Non-Linear Langevin and Fractional Fokker–Planck Equations for Anomalous Diffusion by Lévy Stable Processes
Abstract
1. Introduction
2. The Fokker–Planck and Langevin Equations
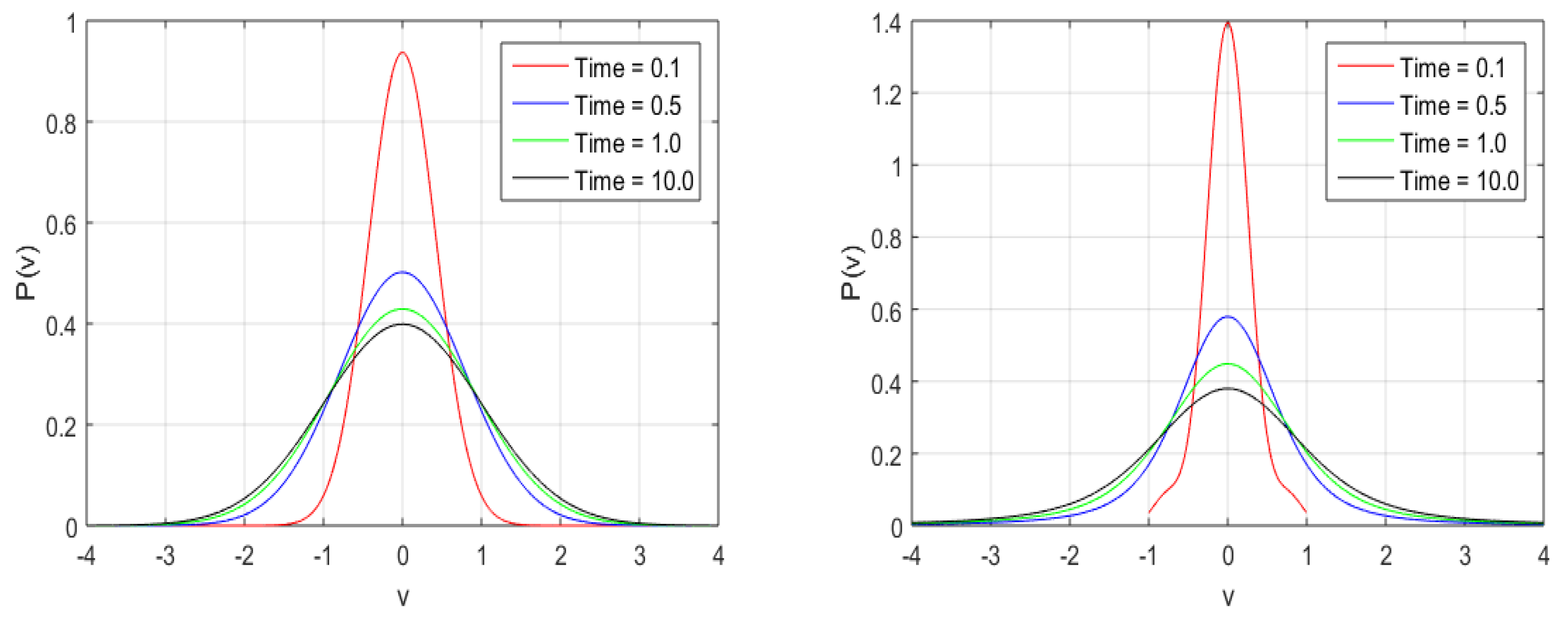
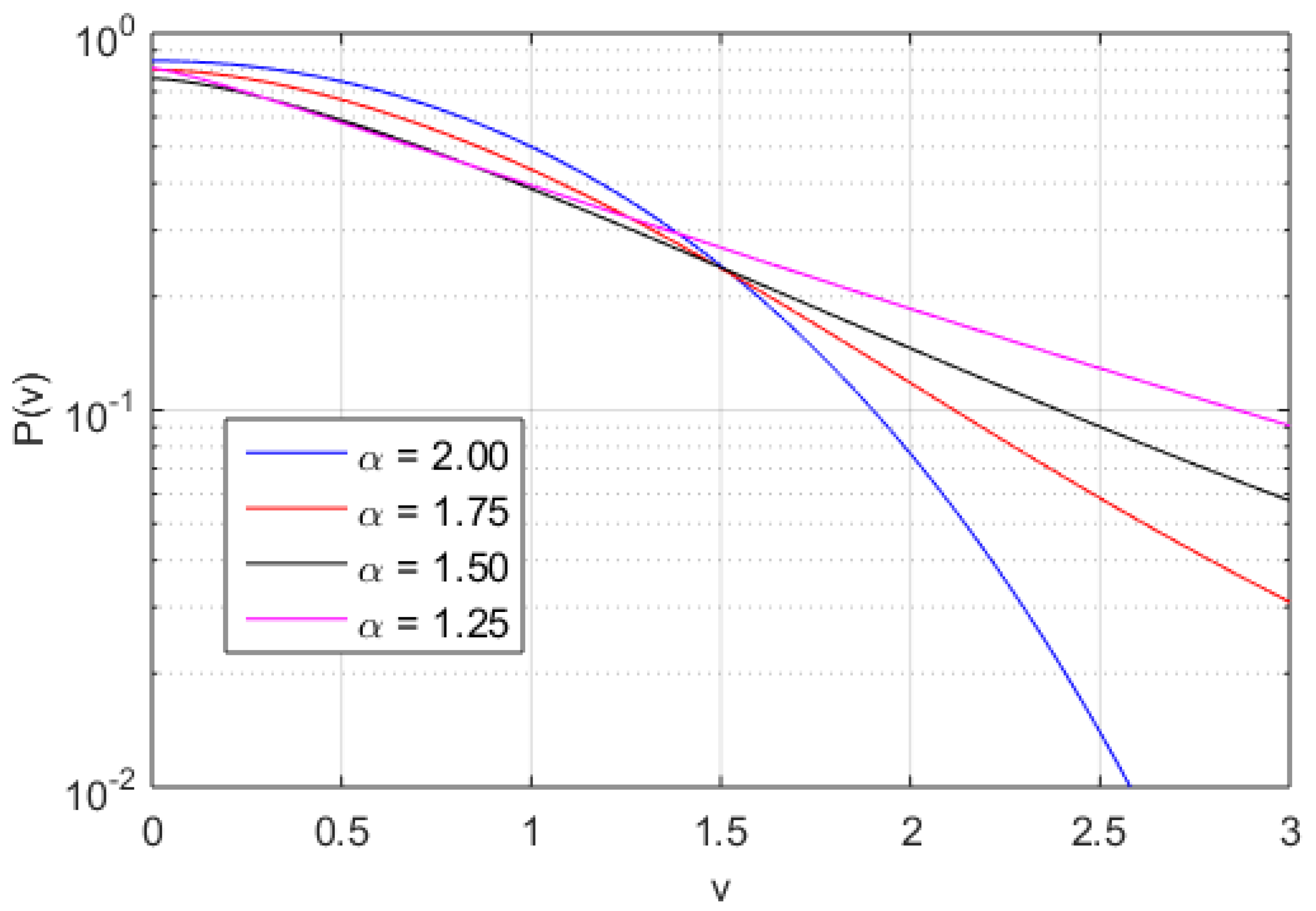
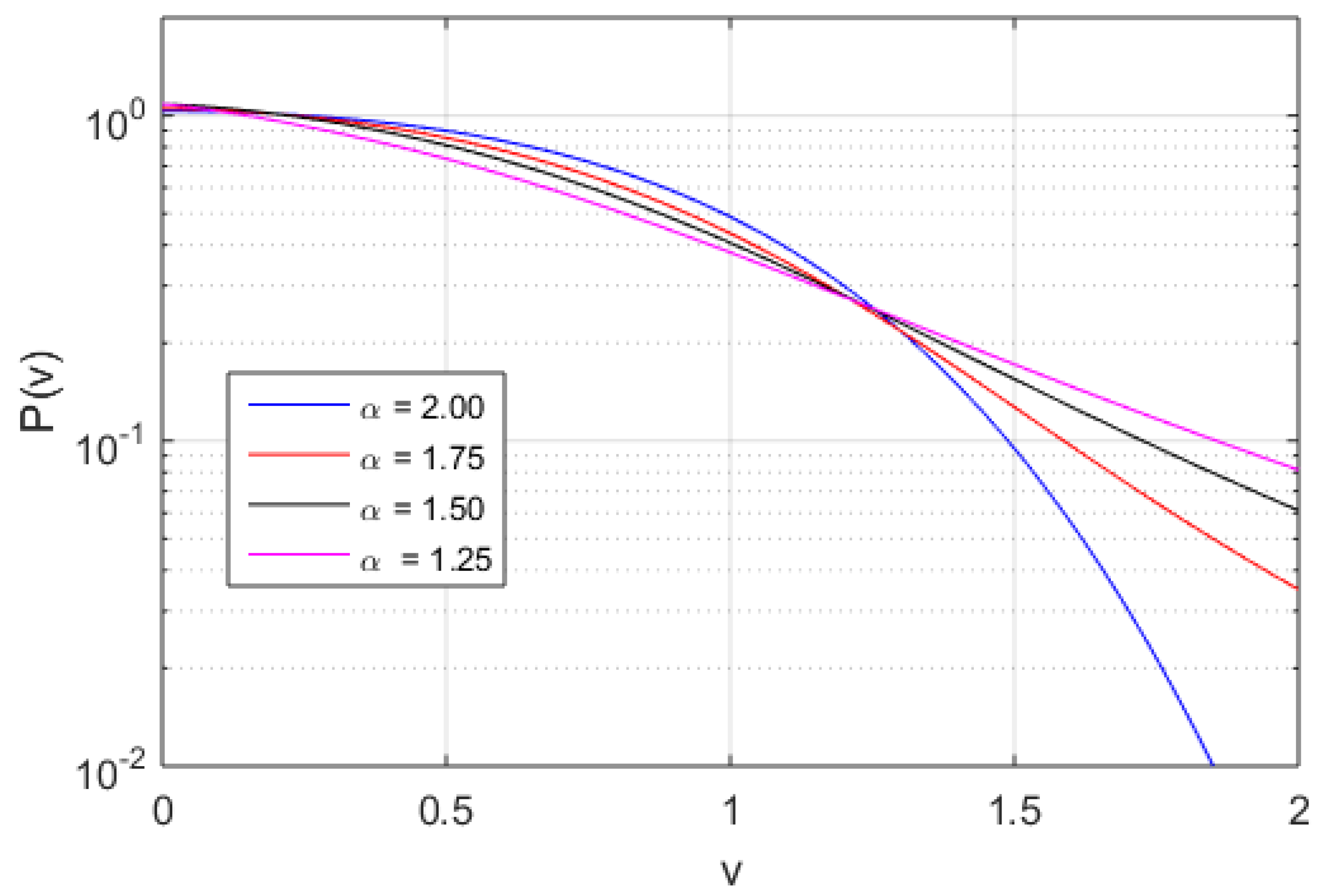
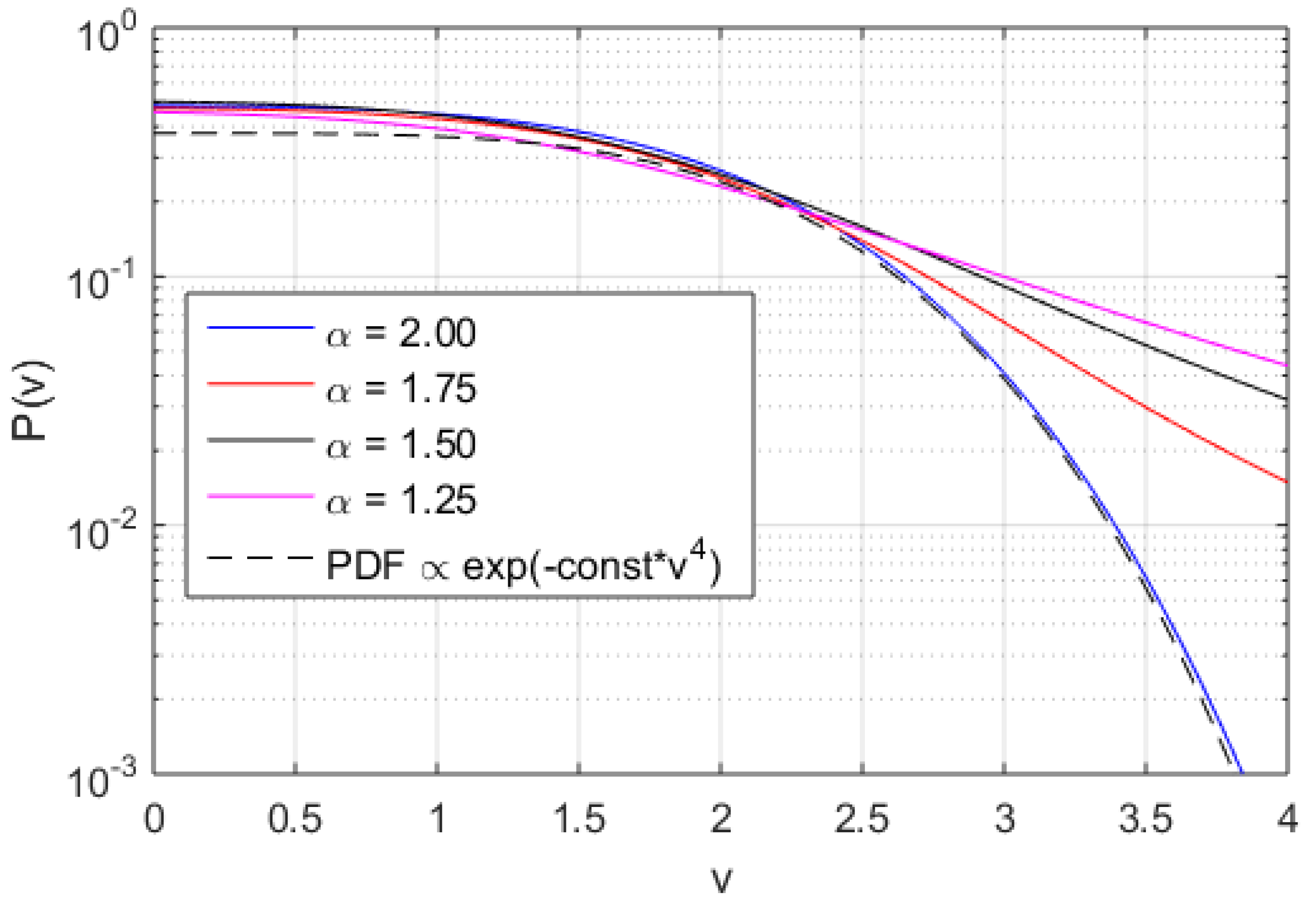
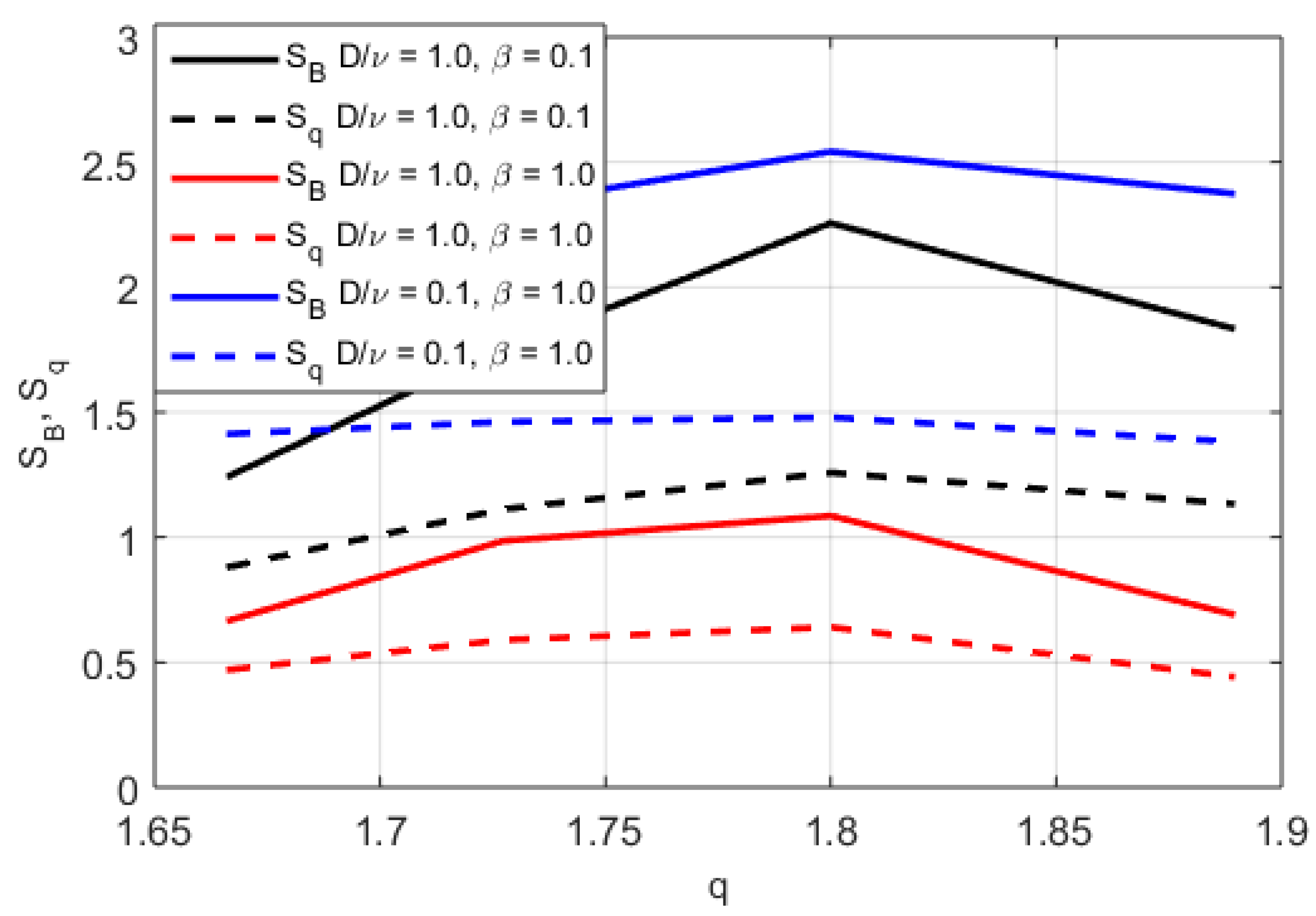
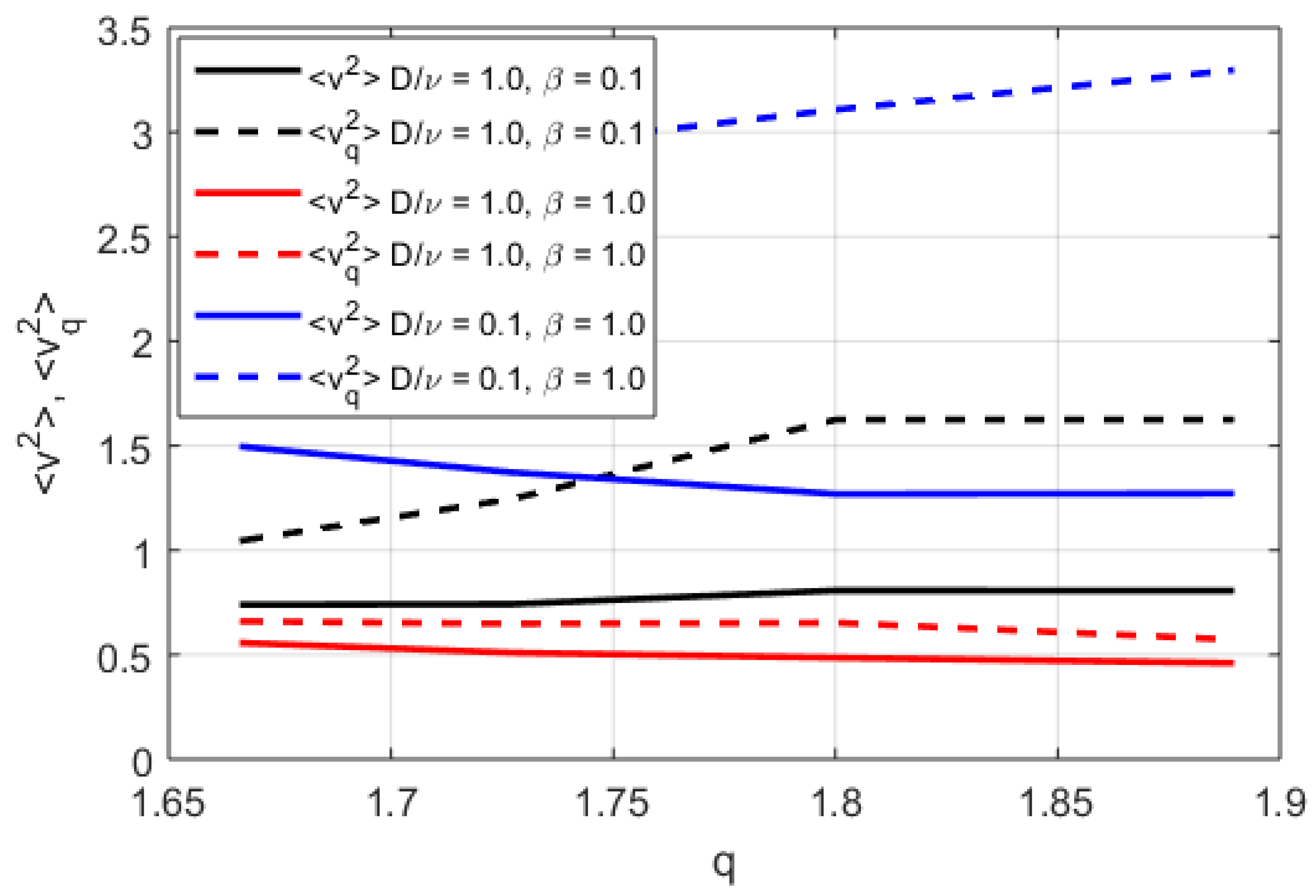
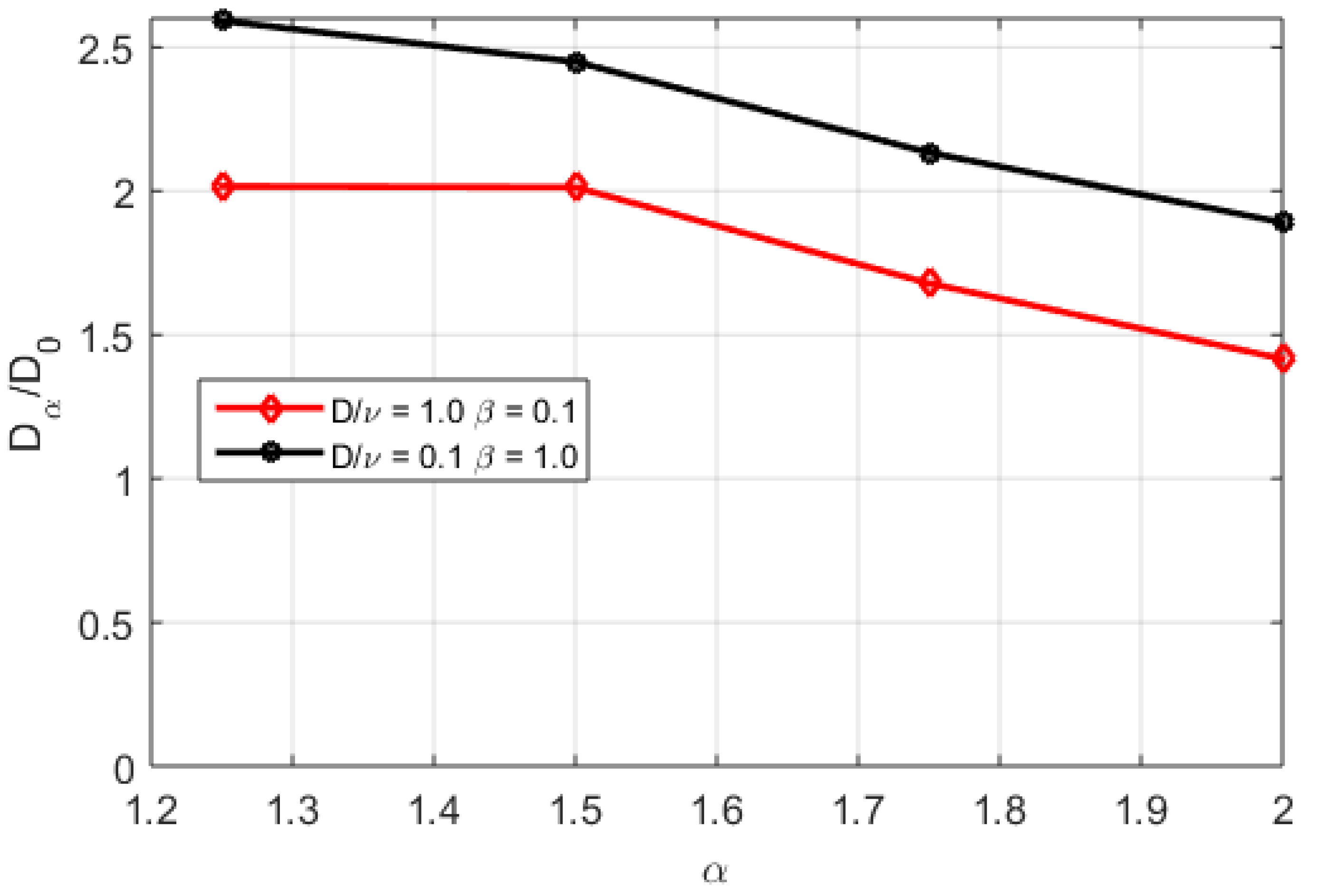
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horton, W. Turbulent Transport in Magnetized Plasmas; World Scientific: Danvers, MA, USA, 2017; ISBN 978-981-3225-88-6. [Google Scholar]
- Krommes, J.A. Fundamental statistical descriptions of plasma turbulence in magnetic fields. Phys. Rep. 2002, 360, 1–352. [Google Scholar] [CrossRef]
- Carreras, B.A.; Hidalgo, C.; Sanchez, E.; Pedrosa, M.A.; Balbin, R.; Garcia, C.I.; van Milligen, B.; Newman, D.E.; Lynch, V.E. Fluctuation-induced flux at the plasma edge in toroidal devices. Phys. Plasmas 1996, 3, 2664–2672. [Google Scholar] [CrossRef]
- Carreras, B.A.; van Milligen, B.; Hidalgo, C.; Balbin, R.; Sanchez, E.; Cortes, I.G.; Pedrosa, M.A.; Bleuel, J.; Endler, M. Self-similarity properties of the probability distribution function of turbulence-induced particle fluxes at the plasma edge. Phys. Rev. Lett. 1999, 83, 3653–3656. [Google Scholar] [CrossRef]
- Van Milligen, B.P.; Sanchez, R.; Carreras, B.A.; Lynch, V.E.; LaBombard, B.; Pedrosa, M.A.; Hidalgo, C.; Gonçalves, B.; Balbín, R.; The W7-AS Team. Additional evidence for the universality of the probability distribution of turbulent fluctuations and fluxes in the scrape-off layer region of fusion plasmas. Phys. Plasmas 2005, 12, 52501–52507. [Google Scholar] [CrossRef]
- Sanchez, R.; Newman, D.E.; Leboeuf, J.N.; Decyk, V.K.; Carreras, B.A. Nature of Transport across Sheared Zonal Flows in Electrostatic Ion-Temperature-Gradient Gyrokinetic Plasma Turbulence. Phys. Rev. Lett. 2008, 101, 205002–205004. [Google Scholar] [CrossRef] [PubMed]
- del-Castillo-Negrete, D.; Carreras, B.A.; Lynch, V.E. Front Dynamics in Reaction-Diffusion Systems with Levy Flights: A Fractional Diffusion Approach. Phys. Rev. Lett. 2005, 94, 18302–18304. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, R.; Carreras, B.A.; Newman, D.E.; Lynch, V.E.; van Milligen, B.P. Renormalization of tracer turbulence leading to fractional differential equations. Phys. Rev. E 2006, 74, 16305–16311. [Google Scholar] [CrossRef] [PubMed]
- Hahm, T.S. Nonlinear gyrokinetic equations for tokamak microturbulence. Phys. Fluids 1988, 31, 2670–2673. [Google Scholar] [CrossRef]
- Zweben, S.J. Search for coherent structure within tokamak plasma turbulence. Phys. Fluids 2007, 28, 974–982. [Google Scholar] [CrossRef]
- Naulin, V. Turbulent transport and the plasma edge. J. Nucl. Mater. 2007, 363–365, 24–31. [Google Scholar] [CrossRef]
- Kaye, S.M.; Barnes, C.W.; Bell, M.G.; DeBoo, J.C.; Greenwald, M.; Riedel, K.; Sigmar, D.; Uckan, N.; Waltz, N. Status of global energy confinement studies. Phys. Plasmas 1990, 2, 2926–2940. [Google Scholar]
- Cardozo, N.J.L. Perturbative transport studies in fusion plasmas. Plasma Phys. Control. Fusion 1995, 37, 799–852. [Google Scholar] [CrossRef]
- Gentle, K.W.; Bravenec, R.V.; Cima, G.; Gasquet, H.; Hallock, G.A.; Phillips, P.E.; Ross, D.W.; Rowan, W.L.; Wootton, A.J. An experimental counter-example to the local transport paradigm. Phys. Plasmas 1995, 2, 2292–2298. [Google Scholar] [CrossRef]
- Mantica, P.; Galli, P.; Gorini, G.; Hogeweij, G.M.D.; de Kloe, J.; Cardozo, N.J.L.; RTP Team. Nonlocal transient transport and thermal barriers in rijnhuizen tokamak project plasmas. Phys. Rev. Lett. 1999, 82, 5048–5051. [Google Scholar] [CrossRef]
- Van-Milligen, B.P.; de la Luna, E.; Tabars, F.L.; Ascasíbar, E.; Estrada, T.; Castejón, F.; Castellano, J.; Cortés, I.G.; Herranz, J.; Hidalgo, C.; et al. Ballistic transport phenomena in TJ-II. Nucl. Fusion 2002, 42, 787–795. [Google Scholar] [CrossRef]
- Anderson, J.; Hnat, B. Statistical analysis of Hasegawa-Wakatani turbulence. Phys. Plasmas 2017, 24, 62301–62308. [Google Scholar] [CrossRef]
- Moradi, S.; Anderson, J.; Romanelli, M. Evidence of non-local heat transport model in JET plasmas. Presented at EU-US Transport Task Force Meeting, Seville, Spain, 11–14 September 2018. [Google Scholar]
- Schlesinger, M.F.; Zaslavsky, G.M.; Klafter, J. Strange kinetics. Nature 1993, 363, 31–37. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. Anomalous diffusion spreads its wings. Phys. World 2005, 18, 29–32. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 2004, 37, 161–208. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals and Geometry of Nature; W. H. Freeman and Company: San Francisco, CA, USA, 1982; pp. 170–180. [Google Scholar]
- Anderson, J.; Xanthopoulos, P. Signature of a universal statistical description for drift-wave plasma turbulence. Phys. Plasmas 2010, 17, 110702–110704. [Google Scholar] [CrossRef]
- Kim, E.; Liu, H.L.; Anderson, J. Probability distribution function for self-organization of shear flows. Phys. Plasmas 2009, 16, 52301–52304. [Google Scholar] [CrossRef]
- Moradi, S.; Anderson, J.; Weyssow, B. A theory of non-local linear drift wave transport. Phys. Plasmas 2011, 18, 062101–062106. [Google Scholar] [CrossRef]
- Moradi, S.; Anderson, J. Non-local gyrokinetic model of linear ion-temperature-gradient modes. Phys. Plasmas 2012, 19, 82301–82307. [Google Scholar] [CrossRef]
- Anderson, J.; Kim, E.; Moradi, S. A fractional Fokker–Planck model for anomalous diffusion. Phys. Plasmas 2014, 21, 122101–122108. [Google Scholar] [CrossRef]
- Moradi, S.; del Castillo, N.D.; Anderson, J. Charged particle dynamics in the presence of non-Gaussian Lévy electrostatic fluctuations. Phys. Plasmas 2016, 23, 907041–907045. [Google Scholar] [CrossRef]
- Montroll, E.W.; Scher, H. Random walks on lattices. IV. Continuous-time walks and influence of absorbing boundaries. J. Stat. Phys. 1973, 9, 101–135. [Google Scholar] [CrossRef]
- Kou, S.C.; Sunney, X. Generalized langevin equation with fractional Gaussian noise: Subdiffusion within a single protein molecule. Phys. Rev. Lett. 2004, 93, 1806031–1806034. [Google Scholar] [CrossRef] [PubMed]
- Combescure, M. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press: Oxford, UK, 2005; pp. 0305–4470. [Google Scholar]
- del Castillo, N.D.; Carreras, B.A.; Lynch, V.E. Fractional diffusion in plasma turbulence. Phys. Plasmas 2004, 11, 3854–3864. [Google Scholar] [CrossRef]
- Del Castillo, N.D. Non-diffusive, non-local transport in fluids and plasmas. Nonlinear Proc. Geophys. 2010, 17, 795–807. [Google Scholar] [CrossRef]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Liouville and BBGKI equations. J. Phys. 2005, 7, 17–33. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional statistical mechanics. Chaos 2006, 16, 331081–331087. [Google Scholar] [CrossRef] [PubMed]
- Lévy, P. Théorie de L’addition des Variables Aléatoires; Gauthier-Villiers: Paris, France, 1937. [Google Scholar]
- West, B.J.; Seshadri, V. Linear systems with Lévy fluctuations. Physical A 1982, 113, 203–216. [Google Scholar] [CrossRef]
- Fogedby, H.C. Langevin equations for continuous time Lévy flights. Phys. Rev. E 1994, 50, 1657–1660. [Google Scholar] [CrossRef]
- Fogedby, H.C. Lévy Flights in Random Environments. Phys. Rev. Lett. 1994, 73, 2517–2520. [Google Scholar] [CrossRef] [PubMed]
- Diethelm, K.; Freed, A.D. The Fractional PECE Subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen; Heinzel, S., Plesser, T., Eds.; Gessellschaft fur Wissenschaftliche Datenverarbeitung: Gottingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Tsallis, C.; de Souza, A.M.C.; Maynard, R. Derivation of Lévy-type anomalous superdiffusion from generalized statistical mechanics. In Lévy Flights and Related Topics in Physics; Springer: New York, NY, USA, 1995; Volume 450, pp. 269–289. [Google Scholar]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, 2197–2200. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physical A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Hamza, A.B.; Krim, H. Jensen-Rényi divergence measure: Theoretical and Computational Perspectives. In Proceedings of the 2003 IEEE International Symposium on Information Theory, Yokohama, Japan, 29 June–4 July 2003. [Google Scholar]
- Barkai, E. Stable equilibrium based on Lévy statistics: Stochastic collision models approach. Phys. Rev. E. 2003, 68, 551041–551044. [Google Scholar] [CrossRef] [PubMed]
- Angulo, J.M.; Esquivel, F.J. Multifractal dimensional dependence assessment based on Tsallis mutual information. Entropy 2015, 17, 5382–5401. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Anastasiadis, A.; Papadimitriou, C.; Mandea, M.; Eftaxiasb, K. Universality in solar flare, magnetic storm and earthquake dynamics using Tsallis statistical mechanics. Physical A 2011, 390, 341–346. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Karkatsanis, L.P.; Xenakis, M.N.; Sarafopoulos, D.; Pavlos, E.G. Tsallis statistics and magnetospheric self-organization. Physical A 2012, 391, 3069–3080. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Karkatsanis, L.P.; Xenakis, M.N. Tsallis non-extensive statistics, intermittent turbulence, SOC and chaos in the solar plasma, Part one: Sunspot dynamics. Physical A 2012, 391, 6287–6319. [Google Scholar] [CrossRef]
- Tsallis, C.; Lévy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of Lévy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef] [PubMed]
- Prato, D.; Tsallis, C. Nonextensive foundation of Lévy distributions. Phys. Rev. E 1999, 60, 2398–2401. [Google Scholar] [CrossRef]
- Milovanov, A.V.; Rasmussen, J.J. Lévy flights on a comb and the plasma staircase. Phys. Rev. E 2018, 98, 222081–222092. [Google Scholar] [CrossRef] [PubMed]
- Jespersen, S.; Metzler, R.; Fogedby, H.C. Lévy flights in external force fields: Langevin and fractional Fokker–Planck equations and their solutions. Phys. Rev. E 1999, 59, 2736–2745. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, J.; Moradi, S.; Rafiq, T. Non-Linear Langevin and Fractional Fokker–Planck Equations for Anomalous Diffusion by Lévy Stable Processes. Entropy 2018, 20, 760. https://doi.org/10.3390/e20100760
Anderson J, Moradi S, Rafiq T. Non-Linear Langevin and Fractional Fokker–Planck Equations for Anomalous Diffusion by Lévy Stable Processes. Entropy. 2018; 20(10):760. https://doi.org/10.3390/e20100760
Chicago/Turabian StyleAnderson, Johan, Sara Moradi, and Tariq Rafiq. 2018. "Non-Linear Langevin and Fractional Fokker–Planck Equations for Anomalous Diffusion by Lévy Stable Processes" Entropy 20, no. 10: 760. https://doi.org/10.3390/e20100760
APA StyleAnderson, J., Moradi, S., & Rafiq, T. (2018). Non-Linear Langevin and Fractional Fokker–Planck Equations for Anomalous Diffusion by Lévy Stable Processes. Entropy, 20(10), 760. https://doi.org/10.3390/e20100760





