Abstract
This paper aims to find a suitable decision rule for a binary composite hypothesis-testing problem with a partial or coarse prior distribution. To alleviate the negative impact of the information uncertainty, a constraint is considered that the maximum conditional risk cannot be greater than a predefined value. Therefore, the objective of this paper becomes to find the optimal decision rule to minimize the Bayes risk under the constraint. By applying the Lagrange duality, the constrained optimization problem is transformed to an unconstrained optimization problem. In doing so, the restricted Bayesian decision rule is obtained as a classical Bayesian decision rule corresponding to a modified prior distribution. Based on this transformation, the optimal restricted Bayesian decision rule is analyzed and the corresponding algorithm is developed. Furthermore, the relation between the Bayes risk and the predefined value of the constraint is also discussed. The Bayes risk obtained via the restricted Bayesian decision rule is a strictly decreasing and convex function of the constraint on the maximum conditional risk. Finally, the numerical results including a detection example are presented and agree with the theoretical results.
1. Introduction
Bayesian, Minimax, and Neyman-Pearson (NP) decisions are three common approaches in the applications of signal detection and processing [1,2,3,4,5,6,7,8]. For instance, a Bayesian approach is proposed in [2] for the signal detection in compressed sensing (CS). In [4], a Minimax framework is introduced for multiclass classification, which can be applied to general data including imagery and other types of high-dimensional data. In order to detect ultra-wideband signals in the presence of dense multipath channels and ambient noise, the NP theorem is used to derive the ultra-wideband (UWB) signal detector [5]. The NP and Bayesian framework are also utilized to access the performance of channel-aware binary-decision fusion over a shared Rayleigh flat-fading channel with multiple antennas at the Decision Fusion Center (DFC) [8], and the DFC is widely used in the spectrum sensing for cognitive radio scenarios [9].
In the classical hypothesis testing problem, a relevant part of uncertainty is usually represented by the prior probability distributions [10]. The aim of the Bayesian criterion is to minimize the Bayes risk [11] and the Bayesian decision rule is determined based on posterior probabilities, where the prior information is assumed to be completely known. On the other hand, no prior information is considered for the Minimax decision rule [12], which minimizes the maximum of the conditional risks given over the parameter space. In addition, the Neyman-Pearson decision rule can be also conceived in the presence of prior distributions [13,14,15]. Therefore, the Bayesian, Neyman-Pearson, and Minimax approaches can be viewed as three different ways of exploiting prior information. In the former two cases, prior information is considered to be completely available, whereas no prior information is required in the latter. In practice, however, the extreme cases rarely happen, and the partial prior information or the prior information with uncertainty is often available, such as the adaptive vector subspace signal detection in partially homogeneous Gaussian disturbance and structured (unknown) deterministic interference within the framework of invariance theory [16].
In most practical cases, the prior distributions are available with certain degree of uncertainty because they are usually obtained based on the previous decisions and experiences [8]. As a result, the Bayesian and Neyman-Pearson approaches are ineffective due to the absence of complete prior information, and the Minimax approach achieves a poor performance since the available partial prior information is ignored. In order to utilize the partial information and to achieve a better performance, several studies have been conducted [8,17,18,19,20,21,22,23,24,25], for example, maximum entropy (ME), Γ-minimax, restricted Bayes, and restricted Neyman-Pearson approaches, to name but a few. For instance, the ME method is utilized in [23] to translate the information contained in the known form of the likelihood into a prior distribution for Bayesian inference. The restricted NP approach is applicable for a binary composite hypothesis-testing problem in the presence of prior information uncertainty [10]. In [25], the group minimax is obtained through the emergent theory of quantizing with Bregman divergences and a closed form Stolarsky mean expression is obtained by optimizing the minimax Bayes risk error divergence for the binary simple hypothesis testing with a partially known prior probability.
To the best of our knowledge, no previous work has focused on the optimal decision rule under the restricted Bayesian criterion for a binary composite hypothesis-testing problem in the presence of prior distribution uncertainty, where the uncertainties may exist not only in the prior probability of the null hypothesis, but also in the distribution probability of each parameter value under the null and the alternative hypotheses. In this paper, we utilize the constraints that the conditional risks should be less than a predefined value to reduce the negative effects of the uncertain prior information, thereby the focus of this paper is to find the optimal decision rule to minimize the Bayes risk on the basis of the constraints and then to explore the relations between the Bayes risk and the predefined value.
In order to solve the optimization problem, the Lagrange duality is applied to convert the minimization of the Bayes risk under the constraints on conditional risks to an unconstrained one. In doing so, the minimization of the Bayes risk under the constraints on conditional risks is equivalent to the minimization of the Bayes risk with a modified prior distribution based on this conversion. Finally, the corresponding theorems and algorithms are developed to search the restricted Bayes decision rule. If there is no uncertainty in the prior distribution, the constraint on the conditional risks is not necessary. In such a case, the classical Bayesian decision rule is applicable, which minimizes the Bayes risk without any constraints. If the value of the constraint is larger than the maximum conditional risk obtained in the classical Bayesian approach, the constraint on the conditional risks is ineffective and the restricted Bayesian decision rule is identical to the classical Bayesian decision rule. On the other hand, if the prior information is full of uncertainty, the Minimax decision rule can be utilized to minimize the worst-case (maximum) conditional Bayes risk. It should be noted that the lowest constraint achieved in the restricted Bayesian approach is equal to the Bayes risk obtained via the Minimax decision rule. Therefore, the classical Bayesian and Minimax approaches are two extreme cases of the restricted Bayesian approaches. In addition, the Bayes risk is a strictly decreasing and convex function of the constraint on conditional risks in the restricted Bayesian approach. The main contributions of this paper are summarized as follows:
- Formulation of the restricted Bayesian framework, which aims to minimize the Bayes risk under the constraint on the conditional risks.
- Derivations of the restricted Bayes decision rule.
- Algorithm for searching the restricted Bayes decision rule.
- Characteristics of the Bayes risk versus the constraint on the conditional risks.
The remainder of this paper is organized as follows: in Section 2, a restricted Bayesian framework is formulated for a binary composite hypothesis-testing problem, which aims to minimize the Bayes risk under the constraint on the conditional risks. The optimal restricted Bayesian decision rule is explored in Section 3 and the corresponding algorithm is provided. Furthermore, the relation between the Bayes risk and the constraint is discussed in Section 4. Finally, numerical examples are presented in Section 5 to illustrate the theoretical results and conclusions are made in Section 6.
2. Problem Formulation
In the theory of signal detection, the detection problems such as radar and communication signal detection are usually formulated as a hypothesis testing problem, and the corresponding framework is developed to provide a theoretical and analytical basis for the detection of useful signal. In this paper, we consider a binary composite hypothesis-testing problem with partially known prior distribution, given by:
where and are the null and the alternative hypotheses, respectively, X is a random variable with the sample space Γ and a K-dimensional observation vector , denotes the pdf of for a given parameter value , and are the respective sets of all possible parameter values of under and . Intuitively, the union of and forms the parameter set Λ, i.e., , and . In addition, the prior distribution of Θ is denoted by , which is usually estimated based on previous observations and known up to a given degree of uncertainty due to the estimation errors.
If the Bayes risk is calculated based on the estimated prior distribution and the minimization of the Bayes risk is performed under the classical Bayesian criterion, then it means that the estimation errors are ignored directly. In doing so, a poor performance is obtained if the estimated distribution differs significantly from the correct one. On the other hand, if the Minimax criterion is utilized and the maximum conditional risk is minimized, then it fails to take the advantage of the useful prior information contained in the estimated prior distribution. In order to utilize the estimated prior distribution and alleviate the negative impact caused by the mismatch between the estimated prior distribution and the correct one, the restricted Bayesian criterion is applied in this paper. More specifically, this paper aims to minimize the Bayes risk, calculated based on the estimated prior distribution, under the constraint that the maximum conditional Bayes risk stays below a significance level that can be adjusted based on the degree of uncertainty in the estimated prior distribution.
Accordingly, the restricted Bayes optimization problem can be formulated by:
subject to:
where denotes the Bayes risk, represents the decision rule which maps the observation vector to 0 or 1, α is the upper limit on the maximum conditional risk, and represents the conditional risk of for Θ = θ and θ ∈ Λ. Prior to calculating the conditional risk , a cost function is used to assign costs to the decision results, where denotes the cost of choosing when Θ = θ and θ ∈ Λ. The can be calculated as the average cost of decision rule for Θ = θ, given by:
In order to solve the constrained optimization problem in (2) and (3), we introduce a regularization parameter to construct an unconstrained optimization problem as below:
which is also a transformation of the Lagrangian of the inequality-constrained optimization problem in (2) and (3), where λ is designed according to α and 0 ≤ λ ≤ 1. In particular, λ decreases as α decreases, and this fact can be utilized to adjust the value of λ. Accordingly, the unconstrained optimization problem in (5) with a suitable λ is an alternative representation of the constrained optimization problem in (2) and (3) according to the Lagrange duality, the equivalence of them will be proved in the next section.
3. Restricted Bayes Decision Rule
In this section, based on the problem formulation in Section 2, the characteristics of the optimal decision rule under the restricted Bayes criterion are investigated first, and then an algorithm for finding the restricted Bayes decision rule is developed.
3.1. Characteristics of the Restricted Bayes Decision Rule
According to the formulation in (5), the following theorems are developed to characterize the restricted Bayes decision rule under certain conditions.
Theorem 1.
Let , where is any valid pdf. If is the classical Bayes decision rule for the modified prior density and satisfies following equality:
then is a solution of the optimization problem in Equation (5).
The proof is presented in the Appendix. Theorem 1 indicates that the solution of the unconstrained optimization problem in (5) is calculated as a classical Bayes decision rule for a modified prior density under certain conditions. In other words, the optimization problem in (5) can be equivalent to a classical Bayesian optimization problem for the modified prior distribution if satisfies the equality in (8).
Next, in order to illustrate the equivalence between the optimization problem in (5) and that in (2) and (3), a proposition is developed as follows.
Proposition 1.
Under the conditions in Theorem 1, is also the solution of the optimization problem in Equations (2) and (3) if .
The proof is given in the Appendix. Proposition 1 implies that if the decision rule defined in Theorem 1 meets the constraint in (3) with equality, then it also provides a solution for the restricted Bayes optimization problem in (2) and (3). In other words, the minimum Bayes risk is achieved when the maximum conditional risk for θ ∈ Λ is equal to the upper limit α. Theorem 1 and Proposition 1 also build a relationship between λ and α. For any λ, the achievable upper limit α can be calculated by the equality in Proposition 1.
In addition, the modified prior distribution specified in Theorem 1 is the least favorable distribution among a family of pdfs, which have the same form with . Explicitly, the achievable minimum Bayes risk corresponding to specified in Theorem 1 is greater than or equal to that corresponding to any other distribution with the pdf form of , where and is any valid pdf. Theorem 2 further states this case.
Theorem 2.
Under the conditions in Theorem 1, the specified in Theorem 1 maximizes the Bayes risk among all probability distributions in the form of , where and is any valid pdf. Equivalently:
where and are the classical Bayes decision rules corresponding to and , respectively.
The proof is presented in the Appendix. As pointed out in Theorem 2, since is the least favorable distribution, this property of can be utilized to search its explicit expression. From the definitions of and , is a special case of and only the case of is concerned in practical applications.
For the rest of this section, we first present the solution to the classical Bayes decision rule, and then develop the algorithm for finding the specified in Theorem 1 and the optimal decision rule for the restricted Bayesian optimization problem.
3.2. Classical Bayes Decision Rule
As discussed above, the classical Bayes decision rule corresponding to can be expressed by:
where . Since , where , the modified Bayes risk is calculated by:
where the last equality holds due to the use of the iterated expectation of . Therefore, can be simply viewed as the cost of using averaged over and x. By using the iterated expectation again, is rewritten as:
According to the Bayes lemma [11], the optimal decision rule to minimize is expressed by:
In many cases, the costs over sets and are uniform, i.e.:
Usually, the cost of a right decision is less than that of a wrong one, i.e., and . Then (11) is simplified as:
where , , and represents the conditional probability for given that . Based on the total probability formula, is calculated by:
where , and denotes the probability of , . Based on the notation introduced in [11], is given as:
where denotes the pdf of given that , and it is:
Accordingly, Equation (13) is rewritten as:
where . As a result, the classical Bayes decision rule is specified by the observation densities of (15), which depends on the probability density of the observation and the conditional densities , and the decision threshold is determined by the prior probabilities and the costs over sets and .
3.3. Algorithm for Finding the Restricted Bayes Decision Rule
Based on the analysis in Section 3.1, the function of and the corresponding classical Bayes decision rule specified in Theorem 1 are required in order to solve the constrained optimization problem in (2) and (3). It also implies that the explicit expression of and the value of should be determined in advance. To achieve this, the condition in Theorem 1 can be expressed as:
with . It is obvious that assigns non-zero probabilities only for the values of that correspond to the global maximum of from Equation (18). In fact, there could be unique, multiple or infinite number of maximizers that achieve global maximum. Therefore, in this work, the solution of the optimization problem in Equations (2) and (3) is discussed under three cases according to the number of the maximizers in the following subsection.
First, assume that has a unique maximizer that achieves the global maximum, then can be expressed by:
where denotes the unique value of corresponding to the maximum and denotes the Dirac delta function, i.e., and . If satisfies the conditions in Theorem 1 and Proposition 1, is the solution of the restricted Bayesian optimization problem in (2) and (3). Based on this assumption, Algorithm 1 is developed to find the restricted Bayes decision rule and .
| Algorithm 1. Restricted Bayes decision rule. |
| 1: Initialize , and . |
| 2: Obtain for all , where denotes the classical Bayes decision rule corresponding to as determined in Section 3.2. |
| 3: Calculate: |
| 4: If , terminate this algorithm, reset and restart the algorithm. When , if the difference between and is less than the predefined precision value, is a solution of the restricted Bayes optimization problem in (2) and (3), and terminate the algorithm. Otherwise, continue to the next step. |
| 5: If , and are replaced with and , respectively. If , and are replaced with and , respectively. |
| 6: If the difference between and is less than the predefined precision value, terminate the algorithm and reset to restart the algorithm; else go to Step 2. |
In Algorithm 1, Step 3 follows from Theorem 2 and Step 4 is developed according to Theorem 1 and Proposition 1. In Step 3, can be treated as the minimum Bayes risk without any constraints on conditional risks corresponding to . It should be noted that the value of is related to through Proposition 1, and increases with the increase of . Hence, the constraint can be achieved by adjusting the value of . For any that satisfies (20), if the corresponding classical Bayes decision rule satisfies and the difference between and is less than the predefined precision value, the is the maximizer that achieves the global maximum of and can be viewed as the solution of the restricted Bayes optimization problem in (2) and (3). In addition, since the classical Bayes decision rule can be obtained based on Section 3.2 for any valid , the solution of the restricted optimization problem in (2) and (3) exists as long as is properly defined. The effective interval of will be discussed in Section 4.
Second, suppose that there are multiple values of corresponding to the global maximum of , should be expressed as:
where , , and denote the number and the value of that achieve the maximum , respectively. For the convenience of analysis, let denote the vector of all unknown components of , i.e.:
In order to solve the restricted Bayes optimization problem in (2) and (3), the Step 3 should be replaced by:
where represents the classical Bayes decision rule for the modified prior distribution . Correspondingly, the condition in Step (4) should be updated by replacing and with and , respectively. Obviously, compared with the case where has only one maximizer, the computational complexity of multiple maximizers increases significantly. In such case, the global optimization algorithms such as the particle swarm optimization algorithm (PSO) and the ant colony algorithm (ACO) can be utilized to find [26,27,28].
Finally, if there are infinitely many values of that correspond to the global maximum of , it is difficult to obtain an accurate solution of the optimization problem in (2) and (3). In this case, an approximate solution can be obtained by employing the Parzen window density estimation to approximate the form of , where is expressed approximately by a convex combination of many window functions, given by:
where , , and denotes a window function which could be a Rectangular, Gauss, or Cosine window function. In order to solve the optimization problem in (2) and (3), Algorithm 1 should be updated by replacing and with and the classical Bayes decision rule corresponding to , respectively.
In real applications, it may be difficult to know all the exact values of that achieve the global maximum of in advance. The practical way is that we start with the assumption that there is a unique that achieves the global maximum. Based on the assumption and Algorithm 1, and the corresponding is obtained. If and satisfy the condition in Step 3, the restricted Bayes optimization problem in (2) and (3) is solved. Otherwise, the number of which are assumed to achieve the global maximum of is increased incrementally until the calculated through the updated Algorithm 1 is verified as the solution of the restricted Bayes optimization problem.
4. Relationship between Bayes Risk and the Constraint
In this section, the relationship between Bayes risk and the constraint on the conditional risks is explored. As the analysis in introduction, the constraint on the conditional risks is introduced from the uncertainty of . Generally speaking, the classical Bayesian criterion is considered to minimize the average Bayes risk when is completely known, and the Minimax decision rule can be utilized to minimize the worst-case (maximum) conditional Bayes risk if the prior information is full of uncertainty. Therefore, the classical Bayesian and Minimax approaches can be viewed as two extreme cases of the restricted Bayesian approaches.
For the notational simplicity, here we respectively denote the classical Bayes and the Minimax decision rules by and , i.e.:
Then define and as the maximum conditional risks achieved by the classical Bayesian and Minimax decision rules, respectively. In addition, the restricted Bayes decision rule where is denoted by . From the definitions of , and , it should be noted that and .
According to the definition of the Minimax criterion, is the achievable minimum of the maximum conditional risk, which means that there is no solution for the optimization problem in (2) and (3) if the value of is less than . On the other hand, it is obvious that the constraint on the conditional risks enforced by is ineffective if is greater than . In other words, the restricted Bayes optimization problem in (2) and (3) is equivalent to the Bayes optimization problem in (25) for any . Namely and if . As a result, should be defined in the interval of ; otherwise the constraint is ineffective or meaningless.
For the restricted Bayes optimization problem formulated in (2) and (3), the maximum conditional risk and the Bayes risk are closely related to the value of the constraint . When , the following conclusion holds that:
A simple contradiction method can be used here to show this conclusion. Suppose that , and let , where and denotes a classical Bayes decision rule obtained in (25), and . There must exist a such that and . Obviously, it contradicts with the definition of . Therefore, the conclusion in (27) is true.
Based on the discussions above, the relationship between the restricted Bayesian decision rule and the value of the constraint on the conditional risks is presented by the Theorem 3.
Theorem 3.
The Bayes risk obtained by the restricted Bayes decision rule is a strictly decreasing and convex function of for .
The proof is provided in the Appendix. Theorem 3 implies the relationship between Bayes risk and the constraint on conditional risks. Moreover, the value of is closely related to the uncertainty of . In general, a smaller value of should be specified for a greater degree of the uncertainty. Therefore, based on these characteristics, one can predefine a suitable value of to obtain the expected Bayes risk in practice. In addition, the restricted optimization problem in (2) and (3) is analyzed and solved in Section 3 from a special perspective that its solution is identical to a classical Bayes decision rule with a modified prior distribution as presented in Theorem 1 and Proposition 1. For any fixed prior distribution, the corresponding classical Bayes decision rule can be obtained from Section 3.2, thereby the solution of the restricted optimization problem in (2) and (3) exists as long as is properly defined in and can be obtained further by the algorithm in Section 3.3.
5. Numerical Results
In this section, a binary hypothesis-testing problem is studied to illustrate theoretical results. The hypotheses are defined as:
where , and denote the sets of all possible values of parameter under and , respectively, which are specified as and , where is a known constant. In addition, denotes a zero mean noise that is a mixture of Rayleigh distributed components; that is, , where for , , and:
In the numerical results, the same variance is assumed, i.e., for . Furthermore, the parameters are specified as , , , , , and for . Then the conditional pdf of for a given value of can be expressed by:
With the assumption, the detection problem in (28) is equivalent to the detection of a signal that employs binary phase shift keying (BPSK). Accordingly, the probability distribution of under is directly expressed as . On the other hand, the probability distribution of under can be modeled as:
where is estimated based on the previous experiences, and it is known with some uncertainty due to the presence of estimation errors. As a result, the probability distribution of can be determined by:
where , and denotes the prior probability of for .
In order to obtain the optimal restricted Bayesian decision rule, the prior distribution should be modified via a pdf according to Theorem 1. Since , the complete form of is expressed as:
where , and are the respective weights assigned for , and , for and .
First, it is assumed that any two of the three assigned weights are zero, i.e., . By employing the algorithm based on (20), the optimal decision rule is obtained if the condition in the third step is satisfied. Otherwise, we assume that only one of the three assigned weights is zero, i.e., , where , , and . In such a case, as is the only one unknown parameter in , the algorithm based on (21) and (22) is used to find the value of and the corresponding that maximizes the Bayes risk. If the corresponding decision rule satisfies the condition in (23), it is the optimal restricted Bayesian rule that we seek. Finally, if the condition is still not met in the second case, the should be determined as and for . If we find the values of and that maximize the Bayes risk corresponding to , the optimal restricted Bayesian rule is also obtained.
In Figure 1, the achievable minimum Bayes risks obtained by the restricted Bayesian decision rule for different values of are plotted against , where , and . As analyzed in Section 4, when is equal to the Bayes risk of the Minimax decision rule, the restricted Bayesian decision rule is identical to the Minimax decision rule. When α is smaller than the Bayes risk of the Minimax decision rule, there is no restricted Bayesian decision rule that satisfies the limit established by α. On the other hand, the detection performance of the restricted Bayesian decision rule is the same with that of the classical Bayesian decision rule when α is greater than and equal to the maximum conditional risk of the classical Bayesian decision rule. As expected, the lowest Bayes risks are obtained by the classical Bayesian decision rule, but it also leads to the highest maximum conditional risk that are 0.3456, 0.3657, 0.3816, 0.4131 and 0.4325 for , 0.65, 0.686, 0.75 and 0.8, respectively. On the contrary, the Minimax decision rule achieves the lowest maximum conditional risk, but it produces the worst Bayes risk. It should be noted that the conditional risks of the Minimax decision rule are equal to each other, which are 0.2381.
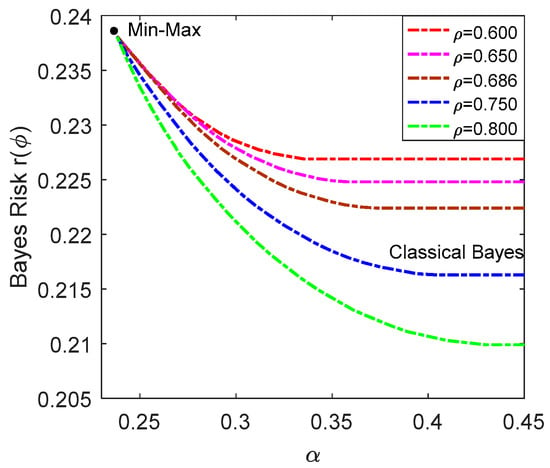
Figure 1.
Bayes risk versus of the restricted Bayesian decision rule for , 0.65, 0.686, 0.75 and 0.8, where , and .
For the restricted Bayesian decision rule, the maximum conditional risk is equal to except for the linear part that corresponds to the classical Bayesian decision rule. In fact, the restricted Bayes decision rule makes a tradeoff between the maximum conditional risk and Bayes risk, and generalizes the Minimax and the classical Bayesian decision rules. It is also shown from the figure that with the increase of , the performance difference of the classical Bayesian and the Minimax decision rules increases for . Specifically, the maximum conditional risk of the classical Bayesian decision rule increases and the corresponding Bayes risk decreases as increases. Furthermore, when α is greater than the maximum conditional risk of the Minimax decision rule and smaller than that of the classical Bayesian decision rule, the Bayes risk is a strictly decreasing and convex function of α. This agrees with the conclusion made in Theorem 3. In addition, Figure 1 acts a guideline for the design of α in practice by observing the corresponding Bayes risk for each α. Hence, instead of assigning a value for α arbitrarily, Figure 1 can be utilized to choose a more appropriate α in practical problems.
Figure 2 compares the achievable lowest maximum conditional risk obtained by the restricted Bayes decision rule and the corresponding Bayes risk versus in (5) for , 0.686 and 0.8, where , and . The maximum conditional risk is equal to the Bayes risk for when 0.8, for when and . This shows that the restricted Bayesian decision rules becomes identical to the Minimax decision rule when reduces to less than or equal to a certain value. For convenience, this value is denoted by , and it is seen that , 0.8207 and 0.8207 for , 0.686 and 0.8, respectively. In fact, the value of increases from 0.7035 to 0.8207 when decreases from 0.8 to 0.686 and maintains at 0.8207 when . In addition, when , the achievable lowest maximum conditional risk increases and the corresponding Bayes risk decreases with the increase of . In order to further illustrate the results in Figure 2, Table 1, Table 2 and Table 3 are provided to show the parameters of , and in , the maximum conditional and Bayes risks of the restricted Bayesian decision rule for different values of for , 0.686 and 0.8.
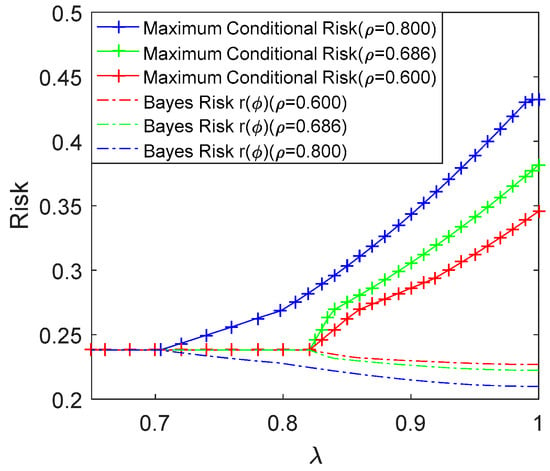
Figure 2.
The maximum conditional and Bayes risks of the restricted Bayesian decision rule versus for , 0.686 and 0.8, where , and .

Table 1.
The parameters of and different risks for various when .

Table 2.
The parameters of and different risks for various when .

Table 3.
The parameters of and different risks for various when .
From the Table 1, Table 2 and Table 3, it is observed that the maximum conditional risk is always equal to the conditional risk for . Actually, the maximum conditional risk can also be viewed as the achievable minimum . Since is independent on , the weight of in is same for each when , 0.686 and 0.8. Conversely, parameters of and change with . In the simulation results, the distribution of based on the Minimax criterion can be calculated as . In order to achieve the same performance with the Minimax decision rule, the in (31) should be modified by making equal to , i.e., . For instance, as listed in Table 1, Table 2 and Table 3, and for , and for , and for . Therefore, Figure 2 and Table 1, Table 2 and Table 3 also provide a guideline to select a suitable value of .
Figure 3a plots the achievable minimum obtained via the restricted Bayesian decision rule versus for , 0.8 and 0.6 when and , and the corresponding minimum Bayes risks are presented in Figure 3b. In general, with the increase of , the achievable minimum and the Bayes risk increase first, and then decrease to troughs, and increase gradually again, all regardless of the values of . In fact, when , the restricted Bayesian decision rule is identical to the classical Bayesian decision rule. In addition, the maximum conditional risk is equal to for any , which agrees with the conclusion in (27). As expected, the classical Bayesian decision rule achieves the highest maximum conditional risk and the minimum Bayes risk. It is also seen that the maximum conditional risk decreases and the Bayes risk increases with the decrease of . In this case, when , it is the same with that of the Minimax decision rule when , which implies for . Similarly, the cases for are the same to that when . From Figure 3a,b, compared with the performance of the classical Bayesian decision rules, the maximum conditional risks obtained via the restricted Bayesian decision rules decrease significantly with much lower increase of the corresponding Bayes risks, especially for and . To clearly investigate the results in Figure 3, the restricted Bayes decision rules for different cases are presented. It should be noted beforehand that the form of the optimal decision rule can be determined as follows:
where represents a part of the sample space. The restricted Bayes decision rules, the constraint and the Bayes risks for different values of σ are provided in Table 4, Table 5 and Table 6 when , 0.8 and 0.6.
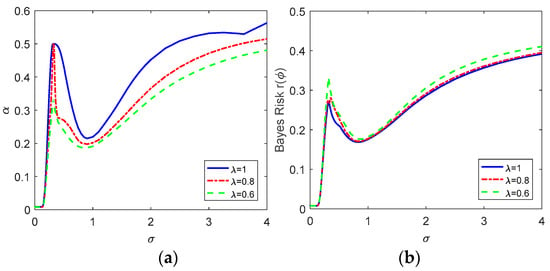
Figure 3.
The achievable minimum and the corresponding minimum Bayes risk as function of for , 0.8 and 0.6 in (a,b), respectively, when and A = 2.

Table 4.
The restricted Bayes decision rules, the achievable minimum α and the corresponding Bayes risk for different σ when λ = 1.

Table 5.
The restricted Bayes decision rules, the achievable minimum α and the corresponding Bayes risk for different σ when λ = 0.8.

Table 6.
The restricted Bayes decision rules, the achievable minimum α and the corresponding Bayes risk for different σ when λ = 0.6.
In Figure 4a, the achievable minimum values of are plotted versus A for , 0.8 and 0.6 when and , where the corresponding minimum Bayes risks are illustrated in Figure 4b. Similarly, the decision rule for is identical to the classical Bayesian decision rule, and the maximum conditional risk is equal to α. When A is small such as , the maximum conditional risk decreases significantly with a small increase of the Bayes risk via the restricted decision rule for both and 0.6. In general, a lower maximum conditional risk and a higher Bayes risk can be obtained for a smaller value of , but it is not true if according to the results shown in Figure 2. Especially, the Bayes risk obtained via the restricted Bayes decision rule when is almost equal to that obtained via the classical Bayes decision rule for some values of A, while it decreases significantly when . The difference between and 0.6 is especially noticeable when . In addition, when , and the Bayes risk decrease gradually to zero as A increases.
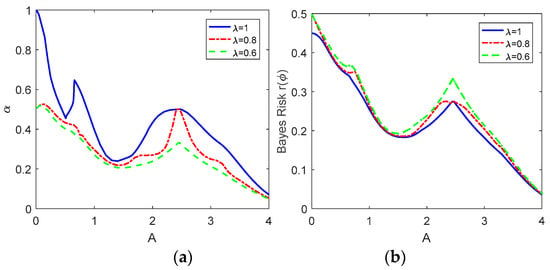
Figure 4.
The achievable minimum and the corresponding minimum Bayes risk versus for , 0.8 and 0.6 in (a,b), respectively when and .
.
6. Conclusions
In this paper, the restricted Bayes decision rule is developed for a binary composite hypothesis-testing problem with a partially known prior distribution. Generally, the prior distribution is estimated based on previous information and is not completely accurate due to the estimate errors. In order to utilize the useful prior information, the Bayes risk is calculated based on the estimated prior distribution. On the other hand, a constraint on the maximum conditional risk is applied to alleviate the negative impact caused by the mismatch between the estimated prior distribution and the correct one. By applying the Lagrange duality, the restricted Bayesian optimization problem is transformed to an unconstrained optimization problem. Based on the transformation, Theorems are derived to provide theoretical supports for the algorithms to find the optimal restricted Bayes decision rule. Specially, an additional conclusion is made that the Bayes risk obtained via the restricted Bayes decision rule is a strictly decreasing and convex function of the constraint on the maximum conditional risk. In addition, the constraint should be defined in an appropriate interval, otherwise the constraint is not effective. Finally, the numerical examples are provided to demonstrate the performance of the proposed decision rule, which are consistent with theoretical results.
The classical Bayes and Minimax decision rules are usually used in two different scenarios from the restricted Bayesian optimization problem, but they can be realized as two special cases of the restricted Bayes decision rule by defining two proper values of the constraint. In fact, the classical Bayesian decision rule achieves the lowest Bayes risk but with the highest maximum conditional risk, whereas the Maximum decision rule obtains the lowest maximum conditional risk but with a worst Bayes risk. By adjusting the constraint, the restricted Bayesian decision rule provides the ability to keep the balance between the maximum conditional risk and the Bayes risk.
Acknowledgments
This research is partly supported by the Basic and Advanced Research Project in Chongqing (Grant No. cstc2016jcyjA0134, No. cstc2016jcyjA0043), graduate scientific research and innovation foundation of Chongqing, China (Grant No. CYB17041), the National Natural Science Foundation of China (Grant No. 61501072, No. 41404027, N0. 61571069, No. 61675036, No. 61471073) and the Fundamental Research Funds for the Central Universities (Grant No. 106112017CDJQJ168817, No. 106112017CDJQJ168819) supported by the Fundamental Research Funds for the Central Universities.
Author Contributions
Shujun Liu raised the idea of the framework to find a suitable decision rule for a binary composite hypothesis-testing problem. Ting Yang and Shujun Liu contributed to the drafting of the manuscript, interpretation of the results, some experimental design and checked the manuscript. Hongqing Liu contributed to analyze the optimal restricted Bayesian decision rule and develop the corresponding algorithm. Ting Yang contributed to the proofs of the theories developed in this paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Theorem 1.
It is obvious that:
where the first inequality holds as . Since is the classical Bayes decision rule, which minimizes the Bayes risk without any constraints for the modified prior distribution of denoted by , one obtains:
If , the following equality holds
Therefore, is a solution of the optimization problem in (5). Especially, the value of the expression in (5) is always greater than or equal to (A3). □
Proof of Proposition 1.
Based on the assumption in Theorem 1,
is the optimal decision rule to minimize the value of the objective function in (5), which means:
Since holds due to the constraint on the conditional risks in (6) and holds based on the assumption in the corollary, should be greater than or equal to in order to satisfy the inequality in (A4). Therefore, is the optimal decision rule that minimizes the Bayes risk under the constraint on the conditional risks if . In other words, is a solution of the optimization problem in (2) and (3). □
Proof of Theorem 2.
Under the conditions in Theorem 1, the minimum Bayes risk corresponding to
is expressed as:
where the second equality holds according to the condition (6) in Theorem 1. Since , one finds:
for any , where the second inequality follows from , and the last inequality holds based on the definition of . Therefore, specified in Theorem 1 is the least favorable distribution that maximizes the Bayes risk among all the probability distributions in the form of for . □
Proof of Theorem 3.
According to the definition of the restricted Bayes optimization problem formulated in (A),
is a non-increasing function in terms of . First, we shall use the contradiction method to prove the strictly decreasing property of . Suppose that and . Actually, is a restricted Bayes rule corresponding to , which means . Obviously, it contradicts with the conclusion in (27). Hence, must be satisfied.
Next, we shall prove the convexity of over by defining a decision rule as follows:
where , , and denote the restricted Bayes decision rules corresponding to the constraint and , respectively. The conditional risks for and the Bayes risk corresponding to are respectively calculated by:
From (A8), the maximum conditional risk is upper bounded by:
where the last equality holds according to (27). Let and , one obtains:
where the first inequality is satisfied since is the optimal decision rule that minimizes the Bayes risk under the constraint on the conditional risks, and the last inequality holds since is non-increasing with respect to (w.r.t.) . Therefore, is a strictly decreasing and convex function of for . □
References
- Madadi, Z.; Anand, G.V.; Premkumar, A.B. Signal detection in generalized gaussian noise by nonlinear wavelet denoising. IEEE Trans. Circuits Syst. I 2013, 60, 2973–2986. [Google Scholar] [CrossRef]
- Cao, J.; Lin, Z. Bayesian signal detection with compressed measurements. Inf. Sci. 2014, 289, 241–253. [Google Scholar] [CrossRef]
- Higger, M.; Akcakaya, M.; Nezamfar, H.; LaMountain, G.; Orhan, U.; Erdogmus, D. A Bayesian framework for intent detection and stimulation selection in SSVEP BCIs. IEEE Signal Process. Lett. 2015, 22, 743–747. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhou, H.; Cheng, J.; Li, H. A Minimax framework for classification with applications to images and high dimensional data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
- Alhakim, R.; Raoof, K.; Simeu, E. Detection of UWB signal using dirty template approach. Signal Image Video Process. 2014, 8, 549–563. [Google Scholar] [CrossRef]
- Shevlyakov, G.; Shin, V.; Lee, S.; Kim, K. Asymptotically stable detection of a weak signal. Int. J. Adapt. Control Signal Process. 2014, 28, 848–858. [Google Scholar] [CrossRef]
- Morey, R.D.; Wagenmakers, E.J. Simple relation between Bayesian order-restricted and point-null hypothesis tests. Stat. Probab. Lett. 2014, 92, 121–124. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Romano, G.; Rossi, P.S. Channel-aware decision fusion in distributed MIMO wireless sensor networks: Decode-and-fuse vs. decode-then-fuse. IEEE Trans. Wirel. Commun. 2012, 11, 2976–2985. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Romano, G. Orthogonality and Cooperation in Collaborative Spectrum Sensing through MIMO Decision Fusion. IEEE Trans. Wirel. Commun. 2013, 12, 5826–5836. [Google Scholar] [CrossRef]
- Bayram, S.; Gezici, S. On the restricted Neyman–Pearson approach for composite hypothesis-testing in presence of prior distribution uncertainty. IEEE Trans. Signal Process. 2011, 59, 5056–5065. [Google Scholar] [CrossRef]
- Poor, H.V. An Introduction to Signal Detection and Estimation; Springer: New York, NY, USA, 1994. [Google Scholar]
- Strawderman, W.E. Minimaxity. J. Am. Stat. Assoc. 2000, 95, 1364–1368. [Google Scholar] [CrossRef]
- Lehmann, E.L. Some history of optimality. Lect. Notes Mono-Graph Ser. 2009, 57, 11–17. [Google Scholar]
- Begum, N.; King, M.L. A new class of test for testing a composite null against a composite alternative hypothesis. In Proceedings of the Australasian Meeting of the Econometric Society, Brisbane, Australia, 3–6 July 2007. [Google Scholar]
- Van Trees, H.L. Detection, Estimation, and Modulation Theory: Part I, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Ciuonzo, D.; Maio, A.D.; Orlando, D. On the Statistical Invariance for Adaptive Radar Detection in Partially Homogeneous Disturbance Plus Structured Interference. IEEE Trans. Signal Process. 2016, 65, 1222–1234. [Google Scholar] [CrossRef]
- Blum, J.R.; Rosenblatt, J. On partial a priori information in statistical inference. Ann. Math. Stat. 1967, 38, 1671–1678. [Google Scholar] [CrossRef]
- Hodges, J.L., Jr.; Lehmann, E.L. The use of previous experience in reaching statistical decisions. Ann. Math. Stat. 1952, 23, 396–407. [Google Scholar] [CrossRef]
- Robbins, H. An empirical Bayes approach to statistics. In Proceedings of the 3rd Berkeley Symposium on Mathematical Statistics and Probability 1, Berkeley, CA, USA, December 1954–July & August 1955; pp. 157–164. [Google Scholar]
- Robbins, H. The empirical Bayes approach to statistical decision problems. Ann. Math. Stat. 1964, 35, 1–20. [Google Scholar] [CrossRef]
- Savage, L.J. The Foundations of Statistics, 2nd ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Watson, S.R. On Bayesian inference with incompletely specified prior distributions. Biometrika 1974, 61, 193–196. [Google Scholar] [CrossRef]
- Caticha, A.; Preuss, R. Maximum entropy and Bayesian data analysis: Entropic prior distributions. Phys. Rev. E 2014, 70. [Google Scholar] [CrossRef] [PubMed]
- Palmieri, F.A.N.; Ciuonzo, D. Objective priors from maximum entropy in data classification. Inf. Fusion 2013, 14, 186–198. [Google Scholar] [CrossRef]
- Varshney, K.R.; Varshney, L.R. Optimal Grouping for Group Minimax Hypothesis Testing. IEEE Trans. Inf. Theory 2014, 60, 6511–6521. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle Swarm Optimization Method for Constrained Optimization Problems; IOS Press: Amsterdam, The Netherlands, 2002; pp. 214–220. [Google Scholar]
- Hu, X.; Eberhart, R. Solving constrained nonlinear optimization problems with particle swarm optimization. In Proceedings of the World Multiconference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 14–18 July 2002. [Google Scholar]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: New York, NY, USA, 2005. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).