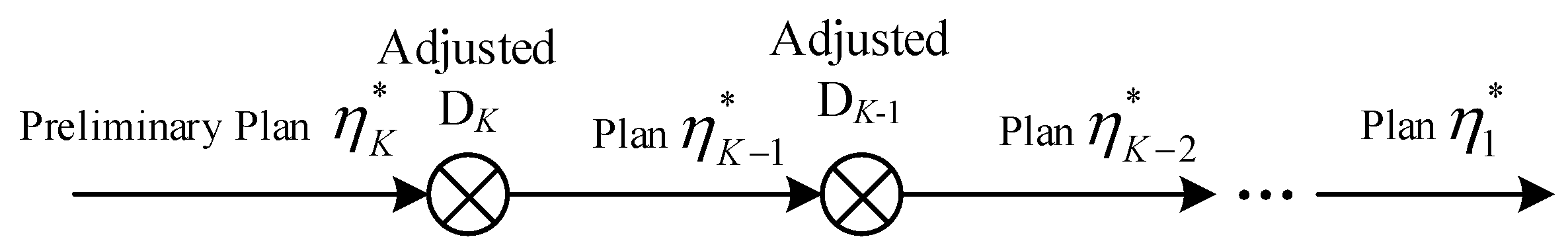A Bayesian Optimal Design for Sequential Accelerated Degradation Testing

Abstract

When optimizing an accelerated degradation testing (ADT) plan, the initial values of unknown model parameters must be pre-specified. However, it is usually difficult to obtain the exact values, since many uncertainties are embedded in these parameters. Bayesian ADT optimal design was presented to address this problem by using prior distributions to capture these uncertainties. Nevertheless, when the difference between a prior distribution and actual situation is large, the existing Bayesian optimal design might cause some over-testing or under-testing issues. For example, the implemented ADT following the optimal ADT plan consumes too much testing resources or few accelerated degradation data are obtained during the ADT. To overcome these obstacles, a Bayesian sequential step-down-stress ADT design is proposed in this article. During the sequential ADT, the test under the highest stress level is firstly conducted based on the initial prior information to quickly generate degradation data. Then, the data collected under higher stress levels are employed to construct the prior distributions for the test design under lower stress levels by using the Bayesian inference. In the process of optimization, the inverse Gaussian (IG) process is assumed to describe the degradation paths, and the Bayesian D-optimality is selected as the optimal objective. A case study on an electrical connector’s ADT plan is provided to illustrate the application of the proposed Bayesian sequential ADT design method. Compared with the results from a typical static Bayesian ADT plan, the proposed design could guarantee more stable and precise estimations of different reliability measures.

1. Introduction

Acceleration degradation testing (ADT) is commonly used to obtain degradation data of products over a short time period, to help extrapolate lifetime and reliability under usage conditions [1]. In an ADT, products are exposed to higher-than-use conditions to get the degradation data in a short time [2,3]. Therefore, ADT is very popular in industrial application [4,5,6]. In planning an ADT, initial values of some unknown model parameters must be specified to optimize a test plan by trading off between constraints and utilities. To capture the uncertainties embedded in these parameters, Bayesian ADT design is utilized, and this method treats model parameters as random variables by assigning prior distributions based on the available historical data and expert’s knowledge. Hence, compared to the traditional ADT optimal design, in which the crisp values are taken for the model parameters, Bayesian optimal design is a global optimal method.

In the last decade, Bayesian ADT design has been widely employed, wherein the optimal ADT plan is designed by maximizing the utility with the constraints of test resource. Liu and Tang [7] proposed a Bayesian design method for ADT, with physically-based statistical models. A single-path power-law statistical degradation model with nonlinear stress life relationships is developed. Based on this model, the optimal objective is to minimize the expected pre-posterior variance of the quantile life at the use condition. Shi and Meeker [8] presented a Bayesian method for accelerated destructive degradation tests (ADDT), under a class of nonlinear degradation models with one accelerating variable. The optimal objective was to maximize the precision of a specified failure-time distribution quantile under usage conditions. Li et al. [1] developed a Bayesian methodology for designing step stress accelerated degradation testing (SSADT) with the objective of relative entropy. It is assumed that the degradation model follows a drift Brownian motion, and the acceleration model follows the Arrhenius equation. The Markov chain Monte Carlo (MCMC) and surface fitting method are chosen to solve for optimality.

For the aforementioned Bayesian ADT design method, the optimal plan depends on the prior information entirely, which is referred to as the static Bayesian design method. However, when the difference between prior information and the actual situation is large, the optimal plan designed by the static Bayesian design method might lead to the over-testing or under-testing problems, which means the test resources have been consumed more or the collected ADT data are insufficient. To avoid these issues, the partial collected ADT data could contribute to updating the prior information so as to modify the test plan by dynamic decision making. Hence, Bayesian optimal design for sequential ADT, referred to as the dynamic Bayesian design method, is proposed in this paper.

For a sequential test design, when the data of the first batch of samples have been obtained, engineers can use this fresh information to optimize or adjust the subsequent test plan. The method has been employed in accelerated life testing (ALT). Liu and Tang [9] presented a sequential constant stress ALT (CSALT) scheme based on the Weibull distribution, and two frameworks of the Bayesian inference method are discussed, i.e., the all-at-one prior distribution construction and the full sequential prior distribution construction. Tang and Liu [10] also proposed the sequential CSALT design method. The objective is to minimize the expectation of the posterior variance of the estimated life percentile at the use condition. Under the sequential scheme, a test at highest stress is first planned and conducted. Using the information obtained at the highest stress level, a Bayesian framework was proposed to optimally determine both the sample allocation and stress combination at lower stress levels of subsequent accelerated tests. Based on the framework in [10], an auxiliary acceleration factor (AAF) was introduced to further amplify the failure probability at low stress levels in [11]. For its good performance of the dynamic decision, the typical application of the sequential test design lies in reliability acceptance sampling testing. Wald [12] proposed a sequential sampling testing method, where a judgment that the batch of the product is accepted, rejected or the test should be continued is proposed when a fault occurs. In this way, the obtained failure information can be fully used to save the test resources. Nezhad et al. [13] introduced a new sequential acceptance sampling plan based on dynamic programming. A suitable cost model was employed for depicting the cost of sampling, accepting or rejecting the lot.

In this paper, a Bayesian optimal design for sequential ADT is proposed to enhance the efficiency and effectiveness of ADT. During the sequential ADT, the test at the highest stress is firstly conducted based on the prior information to quickly generate degradation information. Then, the data collected at the highest stress are used to construct the prior distributions for the test design at lower stress levels using the Bayesian inference method. The proposed methodology can be referred to as the Bayesian sequential step-down-stress ADT. In the proposed sequential scheme, the degradation path is assumed to follow the inverse Gaussian (IG) process, which has been demonstrated as a flexible family for degradation modeling by Ye and Chen [14], Peng et al. [15] and Peng et al. [16]. Moreover, the IG process has also been demonstrated to be more suitable than the Wiener process and the gamma process for degradation modeling in some applications [17,18]. Therefore, it is of interest to further study the sequential scheme based on the IG process model. In addition, Bayesian D-optimality [19] is selected as the objective that minimizes the determinant of the covariance matrix of the model parameter estimates [20]. The remaining paper is organized as follows. In Section 2, the test scheme and Bayesian planning criterion are proposed. In Section 3, the planning of a sequential step-down ADT is presented. In Section 4, the case study is conducted to illustrate the validity and effectiveness of the proposed method. Section 5 concludes this paper.

2. The Test Scheme and Bayesian Optimization

2.1. The Test Scheme

A sequential ADT design is a type of dynamic decision process in which the test plan is dynamically adjusted after the ADT operation on each stress level. As the test at a higher stress level can generate more degradation data in a short time to support the plan design at a lower stress level, the accelerated stress level will be conducted with time in a step-down way; then, an ADT will be first run under the highest stress level.

In order to present the scheme of sequential ADT design, the following settings will be firstly given. In a sequential ADT with $K (K\ge 2)$ accelerated stress levels $S_k$ (i.e., $S_1<S_2<,\cdots ,<S_K$ and $k=1,2,\cdots ,K)$, there are n test items and M total degradation measurements. Let the specified accelerated stress levels be a vector $\mathbf{S}$$=(S_1,S_2,\cdots ,S_K)$ and the specified number of degradation measurements on each accelerated stress level be a vector $\mathbf{m}$$=(m_1,m_2,\cdots ,m_K)$, where $m_k$ denotes the number of degradation measurements on the k-th stress level, and then, $M={\sum }_{k=1}^K{m}_k$. A sequential ADT plan $\mathit{\eta }$, hence, can be written as $\mathit{\eta }\left\{n,M,\mathrm{S},\mathrm{m}\right\}$.

Since there are K accelerated stress levels, correspondingly, the sequential ADT design is divided into K stages; see Figure 1 for the schematic diagram of sequential testing design. $S_0$ denotes the usage stress level at which the product’s certain reliability measure needs to be estimated. The scheme of sequential testing is as follows:

• Stage 1: Both n and M are predefined according to the budget and practical situation before an ADT. The initial optimal test plan ${\eta }_K^{*}$$\left\{\mathrm{S},\mathrm{m}\right\}$ is obtained through the existing Bayesian optimal design method [19] based on the initial prior information. Then, we can make an initial decision $D_K$ to conduct the ADT at the highest stress level based on ${\eta }_K^{*}$.
• Stage 2: After the test under the higher stress level is completed, the corresponding degradation data can be collected. Then, the posterior information could be calculated by the Bayesian inference, which then will be treated as the prior information for the test design at the lower stress level. Hence, the optimal plan for the lower stress level can simultaneously be designed by the Bayesian method, and the decision could be correspondingly adjusted.
• Stage 3: Repeat Stage 2 for $K-1$ times to make $K-1$ decisions, and the whole sequential ADT is completed after finishing the test on the lowest level. Then, the final posterior distributions could be used to estimate the product’s reliability measures under $S_0$.

We remind that the proposed Bayesian sequential scheme is totally different from the empirical Bayesian, since each degradation datum applied in this paper is used only once.

2.2. ADT Model and Assumption

The degradation path of a product is assumed to satisfy the IG process. Let $\left\{X\left(t\right),t\ge 0\right\}$ be the degradation path, and its associated failure is defined to be the event that $X\left(t\right)$ crosses a pre-specified threshold level $X_D$; the corresponding first-passage-time is denoted as $T_D$.

If a degradation process has the following three properties, we say it is an IG process.

(1)

$X\left(0\right)=0$ with probability one;

(2)

$X\left(t\right)$ has independent increments, i.e., $X\left(t_2\right)-X\left(t_1\right)$ and $X\left(t_4\right)-X\left(t_3\right)$ are independent, for $0\le t_1<t_2\le t_3<t_4$;

(3)

each increment follows an IG distribution, i.e., $\Delta X\left(t\right)\sim \mathcal{IG}(\mu \Delta \mathsf{\Lambda }\left(t\right),\lambda {(\Delta \mathsf{\Lambda }\left(t\right))}^2)$, where $\mu >0$, $\lambda >0$, $\Delta \mathsf{\Lambda }\left(t\right)=\mathsf{\Lambda }(t+\Delta t)-\mathsf{\Lambda }\left(t\right)$, $\mathsf{\Lambda }\left(t\right)$ is a given monotone increasing function of time t with $\mathsf{\Lambda }\left(0\right)=0$.

For any $x>0$, the probability density function (PDF) of $\mathcal{I}\mathcal{G}(u,v)$, $\mu >0$, $\lambda >0$, with mean u and variance $u^3/v$, is defined by,

$$f_{\mathcal{I}\mathcal{G}}(x;u,v)=\sqrt{{\displaystyle \frac{v}{2\pi x^3}}}·\exp \left[{\displaystyle -\frac{v{(x-u)}^2}{2u^{2}x}}\right].$$

(1)

Then, the degradation increments x can be described by $\Delta X\left(t\right)\sim \mathcal{IG}(\mu \Delta \mathsf{\Lambda }\left(t\right),\lambda {(\Delta \mathsf{\Lambda }\left(t\right))}^2)$. The mean and variance of $\Delta X\left(t\right)$ are $\mu \Delta \mathsf{\Lambda }\left(t\right)$ and ${\mu }^3\Delta \mathsf{\Lambda }\left(t\right)/\lambda$, respectively. Substituting $u=\mu \Delta \mathsf{\Lambda }\left(t\right)$ and $v=\lambda {(\Delta \mathsf{\Lambda }\left(t\right))}^2$ into Equation (1) yields the PDF of x as,

$$f_{\mathcal{I}\mathcal{G}}(x;\mu ,\lambda )=\sqrt{{\displaystyle \frac{\lambda {\left(\Delta \mathsf{\Lambda }\left(t\right)\right)}^2}{2\pi x^3}}}·\exp \left[{\displaystyle -\frac{\lambda {\left(x-\mu \Delta \mathsf{\Lambda }\left(t\right)\right)}^2}{2x}}\right]$$

(2)

In order to make both the degradation speed and the degradation volatility increase with the stress, the parameter $\mu$ is assumed as the degradation rate of a product [21]. Then, it is a function of the accelerated stress S, i.e., it is an acceleration model denoted by $\mu \left(S\right)$ and could be written as follows,

$$\mu \left(S\right)=\exp \left[a+b\phi \left(S\right)\right]$$

(3)

where the parameters a and b need to be estimated from ADT. For convenience, the stress level can be standardized by using a normalization scheme. In this paper, the linear normalization method is applied. Let $S_0$ and $S_H$ be the usage stress level and operational stress limit, respectively. Then, $\phi \left(S\right)$ is a standardized function of S and expressed as [22],

$${\displaystyle \phi \left(S\right)=\frac{\xi \left(S_k\right)-\xi \left(S_0\right)}{\xi \left(S_H\right)-\xi \left(S_0\right)}}$$

(4)

where $\xi \left(S\right)$ represents a known function of S. For example, if temperature is selected as accelerated stress, $\xi \left(S\right)=1/S$; if the electric stress is accelerated stress, $\xi \left(S\right)=\ln \left(S\right)$.

The parameter $\lambda$ has no physical meaning and is assumed to be a constant in an ADT, i.e., ${\lambda }_1={\lambda }_2=,\cdots ,={\lambda }_K$. Since $\mu$ and $\lambda$ are both time-independent, the process can be called the homogeneous IG process or simple IG process. Generally, there are three different shapes of performance degradation trend: linear, convex and concave. Hence, it is appropriate to assume $\mathsf{\Lambda }\left(t\right)=t^{\beta }(\beta >0)$ [23]. As the path of IG process is strictly increasing, the cumulative distribution function (CDF) of $T_D$ for a given threshold $X_D$ can be expressed as,

$${\displaystyle F_{X_D}\left(t\right)=P(Y\left(t\right)\ge X_D)=\mathsf{\Phi }\left[\sqrt{\frac{\lambda }{X_D}}(t^{\beta }-\frac{X_D}{\mu })\right]-\exp \left(\frac{2\lambda t^{\beta }}{\mu }\right)·\mathsf{\Phi }\left[-\sqrt{\frac{\lambda }{X_D}}\left(t^{\beta }+\frac{X_D}{\mu }\right)\right].}$$

(5)

Let $\tau$ be the non-overlapped interval of degradation measurements and kept constant during ADT, then the test duration $t_k$ on the k-th stress level is $t_k=\tau m_k$. When $X\left(t_{ikj}\right)$ is the measurement result of the j-th measurement of the i-th unit on the k-th stress level at time $t_{ikj}(i=1,2,\cdots ,n,$$k=1,2,\cdots ,K,$$j=1,2,\cdots ,m_k)$, the degradation increment is $x_{ikj}=X\left(t_{ik(j+1)}\right)-X\left(t_{ikj}\right)$ and follows Equation (2). Then, based on Equation (2), the likelihood function is,

$$\begin{array}{c}p\left(x\right|\mathit{\theta })={\displaystyle \prod _{k=1}^K}{\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{j=1}^{m_k}}{\left(\frac{\lambda {\left({\left(m_{ik(j+1)}\tau \right)}_{}^{\beta }-{\left(m_{ikj}\tau \right)}_{}^{\beta }\right)}^2}{2\pi x_{ikj}^3}\right)}^{1/2}\hfill \\ \exp \left[-\frac{\lambda {\left[x_{ikj}-\exp \left[a+b\phi \left(S_k\right)\right]\left({\left(m_{ik(j+1)}\tau \right)}_{}^{\beta }-{\left(m_{ikj}\tau \right)}_{}^{\beta }\right)\right]}^2}{2{\left(\exp \left[a+b\phi \left(S_k\right)\right]\right)}^2{x}_{ikj}}\right]\hfill \end{array}$$

(6)

For the sake of simplicity, we assume that the four parameters (i.e., $a,b,\lambda$ and $\beta$) in Equation (5) are independent of each other and consist of the parameter vector $\mathit{\theta }=(a,b,\lambda ,\beta )$.

2.3. Prior and Posterior Distributions

When the degradation increment x follows an IG distribution, $\lambda$ and $\beta$ should be positive. Therefore, some positive distributions (i.e., Gamma, logistic and Weibull distributions) can be used to depict the uncertainties embedded in $\lambda$ and $\beta$, respectively; while normal, logistic and extreme value distributions can be used to depict uncertainties embedded in a and b.

In our proposed scheme of the sequential ADT, the prior distributions of $\mathit{\theta }$ under the highest stress level are obtained based on the prior information before ADT. For example, when historical degradation data are available as prior information, the mean and the variance of the model parameters can be obtained by using the maximum likelihood estimation method and square root of the determinant of the inverse matrix of the Fisher information matrix. As long as the distribution form of the prior distribution is determined [19], the hyper-parameters can be determined, and the prior distributions are settled. However, the prior distributions under other lower stress levels are obtained by the posterior distributions of the relatively higher stress level.

According to the Bayesian theory, the posterior distributions $p\left(\mathit{\theta }\right|x)$ of $\mathit{\theta }$ can be expressed as [24],

$${\displaystyle p\left(\mathit{\theta }\right|x)=\frac{p\left(x\right|\mathit{\theta }\left)\pi \right(\mathit{\theta })}{{\int }_{\mathrm{\Theta }}p\left(x\right|\mathit{\theta })\pi \left(\mathit{\theta }\right)d\mathit{\theta }}.}$$

(7)

where $\pi \left(\mathit{\theta }\right)$ are the prior distributions of $\mathit{\theta }$. Generally, since it is difficult to derive posterior distributions in a closed form, the MCMC algorithm will be used to generate samples from intractable posterior distributions, which provide the basis for subsequent model inference [25].

2.4. Bayesian Optimal Criterion

According to Li et al. [19], the D-optimality is the most robust optimal objective among the three common objectives (i.e., relative entropy, quadratic loss function and D-optimality) in Bayesian design. Hence, the D-optimality is selected as the optimal objective in this study, which is to maximize the determinant of the Fisher information matrix [26]. It could be written as follows [27],

$$\mathsf{\Phi }\left(\mathit{\eta }\right)=E_{\mathit{\theta }}{E}_x\left[log\left(det\left(I(\mathit{\eta },\mathit{\theta })\right)\right)\right]=\int log\left(det\right(I(\mathit{\eta },\mathit{\theta })\left)\right)\pi \left(\mathit{\theta }\right)d\mathit{\theta }$$

(8)

where the symbol “det” denotes the determinant of the matrix; $I(\mathit{\eta },\mathit{\theta })$ denotes the Bayesian information matrix expressed as follows,

$$I(\mathit{\eta },\mathit{\theta })=\left(\begin{array}{cccc}E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial a^2}\right)& E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial a\partial b}\right)& E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial a\partial \lambda }\right)& E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial a\partial \beta }\right)\\ & E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial b^2}\right)& E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial b\partial \lambda }\right)& E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial b\partial \beta }\right)\\ & & E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial {\lambda }^2}\right)& E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial \lambda \partial \beta }\right)\\ \mathrm{symmetrical}& & & E\left(-\frac{{\partial }^2\ln p\left(\mathit{\theta }\right|x)}{\partial {\beta }^2}\right)\end{array}\right)$$

(9)

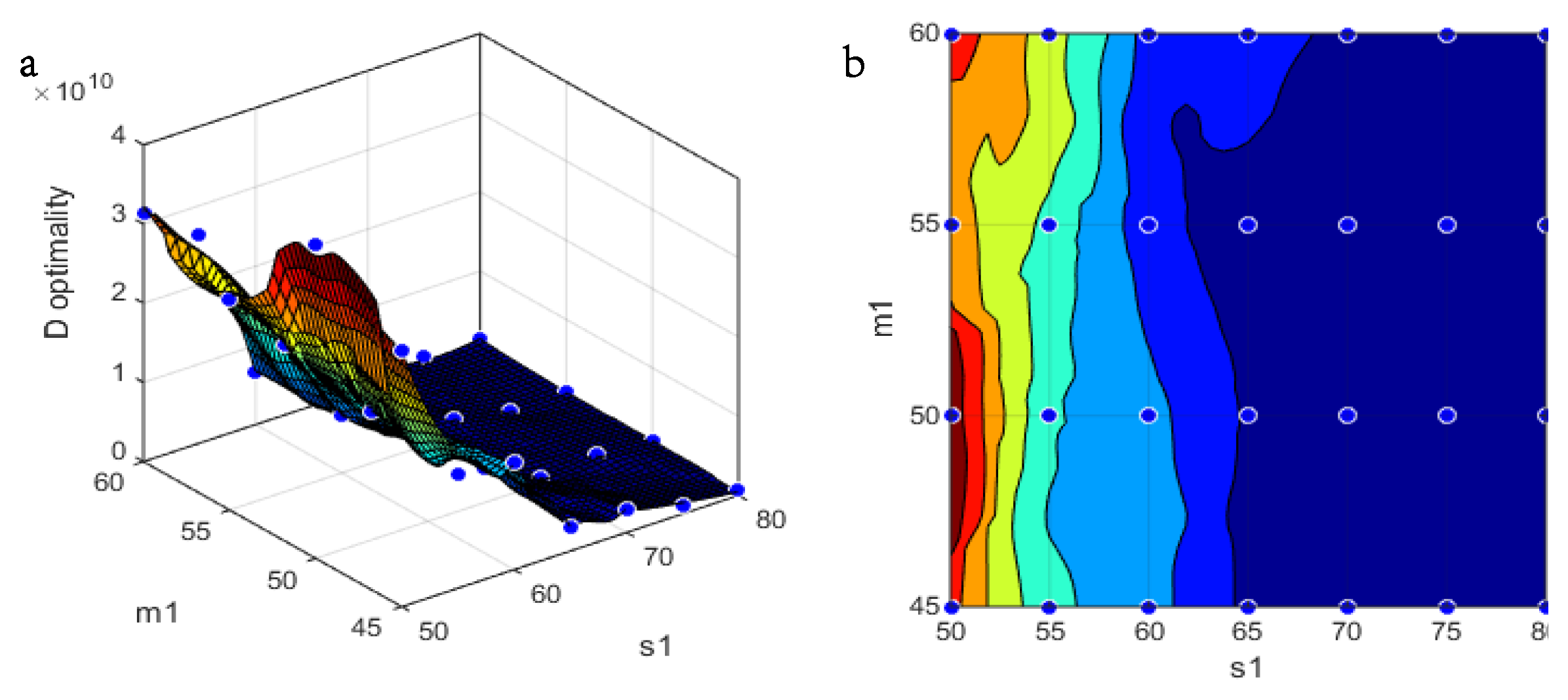
where symmetrical denotes that the matrix is symmetric, and the matrix $I(\mathit{\eta },\mathit{\theta })$ must be non-singular. The expressions for all of the elements in $I(\mathit{\eta },\mathit{\theta })$ are given in Appendix A Then, the Bayesian D-optimality is to maximize Equation (8), which can be expressed as $\max \mathsf{\Phi }\left(\mathit{\eta }\right)$. Due to the complexity of the formulas in Equation (9), a large-sample approximation is utilized to simplify the formulas to numerically calculate the objective of plan $\mathit{\eta }$. Details are given as follows:

• Step 1: A plan space $\mathit{P}$ is firstly defined, which contains R choices of test plans $\mathit{\eta }$. As for ${\mathit{\eta }}_r$, $r=1,2,\cdots ,R$, simulate parameter ${\mathit{\theta }}_{rp}$ from the corresponding $\pi \left(\mathit{\theta }\right)$ for $Q_1$ times ($p=1,2,\cdots ,Q_1$). Based on the simulated ${\mathit{\theta }}_{rp}$, generate degradation data $x_{rpq}$ from the sampling distribution (2) for $Q_2$ times ($q=1,2,\cdots ,Q_2$).
• Step 2: According to the Appendix, calculate the elements of Equation (9) based on the drawn ${\mathit{\theta }}_{rp}$ and $x_{rpq}$.
• Step 3: Numerically calculate the value of Equation (8) based on $\mathsf{\Phi }\left({\mathit{\eta }}_r\right)=\frac{1}{Q_1·Q_2}{\displaystyle \sum _{q=1}^{Q_2}}{\displaystyle \sum _{p=1}^{Q_1}}log\left(\det \left(I_{rpq}({\mathit{\eta }}_r,{\mathit{\theta }}_{rp})\right)\right)$.

3. Planning of a Sequential ADT

Without loss of generality, the number of stress levels $K=3$ is selected to illustrate the optimal design procedure of the sequential ADT.

3.1. Planning ADT under the Highest Stress Level $S_3$

As proposed in Section 2.1, the plan for the highest stress level $S_3$ is an initial plan of the sequential ADT, which is designed based on the initial prior information.

Before the ADT, n and M are supposed to be given according to the budget and practical situation and remain fixed through the test. Then, for the test plan $\mathit{\eta }$, the decision variables include $\mathbf{S}=(S_1,S_2,\cdots ,S_K)$ and $\mathbf{m}=(m_1,m_2,\cdots ,m_K)$. Since the degradation rate under the higher stress level is greater than that under the lower stress level and the time interval is constant, in order to guarantee that enough useful degradation information can be obtained at all accelerated stress levels, the degradation measurements at the lower stress levels are assigned more than that at the higher stress levels, which means $m_1>m_2>,\cdots ,>m_K(k=1,2,\dots ,K)$ [19]. The optimal model could be expressed as follows:

$$\begin{array}{cc}\max \hfill & \mathsf{\Phi }\left(\mathit{\eta }\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & S_0<S_{min}\le S_1<S_2<S_3\le S_{\max }\le S_H\hfill \\ & m_1>m_2>m_3>0,{\sum }_{k=1}^3{m}_{\mathrm{k}}=M\hfill \end{array}$$

(10)

where $S_{min}$ and $S_{\max }$ are the allowable lowest and the highest stress levels in ADT, and generally, the allowable highest stress level in ADT is lower than operational stress limit due to the test facility (i.e., $S_{\max }\le S_H$).

A plan space ${\mathit{P}}_3$ is firstly defined, which contains $R_3$ choices of test plans $\mathit{\eta }$. With the known ${\pi }_3\left(\mathit{\theta }\right)$, the corresponding $\mathsf{\Phi }\left({\mathit{\eta }}_r\right)$ of ${\mathit{\eta }}_r$ in ${\mathit{P}}_3$ could be calculated according to the procedure in Section 2.4. The optimization methodology proposed by Li et al. [19] is applied in our study to solve Model (10), then the initial optimal plan ${\mathit{\eta }}_3^{*}=\left\{(S_1,S_2,S_3),(m_1,m_2,m_3)\right\}$ could be obtained. Next, engineers can run the ADT with n samples under the stress level $S_3$ and collect $m_3$ degradation data.

3.2. Planning ADT under the Middle Stress Level $S_2^{{}^{\prime }}$

After the ADT operation under $S_3$, the degradation data ${\mathit{x}}_3$ under $S_3$ can be collected. Based on ${\mathit{x}}_3$ and ${\pi }_3\left(\mathit{\theta }\right)$, samples from posterior distributions $p_3\left(\mathit{\theta }\right|{\mathit{x}}_3)$ under $S_3$ can be generated by using MCMC according to Section 2.3. Then, the prior distributions ${\pi }_2\left(\mathit{\theta }\right)$ under ${S^{\prime }}_2$ can be built up by the distributions fitting to the samples from $p_3\left(\mathit{\theta }\right|{\mathit{x}}_3)$.

The optimal model is given under $S_2^{\prime }$ with the constraints of the remaining resources $M^{\prime }$,

$$\begin{array}{cc}\max \hfill & \mathsf{\Phi }\left(\eta \right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & S_0<{S_1}^{\prime }<{S_2}^{\prime }<S_3\hfill \\ & {m_1}^{\prime }>{m_2}^{\prime }>0,{\sum }_{k=1}^2{{m_k}^{\prime }=M}^{\prime }\hfill \\ & M^{\prime }=M-m_3\hfill \end{array}$$

(11)

Similar to the method mentioned in Section 3.1, a plan space ${\mathit{P}}_2$ is defined, which contains $R_2$ choices based on the constraints of Model (11), and the optimization methodology in [19] is used to obtain the optimal test plan ${\mathit{\eta }}_2^{*}=\left\{(S_1^{\prime },S_2^{\prime }),(m_1^{\prime },m_2^{\prime })\right\}$. Then, engineers can conduct the test with n samples under the stress level $S_2^{\prime }$ and collect $m_2^{\prime }$ degradation data.

3.3. Planning ADT under the Lowest Stress Level $S_1^{″}$

After the ADT operation under $S_2^{\prime }$, the degradation data ${\mathit{x}}_2$ under $S_2^{\prime }$ can be collected. Similarly, based on ${\mathit{x}}_2$ and ${\pi }_2\left(\mathit{\theta }\right)$, samples from posterior distributions $p_2\left(\mathit{\theta }\right|{\mathit{x}}_2)$ under $S_{\prime }^2$ can be generated by using MCMC according to Section 2.3; then, the prior distributions ${\pi }_1\left(\mathit{\theta }\right)$ under $S_1^{″}$ can be built up by the distributions fitting to the samples from $p_2\left(\mathit{\theta }\right|{\mathit{x}}_2)$. The optimal model is generated under the stress level $S_1^{″}$ with the constraints of the remaining resources $M^{″}$,

$$\begin{array}{cc}\max \hfill & \mathsf{\Phi }\left(\eta \right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & S_0<{S_1}^{″}<{S_2}^{\prime }\hfill \\ & {m_1}^{″}=M^{″}\hfill \\ & M^{″}=M-m_3-{m_2}^{\prime }\hfill \end{array}$$

(12)

The remaining resources $M^{″}$ are fixed according to the Model (12), and the only decision variable is the lowest stress level $S_1^{″}$. The plan space ${\mathit{P}}_1$, which contains $R_1$ choices of test plans $\mathit{\eta }$, is defined by discretizing the range of $S_1^{″}$ (i.e., [$S_0$, $S_2^{\prime }$)). Similar to the method mentioned in Section 3.1, the optimal test plan ${\mathit{\eta }}_1^{*}=\left\{S_1^{″},m_1^{″}\right\}$ can be obtained.

Finally, the whole optimal sequential ADT plan is expressed as ${\mathit{\eta }}^{*}=\left\{(S_1^{″},S_2^{\prime },S_3),(m_1^{″},m_2^{\prime },m_3)\right\}$.

4. Case Study

4.1. Numerical Case

In order to illustrate the proposed method, we assume that a sequential ADT is conduct on the electric connectors given in Yang [28], and their stress relaxation data are used to build up the initial prior distributions in this case study. In Example 8.7 of [28], the electric connector is said to fail when the stress relaxation is over 30%, i.e., $X_D=30$. The ADT data of electric connectors were collected under the conditions of $S_1=65°\mathrm{C}$, $S_2=85°\mathrm{C}$ and $S_3=100°\mathrm{C}$, respectively. These ADT data and the corresponding measurement time are shown in

Table A1. Stress relaxation degradation data of electrical connectors under different accelerated stress levels.

T	ID	Stress Loss
60 °C	1	2.12	2.7	3.52	4.25	5.55	6.12	6.75	7.22	7.68	8.46	9.46
	2	2.29	3.24	4.16	4.86	5.74	6.85	*	7.4	8.14	9.25	10.55
	3	2.4	3.61	4.35	5.09	5.5	7.03	8.24	8.81	9.629	10.27	11.11
	4	2.31	3.48	5.51	6.2	7.31	7.96	8.57	9.07	10.46	11.48	12.31
	5	3.14	4.33	5.92	7.22	8.14	9.07	9.44	10.09	11.2	12.77	13.51
	6	3.59	5.55	5.92	7.68	8.61	10.37	11.11	12.22	13.51	14.16	15
85 °C	7	2.77	4.62	5.83	6.66	8.05	10.61	11.2	11.98	13.33	15.64	-
	8	3.88	4.37	6.29	7.77	9.16	9.9	10.37	12.77	14.72	16.8	-
	9	3.18	4.53	6.94	8.14	8.79	10.09	11.11	14.72	16.47	18.66	-
	10	3.61	4.37	6.29	7.87	9.35	11.48	12.4	13.7	15.37	18.51	-
	11	3.42	4.25	7.31	8.61	10.18	12.03	13.7	15.27	17.22	19.25	-
	12	5.27	5.92	8.05	9.81	12.4	13.24	15.83	17.59	20.09	23.51	-
100 °C	13	4.25	5.18	8.33	9.53	11.48	13.14	15.55	16.94	18.05	19.44	-
	14	4.81	6.16	7.68	9.25	10.37	12.4	15	16.2	18.24	20.09	-
	15	5.09	7.03	8.33	10.37	12.22	14.35	16.11	18.7	19.72	21.66	-
	16	4.81	7.5	9.16	10.55	13.51	15.55	16.57	19.07	20.27	22.4	-
	17	5.64	6.57	8.61	12.5	14.44	16.57	18.7	21.2	22.59	24.07	-
	18	4.72	8.14	10.18	12.4	15.09	17.22	19.16	21.57	24.35	26.2	-

and

Table A2. Inspection time under different stress levels.

T	Performance Inspection Time
65 °C	108	241	534	839	1074	1350	1637	1890	2178	2513	2810
85 °C	46	108	212	408	632	764	1011	1333	1517	2586	-
100 °C	46	108	212	344	446	626	729	972	1005	1218	-

of Appendix B.

Before the sequential ADT of electric connectors, we assume that K is equal to three; three electric connectors are put into the sequential ADT; and the total of the measurements M is equal to 120.

Ye [21] has proven that the collected stress relaxation data follow the IG process, in which stress function $\xi \left(S\right)$ could be rewritten as $1/S$. By using the maximum likelihood estimation method and square root of the determinant of the inverse matrix of the Fisher information matrix, the mean and the variance of the model parameters can be obtained, as shown in

Table 1. Estimated values of the model parameters.

Estimated Parameters	$\widehat{\mathit{a}}$	$\widehat{\mathit{b}}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\beta }}$
Mean	$-1.8966$	1.7379	0.6337	0.4493
Variance	0.1903	0.1738	0.1968	0.0178

.

Now, it is obvious that as long as the distribution form is selected, the hyper-parameters are determined. Suppose that parameters a and b follow normal distributions and parameters $\lambda$ and $\beta$ follow Gamma distributions, then the initial prior distributions ${\pi }_3\left(\mathit{\theta }\right)$ can be determined and are shown in

Table 2. Prior distributions ${\pi }_3\left(\mathit{\theta }\right)$ under $S_3$.

Parameter	a	b	$\mathit{\lambda }$	$\mathit{\beta }$
${\pi }_3\left(\mathit{\theta }\right)$	$Normal(-1.90,0.19)$	$Normal(1.74,0.17)$	$Gamma(2.04,0.31)$	$Gamma(11.34,0.04)$

.

If the usage stress level $S_0$ is 40 °C, then $S_{min}$ and $S_{\max }$ are set to be 50 °C and 100 °C, respectively. For the Bayesian sequential ADT design, the test is supposed to be conducted after each stress level is designed.

In this case, since we do not actually run the test, there is no available practical degradation data for each stress level. Consequently, the numerical simulation based on the “true values” of the parameters will be used to generate the degradation data. The estimations of mean in Table 1 are supposed as the actual situation of the electric connector and to be the “true values” of $\mathit{\theta }$, expressed as ${\mathit{\theta }}_T$. Details about the Bayesian sequential ADT design are illustrated as follows.

4.1.1. The Stage of the Highest Stress Level

According to Li et al. [19], the following simplification is made to obtain plan space ${\mathit{P}}_3$. First, let $S_1=\left[50556065707580\right]$ °C and $S_3=S_{\max }=100$ °C, then, by using the interval between $\xi \left(S_l\right)$ and $\xi \left(S_{l+1}\right)$ constant, $S_2=\left[73767881848789\right]$ °C. Similarly, let $m_1=\left[40506070\right]$, $m_3=\left[40302010\right]$ and $m_2=1/2(m_1+m_3)$, then $m_2=\left[40404040\right]$. With the above simplification, the decision variables are reduced as $(S_1,m_1)$ for $\mathit{\eta }$, since $\mathbf{S}$ and $\mathbf{m}$ will be determined as long as $S_1$ and $m_1$ are chosen, and there are 28 choices of $\mathit{\eta }$ in ${\mathit{P}}_3$. Hence, according to the method introduced in Section 3.1, the fitting surface of the optimal results can be obtained, as shown in Figure 2, and the corresponding initial optimal plan ${\mathit{\eta }}_3^{*}$ is shown in

Table 3. Optimal plan ${\mathit{\eta }}_3^{*}$ at the stage of highest stress level.

${\mathit{S}}_1,{\mathit{S}}_2,{\mathit{S}}_3$ (°C)	${\mathit{m}}_1,{\mathit{m}}_2,{\mathit{m}}_3$	$\mathbf{\Phi }\left(\mathit{\eta }\right)(\times {10}^{10})$
50, 73, 100	50, 40, 30	3.8465

.

4.1.2. The Stage of the Middle Stress Level

A. Prior distributions ${\pi }_2\left(\mathit{\theta }\right)$ under $S_2^{\prime }$:

According to ${\mathit{\eta }}_3^{*}$, the degradation data ${\mathit{x}}_3$ are obtained by the simulation with parameters ${\mathit{\theta }}_T$ under $S_3$. Based on ${\mathit{x}}_3$ and the prior distributions ${\pi }_3\left(\mathit{\theta }\right)$, samples from posterior distributions $p_3\left(\mathit{\theta }\right|{\mathit{x}}_3)$ under $S_3$ can be generated by using MCMC according to Section 3.2. To fit the samples from $p_3\left(\mathit{\theta }\right|{\mathit{x}}_3)$, different distribution types aforementioned in Section 2.3 are considered, and the likelihood ratio test is used to select the appropriate distributions. According to the values of the log likelihood function shown in

Table 4. Results of log likelihood test for samples from $p_3\left(\mathit{\theta }\right|{\mathit{x}}_3)$.

	Distribution Forms	Normal	Extreme Value	Logistic
Parameters
a		−1027.05	−1268.49	−1046.75
b		−1029.14	−1521.26	−1032.19
	Distribution Forms	Gamma	Logistic	Weibull
Parameters
$\lambda$		−350.384	−546.081	−467.518
$\beta$		4955.42	4908.82	4721.6

, the normal and Gamma distributions are used to construct the prior distributions ${\pi }_2\left(\mathit{\theta }\right)$ under $S_2^{\prime }$ as shown in Figure 3 and

Table 5. Prior distributions ${\pi }_2\left(\mathit{\theta }\right)$ under $S_2^{\prime }$.

Parameter	a	b	$\mathit{\lambda }$	$\mathit{\beta }$
${\pi }_2\left(\mathit{\theta }\right)$	$Normal(-1.98,0.12)$	$Normal(1.68,0.12)$	$Gamma(5.48,0.13)$	$Gamma(92.94,0.0049)$

.

B. The middle optimal test plan ${\mathit{\eta }}_2^{*}$:

Given the remaining test resources $M^{\prime }=90$, the following simplification is made to obtain plan space ${\mathit{P}}_2$. First, as $S_3=S_{\max }=100$ °C, the setting for stress levels remains the same with ${\mathit{P}}_3$. Then, $S_1^{\prime }=\left[50556065707580\right]$ °C and $S_2^{\prime }=\left[73767881848789\right]$ °C. As $m_1^{\prime }+m_2^{\prime }=M^{\prime }=90$, let $m_1^{\prime }=\left[45505560\right]$, and $m_2^{\prime }=\left[45403530\right]$. With the above simplification, there are 28 choices of $\mathit{\eta }$ in ${\mathit{P}}_2$. Hence, according to the method introduced in Section 3.2, the fitting surface of the optimal results can be obtained, as shown in Figure 4, and the corresponding optimal plan ${\mathit{\eta }}_2^{*}$ is shown in

Table 6. Optimal plan ${\mathit{\eta }}_2^{*}$ at the stage of the middle stress level.

${\mathit{S}}_1^{{}^{\prime }},{\mathit{S}}_2^{{}^{\prime }}$ (°C)	${\mathit{m}}_1^{{}^{\prime }},{\mathit{m}}_2^{{}^{\prime }}$	$\mathbf{\Phi }\left(\mathit{\eta }\right)(\times {10}^{10})$
50, 73	55, 35	3.9720

.

4.1.3. The Stage of the Lowest Stress Level

A. Prior distributions ${\pi }_1\left(\mathit{\theta }\right)$ under $S_1^{″}$:

The degradation data ${\mathit{x}}_2$ are generated by the simulation with parameters ${\mathit{\theta }}_T$ under $S_2^{\prime }$. Again, with the likelihood ratio test, the normal and Gamma distributions are selected for ${\pi }_1\left(\mathit{\theta }\right)$ under $S_1^{″}$ as shown in Figure 5 and

Table 7. Results of log likelihood test for samples from $p_2\left(\mathit{\theta }\right|{\mathit{x}}_2)$.

	Distribution Forms	Normal	Extreme Value	Logistic
Parameters
a		89.2733	45.8437	−1268.49
b		−872.846	−890.798	−1521.26
	Distribution Forms	Gamma	Logistic	Weibull
Parameters
$\lambda$		697.036	591.541	530.585
$\beta$		6477.74	6444.57	6252.95

. The corresponding values of log likelihood function are shown in

Table 8. Prior distributions ${\pi }_1\left(\mathit{\theta }\right)$ under $S_1^{″}$.

Parameter	a	b	$\mathit{\lambda }$	$\mathit{\beta }$
${\pi }_1\left(\mathit{\theta }\right)$	$Normal(-1.92,0.06)$	$Normal(1.72,0.10)$	$Gamma(13.19,0.0548)$	$Gamma(259.81,0.0017)$

.

B. The last optimal test plan ${\mathit{\eta }}_1^{*}$:

Given the remaining test resources $m_1^{″}=55$, the only decision variable $S_1^{″}$ can be discretized into 12 values with the range of (50, 73). Then, there are 12 choices of $\mathit{\eta }$ in ${\mathit{P}}_1$. The optimal results are shown in Figure 6.

Finally, the optimal plan for Bayesian sequential ADT method is presented in

Table 9. Optimal plan for the sequential method.

Optimal Plan	${\mathit{S}}_1^{{}^{\prime \prime }},{\mathit{S}}_2^{{}^{\prime }},{\mathit{S}}_3$ (${}^{\circ }$ C)	${\mathit{m}}_1^{{}^{\prime \prime }},{\mathit{m}}_2^{{}^{\prime }},{\mathit{m}}_3$	$\mathbf{\Phi }\left(\mathit{\eta }\right)(\times {10}^{10})$
Sequential method	50, 73, 100	55, 35, 30	2.5044

.

4.2. Static Bayesian ADT Design Method vs. Dynamic Sequential ADT Design Method

In this section, comparisons are conducted between the static Bayesian design method in [19] and the proposed dynamic sequential design method. It is known from Section 3.1 that the static Bayesian plan is actually the test plan under the highest stress level ${\mathit{\eta }}_3^{*}$ in the proposed method, which is designed only based on the initial prior distribution ${\pi }_3\left(\mathit{\theta }\right)$.

As previously mentioned in Section 1, when the difference between the prior information and actual situation is large, the optimal plan designed by the static Bayesian method may cause some issues that the implemented ADT following the optimal ADT plan consumes too much testing resources or few accelerated degradation data are obtained during the ADT. It is supposed that the proposed Bayesian sequential ADT design may avoid these issues by dynamic decision-making. Therefore, the “true values” of $\mathit{\theta }$ are assumed as $\pm 2\sigma$ from the mean, respectively, based on ${\pi }_3\left(\mathit{\theta }\right)$ as shown in

Table 10. The assumed model parameter.

“True Values”	a	b	$\mathit{\lambda }$	$\mathit{\beta }$
${\mathit{\theta }}_{T1}(+2\sigma )$	−1.02	2.57	1.52	0.72
${\mathit{\theta }}_{T2}(-2\sigma )$	−2.77	0.90	0.10	0.18

.

Considering the uncertainties embedded in the simulated degradation data, the test plans are designed five times to make the results more convincing. The sequential plans with the true value ${\mathit{\theta }}_{T1}$ and ${\mathit{\theta }}_{T2}$ are shown in

Table 11. Sequential plans with ${\mathit{\theta }}_{T1}$.

Sequential Plan No.	${\mathit{S}}_1^{{}^{\prime \prime }},{\mathit{S}}_2^{{}^{\prime }},{\mathit{S}}_3$ (°C)	${\mathit{m}}_1^{{}^{\prime \prime }},{\mathit{m}}_2^{{}^{\prime }},{\mathit{m}}_3$	$\mathbf{\Phi }\left(\mathit{\eta }\right)(\times {10}^{10})$
1	54, 73, 100	55, 35, 30	4.2332
2	50, 73, 100	60, 30, 30	3.1216
3	50, 73, 100	60, 30, 30	2.8496
4	52, 73, 100	55, 35, 30	2.5196
5	50, 73, 100	55, 35, 30	2.7243

and

Table 12. Sequential plans with ${\mathit{\theta }}_{T2}$.

Sequential Plan No.	${\mathit{S}}_1^{{}^{\prime \prime }},{\mathit{S}}_2^{{}^{\prime }},{\mathit{S}}_3$ (°C)	${\mathit{m}}_1^{{}^{\prime \prime }},{\mathit{m}}_2^{{}^{\prime }},{\mathit{m}}_3$	$\mathbf{\Phi }\left(\mathit{\eta }\right)(\times {10}^{10})$
1	60, 76, 100	45, 45, 30	4.6062
2	62, 73, 100	45, 45, 30	5.4769
3	58, 73, 100	50, 40, 30	1.4460
4	52, 73, 100	50, 40, 30	1.8926
5	54, 73, 100	50, 40, 30	2.6563

.

It is known that an ADT is commonly used to assess the lifetime and reliability; then, to some extent, the more accurate the evaluation is, the better the test plan is. Therefore, the evaluations of the parameters and the p-quantile lifetime are chosen as the measurements for assessing how good the ADT plans are. The mean of the posterior distribution is applied to evaluate the model parameter. The p-quantile lifetime of $X_D$ can be approximately expressed as [21],

$$t_p={\mathsf{\Lambda }}^{-1}\left[{\displaystyle \frac{\mu }{4\lambda }{\left(z_p+\sqrt{{\left(z_p\right)}^2+4X_D\lambda /{\mu }^2}\right)}^2}\right]$$

(13)

where $z_p$ is the standard normal p-quantile and ${\mathsf{\Lambda }}^{-1}\left(.\right)$ is the inverse function of $\mathsf{\Lambda }\left(.\right)$. Then, the Bayesian posterior p-quantile lifetime of $X_D$ is,

$$t(p,\mathit{\theta }|x)={\mathsf{\Lambda }}^{-1}\left(\frac{\mu }{4\lambda }{\left(z_p+\sqrt{{\left(z_p\right)}^2+4X_D\lambda /{\mu }^2}\right)}^2\right)·p\left(\mathit{\theta }\right|x))$$

(14)

The corresponding evaluation results based on the sequential plans listed in Table 11 and Table 12 and the static plan ${\mathit{\eta }}_3^{*}$ are shown in Figure 7, Figure 8, Figure 9 and Figure 10.

To measure the evaluation accuracy of the two design methods better, the “relative deviation” is defined as,

$$\epsilon =\sqrt{\sum {\left(\widehat{w}-w_T\right)}^2}$$

(15)

where $\widehat{w}$ denotes the estimates and $w_T$ denotes the “true values” for both parameters and p-quantile lifetime. The results of the relative deviation are presented in

Table 13. Relative deviation results.

“True Values”	Method	${\mathit{\epsilon }}_{\mathit{a}}$	${\mathit{\epsilon }}_{\mathit{b}}$	${\mathit{\epsilon }}_{\mathit{\lambda }}$	${\mathit{\epsilon }}_{\mathit{\beta }}$	${\mathit{\epsilon }}_{\mathbf{tp}}(\times {10}^{17})$
${\mathit{\theta }}_{T1}$	Static method	0.3940	0.5466	0.5250	0.0582	215.7427
	Sequential method	0.1502	0.3450	0.4954	0.0507	132.9126
${\mathit{\theta }}_{T2}$	Static method	0.7265	1.2556	0.0407	0.0392	11.572
	Sequential method	0.3218	0.8806	0.0388	0.0229	8.0021

.

The following could be true from the “relative deviation” results in Table 13:

(1)

All of the relative deviations obtained by the proposed sequential method are less than that of the static method. That is to say our proposed sequential scheme can ensure better estimates both for the parameters and quantile lifetime.

(2)

There are less fluctuations in the estimates based on the proposed sequential ADT plan than that based on the static ADT plan.

5. Conclusions

A Bayesian sequential step-down-stress ADT design method is proposed, in which the test under the highest stress level is conducted first to quickly generate degradation information. With the prior information and the ADT data collected under the preorder stress levels, the Bayesian interference and design methods are used for planning the subsequent ADT planning. In the proposed sequential scheme, the degradation path is assumed to follow the IG process, and Bayesian D-optimality is selected as the objective.

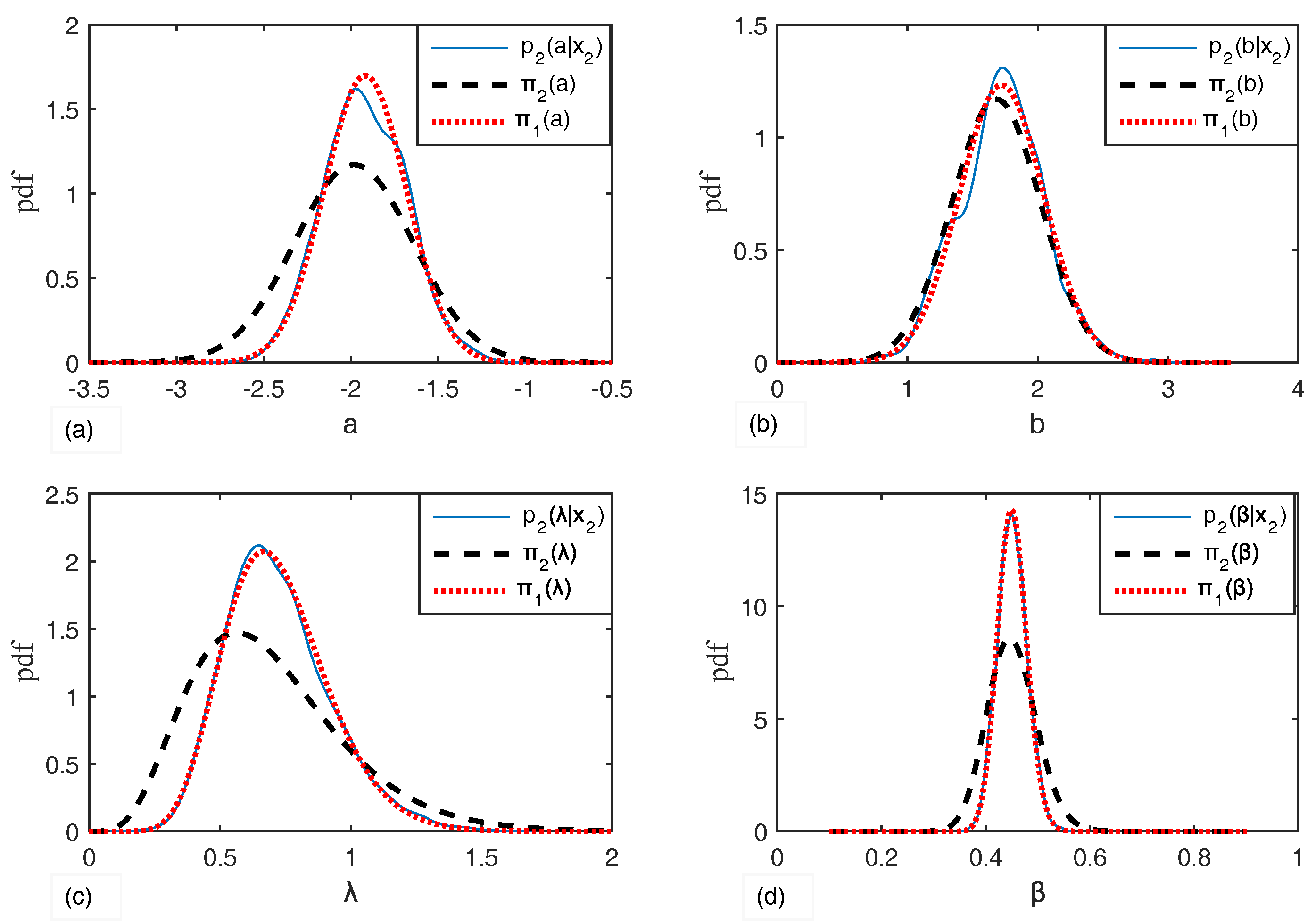
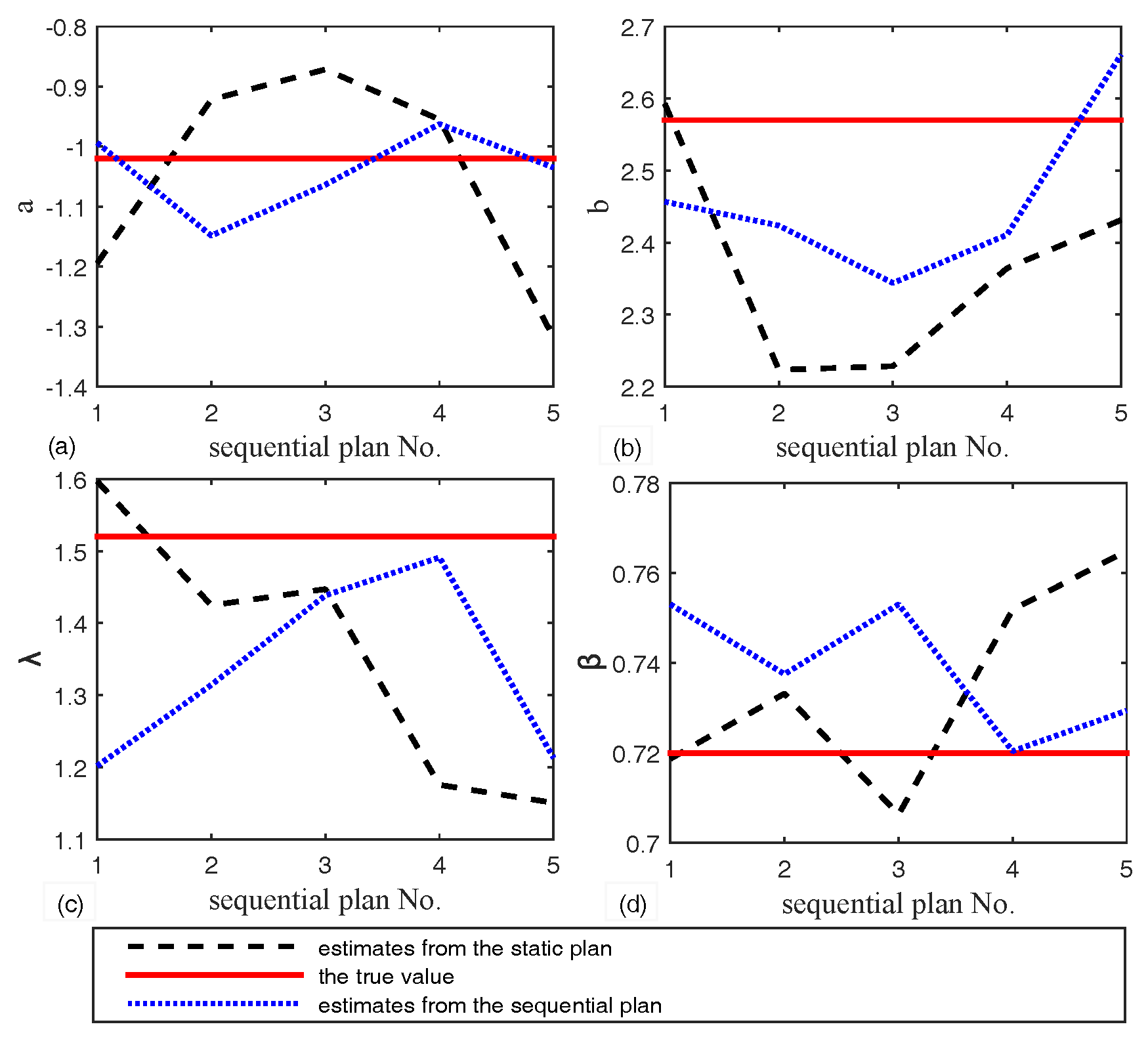
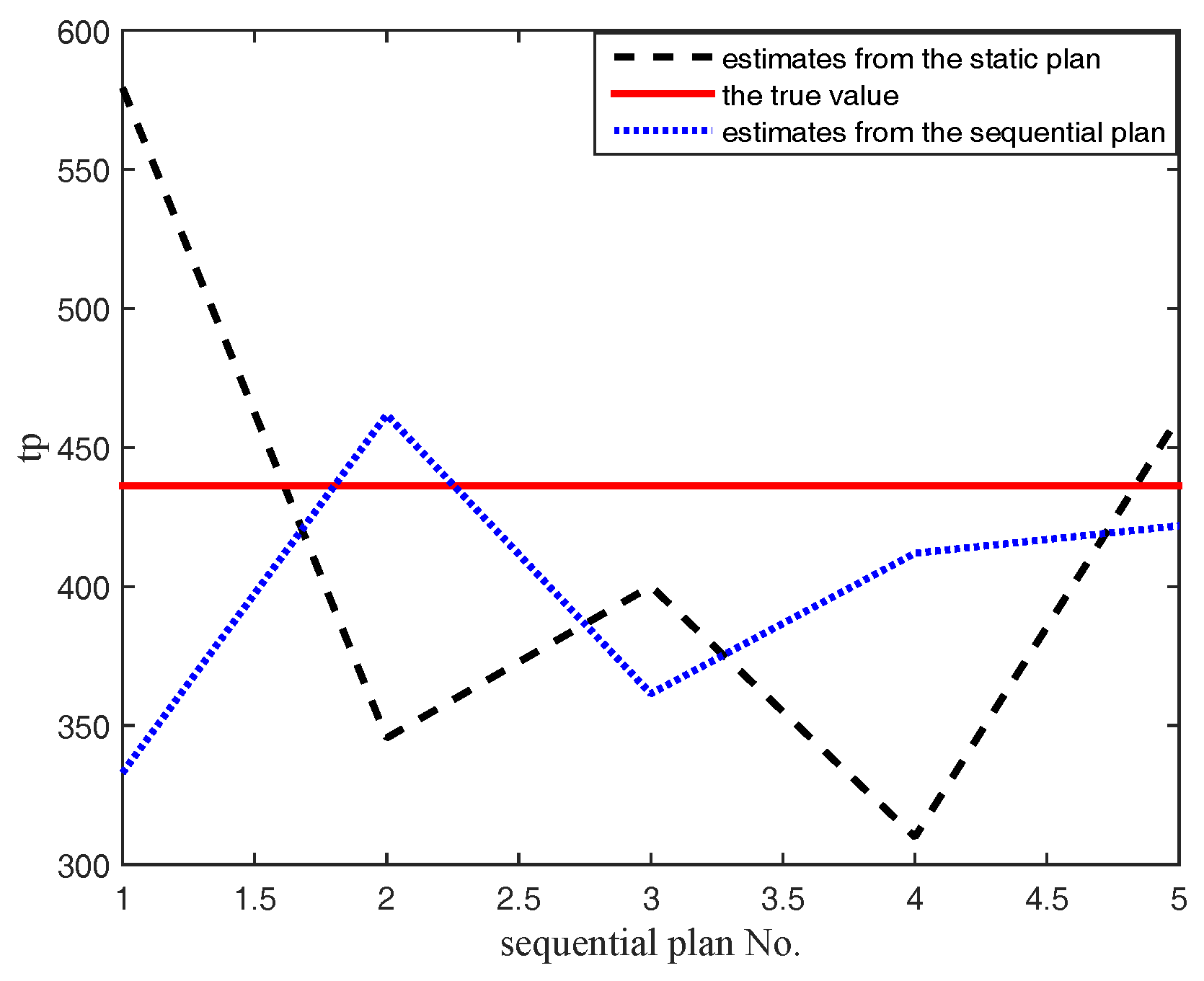
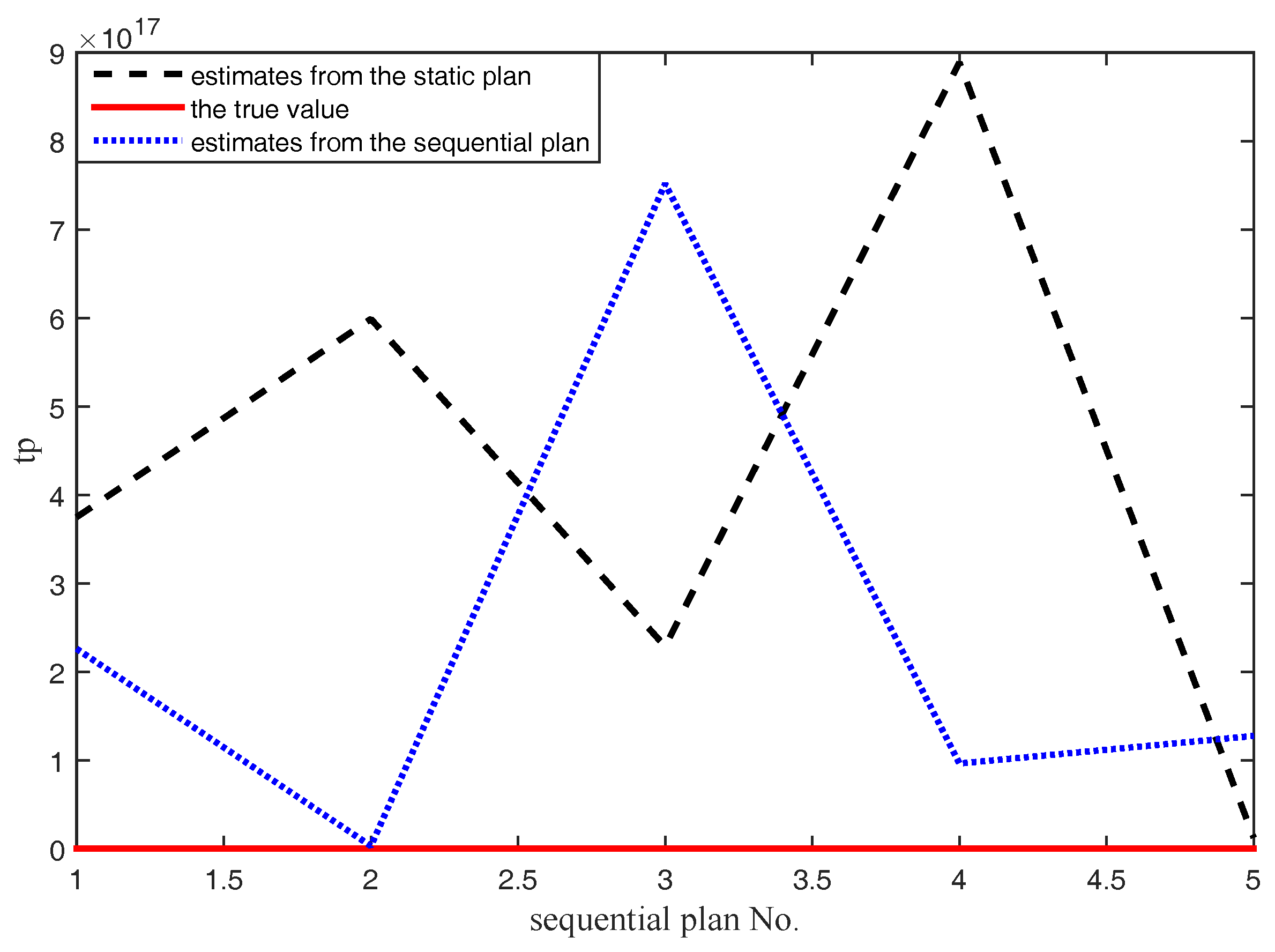
When there is a relatively big difference between priors and actual situations of samples, from the numerical example, we can draw the following conclusions:

(1)

The ADT plan can be dynamically adjusted with the collected ADT data.

(2)

The Bayesian sequential ADT design method outperform the Bayesian static design method on both the accuracy of the evaluation and the robustness of the misspecification of the initial planning parameter value.

The proposed scheme is conducted without the constraints of the total test cost, which could be taken into account in the future work for practical application. In addition, D-optimality is selected as the only objective, which expresses the evaluation precision of model parameters. It is noted that there exist many Bayesian objectives, which express different utilities for ADT design; therefore, it could be considered to design sequential ADT plans under the multi-objective optimization model with different utilities as the objectives.