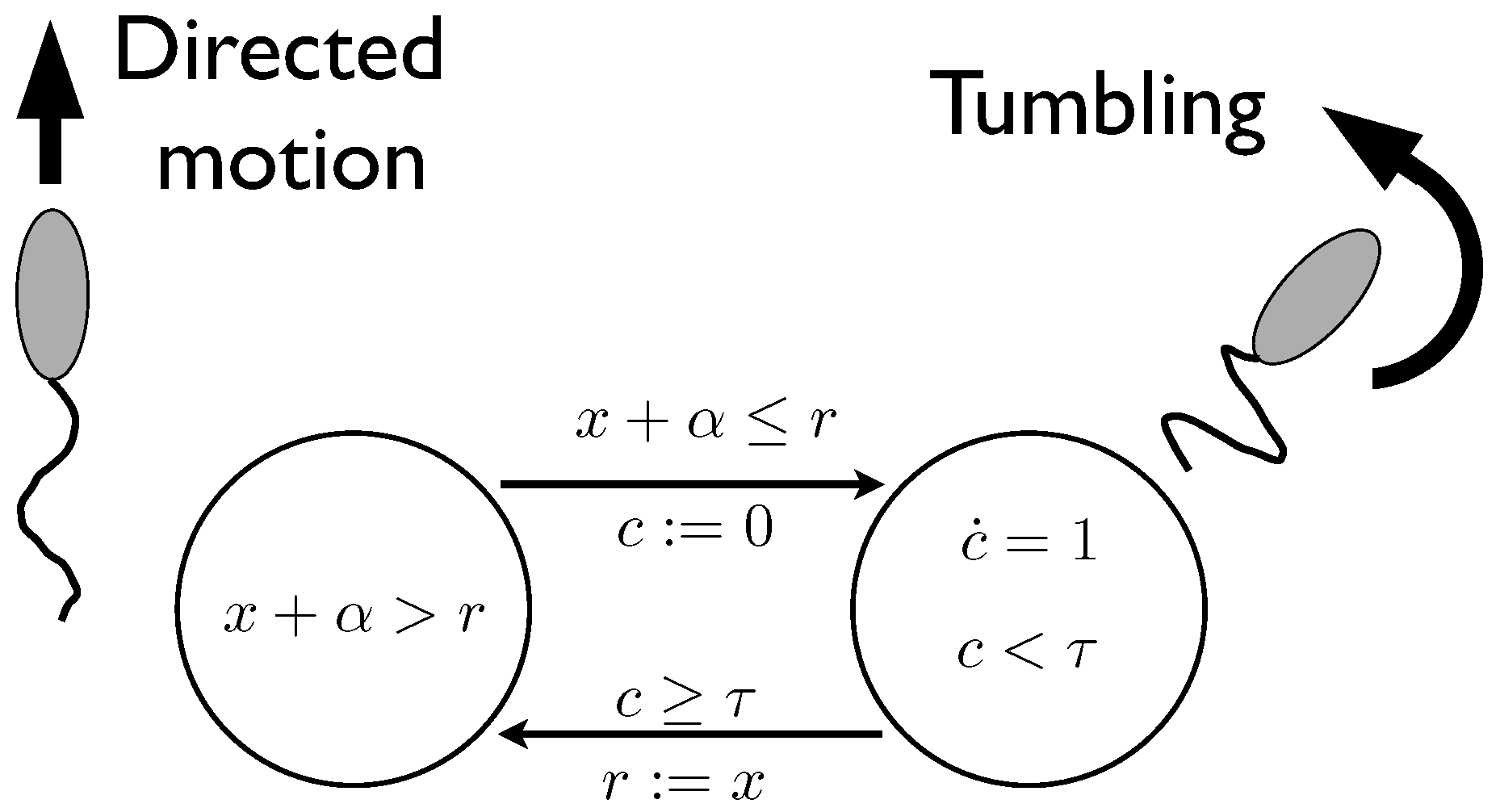
The first criterion (FW1) implies that we need to determine what parts of a system must be included in identifying an agent (i.e., the extent of its identity) before being able to determine if it has free-will or not. Free-will requires a definite boundary between the internal and external, not necessarily a physical boundary (as supplied by e.g., a casing or skin), but more profoundly one of organisation and control. For example a computer controlled robot must have all the necessary provisions for physical independence (as in the extraterrestrial exploration robots), but this still leaves it organisationally linked to humanity because its existence is entirely dependent on our gathering and processing the materials for its “body” and assembling these, implicitly embodying it with functional information [
1] and programming its control computer (including with the goal for operation). For these reasons, such robots remain extensions of ourselves: tools just as sophisticated hammers would be. In general, for free-will, the control information of an agent must be independent of anything beyond a cybernetically meaningful boundary. Put the other way round, for the identification of free-will, we must first identify the boundary of the agent, which is defined by independence of control. The existence of such a cybernetic boundary enclosing the agent is here termed the “closure condition”. Given this, the Mars Rover coupled with its human design team seems to meet the closure condition, but the Mars Rover alone does not.
2.1. Systems with Causal Autonomy
Froese et al. [
22] distinguishes behavioural (based on external behaviour) from constitutive (based on internal organisation) autonomy. They state that for the former, the identity of the system may be imposed by an external observer (it could even be no more than an thermostatic system) and that it is sufficient for the system to demonstrate a capacity for stable and/or flexible interaction with its environment, “without human intervention, supervision, or instruction”. This, they argued, left behavioural autonomy so “ambiguous and inclusive …it threatens to make the concept of autonomy meaningless”. Behavioural definitions of autonomy are inadequate in relation to questions of free will because they do not address the source of will (more precisely, the origin of the goal/s) which motivate the observed actions. To attribute free will to an agent, we need to identify the source of will as a part of the agent (under FW4) and this requires us to consider the composition of the agent. To exclude external (generalised from “human”) “intervention, supervision, or instruction", we must have an agent that is separated from external causation of its actions. According to most authors seeking to explain the apparent independence of action found among living systems, this requirement leads directly to constitutive autonomy, e.g., “every autonomous system is organizationally closed” (Varela [
23], p. 58). This idea has a relatively long history in a multi-disciplinary literature (Froese et al. [
22], Zeleny [
24], Rosen [
25], Vernon et al. [
26], Bich [
27] and references therein), but it is not clear if it is restricted to living systems, or may be broader. Therefore, rather than taking this literature as sufficient justification for a constitutive autonomy requirement, let us examine the options for matching with the following tasks:
to answer Strawson’s [
20] “Basic Argument” of ultimate responsibility;
to separate internal from external (i.e., to give formal meaning to internal and external);
to unambiguously break the physical causal link between the agent and its environment, allowing “leeway” from determinism.
This will start with task (2) because from its conclusion, task (3) may follow, given a specification that relations are strictly causal and if the answer to task (2) does specify constitutive autonomy, then task (1) may be implied from that, though it leaves unproven that a causally autonomous system must be self-made. This gap may not be serious, as later shown.
Therefore, we seek a structure for which “internal” is causally distinct from “external”, giving a clear definition to both. For this we need to define an object
A, properly composed of parts (e.g.,
x,
y), none of which is a part of any other object
B. More formally: ∃
A composed of parts
in which no part of
A is also a part of any object
B unless
B contains or is
A:
. Assume the mereology in which the reflexivity and transitivity principles are true and also the antisymmetry postulate is true. That is: two distinct things cannot be part of each other. This is expressed by the axioms [
28]:
in which P is the “part of” relation. For these, the auxiliary relations are defined:
Therefore, we can define an isolated object
y : no part of
y can overlap with anything other than
y. Hence, Isolation:
, hence
(this definition is not a part of standard mereology). The mereological sum (noting that alternative definitions exist) is defined as: an object
y is a mereological sum of all elements of a set X iff every element of X is a part of
y and every part of
y overlaps some element
x∈ X. (Effingham [
29], p. 153) puts it this way: “the
xs compose
y by definition if (i) each
x is a part of
y; (ii) no two of the
xs overlap; (iii) every part of y overlaps at least one of the
xs”. This definition of sum allows overlap with objects that are not parts of the mereological sum, so
y is not necessarily isolated, therefore also let
denote that
y is an object that is both isolated and composed of a set X (of
xs).
So far, partness (the
relation) has not been defined. The definition of partness depends on what condition must be met for objects to be associated as parts. This is the Van Inwagen [
30] special composition question: “what constitutes being a part; what connection or relationship qualifies as ‘partness’?” Specifically, we need a criterion for “restricted composition” that is relevant to the question of separating internal from external in terms of causation. For this, define causation as a binary relation:
, specifying that the state of object
y is strictly determined by the state of object
x. With this, we can define a transitive closure for causation (transitive closure is the minimal transitive binary relation R on a set X).
First, note that any relation R on a set X is transitive iff
, whenever
and
then
. The conditions for a transitive closure can then be written as follows [
31] (using the notation
to represent a transitive relation): (i) if
(ii) if
(iii) nothing is in
unless by (i) and (ii).
Next, if R is specified as the C relation (from above), then (iii) specifies all the causal relations among members of a set , so that no relation can be causal. This has the effect of causally isolating the elements of as well as ensuring that they are causally related to one another.
Finally, let Y be the set of elements that are included in a transitive causal closure , where is the condition for association as parts: x is a part of y. Under these restrictions, mereologically, the elements of Y are the sum of an object y and . This means that the transitive closure for causation meets the requirement for formally separating internal from external (task 2). Since the relations in the closure are defined to be causal, this achieves task 3 as well. An object (agent) with the property of transitive causal closure among its parts is a causally autonomous system. All that is missing is a way to ensure that the agent is a cause of itself from the beginning of its existence, which requires it to be self-constructing. That will next be addressed with a more concrete example.
2.2. The Kantian Whole as a Material System
A system composed of parts, each of whose existence depends on that of the whole system is here termed a “Kantian whole”, the archetypal example being a bacterial cell [
32]. The origin of this terminology lies in Immanuel Kant’s definition of an organised whole [
33]. To make the closure condition concrete and include an answer to Strawson’s [
20] “Basic Argument” it will now be narrowed to a requirement for self-construction, since this implies the embodiment of self with the pattern-information that will then produce the agents behaviour (i.e., we require strictly constitutive autonomy as defined by Froese et al. [
22]). In other words, we are to consider a cybernetic system that, by constructing itself materially, determines its transition rules, by and for itself (material self-construction may not be essential to ensuring self-determination, but assuming that the cybernetic relations embodied in it are essential, we may proceed without loss of generality). An autocatalytic chemical reaction network with organisational closure (and this is also what Kauffman [
21] considered a Kantian whole) is an anabolic system able to construct itself [
34].
Hordijk and Steel [
34] and Hordijk et al. [
35] define their chemical reaction system by a tuple
, (their symbols) in which
X is a set of molecular types,
a set of reactions and
C a set of catalytic relations specifying which molecular types catalyse each member of
. The system is also provided with a set of resource molecules
, freely available in the environment, to serve as raw materials for anabolism (noting that whilst we are defining an organisational closure, we may (and indeed must) permit the system to be materially and thermodynamically open). The autocatalytic set is that subset of reactions
, strictly involving the subset
, which is:
This definition of an autocatalytic set is an application of the broader mathematical concept of closure and more specifically of transitive closure of a set, since when the autocatalytic set is represented as a network (of reactions), this network has the properties of transitive closure. The concept of autocatalytic set has been implemented in experiments for exploring aspects of the origin of life (e.g., the GARD system simulating “lipid world” [
36]). Clearly with the two conditions for an autocatalytic set met, everything in the system is made by the system, but there is a more important consequence. The system is made from the parts (only) and can only exist if they do. Organisational closure of this kind has been identified as a general property of individual organisms [
37], many biochemical sub-systems of life [
21] and embryonic development [
38].
As it is defined above, living systems fulfil the closure condition, but can we conceive of a non-living system also reaching this milestone? Von Neumann’s [
39] self-replicating automata show that some purely informational (algorithm) systems have the capacity to reproduce within their non-material domain, but they cannot yet assemble the material parts necessary, nor can they build themselves from basic algorithmic components (they rely on a human programmer to make the first copy). What is needed for the physical implementation of a Kantian whole is the ability to “boot-strap” from the assembly of simple physical components to reach the point of autonomous replication (i.e., the system must be autopoietic [
37,
40]. This is necessary to answer Strawson’s [
20] “Basic Argument”: that for deep free-will an entity must be responsible for shaping its own form and it provides a motivation for rejecting dualism (the idea that the “mind” is not created from the material universe).
2.3. Emergence and Downward Causation
Considering the forgoing, we might ask what is responsible for making an autopoietic system (e.g., an organism); is it the components themselves, or is it the organisational system. We might further ask: in either case, what really is the “system”. Cybernetics provides an answer to the second question, in that the system is the organisational pattern-information embodied in a particular configuration of interactions among the component parts. Because it is abstract of its material embodiment, it is “multiply realisable”, i.e., composed of members of functionally equivalent parts (see Auletta et al. [
41]; and Jaeger and Calkins [
42] for biological examples). It is not the identity of the components that matters, rather it is the functions they perform (e.g., a digital computer may be embodied by semiconductor junctions, or water pipes and mechanical valves, without changing its identity). Crucially, “function” is defined by a relationship between a component and the system of which it is a part. According to Cummins [
43], “function” is an objective account of the contribution made by a system’s component to the “capacity” of the whole system. At least one process performed by the component/s is necessary for a process performed by the whole system. This implies that the function of a component is predicated on the function of the whole. This definition was recently modified to more precisely specify the meaning of “capacity” and of whole system, thus: “A function is a process enacted by a system A at organisational level
L which influences one or more processes of a system B at level
, of which A is a component part” [
44].
In this context, organisational level means a structure of organisation that is categorically different from those above and below in the hierarchy because it embodies novel functional information (levels may be ontological or merely epistemic in meaning: that is an open debate in philosophy). The self-organisation of modular hierarchy has been described as a form of symmetry-breaking phase transition [
45], so the categories either side are quantitatively and qualitatively different. Organisational levels were defined precisely in terms of meshing between macro and micro dynamics (from partitioning the state-space of a dynamic system) by Butterfield [
46] and also using category theory to specify supervenience relations and multiple-realisability among levels by List [
47]. Neither definition, though, deals specifically with the phenomenon of new pattern-information “emerging” from the organisation of level
L components at level
, which is responsible for the emergence of new phenomena.
Ellis [
48] shows that a multiply realisable network of functions, self-organised into a functional whole, emerges to (apparently) exercise “downward causation” upon its component parts [
48,
49]. The organisational structure is selecting components from which to construct itself, even though it is materially composed of only the selected components. Since it is purely cybernetic (informational) in nature, the downward control is by pattern-information [
42,
48] which transcends the components from which it is composed. The pattern-information arises from, and is embodied by, the interactions among the components, and for these reasons it was termed a “transcendent complex” by Farnsworth et al. [
50]. Examples are to be found in embryonic development, where a growing cluster of cells self-organises using environmental signals created by the cells taking part [
51] and the collective decision making of self-organising swarms (e.g., honey bees in which the hive acts as a unity [
52]).
There is something significant here for those who conflate determinism with causation. All causal paths traced back would be expected to lead to the early universe. Despite the appearance of near maximum entropy from the uniformity of background microwave radiation, there is broad agreement that the entropy of the early universe was low and its embodied pattern-information (complexity) could not account for the present complexity, including living systems [
53]. Novel pattern-information has been introduced by selection processes, especially in living systems, for which Adami et al. [
54] draw the analogy with Maxwell’s demon. Selection is equivalent to pattern matching, i.e., correlation, and is accompanied by an increase of information. Since its beginning, the entropy of the universe has been increasing [
53] and some of this has been used as a raw material for transformation into pattern-information. This is achieved by creating the “order” of spatial correlation through physical self-assembly (atoms into molecules into molecular networks into living systems). This self-assembly embodies new information in the pattern of a higher level structure through the mutual provision of context among the component parts [
3]. The process of self-assembly is autonomous and follows a boot-strap dynamic, so it provides a basis for answering Strawson’s [
20] “Basic Argument” in which the putative agent of free-will is an informational (pattern) structure of self-assembly.
2.4. Purpose and Will
Much of the literature on downward causation uses the idea of “purpose”, though many are uncomfortable with its teleological implication. The aim of this section is to form a non-teleological account of purpose and its connection with will in non-human agents.
Cause creates correlation (usually, but not necessarily, in a time-series): the pattern of any action having a cause is correlated with its cause. An action without cause is uncorrelated with anything in the universe and accordingly considered random. If an action is fully constrained, then its cause is the constraint. Thus, freedom from at least one constraint allows the cause to be one of either: random, or exogenous control or agent control (in which “control” means non-random cause). By definition the cause is only taken to be the agent’s will if it originated in agent control. Correlation alone, between some outcome variable
x and some attribute
a of the agent, is not sufficient to establish will: (a) because correlation has no direction (but metrics such as “integrated information” [
55] can resolve direction) and (b) because
a may itself be random in origin and thereby not of the agent’s making. Marshall et al. [
56] showed that cause can be established at the “macro” level of agent (as opposed to the “micro” level of its components) using an elaboration of integrated information, so the pattern in
x can be attributed to agent-cause. Because the agent-based cause could be random ((b) above), we must form and test a hypothesis about the effect of
x on the agent before we can attribute the cause to the alternative of agent-will. The hypothesis is that the effect of
a on
x is to increase the overall functioning
F of the agent. If this were true, then to act wilfully is to reduce the entropy of
x, by increasing the probability of an outcome
where
(and
is the average
F). That means that the mutual information between a wilful action
at time
t and the resulting function
,
is greater than zero. This mutual information between action and future functioning is taken to imply a “purpose” for the action, so purpose is identified by the observations that:
where
r is a random (comparator) variable. This is clearly an observational definition and is in some way analogous to the Turing test, but it is a test for purpose rather than “intelligence”. It represents our intuition that if a behaviour repeatedly produces an objectively beneficial outcome for its actor, then it is probably deliberate (repeatedly harmful behaviour is also possibly deliberate, but all such actions are regarded as pathological and thereby a subject beyond the present scope).
To recap, for attributing the action to the agent’s will, we must at least identify a purpose so that Equation (
1) is true. The purpose is a pattern embodied in the agent, which acts as a template for actions of the agent that cause a change in future states (of the agent, its environment, or both). We may call this pattern a “plan” to attain an objective that has been previously set, where the objective is some future state to which the plan directs action. Specifically, let the objective be a state X (of the system or the world, etc.), which can be arrived at through a process P from the current state Y, then the purpose is a “plan” to transform
by the effect of at least one P and at least one function
F is necessary for the process P to complete.
The homoeostatic response to a perturbation, for example, has maintenance at the set-point as its purpose. Y is the perturbed state, F is some function of the internal system having the effect of causing a process P, i.e., some transition . In general there is more than one P and more than one F for achieving each. This results in a choice of which to use: it is a choice for the agent described by the system. To make a choice requires a criterion for choosing (else the outcome is random and therefore not a choice). The criterion for choosing is a “goal” G, consisting of one or more rules, which identify a location in a function describing the outcome (which we may call the objective function). In general, this location could be any and it is essential for freedom of will that it be determined by the agent of action alone. However, in practice it is most likely to be an optimisation point (in living systems, this is implied by Darwinian evolution and in designed systems, it is the basis of rational design). Therefore, narrowing the scope, but with justification, let us take the criterion for choosing to be a goal G, consisting of one or more optimisation rules. For example, of all the possible systems performing homoeostasis, the purposeful one is defined as enacting such that , with , where is an objective function for which the optimisation goal is satisfied, contingent upon the options (e.g., P proceeds as quickly as possible, or with minimum energy expenditure, etc.). Accordingly, “will” is defined by a purpose which is a plan to enact a process causing a transition in state, “as well as possible” (according to ), notwithstanding the earlier comment about pathological purposes. A free-will agent has a choice of transition and a goal which identifies the most desirable transition and the best way to enact it, from those available. These two choices can be united (by intersection), without loss of generality, to one choice of best transition.
One of the reasons for objecting to teleological terms such as “purpose”, “plan” and “goal” in relation to natural systems has been the belief that a plan implies a “designer”, the concept at the centre of the most famous battles between science and religion. This implication is not necessary and is rejected here (following the argument of Mayr [
57]). A plan is merely a pre-set program of steps taking the system from Y to X; it is the concept for which computation theory was developed. It may be designed (the work of an engineer), but also may have evolved by natural selection (which also supplies the goal, in which case it is a teleonomic system (sensu Mayr [
57]).
A plan, as an ordered sequence of transformations, is an abstraction of information from the physical system, which for free-will must be embodied within the system. A more subtle implication of “plan” is that as a path leading from Y to X, it is one among several possible paths: different plans may be possible, perhaps leading to different outcomes. There is a fundamental difference between this and the inevitability of a dynamic system which follows the only path it may, other than by the introduction of randomness. The reason is that for a dynamical system all the information defining its trajectory is pre-determined in the initial (including boundary) conditions and the laws of physics. The initial conditions constitute its one and only “plan”. If a system embodies pattern-information (by its structure) which constitutes a developed plan, then this pattern-information may direct the dynamics of the system along a path other than that set by the exogenous initial conditions (though we may consider the structure of the system to be a kind of initial condition). The point is that the embodied plan gives freedom to the system, since it “might be otherwise’; there could be a different plan and a different outcome. We see this in the variety of life-forms: each follows its own algorithm of development, life-history and behaviour at the level of the individual organism. The existence of a plan as abstract pattern-information is a pre-requisite for options and therefore freedom of action.
2.5. Goal, Master Function and Will Nestedness
Now let us complete the connections between will, goal and function. The previous argument reveals an important difference between downward and any other kind of causation (considered important by Walker [
58]): the former must always be directed by a purpose, for which we need to identify a goal (upward and same level causation are satisfactorily explained by initial conditions [
48]). Viewing entities and actions both as the consequence of information constraining (filtering) entropic systems, then the role that is taken by initial conditions in upward causation, is taken by system-level pattern-information (the transcendent complex [
50]) in downward causation. Since the goal G is a fixed point in an objective function
, it constitutes information (e.g., a homoeostatic set-point) that must be embodied in the agent’s internal organisation. Since the objective function
represents the overall functioning of the system (at its highest level), it matches the definition given by Cummins [
43] and Farnsworth et al. [
44]. The highest level function from which we identify the purpose of a system was termed the “master function” by Jaeger and Calkins [
42], so the will of an agent is instantiated in the master function. This then identifies
with “master function” and “will” with
.
Ellis [
48] identifies five types of downward causation, the second being “non-adaptive information control”, where he says “higher level entities influence lower level entities so as to attain specific fixed goals through the existence of feedback control loops...” in which “the outcome is not determined by the boundary or initial conditions; rather it is determined by the goals”. Butterfield [
46] gives a more mathematically precise account of this, but without elaborating on the meaning or origin of “goals”. Indeed, as both Ellis [
48] and Butterfield [
46] proceed with the third type: downward causation “via adaptive selection” they refer to fitness criteria as “meta-goals” and it is clear that these originate before and beyond the existence of the agent in question. Ellis [
48] describes meta-goal as “the higher level “purpose” that guides the dynamics” and explains that “the goals are established through the process of natural selection and genetically embodied, in the case of biological systems, or are embodied via the engineering design and subsequent user choice, in the case of manufactured systems”.
This suggests a nested hierarchy of goal-driven systems and for each, the goal is the source of causal power and as such may be identified as the “will” (free or otherwise). We may interpret the definition of “deep freedom” [
13] as meaning that an agent has at least two nested levels of causal power, the higher of which, at least, is embodied within the agent (as causal pattern-information). This concept may be formalised after introducing the discrete variable “will-nestedness”
which counts the number of levels of causal power exercised over a system, from within the agent as a whole (i.e., at the level of master function), the
-th level being the highest-level internal cause of its actions.
Among organisms in general, the master function specifies the criteria by which the organism is to assess its possible future reactions to the environment. It is so much an integral part of the organism that without it, the organism would not exist. However, it was not chosen by the organism (in the sense of deep free-will) because it was created by evolutionary filtering and inherited from its parent(s); as all known life has been created by the previous generation copying itself. For single celled organisms the biological master function is to maximise their cell count by survival and reproduction, but in multicellular organisms, this master function exists, by definition, at the level of the whole organism (the unconstrained drive to proliferate a single cell line leads to cancer). Organisms with a central nervous system, regulated by neuro-hormone systems, with their corresponding emotions, can implement more complex (information rich) and adaptable (internally branched) algorithms for the master function, which may include will-nestedness
. In humans, this is taken to such an extent that the biological master function may seem to have been superseded (but the weight of socio-biological evidence may suggest otherwise [
59,
60]).
2.6. The Possibility of Choice and Alternative Futures
So far I have identified organisational-closure and the internal generation of a goal-based plan as prerequisites for free-will, but have not yet addressed the “alternative futures” problem relating to an agent constructed from elemental components that necessarily obey physical determinism. List [
18] provides a philosophical argument for meeting this requirement, constructed from supervenience and multiple realisation of an agent in relation to its underlying (micro) physical level: “an agent-state is consistent with every sequence of events that is supported by at least one of its physical realizations” [
18]. He shows that this may apply not only to multiple micro-histories up to
t, but in principle includes subsequent
sequences at the micro-level, which may map to different agent states and therefore permit different courses of action at the (macro) agent-level. To explain: for any given time
t, the macro-state
is consistent with a set of micro-states
, at least one of which
may lead (deterministically) to a new state
at
, with which a different macro-state
is consistent, thus giving the agent a choice of which micro-state history to “ride” into
(this idea is developed with rigour by List [
18], and illustrated with “real-world” examples; it is the basis on which he concludes that agents may be “free to do otherwise”, despite supervening on deterministic physical processes).
Alternative futures may be produced at multiple levels of system organisation within a hierarchical structure, by re-applying the principles identified by List [
18] for each level of macro-micro relations. For any system level
L to have the potential for alternative futures, it must have the attributes of an “agent-level”: supervenience and multiple realisation such that pattern-information with causal power emerges at level
L from
: i.e., a transcendent complex exists at level
L. However, this does not necessarily give free will to a system of that level, since for that, it must be organisationally closed. If it were not so, we would not be able to identify the system at level
L as an entity to which free-will could be ascribed. Thus will-nestedness cannot be attributed to levels of organisation below that of the Kantian whole. Since the Kantian whole is, by definition, the highest level of organisation to which free-will may be ascribed (any causal power beyond it rules out its free will), then will-nestedness can only apply at the level of the Kantian whole. Given this, the will-nestedness must be constructed from purely organisational, i.e., pattern-informational and therefore be purely computational in nature. This is an important deduction: free-will can only be an attribute of a Kantian whole and it can only result from the cybernetic structure at the level of the Kantian whole.