Abstract
This paper presents an application of Approximate Entropy (ApEn) and Sample Entropy (SampEn) in the analysis of heart rhythm, blood pressure and stroke volume for the diagnosis of vasovagal syndrome. The analyzed biosignals were recorded during positive passive tilt tests—HUTT(+). Signal changes and their entropy were compared in three main phases of the test: supine position, tilt, and pre-syncope, with special focus on the latter, which was analyzed in a sliding window of each signal. In some cases, ApEn and SampEn were equally useful for the assessment of signal complexity (p < 0.05 in corresponding calculations). The complexity of the signals was found to decrease in the pre-syncope phase (SampEn (RRI): 1.20–0.34, SampEn (sBP): 1.29–0.57, SampEn (dBP): 1.19–0.48, SampEn (SV): 1.62–0.91). The pattern of the SampEn (SV) decrease differs from the pattern of the SampEn (sBP), SampEn (dBP) and SampEn (RRI) decrease. For all signals, the lowest entropy values in the pre-syncope phase were observed at the moment when loss of consciousness occurred.
1. Introduction
Syncope is a temporary self-regressing loss of consciousness, usually resulting in a fall. It is assumed that the direct cause of syncope is the short-term reversible global cerebral hypoperfusion. There are three types of syncope: cardiac, orthostatic and neuro-cardiogenic [1]. The causes of cardiac syncope include arrhythmia with slow or fast heart rhythm or organic heart disease (atrium myxoma, myocardial infarction). Patients suffering from cardiac syncope require insightful diagnostics and immediate treatment. The main cause of orthostatic syncope is primary or secondary autonomic failure, resulting from drug intake or dehydration (due to bleeding, diarrhoea or vomiting). The neuro-cardiogenic type includes vasovagal syncope. This is the most common type of syncope [2]. Vasovagal syncope takes place usually due to a long time upright tilt, especially in stuffy rooms or after vein puncture, strong stress or emotions (such as pain and fear). Loss of consciousness might be preceded with a sensation of sudden strong weakening, occurrence of scotoma, nausea, headache or dizziness, sweating or heart palpitations. Common symptoms also include seizures indicative of deep brain ischaemia, secondary to hypotonia and bradycardia. Young people usually have a normal vasovagal history, while elderly people tend to manifest other atypical symptoms.
The exact mechanism of vasovagal syncope is still disputable. While there are some theories explaining the etiology of vasovagal syndrome [3,4,5,6], the main cause remains unknown. Moreover, there is no commonly accepted gold standard diagnostic procedure for vasovagal syncope.
The typical diagnostics for neuro-cardiogenic syncope are based on the patient’s medical history and the results of Head Up Tilt Test (HUTT). Typically, HUTT is performed with a Task Force Monitor device. The Task Force Monitor (TFM) is a device dedicated to the assessment of syncope and hemodynamic and autonomic nervous system dysfunction. The tilt test assesses patient response to orthostatic stress. The patient lies on a table that can tilt to different angles (a 60 to 90 degree angle). A clinician performs the test according to a protocol dedicated to a type of diagnosed dysfunction. In case of syncope, it can be the Westminster protocol, Italian protocol or other protocols. In each protocol, the time in supine position, tilt position and the angle is precisely defined. During the test, the patient’s electrocardiography (ECG), impedance cardiography (ICG), and blood pressure are monitored. All biosignals are recorded and used for further analysis. The observation of the signal changes (especially concerning heart rate and blood pressure) allows classification of the observed neuro-cardiogenic reaction, according to the criteria VAsovagal Syncope International Study (VASIS) [1].
In our study, HUTT was performed with the Task Force Monitor device. The recorded signals were then analyzed in two settings: supine position and tilt, using three windows of 250 consecutive heart beats selected for each body position.
Besides the typical analysis, i.e., comparing mean values of the parameters in each window, we focused on the assessment of the pre-syncopal changes in signal complexity.
There are many investigations and articles dedicated to heart rate variability and heart rate complexity [7,8,9]. It is generally accepted that the loss of complexity of ECG signals is a pathological finding [10,11,12,13]. Our study also demonstrates that the loss of complexity of biosignals is strictly related to the occurrence of neuro-cardiogenic reactions in HUTT. In the typical analysis of syncope, attention is focused on ECG signals and systolic blood pressure. We extended the assessment of the system complexity to analysis of the ICG signal, specifically to stroke volume (SV) determined from the ICG signals. The applications of hemodynamic parameters determined from ICG signals for the diagnosis of syncope are still a subject of discussion [14,15,16,17,18]. Therefore, our study was an attempt to assess the diagnostic usefulness of stroke volume (SV) complexity changes occurring simultaneously with changes in (RR-intervals) RRI-extracted from ECG, systolic blood pressure (sBP) and diastolic blood pressure (dBP) complexity for the diagnosis of syncope.
We used entropy as a measure of signal complexity: Approximate Entropy (ApEn) and Sample Entropy (SampEn) [19,20]. Changes in the entropies (ApEn, SampEn) were already reported in some cardiovascular researches [21,22,23,24], postural control investigations [25,26], physical activity measures [27,28] and in analysis of cardiodepressive vasovagal syncope [24]. The presented analysis of changes in the complexity of joint signals of ECG, ICG and blood pressure during passive provocation of the neuro-cardiogenic reaction will add to further understanding of the course and mechanism of vasovagal syndrome.
2. Materials and Methods
2.1. Approximate Entropy and Sample Entropy
Entropy is a well-known tool used for assessment of dynamic systems complexity. Approximate Entropy (ApEn) is a measure of the complexity proposed by Pincus [19]. The greater irregularity and unpredictability of the system, the greater the entropy. The main idea of the calculation of ApEn is based on measuring the likelihood that similar sequences of points in a time series remain similar for increment sequences. For the analysis of time series with length N, the length of the basic sequence was named as m and the similarity criterion as r. The algorithm for ApEn calculation is well known and its detailed description is available in the literature [19,29,30,31,32]. Here, we only describe it briefly.
Given a time series with length N:
the vector is defined:
where and a set of vectors is formed:
The vectors are similar if they fulfill the following similarity criterion:
where
Then, the sequence is defined
and
In the next step and are analogically calculated and finally the Approximate Entropy is defined according to the following formula:
For large values of N and after some modifications [30,31,32,33,34,35,36], Formula (7) can finally be expressed as:
The presented algorithm was extensively used in many cardiovascular studies [33,34,35,36], but it is known to have some limitations. First of all, ApEn counts a self-match of vectors and hence generates a bias towards regularity [20,30]. Such a limitation is essential in order to avoid the occurrence of in Formula (8) [37,38]. The occurrence of bias results in a strong dependence of ApEn on the quantity of N data points. This limitation is important in case of short data sets [20,37]. The recommended data sets for calculating ApEn for a given m is: points [39]. Another limitation is that ApEn is sensitive to parameters (m,r). In consequence, ApEn is useful as a measure for comparing data sets only for fixed parameters (m,r).
The described limitations became an inspiration for Moormann and Richmann to improve this idea of entropy calculation, by proposing the Sample Entropy (SampEn) [20]. The SampEn (m, r, N) statistic does not count self-matches. It also has better theoretical convergence than ApEn, especially for random numbers with known probabilistic properties and short data, and renders better relative consistency than ApEn. The in-depth description of the comparisons of both of these statistics can be found in the literature [20]. Despite elementary differences between ApEn and SampEn, both statistics are extensively used in cardiovascular physiology [20,22,23,27,28,29,30,31,33,34,35,36,40,41,42]. In this paper we also show the possible applications of ApEn (m, r, N) and SampEn (m, r, N) for the analysis of physiological signals.
2.2. Study Group
The study population consisted of 57 patients: 43 women (age: 35.6 ± 16.2 years) and 14 men (age: 41.7 ± 15.6 years). The youngest female and male participants were both 18 years old and the oldest were 66 and 59 years old, respectively. In all cases, the indication for diagnostic work-up was recurrent syncope. For the purpose of this study, patients with heart and brain diseases were excluded and only patients suffering from neuro-cardiogenic syncope were considered eligible. The patients received full information on the diagnostic methods to be used and gave their informed consent for participation in the study.
2.3. Measurements
In each case, the Head Up Tilt Test (HUTT) was performed with a Task Force Monitor system device (CNSystem, Graz, Austria). All measurements were conducted in the morning, in a quiet room with dimmed lighting and with patients fasting prior to the test. The used protocol was in accordance with the modified Westminster protocol [1]: the patient remained 20 min in the supine position and then was tilted to 60 degrees in 5 s. The passive upright tilt lasted 45 min or until syncope. In three cases after 45 min the syncope did not occur, but the decreasing of the systolic pressure occurred and at the end of the passive upright tilt the systolic pressure was below 100 mmHg. With this indication of onset of the neuro-cardiogenic reaction, the decision was made to prolong the passive tilt phase by another 15 min. In this additional time, each of the three patients eventually experienced syncope. The end point of the tests was full syncope or a pre-syncope condition achieved without pharmacological provocation. The minimal time from the tilt to syncope was 3 min, while the maximal time was 52 min. Average time to syncope after tilt was about 20 min. Based on the HUTT results for each patient, the neuro-cardiogenic reaction was classified according to the VASIS classification [14].
2.4. Data Analysis and Statistical Methods
The HUTT performed with the TFM allows one to record three basic physiological biosignals. The most important is a high resolution ECG signal (2-chanels with the sampling frequency 1000 Hz). From ECG, we extracted the RRI and on such samples we conducted our analysis. The second signal is the signal of sBP and dBP measured continuously. The third signal is ICG. The ICG signal allows us to measure noninvasively the total electrical conductivity of the thorax and its changes in time. Based on the impedance curve, the TFM system determines a time interval from opening to closing of the aortic valve (LVET) and stroke volume (SV). All mentioned signals are used to determine the hemodynamic parameters like cardiac output (CO) and total peripheral resistance (TPR). The algorithms for determining the parameters are implemented in the TFM system. All parameters are presented with beat to beat time intervals; hence the cardiac rhythm indicates the measuring time points. The TFM system allows us to export filtered and not filtered raw data. We exported both types of data, compared them and finally we used the filtered data. All the signals were carefully checked by a clinician. The abnormal data did not exceed 5% of all data obtained during the measurement.
We focused our attention on the basic parameters: RRI, sBP, dBP, SV. In Figure 1 we show an example of recorded parameters and we marked three specific stages of the HUTT: I-supine position, II-tilt, III-syncope. We chose 250 beat-intervals of data from each stage for our analysis. The intervals were named as 250 beat windows, and we marked them as boxes: in the middle of the supine position, when tilt started, and just before the syncope.
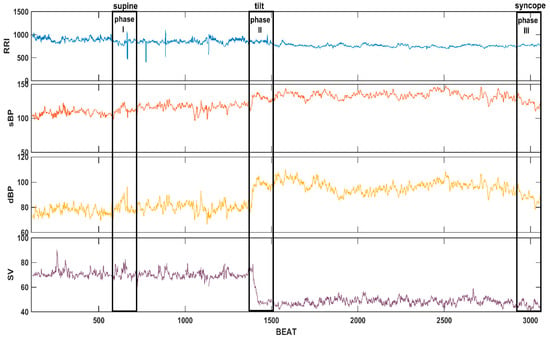
Figure 1.
The recorded parameters: RR-intervals (RRI), systolic blood pressure (sBP), diastolic blood pressure (dBP), stroke volume (SV) and the phases of the measurements (I, II, III) used for calculations.
Firstly we compared the values of RRI, sBP, dBP and SV between registration windows. Then we determined the ApEn and SampEn of the parameters for each window and in the next step we compared the entropies between the windows. In the last stage of our analysis, we focused only on the third window with the data recorded before syncope. We determined the entropies in a sliding window consisting of 100 beats. The window was sliding forward with a 1 beat step. The idea of the sliding windows is as follows:
Let us name the chosen biosignal (RRI, sBP, dBP, SV) as
Let us define a set W of the p-points of the phase III as:
For the window of the width k we define a subset X as:
Now let us define a set Y:
where , SampEn is calculated for a given m and r.
Let us define a function:
The values of are the subsequent values of the entropy calculated “point-by-point” just before the syncope. In our investigations we chose p = 250, k = 100. The obtained vector of entropies (for each signal) shows the changes of the signal complexity before the syncope.
The statistical analysis was performed with nonparametric tests, because the statistical conditions for parametric methods were not fulfilled (normal distribution, variance equality). The comparisons of the parameters were performed with the Friedman test and the post hoc multicomparison test. For all calculations, the statistical significance level was α = 0.05. The entropies (ApEn and SampEn) were determined with the algorithm from Physionet [32]. All calculations were performed with Matlab R2014.
3. Results
3.1. Comparisons of Parameters for Selected HUTT Stages
In Section 2.4, we indicated three phases of the tilt test that were used in our investigations (Figure 1). Figure 2 presents box plots for each analyzed parameter in the three phases. We also compared values of the parameters using the Friedman test and multicomparison post hoc test. Lines linking the boxes represent statistically significant differences between the parameters. The boxes indicate medians and quartiles.
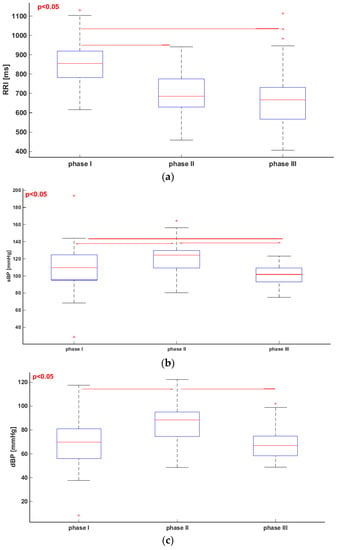
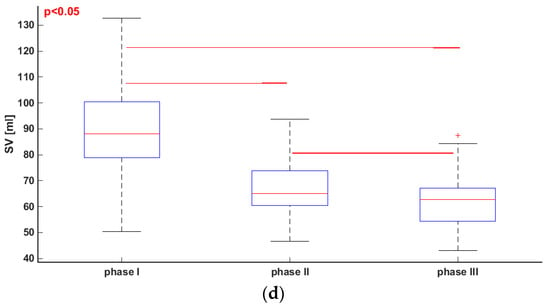
Figure 2.
Friedmann test and multicomparison post hoc test in phase I, II and III of tilt test. (a) RRI; (b) sBP; (c) dBP; (d) SV.
Figure 3 and Figure 4 present box plots for comparisons of the ApEn and SampEn calculated for RRI, sBP, dBP and SV in the 3 phases (I, II, III) of the tilt test. For our calculations we assumed: , , , as proposed in the literature and validated by other investigators for RRI analysis [19,20].
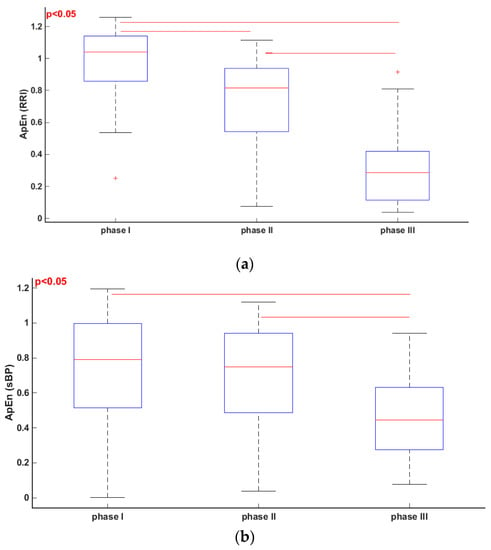
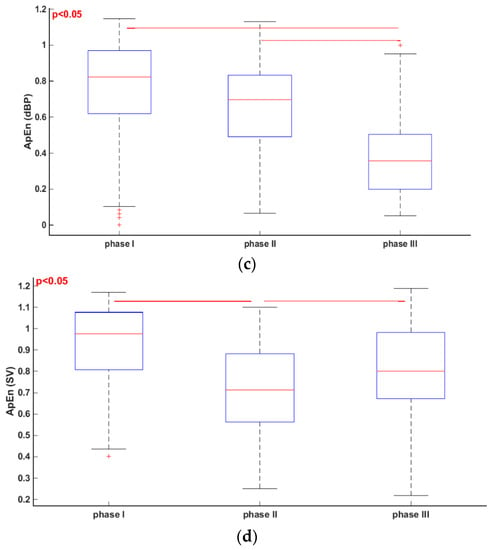
Figure 3.
Friedmann test and multicomparison post hoc test in phase I, II and III of tilt test. (a) ApEn (RRI); (b) ApEn; (sBP); (c) ApEn; (dBP); (d) ApEn (SV).
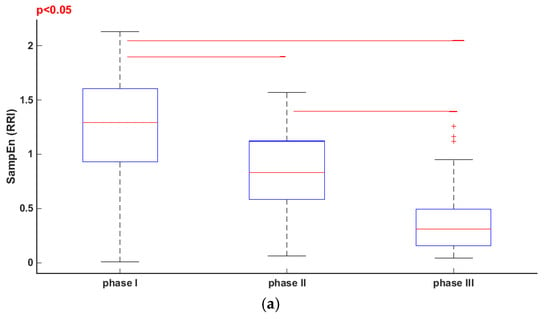
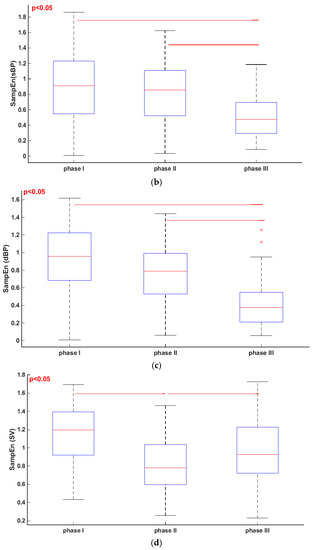
Figure 4.
Friedmann test and multicomparison post hoc test in phase I, II and III of tilt test. (a) Sample Entropy (SampEn) (RRI); (b) SampEn (sBP); (c) SampEn (dBP); (d) SampEn (SV).
Table 1 shows mean values and standard deviation of the parameters and entropies in all 3 phases of the tilt test.

Table 1.
Descriptive statistics for phase I, II and III of tilt test.
3.2. Sample Entropy in Sliding Windows
The main changes in the parameters occur in phase III, that ends with the occurrence of syncope. As we mentioned previously, the most important indicator of syncope is a decrease in sBP and dBP. We analyzed the occurrence of the maximum and minimum values of sBP and dBP in phase III. We also determined the beat number for maximum values of sBP and dBP (Tmax) and the beat number for the minimum values (Tmin). Mean values of these parameters are presented in Table 2.

Table 2.
The characteristics of systolic blood pressure (sBP) and diastolic blood pressure (dBP) changes in the pre-syncope phase (phase III).
Afterwards, we focused on changes of the dynamics of entropy in the pre-syncope phase (III). In a sliding window consisting of 100 beats, we determined SampEn only, since such a window width does not allow reliable ApEn calculations. Figure 5 presents an example of SampEn changes for RRI, sBP, dBP and SV. In each case, SampEn was determined for , , . The window was sliding forward with a 1 beat step each time. According to our observations, syncope was directly preceded with a decrease in the values of SampEn. Table 3 presents the average values of maximum and minimum SampEn (, ). We also determined for each patient the time ( between the time point of and . The average time ( is also included in Table 3.
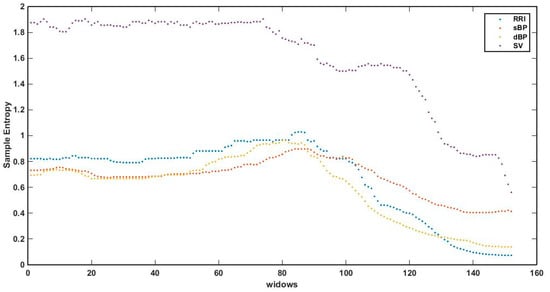
Figure 5.
Sample Entropy (SampEn (0.2 SD, 2, 100)) in a 100 beats sliding window in phase III.

Table 3.
The characteristics of SampEn changes in a 100 beats sliding window in the pre-syncope phase (phase III).
The character of the decrease was similar for each patient. The average values of the entropies (SampEn) for the analyzed parameters (RRI, sBP, dBP, SV) with the SEM (standard error) in each sliding window are shown in Figure 6.
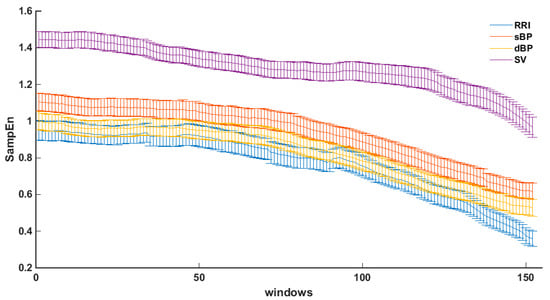
Figure 6.
The average SampEn with standard error (SEM) in the pre-syncope phase (phase III) in sliding windows.
4. Discussion
The results presented in the previous section, based on the analysis of the changes of RRI, sBP, dBP and SV in HUTT, confirm the theory of vasovagal syndrome described in the literature [18,24,43]. As expected, patients with vasovagal syndrome had normal orthostatic reaction on HUTT: heart rate acceleration occurring just after the tilt (RRI in phase II significantly shorter than in phase I (p < 0.05)) and statistically insignificant heart rate changes in phase III, while the deceleration of heart rhythm mostly occurred after syncope.
We also observed another typical manifestation of syncope—a decrease in systolic and diastolic blood pressure (p < 0.05 for comparison of sBP and dBP in phase II vs. III). Loss of consciousness was associated with the lowest value of blood pressure in phase III of HUTT. The mean maximum value of sBP was 133 ± 3.13 mmHg and the mean minimum value of sBP was approximately 63 mmHg, while the mean maximum and minimum value of dBP was about 88 mmHg and 36 mmHg, respectively. The decrease in sBP and dBP lasted for approximately 160 and 172 beats, respectively. We also observed a statistically significant decrease in stroke volume (SV) just after the tilt and before the loss of consciousness. The decrease in SV after tilting was also reported by other researchers [44,45,46]. The decrease in SV before the loss of consciousness directly preceded syncope.
As previously mentioned, entropy had already been used by some researchers for assessment of the changes of RRI complexity in pathological states. In our investigations we also showed the fact that in vasovagal syndrome the entropy of RRI decreases shortly before the loss of consciousness occurs. The difference between the entropy in supine position (II) and during syncope (III) is statistically significant (Table 3, Figure 3). It is also interesting that while the changes of RRI do not meet statistical significance, the changes of the entropy of RRI are significant. In phase II (tilt), the values of SampEn (RRI) reached the level of 1.24 and such entropy characterises a random time series. In the syncope phase (III), the values of the entropies were about 0.36 and such a level corresponds to a dynamic system with periodic evolution. Concerning cardiac rhythm, in vasovagal syndrome, loss of consciousness is predicted by the loss of complexity of RRI rather than the changes of RRI. In the literature, this phenomenon was explained in several ways including that the drop in complexity of RRI is connected with the sympathetic activation or that the main cause of the loss of complexity is the change in vagal activity. We think that both of these (sympathetic activation and vagal activity) modulates the complexity of the autonomic nervous system and these pathological or oversensitive interactions between the sympathetic and parasympathetic branches cause the imbalance in the autonomic reaction to HUTT. We also observed that the entropy of sBP and dBP decreases in phase III. The entropy of sBP decreases approximately 82 beats before syncope and the loss of consciousness is strictly connected with the minimum value of SampEn (sBP). The entropy in the tilt phase (II) reached the level of 0.82 and it dropped to about 0.52 just before the syncope. Such values indicate that the complexity of the sBP signal just after the tilt is similar to chaotic systems, while directly prior to syncope it resembles periodic evolution. Our observations for dBP are similar as for sBP (Table 3, Figure 3). The SampEn (dBP) in phase II and III was about 0.91 and 0.41, respectively.
Another important issue is the analysis of SV. In our investigation, the entropy of SV was decreasing in subsequent phases (I, II, III), but the minimal entropy (SampEn (SV)) occurred in phase II. The highest loss of complexity of SV was observed just after the tilt (0.8). In the syncope phase, the SampEn (SV) increased to 0.95. The values of SampEn (SV) during the tilt differed significantly in comparison with those registered in the supine position and before syncope.
In the numerical calculations, we also compared the complexity of the signals with Approximate Entropy (ApEn) and Sample Entropy (SampEn). Our results remain in line with those previously described in the literature [24,30,47]. In the analysis of signal complexity in a 250 beat window, ApEn is as effective as SampEn and both of the entropy measures lead to identical conclusions despite the values of ApEn being higher than the values of SampEn. As previously explained, this difference arises from the properties of ApEn.
Finally, we also performed the analysis of changes of entropy in the pre-syncope phase. Using a sliding window of 100 beats, we observed changes in the entropy dynamics. The applied window width was obviously too short for ApEn calculations; therefore we analyzed only the SampEn. Some examples of typical changes of SampEn (RRI), SampEn (sBP), and SampEn (SV) are shown in Figure 6. The arrival of loss of consciousness was signaled by a decrease in SampEn (RRI), SampEn (sBP) and SampEn (SV). The decrease in SampEn (RRI) preceded syncope by about 96 beats. Similarly, the decrease in SampEn (sBP) and SampEn (dBP) occured about 82 beats before syncope. The SampEn (SV) decrease was noted about 89 beats before the loss of consciousness, but the changes of SampEn (SV) are diagnostically as effective as changes in SampEn (RRI), SampEn (sBP) and SampEn (SV). The phase shift between the signals (SampEn (RRI) and SampEn (sBP), SampEn (dBP), SampEn (SV)) need deeper investigations. The number of analyses of heart rhythm and heart rate variability in patients with syncope showed that RRI does not have many characteristic features and strongly depends on the type of vasovagal reaction. In the pre-syncope phase (III), the values of SampEn (SV) were higher than SampEn (RRI), SampEn (sBP) and SampEn (dBP). The changes of SampEn (SV) were not as evident as in case of the other signals. This phenomenon requires further study. Analysis of more homogenous groups and the results of ApEn and SampEn between groups should be compared. We hope that the observed ApEn and SampEn results may show clearer associations with syncopy in further larger and more homogenous group studies and reflect the response to the orthostatic test. Extending our investigation to comparisons of our group with patients with a negative result of HUTT(-) may provide further evidence of the utility of using entropy features for the assessment of syncope.
This paper presents an application of entropy in the assessment of RRI, sBP, dBP and SV signal complexity for the diagnosis of vasovagal syndrome. We demonstrated that the complexity of heart rhythm, blood pressure and stroke volume decreases before syncope occurs. The loss of complexity measured as a change of entropy could possibly be an indicator of development of a neuro-cardiogenic reaction. Usually vasovagal syndrome is a mild disease with very typical symptoms and a good prognosis. Finding new parameters that differentiate the vasovagal response from atypical orthostatic hypotension or dysautonomic reaction is important because such reactions may be the first symptoms of neurological disorders such as primary or secondary autonomic failure, multiple systemic atrophy or Parkinson’s disease with autonomic failure, which have worse prognoses. Knowledge of the cause of syncope has a key role in the selection of treatment. Once the cause (bradycardia, hypotension) has been ascertained, the second goal is to assess the mechanism leading to syncope.
5. Limitations
Our analysis did not include the aspect of gender. The unequal proportion in gender reflects the occurrence of syncope in the general population [47,48]. We are also aware that the hemodynamic parameters and their complexity are age-dependent [49,50]. Accounting for gender and age in the analysis would require a breakdown of the study population into small subgroups, not allowing them to reach statistical significance. In further studies, we intend to focus on the possible gender- and age-related differences of biosignal complexity.
Acknowledgments
The study is funded by Collegium Medicum of Nicolaus Copernicus University and did not receive any external funding.
Author Contributions
A.P., E.K. and G.O. conceived and designed the experiments; A.P., E.K. performed the experiments; K.B. analyzed the data; K.B. wrote the paper. All authors have read and approved the final version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moya, A.; Sutton, R.; Ammirati, F.; Blanc, J.-J.; Brignole, M.; Dahm, J.B.; Deharo, J.-C.; Gajek, J.; Gjesdal, K.; Krahn, A.; et al. Guidelines for the diagnosis and management of syncope. Eur. Heart J. 2009, 30, 1–41. [Google Scholar]
- Parry, S.W.; Reeve, P.; Lawson, J.; Shaw, F.E.; Davison, J.; Norton, M.; Frearson, R.; Kerr, S.; Newton, J.L. The Newcastle Protocols 2008: An update on head-up tilt table testing and the management of vasovagal syncope and related disorders. Heart 2009, 95, 416–420. [Google Scholar] [CrossRef] [PubMed]
- Mosqueda-Garcia, R.; Furlan, R.; Tank, J.; Fernandez-Violante, R. The elusive pathophysiology of neurally mediated syncope. Circulation 2000, 102, 2898–2906. [Google Scholar] [CrossRef] [PubMed]
- Abboud, F.M. Neurocardiogenic syncope. NEJM 1993, 328, 1117–1120. [Google Scholar] [CrossRef] [PubMed]
- Flevari, P.P.; Livanis, E.G.; Theodorakis, G.N.; Mesiskli, T.; Zarvalis, E.; Kremastinos, D.T. Baroreflexes in vasovagal syncope: Two types of abnormal response. Pacing Clin. Electrophysiol. 2002, 25, 1315–1323. [Google Scholar] [CrossRef] [PubMed]
- Alboni, P.; Alboni, M.; Bertorelle, G. The origin of vasovagal syncope: To protect the heart or to escape predation? Clin. Auton. Res. 2008, 18, 170–178. [Google Scholar] [CrossRef] [PubMed]
- Heart Rate Variability. Available online: https://doi.org/10.1161/01.CIR.93.5.1043 (accessed on 19 May 2017).
- Denton, T.A.; Diamond, G.A.; Helfant, R.H.; Khan, S.; Karagueuzian, H. Fascinating rhythm: A primer on chaos theory and its application to cardiology. Am. Heart J. 1990, 120, 1419–1440. [Google Scholar] [CrossRef]
- Goldberger, A.L. Non-linear dynamics for clinicians: Chaos theory, fractals, and complexity at the bedside. Lancet 1996, 347, 1312–1314. [Google Scholar] [CrossRef]
- Algra, A.; Tijssen, J.G.; Roelandt, J.R.; Pool, J.; Lubsen, J. Heart rate variability from 24-hour electrocardiography and the 2-year risk for sudden death. Circulation 1993, 88, 180–185. [Google Scholar] [CrossRef] [PubMed]
- Pagani, M.; Lombardi, F.; Guzzetti, S.; Rimoldi, O.; Furlan, R.; Pizzinelli, P.; Sandrone, G.; Malfatto, G.; Dell’Orto, S.; Piccaluga, E.; et al. Power spectral analysis of heart rate and arterial pressure variabilities as a marker of sympatho-vagal interaction in man and conscious dog. Circ. Res. 1986, 59, 178–193. [Google Scholar] [CrossRef] [PubMed]
- Malliani, A.; Pagani, M.; Lombardi, F.; Cerutti, S. Cardiovascular neural regulation explored in the frequency domain. Circulation 1991, 84, 482–492. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, M.K.; Kannankeril, P.J.; Goldberger, J.J. Assessment of autonomic function in cardiovascular disease. Physiological basis and prognostic significance. J. Am. Coll. Cardiol. 2008, 51, 1725–1733. [Google Scholar] [CrossRef] [PubMed]
- Brignole, M.; Menozzi, C.; Del Rosso, A.; Costa, S.; Gaggioli, G.; Bottoni, N.; Bartoli, P.; Sutton, R. New classification of hemodynamics of vasovagal syncope: Beyond the VASIS classification. Analysis of the pre-syncopal phase of the tilt test without and with nitroglycerin challenge. Vasovagal Syncope International Study. Europace 2000, 2, 66–76. [Google Scholar] [CrossRef] [PubMed]
- Demarzo, A.P. Using impedance cardiography to detect asymptomatic cardiovascular disease in prehypertensive adults with risk factors. High Blood Press. Cardiovasc. Prev. 2013, 20, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Cybulski, G. Ambulatory Impedance Cardiography. The Systems and Their Applications, 1st ed.; Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2011; Volume 76, p. 150. [Google Scholar]
- Cybulski, G.; Strasz, A.; Niewiadomski, W.; Gąsiorowska, A. Impedance cardiography: Recent advancements. Cardiol. J. 2012, 19, 550–556. [Google Scholar] [CrossRef] [PubMed]
- Parry, S.W.; Norton, M.; Pairman, J.; Baptist, M.; Wilton, K.; Reeve, P.; Sutcliffe, K.; Newton, J.L. Impedance cardiography: A role in vasovagal syncope diagnosis? Age Ageing 2009, 38, 718–723. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar]
- Vikman, S.; Mäkikallio, T.H.; Yli-Mäyry, S.; Pikkujämsä, S.; Koivisto, A.M.; Reinikainen, P.; Airaksinen, J.; Huikuri, H.V. Altered Complexity and Correlation Properties of R-R Interval Dynamics Before the Spontaneous Onset of Paroxysmal Atrial Fibrillation. Circulation 1999, 100, 2079–2084. [Google Scholar] [CrossRef] [PubMed]
- Tuzcu, V.; Nas, S.; Borklu, T.; Ugur, A. Decrease in the heart rate complexity prior to the onset of atrial fibrillation. Europace 2006, 8, 398–402. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.G.; Yoo, C.S.; Yi, S.H.; Bae, J.H.; Kim, Y.J.; Park, J.S.; Hong, G.R. Prediction of Paroxysmal Atrial Fibrillation Using Nonlinear Analysis of the R-R Interval Dynamics Before the Spontaneous Onset of Atrial Fibrillation. Circ. J. 2006, 70, 94–99. [Google Scholar] [CrossRef] [PubMed]
- Graff, B.; Graff, G.; Makowiec, D.; Kaczkowska, A.; Wejer, D.; Budrejko, S.; Kozłowski, D.; Narkiewicz, K. Entropy Measures in the Assessment of Heart Rate Variability in Patients with Cardiodepressive Vasovagal Syncope. Entropy 2015, 17, 1007–1022. [Google Scholar] [CrossRef]
- Deffeyes, J.E.; Harbourne, R.T.; Stuberg, W.A.; Stergiou, N. Approxcimate entropy used to asses sitting postural sway of infants with developmental delay. Infant Behav. Dev. 2011, 34, 81–99. [Google Scholar] [CrossRef] [PubMed]
- Rhea, C.K.; Silver, T.A.; Hong, S.L.; Ryu, J.H.; Studenka, B.E.; Hughes, M.L.; Haddad, J.M. Noise and complexcity in human postural control: Interpreting the different estimations of entropy. PLoS ONE 2001, 6, e17696. [Google Scholar] [CrossRef]
- Cavanaugh, J.T.; Kochi, N.; Stergiou, N. Nonlinear analysis of ambulatory activity patterns in community-dwelling older adults. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2010, 65, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Sosnoff, J.J.; Goldman, M.D.; Motl, R.W. Real life walking impairment in multiple sclerosis: Preliminary comparison of four methods for processing accelerometry data. Mult. Scler. 2010, 16, 868–877. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.; Huang, W. Approximate entropy-statistical properties and applications. Commun. Stat. Theory Methods 1992, 21, 3061–3077. [Google Scholar] [CrossRef]
- Pincus, S. Approximate entropy as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Graff, B.; Graff, G.; Kolesiak, A. Entropia w badaniach zaburzeń rytmu serca. Mat. Stosow. 2008, 9, 46–52. [Google Scholar]
- PhysioToolkit. Available online: https://www.physionet.org/physiotools/ (accessed on 15 January 2017).
- Ferrario, M.; Signorini, M.G.; Magenes, G.; Cerutti, S. Comparison of Entropy-Based Regularity Estimators: Application to the Fetal Heart Rate Signal for the Identification of Fetal Distress. IEEE Trans. Biomed. Eng. 2006, 53, 119–125. [Google Scholar] [CrossRef] [PubMed]
- Graff, B.; Graff, G.; Kaczkowska, A. Entropy Measures of Heart Rate Variability for Short ECG Datasets in Patients with Congestive Heart Failure. Acta Phys. Pol. B Proc. Suppl. 2012, 5, 153–158. [Google Scholar] [CrossRef]
- Liu, C.; Liu, C.; Shao, P.; Li, L.; Sun, X.; Wang, X.; Liu, F. Comparison of different threshold values r for approximate entropy: Application to investigate the heart rate variability between heart failure and healthy control groups. Physiol. Meas. 2011, 32, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Sarlabous, L.; Torres, A.; Fiz, J.A.; Gea, J.; Martinez-Llorens, J.; Morera, J.; Jane, R. Interpretation of the approximate entropy using fixed tolerance values as a measure of amplitude variations in biomedical signals. IEEE Conf. Proc. Eng. Med. Biol. Soc. 2010, 2010, 5967–5970. [Google Scholar]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The Appropriate Use of Approximate Entropy and Sample Entropy with Short Data Sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef] [PubMed]
- Chon, K.; Scully, C.G.; Lu, S. Approximate entropy for all signals. IEEE Eng. Med. Biol. Mag. 2009, 28, 18–23. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. Heart Circ. Physiol. 1994, 266, H1643–H1656. [Google Scholar]
- Dawes, G.S.; Moulden, M.; Sheil, O.; Redman, C.W. Approximate entropy, a statistic of regularity, applied to fetal heart rate data before and during labor. Obstet. Gynecol. 1992, 80, 763–768. [Google Scholar] [PubMed]
- Fleisher, L.A.; DiPietro, J.A.; Johnson, T.R.; Pincus, S. Complementary and noncoincident increases in heart rate variability and irregularity during fetal development. Clin. Sci. 1997, 92, 345–349. [Google Scholar] [CrossRef] [PubMed]
- Fleisher, L.A.; Pincus, S.M.; Rosenbaum, S.H. Approximate entropy of heart rate as a correlate of postoperative ventricular dysfunction. Anesthesiology 1993, 78, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Koźluk, E.; Cybulski, G.; Piątkowska, A.; Zastawna, I.; Niewiadomski, W.; Strasz, A.; Gąsiorowska, A.; Kempa, M.; Kozłowski, D.; Opolski, G. Early hemodynamic response to the tilt test in patients with syncope. Clin. Res. 2014, 10, 1078–1085. [Google Scholar] [CrossRef] [PubMed]
- Zaidi, A.; Benitez, D.; Gaydecki, P.; Vohra, A.; Fitzpatrick, A. Haemodynamic effects of increasing angle of head up tilt. Heart 2000, 83, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.K.; Low, P.A.; Rea, R.F.; Lohse, C.M.; Hodge, D.O.; Hammill, S.C. Distinct hemodynamic profiles in patients with vasovagal syncope: A heterogeneous population. J. Am. Coll. Cardiol. 2000, 35, 1470–1477. [Google Scholar] [CrossRef]
- Bellard, E.; Fortrat, J.O.; Schang, D.; Dupuis, J.M.; Victor, J.; Leftheriotis, G. Changes in the transthoracic impedance signal predict the outcome of a 70 degrees head-up tilt test. Clin. Sci. (Lond.) 2003, 104, 119–126. [Google Scholar] [PubMed]
- Colman, N.; Nahm, K.; Ganzeboom, K.S.; Shen, W.K.; Reitsma, J.B.; Linzer, M.; Wieling, W.; Kaufmann, H. Epidemiology of reflex syncope. Clin. Auton. Res. 2004, 14, i/9–i/17. [Google Scholar] [CrossRef] [PubMed]
- Kenny, R.A.; Bhangu, J.; King-Kallimanis, B.L. Epidemiology of syncope/collapse in younger and older Western patient populations. Prog. Cardiovasc. Dis. 2013, 55, 357–363. [Google Scholar] [CrossRef] [PubMed]
- Ryan, S.M.; Goldberger, A.L.; Pincus, S.M.; Mietus, J.; Lipsitz, L.A. Gender- and age-related differences in heart rate dynamics: Are women more complex than men? J. Am. Coll. Cardiol. 1994, 24, 1700–1707. [Google Scholar] [CrossRef]
- Catai, A.M.; Takahashi, A.C.; Perseguini, N.M.; Milan, J.C.; Minatel, V.; Rehder-Santos, P.; Marchi, A.; Bari, V.; Porta, A. Effect of the Postural Challenge on the Dependence of the Cardiovascular Control Complexity on Age. Entropy 2014, 16, 6686–6704. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).