Specific and Complete Local Integration of Patterns in Bayesian Networks
Abstract
:1. Introduction
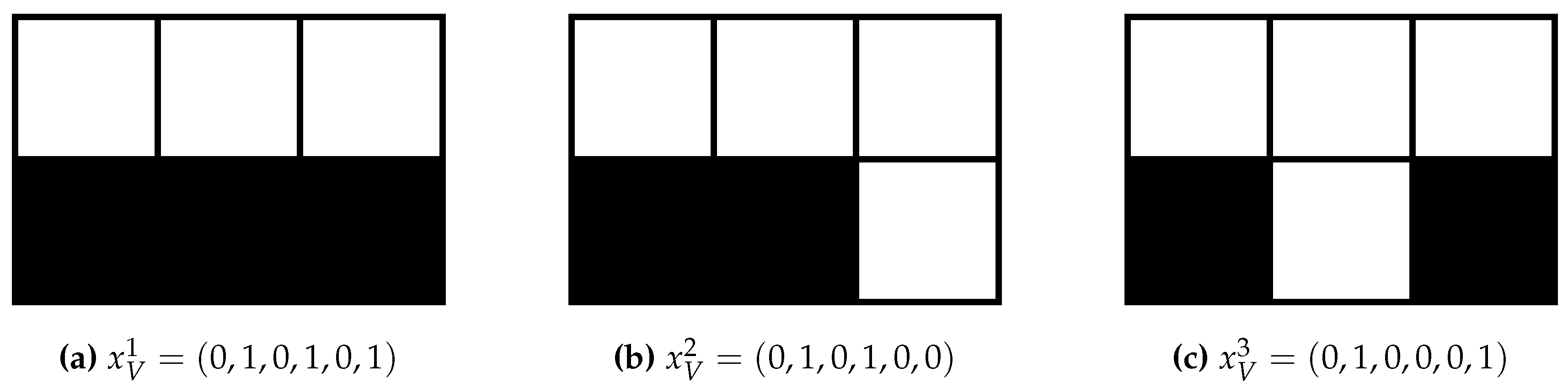
1.1. Illustration
1.2. Contributions
1.3. Related Work
The observer will conclude that the system is an organisation to the extent that there is a compressed description of its objects and of their relations.
2. Notation and Background
- 1.
- as the joint random variable composed of the random variables indexed by A, where A is ordered according to the total order of V,
- 2.
- as the state space of ,
- 3.
- as a value of ,
- 4.
- as the probability distribution (or more precisely probability mass function) of which is the joint probability distribution over the random variables indexed by A. If i.e., a singleton set, we drop the parentheses and just write ,
- 5.
- as the probability distribution over . Note that in general for arbitrary , , and this can be rewritten as a distribution over the intersection of A and B and the respective complements. The variables in the intersection have to coincide:Here δ is the Kronecker delta (see Appendix A). If and we also write to keep expressions shorter.
- 6.
- with as the conditional probability distribution over given :We also just write if it is clear from context what variables we are conditioning on.
- 1.
- Then its partition lattice is the set of partitions of V partially ordered by refinement (see also Appendix B).
- 2.
- For two partitions we write if π refines ρ and if π covers ρ. The latter means that , , and there is no with such that .
- 3.
- We write for the zero element of a partially ordered set (including lattices) and for the unit element.
- 4.
- Given a partition and a subset we define the restricted partition of π to A via:
3. Patterns, Entities, Specific, and Complete Local Integration
3.1. Patterns
- 1.
- A pattern at is an assignmentwhere . If there is no danger of confusion we also just write for the pattern at A.
- 2.
- The elements of the joint state space are isomorphic to the patterns at V which fix the complete set of random variables. Since they will be used repeatedly we refer to them as the trajectories of .
- 3.
- A pattern is said to occur in trajectory if .
- 4.
- Each pattern uniquely defines (or captures) a set of trajectories viai.e., the set of trajectories that occurs in.
- 5.
- It is convenient to allow the empty pattern for which we define .
- Note that for every we can form a pattern so the set of all patterns is .
- Our notion of patterns is similar to “patterns” as defined in [29] and to “cylinders” as defined in [30]. More precisely, these other definitions concern (probabilistic) cellular automata where all random variables have identical state spaces for all . They also restrict the extent of the patterns or cylinders to a single time-step. Under these conditions our patterns are isomorphic to these other definitions. However, we drop both the identical state space assumption and the restriction to single time-steps.Our definition is inspired by the usage of the term “spatiotemporal pattern” in [14,31,32]. There is no formal definition of this notion given in these publications but we believe that our definition is a straightforward formalisation. Note that these publications only treat the Game of Life cellular automaton. The assumption of identical state space is therefore implicitly made. At the same time the restriction to single time-steps is explicitly dropped.

3.2. Motivation of Complete Local Integration as an Entity Criterion
- spatial identity and
- temporal identity.
- The reason for excluding the unit partition of (where see Definition 2) is that with respect to it every pattern has .
- Looking for a partition that minimises a measure of integration is known as the weakest link approach [35] to dealing with multiple partitions. We note here that this is not the only approach that is being discussed. Another approach is to look at weighted averages of all integrations. For a further discussion of this point in the case of the expected value of SLI see Ay [35] and references therein. For our interpretation taking the average seems less well suited since requiring a positive average will allow SLI to be negative with respect to some partitions.
- A first consequence of introducing the logarithm is that we can now formulate the condition of Equation (24) analogously to an old phrase attributed to Aristotle that “the whole is more than the sum of its parts”. In our case this would need to be changed to “the log-probability of the (spatiotemporal) whole is greater than the sum of the log-probabilities of its (spatiotemporal) parts”. This can easily be seen by rewriting Equation (22) as:
- Another side effect of using the logarithm is that we can interpret Equation (24) in terms of the surprise value (also called information content) [36] of the pattern and the surprise value of its parts with respect to any partition . Rewriting Equation (22) using properties of the logarithm we get:Interpreting Equation (24) from this perspective we can then say that a pattern is an entity if the sum of the surprise values of its parts is larger than the surprise value of the whole.
- In coding theory, the Kraft-McMillan theorem [37] tells us that the optimal length (in a uniquely decodable binary code) of a codeword for an event x is if is the true probability of x. If the encoding is not based on the true probability of x but instead on a different probability then the difference between the optimal codeword length and the chosen codeword length isThen we can interpret the specific local integration as a difference in codeword lengths. Say we want to encode what occurs at the nodes/random variables indexed by O, i.e., we encode the random variable . We can encode every event (now a pattern) based on . Let’s call this the joint code. Given a partition we can also encode every event based on its product probability . Let’s call this the product code with respect to π. For a particular event the difference of the codeword lengths between the joint code and the product code with respect to is then just the specific local integration with respect to .Complete local integration then requires that the joint code codeword is shorter than all possible product code codewords. This means there is no partition with respect to which the product code for the pattern has a shorter codeword than the joint code. So -entities are patterns that are shorter to encode with the joint code than a product code. Patterns that have a shorter codeword in a product code associated to a partition have negative SLI with respect to this and are therefore not -entities.
- We can relate our measure of identity to other measures in information theory. For this we note that the expectation value of specific local integration with respect to a partition is the multi-information [9,10] with respect to , i.e.,The multi-information plays a role in measures of complexity and information integration [35]. The generalisation from bipartitions to arbitrary partitions is applied to expectation values similar to the multi-information above in Tononi [38]. The relations of our localised measure (in the sense of [11]) to multi-information and information integration measures also motivates the name specific local integration. Relations to these measures will be studied further in the future. Here we note that these are not suited for measuring identity of patterns since they are properties of the random variables and not of patterns . We also show in Corollary 2 that if is an -entity that (the joint random variable) has a positive for all partitions and is therefore a set of “integrated” random variables.
3.3. Properties of Specific Local Integration
3.3.1. Deterministic Case
3.3.2. Upper Bounds
- It is important to note that for an element of to occur it is not sufficient that does not occur. Only if every random variable with differs from the value specified by does an element of necessarily occur. This is why we call the anti-pattern of .
- for all let , i.e., nodes in O have no parents in the complement of O,
- for a specific and all other let , i.e., all nodes in O apart from j have as a parent,
- for all let , i.e., the state of all nodes in O is always the same as the state of node j,
- also choose and .
- ,
- .
- 1.
- The tight upper bound of the SLI with respect to any partition π with fixed is
- 2.
- The upper bound is achieved if and only if for all we have
- 3.
- The upper bound is achieved if and only if for all we have that occurs if and only if occurs.
- ad 1
- By Definition 5 we haveNow note that for any andThis shows that is indeed an upper bound. To show that it is tight we have to show that for a given and there are Bayesian networks with patterns such that this upper bound is achieved. The construction of such a Bayesian network and a pattern was presented in Theorem 3.
- ad 2
- If for all we have then clearly and the least upper bound is achieved. If on the other hand thenand because (Equation (44)) any deviation of any of the from leads to such that for all we must have .
- ad 3
- By definition for any we have such that always occurs if occurs. Now assume occurs and does not occur. In that case there is a positive probability for a pattern with i.e., . Recalling Equation (43) we then see thatwhich contradicts the fact that so cannot occur without occurring as well.
- Note that this is the least upper bound for Bayesian networks in general. For a specific Bayesian network there might be no pattern that achieves this bound.
- The least upper bound of SLI increases with the improbability of the pattern and the number of parts that it is split into. If then we can have .
- Using this least upper bound it is easy to see the least upper bound for the SLI of a pattern across all partitions . We just have to note that .
- Since it is the minimum value of SLI with respect to arbitrary partitions the least upper bound of SLI is also an upper bound for CLI. It may not be the least upper bound however.
3.3.3. Negative SLI
- for all let
- for every block let ,
- for let:
- The achieved value in Equation (53) is also our best candidate for a greatest lower bound of SLI for given and . However, we have not been able to prove this yet.
- The construction equidistributes the probability (left to be distributed after the probability q of the whole pattern occurring is chosen) to the patterns that are almost the same as the pattern . These are almost the same in a precise sense: They differ in exactly one of the blocks of , i.e., they differ by as little as can possibly be resolved/revealed by the partition .
- For a pattern and partition such that is not a natural number, the same bound might still be achieved however a little extra effort has to go into the construction 3. of the proof such that Equation (59) still holds. This is not necessary for our purpose here as we only want to show the existence of patterns achieving the negative value.
- Since it is the minimum value of SLI with respect to arbitrary partitions the candidate for the greatest lower bound of SLI is also a candidate for the greatest lower bound of CLI.
3.4. Disintegration
- 1.
- 2.
- and for :
- Note that arg min returns all partitions that achieve the minimum SLI if there is more than one.
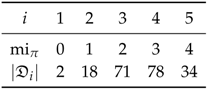
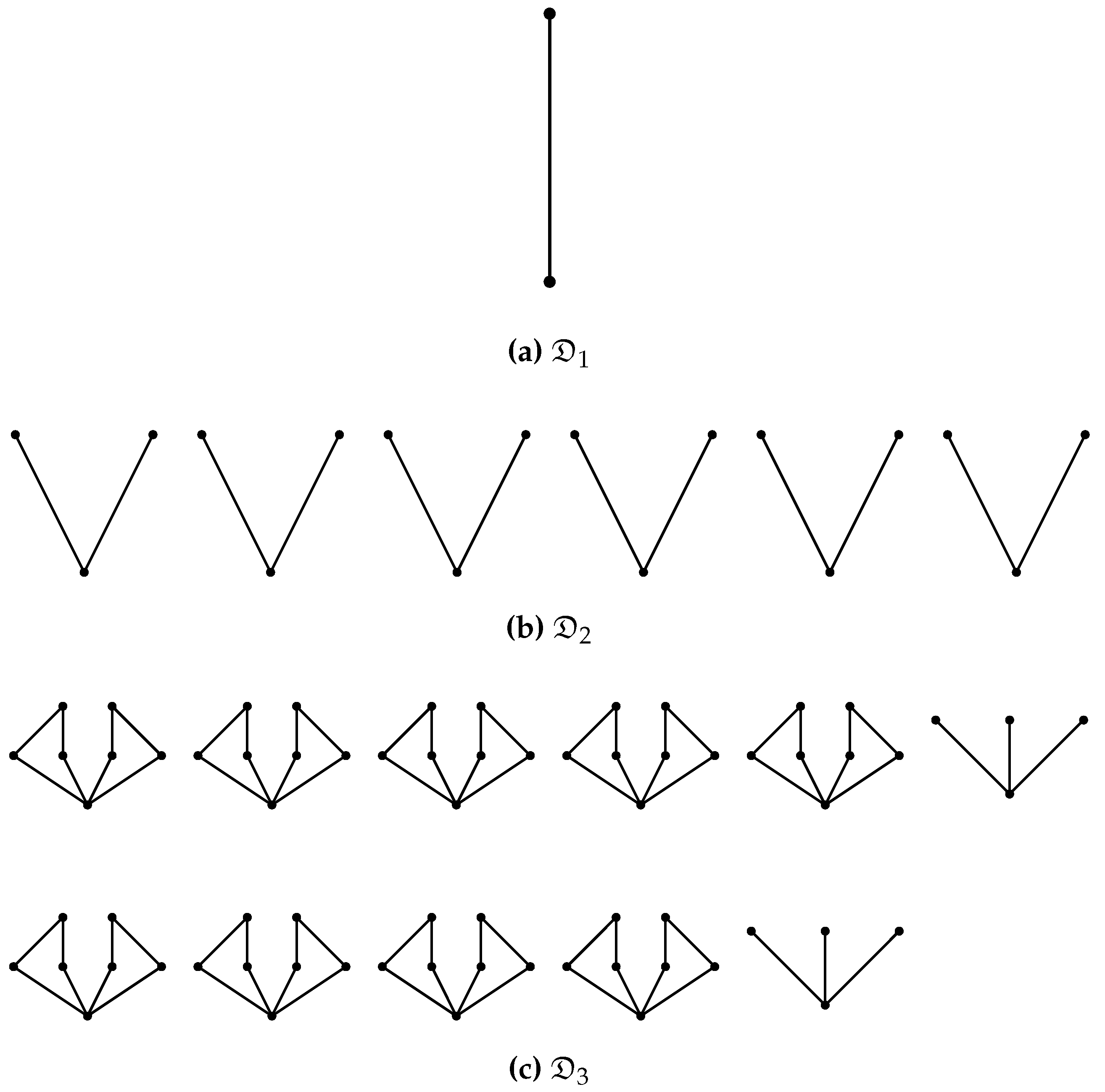
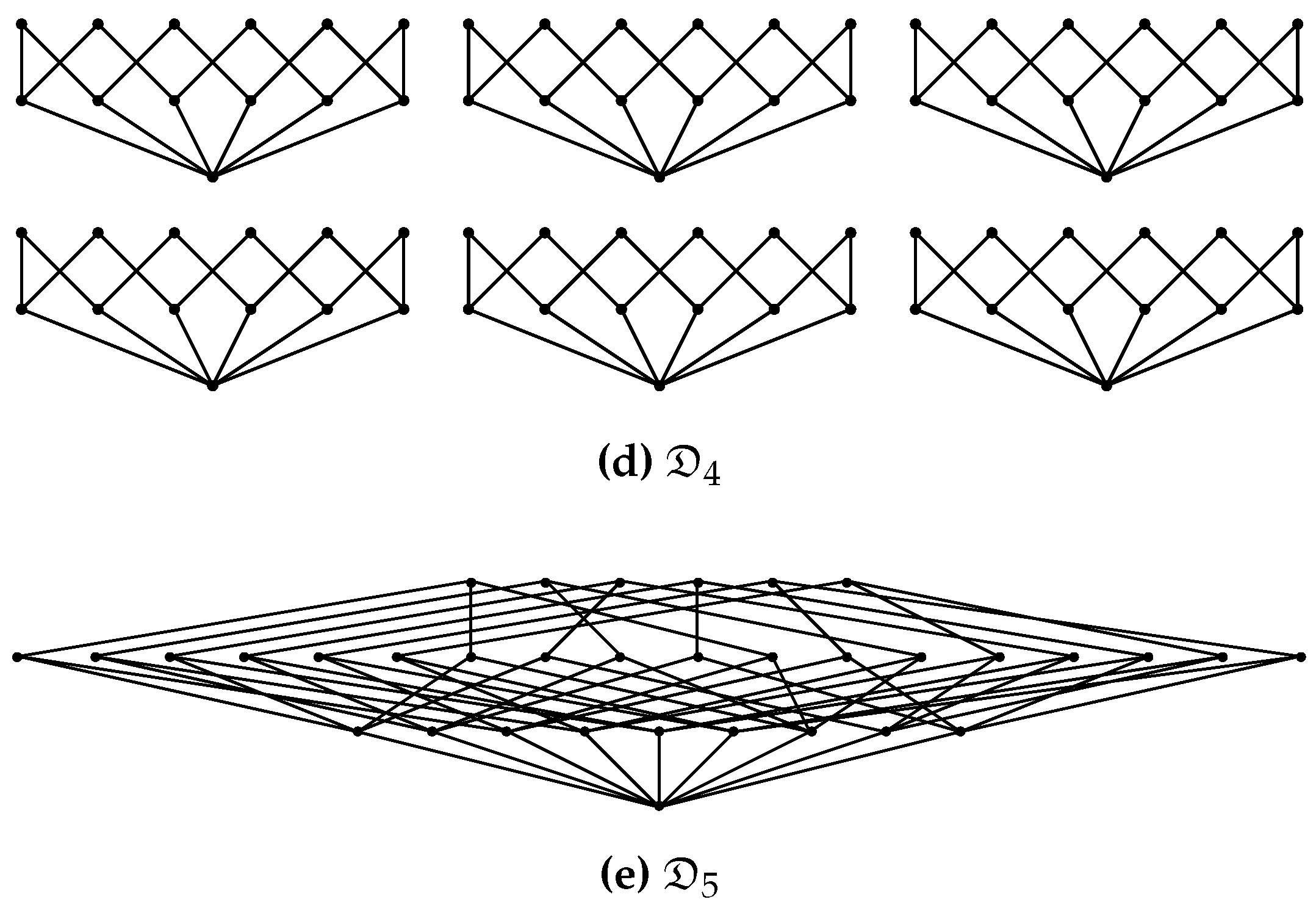
- Since the Bayesian networks we use are finite, the partition lattice is finite, the set of attained SLI values is finite, and the number of disintegration levels is finite.
- In most cases the Bayesian network contains some symmetries among their mechanisms which cause multiple partitions to attain the same SLI value.
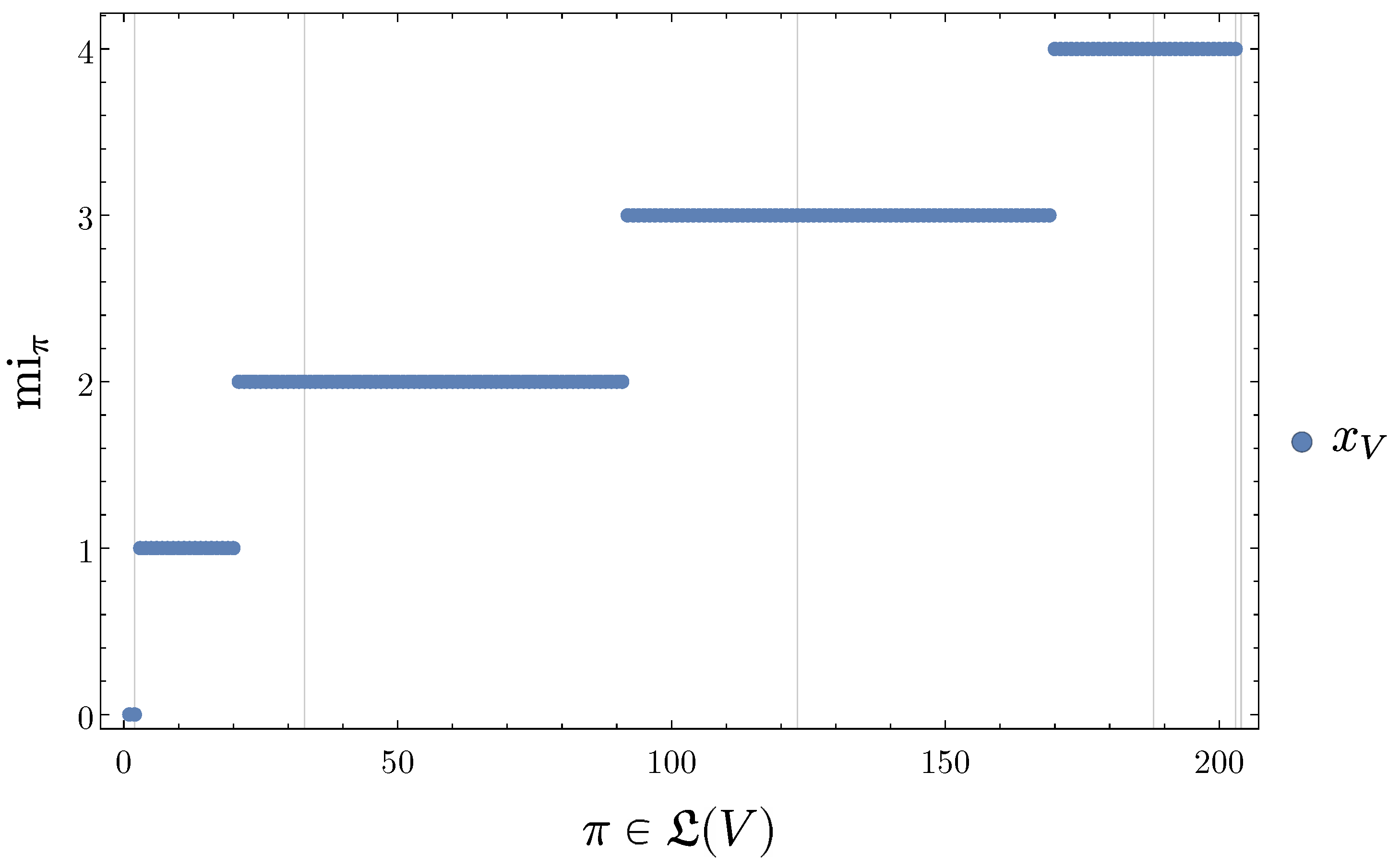
- For each trajectory the disintegration hierarchy then partitions the elements of into subsets of equal SLI. The levels of the hierarchy have increasing SLI.
- 1.
- 2.
- and for :
- Each level in the refinement-free disintegration hierarchy consists only of those partitions that neither have refinements at their own nor at any of the preceding levels. So each partition that occurs in the refinement-free disintegration hierarchy at the i-th level is a finest partition that achieves such a low level of SLI or such a high level of disintegration.
- As we will see below, the blocks of the partitions in the refinement-free disintegration hierarchy are the main reason for defining the refinement-free disintegration hierarchy.
- 1.
- Then for every we find for every with that there are only the following possibilities:
- (a)
- b is a singleton, i.e., for some , or
- (b)
- is completely locally integrated, i.e., .
- 2.
- Conversely, for any completely locally integrated pattern , there is a partition and a level such that and .
- ad 1
- We prove the theorem by contradiction. For this assume that there is block b in a partition which is neither a singleton nor completely integrated. Let and . Assume b is not a singleton i.e., there exist such that and . Also assume that b is not completely integrated i.e., there exists a partition of b with such that . Note that a singleton cannot be completely locally integrated as it does not allow for a non-unit partition. So together the two assumptions imply with . However, thenWe treat the cases of “>” and “=” separately. First, letThen we can define such that
- which implies that because , and
- which contradicts .
Second, letThen we can define such thatwhich contradicts . - ad 2
- By assumption is completely locally integrated. Then let . Since is a partition of V it is an element of some disintegration level . Then partition is also an element of the refinement-free disintegration level as we will see in the following. This is because any refinements must (by construction of break up A into further blocks which means that the local specific integration of all such partitions is higher. Then they must be at lower disintegration level with . Therefore, has no refinement at its own or a higher disintegration level. More formally, let and since only contains singletons apart from A the partition must split the block A into multiple blocks . Since we know thatso that andTherefore is on a disintegration level with , but this is true for any refinement of so and .
- 1.
- b is a singleton, i.e., for some , or
- 2.
- is completely (not only locally) integrated, i.e., .
3.5. Disintegration Interpretation
3.6. Related Approaches
4. Examples
4.1. Set of Independent Random Variables
4.2. Two Constant and Independent Binary Random Variables:
4.2.1. Definition
4.2.2. Trajectories
4.2.3. Partitions of Trajectories

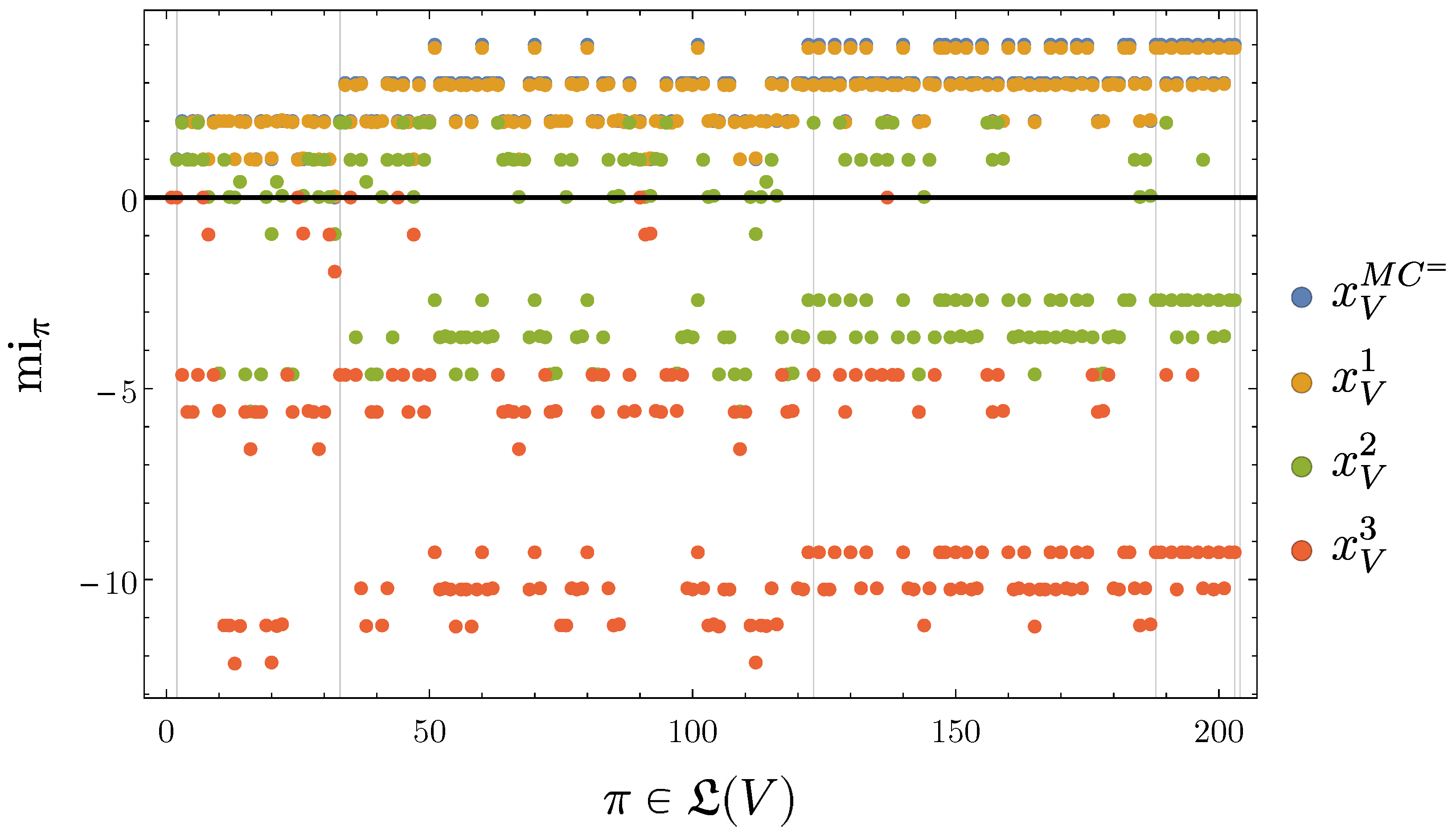
4.2.4. SLI Values of the Partitions
4.2.5. Disintegration Hierarchy
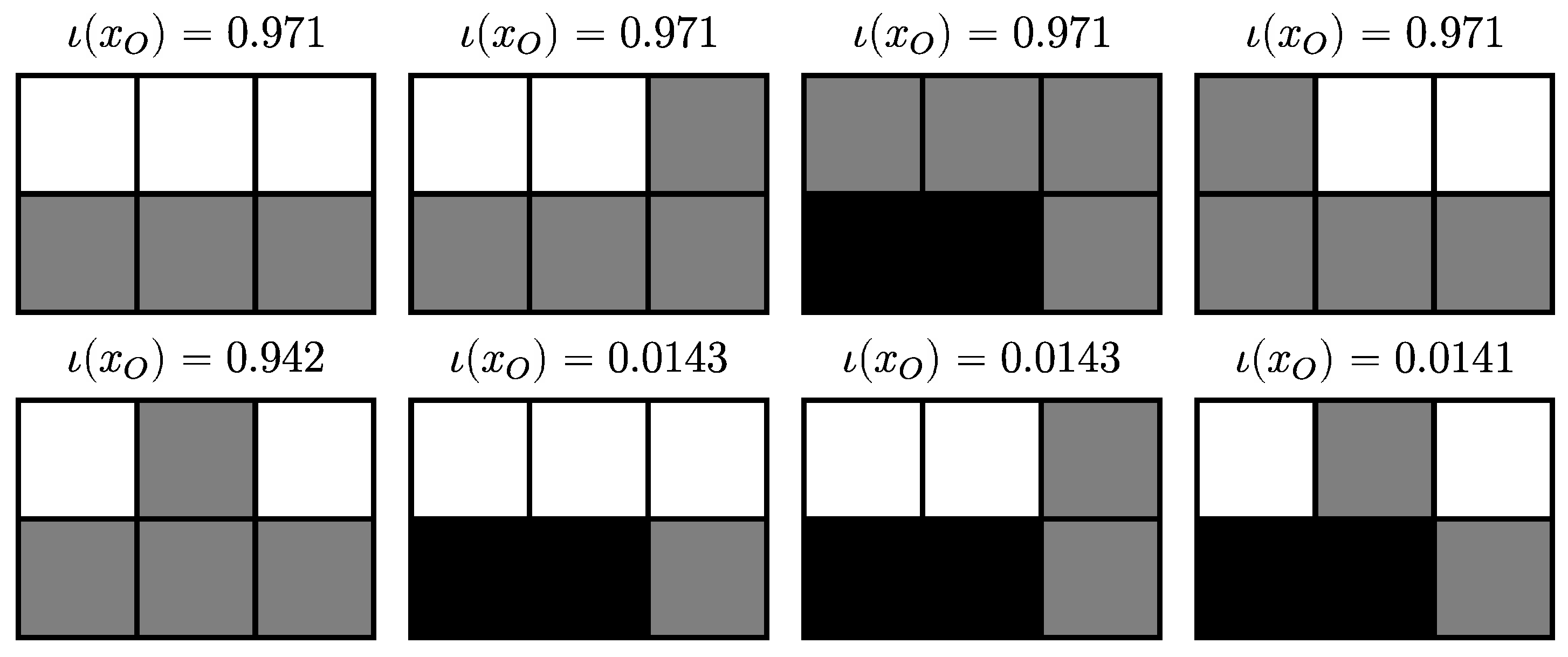
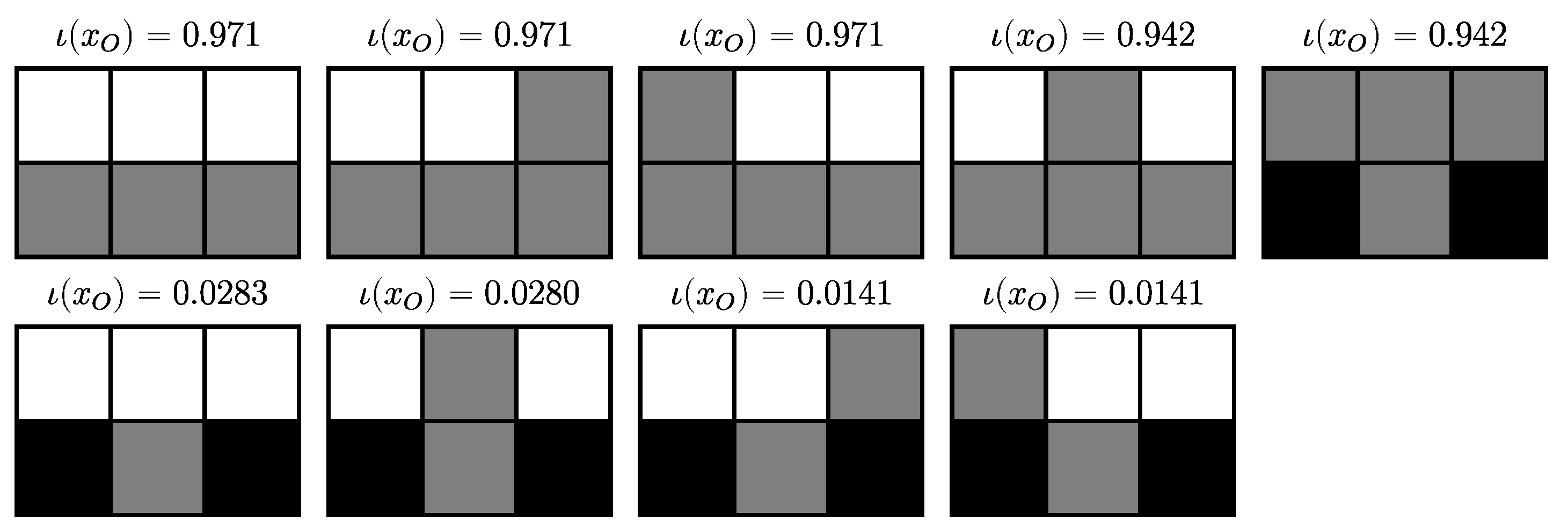
4.2.6. Completely Integrated Patterns
4.3. Two Random Variables with Small Interactions
4.3.1. Definition
4.3.2. Trajectories
4.3.3. SLI Values of the Partitions
4.3.4. Completely Integrated Patterns
5. Discussion
- correspond to fixed single random variables for a set of independent random variables,
- can vary from one trajectory to another,
- and can change the degrees of freedom that they occupy over time,
- can be ambiguous at a fixed level of disintegration due to symmetries of the system,
- can overlap at the same level of disintegration due to this ambiguity,
- can overlap across multiple levels of disintegration i.e., parts of -entities can be -entities again.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SLI | Specific local integration |
| CLI | Complete local integration |
Appendix A. Kronecker Delta
- Let be two random variables with state spaces and a function such thatthen
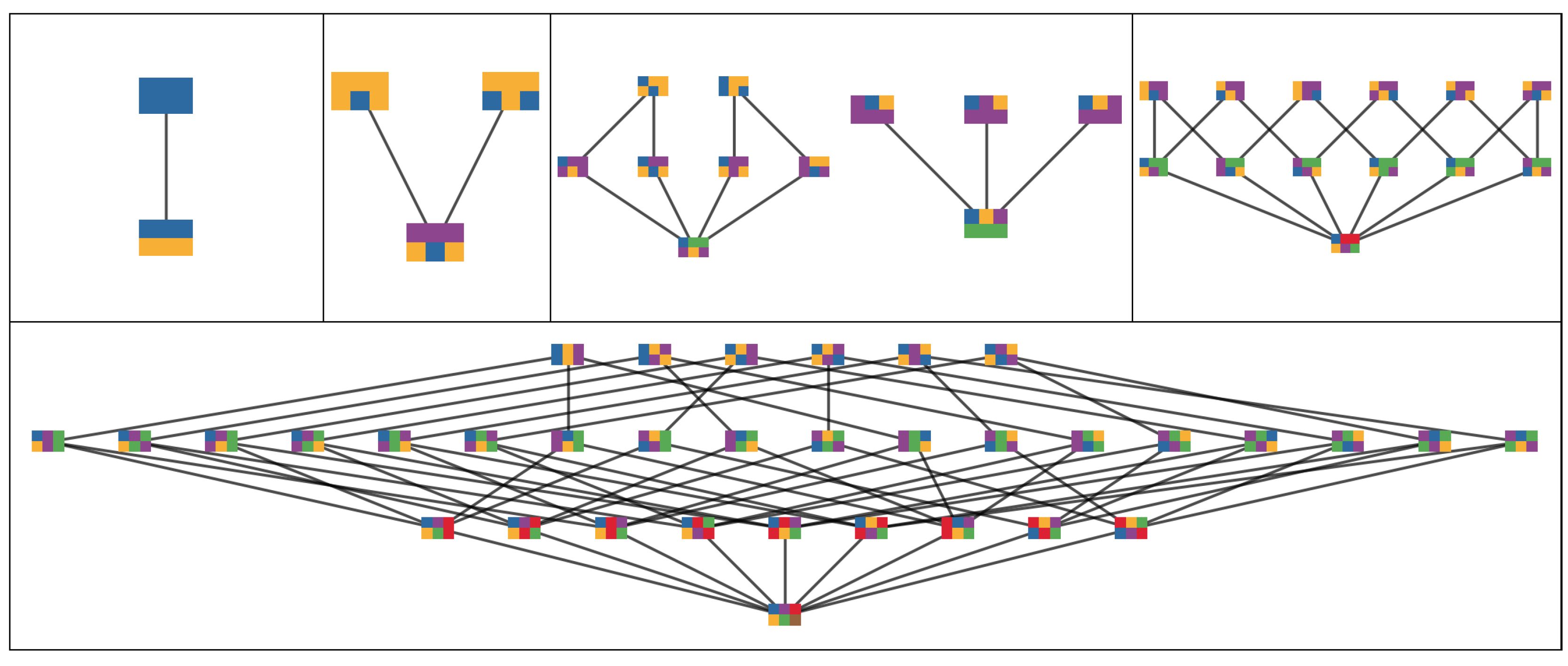
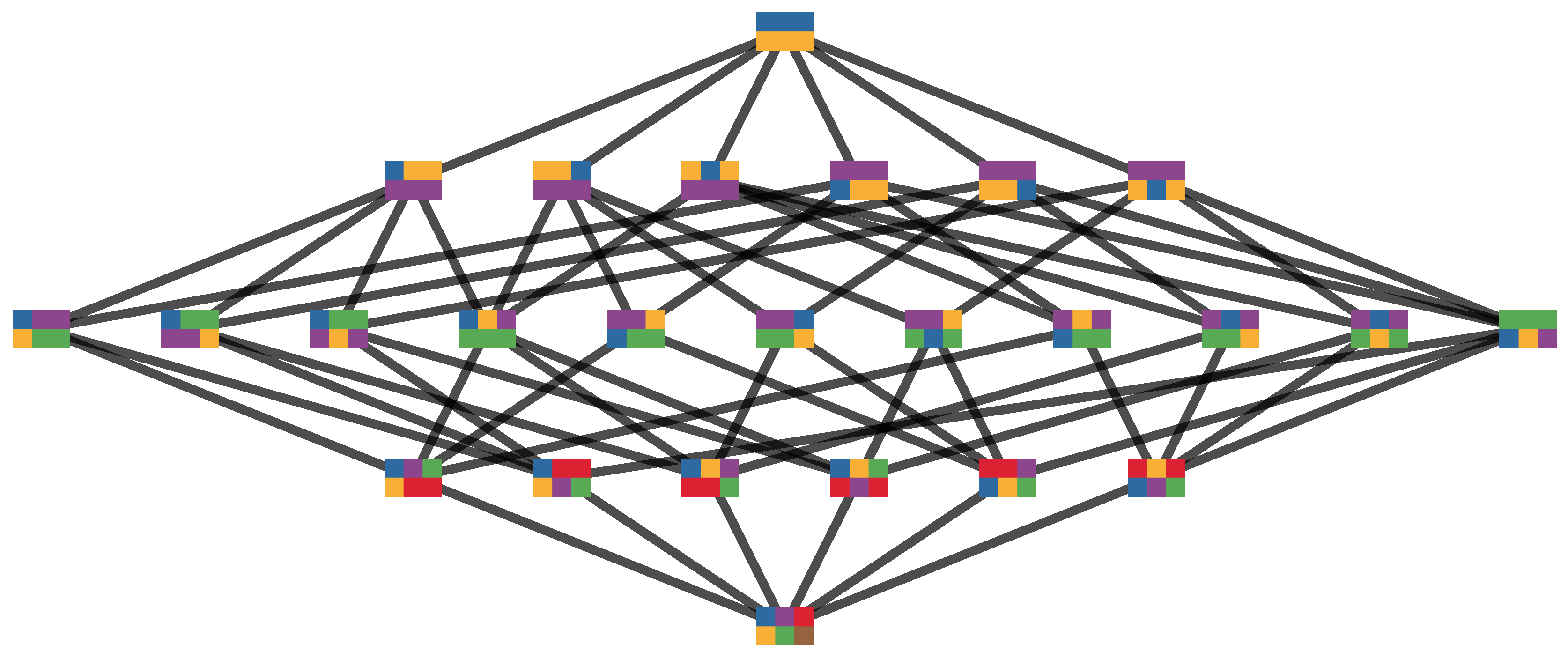
Appendix B. Refinement and Partition Lattice Examples
- 1.
- for all , if , then ,
- 2.
- .
- In words, a partition of a set is a set of disjoint non-empty subsets whose union is the whole set.
- More intuitively, is a refinement of if all blocks of can be obtained by further partitioning the blocks of . Conversely, is a coarsening of if all blocks in are unions of blocks in .
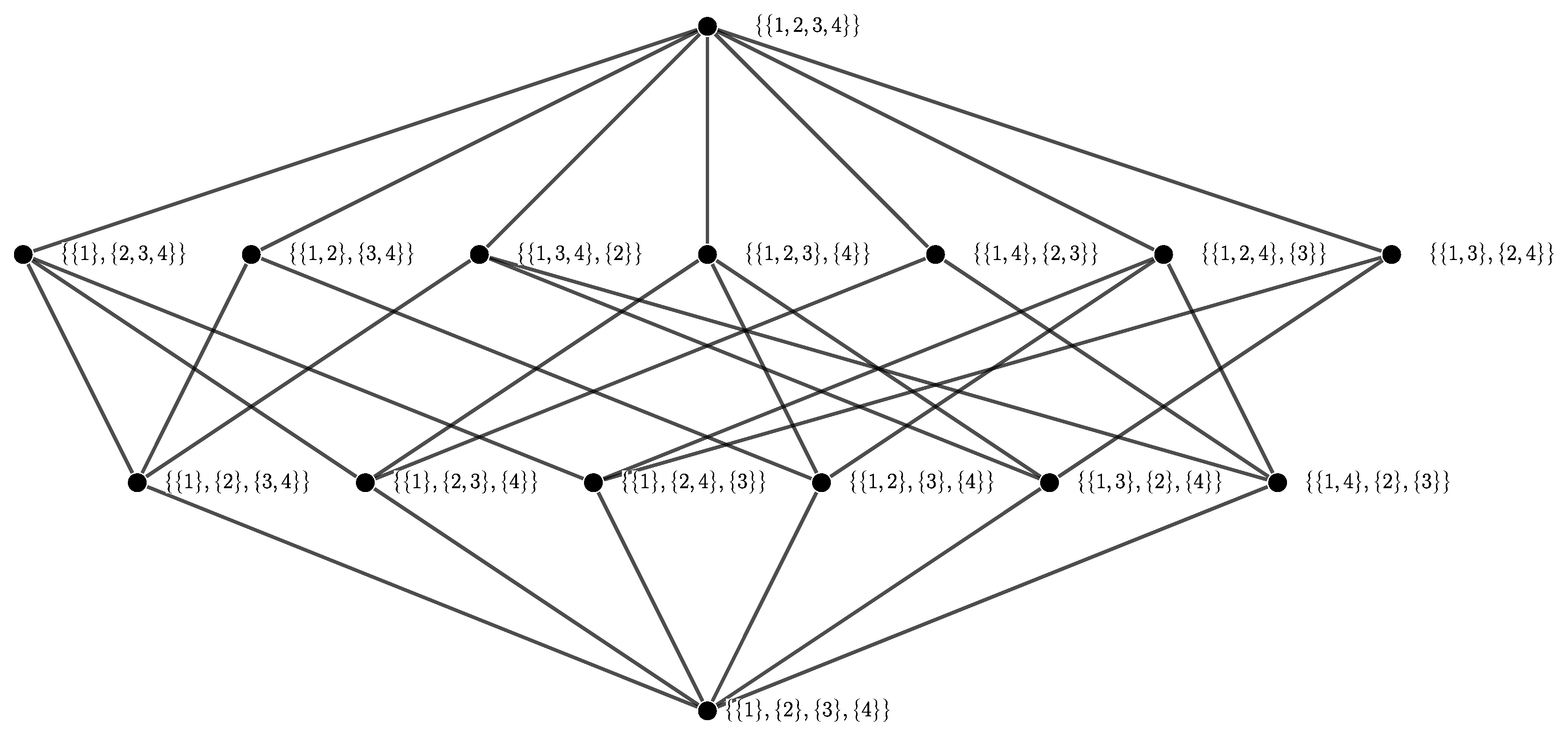
- Examples are contained in the Hasse diagrams (defined below) shown in Figure A1.
- No edge is drawn between two elements if but not .
- Only drawing edges for the covering relation does not imply a loss of information about the poset since the covering relation determines the partial order completely.
- For an example Hasse diagrams see Figure A1.
Appendix C. Bayesian Networks
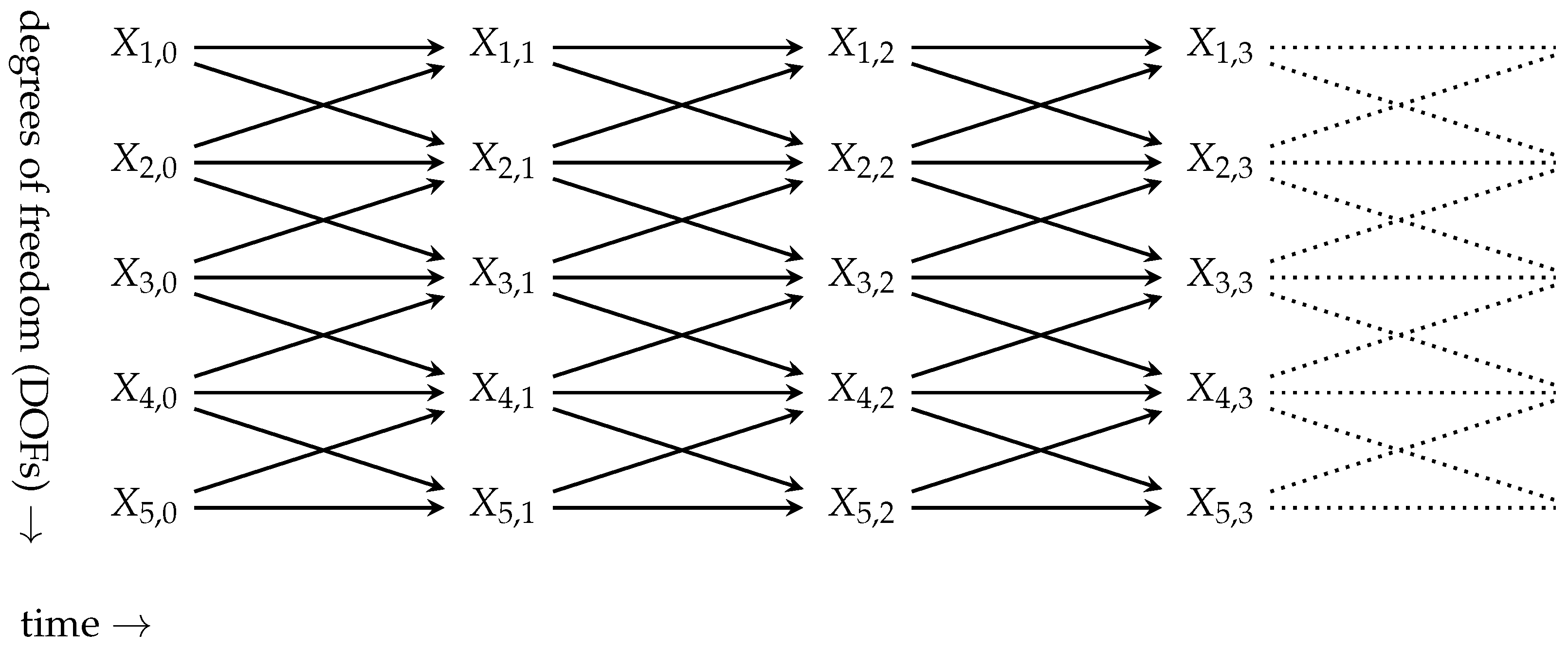
- On top of constituting the vertices of the graph G the set V is also assumed to be totally ordered in an (arbitrarily) fixed way. Whenever we use a subset to index a sequence of variables in the Bayesian network (e.g., in ) we order A according to this total order as well.
- Since is finite and G is acyclic there is a set of nodes without parents.
- We could define the set of all mechanisms to formally also include the mechanisms of the nodes without parents . However, in practice it makes sense to separate the nodes without parents as those that we choose an initial probability distribution over (similar to a boundary condition) which is then turned into a probability distribution over the entire Bayesian network via Equation (A12). Note that in Equation (A12) the nodes in are not explicit as they are just factors with .
- To construct a Bayesian network, take graph and equip each node with a mechanism and for each node choose a probability distribution . The joint probability distribution is then calculated by the according version of Equation (A12):
Appendix C.1. Deterministic Bayesian Networks
- Due to the finiteness of the network, deterministic mechanisms, and chosen uniform initial distribution the minimum possible non-zero probability for a pattern is . This happens for any pattern that only occurs in a single trajectory. Furthermore, the probability of any pattern is a multiple of .
Appendix C.2. Proof of Theorem 2
Appendix D. Proof of Theorem 1
References
- Gallois, A. Identity over Time. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Metaphysics Research Laboratory, Stanford University: Stanford, CA, USA, 2012. [Google Scholar]
- Grand, S. Creation: Life and How to Make It; Harvard University Press: Harvard, MA, USA, 2003. [Google Scholar]
- Pascal, R.; Pross, A. Stability and its manifestation in the chemical and biological worlds. Chem. Commun. 2015, 51, 16160–16165. [Google Scholar] [CrossRef] [PubMed]
- Orseau, L.; Ring, M. Space-Time Embedded Intelligence. In Artificial General Intelligence; Number 7716 in Lecture Notes in Computer Science; Bach, J., Goertzel, B., Iklé, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 209–218. [Google Scholar]
- Barandiaran, X.E.; Paolo, E.D.; Rohde, M. Defining Agency: Individuality, Normativity, Asymmetry, and Spatio-temporality in Action. Adapt. Behav. 2009, 17, 367–386. [Google Scholar] [CrossRef]
- Legg, S.; Hutter, M. Universal Intelligence: A Definition of Machine Intelligence. arXiv, 2007; arXiv: 0712.3329. [Google Scholar]
- Boccara, N.; Nasser, J.; Roger, M. Particlelike structures and their interactions in spatiotemporal patterns generated by one-dimensional deterministic cellular-automaton rules. Phys. Rev. A 1991, 44, 866–875. [Google Scholar] [CrossRef] [PubMed]
- Biehl, M.; Ikegami, T.; Polani, D. Towards information based spatiotemporal patterns as a foundation for agent representation in dynamical systems. In Proceedings of the Artificial Life Conference, Cancun, Mexico, 2016; The MIT Press: Cambridge, MA, USA, 2016; pp. 722–729. [Google Scholar]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Amari, S.I. Information geometry on hierarchy of probability distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems; Springer: Berlin/Heidelberg: Germany, 2012. [Google Scholar]
- Tononi, G.; Sporns, O. Measuring information integration. BMC Neurosci. 2003, 4, 31. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Tononi, G. Integrated Information in Discrete Dynamical Systems: Motivation and Theoretical Framework. PLoS Comput. Biol. 2008, 4, e1000091. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.D. Characterizing autopoiesis in the game of life. Artif. Life 2014, 21, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Fontana, W.; Buss, L.W. “The arrival of the fittest”: Toward a theory of biological organization. Bull. Math. Biol. 1994, 56, 1–64. [Google Scholar]
- Krakauer, D.; Bertschinger, N.; Olbrich, E.; Ay, N.; Flack, J.C. The Information Theory of Individuality. arXiv, 2014; arXiv:1412.2447. [Google Scholar]
- Bertschinger, N.; Olbrich, E.; Ay, N.; Jost, J. Autonomy: An information theoretic perspective. Biosystems 2008, 91, 331–345. [Google Scholar] [CrossRef] [PubMed]
- Shalizi, C.R.; Haslinger, R.; Rouquier, J.B.; Klinkner, K.L.; Moore, C. Automatic filters for the detection of coherent structure in spatiotemporal systems. Phys. Rev. E 2006, 73, 036104. [Google Scholar] [CrossRef] [PubMed]
- Wolfram, S. Computation theory of cellular automata. Commun. Math. Phys. 1984, 96, 15–57. [Google Scholar] [CrossRef]
- Grassberger, P. Chaos and diffusion in deterministic cellular automata. Phys. D Nonlinear Phenom. 1984, 10, 52–58. [Google Scholar] [CrossRef]
- Hanson, J.E.; Crutchfield, J.P. The attractor—Basin portrait of a cellular automaton. J. Stat. Phys. 1992, 66, 1415–1462. [Google Scholar] [CrossRef]
- Pivato, M. Defect particle kinematics in one-dimensional cellular automata. Theor. Comput. Sci. 2007, 377, 205–228. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [PubMed]
- Flecker, B.; Alford, W.; Beggs, J.M.; Williams, P.L.; Beer, R.D. Partial information decomposition as a spatiotemporal filter. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037104. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D. Detecting emergent processes in cellular automata with excess information. arXiv, 2011; arXiv:1105.0158. [Google Scholar]
- Hoel, E.P.; Albantakis, L.; Marshall, W.; Tononi, G. Can the macro beat the micro? Integrated information across spatiotemporal scales. Neurosci. Conscious. 2016, 2016, niw012. [Google Scholar] [CrossRef]
- Grätzer, G. Lattice Theory: Foundation; Springer: New York, NY, USA, 2011. [Google Scholar]
- Ceccherini-Silberstein, T.; Coornaert, M. Cellular Automata and Groups. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 778–791. [Google Scholar]
- Busic, A.; Mairesse, J.; Marcovici, I. Probabilistic cellular automata, invariant measures, and perfect sampling. arXiv, 2010; arXiv: 1010.3133. [Google Scholar]
- Beer, R.D. The cognitive domain of a glider in the game of life. Artif. Life 2014, 20, 183–206. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.R. Autopoiesis and Enaction in the Game of Life; The MIT Press: Cambridge, MA, USA, 2016; p. 13. [Google Scholar]
- Noonan, H.; Curtis, B. Identity. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Metaphysics Research Laboratory, Stanford University: Stanford, CA, USA, 2014. [Google Scholar]
- Hawley, K. Temporal Parts. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Metaphysics Research Laboratory, Stanford University: Stanford, CA, USA, 2015. [Google Scholar]
- Ay, N. Information Geometry on Complexity and Stochastic Interaction. Entropy 2015, 17, 2432–2458. [Google Scholar] [CrossRef]
- MacKay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tononi, G. An information integration theory of consciousness. BMC Neurosc. 2004, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Von Eitzen, H. Prove (1 − (1 − q)/n)n ≥ q for 0 < q < 1 and n ≥ 2 a Natural Number. Mathematics Stack Exchange. 2016. Available online: http://math.stackexchange.com/q/1974262 (accessed on 18 October 2016).
- Bullen, P.S. Handbook of Means and Their Inequalities; Springer Science+Business Media: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Kolchinsky, A.; Rocha, L.M. Prediction and modularity in dynamical systems. In Advances in Artificial Life, ECAL; The MIT Press: Cambridge, MA, USA, 2011; pp. 423–430. [Google Scholar]
- Pemmaraju, S.; Skiena, S. Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica®; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- De Bruijn, N.G. Asymptotic Methods in Analysis; Dover Publications: New York, NY, USA, 2010. [Google Scholar]







© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biehl, M.; Ikegami, T.; Polani, D. Specific and Complete Local Integration of Patterns in Bayesian Networks. Entropy 2017, 19, 230. https://doi.org/10.3390/e19050230
Biehl M, Ikegami T, Polani D. Specific and Complete Local Integration of Patterns in Bayesian Networks. Entropy. 2017; 19(5):230. https://doi.org/10.3390/e19050230
Chicago/Turabian StyleBiehl, Martin, Takashi Ikegami, and Daniel Polani. 2017. "Specific and Complete Local Integration of Patterns in Bayesian Networks" Entropy 19, no. 5: 230. https://doi.org/10.3390/e19050230
APA StyleBiehl, M., Ikegami, T., & Polani, D. (2017). Specific and Complete Local Integration of Patterns in Bayesian Networks. Entropy, 19(5), 230. https://doi.org/10.3390/e19050230






