Multiscale Information Theory and the Marginal Utility of Information
Abstract
1. Introduction
2. Information
- Monotonicity: The information in a subset U that is contained in a subset V cannot have more information than V, that is, .
- Strong subadditivity: Given two subsets, the information contained in both cannot exceed the information in each of them separately minus the information in their intersection:
- Microcanonical or Hartley entropy: For a system with a finite number of joint states, is an information function, where m is the number of joint states available to the subset U of components. Here, information content measures the number of yes-or-no questions which must be answered to identify one joint state out of m possibilities.
- Shannon entropy: For a system characterized by a probability distribution over all possible joint states, is an information function, where are the probabilities of the joint states available to the components in U [9]. Here, information content measures the number of yes-or-no questions which must be answered to identify one joint state out of all the joint states available to U, where more probable states can be identified more concisely.
- Tsallis entropy: The Tsallis entropy [51,52] is a generalization of the Shannon entropy with applications to nonextensive statistical mechanics. For the same setting as in Shannon entropy, Tsallis entropy is defined as for some parameter . Shannon entropy is recovered in the limit . Tsallis entropy is an information function for (but not for ); this follows from Proposition 2.1 and Theorem 3.4 of [53].
- Logarithm of period: For a deterministic dynamic system with periodic behavior, an information function can be defined as the logarithm of the period of a set U of components (i.e., the time it takes for the joint state of these components to return to an initial joint state) [54]. This information function measures the number of questions which one should expect to answer in order to locate the position of those components in their cycle.
- Vector space dimension: Consider a system of n components, each of whose state is described by a real number. Then the joint states of any subset U of components can be described by points in some linear subspace of . The minimal dimension of such a subspace is an information function, equal to the number of coordinates one must specify in order to identify the joint state of U.
- Matroid rank: A matroid consists of a set of elements called the ground set, together with a rank function that takes values on subsets of the ground set. Rank functions are defined to include the monotonicity and strong subadditivity properties [55], and generalize the notion of vector subspace dimension. Consequently, the rank function of a matroid is an information function, with the ground set identified as the set of system components.
3. Scale
4. Systems
- A finite set A of components,
- An information function , giving the information in each subset ,
- A scale function , giving the intrinsic scale of each compoent .
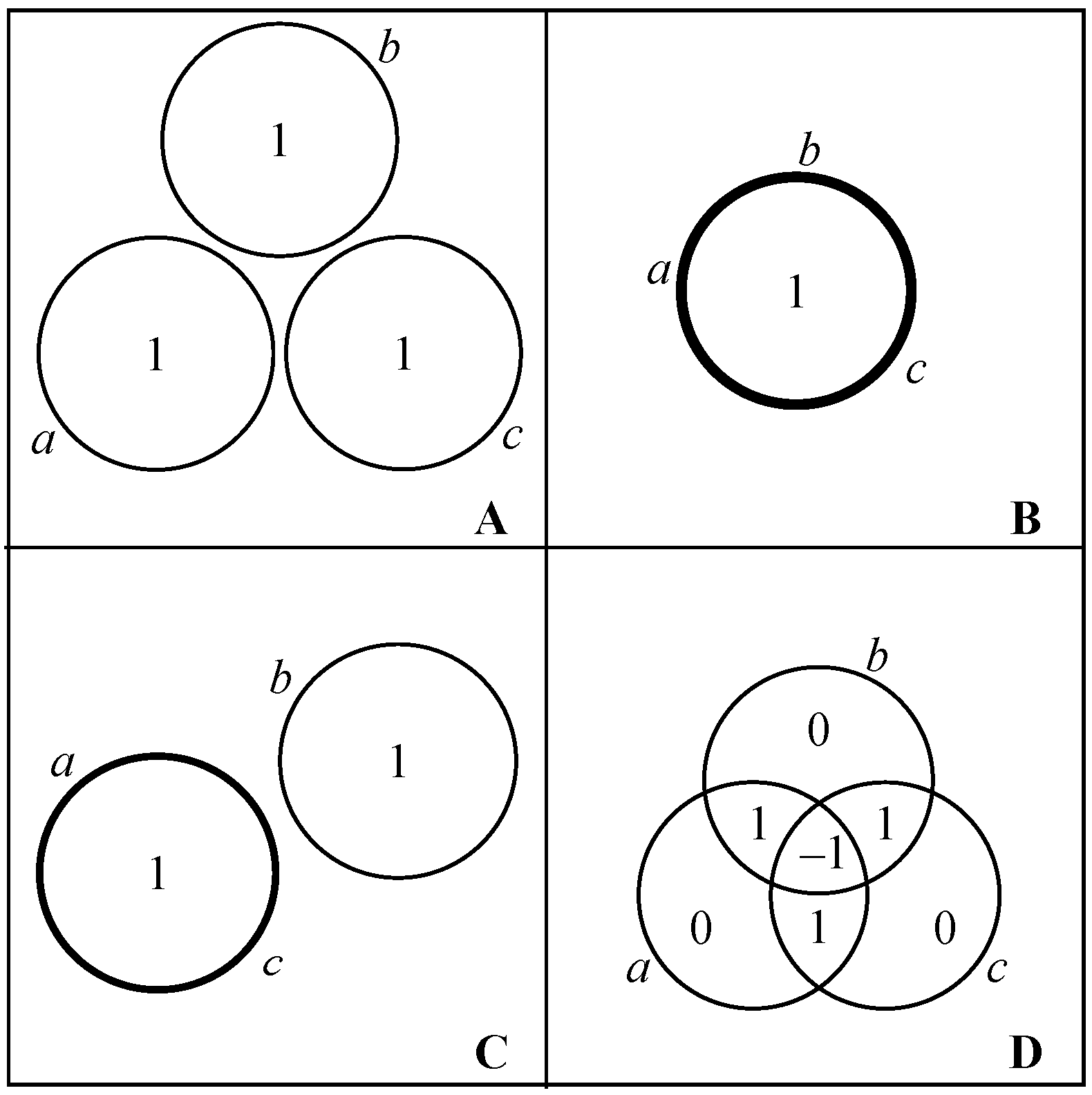
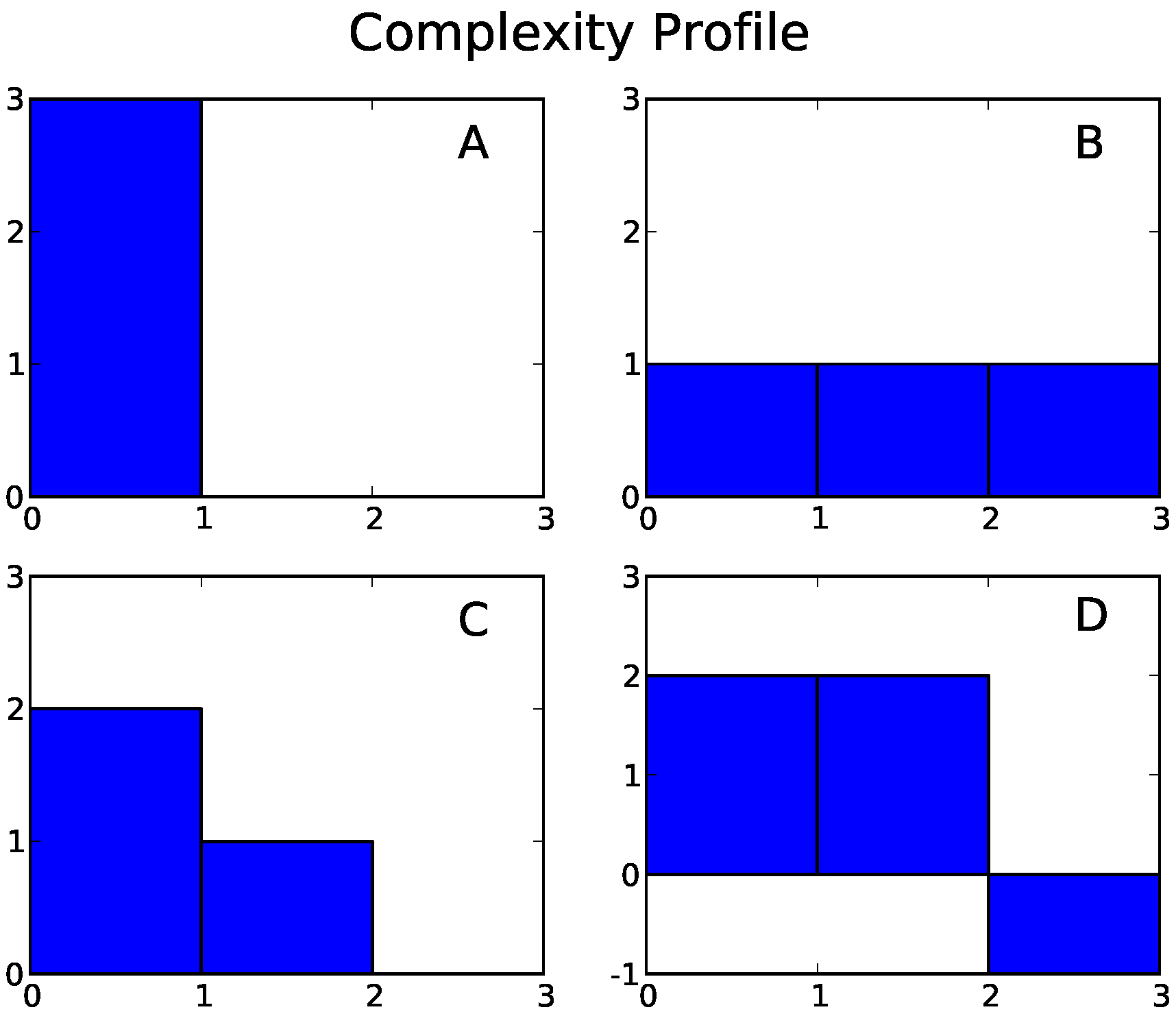
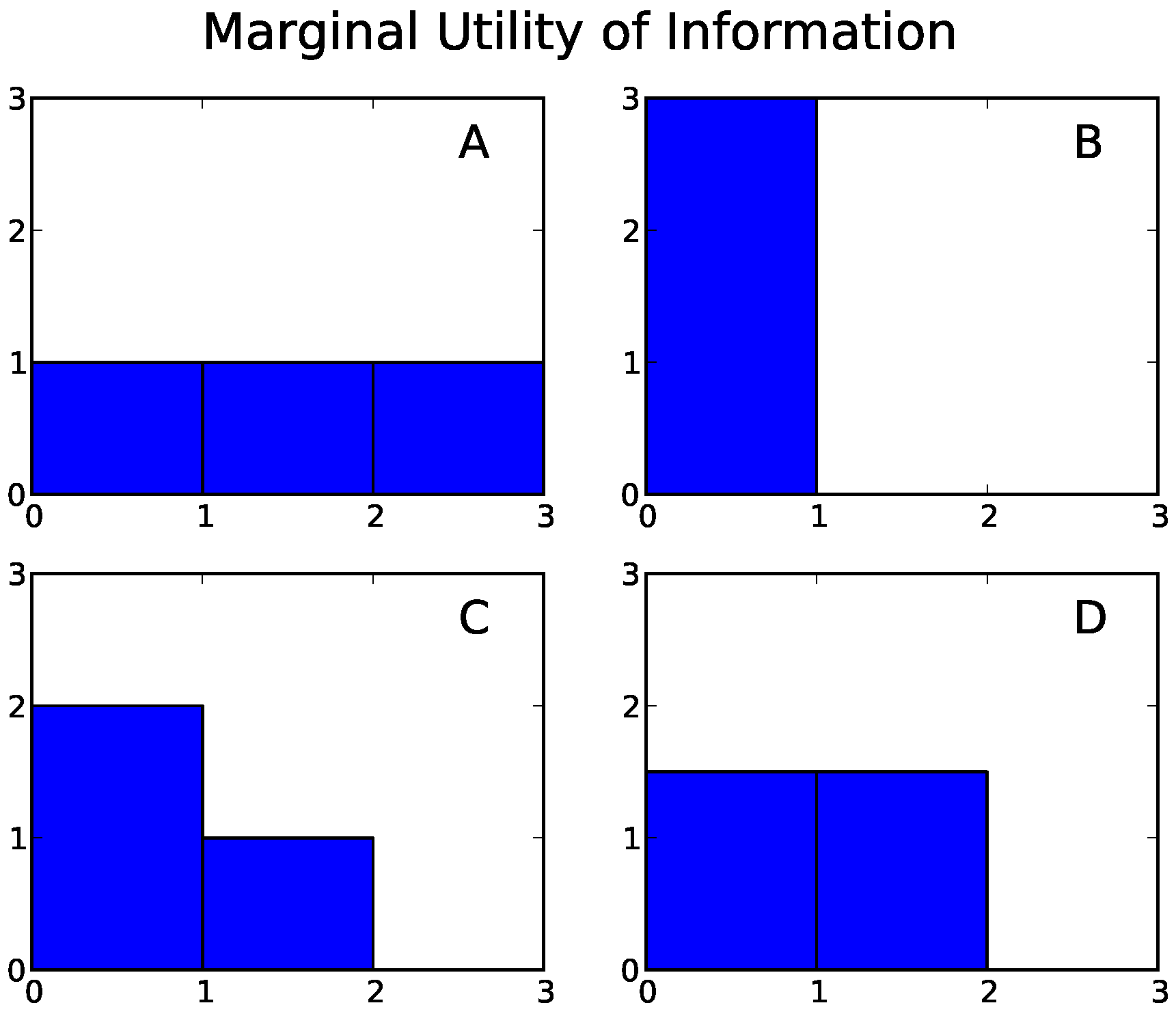
- Example A: Three independent components. Each component is equally likely to be in state 0 or state 1, and the system as a whole is equally likely to be in any of its eight possible states.
- Example B: Three completely interdependent components. Each component is equally likely to be in state 0 or state 1, but all three components are always in the same state.
- Example C: Independent blocks of dependent components. Each component is equally likely to take the value 0 or 1; however, the first two components always take the same value, while the third can take either value independently of the coupled pair.
- Example D: The parity bit system. The components can exist in the states 110, 101, 011, or 000 with equal probability. In each state, each component is equal to the parity (0 if even; 1 if odd) of the sum of the other two. Any two of the component are statistically independent of each other, but the three as a whole are constrained to have an even sum.
5. Multiscale Information Theory
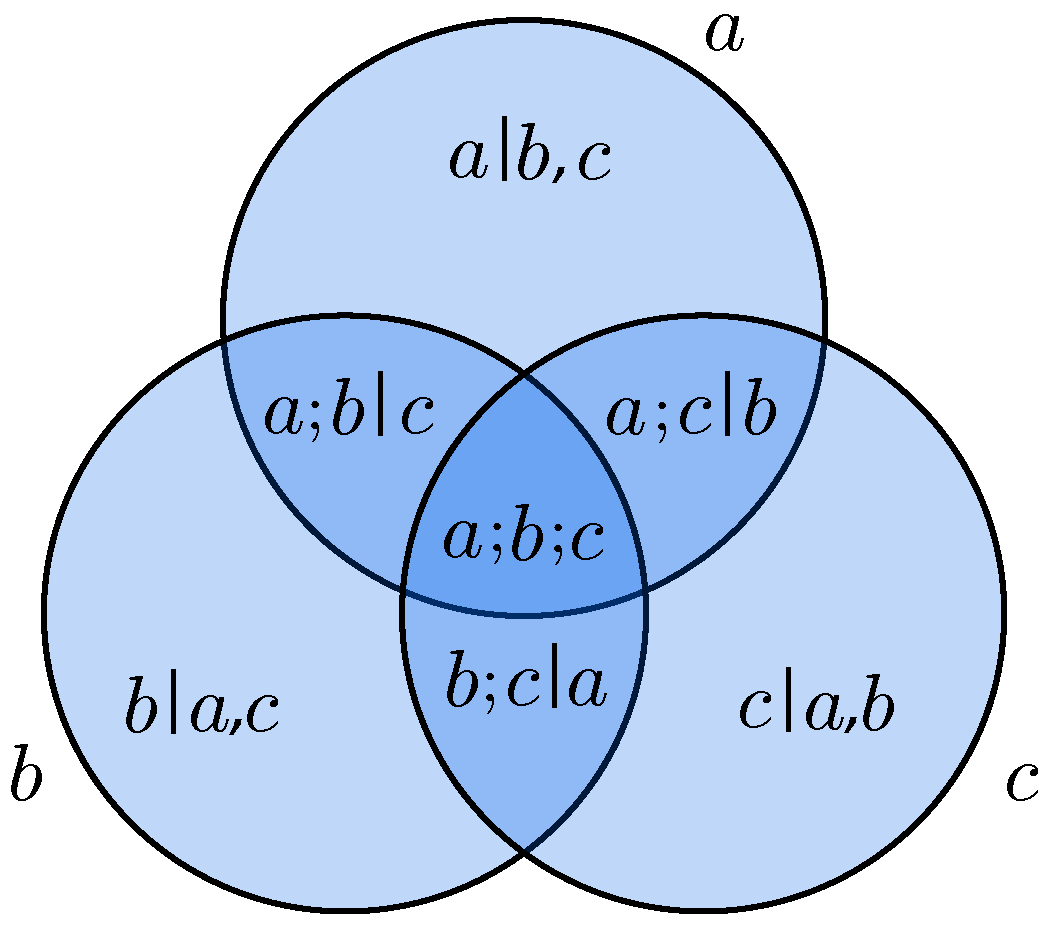
5.1. Dependencies
5.2. Information Quantity in Dependencies
5.3. Scale-Weighted Information
5.4. Independence and Complete Interdependence
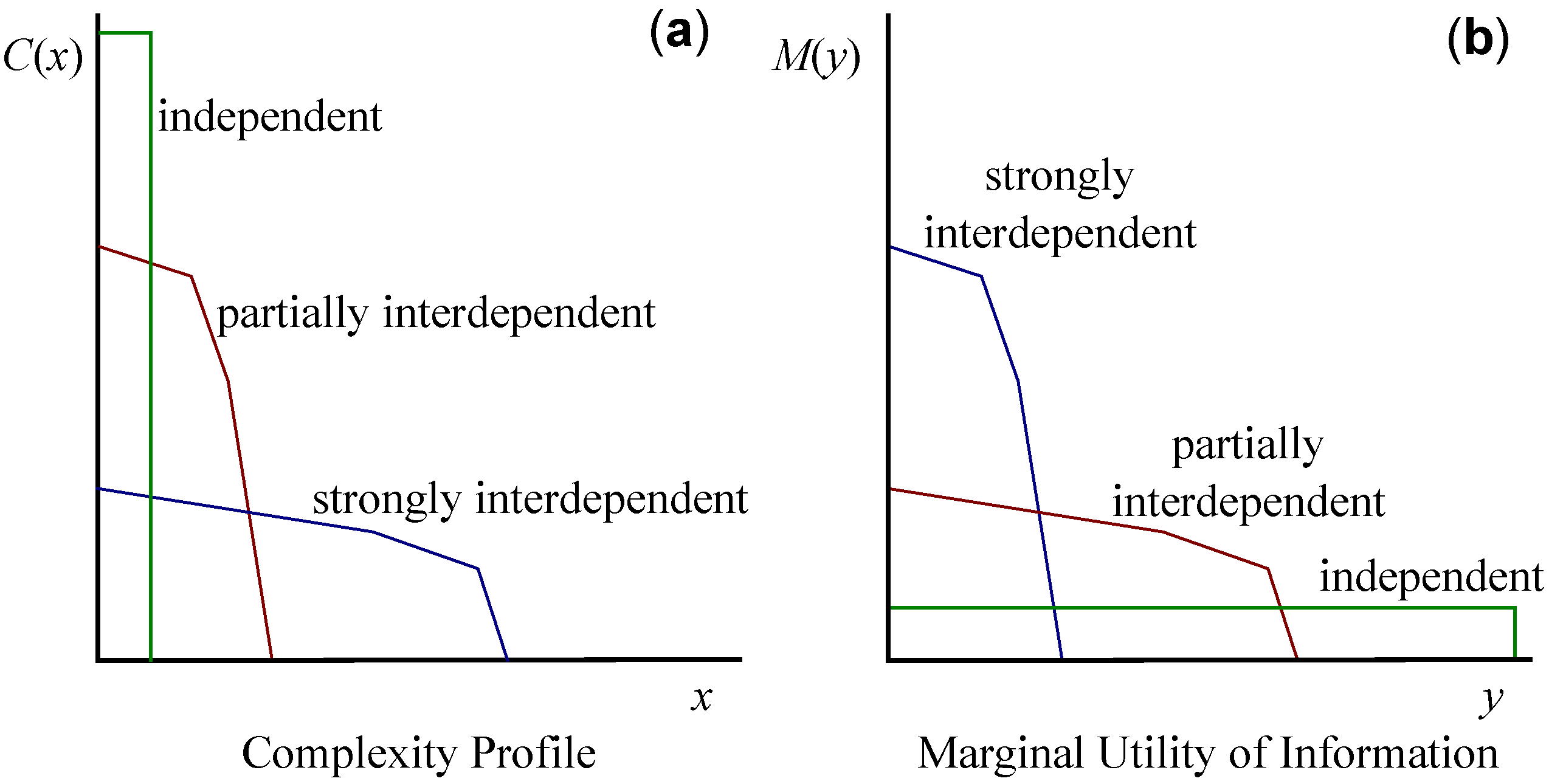
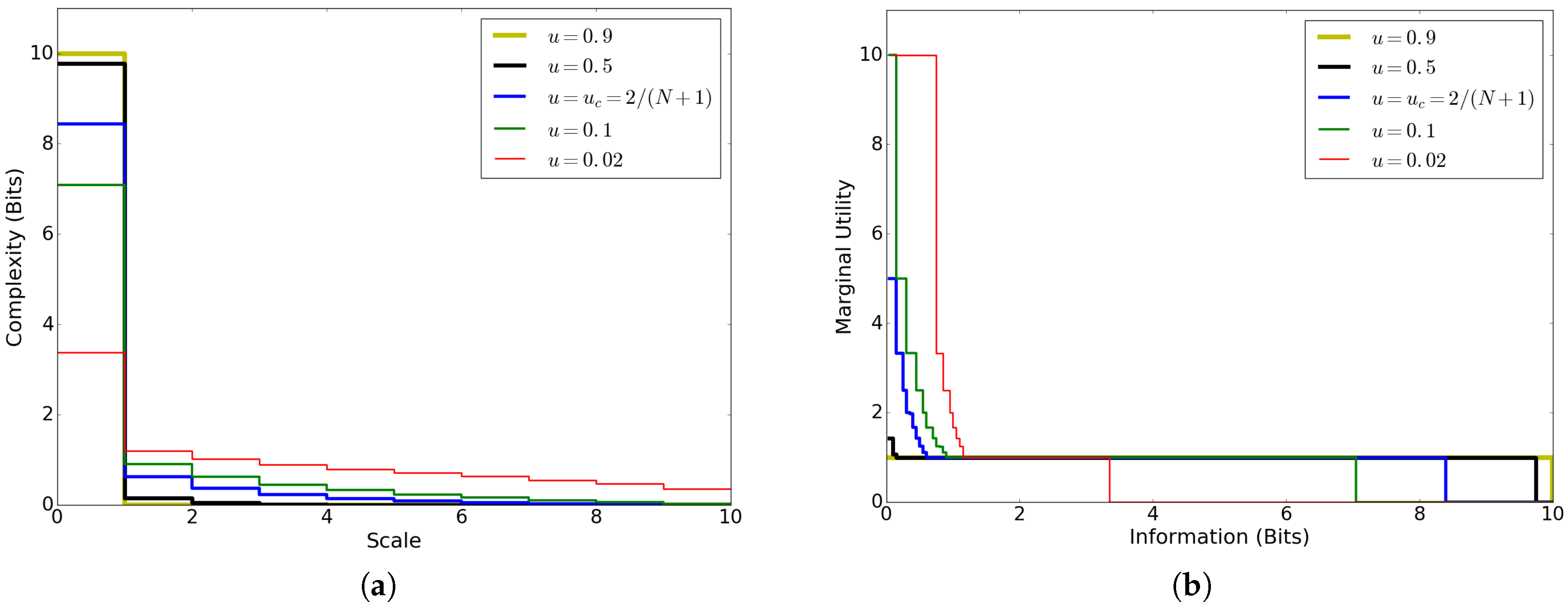
6. Complexity Profile
- Conservation law: The area under is equal to the total scale-weighted information of the system, and is therefore independent of the way the components depend on each other [13]:This result follows from the conservation law for scale-weighted information, Equation (11), as shown in Appendix A.
- Total system information: At the lowest scale , corresponds to the overall joint information: . For physical systems with the Shannon information function, this is the total entropy of the system, in units of information rather than the usual thermodynamic units.
- Additivity: If a system is the union of two independent subsystems and , the complexity profile of the full system is the sum of the profiles for the two subsystems, . We prove this property Appendix D.
7. Marginal Utility of Information
- (i)
- for all subsets .
- (ii)
- For any pair of nested subsets , .
- (iii)
- For any pair of subsets ,
- 1.
- Conservation law: The total area under the curve equals the total scale-weighted information of the system:This property follows from the observation that, since is the derivative of , the area under this curve is equal to the maximal utility of any descriptor, which is equal to since utility is defined in terms of scale-weighted information.
- 2.
- Total system information: The marginal utility vanishes for information values larger than the total system information, for , since, for higher values, the system has already been fully described.
- 3.
- Additivity: If separates into independent subsystems and , thenThe proof follows from recognizing that, since information can apply either to or to but not both, an optimal description allots some amount of information to subsystem , and the rest, , to subsystem . The optimum is achieved when the total maximal utility over these two subsystems is maximized. Taking the derivative of both sides and invoking the concavity of U yields a corresponding formula for the marginal utility M:Equations (21) and (22) are proven in Appendix E. This additivity property can also be expressed as the reflection (generalized inverse) of M. For any piecewise-constant, nonincreasing function f, we define the reflection asA generalized inverse [15] is needed since, for piecewise constant functions, there exist x-values for which there is no y such that . For such values, is the largest y such that does not exceed x. This operation is a reflection about the line , and applying it twice recovers the original function. If comprises independent subsystems and , the additivity property, Equation (22), can be written in terms of the reflection asEquation (24) is proven in Appendix E.
8. Reflection Principle for Systems of Independent Blocks
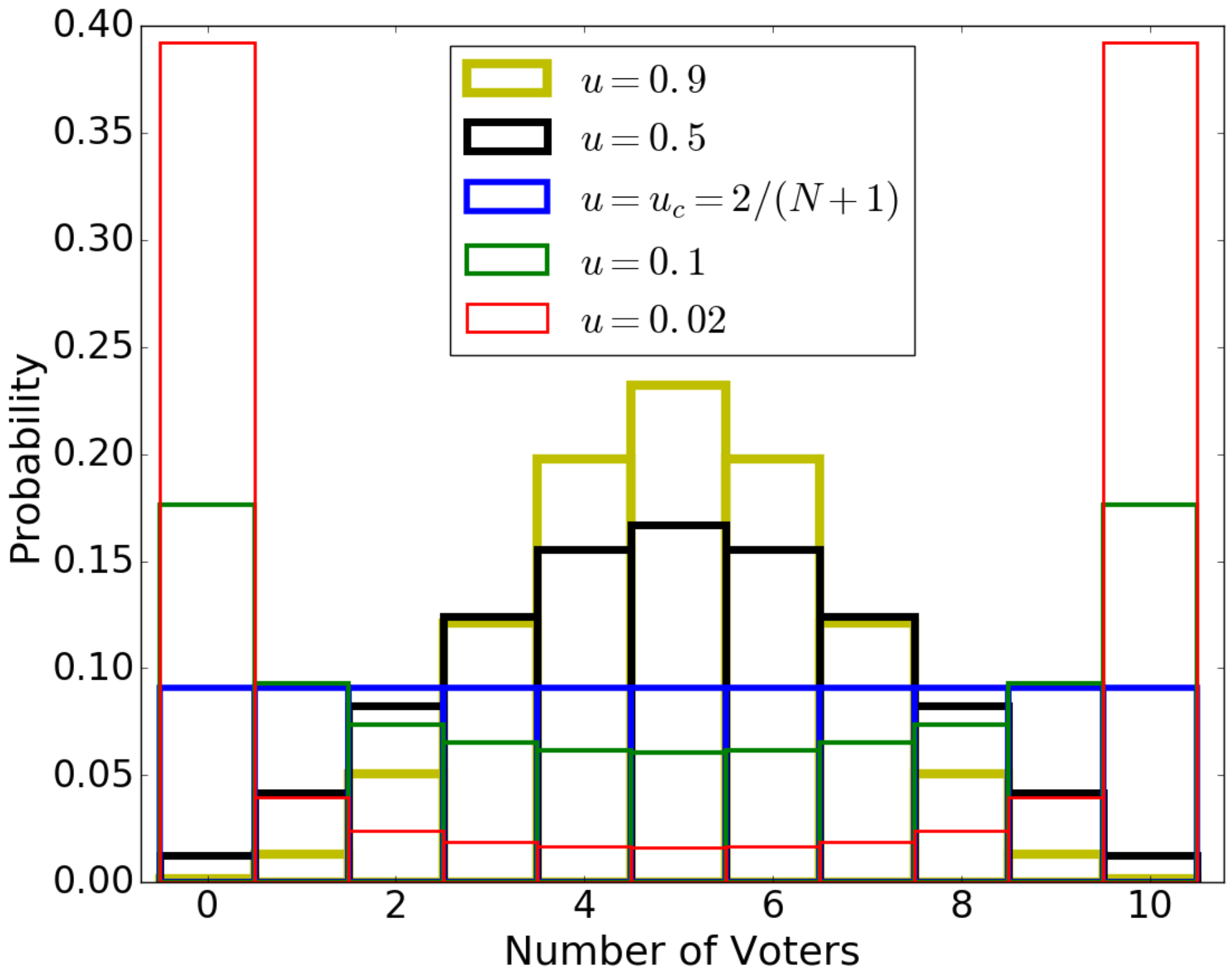
9. Application to Noisy Voter Model
- (i)
- for all ,
- (ii)
- for all ,
- (iii)
- for all .
10. Discussion
10.1. Potential Applications
10.2. Multivariate and Multiscale Information
10.3. Relation of the MUI to Other Measures
10.4. Multiscale Requisite Variety
10.5. Mechanistic versus Informational Dependencies
11. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Total Scale-Weighted Information
Appendix B. Complete Interdependence and Reduced Representations
Appendix C. Properties of Independence
Appendix D. Additivity of the Complexity Profile
Appendix E. Additivity of Marginal Utility of Information
- (i)
- for all .
- (ii)
- For any ,
- (iii)
- For any ,
- (iv)
- .
- (1)
- (2)
- , for all .
- If either
- −
- none of V, W, and belong to S,
- −
- all of V, W, and belong to S,
- −
- V and belong to S while W and do not, or
- −
- W and belong to S while V and do not,
then the difference on the left-hand side of Constraint (iii) has the same value for and —that is, the changes in each term cancel out in the difference. Thus Constraint (iii) is satisfied for since it is satisfied for . - If V, W, and belong to S while does not, thenThe left-hand side of Constraint (iii) therefore decreases when moving from to . So Constraint (iii) is satisfied for since it is satisfied for .
- The nontrivial case is that belongs to S while V, W and do not. ThenBy the definition of S and condition (1) on , we haveSubstituting into (A38) we haveApplying Constraint (iii) on twice to the right-hand side above, we haveBut Lemma A2 implies that for any subset . We apply this to the sets V, W, and to simplify the right-hand side above, yieldingas required.
- (v)
- ,
Appendix F. Marginal Utility of Information for Parity Bit Systems
- (i)
- for all ,
- (ii)
- for all ,
- (iii)
- for all ,
- (iv)
- .
References
- Bar-Yam, Y. Dynamics of Complex Systems; Westview Press: Boulder, CO, USA, 2003. [Google Scholar]
- Haken, H. Information and Self-Organization: A Macroscopic Approach to Complex Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Miller, J.H.; Page, S.E. Complex Adaptive Systems: An Introduction to Computational Models of Social Life; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Boccara, N. Modeling Complex Systems; Springer: New York, NY, USA, 2010. [Google Scholar]
- Newman, M.E.J. Complex Systems: A Survey. Am. J. Phys. 2011, 79, 800–810. [Google Scholar] [CrossRef]
- Kwapień, J.; Drożdż, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Sayama, H. Introduction to the Modeling and Analysis of Complex Systems; Open SUNY: Bunghamton, NY, USA, 2015. [Google Scholar]
- Sethna, J.P. Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Prokopenko, M.; Boschetti, F.; Ryan, A.J. An information-theoretic primer on complexity, self-organization, and emergence. Complexity 2009, 15, 11–28. [Google Scholar] [CrossRef]
- Gallagher, R.G. Information Theory and Reliable Communication; Wiley: Hoboken, NJ, USA, 1968. [Google Scholar]
- Bar-Yam, Y. Multiscale complexity/entropy. Adv. Complex Syst. 2004, 7, 47–63. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Multiscale variety in complex systems. Complexity 2004, 9, 37–45. [Google Scholar] [CrossRef]
- Bar-Yam, Y.; Harmon, D.; Bar-Yam, Y. Computationally tractable pairwise complexity profile. Complexity 2013, 18, 20–27. [Google Scholar] [CrossRef]
- Metzler, R.; Bar-Yam, Y. Multiscale complexity of correlated Gaussians. Phys. Rev. E 2005, 71, 046114. [Google Scholar] [CrossRef] [PubMed]
- Gheorghiu-Svirschevski, S.; Bar-Yam, Y. Multiscale analysis of information correlations in an infinite-range, ferromagnetic Ising system. Phys. Rev. E 2004, 70, 066115. [Google Scholar] [CrossRef] [PubMed]
- Stacey, B.C.; Allen, B.; Bar-Yam, Y. Multiscale Information Theory for Complex Systems: Theory and Applications. In Information and Complexity; Burgin, M., Calude, C.S., Eds.; World Scientific: Singapore, 2017; pp. 176–199. [Google Scholar]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P. The calculi of emergence: Computation, dynamics and induction. Phys. D Nonlinear Phenom. 1994, 75, 11–54. [Google Scholar] [CrossRef]
- Misra, V.; Lagi, M.; Bar-Yam, Y. Evidence of Market Manipulation in the Financial Crisis; Technical Report 2011-12-01; NECSI: Cambridge, MA, USA, 2011. [Google Scholar]
- Harmon, D.; Lagi, M.; de Aguiar, M.A.; Chinellato, D.D.; Braha, D.; Epstein, I.R.; Bar-Yam, Y. Anticipating Economic Market Crises Using Measures of Collective Panic. PLoS ONE 2015, 10, e0131871. [Google Scholar] [CrossRef] [PubMed]
- Green, H. The Molecular Theory of Fluids; North–Holland: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Nettleton, R.E.; Green, M.S. Expression in terms of molecular distribution functions for the entropy density in an infinite system. J. Chem. Phys. 1958, 29, 1365–1370. [Google Scholar] [CrossRef]
- Wolf, D.R. Information and Correlation in Statistical Mechanical Systems. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1996. [Google Scholar]
- Kardar, M. Statistical Physics of Particles; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kadanoff, L.P. Scaling laws for Ising models near Tc. Physics 1966, 2, 263. [Google Scholar]
- Wilson, K.G. The renormalization group: Critical phenomena and the Kondo problem. Rev. Mod. Phys. 1975, 47, 773. [Google Scholar] [CrossRef]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 46, 26–45. [Google Scholar] [CrossRef]
- Han, T.S. Multiple mutual information and multiple interactions in frequency data. Inf. Control 1980, 46, 26–45. [Google Scholar] [CrossRef]
- Yeung, R.W. A new outlook on Shannon’s information measures. IEEE Trans. Inf. Theory 1991, 37, 466–474. [Google Scholar] [CrossRef]
- Jakulin, A.; Bratko, I. Quantifying and visualizing attribute interactions. arXiv, 2003; arXiv:cs.AI/0308002. [Google Scholar]
- Bell, A.J. The co-information lattice. In Proceedings of the Fifth International Workshop on Independent Component Analysis and Blind Signal Separation (ICA), Nara, Japan, 1–4 April 2003; Volume 2003. [Google Scholar]
- Bar-Yam, Y. A mathematical theory of strong emergence using multiscale variety. Complexity 2004, 9, 15–24. [Google Scholar] [CrossRef]
- Krippendorff, K. Information of interactions in complex systems. Int. J. Gen. Syst. 2009, 38, 669–680. [Google Scholar] [CrossRef]
- Leydesdorff, L. Redundancy in systems which entertain a model of themselves: Interaction information and the self-organization of anticipation. Entropy 2010, 12, 63–79. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Rocha, L.M. Prediction and modularity in dynamical systems. arXiv, 2011; arXiv:1106.3703. [Google Scholar]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037109. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef] [PubMed]
- Ay, N.; Olbrich, E.; Bertschinger, N.; Jost, J. A unifying framework for complexity measures of finite systems. In Proceedings of the European Complex Systems Society (ECCS06), Oxford, UK, 25 September 2006. [Google Scholar]
- Bar-Yam, Y. Complexity of Military Conflict: Multiscale Complex Systems Analysis of Littoral Warfare; Technical Report; NECSI: Cambridge, MA, USA, 2003. [Google Scholar]
- Granovsky, B.L.; Madras, N. The noisy voter model. Stoch. Process. Appl. 1995, 55, 23–43. [Google Scholar] [CrossRef]
- Faddeev, D.K. On the concept of entropy of a finite probabilistic scheme. Uspekhi Mat. Nauk 1956, 11, 227–231. [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1957. [Google Scholar]
- Lee, P. On the axioms of information theory. Ann. Math. Stat. 1964, 35, 415–418. [Google Scholar] [CrossRef]
- Rényi, A. Probability Theory; Akadémiai Kiadó: Budapest, Hungary, 1970. [Google Scholar]
- Daróczy, Z. Generalized information functions. Inf. Control 1970, 16, 36–51. [Google Scholar] [CrossRef]
- Dos Santos, R.J. Generalization of Shannon’s theorem for Tsallis entropy. J. Math. Phys. 1997, 38, 4104–4107. [Google Scholar] [CrossRef]
- Abe, S. Axioms and uniqueness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy: Interdisciplinary Applications; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Furuichi, S. Information theoretical properties of Tsallis entropies. J. Math. Phys. 2006, 47, 023302. [Google Scholar] [CrossRef]
- Steudel, B.; Janzing, D.; Schölkopf, B. Causal Markov condition for submodular information measures. arXiv, 2010; arXiv:1002.4020. [Google Scholar]
- Dougherty, R.; Freiling, C.; Zeger, K. Networks, matroids, and non-Shannon information inequalities. IEEE Trans. Inf. Theory 2007, 53, 1949–1969. [Google Scholar] [CrossRef]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Chaitin, G.J. A theory of program size formally identical to information theory. J. ACM 1975, 22, 329–340. [Google Scholar] [CrossRef]
- May, R.M.; Arinaminpathy, N. Systemic risk: The dynamics of model banking systems. J. R. Soc. Interface 2010, 7, 823–838. [Google Scholar] [CrossRef] [PubMed]
- Haldane, A.G.; May, R.M. Systemic risk in banking ecosystems. Nature 2011, 469, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Beale, N.; Rand, D.G.; Battey, H.; Croxson, K.; May, R.M.; Nowak, M.A. Individual versus systemic risk and the Regulator’s Dilemma. Proc. Natl. Acad. Sci. USA 2011, 108, 12647–12652. [Google Scholar] [CrossRef] [PubMed]
- Erickson, M.J. Introduction to Combinatorics; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- James, R.G.; Crutchfield, J.P. Multivariate Dependence Beyond Shannon Information. arXiv, 2016; arXiv:1609.01233. [Google Scholar]
- Perfect, H. Independence theory and matroids. Math. Gaz. 1981, 65, 103–111. [Google Scholar] [CrossRef]
- Studenỳ, M.; Vejnarová, J. The multiinformation function as a tool for measuring stochastic dependence. In Learning in Graphical Models; Springer: Dodrecht, The Netherlands, 1998; pp. 261–297. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [PubMed]
- Polani, D. Foundations and formalizations of self-organization. In Advances in Applied Self-Organizing Systems; Springer: New York, NY, USA, 2008; pp. 19–37. [Google Scholar]
- Wets, R.J.B. Programming Under Uncertainty: The Equivalent Convex Program. SIAM J. Appl. Math. 1966, 14, 89–105. [Google Scholar] [CrossRef]
- James, R.G. Python Package for Information Theory. Zenodo 2017. [Google Scholar] [CrossRef]
- Slonim, N.; Tishby, L. Agglomerative information bottleneck. Adv. Neural Inf. Process. Syst. NIPS 1999, 12, 617–623. [Google Scholar]
- Shalizi, C.R.; Crutchfield, J.P. Information bottlenecks, causal states, and statistical relevance bases: How to represent relevant information in memoryless transduction. Adv. Complex Syst. 2002, 5, 91–95. [Google Scholar] [CrossRef]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. arXiv, 2000; arXiv:physics/0004057. [Google Scholar]
- Ziv, E.; Middendorf, M.; Wiggins, C. An information-theoretic approach to network modularity. Phys. Rev. E 2005, 71, 046117. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Hu, K.; Ivanov, P.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of Trends on Detrended Fluctuation Analysis. Phys. Rev. E 2002, 64, 011114. [Google Scholar] [CrossRef] [PubMed]
- Vereshchagin, N.; Vitányi, P. Kolmogorov’s structure functions and model selection. IEEE Trans. Inf. Theory 2004, 50, 3265–3290. [Google Scholar] [CrossRef]
- Grünwald, P.; Vitányi, P. Shannon information and Kolmogorov complexity. arXiv, 2004; arXiv:cs.IT/0410002. [Google Scholar]
- Vitányi, P. Meaningful information. IEEE Trans. Inf. Theory 2006, 52, 4617–4626. [Google Scholar] [CrossRef]
- Moran, P.A.P. Random processes in genetics. Math. Proc. Camb. Philos. Soc. 1958, 54, 60–71. [Google Scholar] [CrossRef]
- Harmon, D.; Stacey, B.C.; Bar-Yam, Y. Networks of Economic Market Independence and Systemic Risk; Technical Report 2009-03-01 (updated); NECSI: Cambridge, MA, USA, 2010. [Google Scholar]
- Stacey, B.C. Multiscale Structure in Eco-Evolutionary Dynamics. Ph.D. Thesis, Brandeis University, Waltham, MA, USA, 2015. [Google Scholar]
- Domb, C.; Green, M.S. (Eds.) Phase Transitions and Critical Phenomena; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Kardar, M. Statistical Physics of Fields; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Jacob, F.; Monod, J. Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 1961, 3, 318–356. [Google Scholar] [CrossRef]
- Britten, R.J.; Davidson, E.H. Gene regulation for higher cells: A theory. Science 1969, 165, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Carey, M.; Smale, S. Transcriptional Regulation in Eukaryotes: Concepts, Strategies, and Techniques; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2001. [Google Scholar]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.I.; Rinaldi, N.J.; Robert, F.; Odom, D.T.; Bar-Joseph, Z.; Gerber, G.K.; Hannett, N.M.; Harbison, C.T.; Thompson, C.M.; Simon, I.; et al. Transcriptional Regulatory Networks in Saccharomyces cerevisiae. Science 2002, 298, 799–804. [Google Scholar] [CrossRef] [PubMed]
- Boyer, L.A.; Lee, T.I.; Cole, M.F.; Johnstone, S.E.; Levine, S.S.; Zucker, J.P.; Guenther, M.G.; Kumar, R.M.; Murray, H.L.; Jenner, R.G.; et al. Core Transcriptional Regulatory Circuitry in Human Embryonic Stem Cells. Cell 2005, 122, 947–956. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Lloyd-Price, J.; Smolander, O.P.; Baici, W.C.; Hughes, T.R.; Yli-Harja, O.; Chua, G.; Ribeiro, A.S. Information propagation within the Genetic Network of Saccharomyces cerevisiae. BMC Syst. Biol. 2010, 4, 143. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, M.I.; Varona, P.; Selverston, A.I.; Abarbanel, H.D.I. Dynamical principles in neuroscience. Rev. Mod. Phys. 2006, 78, 1213–1265. [Google Scholar] [CrossRef]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef]
- Berdahl, A.; Torney, C.J.; Ioannou, C.C.; Faria, J.J.; Couzin, I.D. Emergent sensing of complex environments by mobile animal groups. Science 2013, 339, 574–576. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef] [PubMed]
- Allen, B.; Lippner, G.; Chen, Y.T.; Fotouhi, B.; Momeni, N.; Yau, S.T.; Nowak, M.A. Evolutionary dynamics on any population structure. Nature 2017, 544, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.; Taylor, H. On the distribution of stock price differences. Oper. Res. 1967, 15, 1057–1062. [Google Scholar] [CrossRef]
- Mantegna, R.N. Hierarchical structure in financial markets. Eur. Phys. J. B Condens. Matter Complex Syst. 1999, 11, 193–197. [Google Scholar] [CrossRef]
- Sornette, D. Why Stock Markets Crash: Critical Events in Complex Financial Systems; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- May, R.M.; Levin, S.A.; Sugihara, G. Complex systems: Ecology for bankers. Nature 2008, 451, 893–895. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer, F.; Fagiolo, G.; Sornette, D.; Vega-Redondo, F.; Vespignani, A.; White, D.R. Economic Networks: The New Challenges. Science 2009, 325, 422–425. [Google Scholar] [PubMed]
- Harmon, D.; De Aguiar, M.; Chinellato, D.; Braha, D.; Epstein, I.; Bar-Yam, Y. Predicting economic market crises using measures of collective panic. arXiv, 2011; arXiv:1102.2620. [Google Scholar] [CrossRef]
- Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell and Mind; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Brillouin, L. The negentropy principle of information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Stacey, B.C. Multiscale Structure of More-than-Binary Variables. arXiv, 2017; arXiv:1705.03927. [Google Scholar]
- Ashby, W.R. An Introduction to Cybernetics; Chapman & Hall: London, UK, 1956. [Google Scholar]
- Stacey, B.C.; Bar-Yam, Y. Principles of Security: Human, Cyber, and Biological; Technical Report 2008-06-01; NECSI: Cambridge, MA, USA, 2008. [Google Scholar]
- Dorogovtsev, S.N. Lectures on Complex Networks; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Dantzig, G.B.; Wolfe, P. Decomposition principle for linear programs. Oper. Res. 1960, 8, 101–111. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allen, B.; Stacey, B.C.; Bar-Yam, Y. Multiscale Information Theory and the Marginal Utility of Information. Entropy 2017, 19, 273. https://doi.org/10.3390/e19060273
Allen B, Stacey BC, Bar-Yam Y. Multiscale Information Theory and the Marginal Utility of Information. Entropy. 2017; 19(6):273. https://doi.org/10.3390/e19060273
Chicago/Turabian StyleAllen, Benjamin, Blake C. Stacey, and Yaneer Bar-Yam. 2017. "Multiscale Information Theory and the Marginal Utility of Information" Entropy 19, no. 6: 273. https://doi.org/10.3390/e19060273
APA StyleAllen, B., Stacey, B. C., & Bar-Yam, Y. (2017). Multiscale Information Theory and the Marginal Utility of Information. Entropy, 19(6), 273. https://doi.org/10.3390/e19060273





