Some Convex Functions Based Measures of Independence and Their Application to Strange Attractor Reconstruction
Abstract
:1. Introduction
2. Quality Factor (QF) of Quasientropy (QE)
2.1. Quasientropy
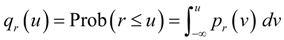 , where Prob(A) denotes the probability that event A occurs, and pr (·) is the probability density function (PDF) of r. Without loss of generality, consider two continuous variables r1 and r2. In the past one or two decades, the study of copulas has become a blooming field of statistical research [20]. Copula is the joint CDF of the transformed variables by their respective CDFs. The rationale of the study of copulas is that, to study the relation between two or more variables, we should nullify the effect of their marginal distributions and concentrate on their joint distribution. Based on this principle, we transform r1 and r2 by their respective CDFs as follows:
, where Prob(A) denotes the probability that event A occurs, and pr (·) is the probability density function (PDF) of r. Without loss of generality, consider two continuous variables r1 and r2. In the past one or two decades, the study of copulas has become a blooming field of statistical research [20]. Copula is the joint CDF of the transformed variables by their respective CDFs. The rationale of the study of copulas is that, to study the relation between two or more variables, we should nullify the effect of their marginal distributions and concentrate on their joint distribution. Based on this principle, we transform r1 and r2 by their respective CDFs as follows:

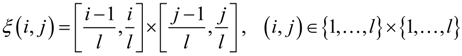
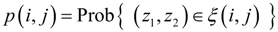
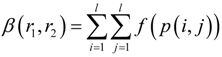
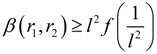
2.2. Quality Factor (QF) of QE
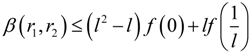
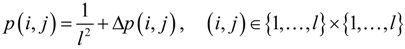
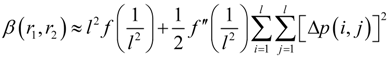
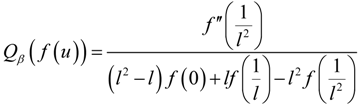
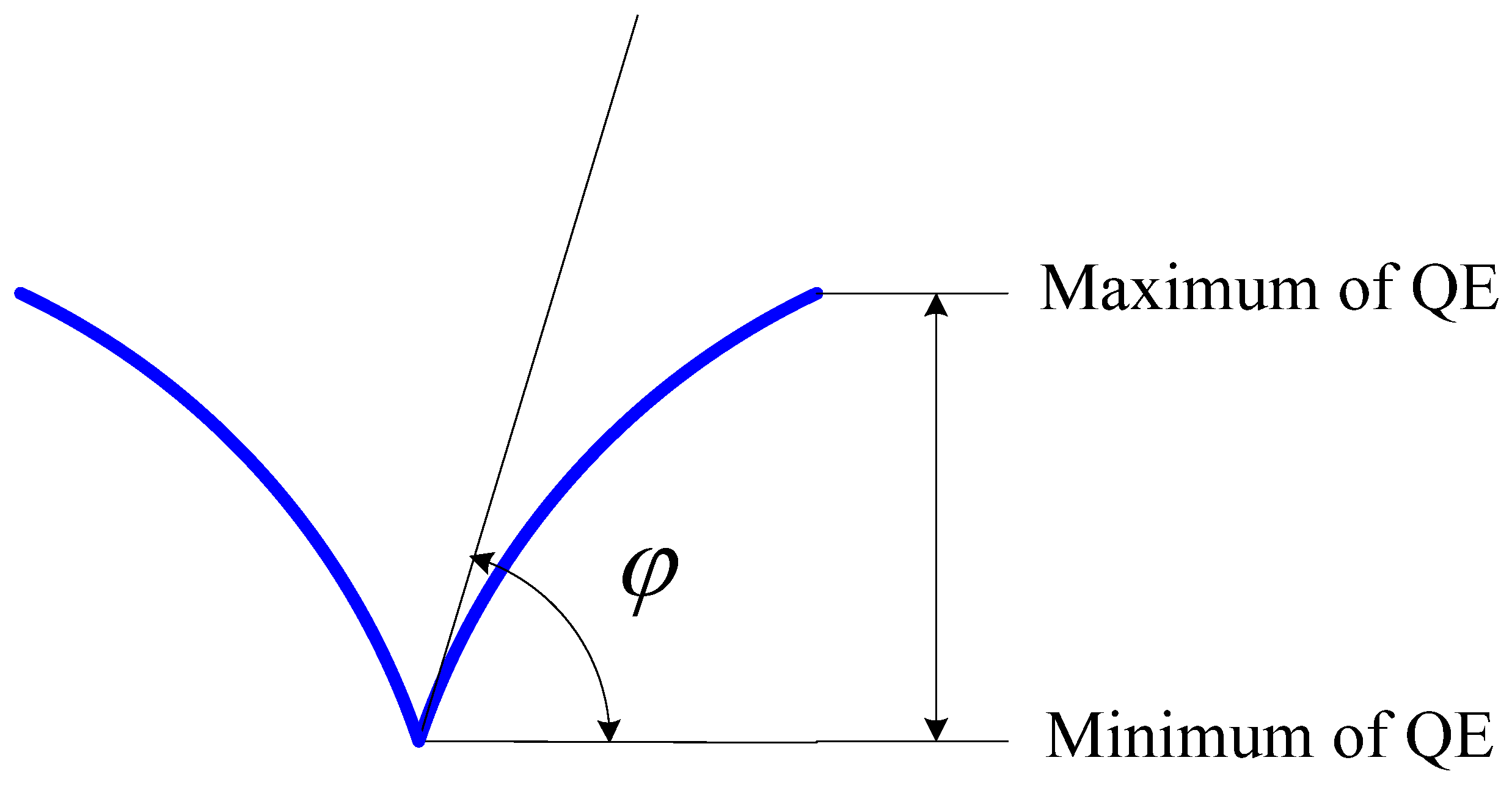
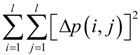 , and φ is the angle that is tangent to the curve of QE at the minimum of QE, then:
, and φ is the angle that is tangent to the curve of QE at the minimum of QE, then:
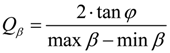
3. QF of Grid Occupancy (GO)
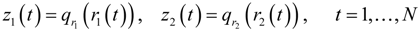
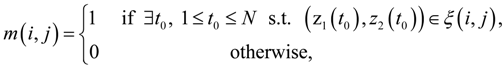
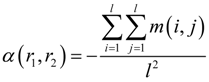
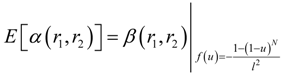
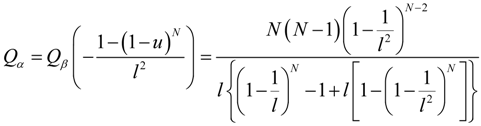
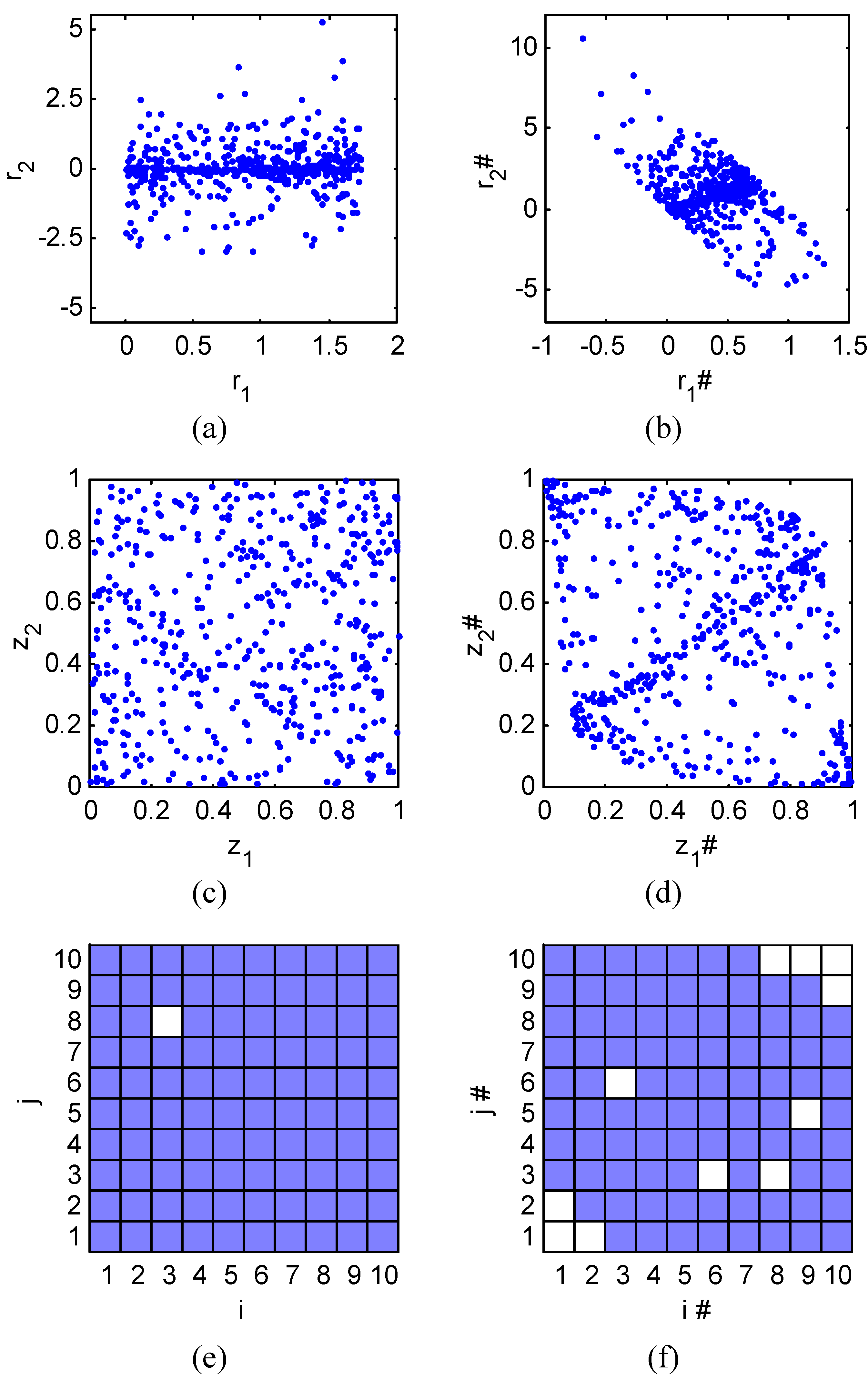
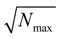 versus l. Right:
versus l. Right: 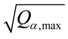 versus l.
versus l.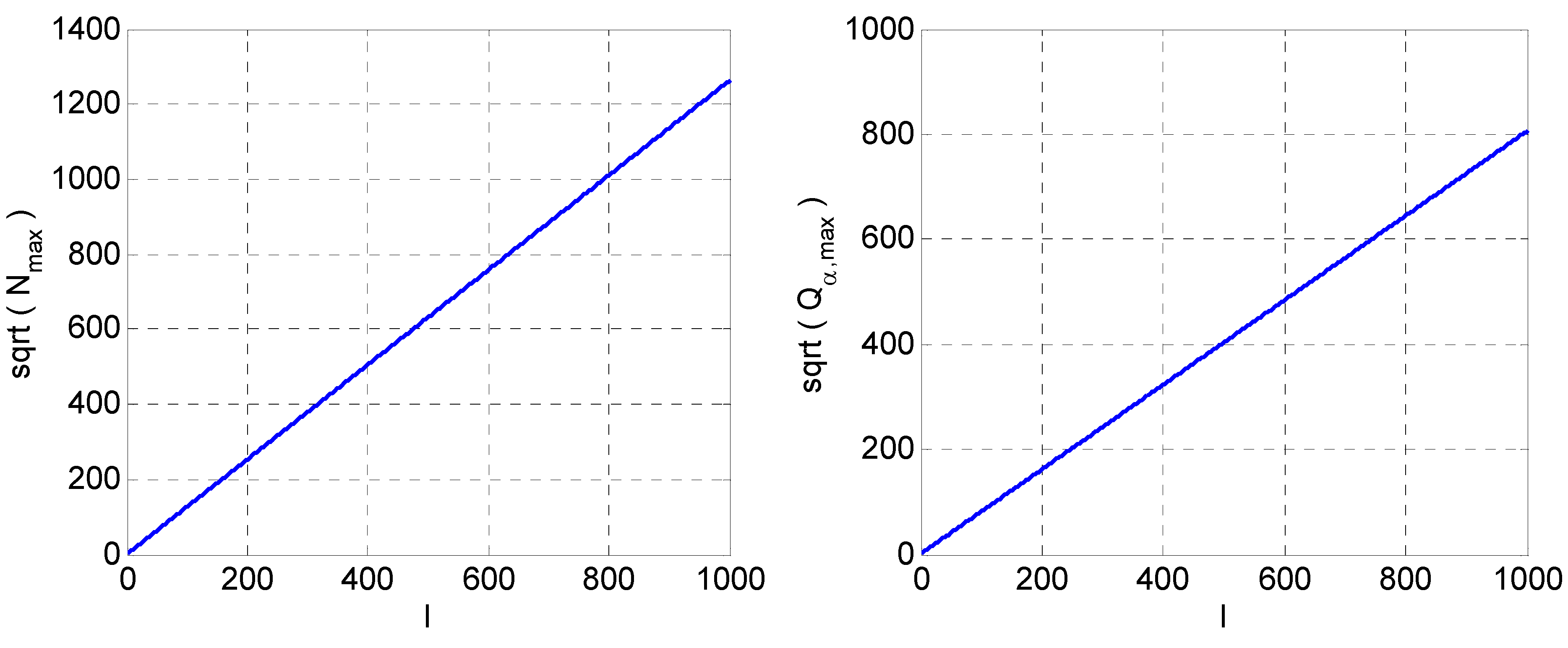
4. QF of Generalized Mutual Information (GMI)
4.1. QF of GMI
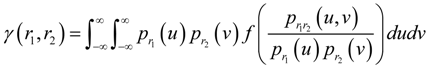
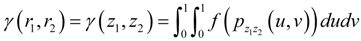
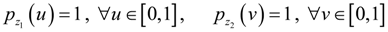
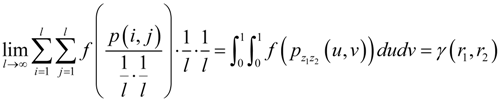
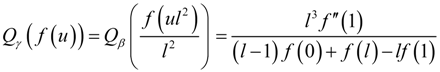
4.2. Existence of GMI
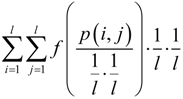 in (21) can be treated as the QE with convex function
in (21) can be treated as the QE with convex function 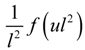 . Thus, (5) and (6) can be applied to this QE, which yield:
. Thus, (5) and (6) can be applied to this QE, which yield:
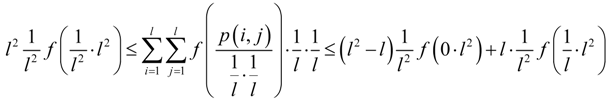
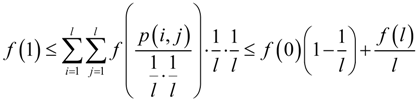
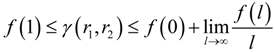
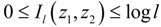
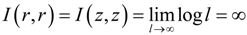
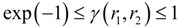
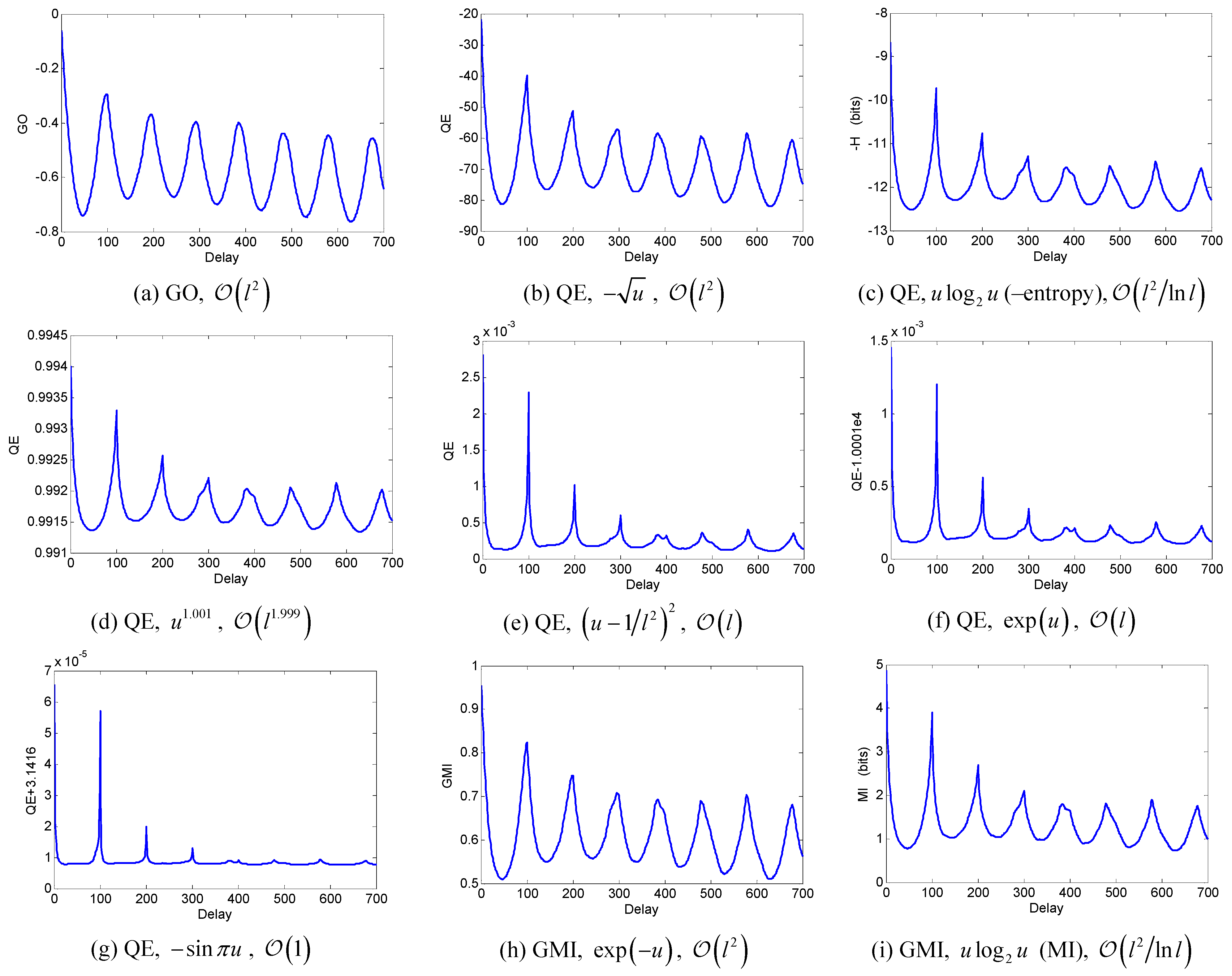
5. Orders of QFs with Respect to l
| f (u) | Qβ (f (u)) | Qγ (f (u)) |
| − ua (0 < a < 1) | 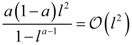 | 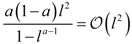 |
| u log u | 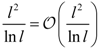 | 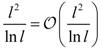 |
| ua (a > 1) | 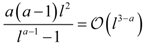 | 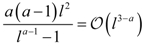 |
| au (a > 0, a ≠ 1) | 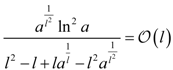 | 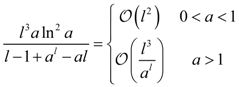 |
| −sin πu | 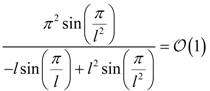 |
6. Numerical Experiments
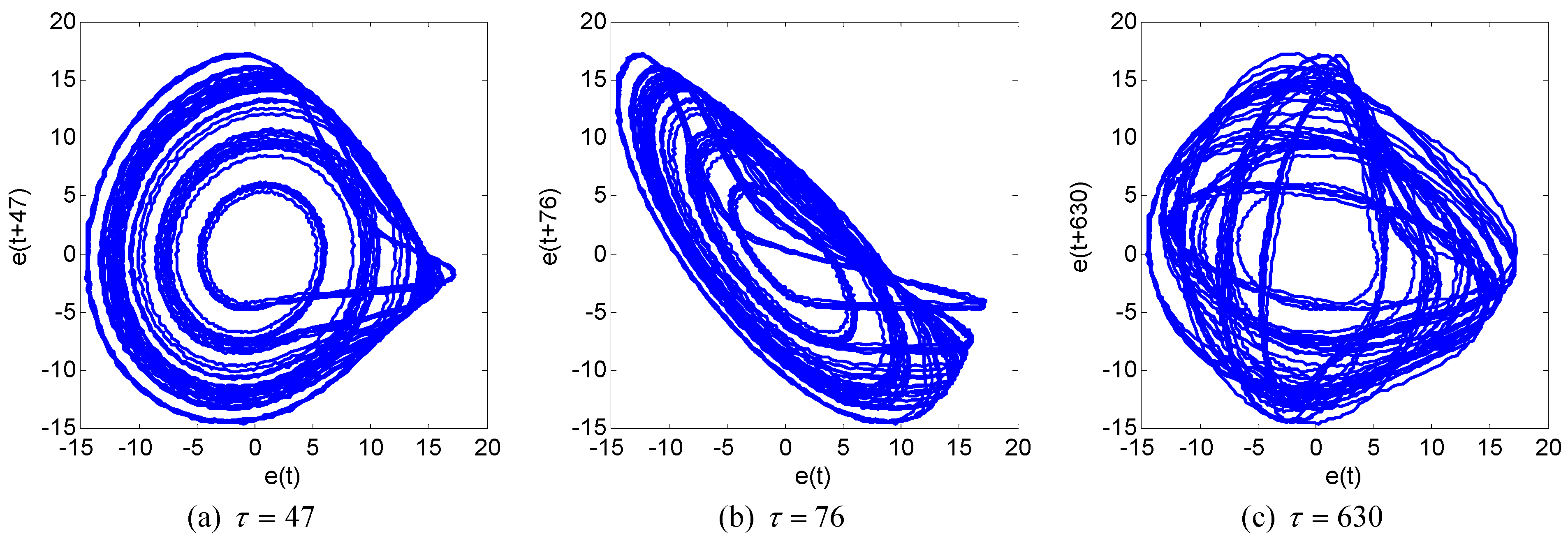
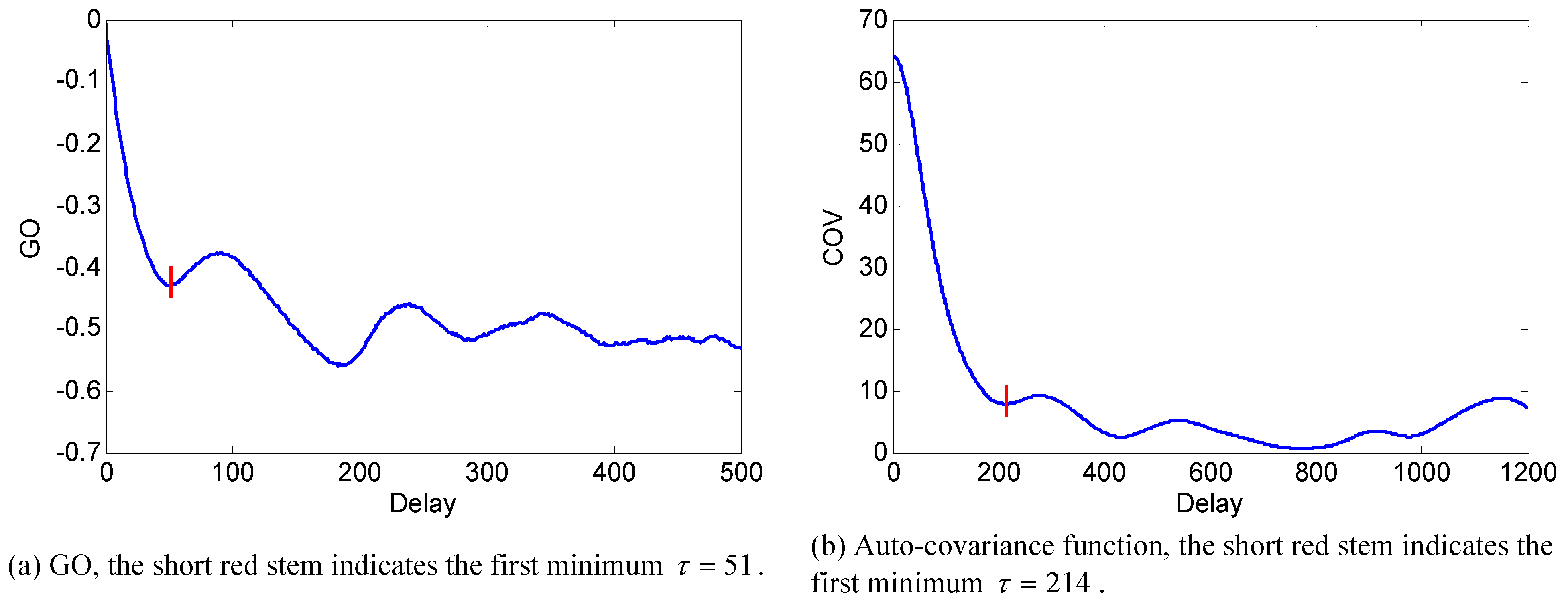
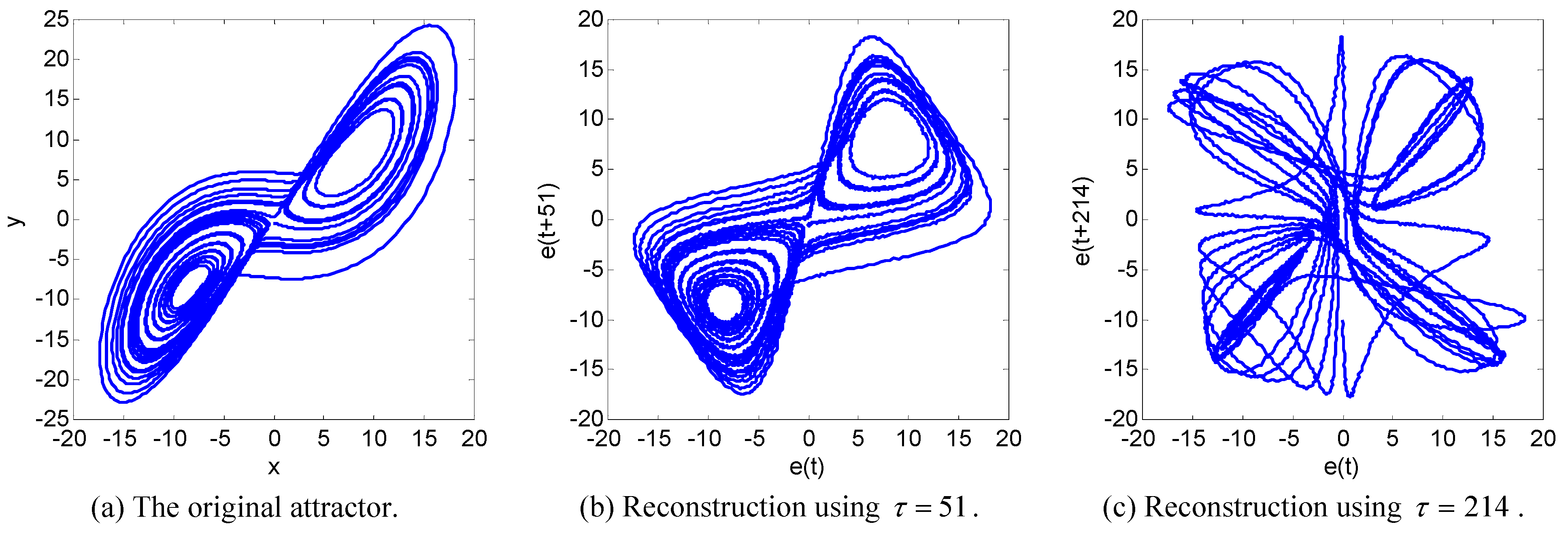
7. Conclusions
Acknowledgements
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Zemansky, M.W. Heat and Thermodynamics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Renyi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Havrda, J.; Charvat, F. Quantification method of classification processes. Kybernetika 1967, 1, 30–34. [Google Scholar]
- Csiszar, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kapur, J.N. Measures of Information and Their Applications; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Chen, Y. A novel grid occupancy criterion for independent component analysis. IEICE Trans. Fund. Electron. Comm. Comput. Sci. 2009, E92-A, 1874–1882. [Google Scholar] [CrossRef]
- Chen, Y. Blind separation using convex functions. IEEE Trans. Signal Process. 2005, 53, 2027–2035. [Google Scholar] [CrossRef]
- Kapur, J.N. Maximum-Entropy Models in Science and Engineering; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Xu, J.; Liu, Z.; Liu, R.; Yang, Q. Information transmission in human cerebral cortex. Physica D 1997, 106, 363–374. [Google Scholar] [CrossRef]
- Kolarczyk, B. Representing entropy with dispersion sets. Entropy 2010, 12, 420–433. [Google Scholar] [CrossRef]
- Takata, Y.; Tagashira, H.; Hyono, A.; Ohshima, H. Effect of counterion and configurational entropy on the surface tension of aqueous solutions of ionic surfactant and electrolyte mixtures. Entropy 2010, 12, 983–995. [Google Scholar] [CrossRef]
- Zupanovic, P.; Kuic, D.; Losic, Z.B.; Petrov, D.; Juretic, D.; Brumen, M. The maximum entropy production principle and linear irreversible processes. Entropy 2010, 12, 996–1005. [Google Scholar] [CrossRef]
- Van Dijck, G.; Van Hulle, M.M. Increasing and decreasing returns and losses in mutual information feature subset selection. Entropy 2010, 12, 2144–2170. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Warwick 1980 Lecture Notes in Mathematics; Springer-Verlag: Berlin, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Gretton, A.; Bousquet, O.; Smola, A.; Scholkopf, B. Measuring statistical dependence with Hilbert-Schmidt norms. In Proceedings of the 16th International Conference on Algorithmic Learning Theory, Singapore, October 2005; pp. 63–77.
- Szekely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, Lecture Notes in Statistics 139; Springer-Verlag: New York, NY, USA, 1999. [Google Scholar]
- Chen, Y. On Theory and Methods for Blind Information Extraction. Ph.D. dissertation, Southeast University, Nanjing, China, 2001. [Google Scholar]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Longstaff, M.G.; Heath, R.A. A nonlinear analysis of the temporal characteristics of handwriting. Hum. Movement Sci. 1999, 18, 485–524. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
Appendix: Recursive Algorithm for Computing GMI and Related Issues
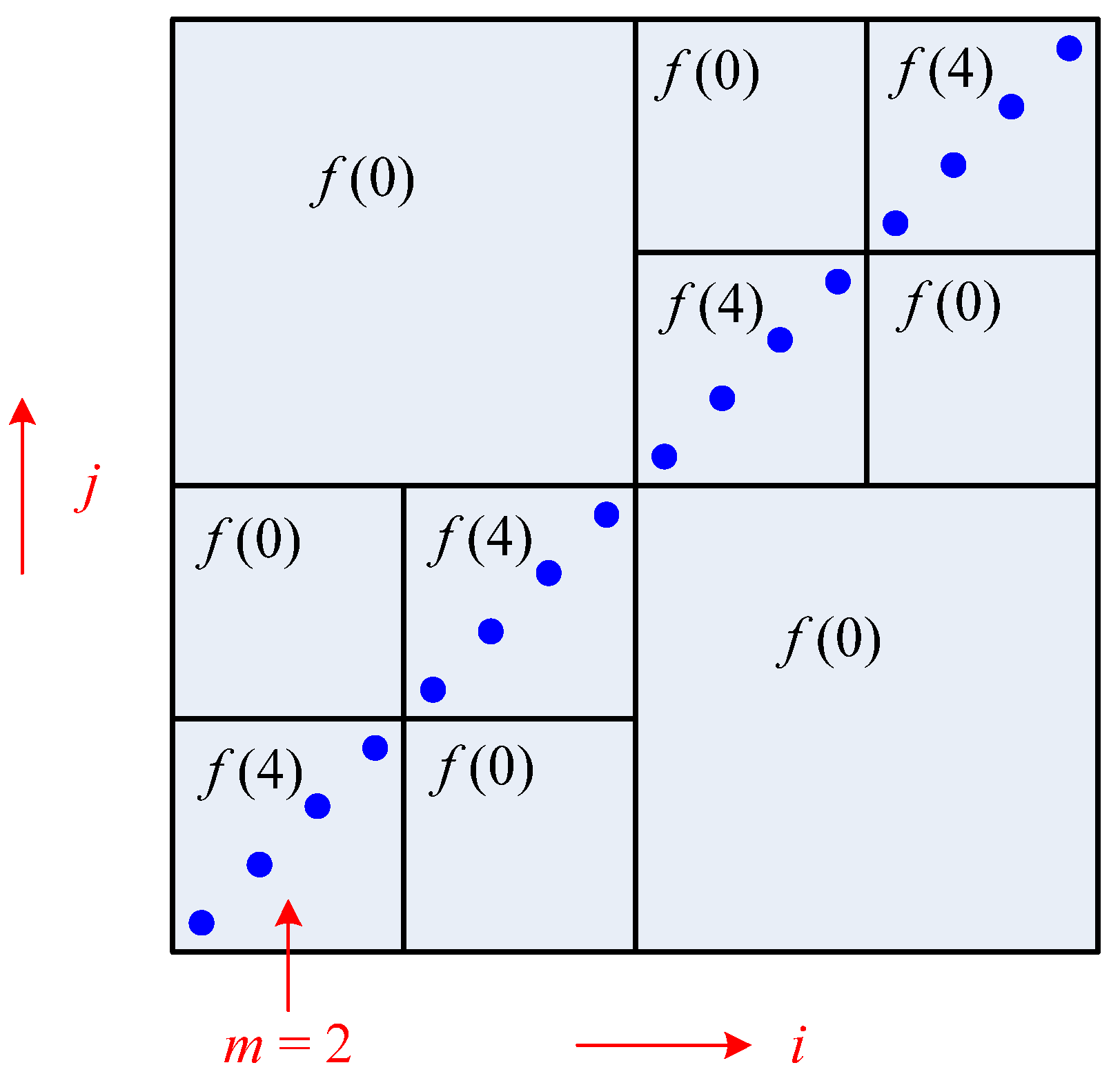
A. Recursive Algorithm for Computing GMI

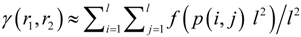 . Alternatively, a more delicate approach can be taken. Namely, different numbers of quantization levels are used according to the bumpiness of pz1z2 in different local regions. Larger l should be taken in more fluctuant regions to avoid the estimated γ from being too small, whereas smaller l should be taken in rather flat regions to avoid the estimated γ from being too large due to limited sample size.
. Alternatively, a more delicate approach can be taken. Namely, different numbers of quantization levels are used according to the bumpiness of pz1z2 in different local regions. Larger l should be taken in more fluctuant regions to avoid the estimated γ from being too small, whereas smaller l should be taken in rather flat regions to avoid the estimated γ from being too large due to limited sample size.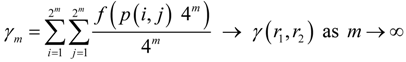
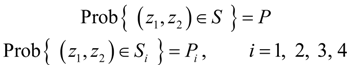
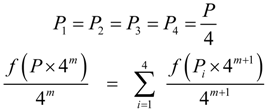
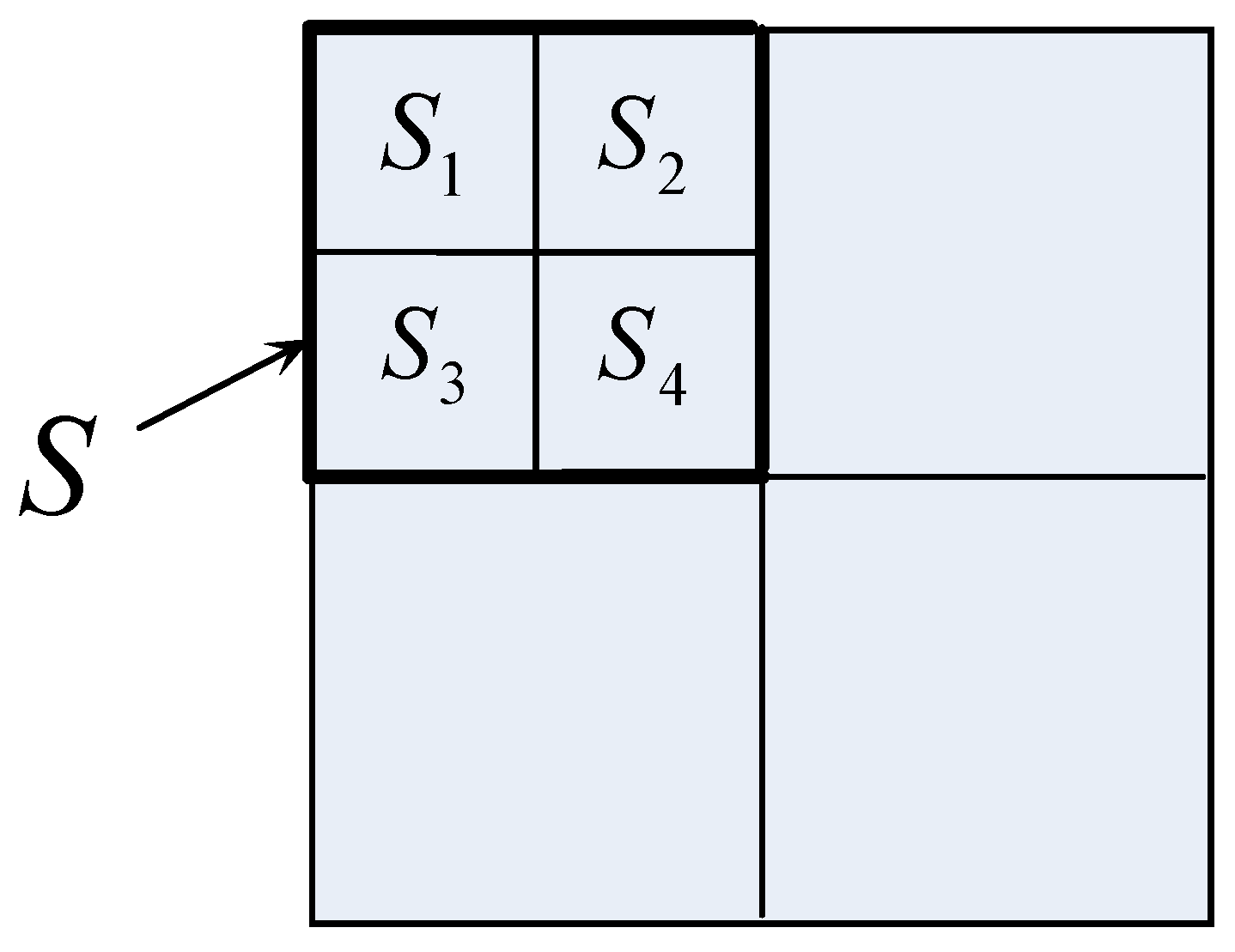
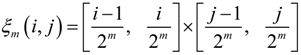
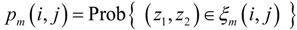
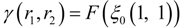
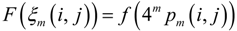
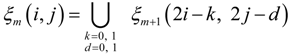
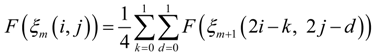
B. Uniformity Test
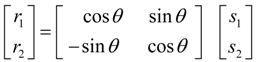
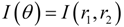
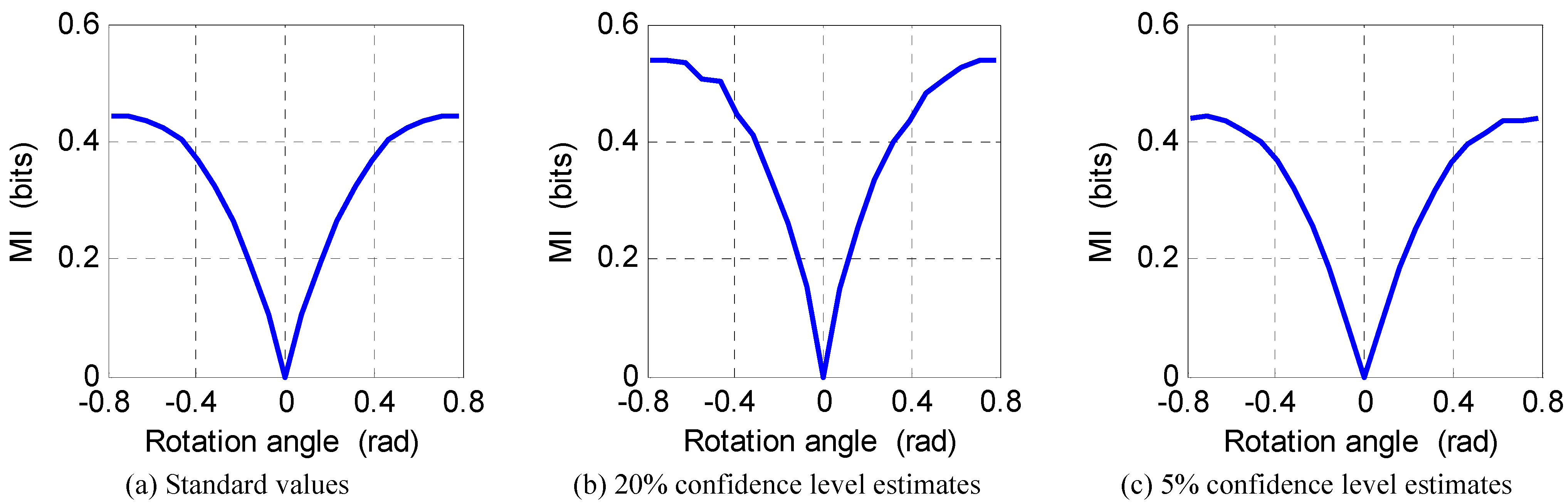
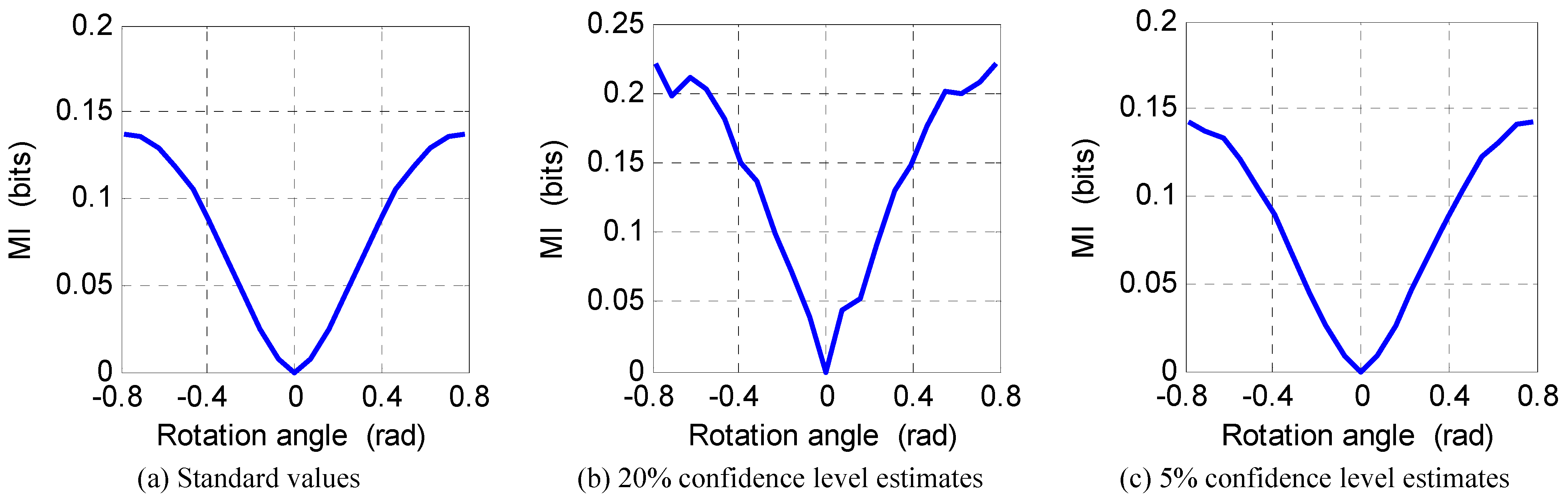
C. Practical Implementation
D. Output of the Recursive Algorithm of GMI
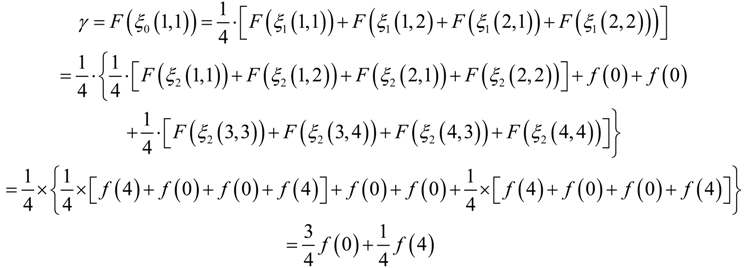
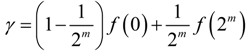
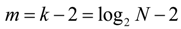
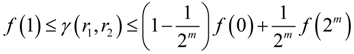
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, Y.; Aihara, K. Some Convex Functions Based Measures of Independence and Their Application to Strange Attractor Reconstruction. Entropy 2011, 13, 820-840. https://doi.org/10.3390/e13040820
Chen Y, Aihara K. Some Convex Functions Based Measures of Independence and Their Application to Strange Attractor Reconstruction. Entropy. 2011; 13(4):820-840. https://doi.org/10.3390/e13040820
Chicago/Turabian StyleChen, Yang, and Kazuyuki Aihara. 2011. "Some Convex Functions Based Measures of Independence and Their Application to Strange Attractor Reconstruction" Entropy 13, no. 4: 820-840. https://doi.org/10.3390/e13040820
APA StyleChen, Y., & Aihara, K. (2011). Some Convex Functions Based Measures of Independence and Their Application to Strange Attractor Reconstruction. Entropy, 13(4), 820-840. https://doi.org/10.3390/e13040820




