Comparative Evaluation of Inductively Coupled Plasma Mass Spectrometry (ICP-MS) and X-Ray Fluorescence (XRF) Analysis Techniques for Screening Potentially Toxic Elements in Soil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Soil Sampling
2.3. Determination of PTE Contents Using XRF and ICP-MS Techniques
2.4. Statistical Analyses
3. Results and Discussion
3.1. Specific-Element Variability and Trends
- Strontium (Sr): ICP-MS and XRF produce similar distributions, though XRF reports a slightly higher median value.
- Nickel (Ni): The ICP-MS distribution appears more skewed, with a few samples displaying significantly higher concentrations than the rest.
- Chromium (Cr): The XRF distribution has a wider tail on the higher concentration side, suggesting a tendency for overestimation in some samples.
- Vanadium (V): ICP-MS and XRF exhibit noticeable differences, with XRF yielding a tighter distribution and less variability.
- Arsenic (As): XRF measurements appear more uniformly distributed, whereas ICP-MS results include a few higher outliers, suggesting greater sensitivity in detecting lower-concentration variations.
- Lead (Pb): Both methods demonstrate high variability, but ICP-MS reports more extreme values, potentially due to its greater sensitivity at lower concentrations.
3.2. Statistical Validation: Paired t-Test and Wilcoxon Signed-Rank Test Analysis
3.3. Bar Chart
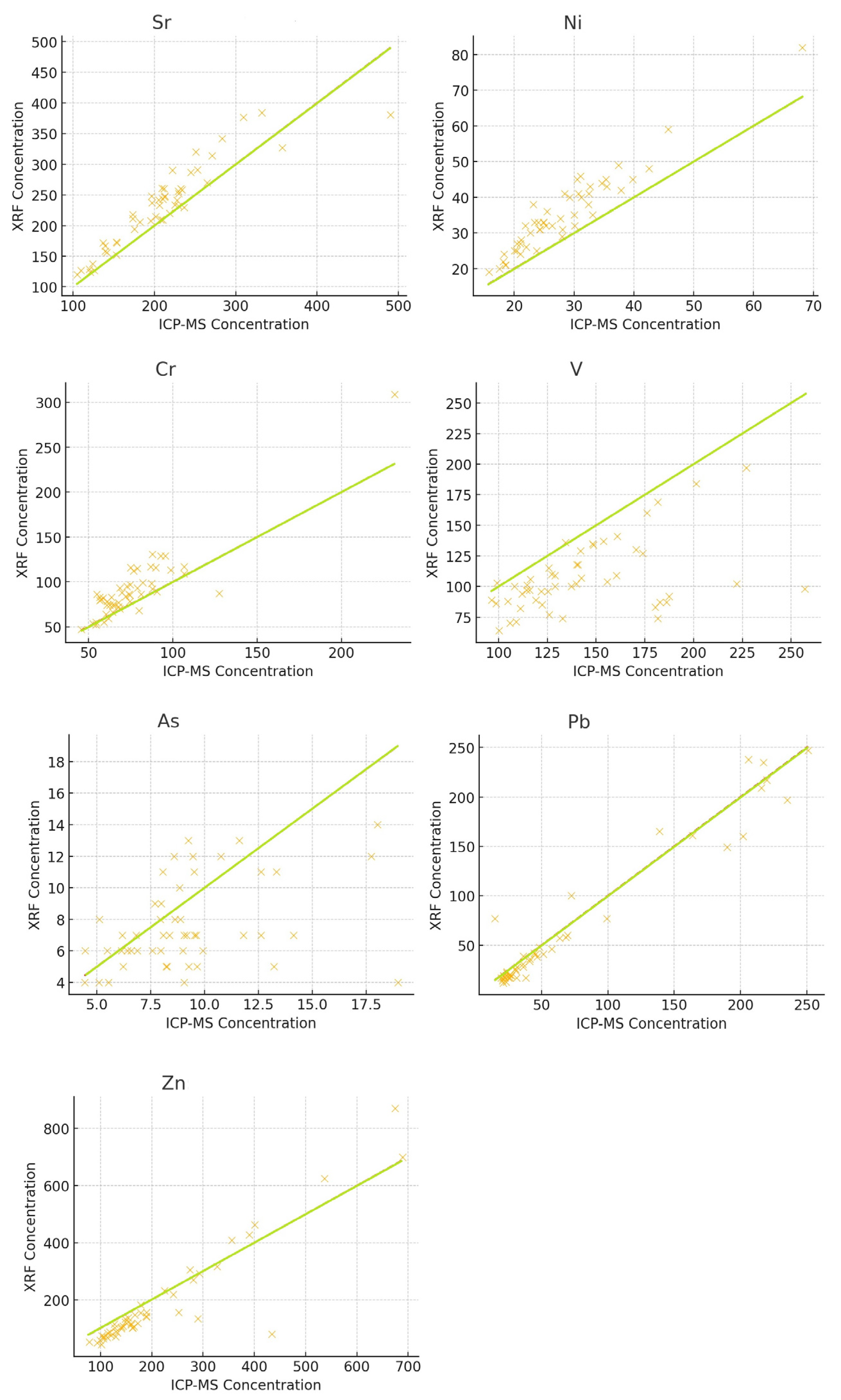
3.4. Regression Trends
3.5. Correlation Analysis
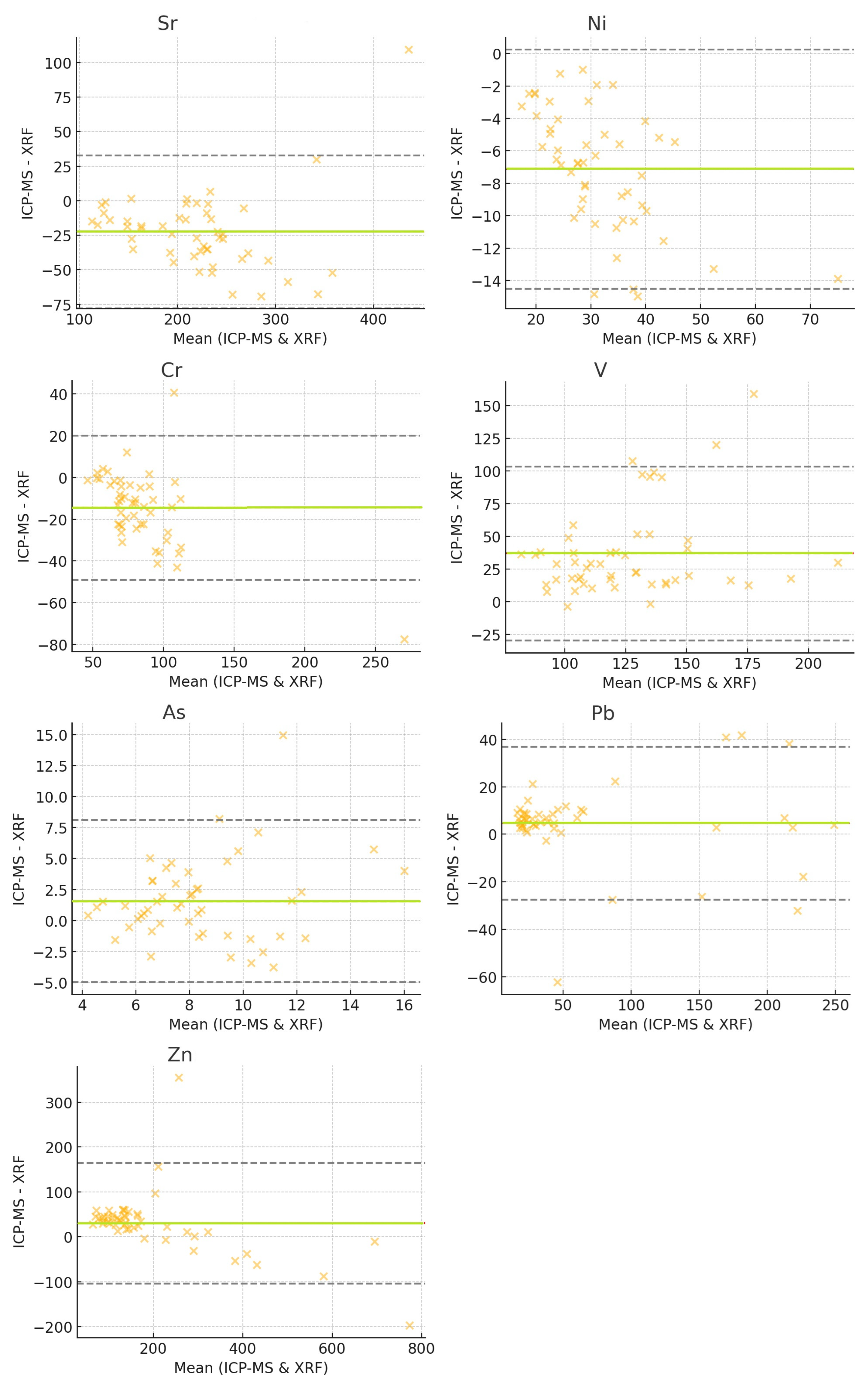
3.6. Bland–Altman Plot Analysis
- the sample CSRN137 exhibited an extreme difference of +109.39, with ICP-MS reporting 490.39 and XRF reporting 381.
- the samples CSRN020, CSRN024, and CSRN126 showed a ~15 unit lower value in ICP-MS compared to XRF.
- the sample CSRN074 showed an ICP-MS value of 231.56 and an XRF value of 309 (−77.44 difference)
- the sample CSRN097 showed an ICP-MS value of 127.61 vs. an XRF value of 87 (+40.61 difference).
- the sample CSRN135, with a +159.03 difference (ICP-MS 257.03 vs. XRF 98),
- the sample CSRN042, with a +107.58 difference,
- the sample CSRN133 with a +120.03 difference.
- the sample CSRN042 (+14.98), with ICP-MS 18.97 and XRF 4.
- with the sample CSRN113 showed a difference of -62.15, with ICP-MS being 14.85 and XRF 77.
- the sample CSRN067: a difference of +355.22, with being ICP-MS 434.22 and XRF 79.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambrosino, M.; Albanese, S.; De Vivo, B.; Guagliardi, I.; Guarino, A.; Lima, A.; Cicchella, D. Identification of Rare Earth Elements (REEs) distribution patterns in the soils of Campania region (Italy) using compositional and multivariate data analysis. J. Geochem. Explor. 2022, 243, 107112. [Google Scholar] [CrossRef]
- Yu, B.; Lu, X.; Fan, X.; Fan, P.; Zuo, L.; Yang, Y.; Wang, L. Analyzing environmental risk, source and spatial distribution of potentially toxic elements in dust of residential area in Xi’an urban area, China. Ecotoxicol. Environ. Saf. 2021, 208, 111679. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Yuan, C.; Hassan Farooq, T.; Chen, P.; Yang, M.; Ouyang, Z.; Fu, Y.; Yuan, Y.; Wang, G.; Yan, W.; et al. Pollution index and distribution characteristics of soil heavy metals among four distinct land use patterns of Taojia River Basin in China. Gondwana Res. 2024, 135, 198–207. [Google Scholar] [CrossRef]
- Su, C.; Yang, Y.; Jia, M.; Yan, Y. Integrated framework to assess soil potentially toxic element contamination through 3D pollution analysis in a typical mining city. Chemosphere 2024, 359, 142378. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Tarvainen, T.; Jarva, J.; Guagliardi, I. Spatial variability and trigger values of arsenic in the surface urban soils of the cities of Tampere and Lahti, Finland. Environ. Earth Sci. 2016, 75, 896. [Google Scholar] [CrossRef]
- Huang, J.; Wu, Y.; Sun, J.; Li, X.; Geng, X.; Zhao, M.; Fan, Z. Health risk assessment of heavy metal(loid)s in park soils of the largest megacity in China by using Monte Carlo simulation coupled with Positive matrix factorization model. J. Hazard Mater. 2021, 415, 125629. [Google Scholar] [CrossRef]
- Xiang, P.; Han, Y.-H.; Li, H.-B.; Gao, P. Editorial: Advanced analytical techniques for heavy metals speciation in soil, crop, and human samples. Front. Chem. 2023, 11, 1151371. [Google Scholar] [CrossRef]
- Guagliardi, I. Editorial for the Special Issue “Potentially Toxic Elements Pollution in Urban and Suburban Environments”. Toxics 2022, 10, 775. [Google Scholar] [CrossRef]
- Haghighizadeh, A.; Rajabi, O.; Nezarat, A.; Hajyani, Z.; Haghmohammadi, M.; Hedayatikhah, S.; Delnabi Asl, S.; Aghababai Beni, A. Comprehensive analysis of heavy metal soil contamination in mining Environments: Impacts, monitoring Techniques, and remediation strategies. Arab. J. Chem. 2024, 17, 105777. [Google Scholar] [CrossRef]
- Gonçalves, D.A.M.; Pereira, W.V.d.S.; Johannesson, K.H.; Pérez, D.V.; Guilherme, L.R.G.; Fernandes, A.R. Geochemical background for potentially toxic elements in forested soils of the state of Pará, Brazilian Amazon. Minerals 2022, 12, 674. [Google Scholar] [CrossRef]
- Ahmed, A.Y.; Abdullah, M.P.; Wood, A.K.; Hamza, M.S.; Othman, M. Determination of some trace elements in marine sediment using ICP-MS and XRF (a comparative study). Orient. J. Chem. 2013, 29, 645–653. [Google Scholar] [CrossRef]
- Elkadi, M.; Pillay, A.; Manuel, J.; Khan, M.R.; Stephen, S.; Molki, A. Sustainability study on heavy metal uptake in neem biodiesel using selective catalytic preparation and hyphenated mass spectrometry. Sustainability 2014, 6, 2413–2423. [Google Scholar] [CrossRef]
- Vrdoljak, G.; Palmer, P.T.; Jacobs, R.M.; Moezzi, B.; Viegas, A. Comparison of XRF, TXRF, and ICP-MS methods for determination of mercury in face creams. J. Med. Radiat. Sci. 2021, 9, 1–8. [Google Scholar] [CrossRef]
- Aarab, I.; Chakir, E.; Maazouzi, Y.; Bounouira, H.; Didi, A.; Amsil, H.; Badague, A. Major and trace elements content in cannabis sativa–l cultivated in north of Morocco and heavy metals health risk assessment. E3S Web Conf. 2023, 469, 00027. [Google Scholar] [CrossRef]
- Lohmeier, S.G.; Lottermoser, B.G.; Schirmer, T.; Gallhofer, D. Copper slag as a potential source of critical elements—A case study from Tsumeb, Namibia. J. South. Afr. Inst. Min. Metall. 2021, 121, 129–142. [Google Scholar] [CrossRef]
- Bowler, R.M.; Beseler, C.L.; Gocheva, V.; Colledge, M.; Kornblith, E.; Julian, J.R.; Lobdell, D.T. Environmental exposure to manganese in air: Associations with tremor and motor function. Sci. Total Environ. 2016, 541, 646–654. [Google Scholar] [CrossRef]
- Delgado, M.; Jason, P.; Humberto, G.; Alba, C.; Gustavo, C.; Alfredo, C.; Alberto, D.; Jorge, G. Comparison of ICP-OES and XRF performance for Pb and As analysis in environmental soil samples from Chihuahua City, Mexico. Phys. Rev. Res. Int. 2011, 1, 29–44. [Google Scholar]
- Congiu, A.; Perucchini, S.; Cesti, P. Trace metal contaminants in sediments and soils: Comparison between ICP and XRF quantitative determination. E3S Web Conf. 2013, 1, 09004. [Google Scholar] [CrossRef]
- Kalnicky, D.J.; Singhvi, R. Field portable XRF analysis of environmental samples. J. Hazard. Mater. 2001, 83, 93–122. [Google Scholar] [CrossRef]
- Roberts, A.A.; Guimarães, D.; Tehrani, M.W.; Lin, S.; Parsons, P.J. A field-based evaluation of portable XRF to screen for toxic metals in seafood products. X-Ray Spectrom. 2023, 53, 506–519. [Google Scholar] [CrossRef]
- Guimarães, D.; Praamsma, M.L.; Parsons, P.J. Evaluation of a new optic-enabled portable X-ray fluorescence spectrometry instrument for measuring toxic metals/metalloids in consumer goods and cultural products. Spectrochim. Acta B 2016, 122, 192–202. [Google Scholar] [CrossRef] [PubMed]
- McComb, J.; Rogers, C.; Han, F.X.; Tchounwou, P.B. Rapid screening of heavy metals and trace elements in environmental samples using portable X-ray fluorescence spectrometer, a comparative study. Water Air Soil Pollut. 2014, 225, 2169. [Google Scholar] [CrossRef] [PubMed]
- Gauglitz, G.; Vo-Dinh, T. Handbook of Spectroscopy; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2003. [Google Scholar] [CrossRef]
- Fukai, M.; Kikawada, Y.; Oi, T. Determination of lanthanoids in seawater by inductively coupled plasma mass spectrometry after pre-concentration with a chelating resin disk. Nat. Sci. 2016, 8, 431–441. [Google Scholar] [CrossRef]
- Palmer, P.T.; Jacobs, R.M.; Yee, S.; Li, T.; Reed, C.; Nebenzahl, D.; Douglas, M. Best practices for the use of portable X-ray fluorescence analyzers to screen for toxic elements in fda-regulated products. J. Regul. Sci. 2019, 7, 1–11. [Google Scholar] [CrossRef]
- Almusawi, A.A.H.; Jebril, N.; AL-Auhaimid, A.A.H.; Hammoodi, Z.H.K. Carpal tunnel syndrome and calcium deposit in the surgically transacted transverse carpal ligament. Sci. World J. 2022, 2022, 2864485. [Google Scholar] [CrossRef]
- McIver, D.J.; VanLeeuwen, J.; Knafla, A.L.; Campbell, J.A.; Alexander, K.; Gherase, M.R.; Fleming, D. Evaluation of a novel portable X-ray fluorescence screening tool for detection of arsenic exposure. Physiol. Meas. 2015, 36, 2443–2459. [Google Scholar] [CrossRef]
- Little, N.C.; Florey, V.; Molina, I.; Owsley, D.W.; Speakman, R.J. Measuring heavy metal content in bone using portable X-ray fluorescence. J. Open Archaeol. 2014, 2, 19–21. [Google Scholar] [CrossRef]
- Ricca, N.; Guagliardi, I. Evidences of Soil Consumption Dynamics over Space and Time by Data Analysis in a Southern Italy Urban Sprawling Area. Land 2023, 12, 1056. [Google Scholar] [CrossRef]
- Iovine, G.; Guagliardi, I.; Bruno, C.; Greco, R.; Tallarico, A.; Falcone, G.; Lucà, F.; Buttafuoco, G. Soil-gas radon anomalies in three study areas of Central-Northern Calabria (Southern Italy). Nat. Hazards 2018, 91, 193–219. [Google Scholar] [CrossRef]
- Tansi, C.; Muto, F.; Critelli, S.; Iovine, G. Neogene-Quaternary strike-slip tectonics in the central Calabrian Arc (southern Italy). J. Geodyn. 2007, 43, 393–414. [Google Scholar] [CrossRef]
- Van Dijk, J.P.; Bello, M.; Brancaleoni, G.P.; Cantarella, G.; Costa, V.; Frixa, A.; Golfetto, F.; Merlini, S.; Riva, M.; Torricelli, S. A regional structural model for the northern sector of the Calabrian Arc (Southern Italy). Tectonophysics 2000, 324, 267–320. [Google Scholar] [CrossRef]
- Gaglioti, S.; Infusino, E.; Caloiero, T.; Callegari, G.; Guagliardi, I. Geochemical Characterization of Spring Waters in the Crati River Basin, Calabria (Southern Italy). Geofluids 2019, 2019, 3850148. [Google Scholar] [CrossRef]
- Guagliardi, I.; Astel, A.M.; Cicchella, D. Exploring Soil Pollution Patterns Using Self-Organizing Maps. Toxics 2022, 10, 416. [Google Scholar] [CrossRef] [PubMed]
- Infusino, E.; Guagliardi, I.; Gaglioti, S.; Caloiero, T. Vulnerability to Nitrate Occurrence in the Spring Waters of the Sila Massif (Calabria, Southern Italy). Toxics 2022, 10, 137. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2006; First Update 2007; World Soil Resources Reports No. 103; FAO: Rome, Italy, 2007. [Google Scholar]
- Soil Survey Staff. Keys to Soil Taxonomy, 11th ed.; USDA-NRCS: Washington DC, USA, 2010. [Google Scholar]
- R.S.S.A. (Agenzia Regionale per lo Sviluppo e per i Servizi in Agricoltura). I suoli della Calabria. Carta dei suoli in scala 1: 250000 della Regione Calabria. In Monografia Divulgativa: Programma Interregionale Agricoltura-Qualità—Misura 5, ARSSA, Servizio Agropedologia; Rubbettino Editore: Catanzaro, Italy, 2003. [Google Scholar]
- Buttafuoco, G.; Caloiero, T.; Guagliardi, I.; Ricca, N. Drought assessment using the reconnaissance drought index (RDI) in a southern Italy region. In Proceedings of the 6th IMEKO TC19 Symposium on Environmental Instrumentation and Measurements, Reggio Calabria, Italy, 24–26 June 2016; pp. 52–55. [Google Scholar]
- Buttafuoco, G.; Caloiero, T.; Ricca, N.; Guagliardi, I. Assessment of drought and its uncertainty in a southern Italy area (Calabria region). Measurement 2018, 113, 205–210. [Google Scholar] [CrossRef]
- Imai, N.; Terashima, S.; Itoh, S.; Ando, A. 1994 compilation values for GSJ reference samples and GSJ reference samples, ‘Igneous rock series’. Geochem. J. 1195, 29, 91–95. [Google Scholar] [CrossRef]
- Balcaen, L.; Bolea-Fernández, E.; Resano, M.; Vanhaecke, F. Inductively coupled plasma—Tandem mass spectrometry (ICP-MS/MS): A powerful and universal tool for the interference-free determination of (ultra)trace elements—A tutorial review. Anal. Chim. Acta 2015, 894, 7–19. [Google Scholar] [CrossRef]
- Greenberg, I.; Sawallisch, A.; Stelling, J.; Vohland, M.; Ludwig, B. Optimization of sample preparation and data evaluation techniques for X-ray fluorescence prediction of soil texture, pH, and cation exchange capacity of loess soils. Soil Sci. Soc. Am. J. 2023, 88, 27–42. [Google Scholar] [CrossRef]
- Al Maliki, A.; Al-lami, A.K.; Hussain, H.M.; Al-Ansari, N. Comparison between inductively coupled plasma and X-ray fluorescence performance for Pb analysis in environmental soil samples. Environ. Earth Sci. 2017, 76, 433. [Google Scholar] [CrossRef]
- Schmidt, K.; Autenrieth, D.; Nagisetty, R. A comparison of field portable X-ray fluorescence (FP XRF) and inductively coupled plasma mass spectrometry (ICP-MS) for analysis of metals in the soil and ambient air. Res. Sq. 2024, rs.3, rs-3849271. [Google Scholar] [CrossRef]
- Chen, Q.; Kissel, C.; Govin, A.; Liu, Z.; Xie, X. Correction of interstitial water changes in calibration methods applied to XRF core-scanning major elements in long sediment cores: Case study from the South China Sea. Geochem. Geophys. Geosyst. 2016, 17, 1925–1934. [Google Scholar] [CrossRef]
- Javadi, S.; Mouazen, A. Data fusion of XRF and Vis-nir using outer product analysis, granger–Ramanathan, and least squares for prediction of key soil attributes. Remote Sens. 2023, 13, 2023. [Google Scholar] [CrossRef]
- Gebregiorgis, D.; Giosan, L.; Hathorne, E.; Anand, P.; Nilsson-Kerr, K.; Plaß, A.; Frank, M. What can we learn from X-ray fluorescence core scanning data? A paleomonsoon case study. Geochem. Geophys. Geosyst. 2020, 21, e2019GC008414. [Google Scholar] [CrossRef]
- Lopresti, M.; Mangolini, B.; Milanesio, M.; Caliandro, R.; Palin, L. Multivariate versus traditional quantitative phase analysis of X-ray powder diffraction and fluorescence data of mixtures showing preferred orientation and microabsorption. J. Appl. Crystallogr. 2022, 55, 837–850. [Google Scholar] [CrossRef]
- Colomban, P.; Gironda, M.; Franci, G.; D’abrigeon, P. Distinguishing genuine imperial Qing dynasty porcelain from ancient replicas by on-site non-invasive XRF and Raman spectroscopy. Materials 2022, 15, 5747. [Google Scholar] [CrossRef]
- Haidous, N.; Sawilowsky, S. Robustness and power of the Kornbrot rank difference, signed ranks, and dependent samples t-test. Am. J. Appl. Math. Stat. 2013, 1, 99–102. [Google Scholar] [CrossRef]
- Wiedermann, W.; Alexandrowicz, R. A modified normal scores test for paired data. Methodology 2011, 7, 25–38. [Google Scholar] [CrossRef]
- Shieh, G.; Jan, S.; Randles, R. Power and sample size determinations for the Wilcoxon signed-rank test. J. Stat. Comput. Simul. 2007, 77, 717–724. [Google Scholar] [CrossRef]
- Ang, J.; Zhang, S. Evaluating long-horizon event study methodology. SSRN Electron. J. 2011. [Google Scholar] [CrossRef]
- Bhatia, M.; Specht, A.; Vallabhuni, R.; Sulaiman, D.; Konda, M.; Balcom, P.; Qureshi, A. Portable X-ray fluorescence as a rapid determination tool to detect parts per million levels of Ni, Zn, As, Se, and Pb in human toenails: A south India case study. Environ. Sci. Technol. 2021, 55, 13113–13121. [Google Scholar] [CrossRef]
- Fleming, D.; Madani, N.; Kaiser, M.; Kim, J.; Keltie, E.; Drage, N.; Brough, L. Portable X-ray fluorescence of zinc and selenium with nail clippings–mother and infant nutrition investigation (mini). PLoS ONE 2024, 19, e0310845. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.H. A novel graphical evaluation of agreement. BMC Med. Res. Methodol. 2022, 22, 51. [Google Scholar] [CrossRef] [PubMed]

| ICP-MS Parameter | Value |
|---|---|
| RF power—W | 1200 |
| Argon plasma gas flow—L min−1 | 15 |
| Nebulizer gas flow—L min−1 | 0.82–0.86 |
| Auxiliary gas flow—L min−1 | 1.15 |
| Lens voltage—V | 6.00 |
| Nebulizer | Cross flow |
| Plasma torch | quartz |
| Sample uptake—mL min−1 | 1 |
| Scanning mode | Peak hop |
| Dwell time—ms | 50 |
| Sweeps/Reading | 20 |
| Number of replicates | 3 |
| Read delay time—s | 15 |
| Cell gas | CH4 |
| DRC gas flow—mL min−1 | 0.7 |
| RPq (rejection parameter q) | 0.65 |
| Isotope ratio precision (RSD for Ag-107/Ag-109) | <0.2% |
| LOD—µg kg−1 | |
| Sr | 0.24 |
| Ni | 0.27 |
| Cr | 5.02 |
| V | 1.9 |
| As | 0.7 |
| Pb | 0.31 |
| Zn | 2.5 |
| U.S.G.S. Standards | Sr | Ni | Cr | V | As | Pb | Zn |
|---|---|---|---|---|---|---|---|
| AGV-1 | 0.51 | 0.01 | 0.008 | 0.12 | 0.09 | 0.03 | 0.08 |
| BCR-1 | 0.31 | 0.01 | 0.13 | 0.4 | 0.61 | 0.01 | 0.12 |
| BR | 1.32 | 0.2 | 0.03 | 0.32 | 0.02 | 0.05 | 0.16 |
| DR-N | 0.4 | 0.01 | 0.04 | 0.22 | 0.003 | 0.05 | 0.14 |
| GA | 0.31 | 0.007 | 0.02 | 0.03 | 0.001 | 0.03 | 0.08 |
| GSP-1 | 0.36 | 0.008 | 0.01 | 0.05 | 0.0001 | 0.05 | 0.1 |
| NIM-G | - | 0.02 | 0.01 | 0.003 | 0.02 | 0.04 | 0.03 |
| Accuracy (%) | 1.1 | 2.4 | 2 | 2.8 | 1.1 | 2.8 | 1.4 |
| RPD (%) | 2.3 | 1.3 | 1.8 | 1.1 | 1.1 | 2.7 | 1.5 |
| Sr | Ni | Cr | V | |||||
| XRF | ICP-MS | XRF | ICP-MS | XRF | ICP-MS | XRF | ICP-MS | |
| N. samples | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| Min | 120.00 | 105.19 | 19.00 | 15.76 | 47.00 | 45.71 | 64.00 | 96.48 |
| Max | 384.00 | 490.39 | 82.00 | 68.11 | 309.00 | 231.56 | 197.00 | 257.03 |
| Median | 233.50 | 209.70 | 33.00 | 25.93 | 85.50 | 72.26 | 100.50 | 135.73 |
| Mean | 231.42 | 208.94 | 35.12 | 27.99 | 91.36 | 76.83 | 107.18 | 143.93 |
| St. dev. | 67.22 | 68.79 | 11.07 | 8.97 | 37.84 | 27.63 | 28.40 | 36.29 |
| CV (%) | 29 | 32.9 | 31.5 | 32 | 41.4 | 36 | 26.5 | 25.2 |
| Skewness | 0.348 | 1.447 | 1.582 | 1.951 | 3.859 | 3.693 | 1.211 | 1.009 |
| Kurtosis | −0.203 | 4.172 | 4.748 | 6.250 | 20.03 | 17.92 | 1.456 | 0.687 |
| Difference mean | −22.48 (ICP < XRF) | −7.12 (ICP < XRF) | −14.53 (ICP < XRF) | +36.75 (ICP > XRF) | ||||
| Largest absolute difference | 109.39 | 14.95 | 77.44 | 159.03 | ||||
| As | Pb | Zn | ||||||
| XRF | ICP-MS | XRF | ICP-MS | XRF | ICP-MS | |||
| N. samples | 50 | 50 | 50 | 50 | 50 | 50 | ||
| Min | 4.00 | 4.43 | 12.00 | 14.85 | 43.00 | 78.36 | ||
| Max | 14.00 | 18.98 | 247.00 | 250.93 | 871.00 | 689.48 | ||
| Median | 7.00 | 8.73 | 32.50 | 36.29 | 116.50 | 160.72 | ||
| Mean | 7.58 | 9.16 | 65.38 | 70.01 | 181.40 | 211.39 | ||
| St. dev. | 2.74 | 3.25 | 71.02 | 70.97 | 172.81 | 138.08 | ||
| CV (%) | 36.2 | 35.5 | 108.6 | 101.4 | 95.3 | 65.3 | ||
| Skewness | 0.735 | 1.238 | 1.467 | 1.459 | 2.328 | 1.986 | ||
| Kurtosis | −0.532 | 1.615 | 0.673 | 0.530 | 5.258 | 3.697 | ||
| Difference mean | +1.58 (ICP > XRF) | +4.63 (ICP > XRF) | +29.99 (ICP > XRF) | |||||
| Largest absolute difference | 14.98 | 62.15 | 355.22 | |||||
| Element | t-Statistic | p-Value |
|---|---|---|
| Sr | 5.63 | 8.80 × 10−7 |
| Ni | 13.40 | 5.22 × 10−18 |
| Cr | 5.84 | 4.14 × 10−7 |
| V | −7.66 | 6.39 × 10−10 |
| As | −3.35 | 1.56 × 10−3 |
| Pb | −1.99 | 5.17 × 10−2 |
| Zn | −3.10 | 3.23 × 10−3 |
| Element | Pearson Correlation (r) | p-Value |
|---|---|---|
| Sr | 0.91 (strong) | 2.01 × 10−20 |
| Ni | 0.95 (very strong) | 3.65 × 10−26 |
| Cr | 0.90 (strong) | 4.01 × 10−19 |
| V | 0.47 (moderate) | 5.46 × 10−4 |
| As | 0.39 (weak) | 4.69 × 10−3 |
| Pb | 0.97 (very strong) | 2.50 × 10−32 |
| Zn | 0.93 (very strong) | 4.34 × 10−22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guagliardi, I.; Ricca, N.; Cicchella, D. Comparative Evaluation of Inductively Coupled Plasma Mass Spectrometry (ICP-MS) and X-Ray Fluorescence (XRF) Analysis Techniques for Screening Potentially Toxic Elements in Soil. Toxics 2025, 13, 314. https://doi.org/10.3390/toxics13040314
Guagliardi I, Ricca N, Cicchella D. Comparative Evaluation of Inductively Coupled Plasma Mass Spectrometry (ICP-MS) and X-Ray Fluorescence (XRF) Analysis Techniques for Screening Potentially Toxic Elements in Soil. Toxics. 2025; 13(4):314. https://doi.org/10.3390/toxics13040314
Chicago/Turabian StyleGuagliardi, Ilaria, Nicola Ricca, and Domenico Cicchella. 2025. "Comparative Evaluation of Inductively Coupled Plasma Mass Spectrometry (ICP-MS) and X-Ray Fluorescence (XRF) Analysis Techniques for Screening Potentially Toxic Elements in Soil" Toxics 13, no. 4: 314. https://doi.org/10.3390/toxics13040314
APA StyleGuagliardi, I., Ricca, N., & Cicchella, D. (2025). Comparative Evaluation of Inductively Coupled Plasma Mass Spectrometry (ICP-MS) and X-Ray Fluorescence (XRF) Analysis Techniques for Screening Potentially Toxic Elements in Soil. Toxics, 13(4), 314. https://doi.org/10.3390/toxics13040314








