Nonsingular Terminal Sliding Mode Control Based on Adaptive Barrier Function for n^th-Order Perturbed Nonlinear Systems

Abstract

In this study, an adaptive nonsingular finite time control technique based on a barrier function terminal sliding mode controller is proposed for the robust stability of n^th-order nonlinear dynamic systems with external disturbances. The barrier function adaptive terminal sliding mode control makes the convergence of tracking errors to a region near zero in the finite time. Moreover, the suggested method does not need the information of upper bounds of perturbations which are commonly applied to the sliding mode control procedure. The Lyapunov stability analysis proves that the errors converge to the determined region. Last of all, simulations and experimental results on a complex new chaotic system with a high Kaplan–Yorke dimension are provided to confirm the efficacy of the planned method. The results demonstrate that the suggested controller has a stronger tracking than the adaptive controller and the results are satisfactory with the application of the controller based on chaotic synchronization on the chaotic system.

1. Introduction

The research in the field of chaos control and synchronization often has shortcomings, such as considering simple models for the system, applying limiting assumptions to system dynamics, and not considering various uncertainties, including variable time indeterminacies [1,2,3,4]. Moreover, considering the global stability and not paying attention to issues such as stimulus saturation and the validity region of state variables is another challenge in this field. In practical applications, actuator saturation is one of the most common nonlinear control inputs encountered in system design [5,6,7]. In particular, the presence of input constraints as a symbol of the physical limitations of control capacity is unavoidable in most stimuli. The constraints routinely impose the limitations on the dynamics and can worsen conditions and lead to unwanted fluctuations and even instability in the system. Therefore, the issue of system design and simultaneous achievement of performance tracking goals is a very practical problem. Much research has been conducted in this field in the recent decade. For instance, in [8], in order to stabilize the linear control systems and improve control performance with actuator saturation, the LMI method is used for compensatory design in controlling and stabilizing a wind turbine. In [9], the axial function neural network method has been used to approximate the amplitude information of the perturbation signal. In [10], the input–output feedback control method is used for systems with unknown nonlinear saturation, despite time delay. In [11], a fuzzy controller for unknown nonlinear systems with input saturation and exterior perturbations via discrete adaptation and dynamic optimal surface control methods is presented. Fuzzy-logic systems have been employed to estimate the dynamics of the unknown system and comparative rules have been used to estimate the parameters of fuzzy-logic systems. Another application of the controller is designed to prevent aggressive actions when input saturation. In [12], a non-singular terminal sliding mode control scheme is planned for a second-order nonlinear system with input saturation. In order to overcome the saturation phenomenon, a non-singular sliding surface is used. Once the uncertainty range is clear, the designed control method can be applied directly to the system based on the designed sliding level. When the range of uncertainty is unknown, a chaotic estimator is used, followed by a hybrid controller containing a finite time scheme and a compensator. The analysis displays that under two recommended control approaches, under the mentioned conditions, the closed-loop system states reach zero in a limited time.

Chaotic systems have been investigated by researchers and scientists for many years, and these systems are found in physical structures and nature. Due to the unwanted behaviors of chaotic systems, their control and synchronization has become one of the new issues. In addition to the implementation and analysis of adsorbents of these systems, their synchronization can be implemented in many applications [13,14,15,16]. In the study of nonlinear behavior of chaotic systems, there are many hidden attractors, each of which can be studied and used in many applications. In chaos control and synchronization, the use of an appropriate control approach can make the proposed design attractive, especially when the chaotic system has a complex dynamic structure [17]. For example, in [18], a complex spiral-shaped chaotic system is used for synchronization. Nonlinear analysis and orbital design of the proposed system have been performed. By analyzing Lyapunov exponents, the proposed system has been shown to be highly chaotic and suitable for chaos synchronization, secure transmission of information and secure communications. In [19], a chaos system with two quadratic nonlinear terms and two transcendental nonlinear terms is used to chaos control. This system has an absorber with a line of fixed points. Passive control has been employed to control this new chaotic system and the results have been done with numerical simulations and orbital implementation. In [20], a class of improved financial chaos based on economic activity is reported. Dynamic behaviors and power spectra of Lyapunov have been analyzed. To synchronize this system, a combination of adaptive control and linear feedback control has been used, which seeks good results for chaos financial systems.

In [21], an adaptive Lyapunov redesign method based on a Barrier Function approach has been investigated for nonlinear systems without a priori knowledge of the perturbations, where the considered barrier function produces a continuous control input with low chattering. In [22], an adaptive sliding mode (ASM) control technique without a priori bounded perturbation is proposed, where the priori bounded uncertainties might impose a priori bounds on states of the system before achieving the closed-loop stability. An adaptive barrier function sliding mode control method with guaranteed performance based on output-feedback for nonlinear systems is proposed in [23], where the finite-time convergence of tracking errors to a neighborhood of origin with guaranteed performance is satisfied. In [24], a tracking control approach for linear motor positioner systems with payload uncertainty and external disturbances by using the barrier function ASM control technique is presented. A barrier function ASM control approach is proposed in [25] for a hybrid AC/DC microgrid system without information of the disturbances bounds. In [26], the barrier function ASM control method is suggested for the vehicle active suspension systems, which satisfies the finite-time convergence of the states of suspension system. A barrier function adaptive high-order sliding mode controller is introduced in [27] for fast stabilization of the perturbed chain of integrators in the presence of bounded uncertainties. In [28], a barrier function adaptive continuous terminal sliding mode control technique for robotic manipulators with external disturbances, which removes the chattering phenomenon caused via switching control and guarantees the high-precision performance, was presented. To the best of the authors’ knowledge, none of the above-mentioned research works have considered the control/synchronization purpose of chaotic system by using the adaptive barrier function-based nonsingular finite time control technique. It motivates the investigators to conduct research on this topic.

This article begins with the design of the barrier function-based adaptive terminal sliding mode (BFATSM) controller. In this two-position controller, there is no need for the high-degree of disturbance usually required in a general sliding mode control. This controller, which is a more complete class of terminal sliding mode controllers, has been designed with regard to issues such as considering variable uncertainties, not applying limiting assumptions to system dynamics, stimulus saturation, and the validity region of state variables. Then, the controller proof is done for all cases. Next, to prove the efficiency of the controller, we went up to the design of an oscillating chaotic system and proved that the designed system is more complex than similar chaotic systems. Finally, by applying a strong BFATSM controller to the proposed chaotic system, we achieved chaotic synchronization.

The rest of this study is organized as follows: the definition of the system is given in Section 2. Section 3 includes two sub-sections as the main results for the BFATSM controller and the new 3D chaotic system. Section 4 also includes two sub-sections as simulation results for the BFATSM controller and chaotic synchronization.

2. System Definition

Consider the n^th-order nonlinear system with external disturbance as

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ ⋮\\ {\dot{x}}_n=f(x,t)+b(x,t)u+w.\end{array}$$

(1)

where $x={[x_1,\dots ,x_n]}^T\in R^n$ specifies the states of the system; $u\in R$ represents the control input; $f(x,t)\in R$ and $b(x,t)\in R$ are the nonlinear continuous functions ($b(x,t)\ne 0$); and $w\in R$ is the matched disturbance with unknown bound $\hslash \in R$, i.e., $\hslash \ge (k_p{c}_n+k_d{c}_{n-1})\left|w\right|+k_d{c}_n\left|\dot{w}\right|$, where $c_{n-1},c_n,k_p,k_d$ denote the positive scalars. The nonlinear functions $f(x,t)$, $b(x,t)$ and $w$ are assumed to be differentiable.

The control aim is to follow the reference states $x_d={[x_{1d},x_{2d},\mathrm{\dots },x_{nd}]}^T$, with ${\dot{x}}_{1d}=x_{2d}$, …, ${\dot{x}}_{(n-1)d}=x_{nd}$, where $x_{nd}$ is considered as a time-differentiable function. Define tracking errors by

$$\begin{array}{l}e=x_1-x_{1d}\\ \dot{e}=x_2-x_{2d}\\ ⋮\\ e^{(n-1)}=x_n-x_{nd}.\end{array}$$

(2)

3. Main Results

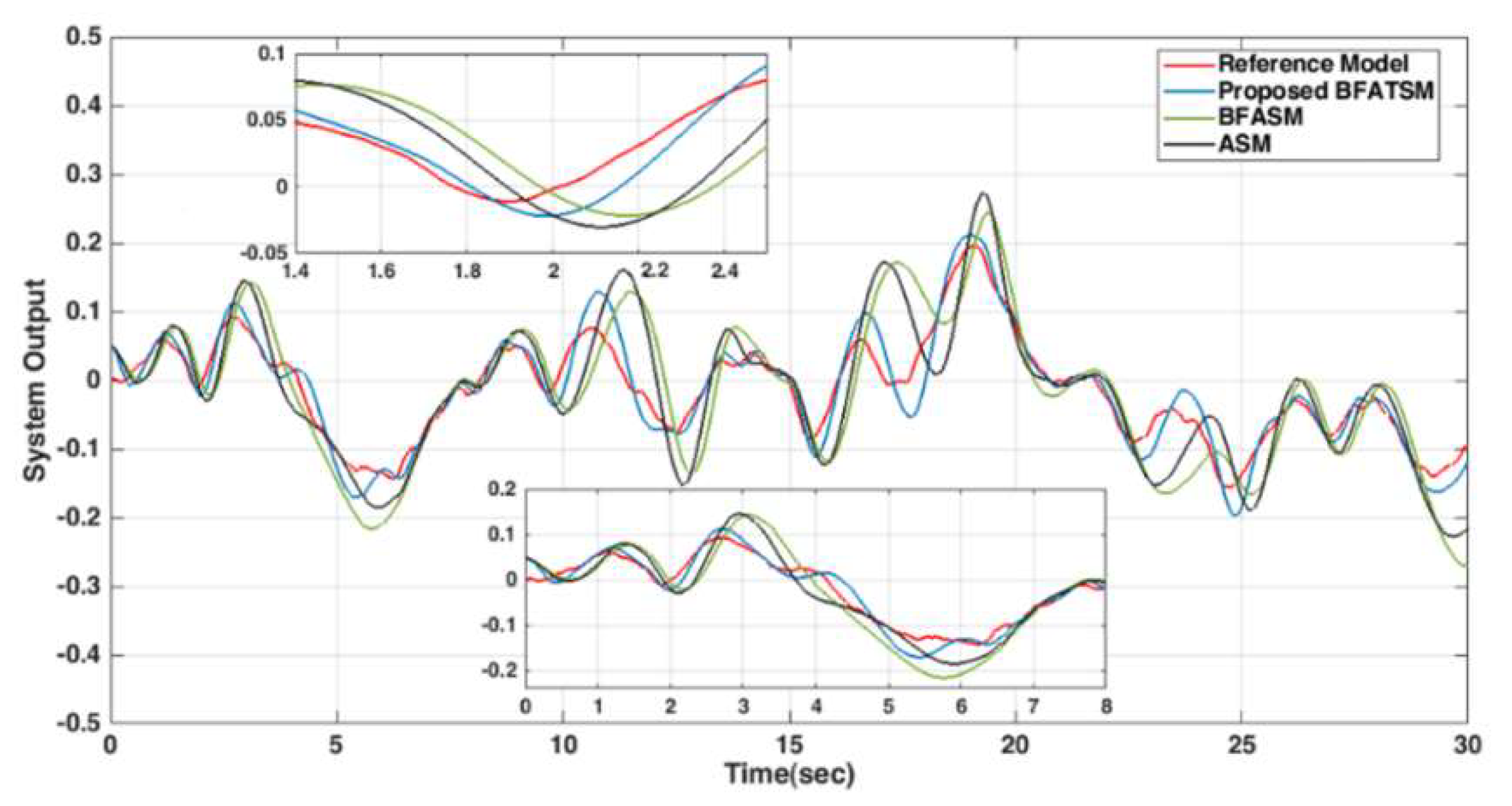
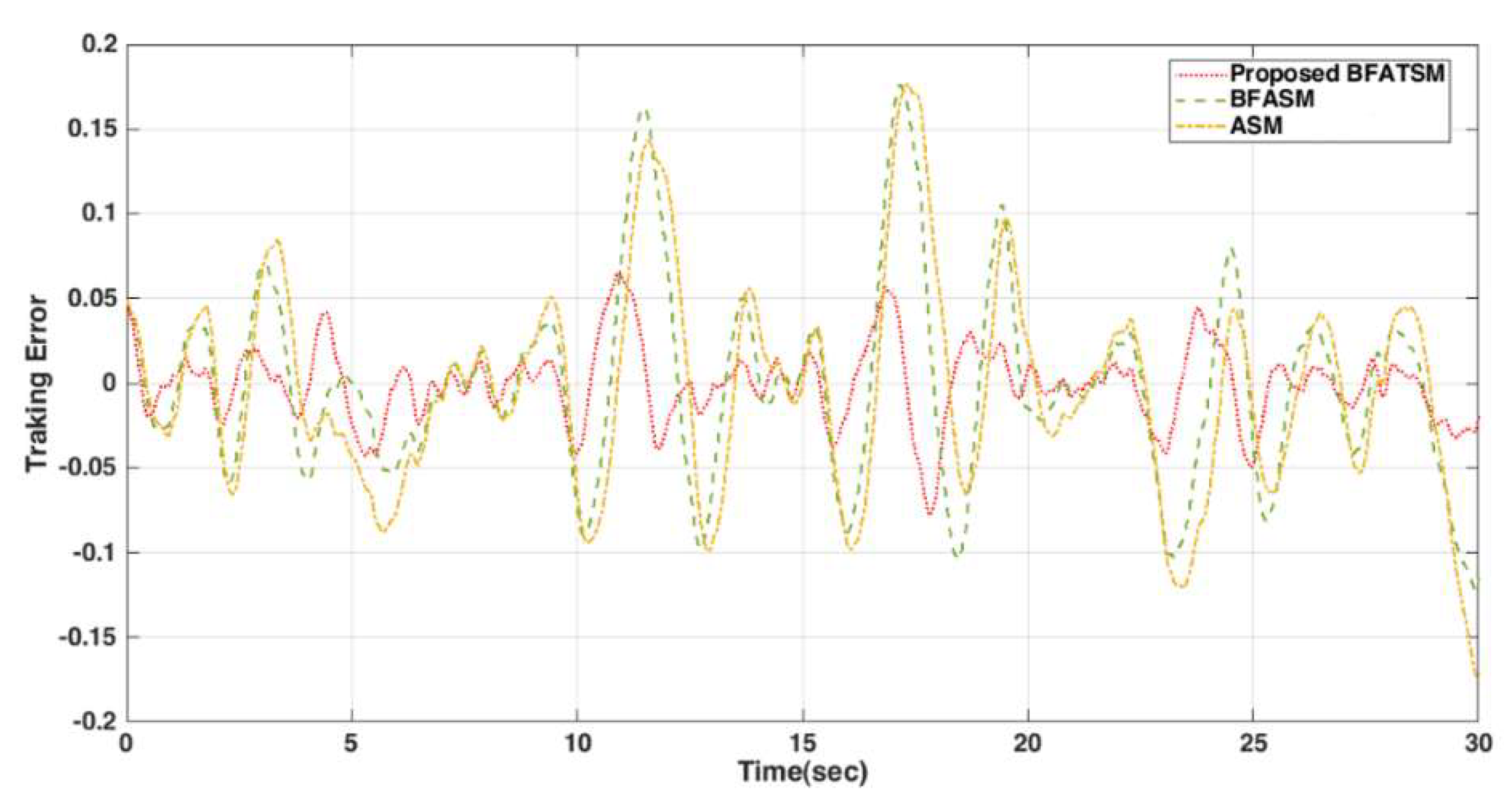
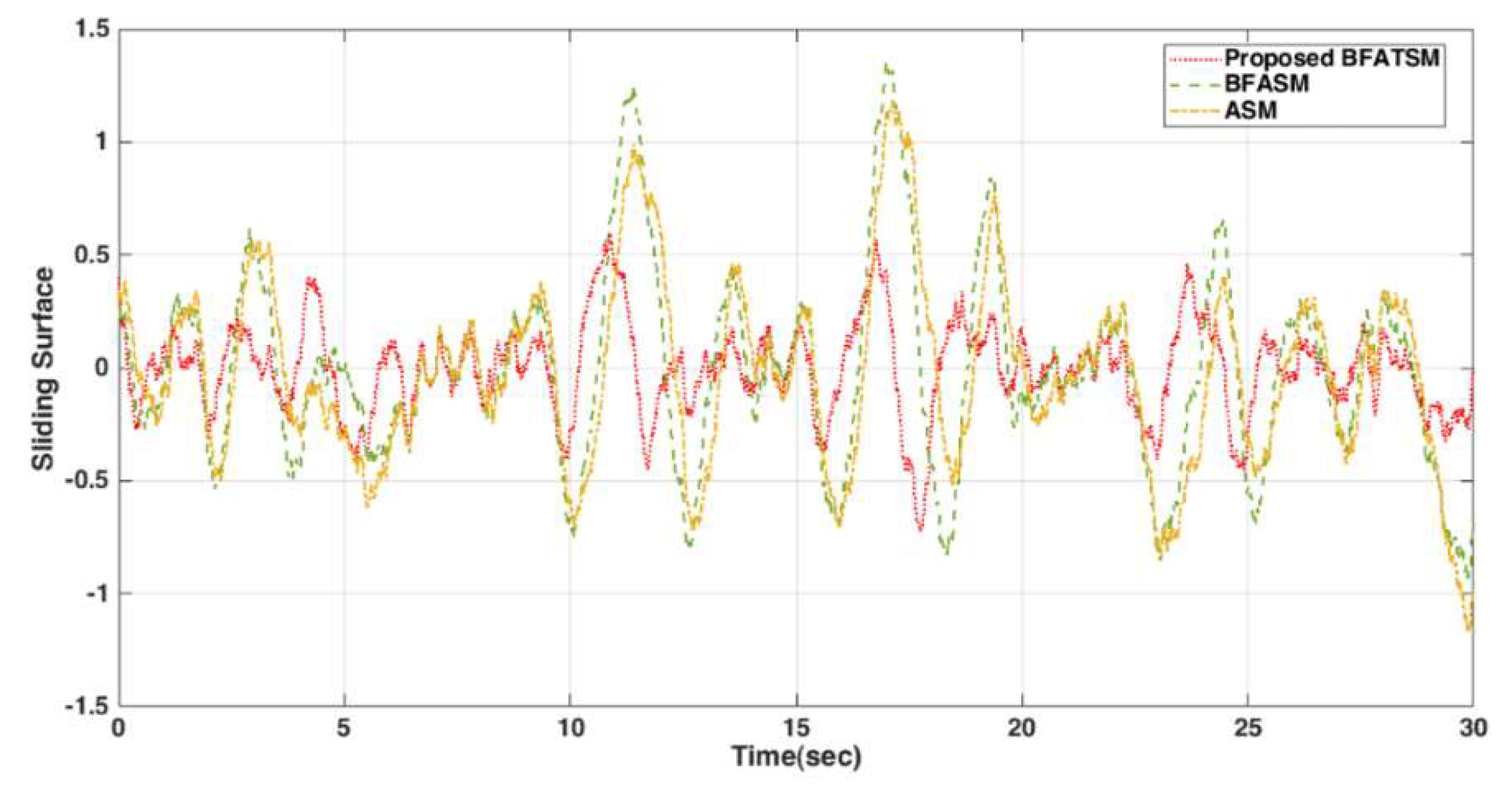
3.1. BFATSM Control

A switching surface function is given as

$$s={\sum }_{i=1}^n{c}_i{e}^{(i-1)},$$

(3)

where $c_1,c_2,\mathrm{\dots },c_n\in R$ are the constants with $c_n\ne 0$. If the switching function is equal to zero, one obtains

$$e^{(n-1)}=-c_n{}^{-1}{\sum }_{i=1}^{n-1}{c}_i{e}^{(i-1)}.$$

(4)

For satisfying the convergence of switching function to origin in the finite time and eliminating the chattering problem, the nonsingular terminal sliding mode surface is proposed by

$$\vartheta =k_{p}s+k_i{\int }_0^{t}s{(\tau )}^{q/r}d\tau +k_d\dot{s},$$

(5)

where $q$ and $r$ denote two odd integers ($1<q/r<2$), and $k_p,k_i,\mathrm{and} k_d$ signify the positive proportional, integral and derivate constants, individually.

In what follows, the convergence of the nonsingular TSMC surface $\vartheta$ to the origin in the finite time is fulfilled and the tracking control of desired trajectory $x_d$ is satisfied.

Theorem 1.

Consider the n^th-order nonlinear system (1) with external disturbance, tracking errors (2), switching function (3), and nonsingular terminal sliding surface (5). If the control signal is designed as

$$\begin{array}{l}\dot{u}=-(k_d{c}_{n}b(x,t){)}^{-1}[k_p\{c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+b(x,t)u-{\dot{x}}_{nd})\}+k_i{s}^{q/r}+k_d\{c_1(x_3-x_{3d})+c_2(x_4\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)+\dot{b}(x,t)u-{\ddot{x}}_{nd})\}+(\hslash +\kappa )sgn(\vartheta )]\end{array}$$

(6)

where $\kappa$ is a positive constant and $\hslash \ge (k_p{c}_n+k_d{c}_{n-1})\left|w\right|+k_d{c}_n\left|\dot{w}\right|$, then the states of the n^th-order nonlinear system (1) with external disturbance converge to the nonsingular terminal sliding surface in the finite time and stay on it thereafter.

Proof. 

The first and second-order time-derivatives of switching function are gotten from (1)–(3) as

$$\begin{array}{l}\dot{s}={\displaystyle \sum _{i=1}^n}{c}_i{e}^{(i)}=c_1\dot{e}+c_2\ddot{e}+\mathrm{\dots }+c_n{e}^{(n)}\\ =c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)+w-{\dot{x}}_{nd}+b(x,t)u)\end{array}$$

(7)

$$\begin{array}{l}\ddot{s}=c_1({\dot{x}}_2-{\dot{x}}_{2d})+c_2({\dot{x}}_3-{\dot{x}}_{3d})+\mathrm{\dots }+c_n(\dot{f}(x,t)+b(x,t)\dot{u}+\dot{w}+\dot{b}(x,t)u-{\ddot{x}}_{nd})\\ =c_1(x_3-x_{3d})+c_2(x_4-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)+b(x,t)\dot{u}+\dot{w}+\dot{b}(x,t)u-{\ddot{x}}_{nd}).\end{array}$$

(8)

Using the Equations (5), (7) and (8), the time-derivative of the nonsingular terminal sliding surface is calculated as

$$\begin{array}{l}\dot{\vartheta }=k_p\dot{s}+k_i{s}^{q/r}+k_d\ddot{s}\\ =k_p\{c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)+w+b(x,t)u-{\dot{x}}_{nd})\}\\ +k_i{s}^{q/r}+k_d\{c_1(x_3-x_{3d})+c_2(x_4-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)+b(x,t)\dot{u}+\dot{w}+\dot{b}(x,t)u-{\ddot{x}}_{nd})\}\end{array}$$

(9)

Consider positive-definite Lyapunov functional as follows:

$$V_1=\frac{1}{2}{\vartheta }^2$$

(10)

where differentiating (10) with respect to time, we have

$$\begin{array}{l}{\dot{V}}_1=\vartheta \{k_p\left\{c_1\left(x_2-x_{2d}\right)+c_2\left(x_3-x_{3d}\right)+\mathrm{\dots }+c_n\left(f\left(x,t\right)-{\dot{x}}_{nd}+b\left(x,t\right)u\right)\right\}+k_i{s}^{q/r}\\ +k_d\left\{c_1\left(x_3-x_{3d}\right)+c_2\left(x_4-x_{4d}\right)+\mathrm{\dots }+c_n\left(\dot{f}\left(x,t\right)+b\left(x,t\right)\dot{u}+\dot{b}\left(x,t\right)u-{\ddot{x}}_{nd}\right)\right\}\\ +(k_p{c}_n+k_d{c}_{n-1})w+k_d{c}_n\dot{w}\}\end{array}$$

(11)

Replacing (6) into (11) gives

$$\begin{array}{l}{\dot{V}}_1=\vartheta \{-(\hslash +\kappa )sgn(\vartheta )+(k_p{c}_n+k_d{c}_{n-1})w+k_d{c}_n\dot{w}\}\\ \le -\kappa \left|\vartheta \right|-\hslash \left|\vartheta \right|+\left|(k_p{c}_n+k_d{c}_{n-1})w+k_d{c}_n\dot{w}\right|\left|\vartheta \right|\\ \le -\kappa \left|\vartheta \right|-\{\hslash -(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|\}\left|\vartheta \right|\\ \le -\sqrt{2}\kappa V_1{}^{\frac{1}{2}}.\end{array}$$

(12)

Consequently, the states of n^th-order nonlinear system are moved from the initial conditions to the switching surface (5) in the finite time and remained on it. □

On the other hand, to remove the effect of external disturbance in practice, the adaptive control law is proposed, where the adaptation laws are designed by the disturbance changes. A novel adaptive terminal sliding mode controller according to the barrier function is planned. Hence, the perturbations can be predicted via the adaptive barrier-based finite time control technique more effectually, and the system is stabilized. The suggested adaptive controller is proposed by

$$\begin{array}{c}\dot{u}=-{(k_d{c}_{n}b(x,t))}^{-1}[k_p\{c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)\\ -{\dot{x}}_{nd}+b(x,t)u)\}\\ +k_i{s}^{q/r}+k_d\{c_1(x_3-x_{3d})+c_2(x_4-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)-{\ddot{x}}_{nd}\\ +\dot{b}(x,t)u)\}+(\kappa +\widehat{\hslash })sgn(\vartheta )]\end{array}$$

(13)

with $\kappa >0$ and

$$\widehat{\hslash }=\{\begin{array}{c}{\hslash }_a, \mathrm{if} 0<t\le \overline{t}\\ {\hslash }_{psb}, \mathrm{if} t>\overline{t}\end{array}$$

(14)

where $\overline{t}$ is the time that the errors are converged to neighborhood $\epsilon$ of the nonsingular surface $\vartheta$. The adaptation law and Positive-Semi-Definite (PSD) barrier function are given as

$${\dot{\hslash }}_a=\mu \left|\vartheta \right|$$

(15)

$${\hslash }_{psb}=\frac{\left|\vartheta \right|}{\epsilon -\left|\vartheta \right|},$$

(16)

where $\epsilon$ and $\mu$ are two positive values. Providing the adaptation law (15), the controller gain ${\hslash }_a$ is adjusted to be increased until the tracking errors reach the neighborhood $\epsilon$ of surface $\vartheta$ at time $\overline{t}$ [29]. For the next times (after $\overline{t}$), the adaptive gain switches to the above-mentioned barrier function that reduces the region of convergence and keeps the tracking errors in there. The system’s stability is proved in the following subsections:

Condition (i): $\mathbf{0}\mathbf{<}\mathit{t}\mathbf{\le }\overline{\mathit{t}}$

Theorem 2.

Consider the n^th-order nonlinear system (1) with external disturbance, switching function (3) and nonsingular TSMC surface (5). Using the adaptive TSMC law (13) with $\widehat{\hslash }={\hslash }_a$ and adaptation law (15), then the error states reach the neighborhood $\epsilon$ of TSMC manifold in the finite time.

Proof. 

Consider the positive-definite Lyapunov function by

$$V_2=\frac{1}{2}({\vartheta }^2+{\gamma }^{-1}{({\hslash }_a-\hslash )}^2),$$

(17)

where $\gamma >0$ and $\hslash$ signifies an unknown constant. Differentiating the Lyapunov function gives

$${\dot{V}}_2=\vartheta \dot{\vartheta }+{\gamma }^{-1}({\hslash }_a-\hslash ){\dot{\hslash }}_a,$$

(18)

where replacing (9) and (15) into (18), one has

$$\begin{array}{l}{\dot{V}}_2=\vartheta (k_p\{c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)+w-{\dot{x}}_{nd}+b(x,t)u)\}\\ +k_i{s}^{q/r}+k_d\{c_1(x_3-x_{3d})+c_2(x_4-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)+b(x,t)\dot{u}+\dot{b}(x,t)u\\ +\dot{w}-{\ddot{x}}_{nd})\})+{\gamma }^{-1}\mu ({\hslash }_a-\hslash )\left|\vartheta \right|\end{array}$$

(19)

Now, substituting the adaptive control law (13) into (19), we attain

$$\begin{array}{l}{\dot{V}}_2=-\vartheta \{(\widehat{\hslash }+\kappa )sgn(\vartheta )-(k_p{c}_n+k_d{c}_{n-1})w-k_d{c}_n\dot{w}\}+{\gamma }^{-1}\mu ({\hslash }_a-\hslash )\left|\vartheta \right|\\ \le -\kappa \left|\vartheta \right|+\left|(k_p{c}_n+k_d{c}_{n-1})w+k_d{c}_n\dot{w}\right|\left|\vartheta \right|-\widehat{\hslash }\left|\vartheta \right|+{\gamma }^{-1}\mu ({\hslash }_a-\hslash )\left|\vartheta \right|\\ \le -\kappa \left|\vartheta \right|-(\widehat{\hslash }-k_d{c}_n\left|\dot{w}\right|-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|)\left|\vartheta \right|+{\gamma }^{-1}\mu ({\hslash }_a-\hslash )\left|\vartheta \right|\end{array}$$

(20)

where adding and subtracting $\hslash \left|\vartheta \right|$ in the above equation yields

$$\begin{array}{l}{\dot{V}}_2\le -\kappa \left|\vartheta \right|-({\hslash }_a-k_d{c}_n\left|\dot{w}\right|-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|)\left|\vartheta \right|+{\gamma }^{-1}\mu ({\hslash }_a-\hslash )\left|\vartheta \right|+\hslash \left|\vartheta \right|-\hslash \left|\vartheta \right|\\ \le -\kappa \left|\vartheta \right|-(\hslash -k_d{c}_n\left|\dot{w}\right|-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|)\left|\vartheta \right|+[{\gamma }^{-1}\mu -1]({\hslash }_a-h)\left|\vartheta \right|\end{array}$$

(21)

where since $\kappa >0$, $\hslash \ge k_d{c}_n\left|\dot{w}\right|+(k_p{c}_n+k_d{c}_{n-1})\left|w\right|$ and $1>\mu /\gamma$, one obtains

$$\begin{array}{l}{\dot{V}}_2\le -\sqrt{2}(\hslash -k_d{c}_n\left|\dot{w}\right|-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|)\frac{\left|\vartheta \right|}{\sqrt{2}}-\sqrt{2\gamma }(1-\frac{\mu }{\gamma })\left|\vartheta \right|\frac{\left|{\hslash }_a-h\right|}{\sqrt{2\gamma }}\\ \le -min\{\sqrt{2}(\hslash -k_d{c}_n\left|\dot{w}\right|-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|),\sqrt{2\gamma }(1-\frac{\mu }{\gamma })\left|\vartheta \right|\}(\frac{\left|\vartheta \right|}{\sqrt{2}}+\frac{\left|{\hslash }_a-h\right|}{\sqrt{2\gamma }})\\ \le -\Theta V_2{}^{0.5}\end{array}$$

(22)

where $\Theta =min\{\sqrt{2}(\hslash -k_d{c}_n\left|\dot{w}\right|-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|),\sqrt{2\gamma }(1-\frac{\mu }{\gamma })\left|\vartheta \right|\}$. □

Condition (ii): $\mathit{t}\mathbf{>}\overline{\mathit{t}}$

Theorem 3.

Consider the n^th-order nonlinear system (1), switching function (3), and nonsingular TSMC manifold (5). Using the adaptive TSMC controller (13) with $\widehat{\hslash }={\hslash }_{psd}$ (Equation (16)), i.e.,

$$\begin{array}{l}\dot{u}=-{(k_d{c}_{n}b(x,t))}^{-1}[k_p\{c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)-{\dot{x}}_{nd}+b(x,t)u)\}\\ +k_i{s}^{q/r}+k_d\{c_1(x_3-x_{3d})+c_2(x_4-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)-{\ddot{x}}_{nd}+\dot{b}(x,t)u)\}\\ +(\left|\vartheta \right|(\epsilon -\left|\vartheta \right|{)}^{-1}+\kappa )sgn(\vartheta )]\end{array}$$

(23)

then the errors reach the region $\left|\vartheta \right|\le \epsilon$ in the finite time.

Proof. 

Consider the Lyapunov function as

$$V_3=0.5({\vartheta }^2+{({\hslash }_{psb}-{\hslash }_{psb}(0))}^2),$$

(24)

where differentiating the above Lyapunov, one achieves

$${\dot{V}}_3=\vartheta \dot{\vartheta }+({\hslash }_{psb}-{\hslash }_{psb}(0)){\dot{\hslash }}_{psb}.$$

(25)

Now, substituting (9) and ${\hslash }_{psb}(0)=0$ in (25), we attain

$$\begin{array}{l}{\dot{V}}_3=\vartheta (k_p\{c_1(x_2-x_{2d})+c_2(x_3-x_{3d})+\mathrm{\dots }+c_n(f(x,t)+w-{\dot{x}}_{nd}+b(x,t)u)\}\\ +k_i{s}^{q/r}+k_d\{c_1(x_3-x_{3d})+c_2(x_4-x_{4d})+\mathrm{\dots }+c_n(\dot{f}(x,t)+b(x,t)\dot{u}+\dot{w}-{\ddot{x}}_{nd}+\dot{b}(x,t)u)\})+{\hslash }_{psb}{\dot{\hslash }}_{psb}\end{array}$$

(26)

Using (23) and (26), we have

$${\dot{V}}_3=-\vartheta \{({\hslash }_{psb}+\kappa )sgn(\vartheta )-(k_p{c}_n+k_d{c}_{n-1})w-k_d{c}_n\dot{w}\}+{\hslash }_{psb}{\dot{\hslash }}_{psb}$$

(27)

or equivalently

$$\begin{array}{l}{\dot{V}}_3\le -\kappa \left|\vartheta \right|-\{{\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|\}\left|\vartheta \right|+\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}{\hslash }_{psb}sgn(\vartheta )\dot{\vartheta }\\ \le -\{{\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|\}\left|\vartheta \right|\\ -\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}{\hslash }_{psb}sgn(\vartheta )((\widehat{\hslash }+\kappa )sgn(\vartheta )-(k_p{c}_n+k_d{c}_{n-1})w-k_d{c}_n\dot{w})\end{array}$$

(28)

where it is expressed as

$$\begin{array}{l}{\dot{V}}_3\le -\{{\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|\}\left|\vartheta \right|-\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}{\hslash }_{psb}\kappa \\ -\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}{\hslash }_{psb}({\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|)\end{array}$$

(29)

where since $\kappa >0$, ${\hslash }_{psb}>0$, $\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}>0$, and ${\hslash }_{psb}\ge (k_p{c}_n+k_d{c}_{n-1})\left|w\right|+k_d{c}_n\left|\dot{w}\right|$, it yields

$$\begin{array}{l}{\dot{V}}_3\le -\sqrt{2}\{{\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|\}\frac{\left|\vartheta \right|}{\sqrt{2}}\\ -\sqrt{2}\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}({\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|)\frac{{\hslash }_{psb}}{\sqrt{2}}\\ \le -\sqrt{2}({\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|)min\{1,\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}\}(\frac{\left|\vartheta \right|}{\sqrt{2}}+\frac{{\hslash }_{psb}}{\sqrt{2}})\\ \le -\Gamma (\frac{\left|\vartheta \right|}{\sqrt{2}}+\frac{{\hslash }_{psb}}{\sqrt{2}})\le -\Gamma V_3{}^{0.5}\end{array}$$

(30)

where $\Gamma =\sqrt{2}({\hslash }_{psb}-(k_p{c}_n+k_d{c}_{n-1})\left|w\right|-k_d{c}_n\left|\dot{w}\right|)min\{1,\epsilon {(\epsilon -\left|\vartheta \right|)}^{-2}\}$. □

Remark 1.

In the n^th-order nonlinear model (1), the external disturbance term is only considered in the last channel $(x_n)$ The suggested method does not support the external disturbances for all of the states, and the system states $x_1,\mathrm{\dots },x_{n-1}$ do not have external disturbances in model (1). If the parametric uncertainties $\mathsf{\Delta }f(x,t)$ and $\mathsf{\Delta }b(x,t)$ are considered in the last equation of (1), such that:

$${\dot{x}}_n=f(x,t)+\mathsf{\Delta }f(x,t)+(b(x,t)+\mathsf{\Delta }b(x,t))u+w,$$

(31)

then the parametric uncertainties and external disturbances terms can be considered as a perturbation term, where

$${\dot{x}}_n=f(x,t)+b(x,t)u+w^{\prime },$$

(32)

with $w^{\prime }=\Delta f(x,t)+\Delta b(x,t)u+w$. In this case, the proposed control technique can be applied for the nonlinear systems with parametric uncertainties and external disturbances.

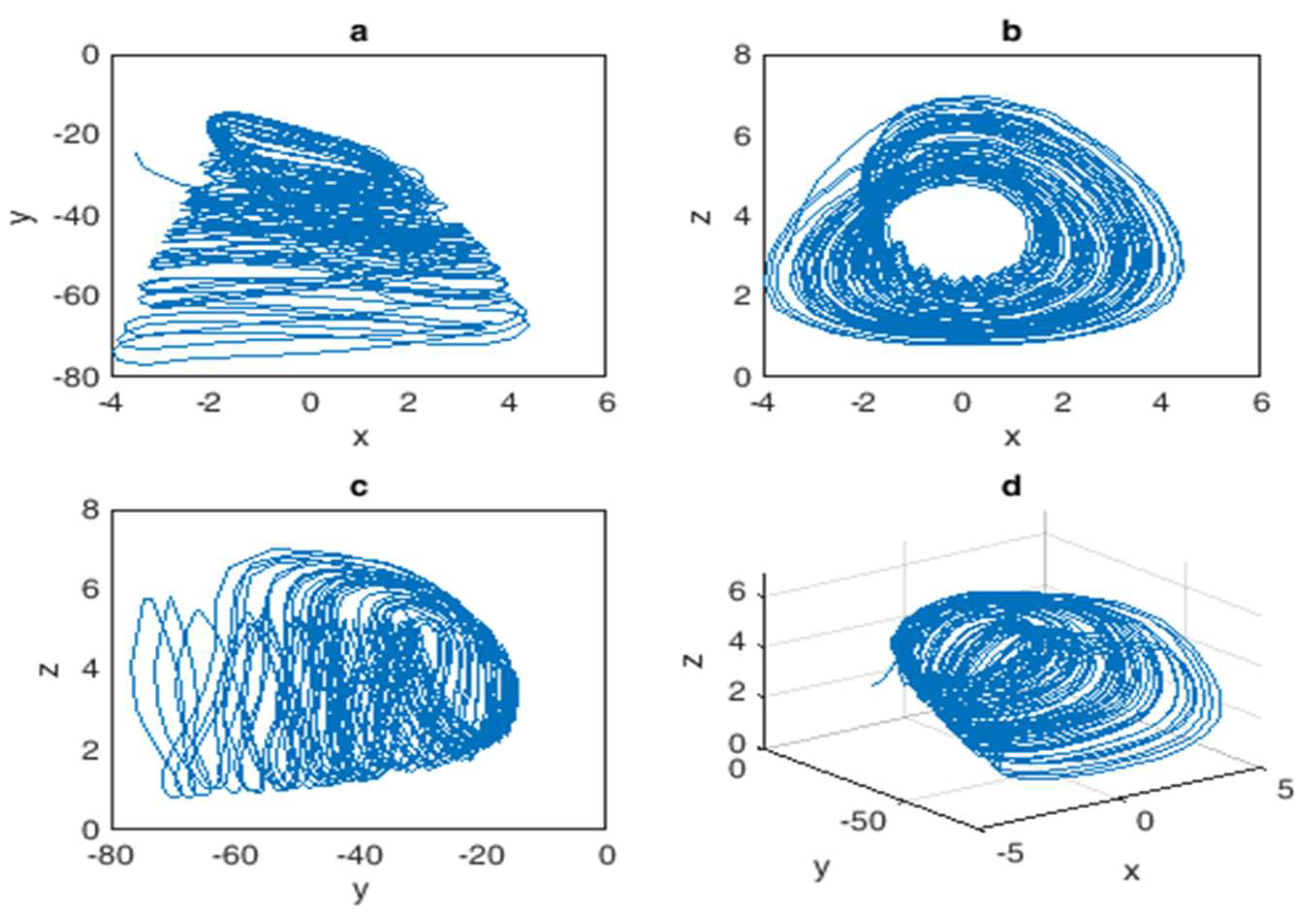
3.2. New 3D Chaotic System

To prove the performance of the barrier function controller, we need a high oscillation system to be able to test the proposed scheme. To this end, we will design an oscillating chaotic system and prove that the proposed system has a higher Kaplan–Yorke dimension than similar nonlinear chaotic systems. The proposed system is as follows:

$$\begin{array}{l}\dot{x}=f_1(x,y,z)\\ \dot{y}=f_2(x,y,z)\\ \dot{z}=f_3(x,y,z)\end{array}$$

(33)

where $f_1(x,y,z)=-ax+ay-byz-c{z}^2$, $f_2(x,y,z)=-dxy-eyz-f{x}^4-gexp(z)$ and $f_3(x,y,z)=xyz-htanh(x)$ with parameters:

$$a=20, b=8.2, c=17, d=2.3, e=11, f=13, g=14.5, h=24$$

(34)

and initial condition:

$$x(0)=-3.5, y(0)=-24.4, z(0)=3.1.$$

(35)

System (33) is a chaotic high-oscillation system. Figure 1 shown the chaotic attractors of system (33).

The degree of divergence and convergence of the paths of the chaotic system is determined by Lyapunov exponents, and the system with a positive Lyapunov exponent is chaotic [30]. Figure 2 shows the Lyapunov exponents of 3D nonlinear system (33). Using the Lyapunov exponents, the Kaplan–Yorke dimension of System (33) can be obtained. This behavior is fractal and, therefore, the complexity of the chaotic system can be evaluated with this index. The higher this index, the more volatile the system behavior [31].

To illustrate the complexity of System (33), a comparison is made between the Kaplan–Yorke dimension of the proposed chaotic system and the well-known new chaotic systems [18]. As it can be seen from

Table 1. Kaplan–Yorke dimension comparison.

No.	System	KYD	No.	System	KYD
1	Singh and Roy [32]	2.16	9	Kapitaniak et al. [33]	2.107
2	Yang and Qiao [34]	2.112	10	Zheng and Zhang [20]	2.594
3	Jinjie and Guangming [35]	2.185	11	Yanmin et al. [36]	2.276
4	Lassoued et al. [37]	2.124	12	Mobayen et al. [38]	2.367
5	Sahin et al. [39]	2.579	13	Benkouider et al. [18]	2.652
6	Lien et al. [40]	2.163	14	Xu et al. [41]	2.074
7	Vaidyanathan et al. [42]	2.162	15	System (33)	2.661
8	Idowu et al. [43]	2.263

, the proposed system has a higher Kaplan–Yorke dimension compared to other systems, so it is more complex.

3.3. New 3D Chaotic System with External Disturbance and Uncertain Parameters

Let’s define the proposed chaotic system with uncertain parameter and external disturbance as follows:

$$\begin{array}{l}\dot{x}=f_1(x,y,z)\\ \dot{y}=f_2(x,y,z)\\ \dot{z}=f_3(x,y,z)+w^{\prime }\end{array}$$

(36)

where $f_1(x,y,z)=-ax+ay-byz-c{z}^2$, $f_2(x,y,z)=-dxy-eyz-f{x}^4-gexp(z)$, $f_3(x,y,z)=xyz-htanh(x)$, and $w^{\prime }=0.1xz-0.2sin(xy)u+0.6sin(3.1t)$. Without the control input u, the 2D and 3D chaotic attractors of the chaotic system (36) with external disturbance and uncertain parameters are shown in Figure 3.

4. Main Results

4.1. BFATSM Controller

In this part, to prove the performance of the planned BFATSM control scheme, a comparison between the proposed controller, BFASM control of [2] and the ASM control designed in [1] is performed. In general, the structure of the ASM controller is as follows:

$$u_{ASM}=-(KB)[KAx+KD+\Gamma s+(\varsigma +\left|KB\right|\widehat{\upsilon })sgn(s)]$$

(37)

where $\upsilon >0$ and $\Gamma$ is a positive fixed number and:

$$\dot{\widehat{\upsilon }}=\{\begin{array}{c}\overline{\widehat{\upsilon }}\left|s\right|sgn(\left|s\right|+\varpi ), \mathrm{if} \widehat{\upsilon }>\psi \\ v,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if} \widehat{\upsilon }\le \psi \end{array}$$

(38)

where $v,\psi ,\overline{\widehat{\upsilon }}$ positive fixed numbers and $\varpi >0$ the size of the dead zone. It is assumed that $KB$ is nonsingular and $s=Kx, K\in {\Re }^{1\times 2}$ is the sliding surface. For simulation, the ASM controller parameters are selected as follows:

$$\varsigma =5, \overline{\widehat{\upsilon }}=2, \psi =0.1, v=0.1, \varpi =0.05, \Gamma =1, K=[1001]$$

(39)

To compare and prove the efficiency of the controllers, a stochastic reference model like Figure 4 has been used.

As demonstrated, the BFATSM controller provides faster and more accurate tracking than the ASM and BFASM controllers [1,2]. Figure 5 shows the tracking errors between the two controllers.

As can be seen, throughout the tracking process, despite speed and acceleration fluctuations, the BFATSM controller had a smaller error range than the ASM and BFASM controllers, resulting in more accurate convergence. Figure 6 compares the inputs of all three controllers and demonstrates that the proposed control signal has low amplitude.

As demonstrated, the amplitude of the BFATSM controller is less than the amplitude of the ASM and BFASM controllers; this is because when the sliding level variable is small, the adaptive control gain in the BFATSM controller decreases due to BF. Furthermore, due to overestimation in ASM, which is based on the applicable law (38), there will be a possibility of control input saturation. As shown in Figure 7, the sliding surface variable in the BFATSM controller is more limited than in the ASM and BFASM controllers, and because we designed the sliding surface based on error, the sliding surface variable changes in proportion to the error changes.

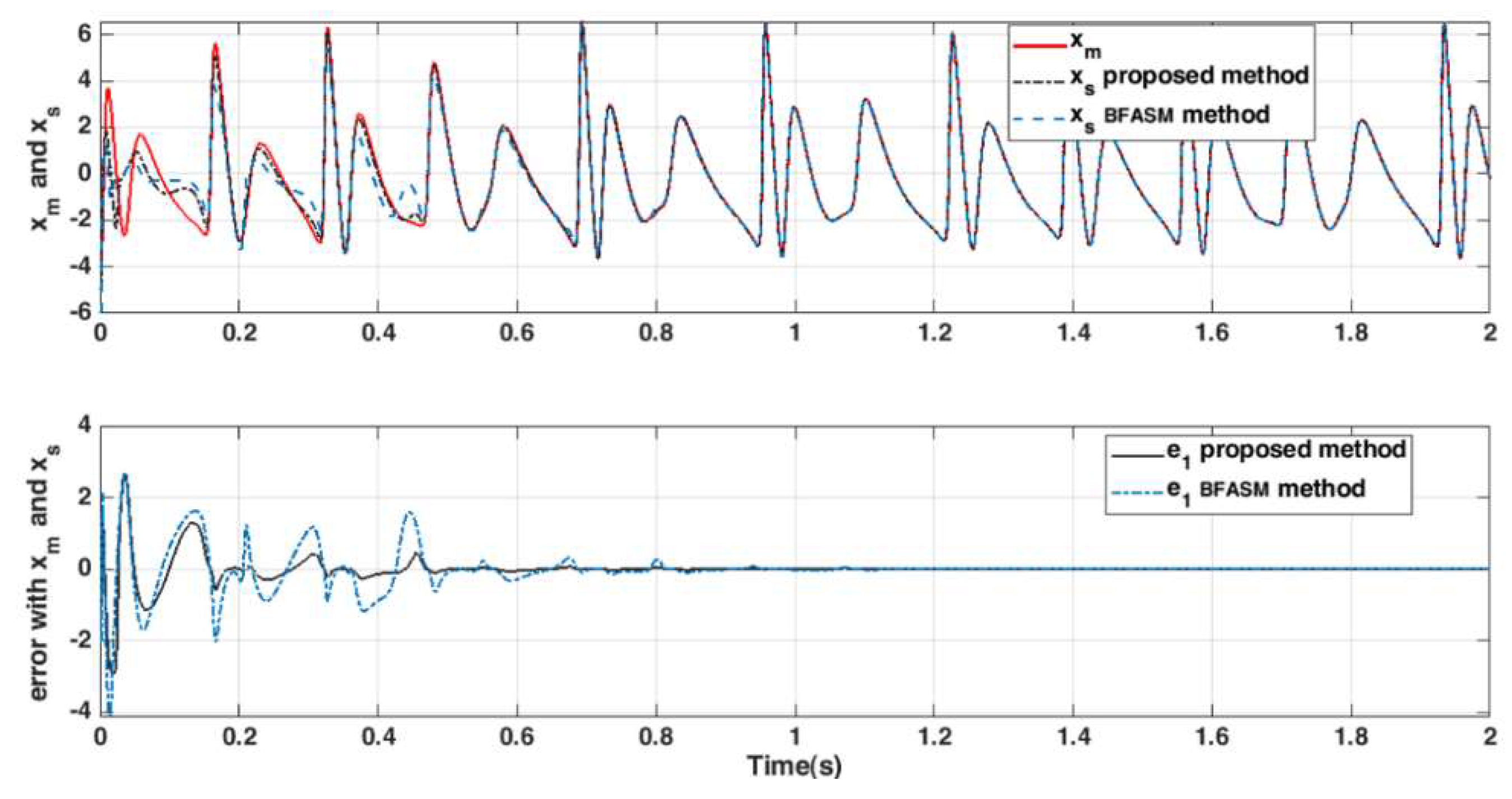
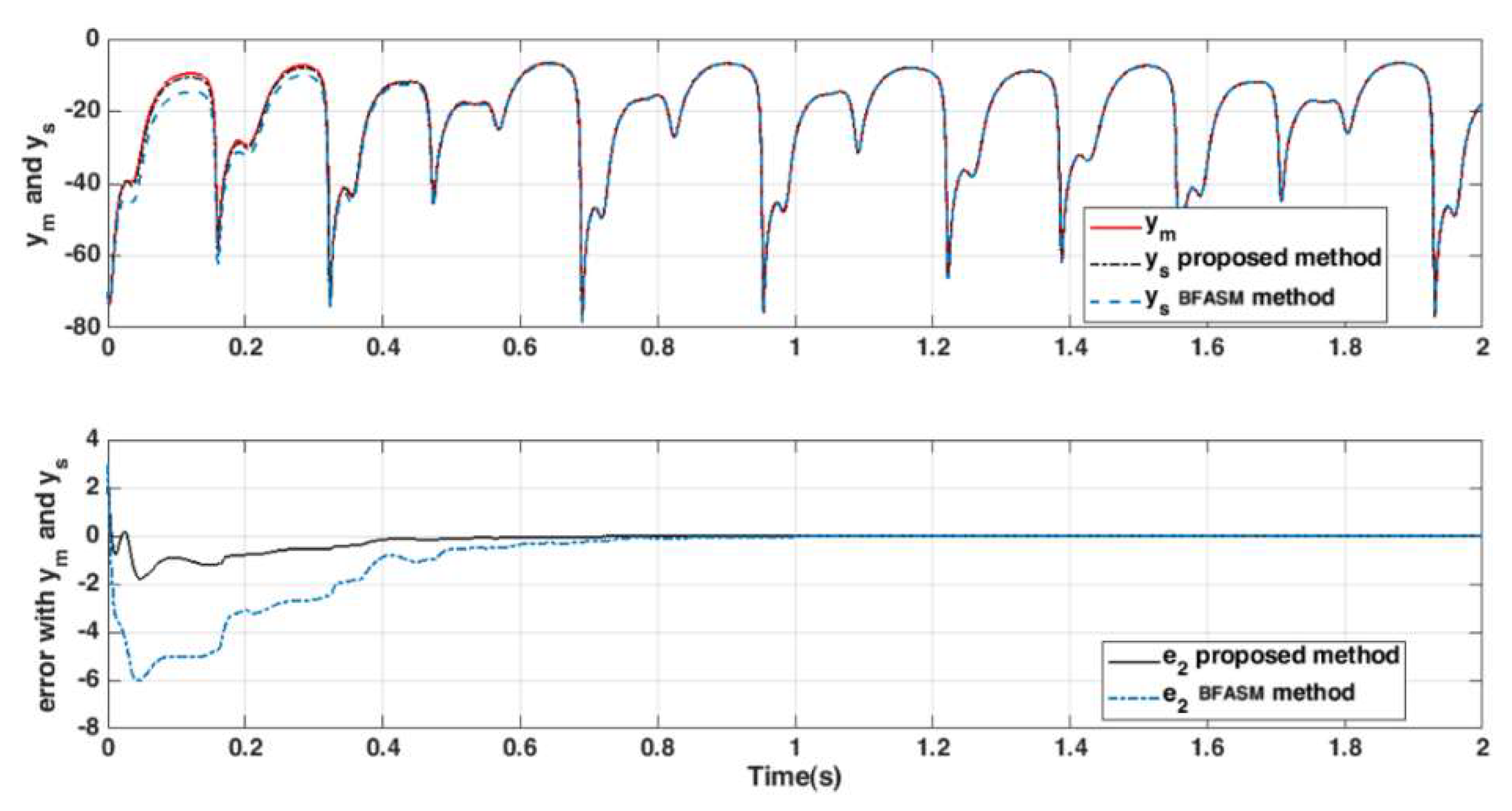
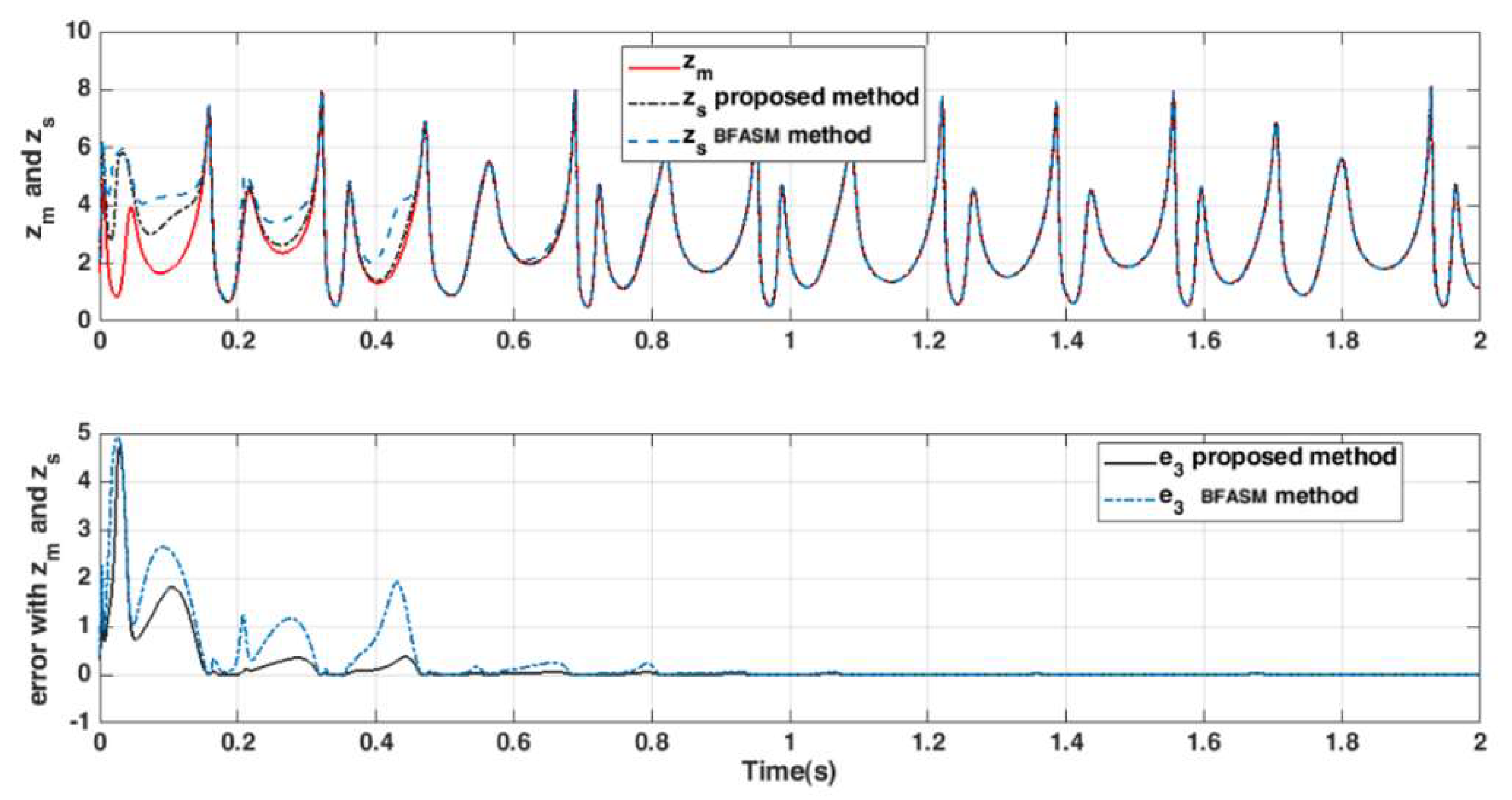
4.2. Chaos Synchronization

For chaotic synchronization, using the nonlinear new system (36) with uncertain parameters, two 3D nonlinear systems are considered. These two systems are referred to as master–slave with different initial conditions and parameters in Equation (40) with subtitles.

$$\begin{gathered} master \mathrm{system}\{\begin{array}{c}{\dot{x}}_m=f_{1m}(x,y,z)\\ {\dot{y}}_m=f_{2m}(x,y,z)\\ {\dot{z}}_m=f_{3m}(x,y,z)\end{array} \\ slave \mathrm{system}\{\begin{array}{c}{\dot{x}}_s=f_{1s}(x,y,z)\\ {\dot{y}}_s=f_{2s}(x,y,z)\\ {\dot{z}}_m=f_{3s}(x,y,z)+b(x,t)u+w^{\prime }\end{array} \end{gathered}$$

(40)

where $f_{1m}(x,y,z)=a{x}_m+a{y}_m-b{y}_m{z}_m-c{z}_m{}^2$, $f_{2m}(x,y,z)=a{x}_m+a{y}_m-b{y}_m{z}_m-c{z}_m{}^2-d{x}_m{y}_m-e{y}_m{z}_m-f{x}_m{}^4-gexp(z_m)$, $f_{3m}(x,y,z)=x_m{y}_m{z}_m-htanh(x_m)$, $f_{1s}(x,y,z)=-a{x}_s+a{y}_s-b{y}_s{z}_s-c{z}_s{}^2$, $f_{2s}(x,y,z)=-d{x}_s{y}_s-e{y}_s{z}_s-f{x}_s{}^4-gexp(z_s)$, $f_{3s}(x,y,z)=x_s{y}_s{z}_s-htanh(x_s)$, $b(x,t)=1$, u is BFATSM control input, and $w^{\prime }=0.6sin(3.1t)$ is external disturbance. The initial conditions and chaos parameters as follows:

$$\begin{gathered} master \mathrm{values}\{\begin{array}{c}{x}_m(0)=-3.5,{ y}_m(0)=-24{.4, z}_m(0)=3.1\\ a_m=20,{ b}_m=8{.2, c}_m{=17, d}_m=2{.3, e}_m{=11, f}_m{=13, g}_m=14{.5, h}_{m }=24\end{array} \\ slave \mathrm{values}\{\begin{array}{c}{x}_s(0)=-4,{ y}_s(0)=-{20, z}_s(0)=2.9\\ a_s=19.2,{ b}_s=7{.9, c}_s=17{.2, d}_s{=2, e}_{s }=10{.8, f}_s{=14, g}_s{=13, h}_s=22.5\end{array} \end{gathered}$$

(41)

The time responses of the chaos synchronization of master–slave systems and synchronization errors by using the proposed technique and the method of [2] are shown in Figure 8, Figure 9 and Figure 10.

4.3. Control Parameters

• Parameters $\epsilon ,c$: Parameter c, as shown in Equation (6), is the coefficient of variation of the sliding surface. Larger c, means faster convergence of system modes. According to Equation (16), smaller $\epsilon$ means less absorption area for the sliding surface variable. If this parameter is selected too small, it may impose a larger control gain on the system. According to Equations (7) and (16), $\epsilon ,c$ determines the size of the state convergence region and must be selected appropriately.
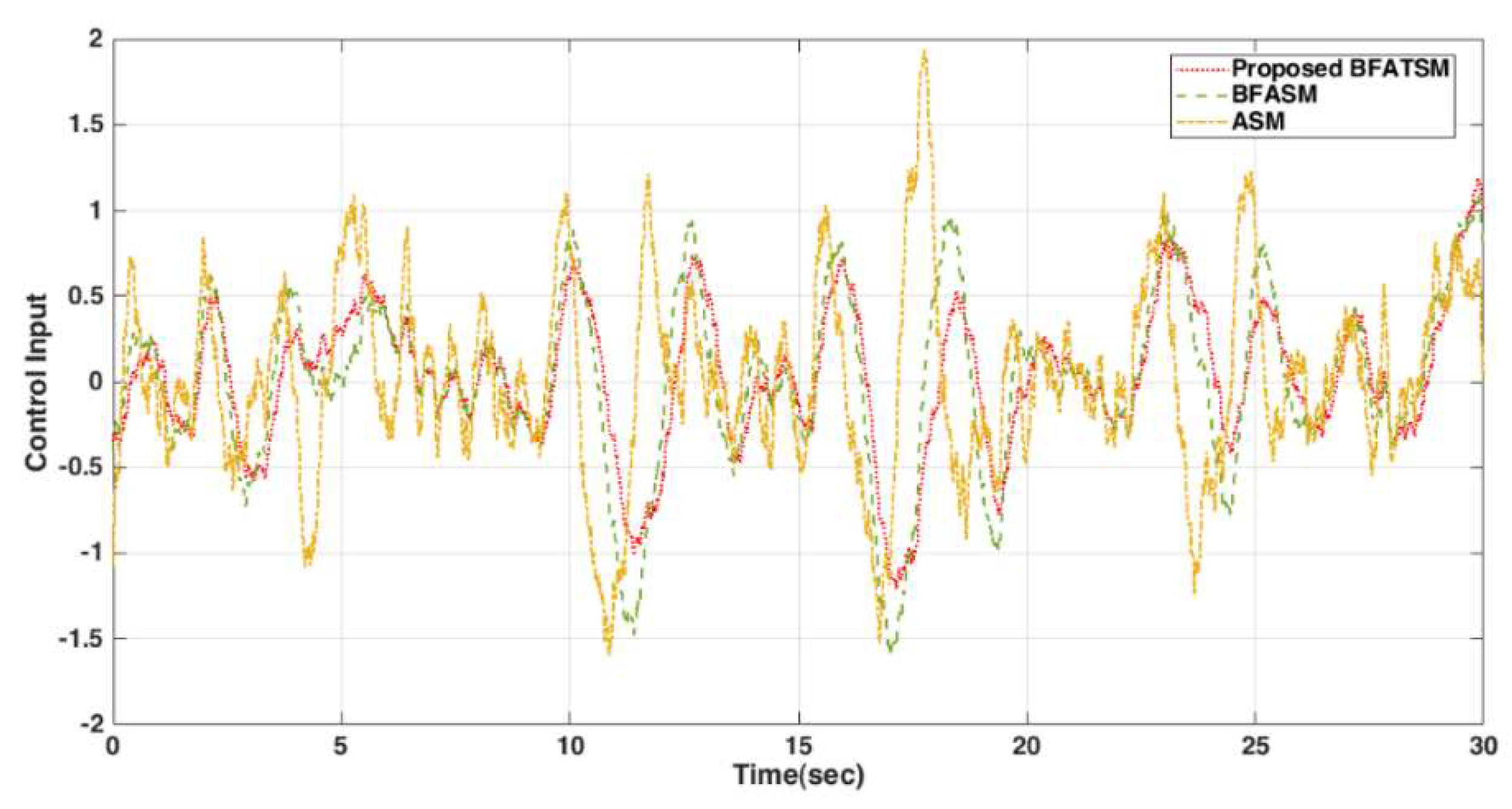
• Parameters $\mu ,\kappa$: in the control laws (13) and (23), $\kappa$ and $\mu$ can effectively increase the efficiency of the controller. If these two parameters are selected too large, it will increase the control gain too much, which will lead to chattering of the control signal.
• The control parameters in the simulation process are exposed in

  Table 2. BFATSM control parameter values.

  Parameters	Values	Parameters	Values
  $k_p$	12.5	$\epsilon$	0.033
  $k_d$	0.61	c	114
  $k_i$	9.3	$\mu$	0.17
  r	19	$\kappa$	11
  q	3	b	1

  .

5. Conclusions

In this study, an adaptive nonlinear finite time control based on the sliding mode controller of the barrier function terminal is proposed for the strong stability of n-order nonlinear dynamic systems with external perturbations. The proposed BFATSM control method causes the tracking errors to converge to an area close to zero in a limited time and, in this method, there is no need for information on the high disturbance boundaries. The new controller, which is a more complete class of terminal sliding mode controllers, is designed with regard to issues such as variable uncertainties, limiting assumptions for system dynamics, actuator saturation, and the validity range of state variables. By analyzing Lyapunov stability, we proved that the errors are convergent to the specified region. In order to make the planned method effective, a new complex chaotic system with a high Kaplan–Yorke dimension was proposed. The results showed that the suggested control technique has stronger tracking than the adaptive controller and produces finite-time chaos synchronization.