Energy-Efficient Training of Memristor Crossbar-Based Multi-Layer Neural Networks
Abstract
1. Introduction
2. Related Works
3. Memristor-Based Neuron and Storage Circuit
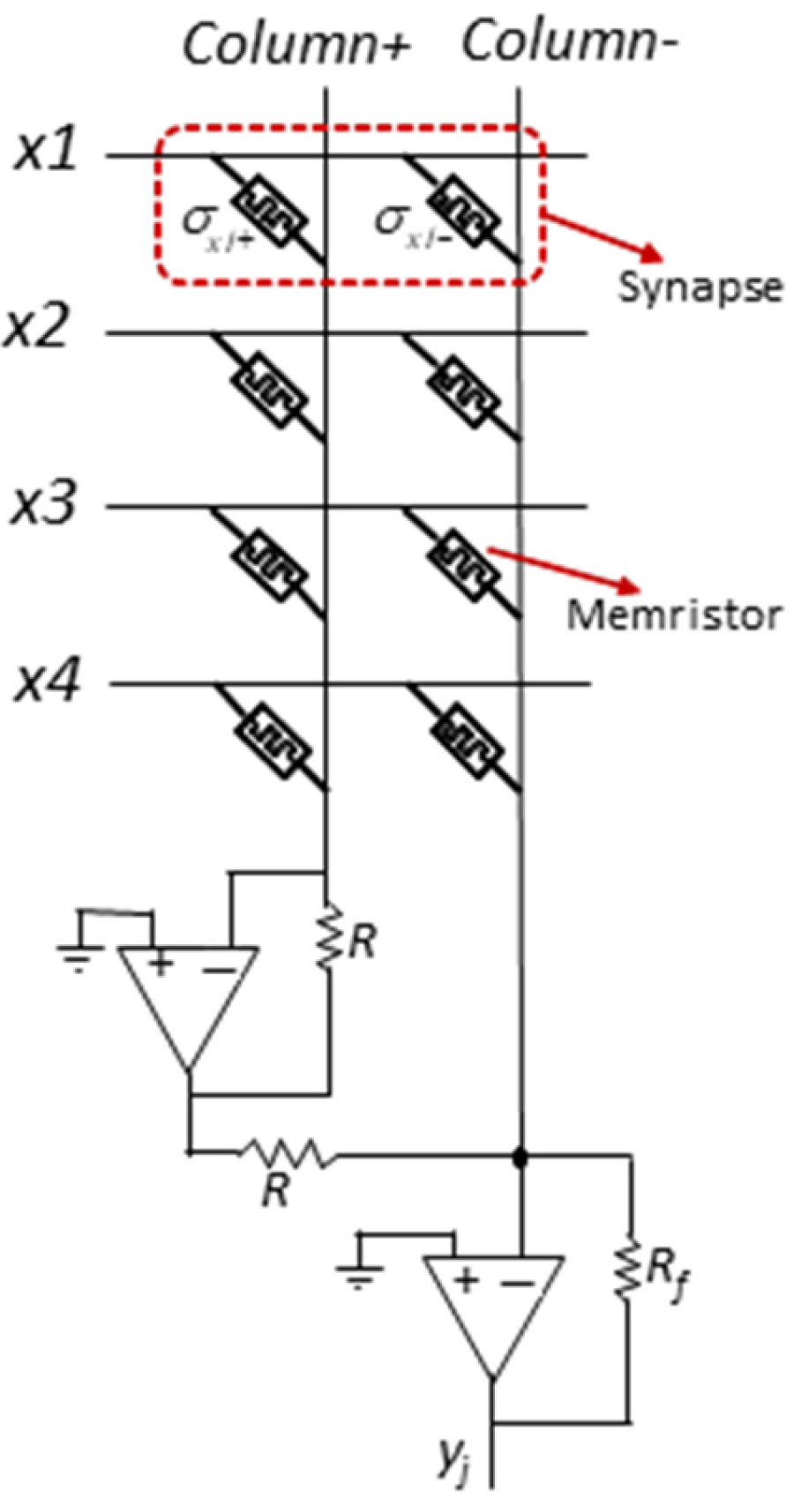
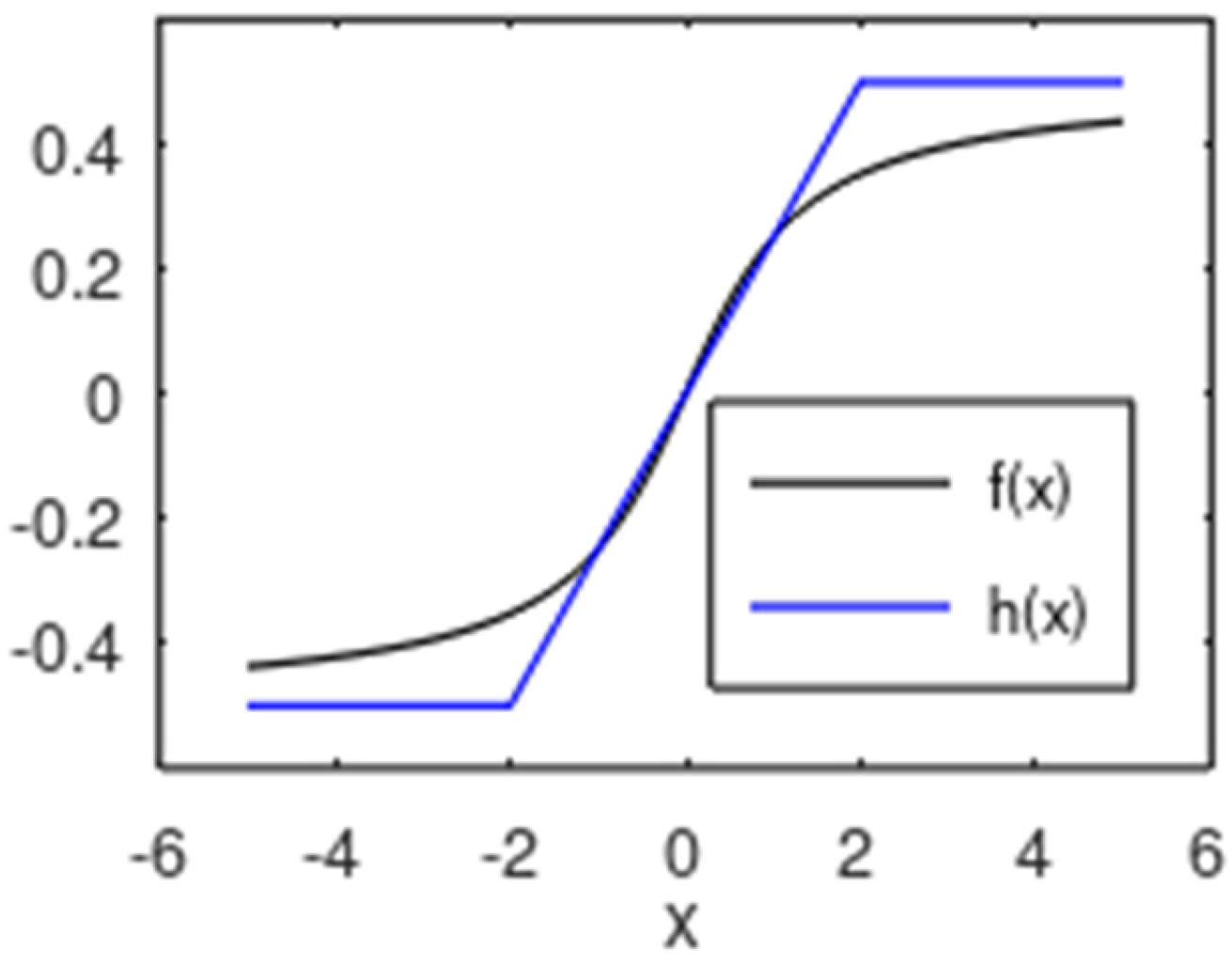
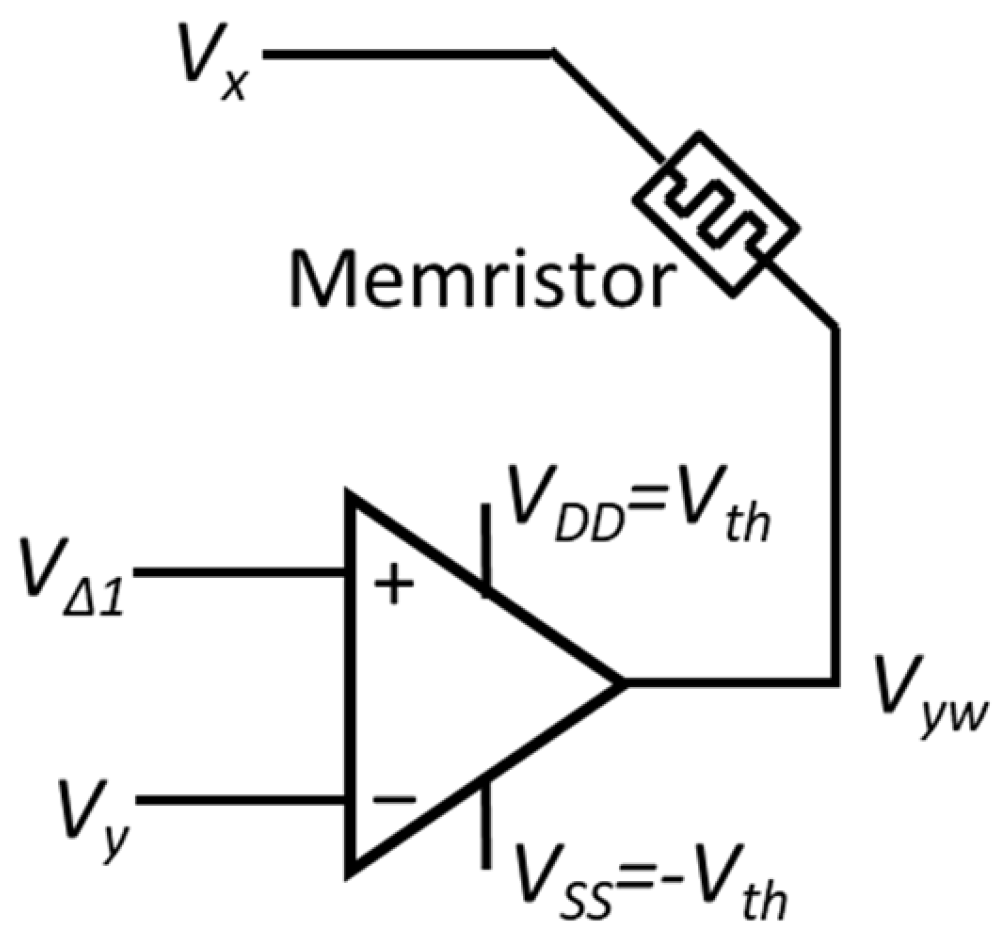
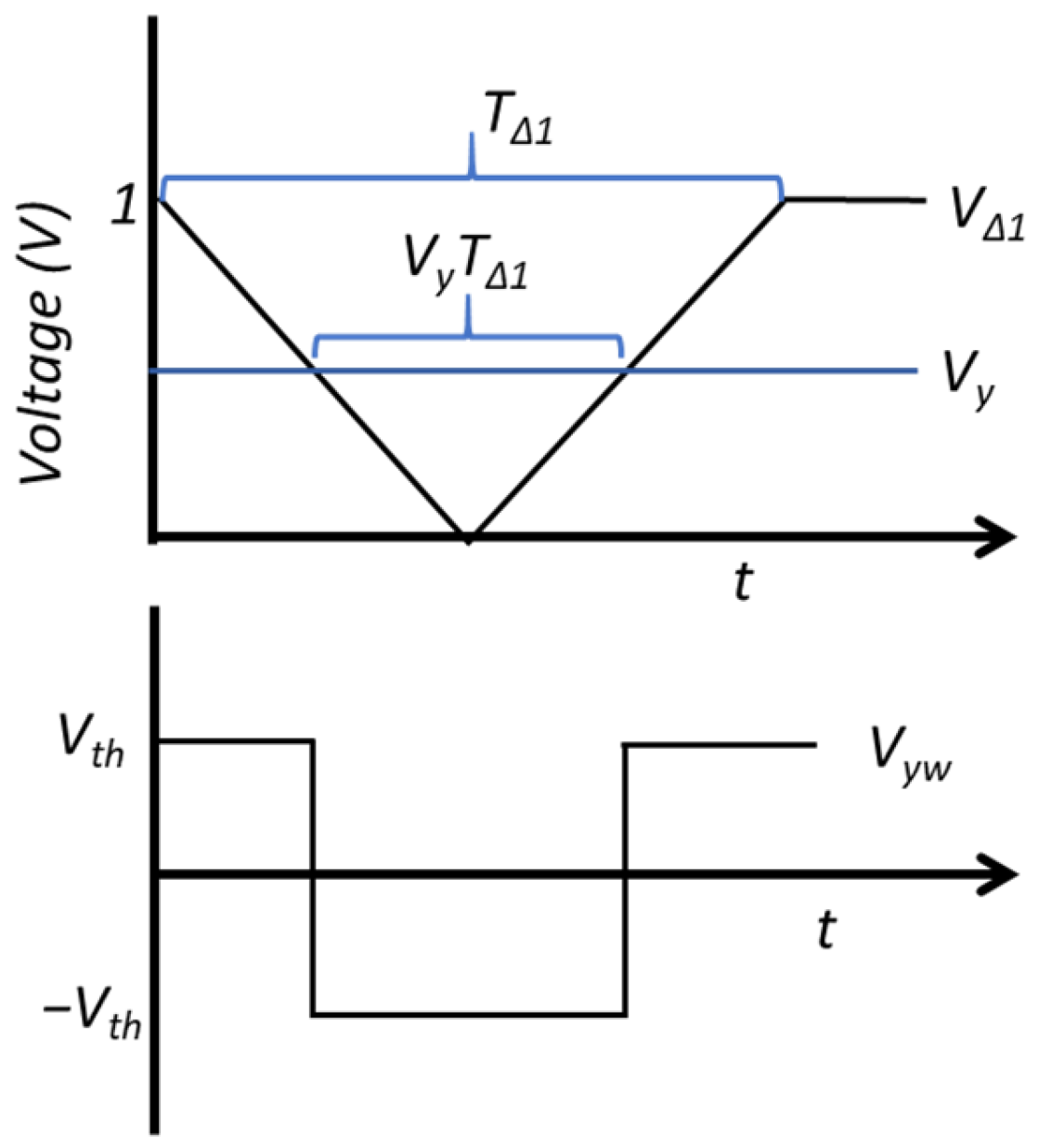
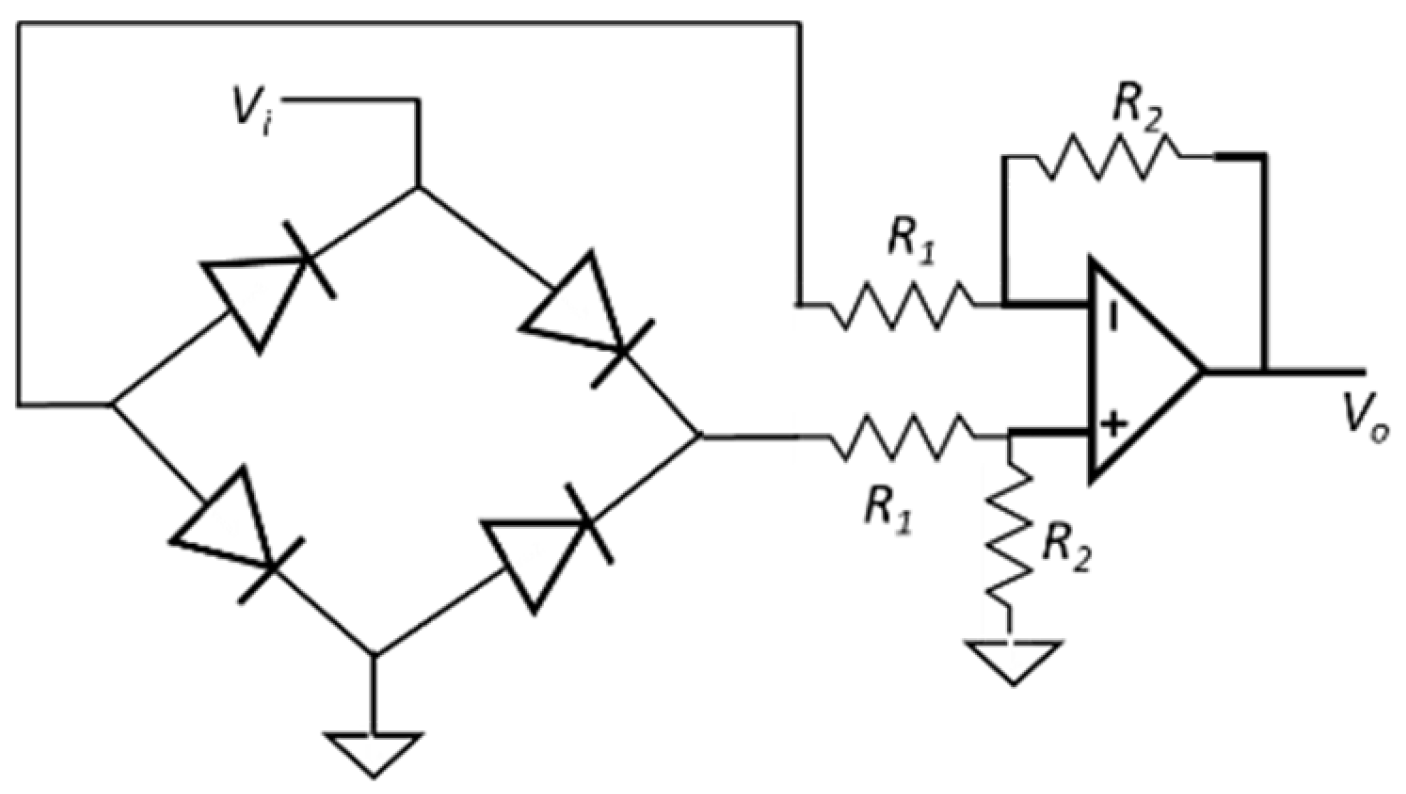
3.1. Neuron Circuit
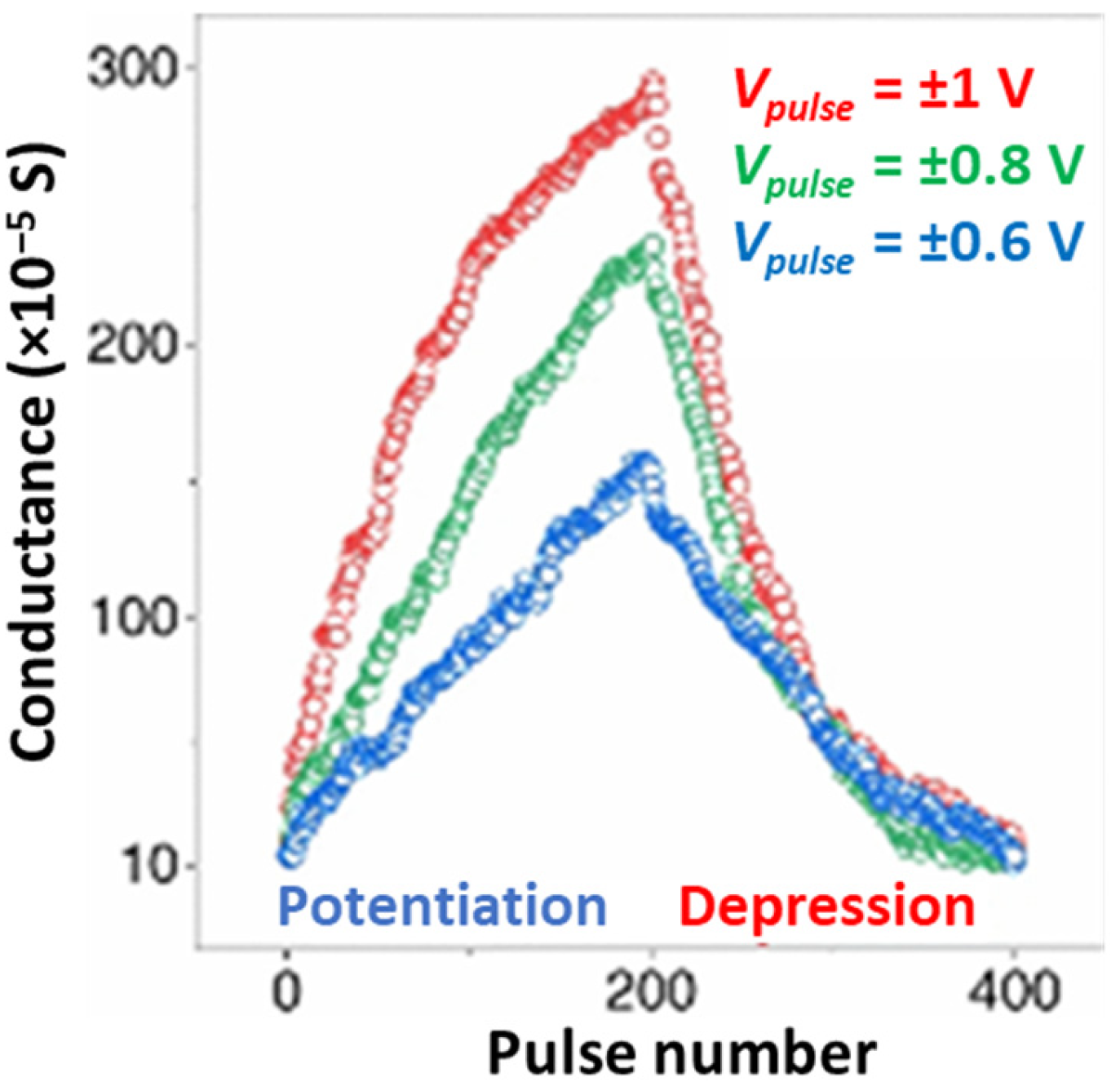
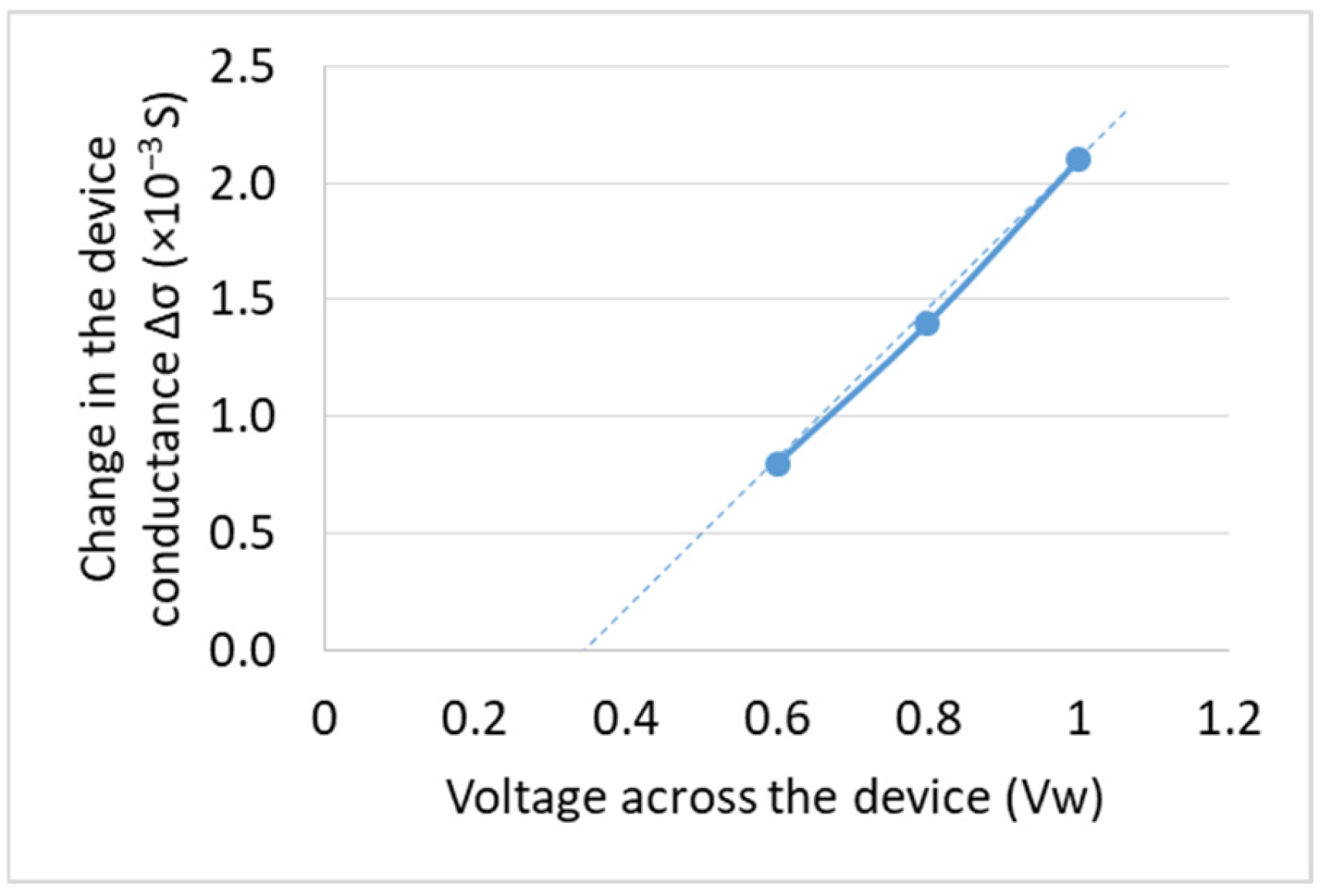
3.2. Memristor-Based Analog Storage Circuit
4. Training of Memristor Crossbar-Based Multi-Layer Neural Networks
4.1. Multi-Layer Neural Network Design
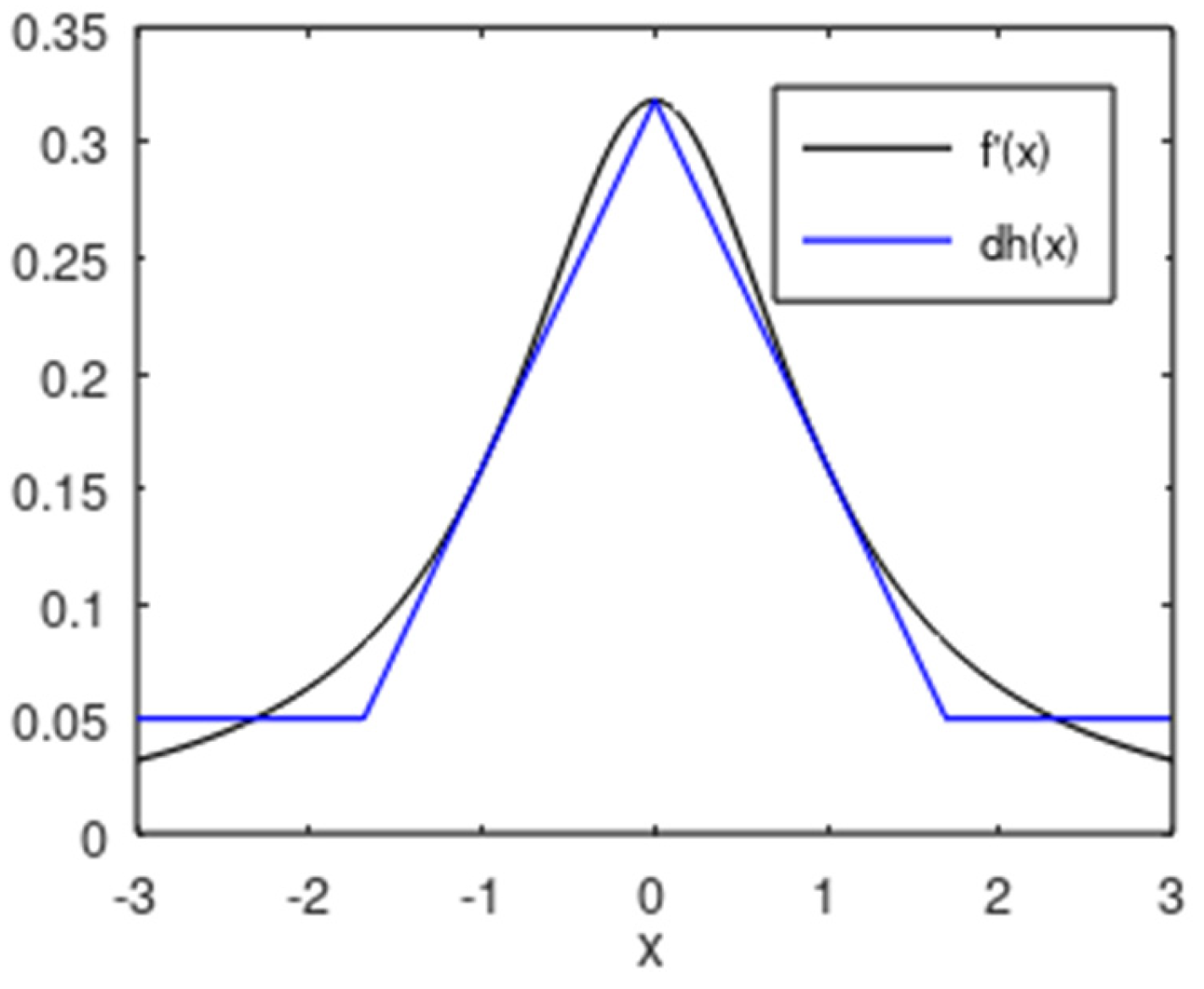
4.2. Training Algorithm
- (1)
- Apply random number of pulses across the memristor devices in the synaptic arrays.
- (2)
- For each training data (x, t), execute the following steps:
- (i)
- Apply the input x to the layer 1 crossbar and evaluate the DPj and, yj values of all the neurons in the system (layer 1 and output layer neurons).
- (ii)
- Calculate the error δj for each output layer neuron j based on Equation (4).
- (iii)
- Assume that the hidden layer neuron j is connected to the output layer neuron k and is the corresponding synaptic weight. Back-propagate the output layer errors for each hidden layer neuron j based on the following formula.
- (iv)
- Determine the amount, Δw, that each neuron’s synapses should be updated.where 2η is the learning rate.
- (3)
- Repeat Step 2 until the output layer error is converged to a sufficiently small value.
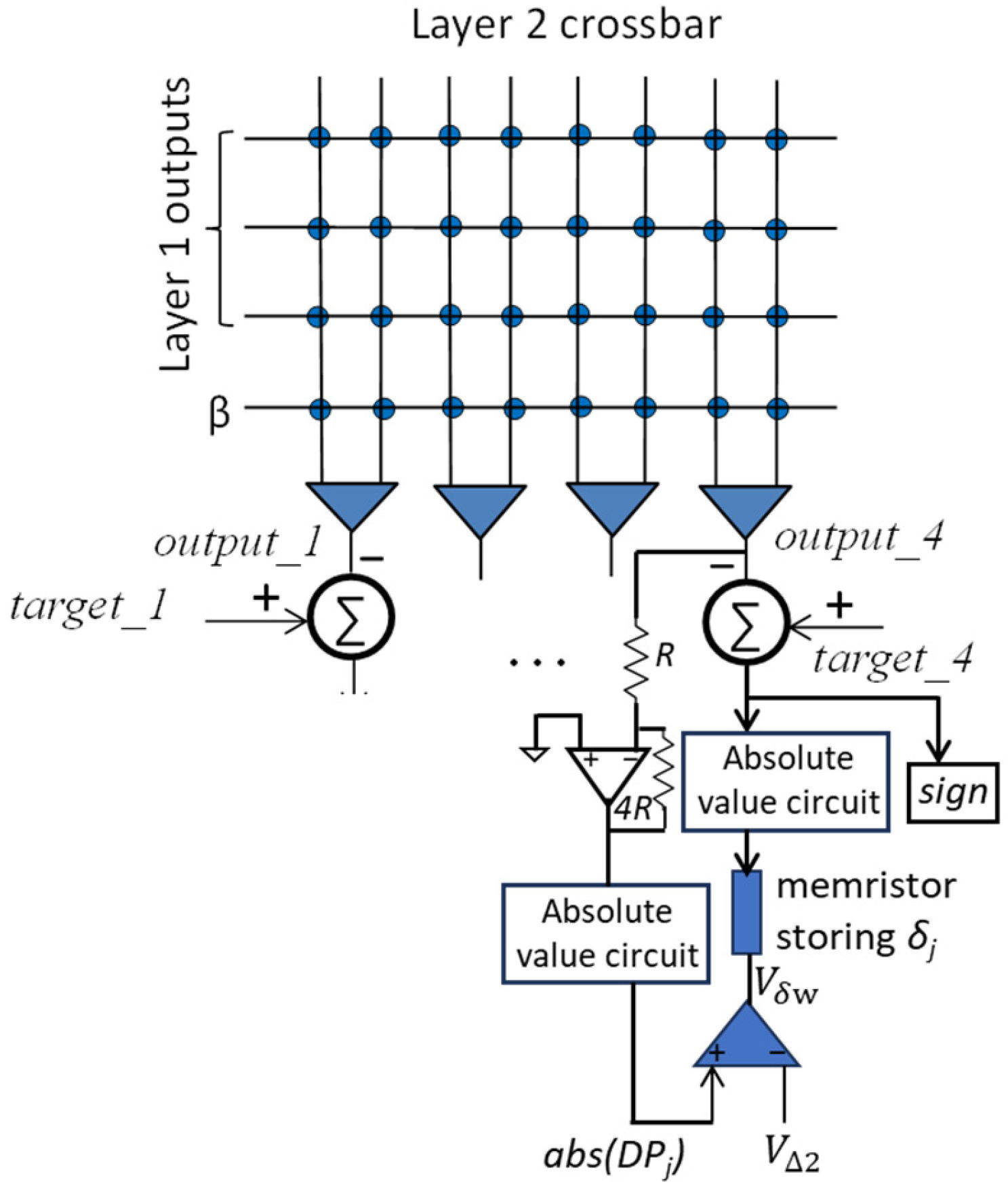
4.3. Hardware Implementation of the Proposed Training Algorithm
- (i)
- Forward pass: Apply input and evaluate the network output.
- (ii)
- Calculate the output layer neuron errors.
- (iii)
- Back-propagate the error for layer 1 neurons.
- (iv)
- Update the synaptic weights.
5. Experimental Setup
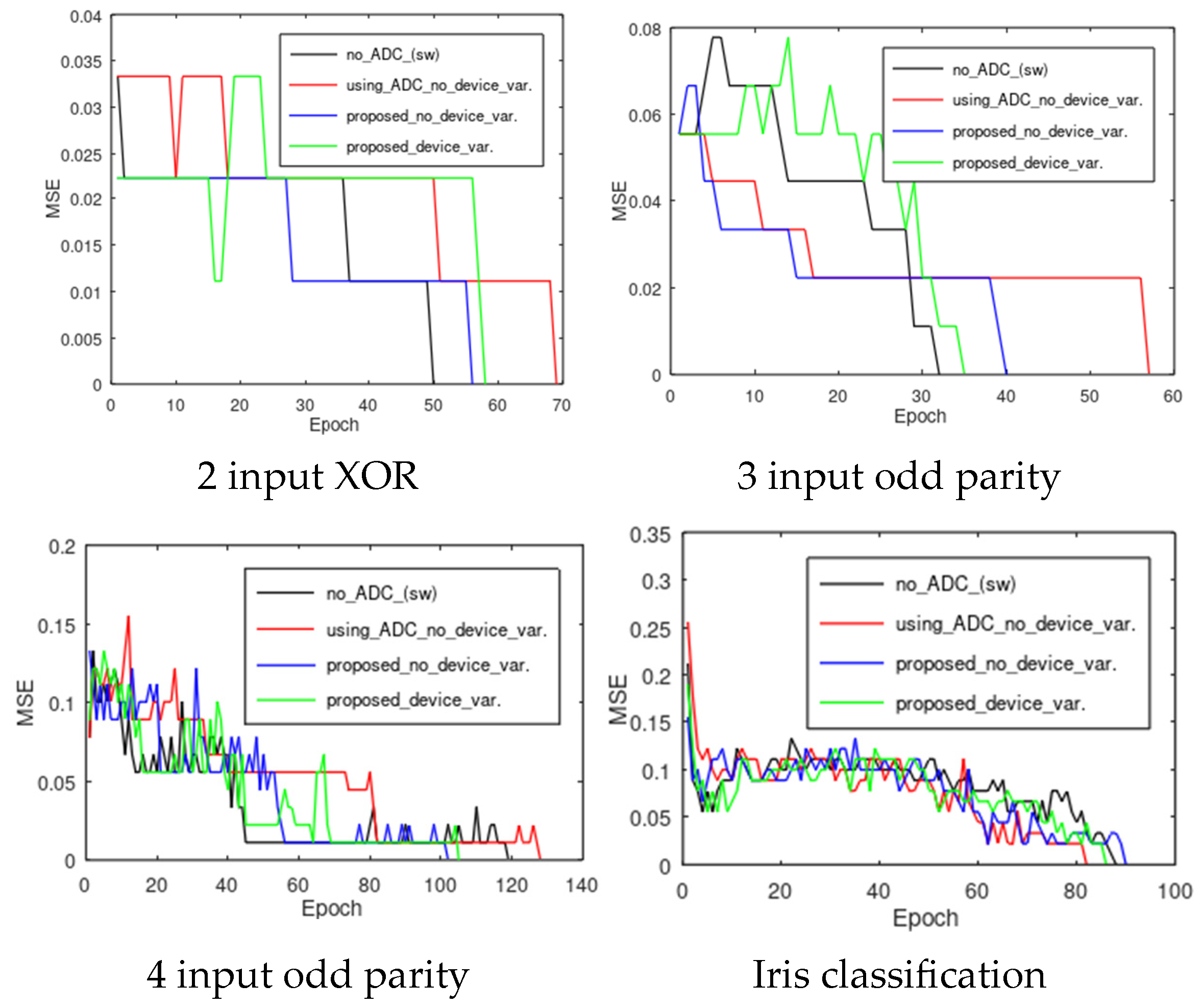
6. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| MCNN | memristor crossbar-based neural network |
References
- Kong, L.; Tan, J.; Huang, J.; Chen, G.; Wang, S.; Jin, X.; Zeng, P.; Khan, M.; Das, S.K. Edge-computing-driven internet of things: A survey. ACM Comput. Surv. 2022, 55, 1–41. [Google Scholar] [CrossRef]
- Taha, T.M.; Hasan, R.; Yakopcic, C.; McLean, M.R. Exploring the Design Space of Specialized Multicore Neural Processors. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013. [Google Scholar]
- Belhadj, B.; Zheng, A.J.L.; Héliot, R.; Temam, O. Continuous real-world inputs can open up alternative accelerator designs. In Proceedings of the 40th Annual International Symposium on Computer Architecture (ISCA), New York, NY, USA, 23–27 June 2013. [Google Scholar]
- Zheng, Y.; Yang, H.; Shu, Y.; Jia, Y.; Huang, Z. Optimizing off-chip memory access for deep neural network accelerator. Trans. Circuits Syst. II Express Briefs 2022, 69, 2316–2320. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor—The Missing Circuit Element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing Memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Ye, L.; Gao, Z.; Fu, J.; Ren, W.; Yang, C.; Wen, J.; Wan, X.; Ren, Q.; Gu, S.; Liu, X.; et al. Overview of memristor-based neural network design and applications. Front. Phys. 2022, 10, 839243. [Google Scholar] [CrossRef]
- Aguirre, F.; Sebastian, A.; Le Gallo, M.; Song, W.; Wang, T.; Yang, J.J.; Lu, W.; Chang, M.F.; Ielmini, D.; Yang, Y.; et al. Hardware implementation of memristor-based artificial neural networks. Nat. Commun. 2024, 15, 1974. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Wu, Y.; Wong, H.-S.P. Investigating the switching dynamics and multilevel capability of bipolar metal oxide resistive switching memory. Appl. Phys. Lett. 2011, 98, 103514. [Google Scholar] [CrossRef]
- Medeiros-Ribeiro, G.; Perner, F.; Carter, R.; Abdalla, H.; Pickett, M.D.; Williams, R.S. Lognormal switching times for titanium dioxide bipolar memristors: Origin and resolution. Nanotechnology 2011, 22, 095702. [Google Scholar] [CrossRef]
- Le Gallo, M.; Khaddam-Aljameh, R.; Stanisavljevic, M.; Vasilopoulos, A.; Kersting, B.; Dazzi, M.; Karunaratne, G.; Brändli, M.; Singh, A.; Mueller, S.M.; et al. A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference. Nat. Electron. 2023, 6, 680–693. [Google Scholar] [CrossRef]
- Soudry, D.; Castro, D.D.; Gal, A.; Kolodny, A.; Kvatinsky, S. Memristor-Based Multilayer Neural Networks With Online Gradient Descent Training. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2408–2421. [Google Scholar] [CrossRef]
- Hasan, R.; Taha, T.M.; Yakopcic, C. On-chip training of memristor crossbar based multi-layer neural networks. Microelectron. J. 2017, 66, 31–40. [Google Scholar] [CrossRef]
- Hasan, R.; Taha, T.M.; Yakopcic, C. A fast training method for memristor crossbar based multi-layer neural networks. Analog. Integr. Circuits Signal Process. 2017, 93, 443–454. [Google Scholar] [CrossRef]
- Boquet, G.; Macias, E.; Morell, A.; Serrano, J.; Miranda, E.; Vicario, J.L. Offline training for memristor-based neural networks. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021; pp. 1547–1551. [Google Scholar]
- Alibart, F.; Zamanidoost, E.; Strukov, D.B. Pattern classification by memristive crossbar circuits with ex-situ and in-situ training. Nat. Commun. 2013, 4, 2072. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Lu, J.; Wang, Z.; Wang, R.; Wei, J.; Shi, T.; Dou, C.; Wu, Z.; Zhu, J.; Shang, D.; et al. Hybrid memristor-CMOS neurons for in-situ learning in fully hardware memristive spiking neural networks. Sci. Bull. 2021, 66, 1624–1633. [Google Scholar] [CrossRef]
- Singh, A.; Lee, B.G. Framework for in-memory computing based on memristor and memcapacitor for on-chip training. IEEE Access 2023, 11, 112590–112599. [Google Scholar] [CrossRef]
- Shen, S.; Guo, M.; Wang, L.; Duan, S. DTGA: An in-situ training scheme for memristor neural networks with high performance. Appl. Intell. 2025, 55, 167. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, P.; Gao, B.; Liu, Q.; Wu, D.; Zhang, Q.; Li, Y.; Qin, Q.; Li, J.; Zhu, Z.; et al. Edge learning using a fully integrated neuro-inspired memristor chip. Science 2023, 381, 1205–1211. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Zhou, Y.; Zhang, Q.; Zhang, S.; Yao, P.; Xi, Y.; Liu, Q.; Zhao, M.; Zhang, W.; Liu, Z.; et al. Memristor-based analogue computing for brain-inspired sound localization with in situ training. Nat. Commun. 2022, 13, 2026. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Wang, Y.; Wang, Y.Z.; Chen, Y.; Yang, H. Training itself: Mixed-signal training acceleration for memristor-based neural network, Design Automation Conference (ASP-DAC). In Proceedings of the 2014 19th Asia and South Pacific, Singapore, 20–23 January 2014. [Google Scholar]
- Fernando, B.R.; Yakopcic, C.; Taha, T.M. 3D memristor crossbar architecture for a multicore neuromorphic system. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef]
- Hu, L.; Yang, J.; Wang, J.; Cheng, P.; Chua, L.O.; Zhuge, F. All-optically controlled memristor for optoelectronic neuromorphic computing. Adv. Funct. Mater. 2021, 31, 2005582. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, M.; Mei, T.; Liu, W.; Wang, L.; Xiao, K. Nanofluidic ionic memristors. ACS Nano 2024, 18, 19423–19442. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Wu, Y.; Jeyasingh, R.; Kuzum, D.; Wong, H.S.P. An electronic synapse device based on metal oxide resistive switching memory for neuromorphic computation. IEEE Trans. Elec. Devices 2011, 58, 2729–2737. [Google Scholar] [CrossRef]
- Dong, X.; Xu, C.; Member, S.; Xie, Y.; Jouppi, N.P. NVSim: A Circuit-Level Performance, Energy, and Area Model for Emerging Nonvolatile Memory. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2012, 31, 994–1007. [Google Scholar] [CrossRef]
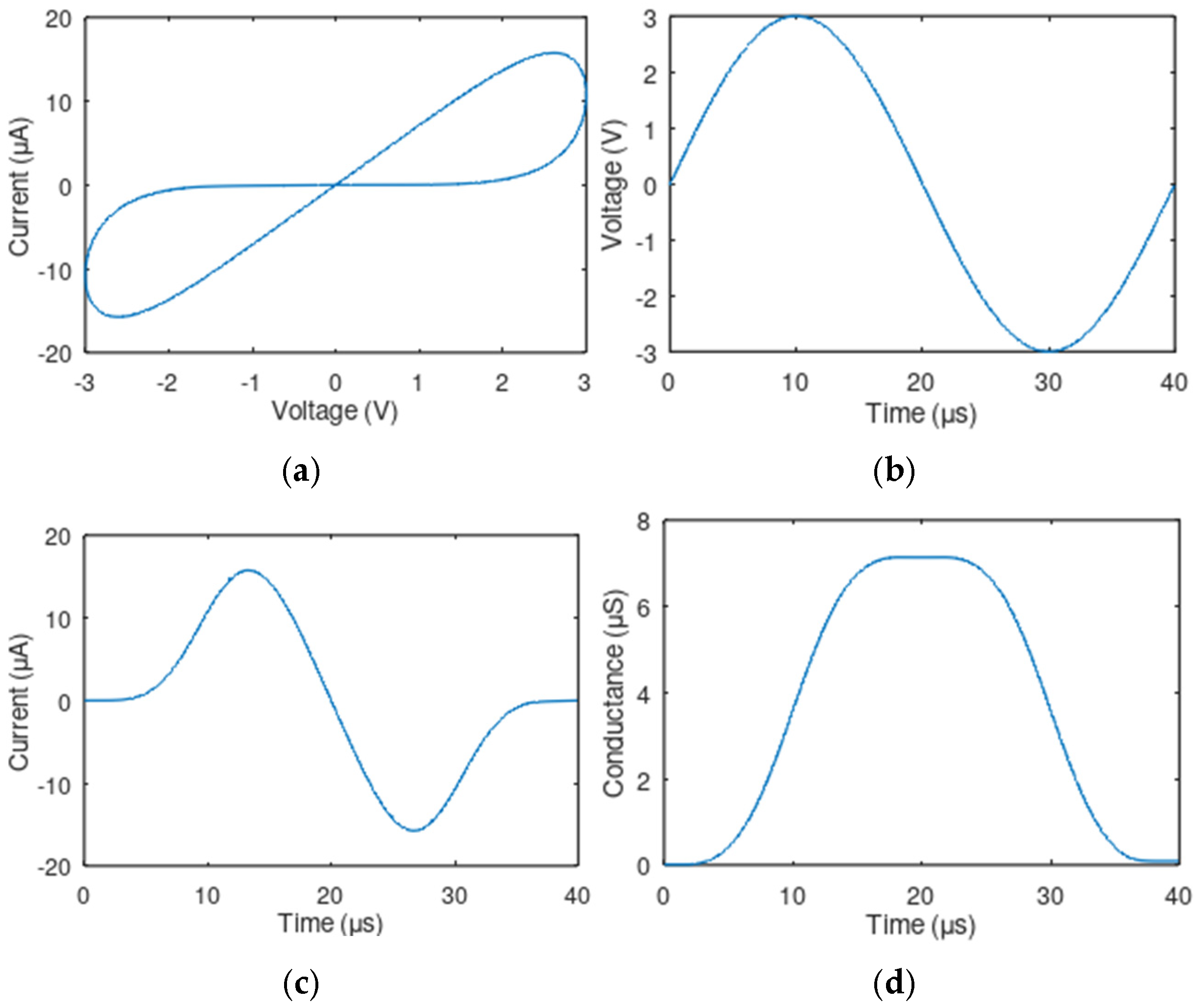
- Qin, F.; Zhang, Y.; Song, H.W.; Lee, S. Enhancing memristor fundamentals through instrumental characterization and understanding reliability issues. Mater. Adv. 2023, 4, 1850–1875. [Google Scholar] [CrossRef]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E. Memristor SPICE model and crossbar simulation based on devices with nanosecond switching time. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–7. [Google Scholar]
- Iris Dataset. Available online: https://archive.ics.uci.edu/ml/datasets/Iris (accessed on 1 November 2024).




| RON (Ω) | 50 kΩ |
| ROFF (Ω) | 10 MΩ |
| Vth (V) | 1.3 V |
| Device switching time for write voltage amplitude 2.5 V | 20 μs |
| Voltage Across Memristor Device (V) | Time (ns) | Change in Conductance (S) |
|---|---|---|
| 1.5 | 35 | 1.65 × 10−8 |
| 2.5 | 70 | 3.46 × 10−7 |
| Sign of xj | Sign of δi | Weight Update | Ip1 | Ip2 | Ip3 | Vwd | Vwai | Vmemristor = Vwai − Vwd | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| For Time TΔ1|δi| | Rem. Time | For time TΔ1|δi| | Rem. Time | ||||||||
| Case 1 | + | + | increase | xi | |δi| | −Vth | Vth | |xi| | |xi| + Vth | |xi| − Vth | |
| Case 2 | + | − | decrease | −xi | |δi| | Vth | −Vth | −|xi| | −(|xi| + Vth) | −|xi| + Vth | |
| Case 3 | − | + | decrease | xi | |δi| | Vth | −Vth | −|xi| | −(|xi|+Vth) | −|xi| + Vth | |
| Case 4 | − | − | increase | −xi | |δi| | −Vth | Vth | |xi| | |xi| + Vth | |xi| − Vth | |
| Maximum read voltage, Vread | 0.5 V |
| Maximum deviation in the response of a memristor device due to device variation and stochasticity | 30% |
| Value of the feedback resistance Rf in Figure 1 circuit | 14 MΩ |
| Learning rate, TΔ1 | 5 ns–8 ns |
| Dataset | Neural Network Configurations | Number of Training Data |
|---|---|---|
| 2 input XOR function | 3→20→1 | 4 |
| 3 input odd parity function | 4→30→1 | 8 |
| 4 input odd parity function | 5→40→1 | 16 |
| Iris classification [31] | 5→20→3 | 90 |
| NN Config. | System Using ADC/DAC [13] | Proposed System | ||
|---|---|---|---|---|
| Time (s) | Energy (J) | Time (s) | Energy (J) | |
| 3→20→1 | 8.25 × 10−7 | 9.32 × 10−11 | 7.80 × 10−7 | 5.85 × 10−11 |
| 4→30→1 | 1.01 × 10−6 | 1.38 × 10−10 | 7.80 × 10−7 | 6.18 × 10−11 |
| 5→80→1 | 1.92 × 10−6 | 3.54 × 10−10 | 7.80 × 10−7 | 1.63 × 10−10 |
| 5→15→3 | 7.71 × 10−7 | 8.13 × 10−11 | 7.80 × 10−7 | 3.64 × 10−11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, R.; Alam, M.S.; Taha, T.M. Energy-Efficient Training of Memristor Crossbar-Based Multi-Layer Neural Networks. Chips 2025, 4, 38. https://doi.org/10.3390/chips4030038
Hasan R, Alam MS, Taha TM. Energy-Efficient Training of Memristor Crossbar-Based Multi-Layer Neural Networks. Chips. 2025; 4(3):38. https://doi.org/10.3390/chips4030038
Chicago/Turabian StyleHasan, Raqibul, Md Shahanur Alam, and Tarek M. Taha. 2025. "Energy-Efficient Training of Memristor Crossbar-Based Multi-Layer Neural Networks" Chips 4, no. 3: 38. https://doi.org/10.3390/chips4030038
APA StyleHasan, R., Alam, M. S., & Taha, T. M. (2025). Energy-Efficient Training of Memristor Crossbar-Based Multi-Layer Neural Networks. Chips, 4(3), 38. https://doi.org/10.3390/chips4030038






