Deep Learning Study on Memory IC Package Warpage Using Deep Neural Network and Finite Element Simulation
Abstract
1. Introduction
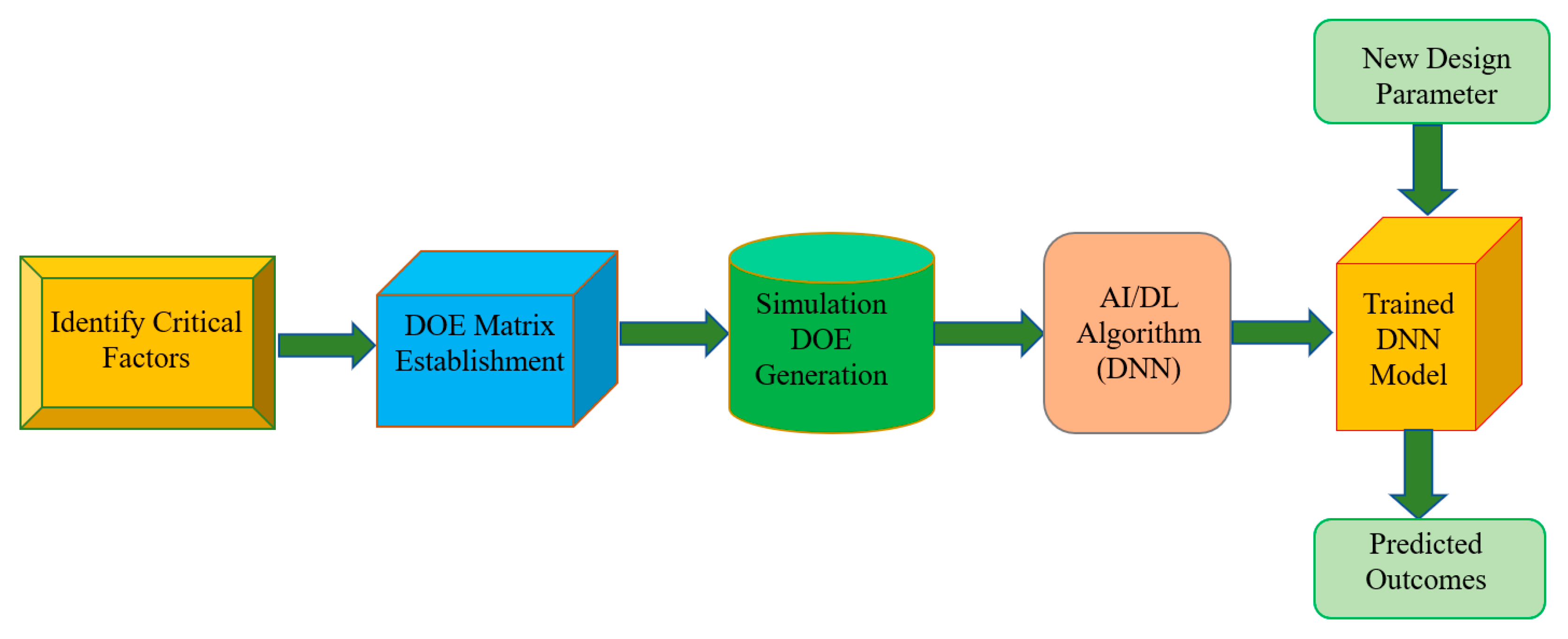
2. Methodology
2.1. Quality Factors and DOE Matrix for DL Model
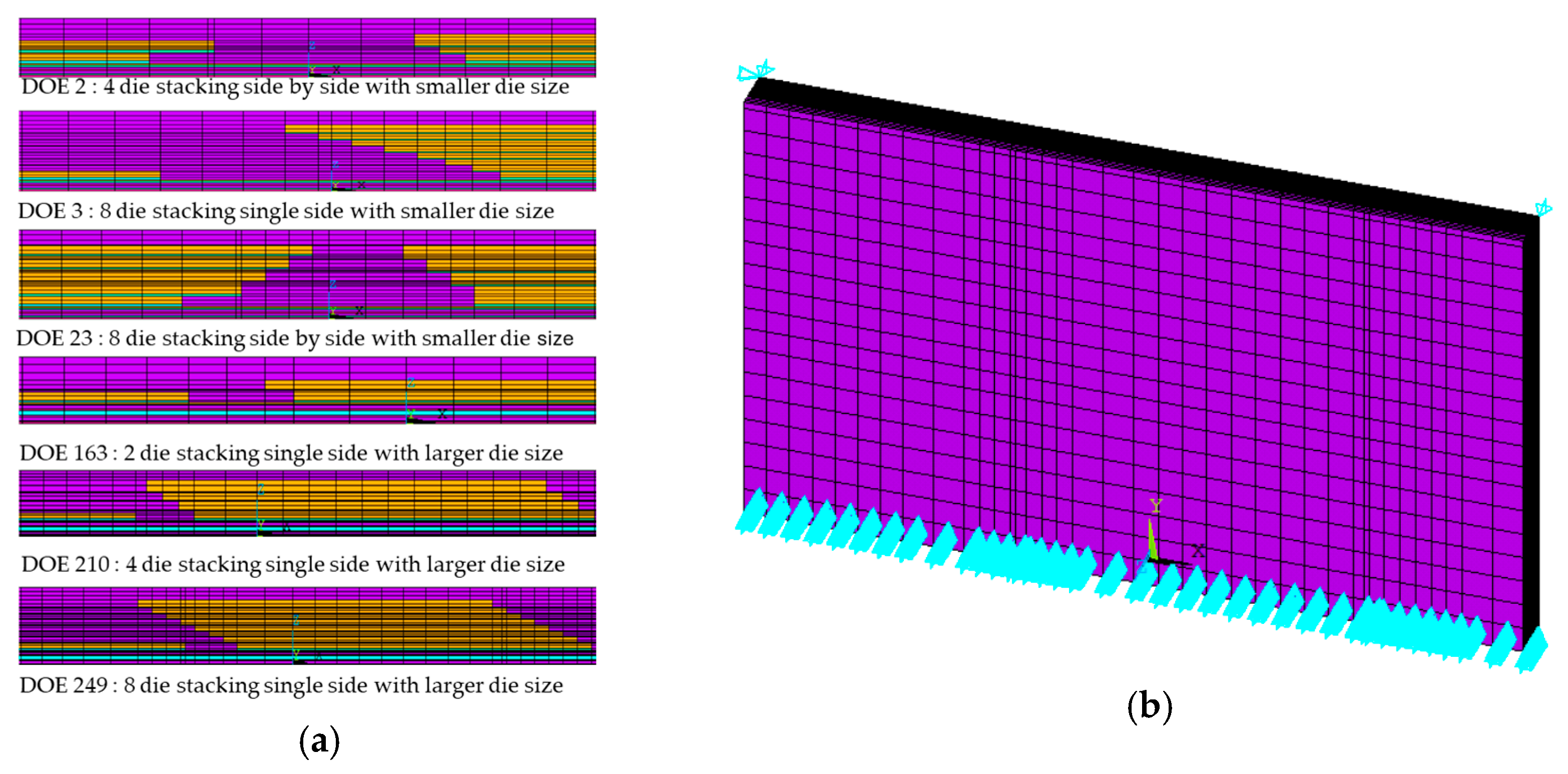
2.2. Finite Element Analysis
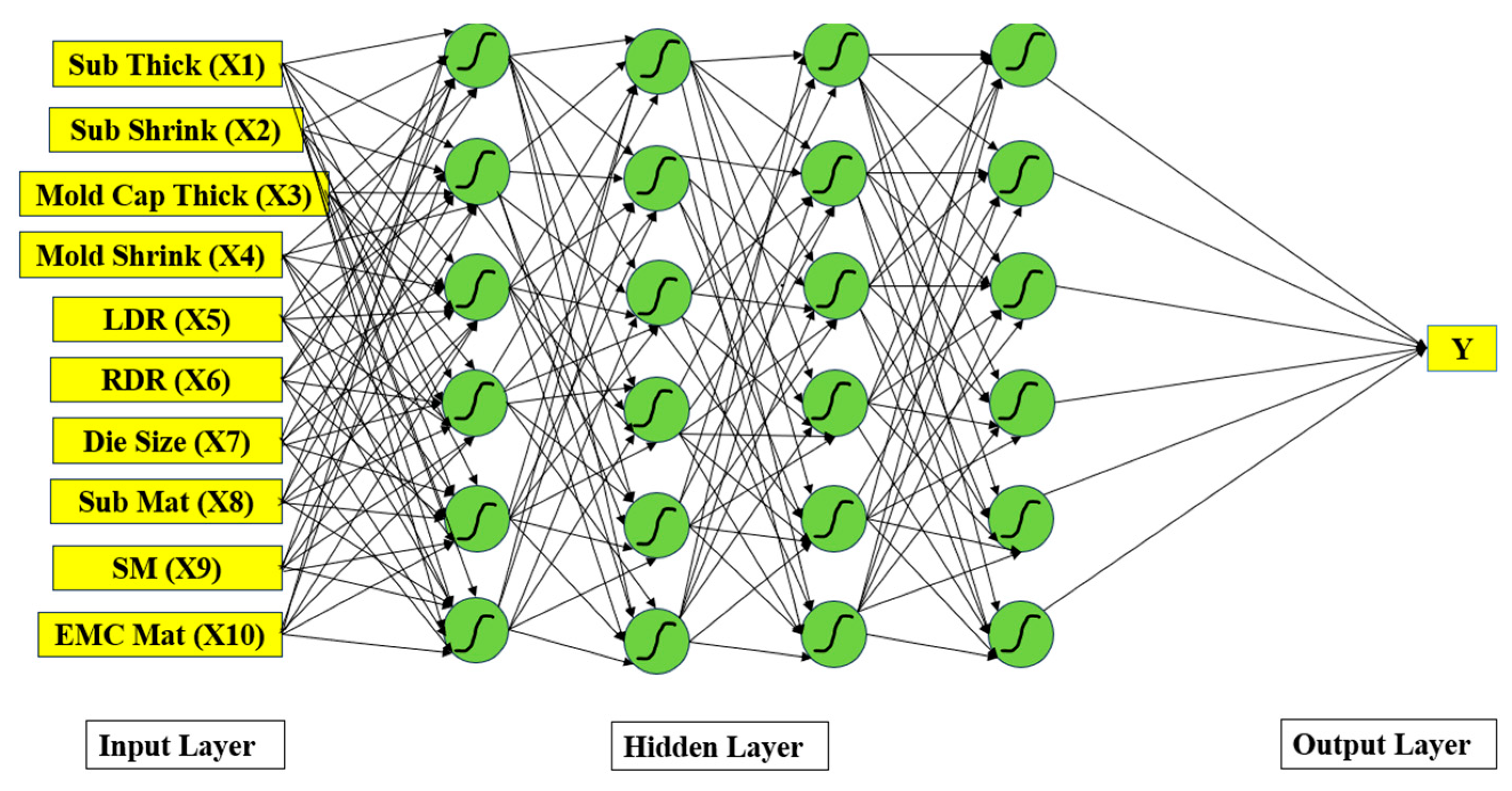
2.3. DNN Regression Model
3. Results and Discussion
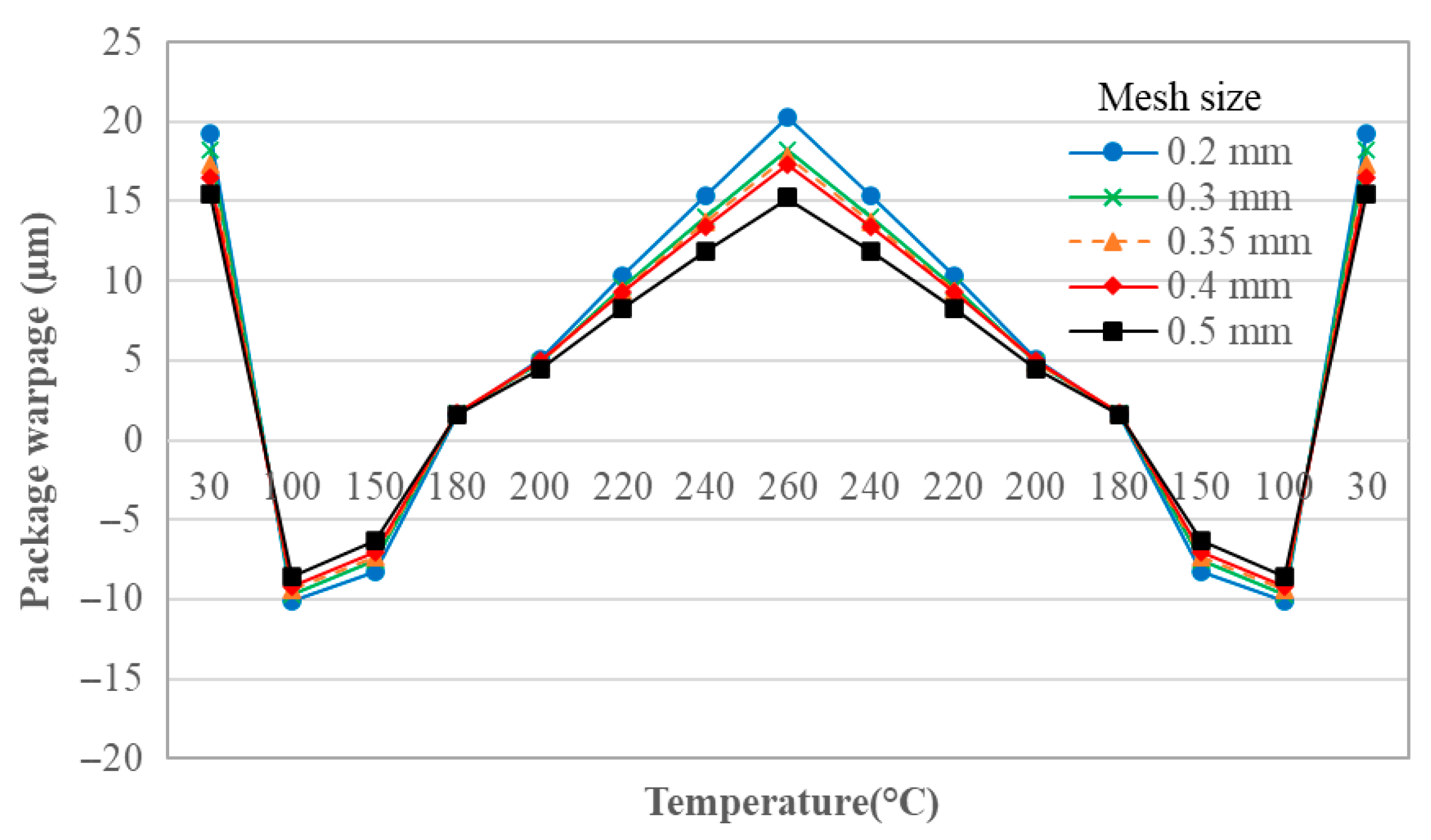
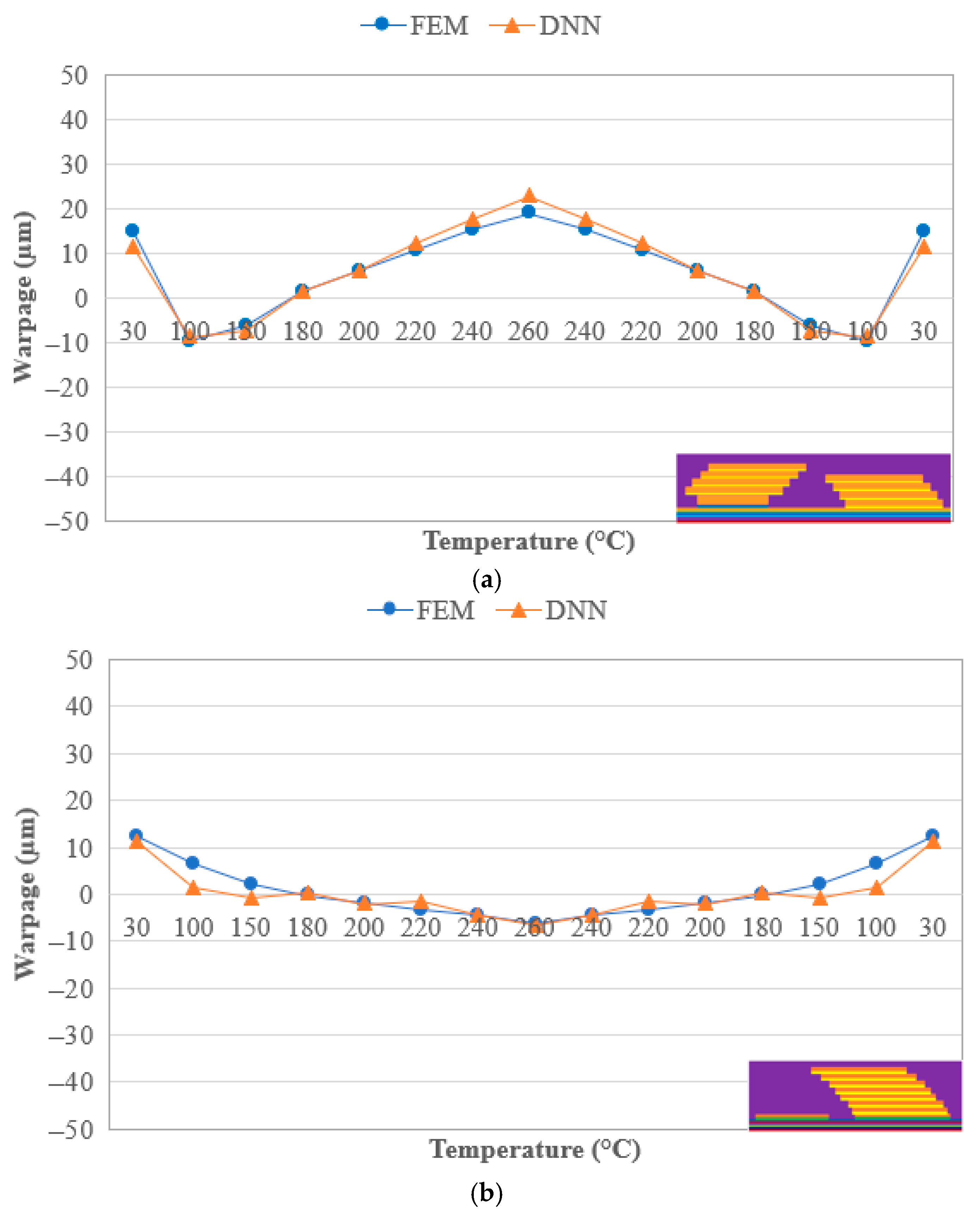
3.1. FEA Simulation Warpage Result
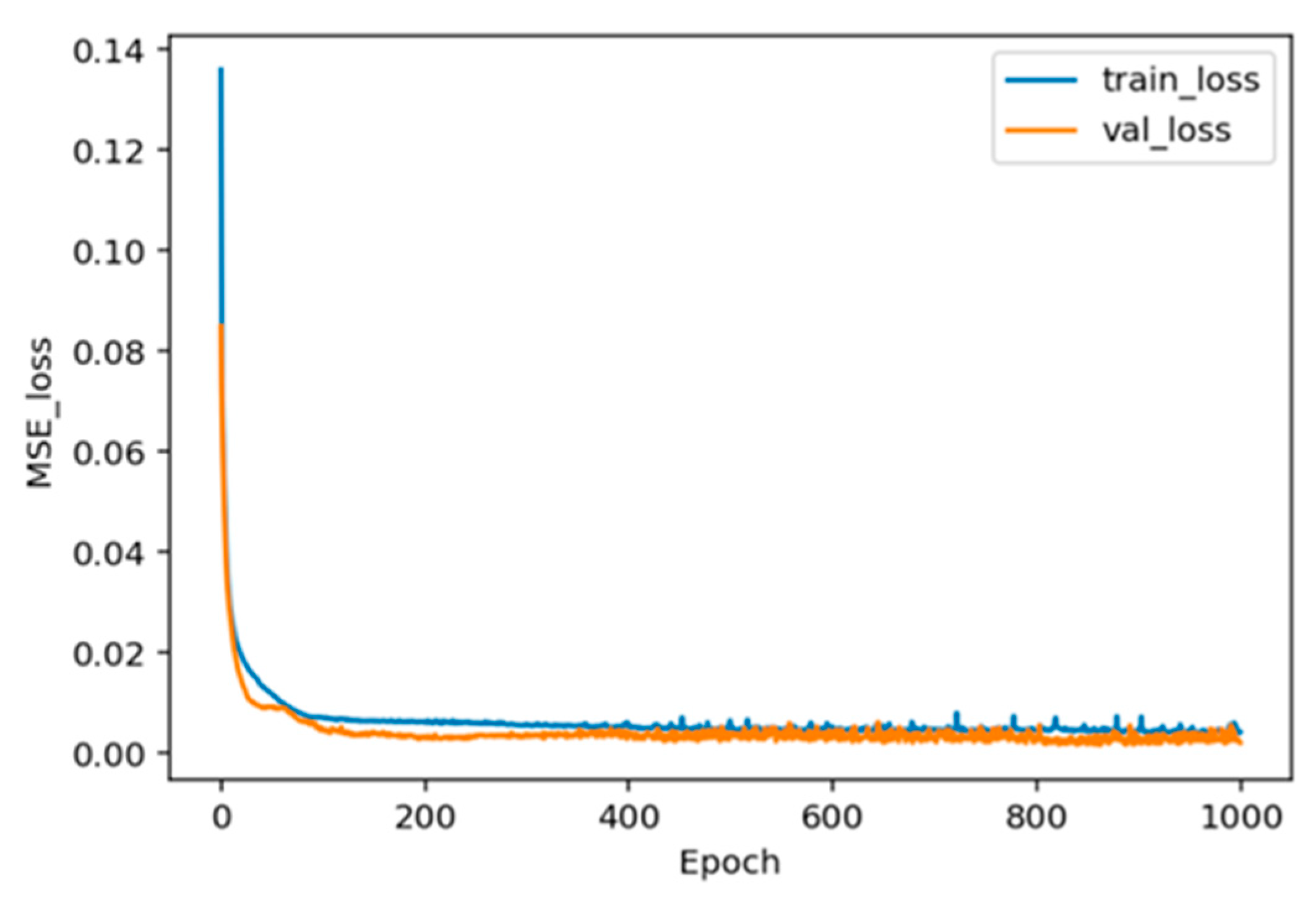
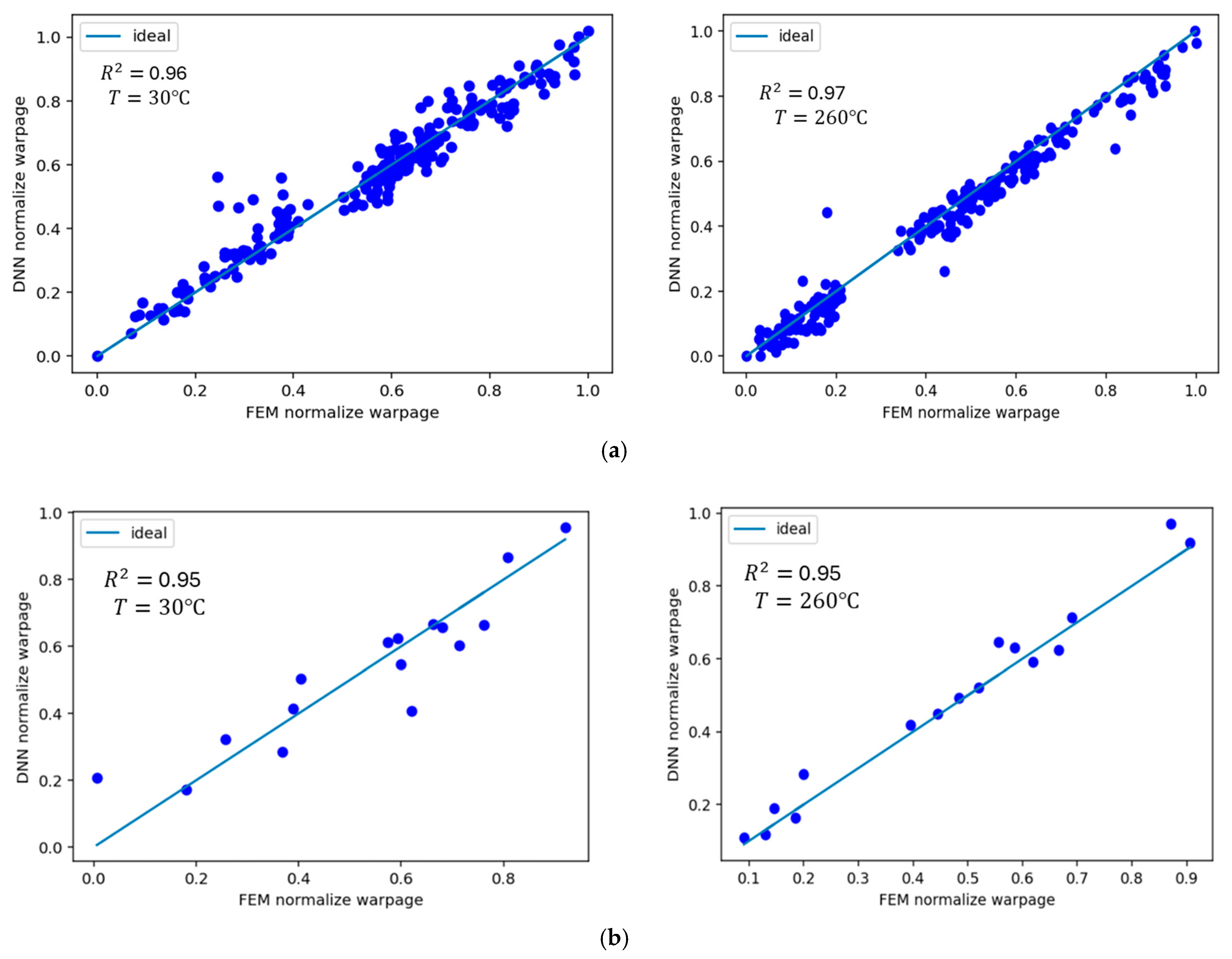
3.2. DNN Trained Model and Validation
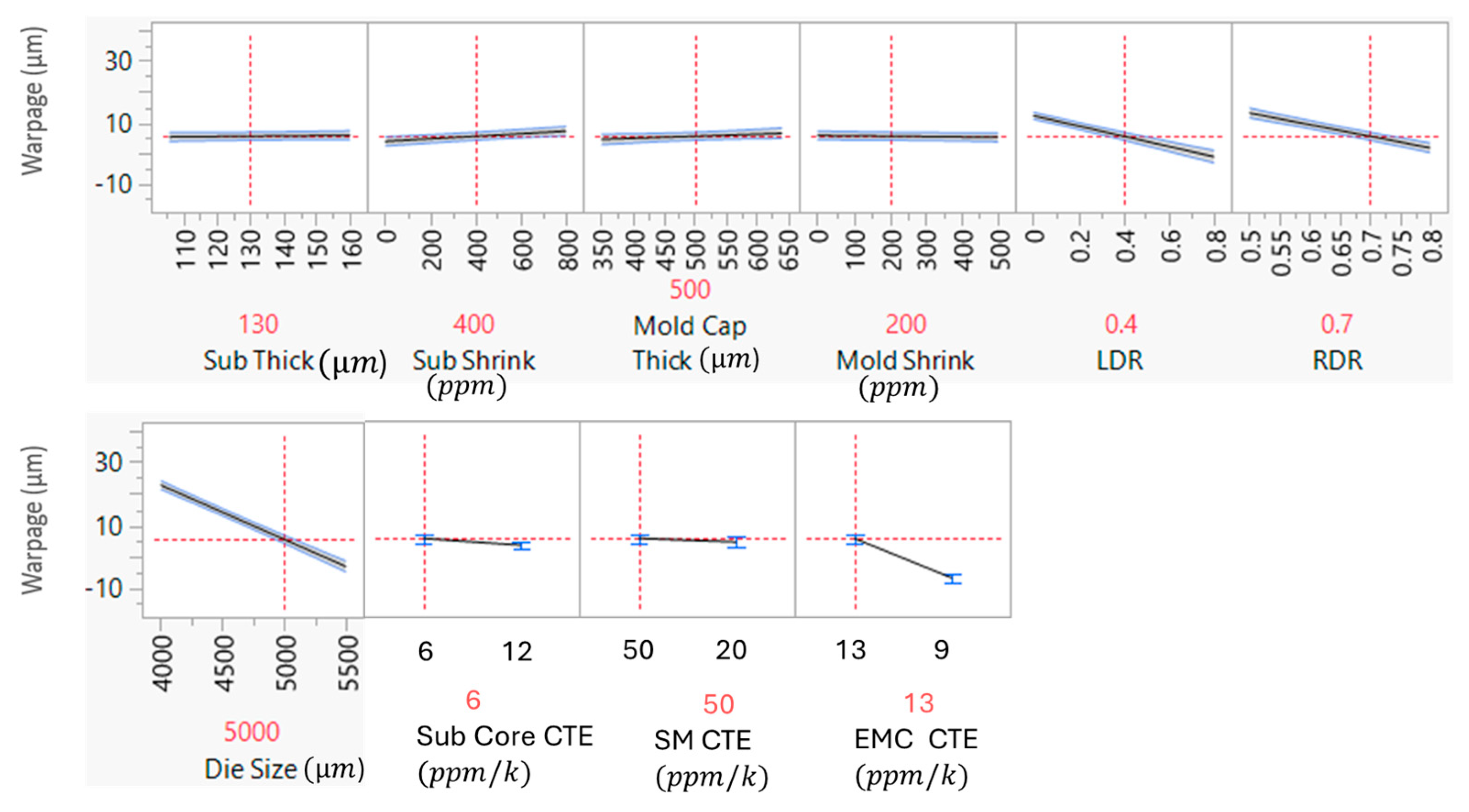
3.3. Factor Sensitivity Study Using Regression Model
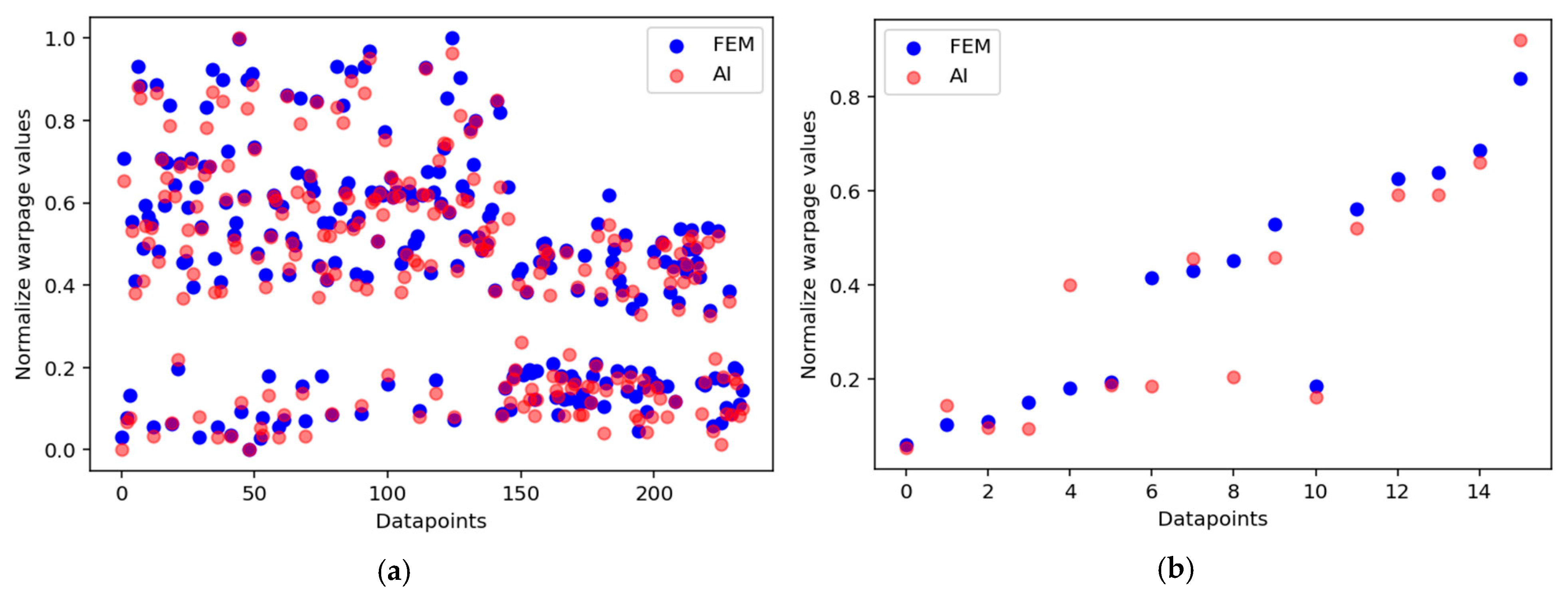
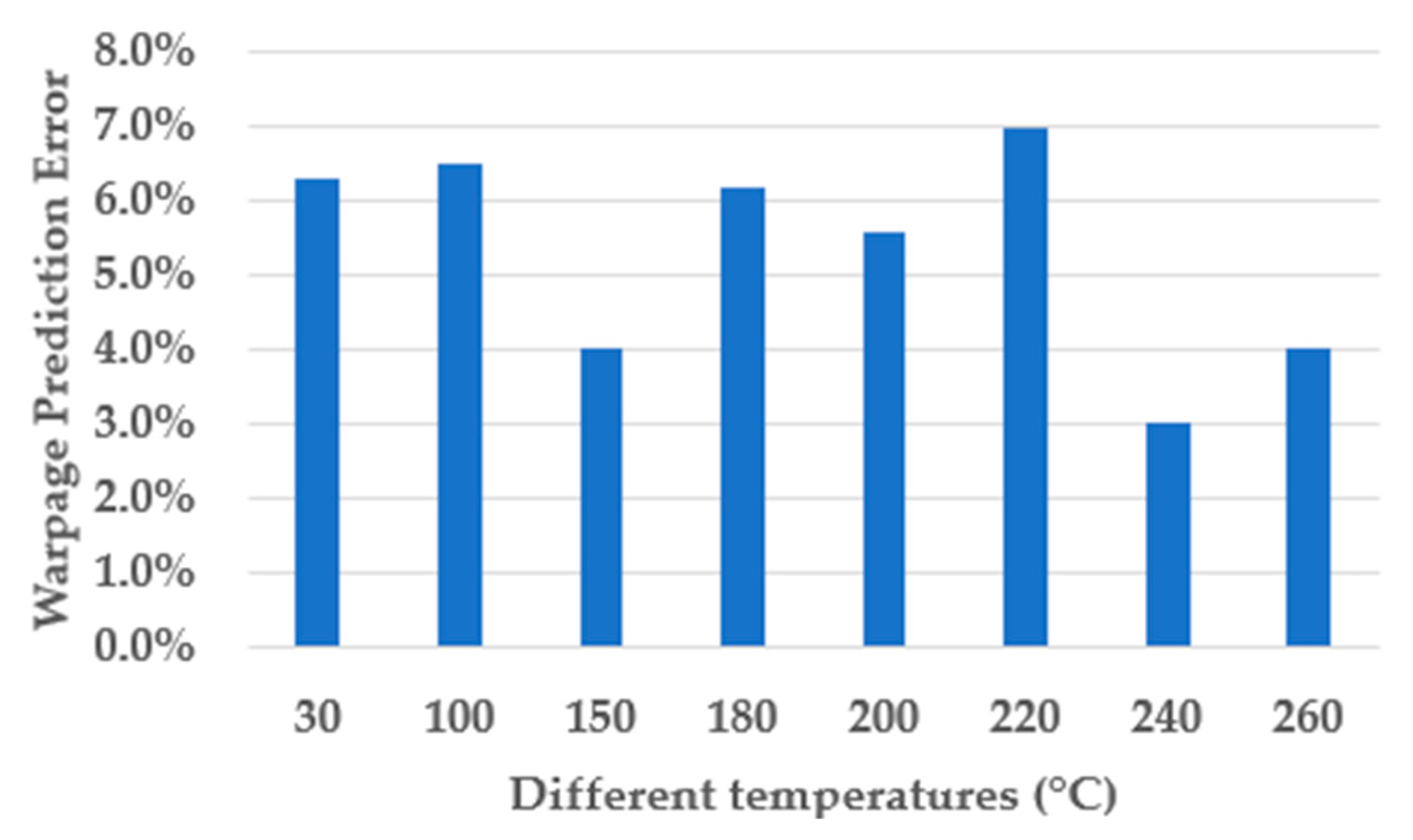
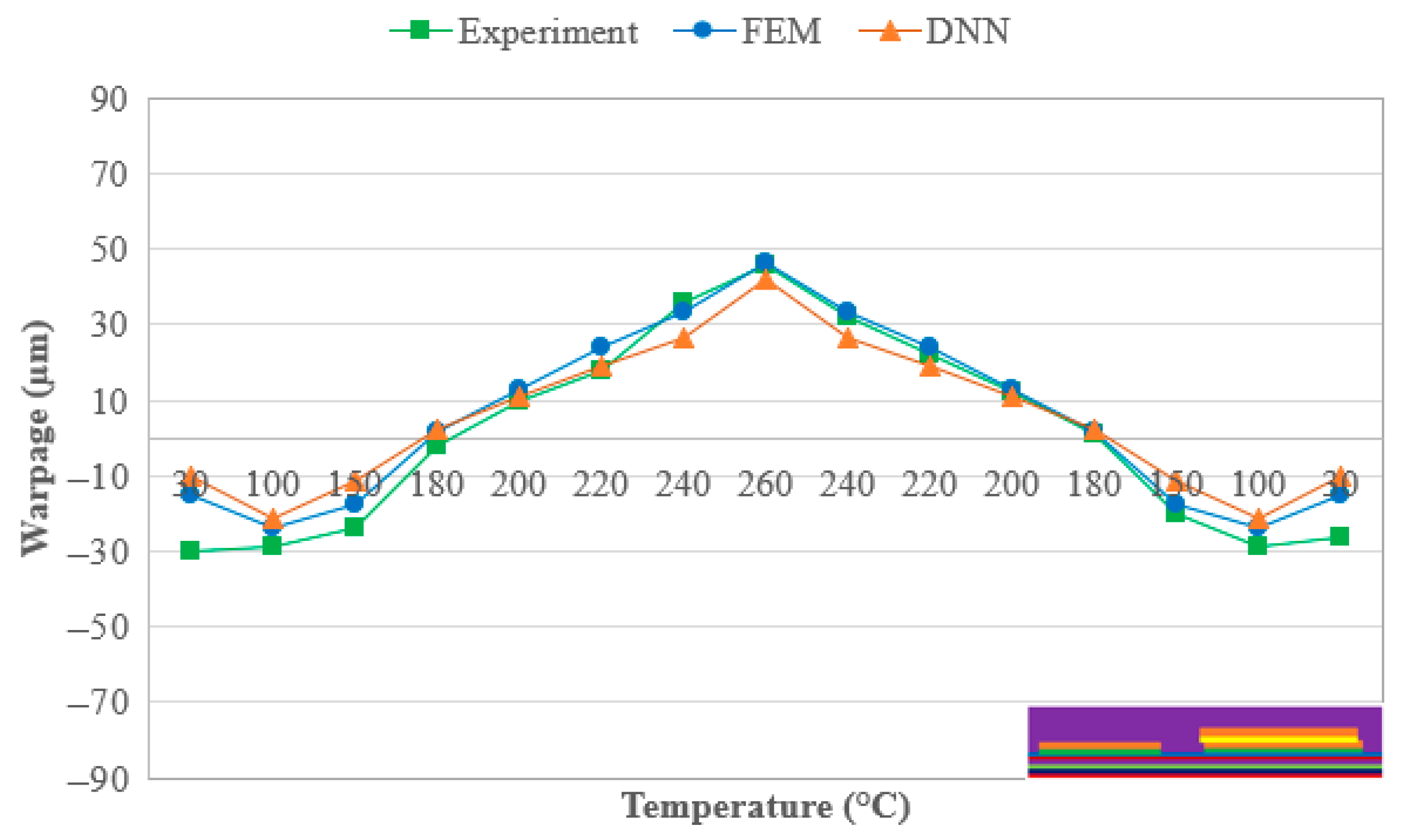
3.4. DNN Regression Model Application on New Package Design
4. Conclusions
- Ten critical factors relating to geometry and materials have been defined based on experience and sensitivity study to develop DNN model for predicting package warpage on UFS memory package.
- To reduce package warpage, wider die size, lower die stacking ratios, lower EMC CTE, thinner die stacking, thicker substrate, and thicker mold cap are recommended based on DNN model prediction on UFS package warpage.
- The implementation of a deep learning model in NPI support significantly reduces cycle time. Compared to traditional methods such as FEA simulation, the AI-based approach achieves approximately 95% reduction in development time and effectively supports for package optimization on UFS package.
- In general, package design and development should leverage AI to optimize structure/performance, reduce costs, and shorten development time. This physics-based DNN model can also be applied to other processes and reliability-related risk assessment areas such as strip warpage, solder joint reliability, thermal analysis, and package strength for advanced packages, which are our on-going and future work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Su, M.; Cao, L.; Lin, T. Warpage Simulation and Experimental Verification for 320 mm × 320 mm Panel Level Fan-Out Packaging Based on Die-First Process. Microelectron. Reliab. 2018, 83, 29–38. [Google Scholar] [CrossRef]
- Onn, S.J.; Tan, K.S.; Tau, T.Y.; Yap, S.S.; Lau, C.S.; Chin, Y.T. Warpage studies of printed circuit boards with Shadow Moir and simulations. In Proceedings of the IEEE 38th International Electronics Manufacturing Technology Conference, Melaka, Malaysia, 4–6 September 2018; pp. 1–5. [Google Scholar]
- Nam, S.; Kang, J.; Lee, I.; Kim, Y.; Yu, H.J.; Kim, D.W. Investigation on Package Warpage and Reliability of the Large Size 2.5D Molded Interposer on Substrate (MIoS) Package. In Proceedings of the 2022 IEEE 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May–3 June 2022; pp. 643–647. [Google Scholar]
- Wang, D.W.; Huang, H.M.; HO, S.C.; Liu, A.H.; Liu, D.S. Study of warpage characteristics of molded stacked-die MCP using Shadow Moiré and Micro Moiré techniques. In Proceedings of the 60th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 27–30 May 2010; pp. 1968–1973. [Google Scholar]
- Geng, M.; Zhang, Y.; Li, X.; Wang, J.; Liu, H. Study on Package Warpage Based on Three-Dimensional Flow Simulation. In Proceedings of the 23rd International Conference on Electronic Packaging Technology (ICEPT), Dalian, China, 10–13 August 2022; pp. 1–4. [Google Scholar]
- Praful, P.; Bailey, C. Warpage in Wafer-Level Packaging: A Review of Causes, Modelling, and Mitigation Strategies. Front. Electron. 2025, 5, 1515860. [Google Scholar] [CrossRef]
- Baek, J.W.; Yang, W.S.; Hur, M.J.; Yun, J.C.; Park, S.J. Representative Volume Element Analysis for Wafer-Level Warpage Using Finite Element Methods. Mater. Sci. Semicond. Process. 2019, 91, 392–398. [Google Scholar] [CrossRef]
- Chen, C.; Yu, D.Q.; Wang, T.; Xiao, Z.Y.; Wan, L.X. Warpage Prediction and Optimization for Embedded Silicon Fan-Out Wafer-Level Packaging Based on an Extended Theoretical Model. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 845–853. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.; Sheng, C.; Feng, Z.; Li, R.; Xue, L.; Liu, J.; Liu, S. Warpage Analysis and Prediction of the Advanced Fan-Out Technology Based on Process Mechanics. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 2201–2213. [Google Scholar] [CrossRef]
- Tsai, C.H.; Liu, S.W.; Chiang, K.N. Warpage Analysis of Fan-Out Panel-Level Packaging Using Equivalent CTE. IEEE Trans. Device Mater. Reliab. 2020, 20, 51–57. [Google Scholar] [CrossRef]
- McCann, S.; Lee, H.H.; Refai-Ahmed, G.; Lee, T.; Ramalingam, S. Warpage and Reliability Challenges for Stacked Silicon Interconnect Technology in Large Packages. In Proceedings of the IEEE 68th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May–1 June 2018; pp. 2345–2350. [Google Scholar]
- Yu, W.; Yang, P.S.Y.; Glancey, C.; Ong, Y.C.; Ng, H.W. Package Warpage Modeling by Considering Shrinkage Behavior of EMC and Substrate. In Proceedings of the 23rd Electronics Packaging Technology Conference, Singapore, 1–3 December 2021; pp. 547–552. [Google Scholar]
- Panigrahy, S.K.; Tseng, Y.C.; Lai, B.R.; Chiang, K.N. An overview of AI-Assisted design-on-Simulation technology for reliability life prediction of advanced packaging. Materials 2021, 14, 5342. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.W.; Panigrahy, S.K.; Chiang, K.N. Prediction of Fan-Out Panel Level Warpage using Neural Network Model with edge Detection Enhancement. In Proceedings of the IEEE 70th ECTC Conference, Virtual, 3–30 June 2020; pp. 1626–1631. [Google Scholar]
- Che, F.X.; Ong, Y.C.; Ng, H.W.; Pan, L.; Shina, K.; Glancey, C.; Kumar, G. Physics-driven Regression Algorithm on Solder Joint Fatigue Life Prediction for Mobile SiP Packages. In Proceedings of the 73rd Electronic Components and Technology Conference, Orlando, FL, USA, 30 May–2 June 2023; pp. 420–425. [Google Scholar]
- Panigrahy, S.K.; Chiang, K.N. Study on an Artificial Intelligence Based Kernel Ridge Regression Algorithm for Wafer Level Package Reliability Prediction. In Proceedings of the IEEE 71st Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 1 June–4 July 2021; pp. 1435–1441. [Google Scholar]
- Chen, C.Y.; Wang, W.C.; Chang, K.S.; Chen, T.Y.; Chen, D.L.; Lin, Y.C. Development of Artificial Neural Network and Topology Reconstruction Schemes for Fan-Out Wafer Warpage Analysis. In Proceedings of the 2021 IEEE 71st Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 1–4 June 2021; pp. 1450–1456. [Google Scholar]
- Gupta, S.; Al-Obaidi, S.; Ferrara, L. Meta-Analysis and Machine Learning Models to Optimize the Efficiency of Self-Healing Capacity of Cementitious Material. Materials 2021, 14, 4437. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Sun, M.; Guo, H.; Yan, P.; Ji, J.; Xu, L. Research on Edge Surface Warping Defect Diagnosis Based on Fusion Dimension Reduction Layer DBN and Contribution Plot Method. J. Mech. 2020, 36, 889–899. [Google Scholar] [CrossRef]
- Kuschmitz, S.; Ring, T.P.; Watschke, H.; Langer, S.C.; Vietor, T. Design and Additive Manufacturing of Porous Sound Absorbers—A Machine-Learning Approach. Materials 2021, 14, 1747. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Ahmad, A.; Ostrowski, K.A.; Dudek, M. Analyzing the Compressive Strength of Ceramic Waste-Based Concrete Using Experiment and Artificial Neural Network (ANN) Approach. Materials 2021, 14, 4518. [Google Scholar] [CrossRef]
- Farooq, F.; Czarnecki, S.; Niewiadomski, P.; Aslam, F.; Alabduljabbar, H.; Ostrowski, K.A.; Sliwa-Wieczorek, K.; Nowobilski, T.; Malazdrewicz, S. A Comparative Study for the Prediction of the Compressive Strength of Self-Compacting Concrete Modified with Fly Ash. Materials 2021, 14, 4934. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wasouf, M.; Sresakoolchai, J.; Kaewunruen, S. Prediction of Healing Performance of Autogenous Healing Concrete Using Machine Learning. Materials 2021, 14, 4068. [Google Scholar] [CrossRef] [PubMed]
- Salazar, A.; Xiao, F. Design of Hybrid Reconstruction Scheme for Compressible Flow Using Data-Driven Methods. J. Mech. 2020, 36, 675–689. [Google Scholar] [CrossRef]
- Song, S.-H. A Comparison Study of Constitutive Equation, Neural Networks, and Support Vector Regression for Modeling Hot Deformation of 316L Stainless Steel. Materials 2020, 13, 3766. [Google Scholar] [CrossRef] [PubMed]
- Papacharalampopoulos, A.; Michail, C.K.; Stavropoulos, P. Manufacturing Resilience and Agility through Processes Digital Twin: Design and Testing Applied in the LPBF Case. Procedia CIRP 2021, 103, 164–169. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhong, C.; Rong, S. Study on Warpage of Flip Chip Structure Based on Finite Element Analysis and Machine Learning Algorithm. In Proceedings of the 25th International Conference on Electronic Packaging Technology (ICEPT), Shenzhen, China, 7–9 August 2024; pp. 1–6. [Google Scholar]
- Yao, P.; Yang, J.; Zhang, Y.; Fan, X.; Chen, H.; Yang, J.; Wu, J. Physics-Based Nested-ANN Approach for Fan-Out Wafer-Level Package Reliability Prediction. In Proceedings of the 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May 2022; pp. 1827–1833. [Google Scholar]
- Lin, Y.C.; Chen, T.Y.; Wang, C.C.; Hung, C.P.; Shou, I.A.; Wang, H.K. GA-NN and Explainable AI for IC Packaging Warpage Optimization: A Case Study on Product Feature. In Proceedings of the 2025 IEEE 75th Electronic Components and Technology Conference (ECTC), Denver, CO, USA, 27–30 May 2025; pp. 1609–1614. [Google Scholar]
- Che, F.X.; Ong, Y.C.; Ng, H.W.; Glancey, C.; Kumar, G. Investigation on memory package crack and prevention under temperature cycling test. Mater. Sci. Semicond. Process. 2024, 180, 108560. [Google Scholar] [CrossRef]
- Huang, S.; Ji, Z.; Liu, Y.; Ye, N.; Takiar, H. Parametric Optimization and Yield Probability Prediction of Package Warpage. In Proceedings of the IEEE 68th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May–1 June 2018; pp. 243–248. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Panigrahy, S.K.; Che, F.X.; Ong, Y.C.; Nune, P.N.; Ng, H.W. Integration of Artificial Neural Network and Finite Element Simulation for Package Warpage Prediction. In Proceedings of the IEEE 25th Electronics Packaging Technology Conference (EPTC), Singapore, 5–8 December 2023; pp. 926–931. [Google Scholar]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar] [CrossRef]


| No of Factors | Factors Name | Level |
|---|---|---|
| X1 | Substrate Thickness (µm) | 106, 127, 160 |
| X2 | Substrate Shrinkage (ppm) | 0, 400, 800 |
| X3 | Mold Cap Thickness (µm) | 350, 500, 640 |
| X4 | EMC Shrinkage (ppm) | 0, 250, 500 |
| X5 | LDR (Left Side Die Stack Ratio) | 0, 0.5, 0.8 |
| X6 | RDR (Right Side Die Stack Ratio) | 0.5, 0.65, 0.8 |
| X7 | Die Width (µm) | 4000, 5500 |
| X8 | Substrate Material CTE (ppm/k) | 6, 12 |
| X9 | Solder Mask CTE (ppm/k) | 20, 50 |
| X10 | EMC Material CTE (ppm/k) | 9, 13 |
| Neural Network Parameter | Attribute Range Setting | Final Attribute/Value |
|---|---|---|
| Neuron Number | 1~10 | 6 |
| Hidden Layer | 2~6 | 4 |
| Activation Function | Sigmoid, Relu, Tanh, SoftMax | Relu |
| Loss Function | MSE | MSE |
| Learning Rate | 0~1 | 0.0001 |
| Batch Size | 2~10 | 2 |
| Epoch (Iteration) | 100~2000 | 500, 1000 |
| Preprocess | Min-Max, Robust, Standard | Min-Max, Standard Scaler |
| Cross-Validation (K-Fold) | 5, 10, 15 | 15 |
| Training/Validation | 234/16 | 234/16 |
| Factors | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
|---|---|---|---|---|---|---|---|---|---|---|
| DOE 1 | 0 | 1 | 0 | 0.5 | 0.625 | 0.5 | 0 | 0 | 0 | 0 |
| DOE 2 | 0 | 0.5 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| DOE 3 | 0.388 | 0 | 0 | 0.5 | 0 | 1 | 1 | 1 | 0 | 0 |
| DOE 4 | 0.388 | 0.5 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| DOE 5 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| DOE 6 | 0 | 1 | 0.517 | 0.5 | 0 | 0.5 | 1 | 1 | 0 | 0 |
| DOE 7 | 1 | 0 | 1 | 0.5 | 0 | 0.5 | 1 | 0 | 0 | 1 |
| DOE 8 | 1 | 0 | 0.517 | 1 | 0 | 0.5 | 1 | 1 | 0 | 1 |
| DOE 9 | 1 | 1 | 0.517 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| DOE 10 | 1 | 0.5 | 0 | 0.5 | 0 | 0 | 1 | 0 | 0 | 1 |
| Temperature °C | Training Score | Validation Score |
|---|---|---|
| 30 | 0.95 | 0.95 |
| 100 | 0.97 | 0.97 |
| 150 | 0.99 | 0.96 |
| 180 | 0.99 | 0.96 |
| 200 | 0.99 | 0.96 |
| 220 | 0.99 | 0.97 |
| 240 | 0.98 | 0.97 |
| 260 | 0.97 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panigrahy, S.K.; Che, F.X.; Ong, Y.C.; Ng, H.W.; Kumar, G. Deep Learning Study on Memory IC Package Warpage Using Deep Neural Network and Finite Element Simulation. Chips 2025, 4, 35. https://doi.org/10.3390/chips4030035
Panigrahy SK, Che FX, Ong YC, Ng HW, Kumar G. Deep Learning Study on Memory IC Package Warpage Using Deep Neural Network and Finite Element Simulation. Chips. 2025; 4(3):35. https://doi.org/10.3390/chips4030035
Chicago/Turabian StylePanigrahy, Sunil Kumar, Fa Xing Che, Yeow Chon Ong, Hong Wan Ng, and Gokul Kumar. 2025. "Deep Learning Study on Memory IC Package Warpage Using Deep Neural Network and Finite Element Simulation" Chips 4, no. 3: 35. https://doi.org/10.3390/chips4030035
APA StylePanigrahy, S. K., Che, F. X., Ong, Y. C., Ng, H. W., & Kumar, G. (2025). Deep Learning Study on Memory IC Package Warpage Using Deep Neural Network and Finite Element Simulation. Chips, 4(3), 35. https://doi.org/10.3390/chips4030035







