Neuromorphic Photonic On-Chip Computing

Abstract

Drawing inspiration from biological brains’ energy-efficient information-processing mechanisms, photonic integrated circuits (PICs) have facilitated the development of ultrafast artificial neural networks. This in turn is envisaged to offer potential solutions to the growing demand for artificial intelligence employing machine learning in various domains, from nonlinear optimization and telecommunication to medical diagnosis. In the meantime, silicon photonics has emerged as a mainstream technology for integrated chip-based applications. However, challenges still need to be addressed in scaling it further for broader applications due to the requirement of co-integration of electronic circuitry for control and calibration. Leveraging physics in algorithms and nanoscale materials holds promise for achieving low-power miniaturized chips capable of real-time inference and learning. Against this backdrop, we present the State of the Art in neuromorphic photonic computing, focusing primarily on architecture, weighting mechanisms, photonic neurons, and training, while giving an overall view of recent advancements, challenges, and prospects. We also emphasize and highlight the need for revolutionary hardware innovations to scale up neuromorphic systems while enhancing energy efficiency and performance.

1. Introduction

The determined pursuit of computational systems mirroring the efficiency of the human brain has served as a compelling impetus with significant industrial implications right from the emergence of artificial intelligence (AI) dating back to the 1950s [1,2]. It has undergone an initial surge of optimism, followed by decades of setbacks, primarily attributed to the dearth of computing power and hardware implementation complexity during that period. Inspired by the human brain’s neurosynaptic framework (Box 1), AI endeavors to attain the level of precision equivalent to human performance in tasks that pose difficulties for conventional computing systems yet come naturally to humans. The brain’s computational power has an efficiency of around aJ/MAC (multiply–accumulate) operation [3]. In contrast, conventional computers generally bound by von Neumann architecture struggled with the architectural scaling, typically consuming 100 pJ/MAC operation [3].

In the present era of prolific data generation and escalating automation, AI has emerged as a transformative force (Box 2) [4], reshaping industries and redefining human–machine interactions through machine learning (ML) [5] and deep learning (DL) [6,7]. These developments are influenced by the advent of computing power reflected in the modern Nvidia graphic processing units (GPUs) [8] and Google’s tensor processing units (TPUs) [9], consuming only around 20 pJ/MAC operation, sustaining Moore’s Law. Some of the current applications of AI extend across various sectors, encompassing autonomous driving, robotic vision, remote sensing, microscopy, surveillance, deterrence, and the Internet of Things [7,10,11,12]. The significant accomplishments of AI algorithms, particularly neural networks (NNs) [13,14], have influenced numerous facets of our daily lives, ranging from language translation [9] to cancer diagnosis [15].

Box 1. Artificial neuron.

The intricate mechanisms of biological neurons have long served as a wellspring of inspiration for neural engineering frameworks [16] to mimic cognitive processes. The Hodgkin–Huxley model [17] explains the working of biological neurons, which are inherently more complex than their artificial counterparts—inspiring models like the Leaky Integrate and Fire (continuous in time) [18] or the Izhikevich (spiking) [19]. Artificial neurons simplify the complexities of biological neurons into functional units comprising the weighted sum and nonlinear activation functions, as shown in Figure below. It mimics synapses and dendrites for weighting and summation, soma for leaky integration, axon hillocks for thresholding, and axon terminals for activation. Direct implementation of neural models in hardware offers unmatched speeds and efficiencies compared to software implementations [3]. This drive toward hardware acceleration for on-chip neuromorphic computing finds isomorphism in electronics [20] and photonics [21,22,23,24]. Artificial neurons mirror the behavior of their natural counterparts, wherein inputs, ${\Psi }_i$, are processed through weighted sums, $U_i$, and nonlinear activation functions, $A_j$, to produce outputs, ${\Psi }_j$. The activation function could be a continuous time [25,26,27,28] or spiking [18,29,30,31,32], which defines the versatility of neural networks tailored to different computational tasks. Here, $W_j$ is the strength between neurons i and j; τ is a leaky integration time constant; $A_{threshold}$ and $A_{reset}$ are the spiking neuron’s threshold and resetting voltages; t is time; and $t_k$ is the spike occurrence point in time when A crosses the $A_{threshold}$.

Biological neuron (left) and its mathematical equivalent model of artificial neuron (right) [33].

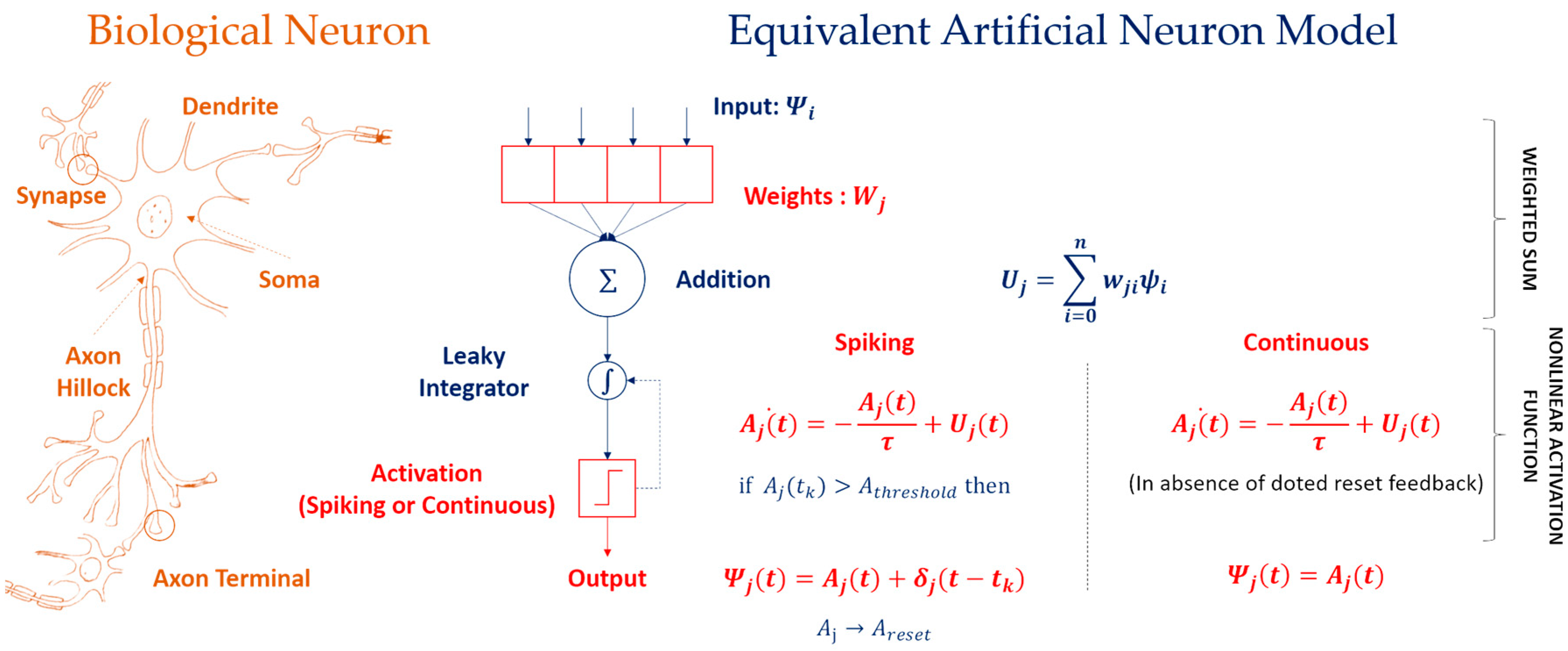
1.1. Neuromorphic Electronic Computing: On-Chip AI

The technology requirements for AI have evolved [34,35]. NN, the backbone of neuromorphic computing for AI algorithms, consists of artificial neurons arranged in layers connected to others through synapses (Box 1), allowing these networks to adapt and learn from data and exhibiting inherent parallelism and distributed computing features that confront significant hurdles when implemented in digital electronics [20]. This misalignment with the sequential nature of von Neumann architecture with separate central processing units and dynamic random-access memory in digital computers has led to a shift toward on-chip electronics, driven by its potential to enhance computational speed and efficiency by co-locating computing and storage units [36,37,38]. State-of-the-Art neuromorphic electronic architectures, which rely on transmission lines and active buffering techniques, face challenges in meeting the demands of massive parallel signal fan-out and fan-in [39]. Architectures resort to digital time-multiplexing, enabling the construction of more extensive NNs at the expense of bandwidth that detours the limitations of electronic writing [20].

Box 2. Neuromorphic Photonics: Through a time-tagged journey.

Timeline of artificial intelligence and optical implementation related to neuromorphic photonics—selected publications [2,5,13,14,16,22,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60].

Industry and research initiatives emphasize the viability of on-chip electronics. Significant achievements in designing application-specific integrated circuits (ASICs) have been observed in noteworthy projects, including IBM’s TrueNorth [61], Neurogrid [38], SpiNNaker [36], Tianjic [11], Microsoft Azure Maia AI Accelerator [62], and Intel’s Loihi [37]. Co-locating computing units and storage units within the same chip addresses the inefficiencies of traditional architectures [3]. However, challenges persist: interconnect density [63] and bandwidth limitations [20], scalability concerns [39], and power consumption issues [64] underscore the need for continued innovation. The future envisions more sophisticated applications, ranging from nonlinear programming [65] to real-time learning [58] and intelligent signal processing [66], evidenced by recent applications, including The Human Brain Project [67], large language model (LLM)–ChatGPT [68], and Tesla’s Dojo Chip [12]. Applications prioritizing bandwidth and low latency necessitate shifting toward direct, non-digital photonic broadcast interconnects [69].

1.2. Photonics: A Bright Solution Looking for a Dark Problem!

Traditional electronics often overshadow the historical development of photonics due to a lack of advantageous parallels in photonic digital logic [70]. Nevertheless, photonics has achieved remarkable milestones in data transmission [71] and communication [72] and is experiencing a renaissance due to its potential to revolutionize information processing [66]. Photonics, harnessing the power of light for communication and computation, presents a promising alternative to overcome the limitations posed by electronic interconnects [63]. Unlike electrons, photons provide diverse dimensions to control, such as wavelength (wavelength-division multiplexing (WDM) allows different wavelengths of light to carry independent information simultaneously), polarization (polarization multiplexing uses orthogonal polarizations to transmit distinct data streams in the same optical channel), and spatial mode (mode multiplexing leverages different transverse modes in multimode waveguides as transmission channels to encode additional parallel data channels). These advantages of photonics properties allow for faster data processing, reduced power consumption, and inherent parallelism at every level of integrated photonic circuits, positioning it as a transformative solution for contemporary AI [33]. Non-digital computing models, particularly those enabled by photonics, promise solutions to challenges like low latency [3], high bandwidth [39], and low energies [64], giving rise to a field of neuromorphic photonics at the intersection of photonics and the neural-engineering framework [53].

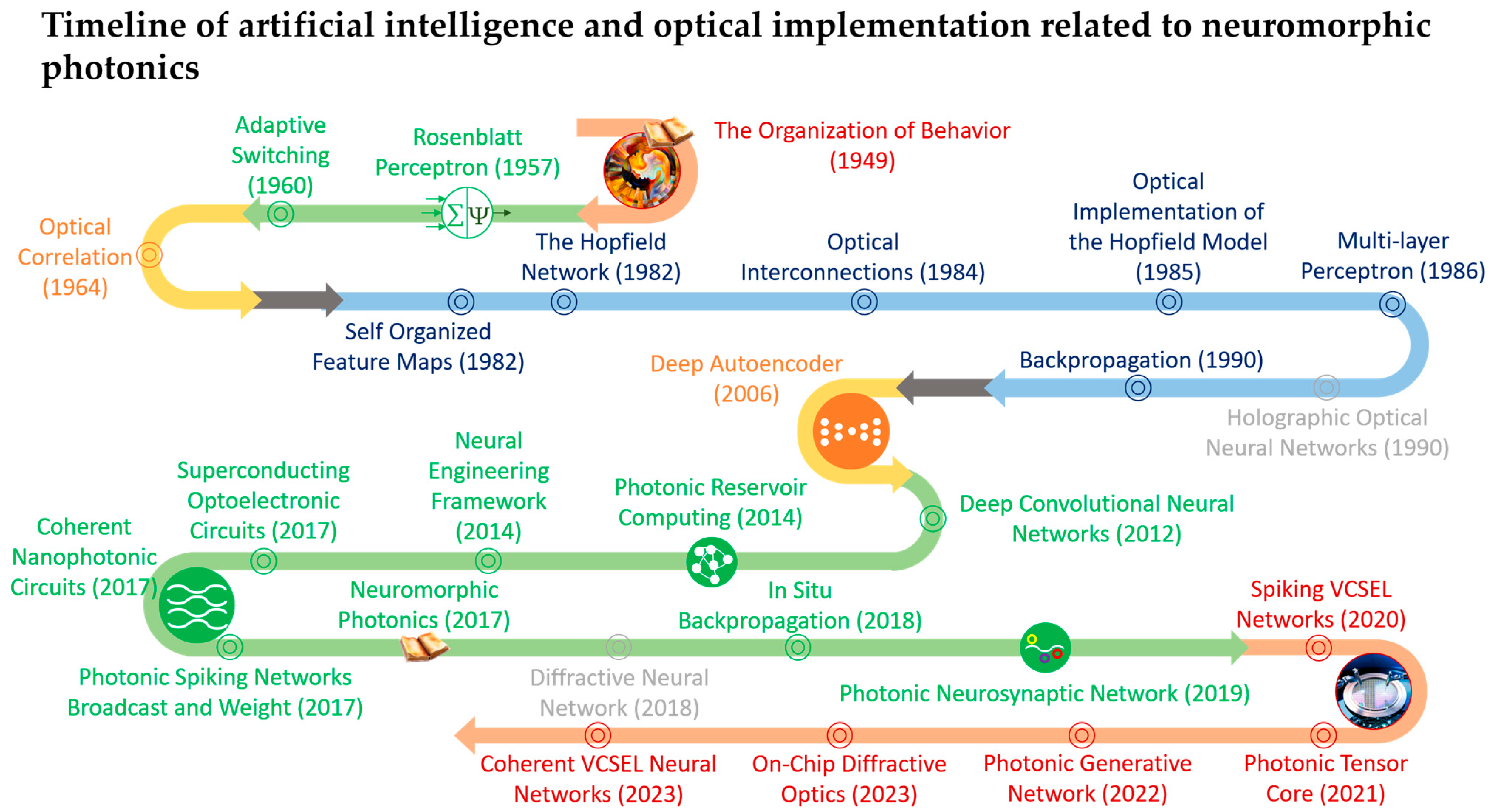
1.3. Neuromorphic Photonics in the Background of AI Technology Revolution

Neuromorphic photonics aims to facilitate matching hardware to the algorithm, supporting many-to-many communication and overcoming the trade-offs inherent in electronic approaches, which are power-hungry [64] and trade-off bandwidths for interconnectivity [20]. With its interconnectivity [69] and matrix multiplication advantages [73], photonic channels are promising candidates, as they do not suffer from the limiting features of their electronic counterpart, though the latter has its own merit as well. The maturity of enabling technologies in this domain provides a pathway to achieve cascadability and nonlinearity in neuromorphic systems. In particular, demonstrated scalable silicon photonic devices, including waveguide, Mach–Zehnder Interferometer (MZI) [74], micro-ring resonator (MRR) [75], micro comb [76], photonic crystals [77,78], and phase-change material (PCM) [22], contribute and emerged as a promising technology. Leveraging existing Complementary Metal–Oxide–Semiconductor (CMOS) compatibility [79], silicon photonics can be seamlessly integrated with available lightspeed active optoelectronic and CMOS circuits without requiring additional complex processes [80]. This co-design with mature electronics provides a versatile component sensitivity [81] for large-scale photonic fabrication and integration platforms [79], along with calibration and control [82]. In specific applications, such as autonomous driving, the combination of neuromorphic photonics facilitates real-time decision-making with unparalleled efficiency. In healthcare, the ability of photonics to handle vast amounts of medical data accelerates diagnostic processes [15]. Intelligent systems for smart cities leverage photonics’ speed and bandwidth advantages for seamless data processing [66].

As neuromorphic photonics continues to push boundaries, research and technology will play pivotal roles. Challenges arise in storing and retrieving neuron weights within on-chip memory [83,84]. Ongoing efforts in optical memories, particularly “in-memory” computing, have been explored [83,85,86,87]; however, their limitations include difficulties in high-frequency read and write operations [22]. The concept of electronic–photonic co-design emerges as a highly promising approach for implementing neuromorphic photonic systems [33]. This integration should leverage the characteristics of memory types (volatile and non-volatile) in digital or analog domains tailored to ASIC and computational requirements. The envisaged future demands of AI, marked by increased complexity and diverse applications [88], align seamlessly with the strengths of photonics [81]. Research efforts into architectures and algorithms for neuromorphic photonic processors (NPPs) [33,89] signal new directions that hold tremendous promise for the trajectory of AI with a potential of aJ per MAC energy efficiencies and P-MAC/s/mm² processing speed [3]. However, nurturing this synergy will require collaborative efforts to overcome integration, scalability, and compatibility challenges and explore novel applications to propel the field toward new frontiers in intelligent computing on chips. Here, we explore the transformative domain of neuromorphic photonics, with a focus on neuromorphic photonic processing node (NPPN), from signal-weighting mechanisms and photonic neuron (PN) intricacies to the architecture of neuromorphic photonic networks (NPNs) and training. Additionally, recent advancements in experimentally demonstrated on-chip neuromorphic photonic approaches are discussed, along with potential applications and the hurdles they encounter in scaling up for widespread deployment. There is a strong emphasis on the necessity for groundbreaking on-chip hardware innovations to be compatible with fabrication technology to enhance energy efficiency, performance, and scalability within neuromorphic systems. This extensive exploration aims to provide valuable insights into the present status, challenges, and future possibilities of photonic and neuromorphic computing on-chip.

2. Neuromorphic Photonics Processing Node

The convergence of neuromorphic photonics potentially revolutionizes the computing paradigm [53], where the complexities of brain-inspired processing merge with the capabilities of light-based technologies [45] by harnessing the optical system’s inherent direct multiplication [73], multiplexing techniques [90], energy efficiency [64], and speed [3]. At the heart of this endeavor lies the design of a NPPN (Figure 1) which is inspired by the fundamental components and scheme of the brain’s neural architecture given in Box 1 [33]. Designing a NPPN that encapsulates these functionalities necessitates a multidisciplinary approach, integrating insights from neuroscience, materials science, photonics engineering, fabrication technology, system integration, platform co-integration, and packaging [34,91].

Different hardware implementations of neuromorphic photonics have been demonstrated, with each having been designed for specific application classes. These implementations typically involve NPPNs, which consist of nonlinear PN interconnected through configurable photonic synapses (further referred as synapses) for linear weighting. These models differ in PN signal representation (continuous or spiking) and weight configuration (tunable criterion [5] or fixed [92]) to accomplish a particular task per the learning algorithm. In general, continuous-variable nonlinear neurons can be trained using backpropagation [5], while spike-timing-dependent update rules are well-suited for spiking neurons [93,94].

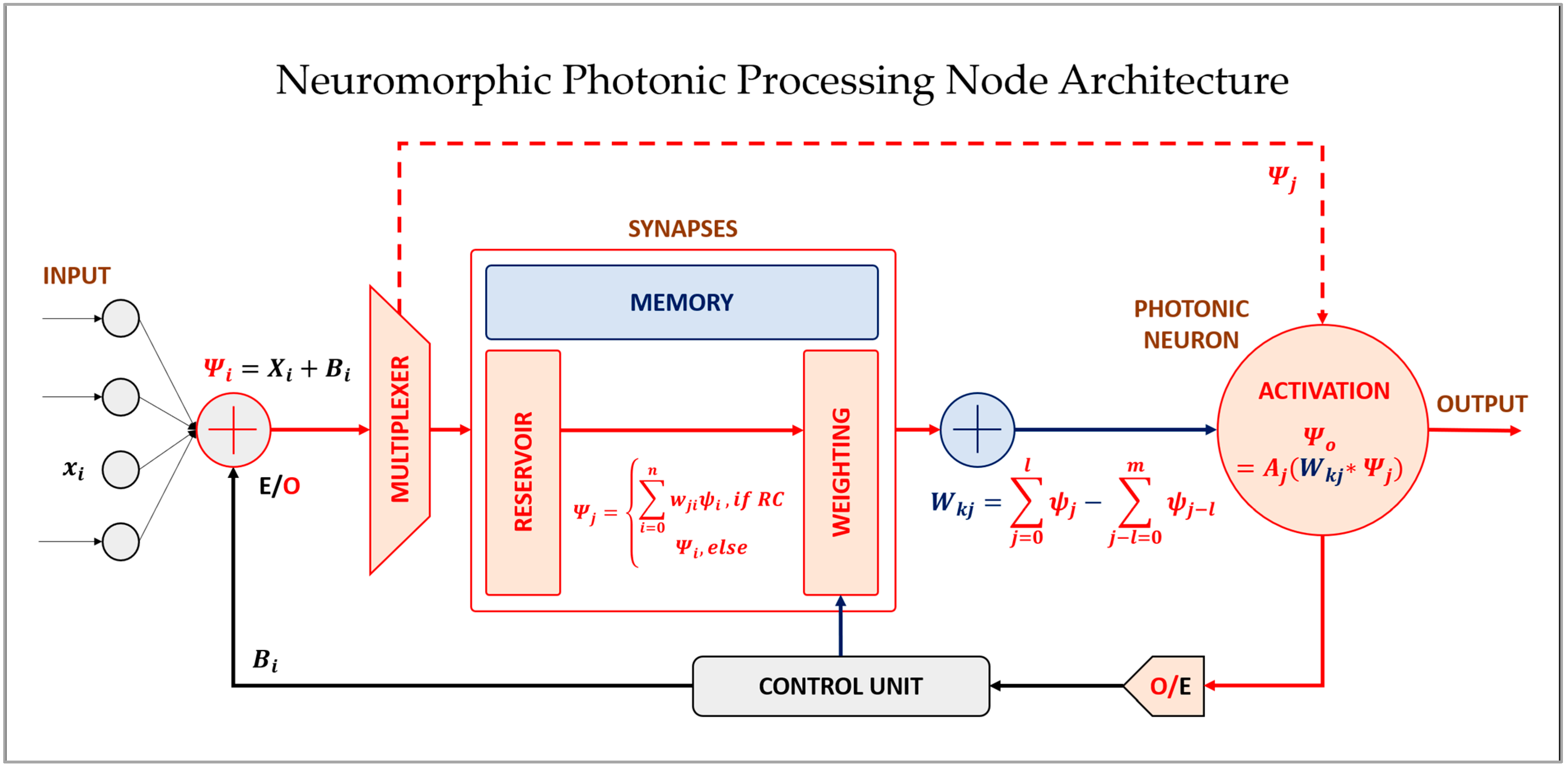
2.1. Neuromorphic Photonic Processing-Node Architecture

NPPN architecture is designed to emulate the functionality of traditional neurons while operating in the optical domain (Box 1). At its core, the NPPN comprises two main components: linear operation weighting and nonlinear activation, supplemented by interconnects, memory, and photonic components. Ideal NPPN should consume minimal energy; possess high endurance; enable easy addressing in large, interconnected networks; provide signal gain and on-chip memory; and offer tunability, active dynamism, reconfigurability, and multifunctionality. Additionally, they should support large fan-in and fan-out, extensive interconnectivity, self-assembly capability, formation of 3D interconnects, and easy manufacturability in large quantities, all at a low cost [91].

In the NPPN architecture (Figure 1), input signals are received as optical pulses (Ψ_j) from a multiplexer after adding the bias (B_i) signal to the actual input signal (X_i), representing incoming information. Optical synapses adjust the strength of connections through externally controlled feedback tuning to matrix multiply, simulating synaptic weights that may have on-chip synaptic memory (volatile or non-volatile) for storage. The weighted signals are then linearly summed (W_kj) to control PN dynamics. The PN executes the nonlinear activation, generating optical output signals (Ψ_o) based on modulation and interaction within the components. Moreover, the NPPN architecture exhibits similarities to an artificial neural network (ANN) [58] and reservoir computing (RC) [49] when serving as a reservoir in absence of dashed interconnects, due to the inherent parallelism supported in photonics through multiplexing. This versatility underscores the adaptability and potential of the NPPN architecture to serve as a robust platform for advanced neuromorphic computing tasks. Demonstrated NPNs utilized a variety of PNs and synapses. However, one particular interest involves the creation of synapses and PNs using identical technologies to facilitate seamless integration within expansive systems and enable the implementation of NN algorithms leveraging the innate physics of optical components.

2.2. Weights (Synapses): Linear Operation

Photonic synapses play a pivotal role in neuromorphic photonic computing, enabling the manipulation and processing of network signals. These synapses govern the strength of connections between neurons by assigning scalar multipliers, known as synaptic weights, to the signals transmitted across them. The weighted signals from upstream neurons are aggregated and modulated by the synaptic weights before being transmitted to downstream neurons, facilitating information and computation integration within the network.

Various integrated photonic devices have been developed to implement weighted interconnection (Figure 2). These implementations can be broadly categorized into two groups based on wavelength multiplexing and interference in optical modes. However, they are not limited to and are extensively explored within the scientific community, particularly in RC. Mode-based approaches leverage interference between different optical paths and coherent input light to implement unitary matrix transforms for weighted interconnection (Figure 2a) [51]. These techniques utilize beam splitters, phase shifters, and MZIs to modulate the power and phase of light signals, enabling control over synaptic weights and interconnection matrices [74,95]. Additionally, advancements in cryogenic architectures and index-tuning mechanisms have expanded the scope of mod-based approaches (Figure 2b) [96], offering enhanced performance and flexibility in weight configuration. On the other hand, in the wavelength-based approach, signals are weighted in parallel using WDM techniques [90] and tunable filters [82,97,98], such as MRRs [99]. Although they differ in weighting mechanism, these approaches, exemplified by architectures like broadcast-and-weight (B&W, Figure 2c) [82,100] and photonic cross-connect using indium phosphide (InP) semiconductor optical amplifiers (SOAs, Figure 2d) [101], offer efficient methods for multiwavelength synapses for NPPN, with different architectures employing variations in weighted addition and attenuation mechanisms.

RC uses weighted transient states of a nonlinear element with delayed feedback or time-division multiplexing (Figure 2e) [102]. Non-volatile synapse implementations represent another significant advancement in neuromorphic photonic approaches (Figure 2f) [85], offering solutions that eliminate the need for electrical inputs for tuning. These approaches depend on optically induced alterations in materials like chalcogenides to regulate light propagation within waveguides. By leveraging the unique properties of non-volatile optical materials, these implementations address challenges related to electrical input/output and heat dissipation, paving the way for more efficient and robust NPNs. A variety of weighting mechanisms are explored [71,97,103,104,105,106,107] for developing weighted interconnects in neuromorphic photonics, realizing high-performance and energy-efficient computing systems [73,90]. By leveraging the capabilities of integrated photonic circuits and novel materials, researchers are unlocking new possibilities for designing and implementing advanced NPNs with unprecedented functionality and adaptability.

2.3. Photonic Neuron: Nonlinear Activation

The PN represents a critical component to emulate the functionality of biological neurons for advanced information-processing tasks [75], which still face the challenge of achieving nonlinear activation while ensuring compatibility with network architectures, including fan-in [39] and cascadability [39]. Researchers have explored the multifaceted devices utilized for implementing PNs (Figure 3 and Figure 4), signifying two categories per the physical representation of signals: all-optical and optical/electrical/optical (O/E/O). In the all-optical PN design, the neuron signal is represented solely by material properties or changes in optical susceptibilities. While all-optical neurons offer inherent speed advantages over O/E/O implementations, they face significant challenges in achieving sufficient output strength to drive subsequent neurons.

Solutions to this challenge involve integrating carrier regeneration mechanisms [108], wherein each neuron produces a renewed carrier wave modulated by its output signal, thereby enhancing its strength for downstream transmission. This approach has been demonstrated through various techniques, such as semiconductor carrier populations using cross-gain modulation (Figure 3a) [28], and structural phase transitions (Figure 3b) [22], enabling the realization of all-optical PN with enhanced functionality and cascadability. Despite introducing a new challenge of differentiating controller signals from controlled signals, carrier regeneration enables the amplification of output signals to drive downstream PN efficiently. Another avenue of exploration in PN design involves the O/E/O signal pathway, and optical signals are transduced into electrical currents and back into optical signals within the primary signal pathway (Figure 3c–g). The nonlinear dynamics of PNs using a superconducting electronic signal pathway (Figure 3c) [24,27] and a photodetector–modulator PN for MZI meshes (Figure 3d) [23] were proposed and implemented. Not only that, but this pathway enables the implementation of nonlinearities either in the electronic domain or through optical–electrical conversion stages utilizing modulators (Figure 3e,f) [21,25] or lasers (Figure 3g) [26]. By leveraging electronic components for nonlinear processing, O/E/O neurons can achieve high-bandwidth nonlinear transfer functions unconstrained by the characteristics of input signals to facilitate the generation of output signals more potent than the input essential for neural computation.

Furthermore, spiking laser neurons (Figure 4), classified as all-optical or O/E/O, have showcased robust nonlinearity, carrier regeneration, and neural dynamics within a singular device. This is achieved by harnessing gain, cavity, and saturable processes. Spiking neurons have been demonstrated utilizing various technologies, including mode competition (Figure 4a,b) [30,31], saturable semiconductor media (Figure 4c–e) [18,32,59,109], and resonant tunneling diodes (Figure 4f) [29].

When comparing all-optical and O/E/O implementations of PNs, the apparent advantage of all-optical approaches lies in their intrinsic speed, often ascribed to the comparatively sluggish carrier drift and current flow phases in O/E/O designs. However, recent developments have challenged this notion, revealing that analog O/E/O devices can exhibit comparable or even superior bandwidth and energy performance [64] compared to their all-optical counterparts. It is worth noting that in PNs applying nonlinearities in the digital domain, the maximum system bandwidth is often dictated by the efficiency of the digital subsystem, underscoring the importance of efficient digital processing. Moreover, in PN design, a crucial consideration is the ability to configure and customize nonlinear transfer functions to align with specific NPN tasks. Analog PNs offer flexibility in configuring transfer functions through electrical biasing [21].

Conversely, digital counterparts offer the flexibility to implement arbitrary transfer functions. Surprisingly, recent research advancements have demonstrated that programming techniques and neural training can adapt to analog photonic devices’ inherent transfer functions, showcasing these devices’ potential for efficient and adaptable neural computation [110,111]. Therefore, integrating PN with silicon photonics platforms holds promise for scalable and cost-effective implementation of large-scale on-chip neuromorphic photonic integrated circuits (nPICs) for information processing. Silicon photonics provide a stable ecosystem for research and development, facilitating advancements in technology road mapping, standardized fabrication processes, and broad accessibility to academic research [34]. This integration enables harnessing the scalability and feasibility of photonic integrated circuits for realizing advanced NPNs.

Figure 4. Spiking photonic neurons. All-optical: (a) A semiconductor-ring laser featuring an electrically pumped group III–V MRR coupled to a waveguide (top) [112]. Bistability arises from excitable behavior (bottom) [113] when the symmetry of the two counter-propagating (clockwise or anticlockwise) modes per frequency is disrupted [30]. (b) On the left, an InP-based two-dimensional photonic crystal features a L3 cavity (three holes removed, incorporating quantum wells) that leverages fast third-order nonlinearity to achieve excitability. On the right, hysteresis cycles demonstrate bistability with varying detuning values relative to the cavity resonance, displayed in arbitrary units [31]. (c) On the left is an optically pumped group III–V micropillar laser with a SA. The amplitude response to a single-pulse perturbation versus perturbation energy is depicted for bias pump power relative to the self-pulsing threshold on the right. This illustrates the differentiation between the excitable and self-pulsing thresholds [109]. (d) Pre-weighted optically encoded input is injected into the vertical-cavity surface-emitting laser (VCSEL)–neuron and integrated over time (top)—recorded spike response of multiple pulses with varying amplitude close to threshold operation points (bottom) [59]. Optical–electronic–optical: (e) A two-section gain–SA setup on the left, functioning as an integrate-and-fire mechanism. At the bottom is a micrograph of an electrically injected excitable distributed feedback laser used to selectively disturb the gain, driven by a balanced photodetector pair. On the right, the measured excitable power of the input pulses is displayed at the top, while the laser output is at the bottom [18]. (f) On the left is a resonant-tunneling diode layer stack, photodetector, and laser diode (RTD-LD), constituting an excitable optoelectronic device. On the right, excitability is attained by biasing a double-barrier quantum well within the RTD in the negative differential resistance region of its direct current–voltage curve [29]. Figures adapted with permission from Ref. [112], Elsevier (a, bottom); and Ref. [114], IEEE (e). Figures reproduced with permission from Ref. [113], APS (a, top); Ref. [31], APS (b); Ref. [109], APS (c); Ref. [59], author(s) (d); and Ref. [29], OPG (f).

Figure 4. Spiking photonic neurons. All-optical: (a) A semiconductor-ring laser featuring an electrically pumped group III–V MRR coupled to a waveguide (top) [112]. Bistability arises from excitable behavior (bottom) [113] when the symmetry of the two counter-propagating (clockwise or anticlockwise) modes per frequency is disrupted [30]. (b) On the left, an InP-based two-dimensional photonic crystal features a L3 cavity (three holes removed, incorporating quantum wells) that leverages fast third-order nonlinearity to achieve excitability. On the right, hysteresis cycles demonstrate bistability with varying detuning values relative to the cavity resonance, displayed in arbitrary units [31]. (c) On the left is an optically pumped group III–V micropillar laser with a SA. The amplitude response to a single-pulse perturbation versus perturbation energy is depicted for bias pump power relative to the self-pulsing threshold on the right. This illustrates the differentiation between the excitable and self-pulsing thresholds [109]. (d) Pre-weighted optically encoded input is injected into the vertical-cavity surface-emitting laser (VCSEL)–neuron and integrated over time (top)—recorded spike response of multiple pulses with varying amplitude close to threshold operation points (bottom) [59]. Optical–electronic–optical: (e) A two-section gain–SA setup on the left, functioning as an integrate-and-fire mechanism. At the bottom is a micrograph of an electrically injected excitable distributed feedback laser used to selectively disturb the gain, driven by a balanced photodetector pair. On the right, the measured excitable power of the input pulses is displayed at the top, while the laser output is at the bottom [18]. (f) On the left is a resonant-tunneling diode layer stack, photodetector, and laser diode (RTD-LD), constituting an excitable optoelectronic device. On the right, excitability is attained by biasing a double-barrier quantum well within the RTD in the negative differential resistance region of its direct current–voltage curve [29]. Figures adapted with permission from Ref. [112], Elsevier (a, bottom); and Ref. [114], IEEE (e). Figures reproduced with permission from Ref. [113], APS (a, top); Ref. [31], APS (b); Ref. [109], APS (c); Ref. [59], author(s) (d); and Ref. [29], OPG (f).

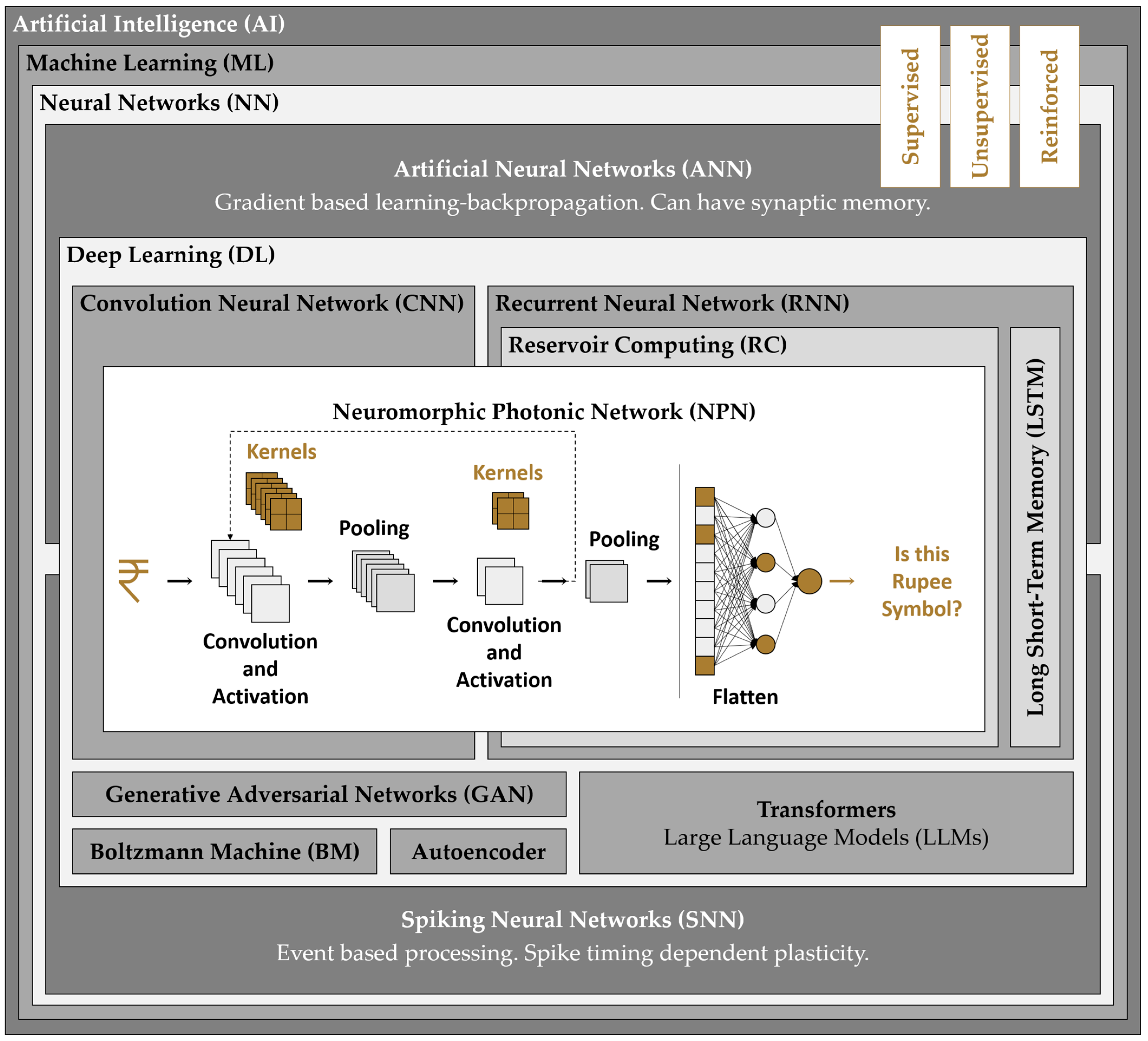
3. Neuromorphic Photonic Networks

Data-centric AI-driven applications predict the urgent need for high-efficiency and ultralow-power-consumption solutions [115]. On-chip neuromorphic photonics has garnered attention as a complementary approach [33,116]. However, synergetic research is needed to identify optimized network topology and algorithms for NPNs [117]. ML and DL breakthroughs have propelled advancements across the hierarchy of networks, driven by various training algorithms that enable networks to adapt to diverse tasks [6,48]. Within this landscape, computational models inspired by the human brain’s structure and function, such as NNs [5,14], have gained prominence, leading to the exploration of various architectures and algorithms to enhance their capabilities. Moreover, integrating photonics into NN design has opened new avenues for achieving high-speed, wide-bandwidth, energy-efficient computing supporting massive parallelism [117]. Figure 5 illustrates the evolution from essential ANNs to cutting-edge spiking neural networks (SNNs) and photonic architectures, highlighting the algorithms and architectures that drive their functionality.

At the heart of ML is the concept of ANNs, computational models comprising interconnected nodes, or neurons, organized into layers. ANNs can learn complex patterns and relationships from data through a process known as training. Backpropagation, a fundamental algorithm ANNs use, adjusts synaptic weights based on the error gradient concerning each weight during training [5,52]. This iterative optimization process minimizes the difference between calculated and actual outputs, allowing the network to learn from labeled data. SNNs emulate the event-driven processing of the human brain, utilizing spikes to encode information and achieve efficient computation [16,22,93]. Neurons in SNNs integrate input spikes over time, generating output spikes when the membrane potential exceeds a threshold. This threshold-based firing mechanism, combined with spike-timing-dependent plasticity (STDP) [94], enables SNNs to learn from temporal patterns in data and exhibit robust adaptive behavior. DL represents a paradigm shift in ML, leveraging NN with multiple hidden layers (GAN, autoencoders, LLMs, etc.) to extract intricate features from raw data. Training through stochastic gradient descent (SGD) and its variants optimize the complex parameters of deep neural networks (DNNs) by efficiently navigating the high-dimensional parameter space [6,118]. Convolution neural network (CNNs) are prime examples of DL architectures widely employed in image-recognition and computer-vision tasks [7,55]. CNNs utilize convolutional layers to detect hierarchical features in input data and then pool layers for dimensionality reduction and fully connected layers for classification. Recurrent NNs (RNNs) excel in sequential data by maintaining internal states or memory across time steps–long short-term memory, making them suitable for natural-language-processing [9] and time-series-prediction tasks [118]. RC offers a unique approach to neural network training, focusing on adapting only the readout layer while keeping the internal parameters fixed, simplifying the training process, and enhancing scalability, particularly in hardware-constrained environments [92,102]. RC architectures, characterized by interconnected nonlinear nodes forming a fixed RNN, have shown promise in emulating complex behaviors and achieving efficient information processing.

Supervised [51], unsupervised [22], and reinforced [119] learning represent fundamental techniques in ML, with each offering unique approaches to training. These methodologies provide versatile frameworks for optimizing the NN to accomplish specific tasks within various network topologies (Figure 5). Labeled data guides the NN to establish correlations between input data and corresponding output labels in supervised learning, encompassing classification [57], regression, and sequence-prediction tasks. Unsupervised learning, conversely, entails training the NN on unlabeled data to unveil latent patterns or structures within the dataset, beneficial for tasks such as clustering, dimensionality reduction, and anomaly detection, enabling the extraction of meaningful representations from the data without predefined labels [22]. Reinforcement learning operates within a framework where an agent learns to navigate an environment by taking actions and receiving feedback through rewards or penalties [119]. This adaptive approach is instrumental in training NN for tasks requiring sequential decision-making, such as game-playing, robotics, and autonomous systems. As we navigate the landscape of network topologies, from ANNs and SNNs to NPNs, we witness the convergence of AI-driven technologies and cutting-edge research [116]. By embracing the complexity of NNs and harnessing the power of photonics, researchers are poised to unlock new frontiers in intelligent computing.

3.1. Neuromorphic Photonic Network: A Combined Structure

The NPN represents a pioneering advancement in DL architectures specifically tailored for photonic applications harnessing NPPNs as the fundamental building blocks. This innovative NN architecture integrates principles from CNNs [7,55] and RNNs [52,120], leveraging the unique properties of light for efficient computation. The network consists of two primary components: convolutional layers with activation functions, followed by pooling layers and a recurrent feedback loop. The architecture is structured to exploit spatial and temporal correlations in input data, making it well-suited but not limited to tasks such as pattern recognition, classification, and sequential data processing. The schematic of the approach to recurrent convolutional neuromorphic photonic networks (ReConN, Figure 5) has been combined and framed here in the context of neuromorphic photonic computing:

• Instead of traditional convolutional layers, the ReConN employs NPPNs to perform convolutional operations directly on input photonic signals, enabling them to extract spatial features from the input data and apply nonlinear activation functions simultaneously.
• NPPNs in RC mode, followed by unit weighting within the synapse for pooling operations (Figure 1), eliminate the need for different variety of layers. NPPNs dynamically aggregate information across spatial dimensions of the input data, facilitating downsampling and feature selection, while preserving the advantages of photonic processing.
• A defining feature of the ReConN’s is its incorporation of a recurrent feedback loop enabled by the inherent memory (synaptic or delayed) properties of NPPNs. The output from the post-NPPNs is fed back into the pre-NPPNs in the network, allowing for iterative refinement of representations over multiple time steps and capturing temporal dependencies in the input data.
• Following the recurrent processing stage, the output is flattened for processing (say classification). This final layer utilizes standard classification techniques to map the learned features to specific output classes, enabling the network to make accurate predictions based on the input data.

3.2. Neuromorphic Photonic Approaches

State-of-the-Art neuromorphic photonic approaches represent AI, leveraging the principles of neuroscience and photonics to develop energy-efficient and high-performance computing systems. Various NPNs proposed and experimentally demonstrated (Figure 6) the potential across different architectures. These approaches encompass different topologies (NPNs), weighting (synapse), and photonic signal representations (PNs). Each approach offers unique achievements and challenges, paving the way for innovative solutions in neuromorphic computing (

Table 1. On-chip approaches for neuromorphic photonic networks.

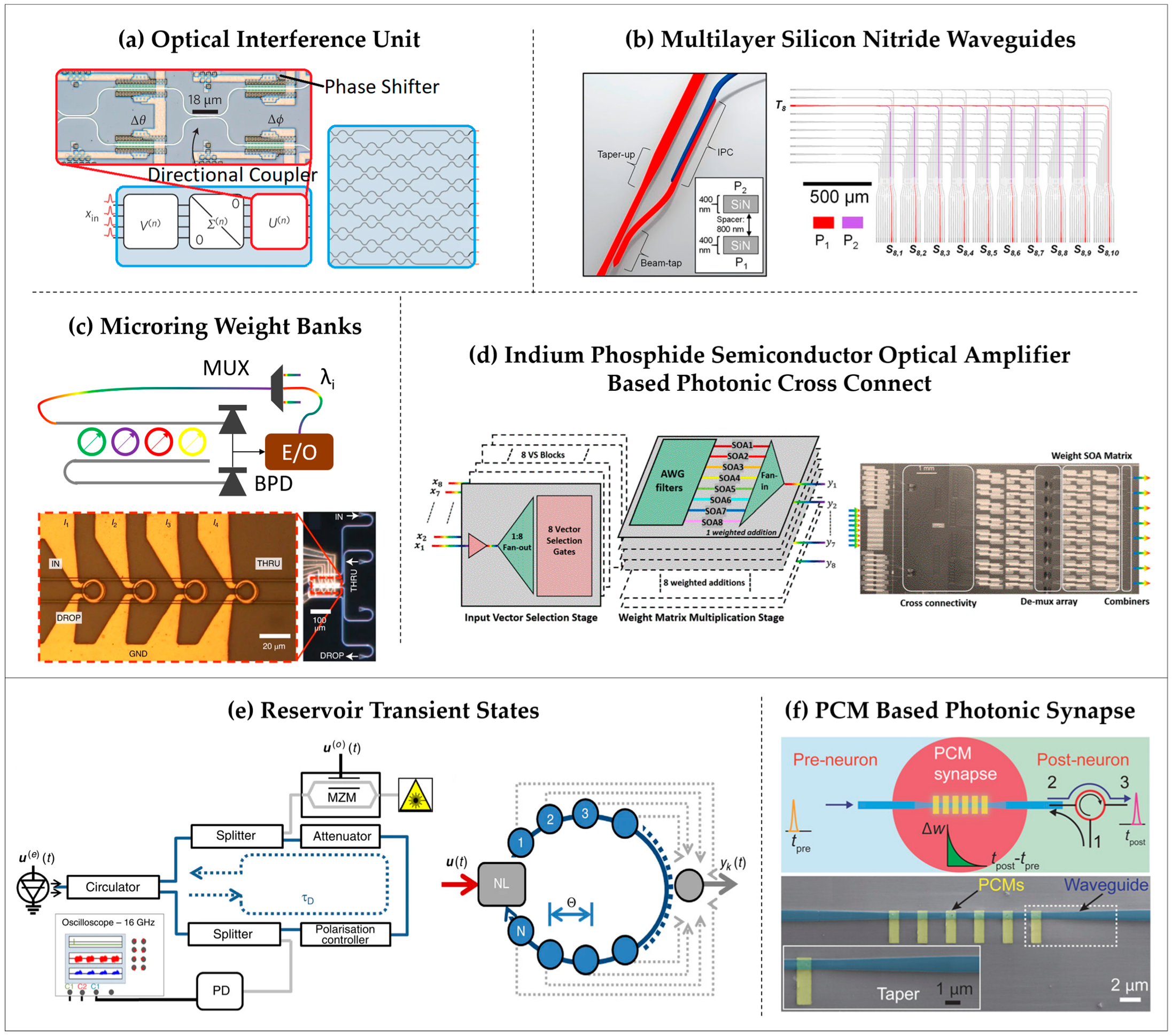
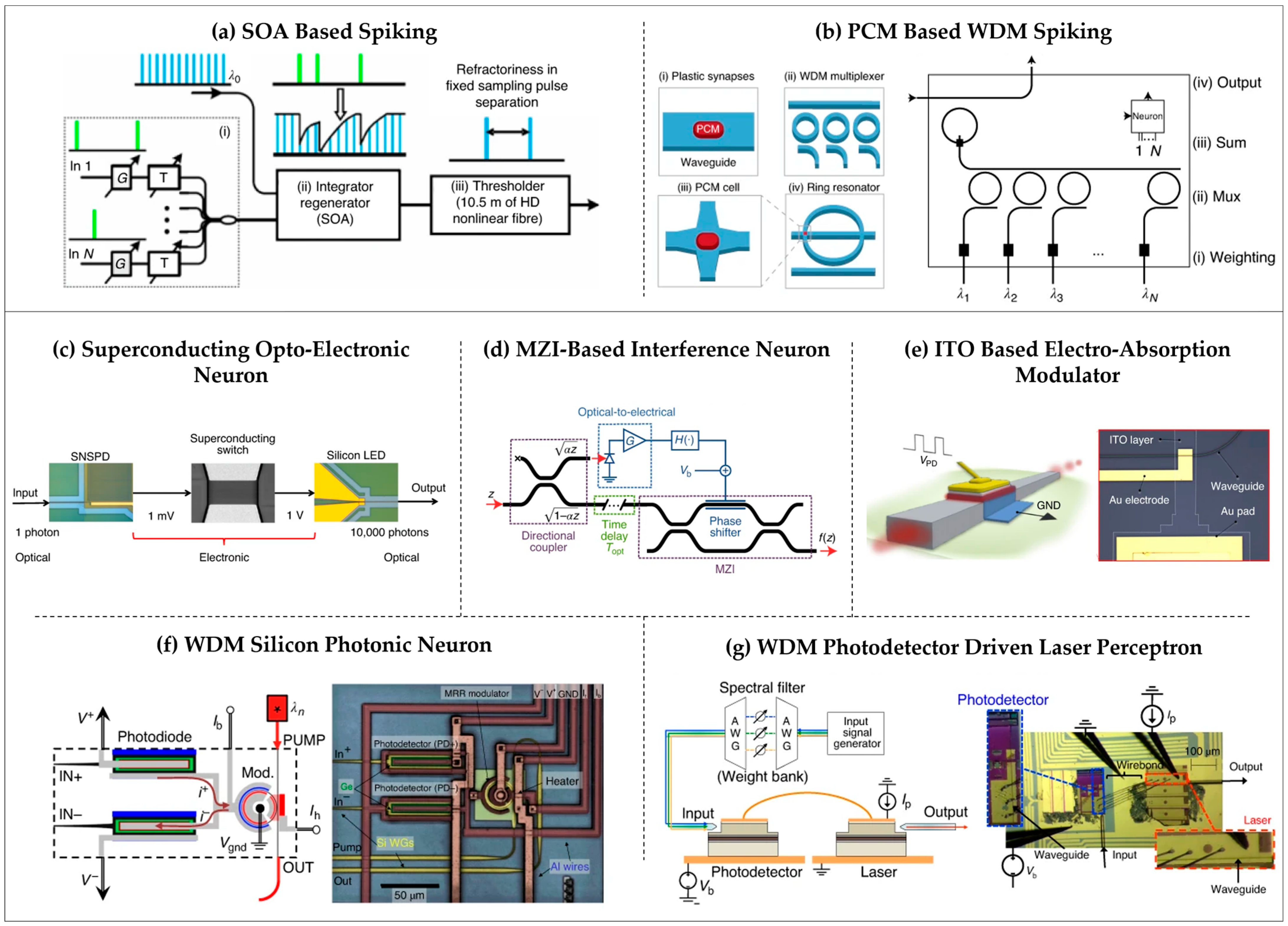
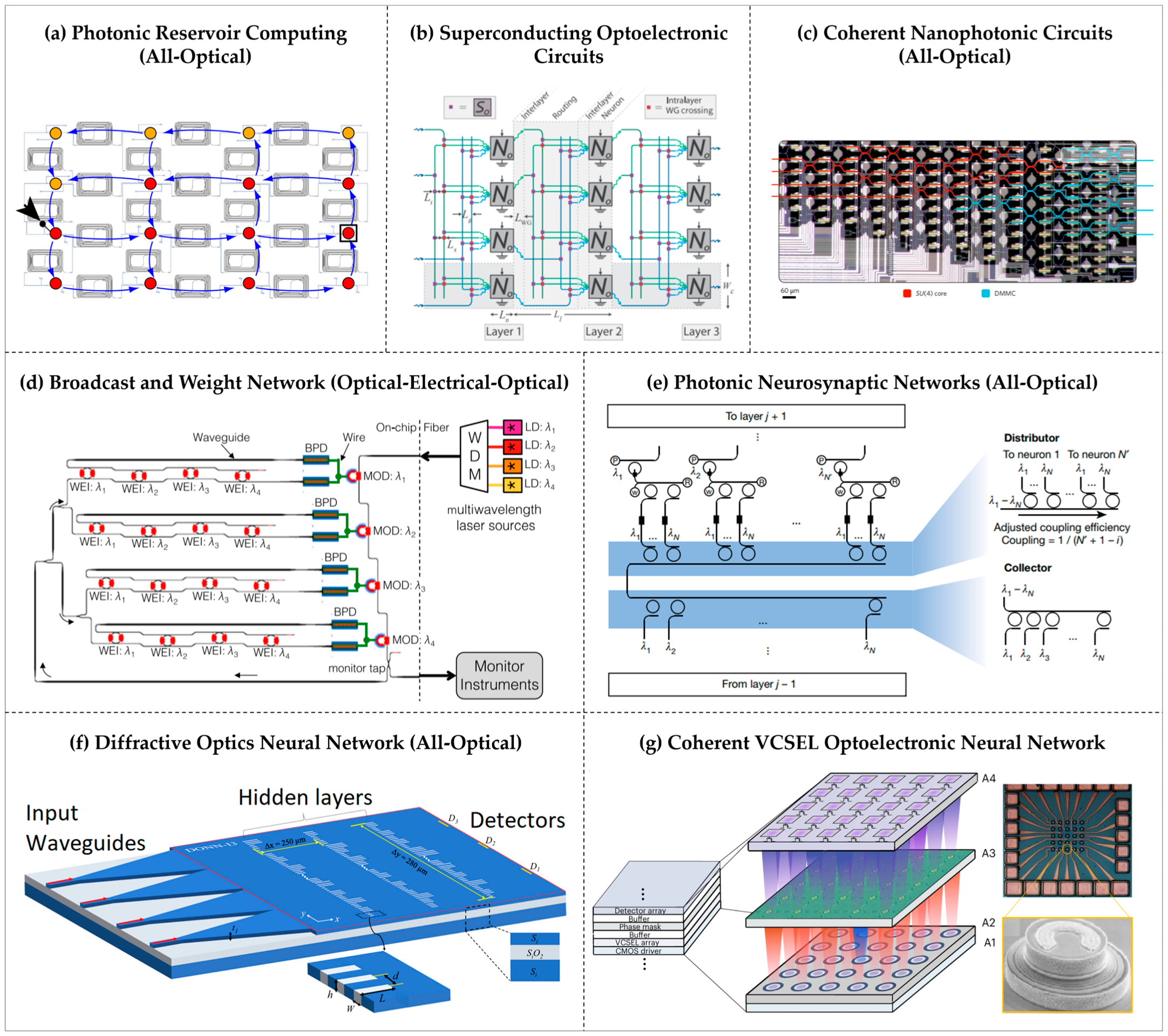
NPN Type [Ref.]	Synapse	Synaptic Memory	Photonic Neuron	Physics	Topology	Remarks
RC [49]	Node of reservoir with multiple feedback loops	280 spy interconnection delay	Intrinsic nonlinearity of photodetector	Superposition principle	Reservoir	No power consumption in the reservoir and high bit rate scalability (>100 Gbit/s). Cannot be generalized for complex computing application.
SOC [50]	Interplanar or lateral waveguide coupler with electromechanically tunable coupling	MEMS capacitor.	Phase-change nanowires from superconducting-to-normal metal above a threshold induced by photon absorption arranged in parallel or series detector	Superconductivity and MEMS capacitance	ANN and SNN	Highly scalable, zero static power dissipation, extraordinary device efficiencies. Require cryogenic temperature (2K). Bandwidth limited to 1 GHz.
CNC [51]	OIU consisting of beamsplitters and phase shifters for unitary transformation and attenuators for diagonal matrix	NA	Nonlinear mathematical saturable absorber function	TO effect	Two-layer DNN	Can implement any arbitrary ANN. May allow online training. Bulky and requires high driving voltage.
B&W [52]	Reconfigurable TO-MRR filters	NA	Mach–Zehnder modulator	TO effect	CTRNN	Capable of implementing generalized reconfigurable RNN. Bandwidth limited to 1 GHz.
MN [22]	Optical waveguides integrated PCM on top, controlling propagating optical mode	GST Phase.	Optical ReLU designed via MRR-PCM on top	WDM and PCM dynamic	ANN	No waveguide crossings, no accumulation of errors and signal contamination. The endurance of GST is of ~104 switching cycles and sub-nanosecond operation speed.
DO [57]	Pretrained phase values on distinct hidden layers via SSSD	NA	Diffractive unit composed of three identical SSSD	Huygens–Fresnel principle and TO effect	Three-layer DNN	Scalable, simple structure design, and all-optical passive operation. Requiring external algorithmic compensation.
VNN [60]	Homodyne detection with phase-encoding	NA	Homodyne VCSEL nonlinearity	Lasing principle	Three-layer ANN	Scalable and can be integrated into 2D/3D arrays and inline nonlinearity. Limited by phase stability and integration scale.

Optical interference unit (OUI); thermo-optic (TO); continuous-time RNN (CTRNN); not applicable (NA). Selected publications based on novelty or experimental demonstration.

, “Remarks” column). Solutions to the challenges of these approaches are promising for revolutionizing computing paradigms and enabling advanced AI applications in various domains.

RC leverages the complex dynamics of optical systems to perform computation. By utilizing interconnected delays between the fixed nonlinear nodes with multiple feedback loops, RC architectures demonstrate remarkable capabilities in emulating complex behaviors and processing information efficiently (Figure 6a) [49]. Recent advancements in RC have focused on integrating passive photonic elements, such as waveguides and resonators, to achieve scalable and high-performance computing [121]. Experimental demonstrations have showcased the ability of photonic RC to perform application-specific tasks such as spoken-digit recognition, time-series prediction, and signal optimization, making it a promising candidate for various real-world applications. However, it cannot be generalized to complex problems [102,122].

Superconducting optoelectronic circuits (SOCs) combine the advantages of superconducting electronics and photonics to achieve ultrafast and energy-efficient computing optimized for scalability (Figure 6b) [50]. These circuits exploit the superconducting nanowires, single-photon detectors, and capacitive micro-electromechanical system (MEMS)-based modulators to perform unprecedentedly efficient NN operations on a chip, paving the way for scalable and high-performance neuromorphic computing platforms with an energy cost associated with cooling at cryogenic temperature necessary for operation with maximum bandwidth limited to 1GHz [24,96,123].

The MZI-based coherent nanophotonic circuits (CNCs) leverage coherent light manipulation to perform complex computational tasks (Figure 6c) [51]. Integrating beamsplitters and phase shifters enables these circuits to control optical signals and facilitate high-speed processing, but they are bulky and require high driving voltages [23,74,95]. Experimental demonstrations have shown the potential of CNC for implementing neuromorphic algorithms such as in situ backpropagation [58], self-calibration [110], and asymptotically fault-tolerant programable photonic circuits [111], opening new avenues for ultrafast and energy-efficient computing [124,125,126].

B&W utilizes the concept of WDM to perform matrix–vector multiplication efficiently (Figure 6d) [52]. These networks can achieve parallel processing of NN operations by modulating optical signals at specific wavelengths and tuning MRRs [82,98]. Experimental implementations have demonstrated its scalability and energy efficiency for solving differential equations, making them promising candidates for nPIC for computing, but their bandwidth is limited to 1GHz [21,100].

Multiwavelength photonic neurosynaptic networks (MNs) integrate PCM–germanium–antimony–tellurium (GST)-based PN (Figure 6e) [22] and synapses [85] on silicon nitride on a silicon dioxide platform with inherent synaptic memory associated with PCM with no energy requirement to maintain its states in case of offline learning. Online learning can be challenging, with individual PCM devices’ endurance up to 10⁴ switching cycles requiring nJ of energy per cycle with sub-nanosecond operation speed. These networks leverage the optical mode in a controlled manner to perform complex cognitive tasks. Experimental demonstrations have shown the feasibility of implementing MN for tasks such as pattern recognition and associative memory with supervised and unsupervised learning, highlighting their potential for next-generation nPIC [55,118].

On-chip diffractive neural networks (DO) harness the principles of diffractive optics to perform computational operations passively. By integrating diffractive elements in silicon slots filled with silicon dioxide (SSSD), these networks can achieve parallel processing of optical signals with minimal power consumption (Figure 6f) [57]. Experimental implementations have demonstrated the ability of DO to perform image classification [57,126]. DO is highly susceptible to noise and fabrication errors, requiring algorithmic compensation.

Vertical-cavity surface-emitting laser optoelectronic neural network (VNN) architecture utilizing spatial–temporal multiplexing and coherent detection mechanisms is a method that achieves significant breakthroughs in energy efficiency and compute density (Figure 6g). The VNN has compact device footprints and near-instantaneous inline nonlinearity through homodyne photoelectric multiplication. Challenges involve enhancing photonic integration to reduce phase instability and scaling VCSEL arrays for even larger neural network models [60].

3.3. Algorithms and Methods for Training Neuromorphic Photonic Networks

NPNs represent a burgeoning frontier ripe with promise. However, training algorithms face unique challenges due to the nonlinear nature of optical components and the need for efficient optimization techniques for a delicate balance between processing and memory access [116,117]. Unlike conventional AI algorithms deployed in software applications, developing customized training algorithms tailored for photonic hardware implementation could herald a transformative shift in this domain (

Table 2. Applied training and comparison of on-chip neuromorphic photonic networks.

NPN Type	Device Basic Unit [Reference]	Networks and Training					Comparison
		Topology	Training	Data (Train/Test) %	Application	Remark or Accuracy Exp. (Sim.)	NBUs/mm2	Operational Power (pJ/FLOP)	Throughput (TOPS)
RC	Spiral nodes [49]	Reservoir	Fivefold cross-validation, ridge regression, and winner-takes-all approach	10000 bits for Boolean task and 5-bit headers	Arbitrary Boolean logic and 5-bit header recognition	>99 (-)	62,500	0	0.4
SOC	SNSPD [50]	ANN And SNN	Backpropagation and STDP	-	-	Designed for Scalability	7 to 4000	0.00014	19.6
CNC	Tunable MZI [51]	Two-layer DNN	SGD	360 data points (50:50)	Vowel recognition	76.7 (91.7)	<10	0.07600	6.4
B&W	TO-MMR [52]	CTRNN	Bifurcation analysis	500 data points from 0.05 to 0.85	Lorenz attractor	B&W is Isomorphic to CTRNN	1600	288.0000	1.2
MN	X-PCM [55]	CNN	Backpropagation	MNIST handwritten digits	Digit recognition	95.3 (96.1)	<5	0.00590	28.8
DO ##	SWU [57]	Three-layer DNN	Pretrained backpropagation (adaptive moment estimation)	Iris (80:20) and MNIST handwritten digits (85:15)	Classification	90 (90) and 86 (96.3)	2000	0.00001	13,800.0
VNN	VCSEL arrays [60]	Optical NN	Backpropagation	MNIST handwritten digits	Image classification	93.1 (95.1)	6	0.007	50
For more comprehensive information, readers may also refer to other reported works [56,58,59,110,111,118,127,128,129,130,131].

No. of basic unit (NBU); trillions of operations per second (TOPS) = 2 x No. of layers in network x No. of rows x No. of columns x Detection rate; floating point operations (FLOPs); X represents ring or MAC unit; sub-wavelength unit (SWU); ^## reported 30% fabrication error; selected publications based on novelty or experimental demonstration.

). One of the key challenges in training NPNs lies in achieving precision (Table 2, “Networks and Training” column). Traditional backpropagation algorithms, which are highly effective for training deep AI networks, require precise adjustments of weights based on slight variations in error gradients. However, most nanodevices used in NPN are inherently noisy, making it challenging to achieve such fine adjustments. Novel training algorithms that can adapt to the imperfections and variability of physical devices can cash in on the inherent properties of photonics. Several strategies are proposed to address the precision challenge in photonic training, including the photonic generative network that harnesses noises of photonic hardware [56], a heuristic photonic recurrent algorithm for the Ising problem [127], and the photonic analog of the backpropagation leveraging adjoint variable methods that can significantly reduce complexity by simplifying the mathematical model associated with training [58] algorithms.

Additionally, statistical optimization tools, including genetic algorithms [132], Bayesian optimization [133], nonlinearity inversion [120], and equilibrium propagation [134], have been investigated for optimizing weights in NPNs. These gradient-free algorithms show promise for training NPNs efficiently, particularly for classification tasks with different datasets [135]. Another essential consideration in NPN training is the need for weight-independent variations using external signals (electrical or optical). Furthermore, modifying existing algorithms to work effectively despite device imperfections is crucial, as demonstrated in self-calibrated [110] and asymptotically fault-tolerant [111] programmable NPNs. Unsupervised learning algorithms are particularly intriguing for NPNs and are highly adaptable to device imperfections. STDP is a popular unsupervised learning rule inspired by neuroscience [119]. In STDP, synaptic weights are modified based on the temporal relationship between pre-synaptic and post-synaptic activities, making it suitable for implementation in NPNs (Table 2, “Networks and Training” column) [22,50]. In addition to precision and unsupervised learning, optimizing nPIC presents challenges. Mitigating the complexity of probing local optical intensities across the circuit is essential for efficient training. Recent advancements propose on-chip reconfigurable [136] and control-free hardware-aware [135] training for NPNs. In contrast, Boolean learning via coordinate descent offers a practical and efficient alternative to error backpropagation [119], enabling high-performance NPNs with programmable connections. These novel training schemes (Table 2), proposed or experimentally validated for NPNs, underscore a dynamic landscape characterized by notable achievements, persistent challenges, and promising prospects also highlighted in State-of-the-Art NPN demonstrations [118,128,129,130]. By addressing the challenges and exploring innovative training algorithms, NPNs hold the potential to revolutionize neuromorphic computing paradigms, offering energy-efficient and high-performance solutions for a wide range of applications (Figure 7).

4. Discussion

The demand for AI and its multifaceted applications is accelerating rapidly, exemplified by recent advancements such as DALL-E3 and Sora [88], which require massive computational power for training models with billions of parameters. Such tasks have relied on large-scale clusters of accelerators, like GPUs or TPUs [115]. Neuromorphic photonics holds the potential to support these power-hungry processors, particularly for ASIC demands. Photonics leverage its inherent bandwidth, parallelism [39], picosecond latencies [64], and energy efficiency (measured in pJ/FLOP) [3]. Mainstream silicon photonic platforms offer a fundamental device library encompassing modulators, waveguides, and detectors, crucial for constructing signal pathways within diverse neuromorphic architectures [79,80,81]. Innovations in conventional manufacturing processes, including the integration of PCMs [22,55,130,137] or vanadium dioxide [86], superconducting electronics [24,27,50,123] and magneto-optic (MO) memory cells comprising heterogeneously integrated cerium-substituted yttrium iron garnet (Ce:YIG) on silicon MRR [87], are being investigated to broaden the range of achievable architectures.

4.1. Exploring the Current State of the Art: Challenges and Solutions

4.1.1. Synergistic Co-Integration of Photonics with Electronics

Silicon photonics has its advantages but still faces challenges yet to be solved. Coherent on-chip architectures utilizing components like MZIs are susceptible to thermal and fabrication processes, leading to variations in phase, interference, and diffraction. This results in inaccuracies in NPNs, emphasizing the need for strategies to mitigate these effects during training and tuning. Non-coherent architectures face challenges such as heterodyne crosstalk in MRRs and the requirement for numerous modulation resources, limiting scalability and energy efficiency. Efforts to address these challenges include exploring parallel arrangements of MRRs, leveraging microdisks, and facilitating increased integration density on-chip. Variations and reliability issues also present significant hurdles in silicon photonic devices, affecting their performance and stability. Therefore, electronic controllers for feedback and algorithm (calibration), direct-current analog signal for biasing, analog to digital, and digital to analog for trans-impedance amplification pose a solution in managing photonic devices and ensuring the stable operation of NPNs [138]. However, high latencies and frequency mismatches between electronic controllers and optical networks pose real-time, high-speed operation challenges.

Thus, integrating on-chip active electronics becomes crucial, and a significant challenge is the need for more complex on-chip electronic circuitry, which demands a higher density of electrical ports than optical ports, with the number of electrical ports scaling quadratically with the optical ports. Despite the challenges, the co-integration of CMOS electronics and photonics holds promise for overcoming many limitations by leveraging the advantages of both technologies while mitigating their drawbacks. Technologies including flip-chip bonding, wire bonding, and monolithic fabrication enable the integration of CMOS electronics optimized for digital control with silicon photonic chips [79,81], offering advantages such as increased interconnection density and reduced parasitic impedance.

4.1.2. On-Chip Light Sources on Semiconductor Platform

Power efficiency is critical in neuromorphic photonics, with O/E/O conversions consuming considerable power. At the same time, all-optical neurons offer better power efficiency. Additionally, off-chip lasers contribute significantly to power consumption, necessitating research into power-efficient on-chip light sources. Efforts to tackle this challenge involve integrating light sources directly into the silicon waveguide layer [139], employing methods such as rare-earth-element doping, strain engineering of germanium, and all-silicon emissive defects [24]. This is advantageous, as it eliminates the need to send the optical signal off-chip for computation, which is particularly beneficial for neuromorphic photonics systems employing NPNs. The selection of lasers for neuromorphic photonics depends on the type of neuron involved. Multi-die techniques are applicable for systems utilizing modulator-class neurons, where the light source can be positioned outside the chip. However, precise integration of optical gain onto waveguides is essential for laser-class neurons.

4.2. Advancements and Future Directions in Scientific Inquiry

4.2.1. Fabrication Challenges

An essential aspect of advancing neuromorphic photonics involves enhancing the robustness of systems to environmental fluctuations and overcoming fabrication challenges. Analog circuits, typical in neuromorphic processors, often require trimming to address manufacturing variabilities and environmental sensitivities. In integrated photonics, resonant devices like MRRs pose challenges due to their sensitivity to variations [99]. One approach to mitigate these challenges is resonance trimming, which involves inducing changes in the refractive index of waveguides. Active trimming methods, including heating waveguides to environmental variability, require constant power input and fast response times. Alternatively, passive trimming methods utilize permanent or non-volatile techniques to adjust the refractive index of devices. These methods, including electron beam-induced compaction [140], ion implantation [141], and strain of oxide cladding [142], offer solutions for correcting fabrication variations or preprogramming circuits to default states. Moreover, the integration of field-programmable PCMs allows for in-place reconfiguration [84], further enhancing robustness to fabrication discrepancies. In addition to addressing variability, advancements in neuromorphic photonics necessitate the development of analog-aware compilers to map application tasks to photonic hardware effectively [143]. Unlike traditional compilers for electronic systems, photonic compilers must account for idiosyncrasies inherent in representing signals in WDM light waves, including nonlinear distortion and limited dynamic range. Collaborative efforts within the academic community are underway to develop these compilers tailored for neuromorphic and programmable photonics [51,66,110,144], enabling efficient task mapping and optimization for photonic systems. By addressing these challenges and embracing innovative solutions, the field of neuromorphic photonics can enhance its resilience to environmental fluctuations and fabrication complexities, thereby facilitating the realization of robust and reliable neuromorphic computing systems.

4.2.2. Integration of Photonic Components

Efficient integration of diverse material systems in photonic circuits is pivotal for advancing neuromorphic photonic computing [145]. The primary challenge is seamlessly combining materials like silicon, III-V semiconductors (e.g., GaAs and InP), and lithium niobate-on-insulator (LNOI) to create a unified, high-performance platform [101,146,147]. Silicon photonics is the cornerstone of passive components, leveraging CMOS compatibility to enable mass production and scalability [81]. However, silicon’s indirect bandgap limits its ability to generate or amplify light, necessitating the integration of III-V materials for efficient light sources, like lasers and photodetectors. With their direct bandgap properties, these materials excel in light emission and detection but face cost, CMOS compatibility, and integration-density challenges [148].

Three integration approaches address these challenges: hybrid, heterogeneous, and monolithic integration. Hybrid integration involves physically aligning separate III-V and silicon chips through photonic wire bonding or flip-chip packaging. While effective for pre-tested components, its alignment precision and limited density hinder scalability. Heterogeneous integration advances this by wafer bonding III-V materials onto silicon, enabling high-density integration and efficient vertical coupling. For instance, distributed feedback lasers integrated heterogeneously on silicon have achieved ultra-narrow linewidths and high power efficiency. Monolithic integration, the ultimate goal, involves directly growing III-V materials on silicon substrates. Though promising in eliminating coupling losses, it faces significant challenges from lattice mismatches and thermal-expansion differences [81,148].

LNOI introduces another dimension to photonic integration, offering exceptional electro-optic modulation capabilities. Its high refractive-index contrast facilitates tightly confined optical modes, while its low-voltage-length product enables energy-efficient operations. Advanced fabrication techniques, such as smart-cut and wafer bonding, now allow the integration of submicron-thick lithium niobate films onto silicon substrates. This combination enhances the functionality of photonic circuits, making them suitable for high-speed, low-power applications in neuromorphic photonics [147].

The development of integrated photonic systems is not limited to material integration. However, it extends to the functional integration of components like photonic digital-to-analog converters (DACs), frequency comb sources, and multifunctional photonic memory cells. Photonic DACs, utilizing techniques like optical intensity weighting with MRRs, provide high precision, reduced distortion, and immunity to electromagnetic noise [149]. Similarly, frequency combs based on soliton microcombs offer chip-scale solutions for generating broadband, stable, and precisely aligned optical signals, essential for neuromorphic architectures [76]. Multifunctional photonic memory cells represent yet another innovation, where PCMs are integrated with silicon PN junctions or non-reciprocal magneto-optic materials wafer bonded on silicon-on-insulator (SOI) technology. These cells support nonvolatile optical weighting and high-speed tuning, enabling dynamic in situ training and adaptability in neuromorphic systems. Such devices demonstrate how heterogeneous integration combines materials and leverages their unique properties to enhance system-level performance.

Achieving full photonic integration requires addressing key challenges, including minimizing thermal dissipation, optimizing optical coupling, and reducing fabrication variability [138]. Advances in hybrid and heterogeneous integration and innovations in packaging and alignment are essential for creating a cohesive platform. Furthermore, the co-integration of electronics and photonics through co-packaged architectures offers a pathway to achieve energy-efficient, high-performance systems capable of supporting nPIC’s demands [79,81].

4.2.3. Synaptic Memory

The integration of synaptic memory stands out as a critical area of exploration. Conventional approaches have typically depended on a blend of specialized photonic devices controlled by generalized electronic circuits. However, the absence of standard building blocks like high-level compilers, logic gates, and memory within current photonic platforms necessitates innovative strategies to incorporate memory into neuromorphic processors effectively. For specific ML and neuromorphic applications, such as DL inference, synaptic weights, once trained, may not require frequent updates. In these scenarios, non-volatile analog memory, such as in-memory computing utilizing PCMs and non-reciprocal phase shift in magneto-optic materials, presents a promising solution [83,87,137]. By interfacing with digital electronic drivers, these memory systems enable real-time NN operation, precomputed weight storage, and direct inference task execution on the hardware [55]. Nevertheless, challenges persist in scenarios where temporary storage of neuron outputs is required, as seen in long short-term memory RNNs. In such cases, alternative memory technologies, including digital or short-term analogue electronic memory with electro-optic interfaces to analog photonics, may be better suited. While analog memory may exhibit limitations in precision and noise compared to digital memory, recent studies have shown that even low precision can support effective deep RNN operations. As neuromorphic photonics progress, they are expected to adopt heterogeneous memory technologies, akin to modern computers, comprising various memory types within a single system [144,150]. This evolution may involve integrating electronic memory components alongside novel photonic memory technologies, offering non-volatile and reconfigurable capabilities essential for dynamic neural network operations.

4.3. Envisioning the Future of Neuromorphic Photonics: A Visionary Perspective

Neuromorphic photonics represents a cutting-edge fusion of advanced technologies and innovative architectural designs, offering transformative solutions pivotal for constructing NNs for emerging applications. In LLMs, parallel matrix–vector multiplications are enabled, which is critical for efficient training and inference [73]. For digital twins, neuromorphic photonics supports on-chip, real-time simulations, enhancing predictive modeling and decision-making [57,136]. In data centers, it eliminates the need for electronic-to-optical signal conversions by achieving seamless communication through WDM, significantly reducing energy consumption [3,73,90]. Furthermore, the extreme demands of 6G communications—such as ultra-high bandwidth, minimal latency, and efficient signal processing—are met through photonic broadcast interconnects, which deliver low latency and high throughput while conserving energy [39,46,63,145].

These unique attributes position neuromorphic photonics as a game-changing paradigm for tackling the challenges of modern computational and communication technologies. A prominent concept, the NPP [33], embodies this integration by leveraging State-of-the-Art photonic packaging and emerging integrated photonics. The NPP seamlessly merges optical and electronic components within a system-in-package framework, enabling versatile signal processing and control functionalities. Here, we deal with two fundamental architectures, the NPPN and the ReConN, as contributions to the evolving field of neuromorphic photonics, offering blueprints for realizing large-scale NNs. The convergence of photonics and neuromorphic computing signifies a transformative era of technological advancement and scientific exploration. Embracing perspectives and pioneering research endeavors will unlock the vast potential of neuromorphic photonics, reshaping the landscape of on-chip neuromorphic computing for application-specific AI.

5. Conclusions

Neuromorphic photonics based photonic integrated circuits represents a transformative approach to optoelectronic (grabbing the lower-hanging fruit first) or all-optical (too early to demand, requires technological advancement) hardware design, aiming to create systems that mirror the structure and functionality of NNs. This isomorphic relationship between NPNs and their biological counterparts promises remarkable capabilities and has sparked significant technological and societal interest. Over recent years, research in NPNs has witnessed rapid growth, leading to the exploration of diverse architectural concepts, PN models, training techniques, and network topologies. This diversity highlights the dynamic nature of the field, with ongoing efforts aimed at identifying optimal applications where photonics can outperform traditional electronic computing methods. Real-time applications requiring rapid decision-making are particularly promising areas for deploying neuromorphic photonics. A key focus will be on scaling the integration of PN within single networks. Despite challenges such as the co-packaging of control electronics and light sources, advancements in scalable photonics platforms offer promising avenues for overcoming these obstacles. With modern integrated platforms and innovative ideas and devices for on-chip functionality, neuromorphic photonics is poised to push the boundaries of ML and information processing, unlocking new frontiers in AI and computational capabilities.