Wind Resource Assessment over Extremely Diverse Terrain

Abstract

The current study investigates the effect of terrain features on wind resources in a region with extremely diverse terrain. To that end, a case study of Nepal based on annual wind data collected from 10 different sites is performed. The evaluation of mean wind speeds using Weibull probability density functions (PDFs) shows that complex-terrain sites exhibit greater variability in 10-min average wind speeds relative to the annual average wind speeds. This pattern is also evident in comparisons of short- and long-term average wind speeds. At the complex-terrain sites, the wind speeds exhibited strong short-term variations, suggesting that local terrain effects dominate over seasonal wind variation. Terrain complexity also strongly affected turbulence. The flat-terrain sites showed turbulence intensities below the lowest IEC category turbulence profile, while the complex-terrain sites exceeded the highest IEC profile. This indicates that the IEC standard may require modification based on site complexity parameters, such as the standard deviation of elevation fluctuations. The power law exponent ($\alpha$), used to extrapolate wind speeds to higher elevations, deviated notably from the typical 1/7 value, even in flat terrain. Finally, a power potential analysis indicated that three sites with higher mean wind speeds achieved higher capacity factors.

1. Introduction

Massive deployment of renewable energy, such as wind and solar energy, is crucial to reduce our dependency on fossil fuel-based energy systems and to control the current rate of global warming by cutting the emission of greenhouse gases. The worldwide transition to renewable energy is also necessary to meet our objective of a carbon-neutral economy by 2050. In this regard, wind energy has received significant interest in the past two decades, with governments (mostly in developed countries) adopting green energy-friendly policies, which consequently have encouraged major investment from the industrial sector. According to the Global Wind Energy Council (GWEC), just in 2023, more than 116 GW of new wind power capacity was installed worldwide, bringing the cumulative global capacity to 1021 GW [1]. Although the numbers are promising, considering the market share, around 90% of those wind turbines are installed in economic powerhouses like China, the US, the EU, and other developed countries. In most developing countries, there have either been no utility-scale wind turbines installed to date or the share of wind energy is negligibly small. A lack of infrastructure, a poor investment environment, and a lack of government policies are some of the factors attributed to the slow or absent growth of wind energy in those countries.

In terms of technical aspects, most developing countries do not have sufficient wind data to assess their wind energy potential. Furthermore, these regions may have unique terrain features and localized wind conditions. As also shown in this study, due to the complexity of terrain, the wind characteristics (e.g. shear and turbulence intensities) of these sites may deviate significantly from those defined in the international standards [2]. The current study therefore investigates the effect of terrain features on wind resources in a region with extremely diverse terrain. To that end, a case study of Nepal based on annual wind data collected from 10 different sites is performed.

Investigating the effect of terrain features (specifically complex terrain) on flow physics poses significant challenges. It is difficult to predict the impact of complex terrain over the atmospheric boundary layer (ABL) flow since terrain induces turbulence and shear, which further interact with other ABL dynamics, such as atmospheric stability [3,4]. In the large-eddy simulation (LES) of a wind farm over complex terrain, Bernardoni et al. showed that turbulence and topographic wakes affect both power production and turbine loads [5]. For example, the wind direction varied significantly between the bottom and top of the rotor, leading to off-design operation and large fluctuations in the loads experienced by the blades. However, data from the numerical flow models, particularly in complex terrains, have higher uncertainties and generally are not well quantified [6]. Therefore, more recently, on-site measurements have been used to calibrate numerical flow models or their outputs and improve the final wind resource estimation [6,7]. In order to obtain an accurate picture of the wind characteristics at complex-terrain sites, direct measurement—using met-masts and remote sensing devices—for an extended period of time remains the only option.

In their review of boundary-layer studies over complex terrain, Rotach and Zardi [8] combined high-resolution turbulence observations with numerical simulations. Their work suggested that turbulence exchange processes over complex topography can be parametrized based on terrain characteristics, although a detailed theoretical framework was not provided. Beyond turbulence, complex terrain is also known to induce distinct local wind phenomena. For instance, in terrain with unique topographic features, turbulent transport can play a crucial role in driving highly localized mountain–plain breeze circulations [9]. However, despite extensive research on wind flow in complex terrain, two important aspects warrant further investigation. First, the influence of terrain-induced local wind conditions on seasonal atmospheric variability requires closer examination, particularly because of its direct implications for wind resource assessment and energy production. Second, the development of methods to quantify terrain complexity and relate it to site-specific turbulence intensity remains a challenging but essential task.

The primary research question of this study is how terrain complexity can be related to local and seasonal atmospheric variability as well as to the turbulence intensity at the sites. To address this, the current study investigates the influence of terrain features on local wind characteristics in a region with highly diverse topography by using available field measurements. The study also discusses the potential modification of the IEC standard for turbulence intensity by defining its parameters based on terrain complexity. Furthermore, the wind energy potential of the sites is also evaluated and discussed. The remainder of the paper is organized as follows. Section 2 introduces the measurement sites and the meteorological masts installed at those sites. It also describes the 10-min averaged wind data, their availability, and the analysis methods applied in the study. Section 3 presents the mean wind speeds and wind direction distributions, highlighting their relationship to terrain complexity. This is followed by an analysis of turbulence intensities and peak wind speeds. The section also evaluates the reliability of the power law for extrapolating wind speeds at higher elevations. Section 4 evaluates the power potential of the sites using measured wind data for a reference wind turbine. To that end, power distributions are computed and used to estimate annual energy production and capacity factors. Section 5 presents a discussion based on the analysis and interpretation of the results. Finally, the main conclusions are summarized in Section 6.

2. Materials and Methods

2.1. Measurement Sites

Nepal has one of the most complex terrains in the world. The country extends from northwest to southeast, and, just within the latitude range from around ${26}^{\circ }$ to ${30}^{\circ }$, the elevation varies from 50 m to more than 8000 m. The southern part of the country is flat, with negligible elevation features, but the mountainous region starts just about 20 to 30 km north of the southern border. Extreme variations in geographical features contribute to the highly localized atmospheric dynamic, especially in the north of the country. The complex terrain and the localized behavior of the atmosphere are the reasons why the wind resources of Nepal cannot be accurately predicted with mesoscale simulation tools such as Weather Research and Forecasting (WRF). Extended and distributed measurement campaigns, which, in addition to providing an actual picture of available wind resources, are necessary to calibrate and improve the performance of simulation tools like WRF.

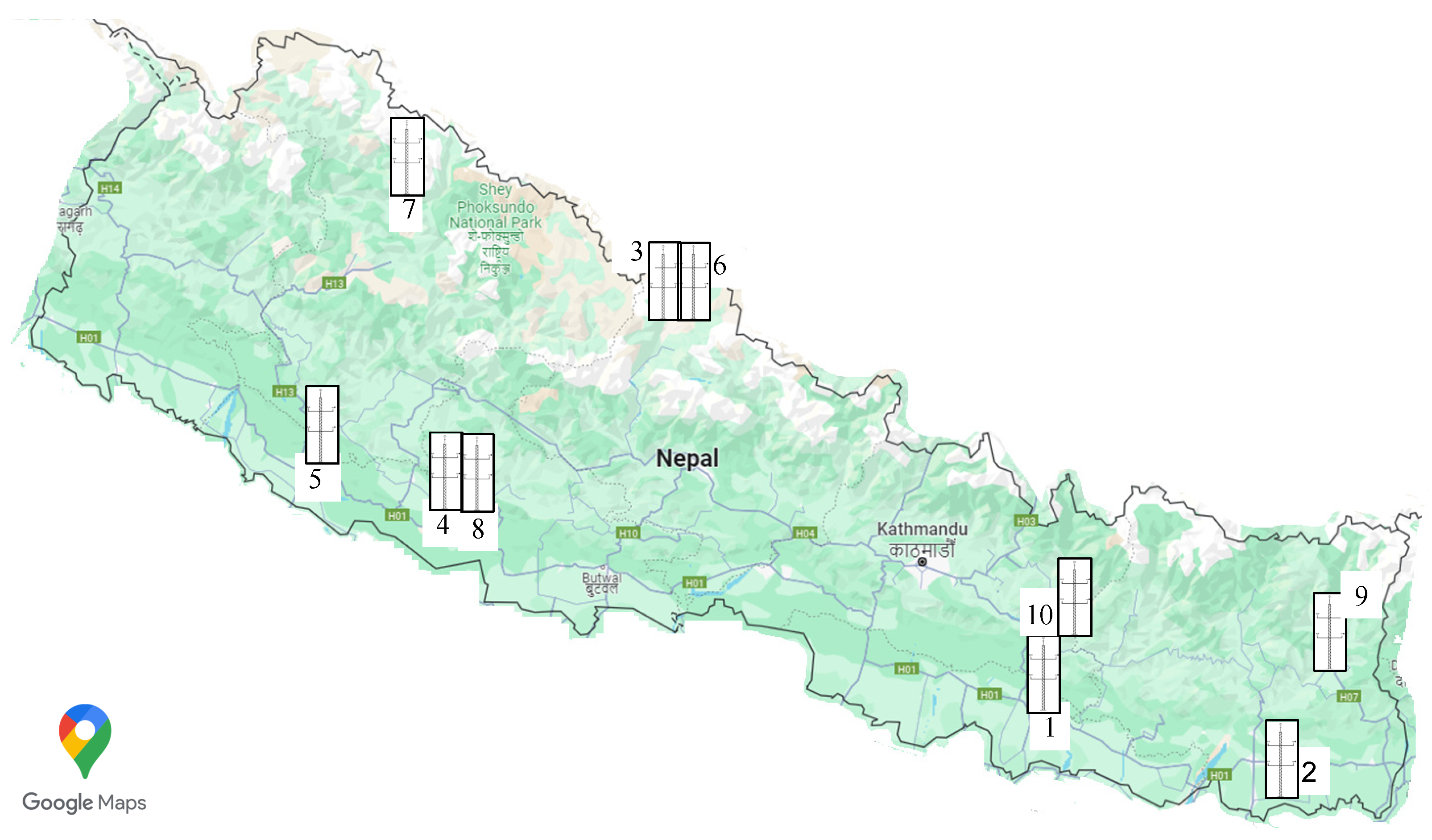
The Energy Sector Management Assistance Program (ESMAP) funded and supported the project of identifying and geospatial planning of renewable energy resources for Nepal [10]. The project is administered by the World Bank and has installed 10 meteorological masts (met-masts) in the various regions of Nepal [11], as summarized in Table 1. Their rough locations are also shown in Figure 1, with site numbers corresponding to those in the table. Details about mast installation and instrumentation can be found in the World Bank Report [11]. All 10 met-masts are composed of square lattice towers supported by guy wires, and they have the height of 80 m. They were designed according to the IEC Standard 61400-12-1. Met-masts are equipped with cup anemometers (Thies 4.3351.10.000) from 20 m through 80 m height at an interval of 20 m, while wind vanes (Thies 4.3151.00.901) are installed at 58.5 m and 78.5 m. Cup anemometers have accuracy class of 0.5 (class S classification). Both cup anemometers and wind vanes collect horizontal wind speeds and directions at a sampling frequency of 1 Hz. The measured data has been publicly available since 2019 in the ESMAP repository via ENERGYDATA.info [12]. In terms of terrain complexity, sites 1, 2, 5, 8, and 10 can be considered to have flat terrain, and sites 3, 4, 6, 7, and 9 can be considered to have highly complex terrain.

Table 1. Summary of the sites where met-masts are installed. The height of the met-masts at all the sites is 80 m.

Site No.	Site Name	Latitude (deg)	Longitude (deg)	Elevation (m)	Administrative Profile
1	Sitapur	26.6533	86.4154	95	Laxmipur Gaunpalika-6, Siraha
2	Pidari	26.4253	87.6677	70	Mahadeva-1, Morang
3	Tangbe	28.8805	83.7995	3040	Green Tangbe Limited, Tangbe, Mustang
4	Purungchheda	28.0449	82.5888	1448	Purungcheda, Kabre VDC-1, Dang
5	Khajura	28.1089	81.5939	150	Khajura, Nepalgunj, Banke
6	Kagbeni	28.8322	83.7880	3036	Kagbeni, Mustang
7	Dangibada	29.2342	82.0689	2311	Dangibada, Tatopani-5, Jumla
8	Koilabas	27.6897	82.5265	210	Koilabas Bazaar, Gadhawa Ghaunpalika-8, Dang
9	Saptami	26.9744	87.6865	2181	Saptami, Panchthar
10	Birtabesi	27.2768	86.0805	454	Birtabesi, Ramechap

Figure 1. Rough locations of all 10 measurement sites.

2.2. Data and Methodology

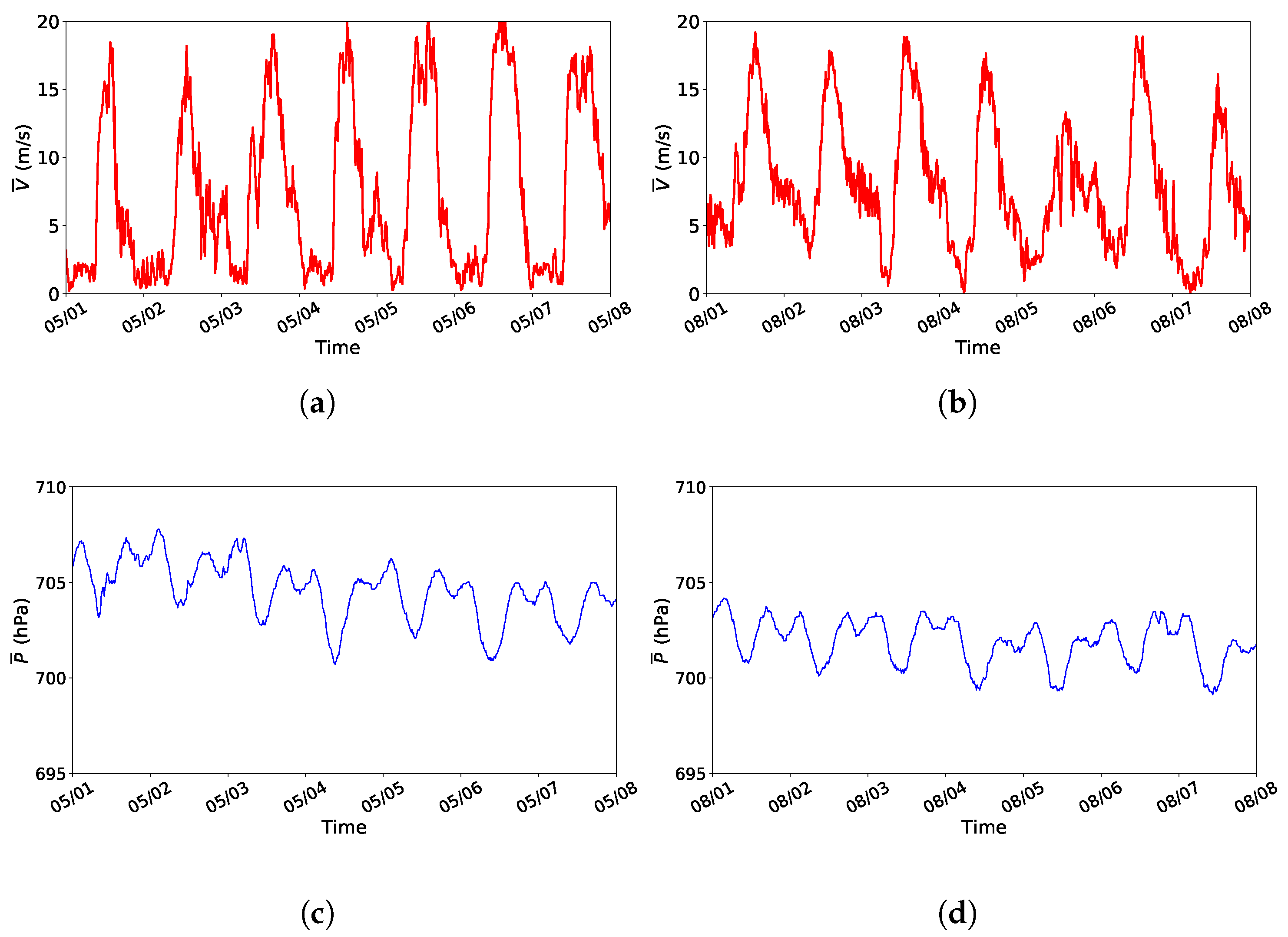
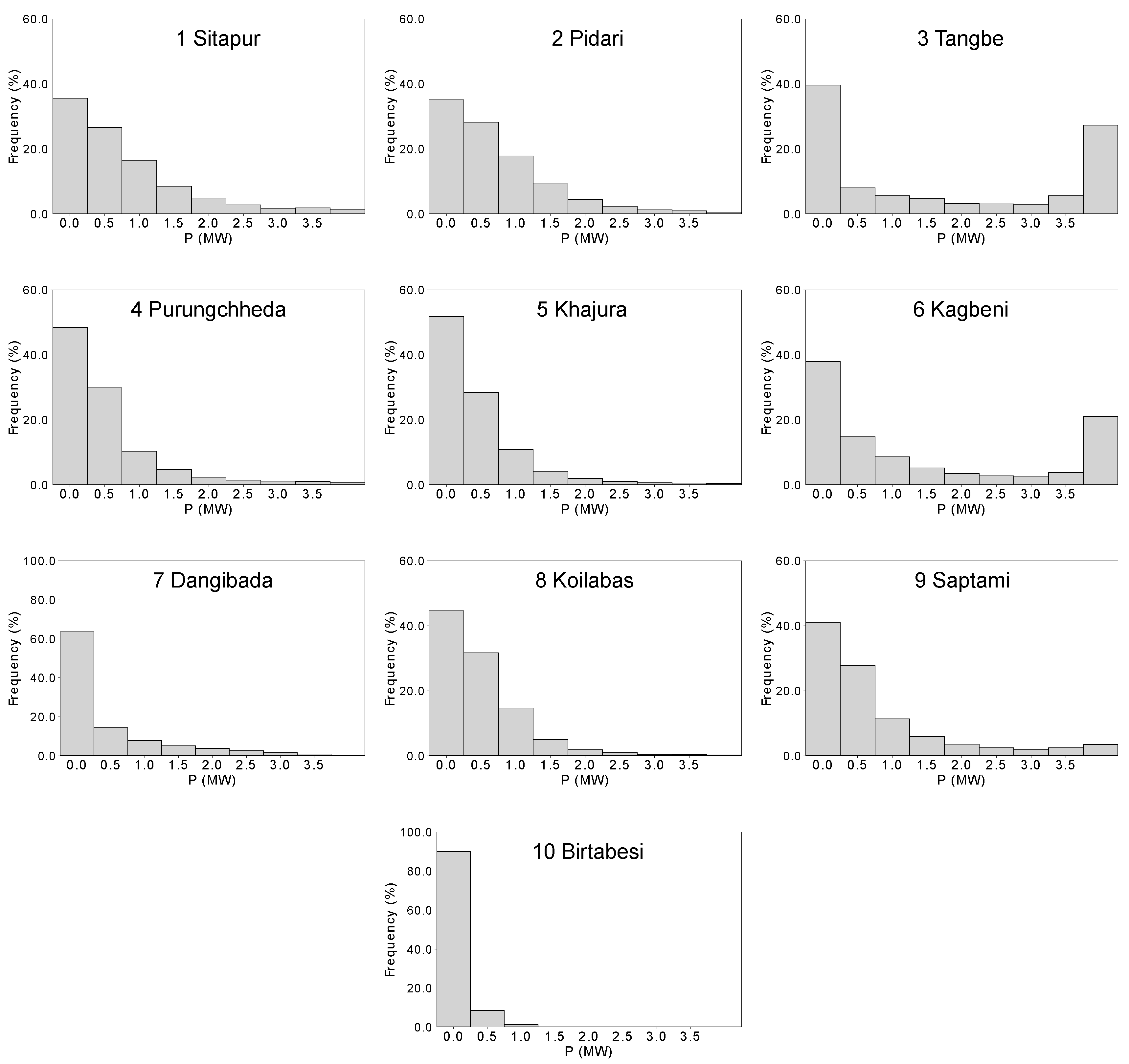
This study uses data from the repository under the open data license terms of Creative Commons Attribution 4.0 [13]. It is noted that the author was not involved in the actual measurement campaigns. Wind speeds and wind directions data for the period of one year are analyzed from all 10 met-masts. For site number 1 Sitapur, data from October 2018 through September 2019, for site number 4 Purungchheda and site number 7 Dangibada, data from January through December 2019 are processed. For all other sites, data from April 2019 through March 2020 is used. Wind speed and wind direction data at 80 m and 78.8 m, respectively, are primarily analyzed for evaluating wind energy potential at those sites. All analyses are conducted using 10-min averaged data derived from measurements at a 1 Hz sampling frequency. To mitigate the influence of extreme outliers caused by measurement uncertainties, the 90th percentile values of turbulence intensity and peak wind speed are used in the analysis. In addition, mean wind speeds below 0.2 m/s are excluded when calculating the power law exponent ($\alpha$).

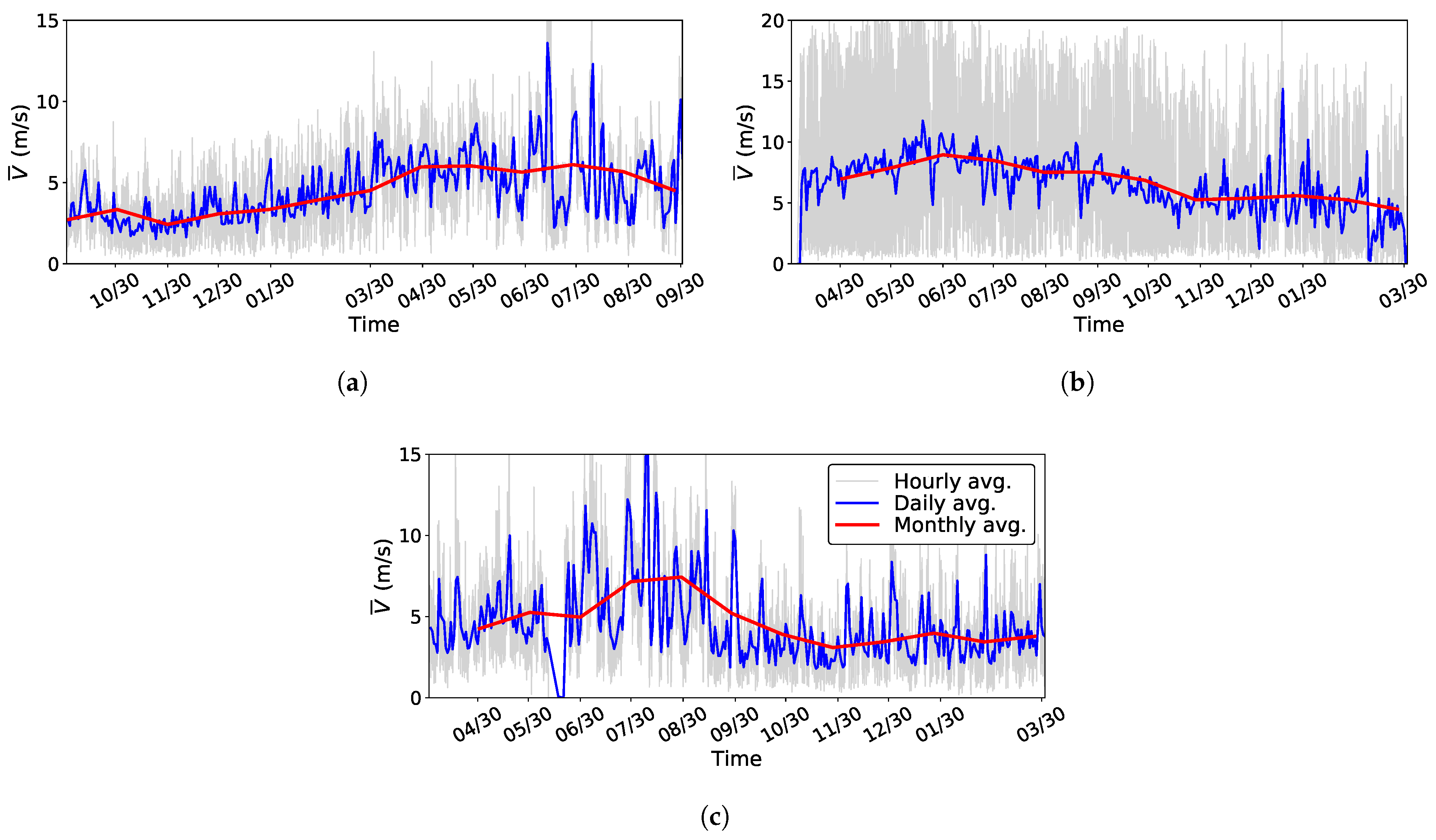
Figure 2 shows the availability ($\eta$) of the 10-min average wind speeds during the one-year analysis period. $\eta$ is defined as [14]

$$\eta ={\displaystyle \frac{N_{\mathrm{meas}}}{N_{\max }}}$$

(1)

where $N_{\max }$ and $N_{\mathrm{meas}}$ are the maximum and the actual number of 10-min averaged wind data that the anemometer can measure in one year. It can be observed that, except for site 3 Tangbe, availability is almost 100% for all sites. Therefore, the data can be considered sufficiently reliable for accurate wind resource analysis. For Tangbe, data was unavailable for approximately six month period, resulting in η < 50%. However, since sites 3 and 6 are close to each other, lower availability at site 3 does not affect the results and conclusions of this study.

Figure 2. Availability of the 10-min average wind speed for all 10 sites during the one-year analysis period. Measured data at the height of 80 m above ground level (AGL) are used.

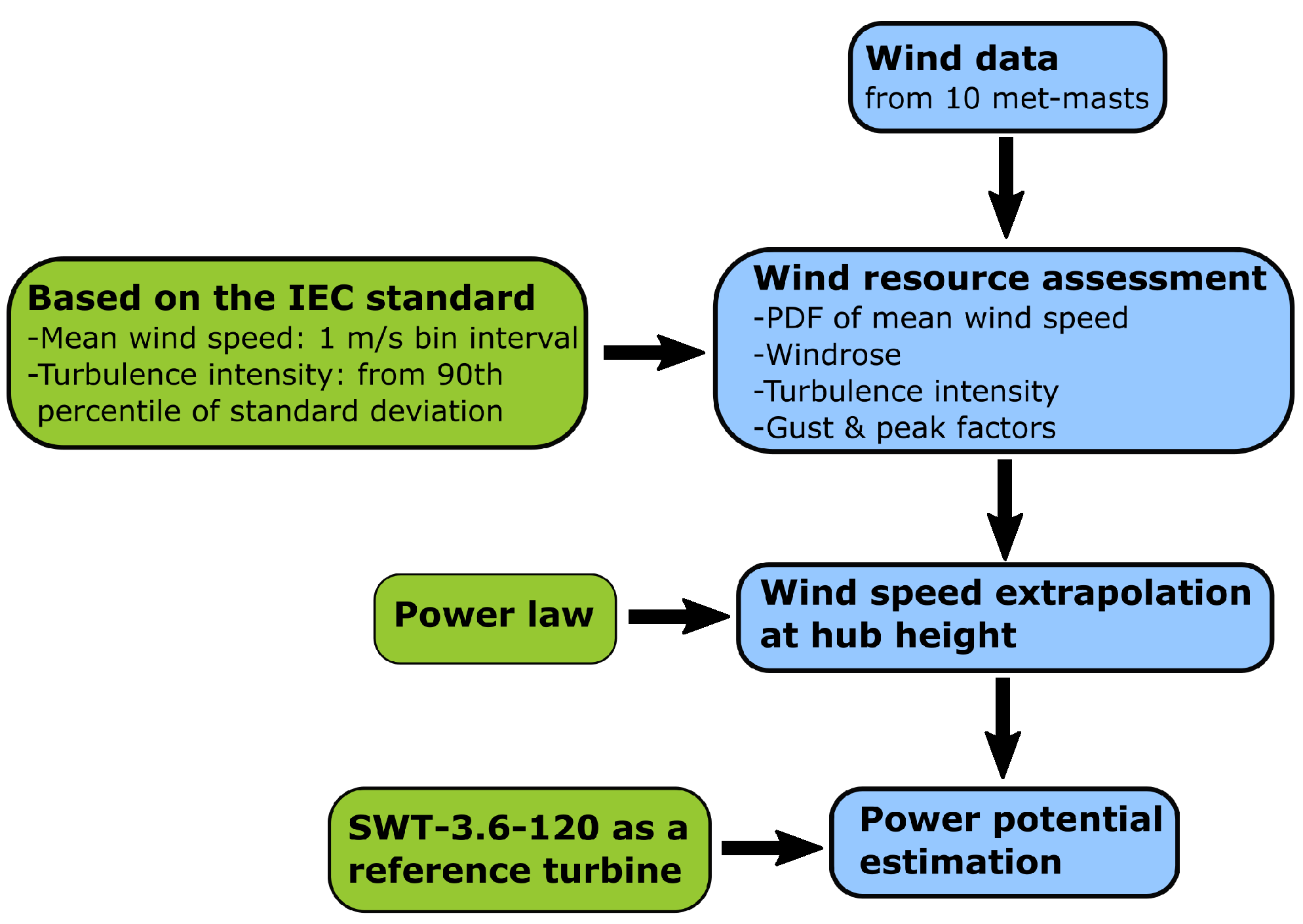
Figure 3 shows the flowchart describing the research methodology employed in this study. Wind resource assessment is performed based on the IEC standard. The methods applied, along with their corresponding formulations, are outlined here.

Figure 3. Flowchart of research methodology.

First of all, the mean wind speed distributions are analyzed using the Weibull probability distribution (PDF), which is defined as

$$p\left(\overline{V}\right)=\left({\displaystyle \frac{k}{c}}\right){\left({\displaystyle \frac{\overline{V}}{c}}\right)}^{k-1}exp\left[-{\left({\displaystyle \frac{\overline{V}}{c}}\right)}^k\right]$$

(2)

where k and c are the shape and scale factors, respectively. Since the Weibull PDF is based on two parameters, it can better represent a wider variety of wind regimes and therefore is also one of the most commonly used probability distributions in wind data analysis [4].

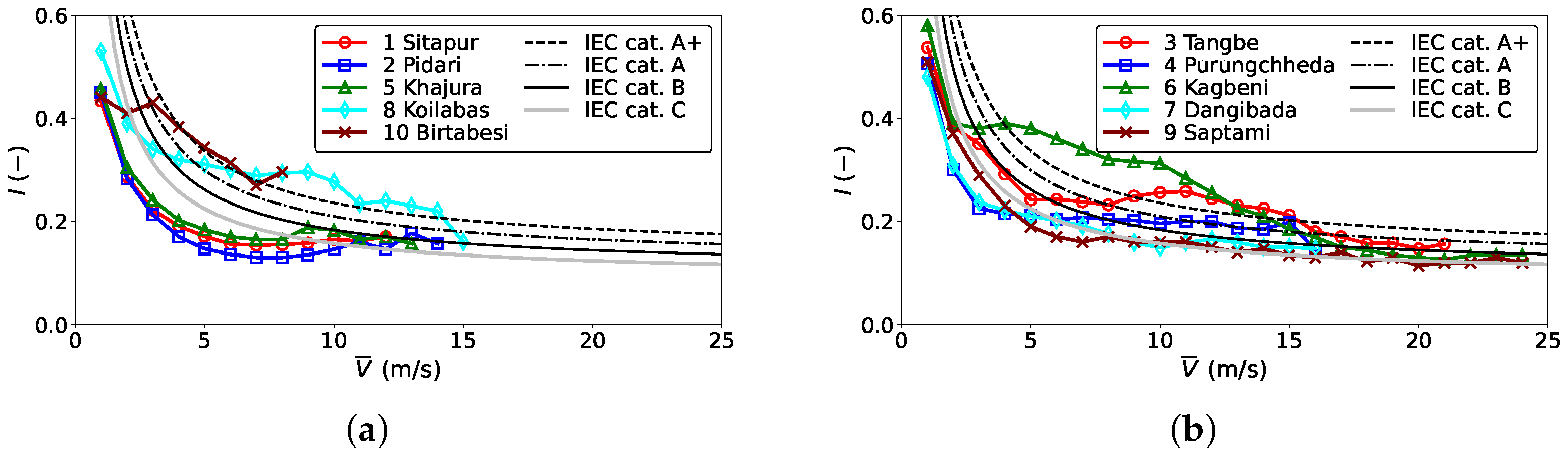
Fluctuations in wind speed are quantified using turbulence intensity (I), which is the ratio of the standard deviation ($\sigma$) to the mean wind speed ($\overline{V}$):

$$\begin{array}{cc}\hfill I& ={\displaystyle \frac{\sigma }{\overline{V}}}\hfill \end{array}$$

(3)

The study compares the measured turbulence intensities with those specified by the IEC standard. The turbulence intensity profiles in the IEC standard are given by

$$I_{\mathrm{IEC}}={\displaystyle \frac{I_{\mathrm{ref}}(0.75{\overline{V}}_{\mathrm{h}}+b)}{{\overline{V}}_{\mathrm{h}}}},$$

(4)

where $I_{\mathrm{ref}}$ is the reference value of the turbulence intensity, ${\overline{V}}_{\mathrm{h}}$ is the wind turbine hub height wind speed, and $b=5.6$ m/s. In the IEC standard, $I_{\mathrm{ref}}$ is defined as the turbulence intensity corresponding to the 70% quantile at 15 m/s. There are four categories of reference turbulence intensities, namely A + ($I_{\mathrm{ref}}=0.18$): very high turbulence; A ($I_{\mathrm{ref}}=0.16$): higher turbulence; B ($I_{\mathrm{ref}}=0.14$): medium turbulence; and C ($I_{\mathrm{ref}}=0.12$): lower turbulence. There is an additional wind turbine class, Class S, for which the wind speed and turbulence intensity are specified by the designer [15].

Turbulence intensity is also related to ABL stability, which is quantified using the Bulk Richardson number ($R_B$) in this study. $R_B$ is defined as

$$R_B={\displaystyle \frac{\frac{g}{\theta }\Delta \theta \Delta z}{{(\Delta V)}^2}}$$

(5)

where g is the acceleration due to gravity, $\theta$ is the mean potential temperature, $\Delta \theta$ is the potential temperature difference between vertical levels separated by $\Delta z$, and $\Delta V$ is the wind speed difference. By definition, $R_B$ is negative under unstable stratification and positive under stable stratification. A critical Richardson number of $R_{B,c}\approx 0.25$ is commonly used as a threshold above which atmospheric turbulence is suppressed [16].

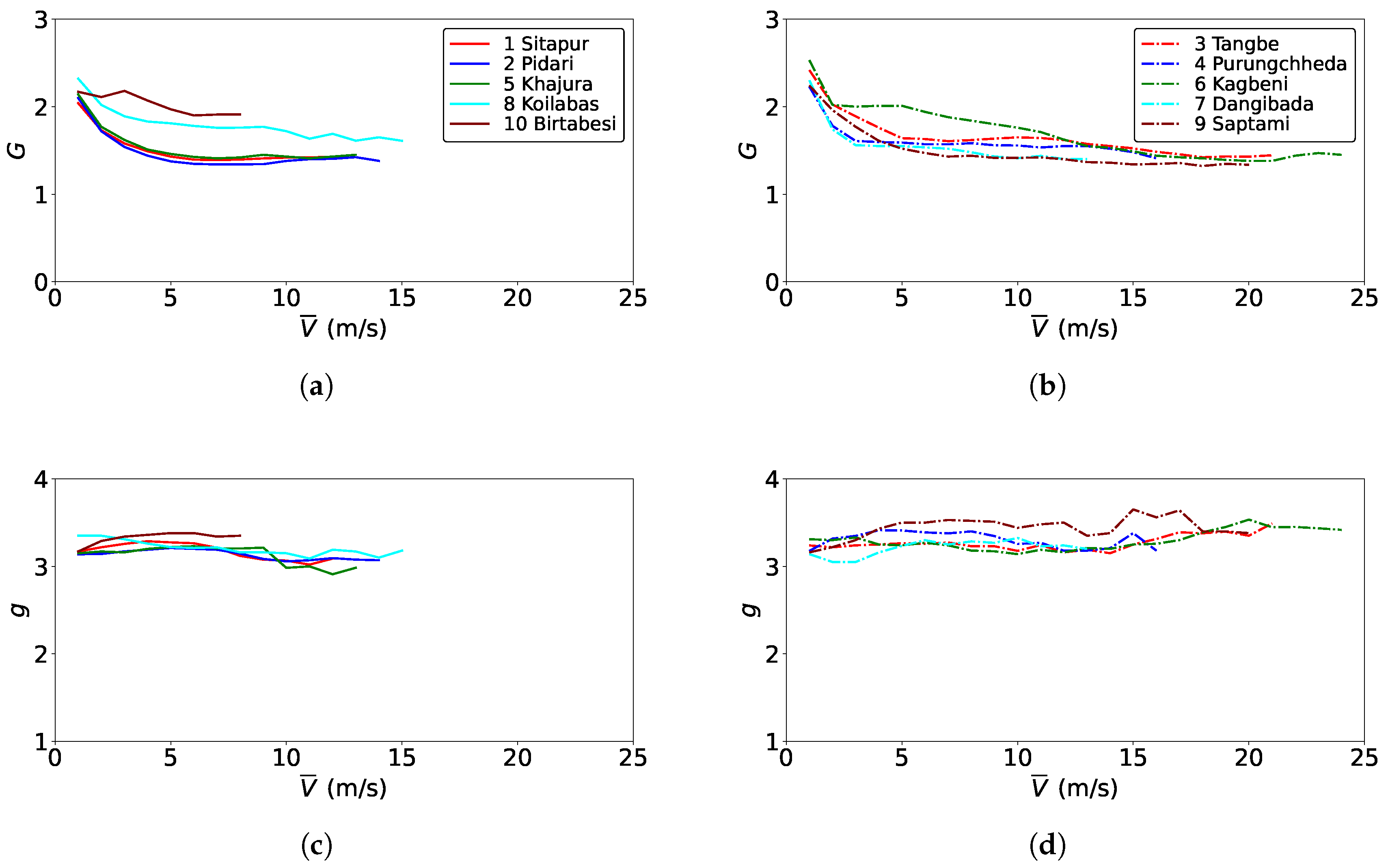
The peak gust wind speeds are required for estimating the extreme load that a wind turbine may experience at the site. To that end, gust factor (G) and peak factor (g) are used to define an expected value of peak wind speed ($\widehat{V}$) as required by the IEC standard [15].

$$\widehat{V}=(1+gI)\overline{V}=G\overline{V}.$$

(6)

Here, gust factor $G=\widehat{V}/\overline{V}$, peak factor $g=(\widehat{V}-\overline{V})/\sigma$, and $\sigma$ is the standard deviation.

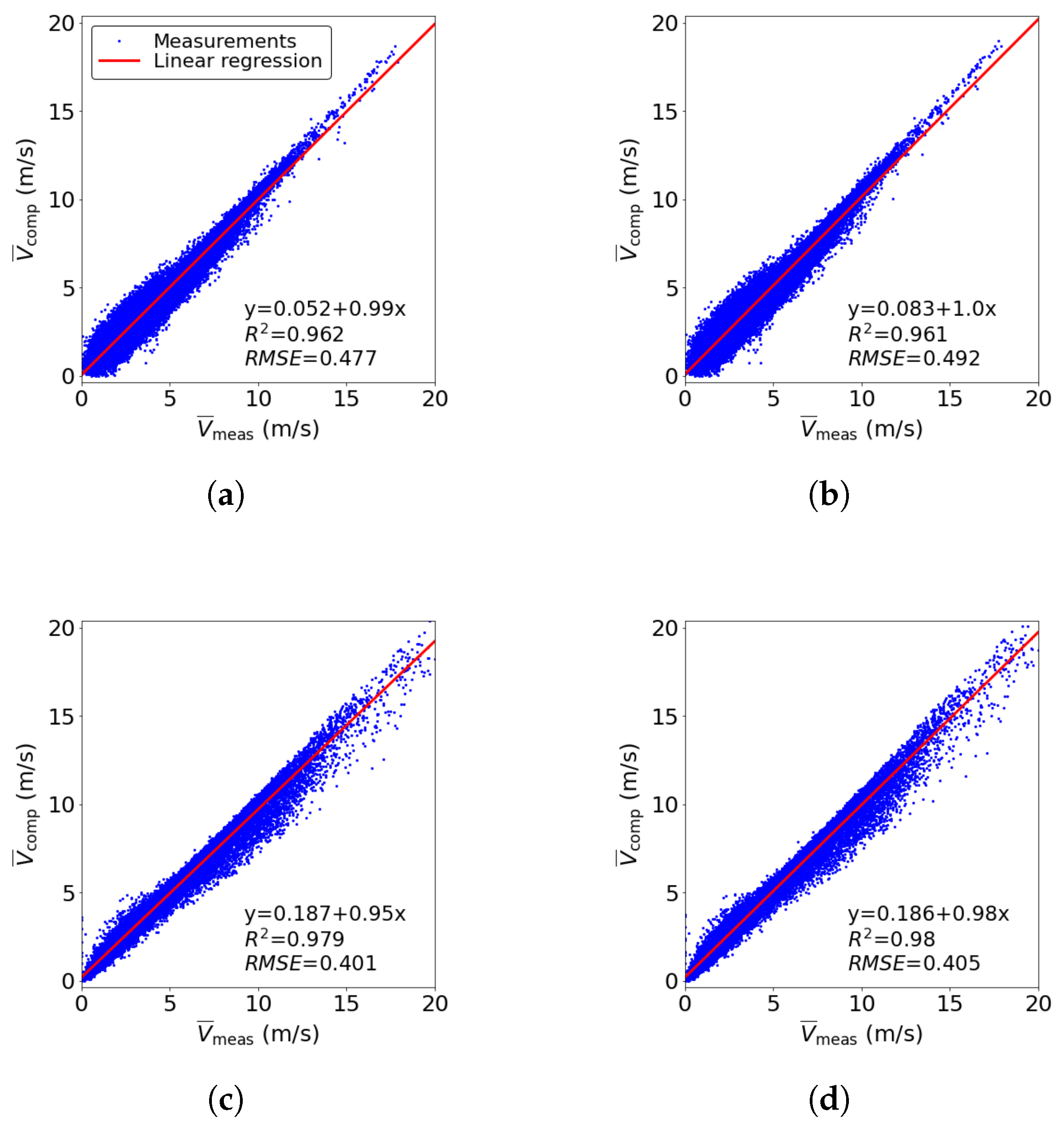
For accurate wind resource assessment, wind speeds at higher points (corresponding to the wind turbine hub height) can be extrapolated using logarithmic or power law profiles; i.e.,

$$\overline{V}\left(z\right)={\displaystyle \frac{u_{\tau }}{\kappa }}\ln \left({\displaystyle \frac{z}{z_0}}\right),$$

(7)

$${\displaystyle \frac{\overline{V}\left(z\right)}{\overline{V}\left(z_{\mathrm{ref}}\right)}}={\left({\displaystyle \frac{z}{z_{\mathrm{ref}}}}\right)}^{\alpha }.$$

(8)

In Equation (7), $u_{\tau }$ is a friction velocity, $\kappa =0.4$ is the von Karman’s constant, and $z_0$ is the surface roughness height. Similarly, in Equation (8), $z_{\mathrm{ref}}$ is a reference height at which measured wind speed $\overline{V}\left(z_{\mathrm{ref}}\right)$ is available, and $\overline{V}\left(z\right)$ is a wind speed that needs to be estimated. $\alpha$ is the power law exponent, and its value is strongly influenced by the nature of the terrain, atmospheric stability, and other thermal and mechanical parameters [17]. Logarithmic profile requires terrain roughness height, which is not always known. The study therefore uses power law representation of wind speed profiles. To that end, $\alpha$ values for each site are computed using wind data at two lower heights using

$$\alpha ={\displaystyle \frac{\ln \left(\overline{V}\left(z_2\right)/\overline{V}\left(z_1\right)\right)}{\ln \left(z_2/z_1\right)}}$$

(9)

where $z_1$ and $z_2$ are lower heights (80 m or below) for which measurement data is available.

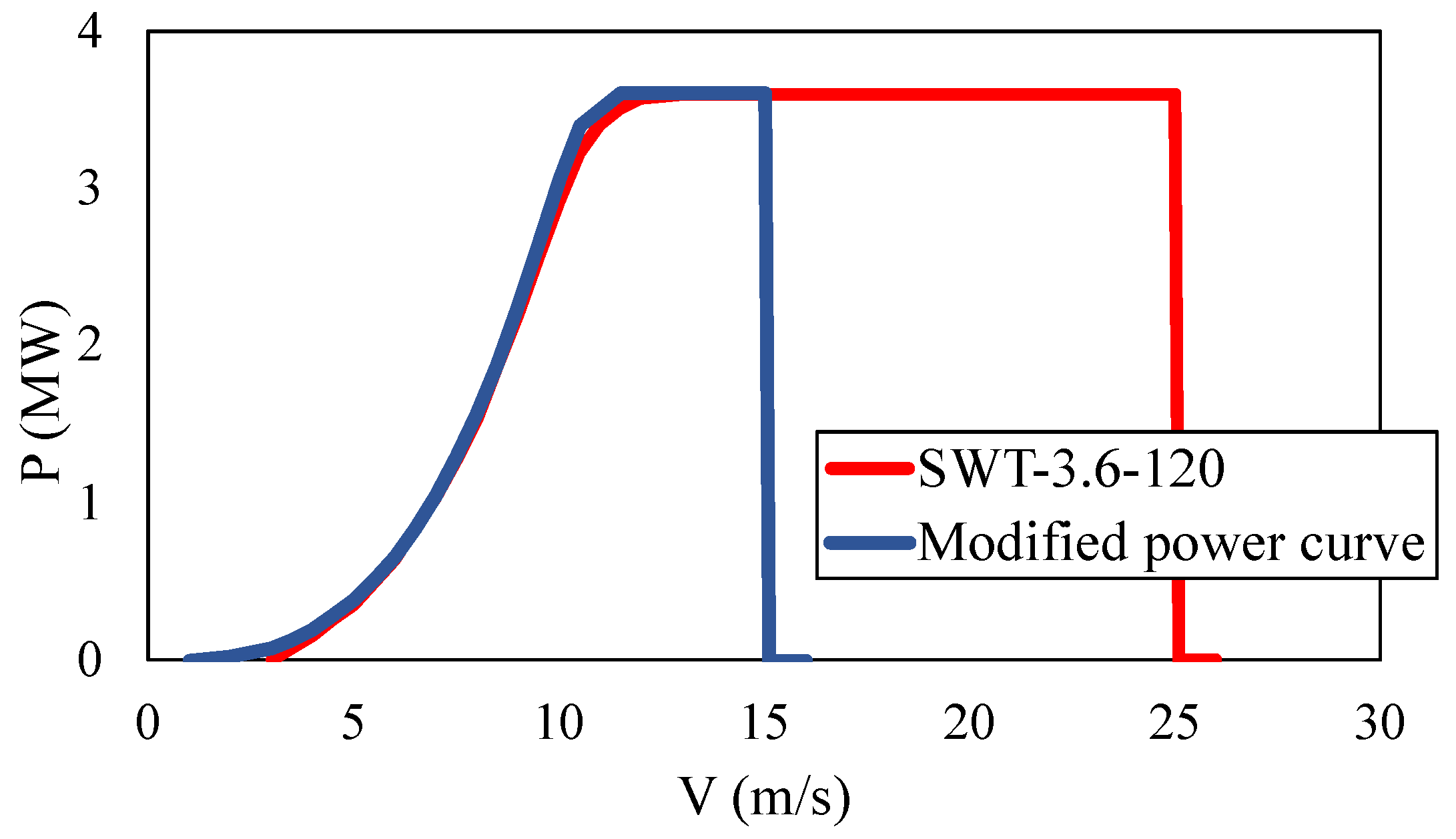
Next, the potential power outputs of the sites are computed using the power curve of SWT-3.6-120 wind turbine. This turbine has a rotor diameter (D) of 120 m and a rated power ($P_{\mathrm{r}}$) of 3.6 MW. Its cut-in ($V_{\mathrm{in}}$), rated ($V_{\mathrm{r}}$), and cut-out ($V_{\mathrm{out}}$) wind speeds are 3.5 m/s, 14 m/s, and 25 m/s, respectively. The power curve and other details about the turbine are accessible at thewindpower.net [18]. The power outputs of the sites are computed using

$$\begin{array}{cc}\hfill P\left(\overline{V}\right)=& \left\{\begin{array}{cc}0\hfill & \overline{V}<V_{\mathrm{in}},\hfill \\ \\ {\displaystyle \frac{P_{i+1}-P_i}{V_{i+1}-V_i}}(\overline{V}-V_i)+P_i\hfill & V_{\mathrm{in}}\le \overline{V}<V_{\mathrm{r}},\hfill \\ \\ P_{\mathrm{r}}\hfill & V_{\mathrm{r}}\le \overline{V}<V_{\mathrm{out}},\hfill \\ \\ 0\hfill & \overline{V}\ge V_{\mathrm{out}},\hfill \end{array}\right.\hfill \end{array}$$

(10)

where $P_{i+1}$ and $P_i$ are discrete power outputs of SWT-3.6-120 at wind speeds $V_{i+1}$ and $V_i$, respectively.

The available wind power ($P_{\mathrm{wind}}$), which is used in power duration curve analysis, is computed using the swept area of the SWT-3.6-120 wind turbine; i.e.,

$$P_{\mathrm{wind}}={\displaystyle \frac{1}{2}}\rho A_T{\overline{V}}^3$$

(11)

where $\rho =1.22\mathrm{kg}/{\mathrm{m}}^3$ is the air density, and $A_T=\pi /4D^2$.

3. Wind Resources and Terrain Complexity

This section presents the annual wind resources of the sites and also discusses the relationship between terrain complexity and the mean and turbulence characteristics of those sites. First, the mean wind speed distributions are discussed. Next, the turbulence statistics and peak wind speeds are presented. Finally, this section discusses the effect of terrain features on the power-law-based wind speed extrapolation at higher altitude.

3.1. Mean Wind Speed Distribution

Figure 4 shows the mean wind speed ($\overline{V}$) distributions at the sites for the one-year measurement period. Frequency of occurrences of $\overline{V}$ and their corresponding Weibull PDFs (see Equation (2)) are shown in the figure. The wind speed frequencies peak at $\overline{V}<5$ m/s at all ten sites. At six of the sites, peak frequency of occurrence is observed at $\overline{V}=3$ m/s. Sites 3 Tangbe and 6 Kagbeni have comparatively higher frequencies of occurrences for wind speed bins between 5 and 15 m/s. It can be observed that the Weibull PDFs reproduce wind speed distributions fairly accurately.

Figure 4. Frequency of occurrence of 10-min average wind speeds and the corresponding Weibull distribution of the PDFs. Weibull PDFs are represented by lines.

Table 2 summarizes the Weibull parameters and the annual average wind speeds at all sites. Sites with higher values of k (>2) are those where the variation in 10-min average wind speeds regarding the annual average wind speeds is small [4]. In this study, this is the case with most flat-terrain sites. On the other hand, sites with more complex terrain tend to have lower k values, indicating greater variability. In particular, at sites 3 and 6, 10-min average wind speeds show significant variation. Although most of the sites presented in this study can be considered to have low wind energy potential, site 6 Kagbeni has higher annual average wind speeds. Tangbe and Kagbeni, which are close to each other, have annual average wind speeds greater than 6.5 m/s. Similarly, sites 1, 2, and 9, with wind speeds higher than 4 m/s, can still be considered suitable for utility-scale wind turbines with larger rotor area, which can help to maintain higher capacity factor.

Table 2. Annual average wind speeds and Weibull shape and scale factors for wind data for all 10 sites.

Site No.	Site Name	Annual Average Wind Speed (m/s)	Shape Factor (k)	Scale Factor (c)
1	Sitapur	4.571	2.086	5.602
2	Pidari	4.419	2.222	5.601
3	Tangbe	6.659	0.748	5.016
4	Purungchheda	3.908	2.272	4.580
5	Khajura	3.525	2.153	4.306
6	Kagbeni	6.682	1.187	7.717
7	Dangibada	3.309	1.316	3.540
8	Koilabas	3.793	2.416	4.718
9	Saptami	4.653	1.962	5.307
10	Birtabesi	1.518	1.695	1.727

Figure 5 shows wind rose of the sites. It can be observed that most sites have one or two dominant wind directions. The dominant wind directions for sites 1 Sitapur, 5 Khajura, 9 Saptami, and 10 Birtabesi are E and ESE. These sites receive wind from the Bay of Bengal, which lies to the southeast of Nepal. Sites 3 Tangbe, 6 Kagbeni, and 7 Dangibada have complex mountainous terrain. In general, wind directions and wind speeds at these sites are dictated by the local climate and terrain features. Dominant wind directions at these sites are S, SSW, and SW.

Figure 5. Wind rose showing distribution of wind speeds and wind directions. Wind speed colobar in (10 Birtabesi ) is common for eight of the sites. For (3 Tangbe and 6 Kagbeni), corresponding colobars are included in those subfigures.

In order to evaluate whether the effect of seasonal variation or terrain feature is dominant, Figure 6 presents the hourly, daily, and monthly average wind speeds. Since sites 1 Sitapur, 6 Kagbeni, and 9 Saptami have the highest annual average wind speeds, the figure only shows times series of those three sites. Data availability at site 3 Tangbe is small, and therefore this site is not considered. One would expect that, if the effect of terrain is dominant, the difference between the short-term (e.g., hourly average) and long-term (e.g., monthly average) average wind speeds would be larger. This is observed at site 6 Kagbeni. As shown in Figure 7, this site is located at an elevation of 3036 m and is surrounded by mountainous terrain on all sides. In the SSW direction (i.e., the dominant wind direction), the maximum terrain variation within the 5 km radius from the met-mast site is 625 m. The variation is much higher when the entire area shown in the figure is considered. While a seasonal effect is observed in the monthly average time series, the difference is not significant when compared to the daily average. Site 9 Saptami has less complex terrain; thus, the variation in hourly, daily, and monthly average wind speeds is comparatively low. At site 1 Sitapur, the hourly, daily, and monthly averages of wind speeds follow the same trend, showing that the seasonal variation is dominant. There are spikes in the hourly average time series data, but they can be attributed to the atmospheric stability of the site. In the east direction (i.e., the dominant wind direction), the maximum terrain variation within a 5 km radius from the met-mast site is about 10 m. This variation is much smaller compared to the other two sites.

Figure 6. Time series of the hourly, daily, and monthly averaged wind speeds. (a) Site 1 Sitapur; (b) site 6 Kagbeni; (c) site 9 Saptami.

Figure 7. Distributions of the elevation fluctuation within the 5 km radius from the met-mast locations indicated by dark or gray markers. (a) Site 1 Sitapur; (b) site 6 Kagbeni; (c) site 9 Saptami.

The wind speed at site 6 Kagbeni exhibited interesting diurnal patterns; thus, we briefly discuss them here. Figure 8 shows the time series of 10-min average wind speeds for a week each in May and August. Almost every day, the wind speed begins to increase around 9:00 in the morning and reaches the daily peak of more than 15 m/s in the afternoon (usually between 14:00 and 15:00). After that, the speed gradually decreases until the next morning. With some exceptions from December to February, this cycle repeats throughout the year. The probable cause of this daily cycle involves the mountain and valley breezes induced by the local terrain features of the site. As shown in Figure 7, the site is characterized by a steep slope in the SSW direction, which coincides with the dominant wind direction (see Figure 5, 6 Kagbeni). During the daytime, solar heating warms the upper slopes more rapidly than the lower portions, causing the air near the upper slopes to rise and thus creating a local reduction in atmospheric pressure. This effect is evident in the pressure time series presented in Figure 8c,d. Consequently, air flows from the relatively higher-pressure region at the base of the slope toward the lower-pressure region at the met-mast location. At night, the process reverses: the slopes cool rapidly, producing denser higher-pressure air that flows downslope into the valley. However, wind speeds in Kagbeni are considerably weaker during nighttime. For a detailed discussion of mountain and valley breezes, see Stull [19].

Figure 8. Time series of 10-min average wind speeds and pressures from site 6 Kagbeni. (a,b) Wind speeds; (c,d) pressures. (a,c) From 1 May through 8 May 2019; (b,d) from 1 August through 8 August 2019.

3.2. Turbulence Intensity and Peak Wind Speed

Figure 9 shows the distribution of turbulence intensity as a function of wind direction for the three sites shown in Figure 6 above. Site 6 Kagbeni with the most complex terrain experiences the highest turbulence. It has turbulence range of 20–30% for more than 10% of the time. The occurrence frequency of the turbulence range of 15–20% is about 10%, while that of 10–15% is around 20%. In comparison, site 1 Sitapur experiences a lower turbulence intensity distribution. The site has 15–20% turbulence intensity range for 5% of the time, 10–15% for around 20% of the time, and 5–10% for around 15% of the time. The turbulence distribution at site 9 Saptami lies between that of sites 1 and 6. The higher turbulence intensities at site 6 can be attributed to the complex terrain. However, site 1, despite having flat terrain, also experiences a significant fraction of turbulence in the higher range of 10–15%. This is further discussed using ABL stability.

Figure 9. Turbulence rose showing distribution of turbulence intensity and wind directions. (a) Site 1 Sitapur; (b) site 6 Kagbeni; (c) site 9 Saptami.

Figure 10 presents the distribution of the Bulk Richardson number ($R_B$) as a function of mean wind speed at site 1 (Sitapur). A critical Richardson number, $R_{B,c}\approx 0.25$, is indicated by the horizontal dark line in the figure. Data with mean wind speeds $\overline{V}<0.5$ m/s are excluded due to potential measurement uncertainties at low wind speeds. The results clearly show a larger proportion of unstable points, particularly at higher wind speeds (e.g., $\overline{V}>5$ m/s). Over the one-year period, the atmospheric boundary layer (ABL) was unstable 41% of the time, stable for 33%, and near-neutral ($0<R_B<R_{B,c}$) for the remaining 26%. The higher frequency of unstable stratification suggests enhanced turbulence at the site despite having flat terrain.

Figure 10. Bulk Richardson number ($R_B$) as a function of mean wind speed at site 1 Sitapur. The horizontal line at $R_{B,c}=0.25$ is a critical Richardson number.

Figure 11 compares the measured turbulence intensities (I) with those specified by the IEC standard [15]. The measured turbulence intensities are calculated using the 90th percentile of the standard deviation for wind speed bins of 1 m/s interval. These 90th percentile lines are considered as representative turbulent characteristics of sites. IEC standard [15] also recommends this definition of turbulence intensities for the normal turbulence model (NTM), which is used for fatigue load calculation. Note that the IEC categories are not defined to precisely represent any specific site; instead, they are intended to represent many different sites. However, wind speed of 15 m/s is too high for defining $I_{\mathrm{ref}}$ values since many modern wind turbines predominantly operate at lower wind speeds (10 m/s or below). Furthermore, the NTM may have been designed based on data from flat- and moderately complex-terrain sites, making them less applicable to complex-terrain sites.

Figure 11. Comparison of the measured turbulence intensities against the IEC-specified turbulence categories [15]. (a) Flat-terrain sites; (b) complex-terrain sites. The measured turbulence intensities are computed from the 90th percentile of the standard deviation for the wind speed bin. Bin size is set to 1 m/s.

For clarity, Figure 11a presents turbulence intensities of sites with relatively flat terrain, while Figure 11b shows those of sites with complex mountainous terrain. Three of the flat-terrain sites have I values lower than IEC category C for $\overline{V}\le 10$ m/s, and for higher wind speeds I values roughly overlap with IEC category B line. Three of the complex-terrain sites appear to experience highly turbulent winds. In particular, sites 3 Tangbe and 6 Kagbeni have even higher turbulence intensities than IEC category A+ for a large wind speed range. This indicates that the IEC standard, which is commonly used for wind turbine design, may not be fully applicable for new sites; in particular, the specifications need to be modified for regions with extremely diverse terrain features. A potential model for turbulence intensity profiles based on terrain complexity parameters is proposed in the Discussion (see Section 5).

Figure 12 shows the gust and peak factors (see Equation (6)) for all 10 sites computed from the 90th percentile of the corresponding parameters for the wind speed bin. For clarity, (a) and (c) show the parameters for the sites with relatively flat terrain, while (b) and (d) present those for sites with complex mountainous terrain. It is interesting to observe that gust factors and peak factors at most of the sites converge to similar values at higher wind speeds. However, this is not the case for site 8 Koilabas and site 10 Birtabesi. Studies have shown that gust factor (G) values lie between 1.2 and 1.8, while the expected values of peak factor (g) generally lie between 3 and 4 (see, e.g., Holmes [20]). The IEC standard recommends $G=1.4$ and $g=3.5$. Table 3 summarizes gust and peak factors at the maximum mean wind speeds observed in Figure 12. Except for sites 8 and 10, gust factor values are roughly around 1.4. Similarly, peak factor values are around 3 for most of the flat-terrain sites and around 3.4 for most of the complex-terrain sites.

Figure 12. Gust and peak factors as a function of mean wind speed at all 10 sites. The profiles are obtained from the 90th percentile of the parameters for the wind speed bin. Bin size is set to 1 m/s. (a) Gust factors at flat-terrain sites; (b) gust factors at complex-terrain sites; (c) peak factors at flat-terrain sites; (d) peak factors at complex-terrain sites.

Table 3. Peak and gust factors for all 10 sites. Note that mean wind speeds are the speeds at which these parameters are obtained.

Site No.	Site Name	Mean Wind Speed $\overline{\mathit{V}}$ (m/s)	Gust Factor G	Peak Factor g
1	Sitapur	12	1.42	3.08
2	Pidari	14	1.38	3.07
3	Tangbe	21	1.44	3.49
4	Purungchheda	16	1.41	3.18
5	Khajura	13	1.45	2.98
6	Kagbeni	24	1.45	3.41
7	Dangibada	13	1.40	3.20
8	Koilabas	15	1.60	3.18
9	Saptami	20	1.33	3.38
10	Birtabesi	8	1.91	3.35

3.3. Power Law Exponent

One of the main challenges in wind resource assessment is the scarcity of wind data at higher elevations corresponding to the size of large utility-scale wind turbines, with hub heights exceeding 100 m and rotor diameters ranging from 100 to 200 m. This is particularly an issue in developing countries, where the installation of tall met-masts is not always economically feasible. Considering that the annual average wind speeds of most sites discussed in this study are below 5 m/s (see Table 2), wind turbines with larger rotor diameter need to be installed to achieve economically viable capacity factors. Thus, for accurate wind resource assessment, this study uses power law representation of wind speed profiles (see Equation (8)).

For the given site, $\alpha$ values in Equation (9) can be computed using one of the following two methods.

• Sector-averaged wind speed: Divide measured wind speeds into sectors corresponding to the wind directions. The current study employs 12 sectors, and each sector is of size 30°. Next, take mean of the wind speeds from each sector. The sector-averaged wind speeds are then substituted into Equation (9) to compute $\alpha$ for each corresponding sector.
• Sector-averaged $\alpha$: Compute $\alpha$ from the measured 10-min average wind speeds from the two lower heights using Equation (9). Divide the $\alpha$ values into sectors corresponding to the wind directions and then take average of the $\alpha$ from each sector.

In order to evaluate the uncertainties in the $\alpha$ values estimated using the two methods, the computed wind speeds are compared against the corresponding measured wind speeds. To that end, $\alpha$ is computed using wind speeds at 40 and 60 m. This is then used to estimate time series of wind speeds at 80 m. Figure 13 compares the estimated wind speeds with the measured data for the two methods of computing $\alpha$. Note that Sitapur is a flat-terrain site, while Saptami is a complex-terrain site. Due to higher uncertainty, wind speeds below 1 m/s are removed from the comparison. The two methods show comparable degrees of accuracy at the two sites. The slopes of the regression line are 0.99 and 1 at Sitapur, while at Saptami, the values are 0.95 and 0.98 for methods 1 and 2, respectively. Interestingly, the coefficient of determination ($R^2$) values are higher at Saptami, which features complex terrain. The RMSE ranges between 0.4 and 0.5 m/s in all four comparisons. However, method 1 shows slightly lower RMSE values at both sites.

Figure 13. Comparison of wind speeds obtained from the power law against the measured wind speeds at the height of 80 m. (a) Sitapur: from sector-averaged wind speed; (b) Sitapur: from sector-averaged $\alpha$; (c) Saptami: from sector-averaged wind speed; (d) Saptami: from sector-averaged $\alpha$.

The uncertainties in the estimated wind speed using the two methods are comparable, although method 1 demonstrates slightly better accuracy in terms of RMSE. This study therefore uses method 1, i.e., $\alpha$ computed from the sector-averaged wind speeds. Table 4 lists the $\alpha$ values from the 12 sectors at all 10 sites. Note that the $\alpha$ values in the table are estimated using wind speeds measured at 60 m and 80 m. This approach enables a more accurate extrapolation of the wind speed at the hub height of 100 m compared to using $\alpha$ values derived from measurements at 40 m and 60 m. One can appreciate that, even for the same site, $\alpha$ varies significantly with wind direction. For flat terrain and during neutral atmospheric stability, $\alpha$ is supposed to be around 1/7 (≈0.14) (see Manwell et al. [4]). However, with some exceptions, $\alpha$ is different for most sectors even at flat-terrain sites. For example, at site 1 Sitapur, $\alpha$ is 0.3 for the sector ${105}^{\circ }-{135}^{\circ }$.

Table 4. Power law exponent ($\alpha$) for all 10 sites. $\alpha$ values are computed from the sector-averaged wind speeds at 60 and 80 m heights.

Site No.	Site Name						Sectors (°)
		345-15	15-45	45-75	75-105	105-135	135-165	165-195	195-225	225-255	255-285	285-315	315-345
1	Sitapur	0.22	0.44	0.38	0.30	0.19	0.20	0.47	0.49	0.33	0.44	0.61	0.52
2	Pidari	0.25	0.26	0.33	0.24	0.19	0.22	0.34	0.18	0.28	0.42	0.38	0.29
3	Tangbe	0.05	0.12	0.11	0.0	0.34	0.12	0.02	0.0	0.27	0.0	0.01	0.0
4	Purungchheda	0.17	0.17	0.14	0.18	0.18	0.19	0.13	0.17	0.08	0.25	0.31	0.18
5	Khajura	0.34	0.31	0.14	0.25	0.37	0.27	0.12	0.42	0.23	0.29	0.44	0.45
6	Kagbeni	0.11	0.05	0.0	0.0	0.11	0.0	0.0	0.0	0.0	0.0	0.1	0.0
7	Dangibada	0.0	0.07	0.17	0.09	0.0	0.07	0.0	0.12	0.01	0.0	0.0	0.0
8	Koilabas	0.0	0.0	0.48	0.6	0.4	0.22	0.27	0.19	0.4	0.41	0.28	0.2
9	Saptami	0.11	0.05	0.02	0.25	0.18	0.02	0.02	0.25	0.13	0.14	0.18	0.16
10	Birtabesi	0.01	0.0	0.0	0.0	0.0	0.0	0.0	0.13	0.1	0.08	0.09	0.03

4. Power Potential Estimation

Next, we compute the potential power outputs of the sites for the measured wind data using the SWT-3.6-120 as a reference turbine. The current study considers a turbine hub height of 100 m and extrapolates the wind speeds to this height using the power law exponent ($\alpha$) values listed in Table 4.

Figure 14 shows the power distribution at all 10 sites. The frequency of occurrence for 0 MW, i.e., when turbine is not in the power production mode, is dominant at all 10 sites. Except for Tangbe and Kagbeni, the largest power production bin is 0.5 MW, thus indicating that the sites have low wind energy potential. Only four sites—Sitapur, Tangbe, Kagbeni, and Saptami—experience sufficiently high wind speeds to generate rated power of 3.6 MW. Although most of the sites presented in this study can be considered to have low wind energy potential, site 6 Kagbeni has higher annual average wind speeds. Similarly, sites 1, 2, and 9, with wind speeds higher than 4 m/s, can still be considered suitable for utility-scale wind turbines with larger rotor areas, which can help to maintain a higher capacity factor.

Figure 14. Power distribution of all 10 sites for the SWT-3.6-120 wind turbine. Bin size is set to 0.5 MW.

Table 5 summarizes the energy production and capacity factors of the sites. Note that we have computed the capacity factors for the time length for which wind speed data was available. While this is close to the annual capacity factor for most sites, in the case of Tangbe—where data availability is less than 50% (see Figure 2)—the number may not represent the actual annual capacity factor. Nevertheless, Tangbe being close to Kagbeni, the capacity factor from the latter can be used as a representative value. The Kagbeni site is promising for wind energy development, with a capacity factor of 34%. Among the remaining sites, Sitapur, Pidari, and Saptami have capacity factors of more than 15%. This value is still low, and, for profitable land-based wind energy development, a minimum capacity factor of around 25% is typically expected during the wind resource assessment phase. However, the 25% value is based on the assessment of wind turbine installation in developed countries. For a lower levelized cost of energy (LCOE), which may be expected from a developing country, even lower capacity factors can be profitable.

Table 5. Annual energy production and capacity factors for all 10 sites estimated using wind speeds at 100 m height. The SWT-3.6-120 is used as a reference wind turbine [18].

Site No.	Site Name	Power Density $\mathbf{W}/{\mathbf{m}}^2$	Energy Production (MW.h)	Capacity Factor (%)
1	Sitapur	58.5	5200	17
2	Pidari	52.8	4666	15
3	Tangbe	180.8	1087	41
4	Purungchheda	36.5	3191	10
5	Khajura	26.8	2710	9
6	Kagbeni	182.7	10407	34
7	Dangibada	22.2	3141	10
8	Koilabas	33.4	2928	9
9	Saptami	61.7	4380	17
10	Birtabesi	2.14	270	1

It should be noted that the present analysis does not account for wake interactions arising when multiple wind turbines are installed; energy production has been evaluated only for a single turbine. On flat terrain, wake interactions are generally expected to reduce overall energy production. Previous studies have reported that the power output of downstream turbines can decrease by up to 40% [21]. In contrast, on complex terrain, wind farm layouts can be optimized to exploit speed-up effects over topographic high points and to alter wake trajectories [22]. Addressing these effects requires dedicated investigations that combine complex terrain features with wind farm layout considerations in high-fidelity simulations for each site.

Figure 15 shows the power duration curves describing the number of hours in the measurement period (one year in the current study) for which the wind power and power output of the reference turbine are equal to or higher than each particular value. Turbine power is obtained from the measured wind speeds, and the corresponding power output is determined using the power curve. For reference, the available wind power ($P_{\mathrm{wind}}$) is also shown. Of the 10 sites, only Kagbeni is capable of producing the rated power of 3.6 MW for a significantly long duration (more than 1800 h). However, the total duration for which the wind turbine could have generated 1 MW or more is more than 1500 h for the three sites with capacity factors greater than 15% in Table 5.

Figure 15. Power duration curve of all 10 sites for the SWT-3.6-120 wind turbine.

5. Discussion

The analysis of mean wind speeds revealed that seasonal variations predominantly influence the wind characteristics at flat-terrain sites, whereas terrain-induced effects play a more significant role at complex-terrain sites, leading to localized atmospheric conditions. An example of such a localized effect observed in this study is the diurnal cycle of mountain and valley breezes at site 6 Kagbeni. This strong dependence of atmospheric behavior on terrain features has direct implications for wind speed modeling at these sites.

For reference, Figure 16 compares the annual average wind speeds listed in Table 2 against the wind speeds obtained from the Global Wind Atlas (GWA) [23]. The GWA uses WRF-based mesoscale simulation followed by WAsP-based microscale modeling to estimate wind speeds. The wind speed estimates from the GWA exhibit trends consistent with the measurements. The GWA-estimated wind speeds at sites 1, 2, and 5—located in flat plains—show errors of approximately 5%. In contrast, at sites 3, 4, 6, 7, and 9, which are characterized by highly complex terrain, the errors increase to about 10–15%. The comparison shows that the agreement is stronger in regions with relatively flat terrain, while discrepancies increase at sites with complex topography. Therefore, direct field measurements remain essential for accurately assessing wind resources and for improving the reliability of modeling tools such as WRF, especially for highly complex-terrain sites.

Figure 16. Comparison of annual average wind speeds for all 10 sites against the wind speed obtained from the Global Wind Atlas. (a) Bar diagram; (b) distribution plot with a linear regression line.

However, the investigations are based solely on one set of field measurement data. Comparison with previous studies—which could have enhanced the reliability of the presented analyses—is limited as there are currently no significant studies on wind resource characterization in Nepal. In this regard, the present study serves as an important reference for future wind resource assessments and wind energy project development in the country.

Regarding the turbulence intensities, the values observed at flat-terrain sites are lower, whereas those at complex-terrain sites are higher than the IEC profiles. This indicates that the IEC standard, which is commonly used for wind turbine design, should be revised to better account for local terrain features and atmospheric conditions. The relation between turbulence intensities and site complexity and how that can be used to modify the existing IEC standard is further discussed. To that end, Equation (4) can be rewritten as

$$I_{\mathrm{IEC}}=a_c+{\displaystyle \frac{b_c}{{\overline{V}}_{\mathrm{h}}}},$$

(12)

where $a_c=0.75I_{\mathrm{ref}}$ and $b_c=I_{\mathrm{ref}}b$ are constants. These two parameters are obtained from the fitting to the measured turbulence profiles (c.f. Figure 11). Table 6 compares $a_c$ and $b_c$ values against the standard deviation of the elevation fluctuation (${\sigma }_z$) for the three sites. ${\sigma }_z$ has been normalized by the turbine hub height ($z_h$), which is 100 m in this study. As can be expected, ${\sigma }_z$ is large for complex-terrain sites and small for flat-terrain sites. One can appreciate that both $a_c$ and $b_c$ increase with site complexity. Therefore, instead of specifying turbulence categories, the IEC standard can redefine turbulence profiles using site complexity parameters such as ${\sigma }_z$.

Table 6. Elevation fluctuation and parameters $a_c$ and $b_c$ in Equation (12).

Site No.	Site Name	${\mathit{\sigma }}_{\mathit{z}}/{\mathit{z}}_{\mathit{h}}$	${\mathit{a}}_{\mathit{c}}$	${\mathit{b}}_{\mathit{c}}$
1	Sitapur	0.061	0.12	0.3
6	Kagbeni	3.2	0.25	0.625
9	Saptami	2.9	0.15	0.375

As an extension of the current study, we plan to develop a model to quantify terrain complexity based on the vertical and horizontal extent of the terrain features. The standard deviation of the elevation fluctuation and terrain slope can be two potential parameters. These parameters can be computed for the circular area around the target point and can have a radius of 5 or 10 times the wind turbine hub height. Terrain slope can also be used to estimate the length scale of the terrain type for the given sector. It will also be interesting to propose models of mean wind speed and turbulence intensity profiles based on these complexity parameters. Such models will be useful for performing initial wind energy potential evaluation as well as a rough cost analysis for sites where measured data is not available.

Measured data can also be coupled with geostatistical interpolation schemes or machine learning techniques to develop a regional wind resource map. However, in order to tune and validate these models, a large amount of field data will be necessary. Therefore, it will be important to search and collect openly available data from other sites around the world.

From the power potential analysis (see Figure 14), it is clear that most of the sites presented in this study exhibit relatively low wind energy potential. However, many emerging wind energy markets worldwide are also characterized by similar low-wind-speed conditions. Therefore, utility-scale wind turbines must be adapted to generate power more efficiently under such conditions. This is an active area of research, focusing primarily on reducing the cut-in wind speed and increasing the power coefficient [24].

To evaluate the potential benefits of such design modifications, this study introduces a modification of the SWT-3.6-120 turbine power curve, as shown in Figure 17. In the modified curve, the cut-in wind speed is reduced from 3.5 m/s to 1.5 m/s, the rated wind speed from 14 m/s to 10.5 m/s, and the cut-out wind speed from 25 m/s to 15 m/s. Note that the modified turbine maintains the same power coefficient characteristics as the original model; in other words, no improvement in aerodynamic efficiency is assumed. With this modification, the annual energy production at site 1 Sitapur increased from 5200 MW.h to 5410 MW.h—an improvement of approximately 4.2%. Further gains may be achieved if the turbine were fully optimized for low-wind-speed operation. Interestingly, reducing the cut-out wind speed to 15 m/s has a negligible impact on energy production. This is because the occurrence frequency of higher wind speeds is extremely low at most of the sites in this study (see Figure 4), and it should be the case for other sites characterized by lower wind speeds. An additional advantage of lowering the cut-out wind speed is that the turbine would no longer need to be designed to withstand higher wind speeds (e.g., 25 m/s). Consequently, the structural loads and material requirements could be reduced, potentially lowering the LCOE.

Figure 17. Power curve of SWT-3.6-120 and modified power curve with reduced cut-in, rated, and cut-out wind speeds.

6. Conclusions

This study has evaluated the effects of terrain features on local wind characteristics in a region with extremely diverse terrain. To that end, wind data from ten meteorological masts installed across different regions of Nepal were used to conduct a detailed assessment of wind resources and to estimate the wind energy potential at these sites.

At complex-terrain sites, wind characteristics are primarily influenced by local terrain features, whereas, at flat-terrain sites, seasonal variations are more dominant. This pattern is evident in both the Weibull probability density functions and in the comparisons of hourly, daily, and monthly average wind speeds. Clear differences were also observed in turbulence characteristics between the flat-terrain and complex mountainous sites. The complex-terrain sites experienced higher turbulence intensity over longer periods compared to the flat-terrain sites. However, atmospheric boundary layer (ABL) stability also plays an important role and can significantly alter turbulence characteristics, particularly at flat-terrain sites. At most flat-terrain locations, the turbulence intensities were even lower than the profiles defined by the IEC standard, whereas some complex-terrain sites experienced higher turbulence intensities than the IEC profiles.

In order to estimate the potential power output of the sites, the power characteristics of the SWT-3.6-120 utility-scale wind turbine were used. Since the hub height of the turbine was considered to be 100 m, wind speeds from the lower height of 80 m had to be extrapolated using the power law. The capacity factor at site 6 Kagbeni was significantly high at 34%. Sites 1 Sitapur and 9 Saptami, with comparatively stronger wind, demonstrated capacity factors of 17%, while all the other sites had smaller values. In this study, the power potential analysis does not account for wake interactions that may arise when multiple turbines are installed at a site. At flat-terrain locations, wake interactions are expected to reduce the overall energy production, whereas, at complex-terrain sites, topographic effects are likely to be more dominant. Addressing wake effects, however, requires future investigations employing site-specific high-fidelity simulations.