Abstract
The G-modified Helmholtz equation is a partial differential equation that enables us to express gravity intensity g as a series of spherical harmonics having radial distance r in irrational powers. The Laplace equation in three-dimensional space (in Cartesian coordinates, is the sum of the second-order partial derivatives of the unknown quantity equal to zero) is used to express the Earth’s gravity potential (disturbing and normal potential) in order to represent other useful quantities—which are also known as functionals of the disturbing potential—such as gravity disturbance, gravity anomaly, and geoid undulation as a series of spherical harmonics. We demonstrate that by using the G-modified Helmholtz equation, not only gravity intensity but also disturbing potential and its functionals can be expressed as a series of spherical harmonics. Having gravity intensity represented as a series of spherical harmonics allows us to create new Global Gravity Models. Furthermore, a more detailed examination of the Earth’s isogravitational surfaces is conducted. Finally, we tabulate our results, which makes it clear that new Global Gravity Models for gravity intensity g will be very useful for many geophysical and geodetic applications.
Keywords:
gravity; gravity anomaly; gravity disturbance; vertical gradient of gravity; disturbing potential; spherical harmonics; isogravitational surfaces MSC:
35A09; 35C10; 35J25; 33C05; 33C75
1. Introduction
Spherical harmonics are important in many theoretical and practical applications (electromagnetic fields, electron configurations, gravitational fields, geoids, computer graphics, cosmic microwave background radiation, etc.). Some of these applications are briefly mentioned in this work. Spherical harmonics have been extensively studied and are widely applicable due to their numerous convenient properties. In computer graphics [1], they are quite useful since they share many of the same strengths as Haar wavelets, and there are techniques that bridge the gap between them. This enables the representation of low-frequency and high-frequency functions. Additionally, in [2,3,4], they are used in the formation of a realistic global lightning model.
Gravity potential is a quantity expressed as a series of spherical harmonics. This series is utilized for formulating Global Gravity Models and Local Gravity Models. A Global Gravity Model [5], also referred to as a Global Geopotential Model, serves as a mathematical representation of the external gravitational potential of a celestial body. Here, we focus on the scenario where the Earth is the attracting body. The use of Global Gravity Models enables us to determine all the related gravity field functionals—for example, gravity vectors and gravity.
It is important to note that these models [6,7,8,9] are crucial as they offer valuable insights into Earth’s features, including geoid undulation, gravity anomalies, gravity disturbances, and vertical deflection. It is worth mentioning that these models have wide-ranging applications, including orbit determination, inertial navigation for airplanes and missiles, oceanographic studies of ocean circulation, and geophysical research into density distributions.
The Earth’s magnetic vector field [10] is related to the scalar geomagnetic potential that obeys the Laplace equation and can be represented as a series of spherical harmonics. The applications of the geomagnetic potential [11,12] are incredibly vast; they range from studying hydromagnetic wave propagation and ionospheric currents to investigating tides, monitoring changes in tropospheric weather, and exploring the Earth’s crust.
The intensity of gravity and electrostatic forces can be mathematically expressed as a series of spherical harmonics. This series arises from the solution of the G-modified Helmholtz equation. The intensity of electrostatics plays a critical role in a diverse array of applications [13], ranging from heat and mass transfer to the synthesis of nanomaterials and the reduction inCO2 emissions. Furthermore, spheroids [14,15,16] have been employed to address electromagnetic scattering problems and analyze electrostatic interactions between spheroidal particles in different scenarios. The intensity of gravity is very valuable in various applications. It plays a crucial role [17,18] in detecting seismic faults, estimating simple spherical structures within the Earth, determining geoid and quasi-geoid (which define the physical shape of the Earth and reference surface of physical heights), [19] analyzing sea surface topography, understanding the structure of the lithosphere, inferring the thickness of floating ice, and [20] even detecting archaeological structures during exploration.
In this study, we present a novel method for determining the disturbing potential that is independent of the Laplace equation. By expressing [21] gravity anomaly and gravity disturbance as series of spherical harmonics using the modified Helmholtz equation (with the radial distance, r, raised to irrational powers), we can effortlessly determine the disturbing potential through a simple partial differential equation. This new approach allows us to represent relative quantities associated with gravitational potential (i.e., its functionals) in a new series of spherical harmonics. In addition, by expressing gravity intensity as a series of spherical harmonics, we can conduct a more thorough analysis of isogravitational surfaces. It is important to emphasize that, in this context, the Earth is regarded as a non-rotating body.
2. Laplace Equation, Disturbing Potential, and Relative Quantities
Focusing on the case of the Earth, the disturbing potential T [22] (which is the difference between Earth’s actual gravity potential W and the normal potential U generated by a suitable ellipsoid of revolution) is a solution of the Laplace equation.
The concept of disturbing potential holds significant importance, as it is vital for calculating the geoid undulation N, which represents the distance between the geoid’s surface and the surface of a suitable ellipsoid of revolution. Additionally, it plays a crucial role in determining other important quantities such as gravity disturbance δg, gravity anomaly Δg, and deflections of the vertical. There are three classical problems [5] for determining the disturbing potential T from boundary values on a sphere: (a) the Poisson problem, (b) the Hotine problem, and (c) the Stokes problem.
The first problem is a Dirichlet problem on a sphere with a radius of R, where the values of T are given on the sphere. The second problem, as a spherical approximation, involves solving a Neumann problem. In this problem, we are provided with the values of gravity disturbance δg (representing the radial derivative of the disturbing potential T). The third problem (as a spherical approximation) is a Robin problem in which the values of gravity anomaly Δg are given on the geoid fulfilling the following relation:
Instead of solving boundary value problems to determine the disturbing potential T, we use Global Geopotential Models (GGMs). A Global Geopotential Model [5,23] is a mathematical expression that enables the calculation of the disturbing potential through spherical harmonic expansion. The harmonic series of a GGM is finite and also provides a collection of mathematical expressions, numerical values, and algorithms. With these tools, users can easily perform computations to determine numerical values of quantities associated with the disturbing potential (such as gravity disturbance and gravity anomaly). Additionally, these computations enable the evaluation of specific errors that are linked to these quantities.
We present some finite series expressions [22,23,24], in spherical coordinates (r, θ, λ) (θ is measured from the z-axis, (normalized coefficients).
Geoid undulation is calculated by
where γ is the value of normal gravity [22] on the ellipsoid, G is the gravitational constant and M is the mass of the Earth. Components of the deflection of the vertical [23] are
In Equations (7) and (8) normal gravity [22] is determined on a suitable point which is located on an appropriate equipotential surface of the normal gravity field. The disturbing potential, T, is a quantity that cannot be directly measured. Therefore, other measurable quantities are required to determine its value. However, we will demonstrate an alternative method for determining T in the following paragraph.
3. G-Modified Helmholtz Equation, Disturbing Potential, and Relative Quantities
Assuming that the gravity disturbance δg is a continuous function on the surface of the geoid, we can determine it by solving the Dirichlet problem that involves the G-modified Helmholtz equation.
The expression of gravity disturbance in spherical harmonics [21] is as follows:
According to [22], on the surface of the geoid, which, as a spherical approximation, corresponds to a sphere of radius R, we can derive
Putting
The series in Equation (13) becomes
Thus,
and the coefficients [22] of series (17) are equal to
Hence, the desirable expression for gravity disturbance is
Gravity anomaly can also be identified through a similar Dirichlet problem if the values of gravity anomaly Δg are known on the geoid’s surface.
The expression of gravity anomaly is
Now, we are ready to find the disturbing potential. The function T will be determined [22] from the following partial differential equation:
The solution of this partial differential equation is
The function fδg is an arbitrary function, but it can be determined from the following boundary condition [22]:
Substituting the necessary quantities from Equations (21), (23), and (25) we have
Therefore, the function fδg is expressed as a series of spherical harmonics.
The coefficients of the above series are equal to
Finally, the disturbing potential T is given as
The procedure of finding Equation (31) can be named the alternative gravimetric determination of the disturbing potential.
The expression for the disturbing potential given by Equation (31) can be replaced with a finite series of spherical harmonics in order to develop a new Global Geopotential Model. Following geodetic terminology, in this model, the disturbing potential is a functional of gravity disturbances. For n = Nmax, Equation (31) becomes a finite series and allows us to determine the third-order partial derivatives of the disturbing potential in spherical coordinates. These derivatives can be expressed in different Cartesian systems [25] and effectively used in various geophysical studies and explorations.
In Equation (31), for r = R, the disturbing potential is determined on the surface of the geoid. The result is as follows:
The above formula can be written as
Hence, on the surface of the geoid, the disturbing potential is equal to the difference between gravity disturbance and gravity anomaly, multiplied by R/2.Using Equation (6), the geoid undulation can be expressed in a new alternative form.
Equations (33) and (34) also represent the significance of gravity disturbance and gravity anomaly (determined by measurements). An interesting theoretical result occurs if δg and Δg are substituted with their equals.
Therefore, if the value of normal gravity γ is known on the surface of the geoid, then the disturbing potential (on this surface) and the geoid’s undulation are known (again as a series of spherical harmonics).
The intensity of gravity g is a highly significant quantity that can be expressed as a series of spherical harmonics.
This formula is much more manageable than the typical formula.
where VE stands for the Earth’s Newtonian gravity potential. Equation (33) is also valuable for various conversions between different types of heights, such as orthometric height correction and dynamical correction.
As a spherical approximation, the vertical gradient of gravity is equal to the radial derivative of gravity intensity; thus [22] (we remind that we are dealing with a non-rotating Earth),
where J is the mean curvature of the relative equipotential surface.
By combining Equations (39) and (40), we can determine the mean curvature of the equipotential surfaces of the Earth’s gravity field.
4. Study of the Earth’s Isogravitational Surfaces
Equation (37) enables us to investigate the isogravitational surfaces of the Earth’s gravity field. On these surfaces, the value of gravity remains constant. As indicated in [26], isogravitational surfaces closely resemble spheres. In order to conduct a localized study of the isogravitational surfaces, we initiate the following transformation:
The Cartesian system (X, Y, Z) [22] has its center at the Earth’s center of gravity, the Z-axis coincides with the Earth’s mean axis of rotation, the X-axis is on the meridian plane of Greenwich pointing outwards, and the Y-axis makes the system right-handed. Then,
The unit normal vectors are
Let P an arbitrary point with spherical coordinates (rP, θP′, λP). We define a second Cartesian system (x, y, z), such that its center is at point P, and the z–axis has the same direction asthe vector ε1 (Equation (43)). Τhe x-axis is tangent to the meridian of a sphere of radius rP and center the Earth’s center of gravity, and it has the same direction as the vector ε2. The y-axis makes the system right-handed. The transformation between (X, Y, Z) and (x, y, z) [27] is
The first- and second-order partial derivatives of gravity intensity expressed in the (x, y, z) system [27] are given as follows:
The above equations (Equation (47) to Equation (55)) are referred to as point P. Due to the non-zero partial derivative of g with respect to r, a parameterization of the isogravitational surface [21] for a small region near point P is
The function z is not known, but its partial derivatives can be determined. Hence, the coordinate vectors are
The normal vector is
The unit normal vector is
Fundamental elements [21] of the first kind are
Fundamental elements of the second kind are
Let P be a point far away from the Earth, i.e., rP takes a large value. As we slowly approach Earth along the polar axis r = rP, gx and gy are small quantities. Thus, Equation (61) to Equation (66) become
At point P, the principal curvatures, k1 and k2, of the isogravitational surface [28] are the roots of the following equation:
Hence,
The mean and Gaussian curvatures of the isogravitational surface at point P are equal to
If point P is far away from the Earth, Equations (76) and (77) become
Therefore, for large values of r, the isogravitational surfaces are spheres of radius rP. Approaching the Earth along polar axis r = rP, the mean curvature is given by Equation (76) and the Gauss curvature is derived from the following relation:
The Gauss curvature at point P characterizes the shape of the isogravitational surface around that point. The second term of Equation (80) describes the deviation of the isogravitational surface’s shape from that of a sphere. As point P gradually approaches Earth (with a small δr), isogravitational surfaces form closed surfaces with a positive Gauss curvature. Around point P, the shape of the isogravitational surface is an elliptic paraboloid.
Figure 1 shows the shape of the isogravitational surface around point P which is a paraboloid. The shape of isogravitational surfaces becomes more complicated when point P is close to the Earth. Assuming the geoid represents the true shape of the Earth, let P be a point on the geoid, particularly at the North Pole (θ’ = π/2). The isogravitational surface passing through point P cannot intersect the geoid. Hence, both surfaces are tangent at point P, i.e., they have common tangent plane. Around point P, the z - coordinates of the neighboring points have a positive sign.
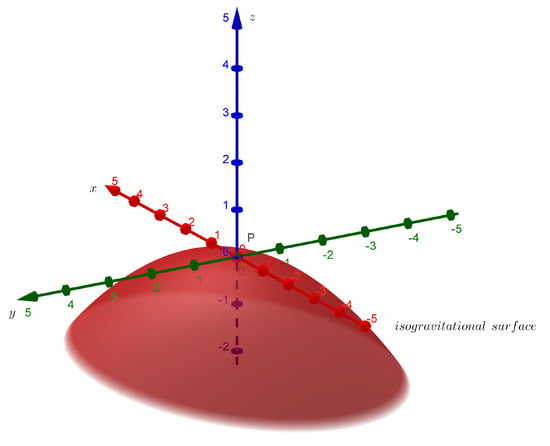
Figure 1.
Isogravitational Surface.
Let γ be a curve on the isogravitational surface that is formed by the intersection of the isogravitational surface and a meridian plane. Since isogravitational surfaces are closed surfaces, this means that as we move further from point P along the curve γ, we reach a point A where the Gauss curvature is positive and the neighboring points of the isogravitational surface have negative z-coordinates. Consequently, on the curve γ between point P and A, there is a point, Q, where the Gauss curvature is equal to zero and the z-coordinates of the neighboring points are also equal to zero. This means that point Q is a singular point, i.e., LQ = MQ = NQ = 0.
The isogravitational surface that passes through point P intersects the equatorial plane and lies outside the geoid, without any singular points. The set of points that have a zero Gauss curvature is defined as a singular ring of the isogravitational surface. Close to the surface of the geoid, each isogravitational surface has at least one singular ring.
Figure 2 shows a simplified representation of a singular ring. As point P moves along the z-axis, rP increases. We have demonstrated that as the polar distance r reaches high values, the isogravitational surfaces become spheres. This indicates that the Gauss curvature at point P approaches zero. Simultaneously, as the singular rings slowly shrink, they reach a critical point when the Gauss curvature at point P becomes zero. Point P represents the location of the singular ring on this surface. If rP surpasses the critical value, the isogravitational surfaces will exhibit a positive Gauss curvature throughout, resulting in the absence of singular rings. Finally, as rP takes on large values, isogravitational surfaces become spheres with a radius of rP.
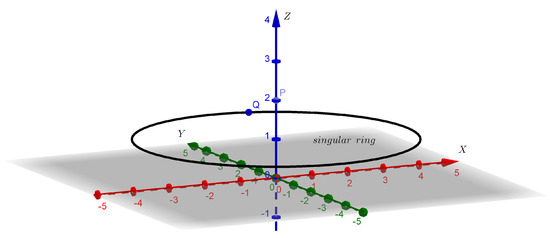
Figure 2.
Singular Ring.
Figure 3 shows a simplified image of a family of singular rings.
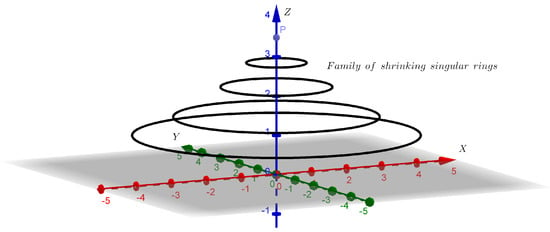
Figure 3.
Family of Singular Rings.
5. Disturbing Isogravitational Surfaces, Anomalistic Isogravitational Surfaces, and a Comparison between the Two Methods of Determining Disturbing Potential
A disturbing isogravitational surface is characterized by a constant value of gravity disturbance δg. Similarly, an anomalistic isogravitational surface is characterized by a constant value of gravity anomaly Δg. This local study is similar to that of the isogravitational surfaces, where the mean and Gaussian curvatures are given by Equations (76) and (77), respectively, with g replaced by δg (or Δg).
In the table below, we present a summary of the findings from Section 3 and Section 4. The first column lists the gravitational quantities, while the second column indicates whether each quantity is expressed as a series of spherical harmonics provided by the Laplace equation. We use “yes” to indicate when the quantity is explicitly expressed as such and “no” when it is not. In the third column, “yes” is selected when the quantity is represented as a series of spherical harmonics obtained from the G-modified Helmholtz equation. The term “direct” is used to describe a quantity that satisfies the chosen partial differential equation and remains either measurable or constant on the boundary. Conversely, we utilize the term “indirect” when the conditions mentioned above are not met. In addition, the symbols “Ve” and “VE” represent the Earth’s and ellipsoid’s Newtonian gravitational potential, respectively.
From Table 1, we can observe that the Laplace equation offers an advantage in the analysis of gravitational potential, whereas the G-modified Helmholtz equation has an edge in the study of gravity intensity, gravity disturbance, and gravity anomaly. It is worth noting that the process of determining the disturbing potential using the G-modified Helmholtz equation is quite straightforward, as it only involves solving a simple partial differential equation (see Equation (24)).

Table 1.
Comparison between Laplace and G – modified Helmholtz equation.
6. Summation of the Results
In this section, we tabulate the new results that were presented in Section 3.
Table 2 represents the significance of the G–modified Helmholtz equation, which enables us to study gravitational quantities independently of gravity potential and express them as a new kind of series of spherical harmonics. We chose to express the most significant formulae in detail, which are related to gravity g, gravity disturbance δg, gravity anomaly Δg, disturbing potential T, geoid undulation N, vertical gradient of gravity, and normal gravity on the geoid (marked in bold). Moreover, Table 2 also includes the components of the deflection of the vertical.

Table 2.
New spherical harmonic expressions occured from G—modified Helmholtz equation.
Along with the Laplace equation, the G-modified Helmholtz equation can also be classified as a fundamental partial differential equation of Physical geodesy.
7. Conclusions
In this work, we presented new alternative formulae for various quantities related to the Earth’s gravity field.
The G-modified Helmholtz equation is a partial differential equation that allows us to calculate the intensity of gravity as a series of spherical harmonics. The intensity of gravity plays a crucial role in a wide range of applications. The harmonic series of gravity intensity is a series in which the powers of the radial distance are irrational numbers. This series allows us to represent the vertical gradient of gravity as a series of spherical harmonics. The vertical gradient of gravity is very important for numerous geophysical applications.
Gravity disturbance and gravity anomaly are very significant. They are expressed as a series of spherical harmonics, as provided by the Laplace equation or the G-modified Helmholtz equation. In the first scenario, their determination is not straightforward, as we have to solve either a Neumann (Hotine problem) or Robin (Stokes problem) boundary value problem. In the second case, their determinations occur as solutions to Dirichlet boundary value problems, which are simpler than the previous two cases.
The G-modified Helmholtz equation offers an additional advantage: it enables us to calculate the Earth’s disturbing potential using a simple partial differential equation. The solution of this equation involves only the integration of the harmonic series of gravity anomaly with respect to radial distance, r. Moreover, the G-modified Helmholtz equation can also be used to find the components ξ and η of the deflection of the vertical and the geoid undulation.
In addition, on the surface of the geoid, the disturbing potential and the geoid undulation take the elegant form of a series of spherical harmonics, which shows the dependence on the difference between gravity disturbance and gravity anomaly on this surface. An interesting theoretical result that occurs is that both disturbing potential and geoid undulation can be determined if the value of normal gravity is known on the surface of the geoid. All the new formulae that occur from the G-modified Helmholtz equation are tabulated in Section 6.
The harmonic series of gravitational intensity gives us a significant advantage in studying the Earth’s isogravitational surfaces. The Earth’s gravitational potential’s first- and second-order partial derivatives can be conveniently expressed in Cartesian systems. This simplifies the expressions of the partial derivatives and the required approximations. It is shown that isogravitational surfaces are closed surfaces with a non-negative Gauss curvature.
At very high altitudes, when the value of the radial distance “r” is large, isogravitational surfaces are spheres with a radius equal to the selected radial distance. As we move closer to Earth, their appearance becomes progressively more intricate. Each isogravitational surface near Earth has at least one set of points defined as a singular ring. This name is attributed to the fact that all points belonging to this set are singular points. The family of singular rings converges to a single point located on Earth’s mean axis of rotation.
Future work could involve the development of new Global Gravity Models for gravity intensity g, gravity disturbance δg, and gravity anomaly Δg. A Global Gravity Model for gravity intensity would represent a significant advancement with a wide range of applications, such as in the fields of geophysics, archaeology, geodesy, orbit determination, and inertial navigation. Furthermore, it would be advantageous to develop new Global Gravity Models for gravity anomaly and gravity disturbance, separate from Global Geopotential Models. This evolution may present us with opportunities to improve present techniques for manipulating gravity data, leading to a deeper comprehension of the Earth’s gravity field.
Funding
This research received no external funding.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data was used.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Jarosz, W.; Carr, N.A.; Jensen, H.W. Importance Sampling Spherical Harmonics. Comput. Graph. Forum 2009, 28, 577–586. Available online: http://graphics.ucsd.edu/~henrik/papers/importance_sampling_spherical_harmonics.pdf (accessed on 2 February 2024). [CrossRef]
- Silvennoinen, A.; Sloan, P.P. Moving Basis Decomposition for Precomputed Light Transport. Comput. Graph. Forum 2021, 40, 127–137. Available online: https://www.ppsloan.org/publications/mbd.pdf (accessed on 2 February 2024). [CrossRef]
- Wang, J.; Xu, K.; Zhou, K.; Lin, S.; Hu, S.; Guo, B. Spherical Harmonics Scaling. Vis. Comput. 2006, 22, 713–720. Available online: https://link.springer.com/article/10.1007/s00371-006-0057-8 (accessed on 2 February 2024). [CrossRef]
- Annen, T.; Kautz, J.; Durand, F.; Seidel, H.P. Spherical Harmonic Gradients for Mid-Range Illumination. In Proceedings of the 15th Eurographics Workshop in Rendering Techniques, Norrköping, Sweden, 21–24 June 2004; pp. 331–336. Available online: https://diglib.eg.org/bitstream/handle/10.2312/EGWR.EGSR04.331-336/331-336.pdf?sequence=1&isAllowed=y (accessed on 2 February 2024).
- Sanso, F.; Sideris, M. Geoid Determination Theory and Methods; Springer Science & Business Media: Berlin, Germany, 2013; Chapter 6; Volume 262, p. 131. Available online: https://link.springer.com/book/10.1007/978-3-540-74700-0 (accessed on 2 February 2024).
- Shouny, A.; Khalil, R.; Kamel, A.; Miky, Y. Assessments of recent Global Geopotential Models based on GPS levelling and gravity data along coastal zones of Egypt. Open Gosciences 2023, 15, 20220450. Available online: https://www.degruyter.com/document/doi/10.1515/geo-2022-0450/html (accessed on 2 February 2024). [CrossRef]
- Wu, Y.; He, X.; Luo, Z.; Shi, H. An Assessment of Recently Released High Degree Global Geopotential Models Based on Heterogeneous Geodetic and Ocean Data. Front. Earth Sci. 2021, 9, 749611. Available online: https://www.frontiersin.org/articles/10.3389/feart.2021.749611/full (accessed on 2 February 2024). [CrossRef]
- Isik, M.S.; Çevikalp, M.R.; Erol, B.; Erol, S. Improvement of GOCE-Based Geopotential Models for Gravimetric Geoid Modeling in Turkey. Geosciences 2022, 12, 432. Available online: https://www.mdpi.com/2076-3263/12/12/432 (accessed on 2 February 2024). [CrossRef]
- Elizondo, N.A.; Lopez, R.V.G.; Carillo, X.G.T.; Becerra, G.E.V. Combining Global Geopotential Models, Digital Elevation Models, and GNSS/Leveling for Precise Local Geoid Determination in Some Mexico Urban Areas: Case Study. ISPRS Int. J. Geo-Inf. 2021, 10, 819. Available online: https://www.mdpi.com/2220-9964/10/12/819 (accessed on 2 February 2024). [CrossRef]
- Roithmayr, C.M. Contributions of Spherical Harmonics to Magnetic and Gravitational Fields; NASA TM-2004-213007; National Aeronautics and Space Administration: Washington, DC, USA, 2004. Available online: https://ntrs.nasa.gov/api/citations/20040047194/downloads/20040047194.pdf (accessed on 2 February 2024).
- Campbell, W.H. Geomagnetism Applications; U.S. Geological Survey Sircular 1109; United States Government Printing Office: Washington, DC, USA, 1995. Available online: https://pubs.usgs.gov/circ/1995/1109/report.pdf (accessed on 2 February 2024).
- Prada, K.O.; Antelo, M.J.; Murillo, N.A.; Cózar, J.R.; Contreras–de–Villar, F.; Pérez, J.J.M. A New Method for the Collection of Marine Geomagnetic Information: Survey Application in the Colombian Caribbean. J. Mar. Sci. Eng. 2021, 9, 10. Available online: https://www.mdpi.com/2077-1312/9/1/10 (accessed on 2 February 2024). [CrossRef]
- Zigan, L. Overview of Electric Field Applications in Energy and Process Engineering. Energies 2018, 11, 1361. Available online: https://www.mdpi.com/1996-1073/11/6/1361 (accessed on 15 February 2024). [CrossRef]
- Tognolatti, L.; Ponti, C.; Santarsiero, M.; Schettini, G. An Efficient Computational Technique for the Electromagnetic Scattering by Prolate Spheroids. Mathematics 2022, 10, 1761. Available online: https://www.mdpi.com/2227-7390/10/10/1761 (accessed on 15 February 2024). [CrossRef]
- Vafeas, P.; Perrusson, G.; Lesselier, D. Low-frequency scattering from perfectly conducting spheroidal bodies in a conductive medium with magnetic dipole excitation. Int. J. Eng. Sci. 2009, 47, 372–390. Available online: https://www.researchgate.net/publication/222923079_Lowfrequency_scattering_fro_perfectly_conducting_spheroidal_bodies_in_a_conductive_medium_with_magnetic_dipole_excitation (accessed on 15 February 2024). [CrossRef]
- Perrusson, G.; Vafeas, P.; Chatjigeorgiou, I.K.; Lesselier, D. Low-frequency on-site identification of a highly conductive body buried in Earth from a model ellipsoid. IMA J. Appl. Math. 2015, 80, 963–980. Available online: https://www.researchgate.net/publication/274162167_Low-frequency_onsite_identification_of_a_highly_conductive_body_buried_in_Earth_from_a_model_ellipsoid (accessed on 15 February 2024). [CrossRef]
- Ming, Y.; Niu, X.; Xie, X.; Han, Z.; Li, Q.; Sun, S. Application on Gravity Exploration in Urban Active Fault Detection. In The 9th International Conference on Environmental and Engineering Geophysics 2021, Proceedings of the IOP Conference Series: Earth and Environmental Sciences, Changchun, China, 11–14 October 2020; IOP Publishing: Bristol, UK, 2021; Volume 660, p. 012057. Available online: https://www.researchgate.net/publication/349532168_Application_of_gravity_exploration_in_urban_active_fault_detection (accessed on 21 February 2024).
- Sjöberg, L.E.; Bagherbagdi, M. Gravity Inversion and Integration. In Theory and Applications in Geodesy and Geophysics; Springer: Basel, Switzerland, 2017; p. 251. Available online: https://www.geokniga.org/bookfiles/geokniga-gravity-inversion-and-integration.pdf (accessed on 21 February 2024).
- Scheinert, M.; Ferranccioli, F.; Schwabe, J.; Studinger, M.; Damaske, D.; Jokat, W.; Aleshkova, N.; Jordan, T.; Leitchenkov, G.; Blankenship, D.D.; et al. New Antarctic gravity gnomaly grid for enhanced geodetic and geophysical studies in Antarctica. Geophys. Res. Lett. 2016, 43, 600–610. Available online: https://www.researchgate.net/publication/289983658_New_Antarctic_Gravity_Anomaly_Grid_for_Enhanced_Geodetic_and_Geophysical_Studies_in_Antarctica (accessed on 21 February 2024). [CrossRef] [PubMed]
- Ismail, N.; Yanis, M.; Abdullah, F.; Irfansyam, A.; Atmojo, B.S.W. Mapping buried ancient structure using gravity method: A case study from Cot Sidi Abdullah North Aceh. J. Phys. 2018, 1120, 012035. Available online: https://iopscience.iop.org/article/10.1088/1742-6596/1120/1/012035/pdf (accessed on 21 February 2024). [CrossRef]
- Manoussakis, G. The Gravity Force Generated by a Non-Rotating Level Ellipsoid of Revolution with Low Eccentricity as a Series of Spherical Harmonics. Mathematics 2023, 11, 1974. Available online: https://www.mdpi.com/journal/mathematics/special_issues/Applications_Partial_Differential_Equations_Mathematical_Physics (accessed on 21 February 2024). [CrossRef]
- Heiskanen, W.; Moritz, H. Physical Geodesy. W.H. Freeman Co. 1967, 82–112. Available online: https://archive.org/details/heiskanen_morits_1967_physical_geodesy/page/n89/mode/2up?view=theater (accessed on 3 March 2024).
- Bagherbandi, M.; Jouybari, A.; Niflourousan, F.; Ägren, J. Deflection of vertical effect on direct georeferencing in aerial mobile mapping systems: A case study in Sweden. Photogramm. Rec. 2022, 37, 285–305. Available online: https://www.diva-portal.org/smash/get/diva2:1684428/FULLTEXT01.pdf (accessed on 3 March 2024). [CrossRef]
- Barzaghi, R.; Carrion, D.; Pepe, M.; Prezioso, G. Computing the Deflection of the Vertical for Improving Aerial Surveys: A Comparison between EGM2008 and ITALGEO05 Estimates. Sensors 2016, 16, 1168. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5017334/pdf/sensors-16-01168.pdf (accessed on 3 March 2024). [CrossRef] [PubMed]
- Šprlák, M.; Novak, P. Integral formulas for computing a third order gravitational tensor from volumetric mass density, disturbing gravitational potential, gravity anomaly and gravity disturbance. J. Geod. 2015, 89, 141–157. Available online: https://www.researchgate.net/publication/271211475_Integral_formulas_for_computing_a_thirdorder_gravitational_tensor_from_volumetric_mass_density_disturbing_gravitational_potential_gravity_anomaly_and_gravity_disturbance (accessed on 5 March 2024). [CrossRef]
- Gorshkov, G.P. Isogravitational surfaces. Geophys. Abstr. 1934, 82. Available online: https://books.google.gr/books?id=1RxUCPOWOtEC&pg=PA1738&lpg=PA1738&dq=isogravitational+surfaces+of+the+Earth&source=bl&ots=9VnOhvB6Cs&sig=ACfU3U2hlSJxufGjWTktf6yfI13mwKuylA&hl=el&sa=X&ved=2ahUKEwjx8pD85tqEAxVh9LsIHbuUA_E4ChDoAXoECAYQAw#v=onepage&q=isogravitational%20surfaces%20of%20the%20Earth&f=false (accessed on 5 March 2024). [CrossRef]
- Koop, R. Global Gravity Field Modelling Using Satellite Gravity Gradiometry; Nederlandse Commissie voor Geodesie: Delft, Netherlands, 1993; Volume 38, pp. 32–183. Available online: https://ncgeo.nl/index.php/en/publicatiesgb/publications-on-geodesy/item/2544-pog-38-r-koop-global-gravity-modelling-using-satellite-gravity-gradiometry (accessed on 5 March 2024).
- Giblin, P. Differential Geometry of Curves and Surfaces; Department of Mathematical Sciences, University of Liverpool: Liverpool, UK, 1999; pp. 32–39. Available online: https://www.liverpool.ac.uk/~pjgiblin/papers/diff-geom-book.pdf (accessed on 5 March 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).