Improvement of GOCE-Based Global Geopotential Models for Gravimetric Geoid Modeling in Turkey
Abstract
1. Introduction
2. Materials and Methods
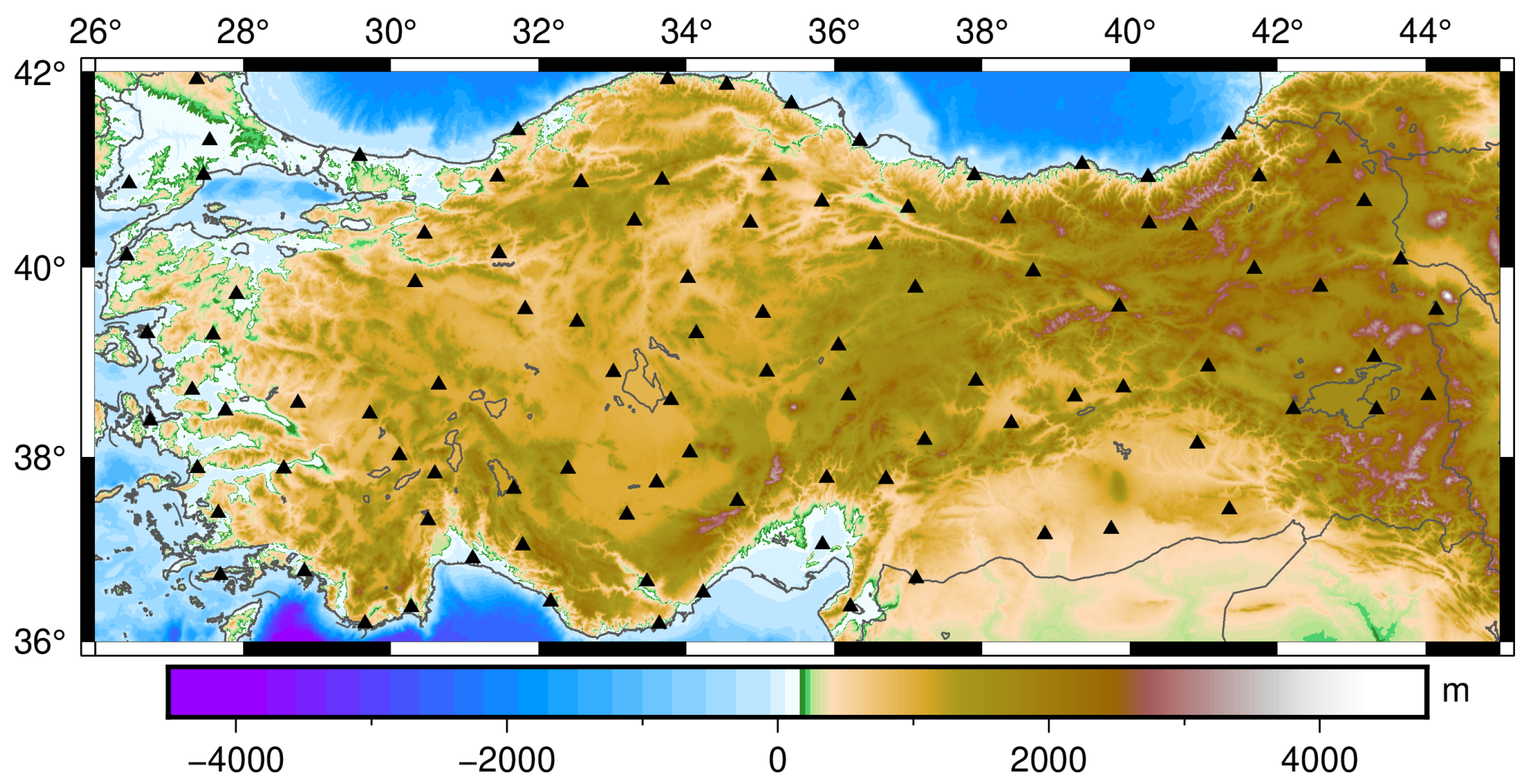
2.1. Study Area and Data Set
2.1.1. Global Geopotential Models
2.1.2. Residual Terrain Model
2.1.3. Gravity Data
2.1.4. Validation Data Set
2.2. Methodology
2.2.1. Spectral Enhancement Method
2.2.2. Gravimetric Geoid Modeling
3. Results and Discussions
3.1. Assessment of Global Geopotential Models
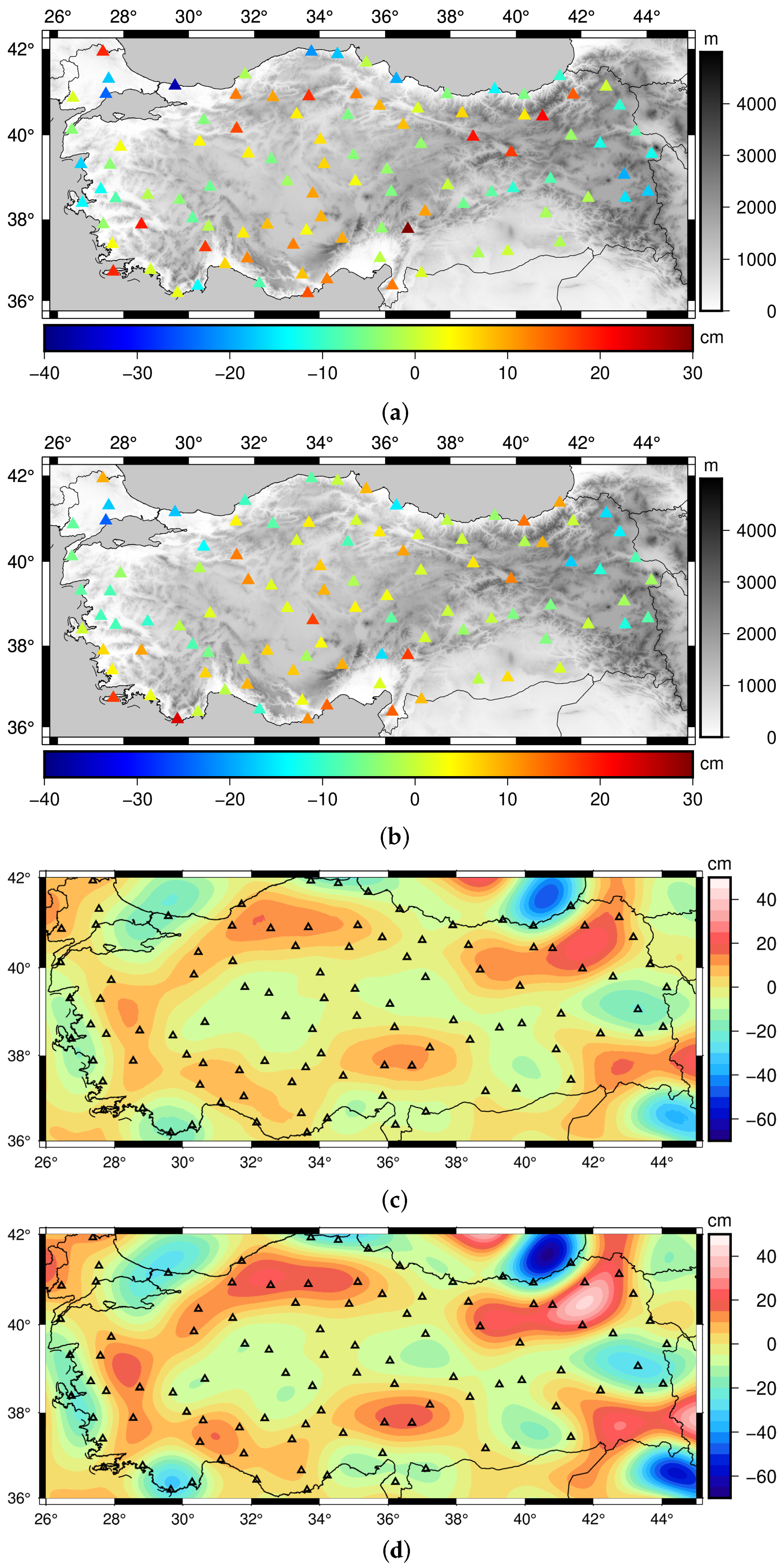
3.2. Determination and Validation of Gravimetric Geoid Models
3.3. Discussion on the Use of Geoid Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CHAMP | Challenging Minisatellite Payload |
| DIR | Direct |
| GDMRE | General Directorate of Mineral Research and Exploration |
| GGM | Global Geopotential Model |
| GMT | Generic Mapping Tools |
| GNSS | Global Navigational Satellite System |
| GOCE | Gravity Field and Steady-State Ocean Circulation Explorer |
| GOCO | Gravity Observation Combination |
| GRACE | Gravity Recovery and Climate Experiment |
| hl-SST | High-to-low Satellite to Satellite Tracking |
| HPF | High Processing Facility |
| ICGEM | International Centre for Global Earth Models |
| IGSN71 | International Gravity Standardization Net 1971 |
| ITRF96 | International Terrestrial Reference Frame 1996 |
| LSMSA | Least Squares Modification of Stokes Integral with Additive corrections |
| RTE | Residual Terrain Effect |
| RTM | Residual Terrain Model |
| SD | Standard Deviation |
| SGG | Satellite Gravity Gradiometry |
| SPW | Space-wise |
| SRTM | Shuttle Radar Topography Mission |
| TIM | Time-wise |
| TUDKA99 | Turkish National Vertical Control Network 1999 |
| TUTGA | Turkish National Fundamental GPS Network |
References
- Barthelmes, F. Definition of Functionals of the Geopotential and Their Calculation from Spherical Harmonic Models; Technical Report; Deutsches GeoForschungs Zentrum GFZ: Potsdam, Germany, 2009. [Google Scholar]
- Eshagh, M.; Ebadi, S. Geoid modelling based on EGM08 and recent Earth gravity models of GOCE. Earth Sci. Inform. 2013, 6, 113–125. [Google Scholar] [CrossRef]
- Saari, T.; Bilker-Koivula, M. Applying the GOCE-based GGMs for the quasi-geoid modelling of Finland. J. Appl. Geod. 2018, 12, 15–27. [Google Scholar] [CrossRef]
- Matsuo, K.; Kuroishi, Y. Refinement of a gravimetric geoid model for Japan using GOCE and an updated regional gravity field model. Earth Planets Space 2020, 72, 33. [Google Scholar] [CrossRef]
- Borghi, A.; Barzaghi, R.; Al-Bayari, O.; Madani, S.A. Centimeter Precision Geoid Model for Jeddah Region (Saudi Arabia). Remote Sens. 2020, 12, 2066. [Google Scholar] [CrossRef]
- Barzaghi, R.; Carrion, D.; Kamguia, J.; Kande, L.; Yap, L.; Betti, B. Estimating gravity field and quasi-geoid in Cameroon (CGM20). J. Afr. Earth Sci. 2021, 184, 104377. [Google Scholar] [CrossRef]
- Gruber, T.; Gerlach, C.; Haagmans, R. Intercontinental height datum connection with GOCE and GPS-levelling data. J. Geod. Sci. 2012, 2, 270–280. [Google Scholar] [CrossRef]
- Kotsakis, C.; Katsambalos, K.; Ampatzidis, D. Estimation of the zero-height geopotential level W o LVD in a local vertical datum from inversion of co-located GPS, leveling and geoid heights: A case study in the Hellenic islands. J. Geod. 2012, 86, 423–439. [Google Scholar] [CrossRef]
- Vergos, G.S.; Erol, B.; Natsiopoulos, D.A.; Grigoriadis, V.N.; Isik, M.S.; Tziavos, I.N. Preliminary results of GOCE-based height system unification between Greece and Turkey over marine and land areas. Acta Geod. Geophys. 2018, 53, 61–79. [Google Scholar] [CrossRef]
- Zhang, P.; Bao, L.; Guo, D.; Li, Q. Estimation of the height datum geopotential value of Hong Kong using the combined Global Geopotential Models and GNSS/levelling data. Surv. Rev. 2022, 54, 106–116. [Google Scholar] [CrossRef]
- Braitenberg, C. A Grip on Geological Units with GOCE. In Gravity, Geoid and Height Systems; Marti, U., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 309–317. [Google Scholar]
- van der Meijde, M.; Julià, J.; Assumpç ao, M. Gravity derived Moho for South America. Tectonophysics 2013, 609, 456–467. [Google Scholar] [CrossRef]
- van der Meijde, M.; Pail, R.; Bingham, R.; Floberghagen, R. GOCE data, models, and applications: A review. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 4–15. [Google Scholar] [CrossRef]
- Bouman, J.; Ebbing, J.; Meekes, S.; Abdul Fattah, R.; Fuchs, M.; Gradmann, S.; Haagmans, R.; Lieb, V.; Schmidt, M.; Dettmering, D.; et al. GOCE gravity gradient data for lithospheric modeling. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 16–30. [Google Scholar] [CrossRef]
- Shin, Y.H.; Shum, C.; Braitenberg, C.; Lee, S.M.; Na, S.H.; Choi, K.S.; Hsu, H.; Park, Y.S.; Lim, M. Moho topography, ranges and folds of Tibet by analysis of global gravity models and GOCE data. Sci. Rep. 2015, 5, 11681. [Google Scholar] [CrossRef]
- Eshagh, M.; Ebadi, S.; Tenzer, R. Isostatic GOCE Moho model for Iran. J. Asian Earth Sci. 2017, 138, 12–24. [Google Scholar] [CrossRef]
- Abrehdary, M.; Sjöberg, L.E. Moho density contrast in Antarctica determined by satellite gravity and seismic models. Geophys. J. Int. 2021, 225, 1952–1962. [Google Scholar] [CrossRef]
- Kaban, M.K.; El Khrepy, S.; Al-Arifi, N.; Tesauro, M.; Stolk, W. Three-dimensional density model of the upper mantle in the Middle East: Interaction of diverse tectonic processes. J. Geophys. Res. Solid Earth 2016, 121, 5349–5364. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Sampietro, D.; Sansò, F. Global Moho from the combination of the CRUST2.0 model and GOCE data. Geophys. J. Int. 2013, 195, 222–237. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Sampietro, D. GEMMA: An Earth crustal model based on GOCE satellite data. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 31–43. [Google Scholar] [CrossRef]
- Braitenberg, C. Exploration of tectonic structures with GOCE in Africa and across-continents. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 88–95. [Google Scholar] [CrossRef]
- Eppelbaum, L.; Katz, Y. A new regard on the tectonic map of the Arabian–African region inferred from the satellite gravity analysis. Acta Geophys. 2017, 65, 607–626. [Google Scholar] [CrossRef]
- Ebbing, J.; Haas, P.; Ferraccioli, F.; Pappa, F.; Szwillus, W.; Bouman, J. Earth tectonics as seen by GOCE—Enhanced satellite gravity gradient imaging. Sci. Rep. 2018, 8, 16356. [Google Scholar] [CrossRef]
- Gruber, T.; Visser, P.N.A.M.; Ackermann, C.; Hosse, M. Validation of GOCE gravity field models by means of orbit residuals and geoid comparisons. J. Geod. 2011, 85, 845–860. [Google Scholar] [CrossRef]
- Hirt, C.; Gruber, T.; Featherstone, W.E. Evaluation of the first GOCE static gravity field models using terrestrial gravity, vertical deflections and EGM2008 quasigeoid heights. J. Geod. 2011, 85, 723–740. [Google Scholar] [CrossRef]
- Pail, R.; Bruinsma, S.L.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.D.; Höck, E.; Reguzzoni, M.; Brockmann, J.M.; Abrikosov, O.; et al. First GOCE gravity field models derived by three different approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C.; Pail, R.; Claessens, S. Evaluation of the third- and fourth-generation GOCE Earth gravity field models with Australian terrestrial gravity data in spherical harmonics. J. Geod. 2014, 88, 319–333. [Google Scholar] [CrossRef]
- Godah, W.; Krynski, J.; Szelachowska, M. The use of absolute gravity data for the validation of Global Geopotential Models and for improving quasigeoid heights determined from satellite-only Global Geopotential Models. J. Appl. Geophys. 2018, 152, 38–47. [Google Scholar] [CrossRef]
- Ince, E.S.; Erol, B.; Sideris, M.G. Evaluation of the GOCE-Based Gravity Field Models in Turkey. In Gravity, Geoid and Height Systems; Marti, U., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 93–99. [Google Scholar] [CrossRef]
- Erol, B.; Isik, M.S.; Erol, S. An Assessment of the GOCE High-Level Processing Facility (HPF) Released Global Geopotential Models with Regional Test Results in Turkey. Remote Sens. 2020, 12, 586. [Google Scholar] [CrossRef]
- Simav, M.; Yildiz, H. Evaluation of EGM2008 and latest GOCE-based satellite only global gravity field models using densified gravity network: A case study in south-western Turkey. Boll. Geofis. Teor. Appl. 2019, 60, 49–68. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Hirt, C.; Kuhn, M.; Claessens, S.; Pail, R.; Seitz, K.; Gruber, T. Study of the Earth’s short-scale gravity field using the ERTM2160 gravity model. Comput. Geosci. 2014, 73, 71–80. [Google Scholar] [CrossRef]
- Gilardoni, M.; Reguzzoni, M.; Sampietro, D.; Sanso, F. Combining EGM2008 with GOCE gravity models. Boll. Geofis. Teor. Appl. 2013, 54. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A general model for modifying Stokes’ formula and its least-squares solution. J. Geod. 2003, 77, 459–464. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.; Abrikosov, O.; Flechtner, F.; Marty, J.C.; Lemoine, J.M.; Dahle, C.; Neumayer, H.; Barthelmes, F.; König, R.; et al. EIGEN-6C4—The latest combined global gravity field model including GOCE data up to degree and order 1949 of GFZ Potsdam and GRGS Toulouse. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; p. 3707. [Google Scholar]
- Isik, M.S.; Erol, S.; Erol, B. Investigation of the Geoid Model Accuracy Improvement in Turkey. J. Surv. Eng. 2022, 148, 1–14. [Google Scholar] [CrossRef]
- Rummel, R. Height unification using GOCE. J. Geod. Sci. 2012, 2, 355–362. [Google Scholar] [CrossRef]
- Pail, R.; Goiginger, H.; Schuh, W.D.; Hck, E.; Brockmann, J.M.; Fecher, T.; Güruber, T.; Mayer-Gürr, T.; Kusche, J.; Jäggi, A.; et al. Combined satellite gravity field model GOCO01S derived from GOCE and GRACE. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Bruinsma, S.L.; Marty, J.C.; Balmino, G.; Biancale, R.; Förste, C.; Abrikosov, O.; Neumayer, K.H. GOCE Gravity Field Recovery by Means of the Direct Numerical Method. In Proceedings of the 2010 ESA Living Planet Symposium, Bergen, Norway, 28 June–2 July 2010. [Google Scholar]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Marty, J.C.; Rio, M.H.; Mulet, S.; Bonvalot, S. The new ESA satellite-only gravity field model via the direct approach. Geophys. Res. Lett. 2013, 40, 3607–3612. [Google Scholar] [CrossRef]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Lemoine, J.M.; Marty, J.C.; Mulet, S.; Rio, M.H.; Bonvalot, S. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys. Res. Lett. 2014, 41, 7508–7514. [Google Scholar] [CrossRef]
- Pail, R.; Goiginger, H.; Mayrhofer, R.; Schuh, W.D.; Brockmann, J.M.; Krasbutter, I.; Höck, E.; Fecher, T. GOCE gravity field model derived from orbit and gradiometry data applying the time-wise method. In Proceedings of the ESA Living Planet Symposium, Bergen, Norway, 28 June–2 July 2010; Volume 28, p. 8. [Google Scholar]
- Brockmann, J.M.; Zehentner, N.; Höck, E.; Pail, R.; Loth, I.; Mayer-Gürr, T.; Schuh, W.D. EGM-TIM-RL05: An independent geoid with centimeter accuracy purely based on the GOCE mission. Geophys. Res. Lett. 2014, 41, 8089–8099. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Schubert, T.; Mayer-Gürr, T.; Schuh, W.D. The Earth’s Gravity Field as Seen by the GOCE Satellite—An Improved Sixth Release Derived with the Time-Wise Approach (GO_CONS_GCF_2_TIM_R6); GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Migliaccio, F.; Reguzzoni, M.; Sanso, F.; Tscherning, C.C.; Veicherts, M. GOCE data analysis: The space-wise approach and the first space-wise gravity field model. In Proceedings of the ESA Living Planet Symposium, Bergen, Norway, 28 June–2 July 2010; Citeseer: Forest Grove, OR, USA, 2010; Volume 28. [Google Scholar]
- Migliaccio, F.; Reguzzoni, M.; Gatti, A.; Sansò, F.; Herceg, M. A GOCE-only global gravity field model by the space-wise approach. In Proceedings of the 4th International GOCE User Workshop, Munich, Germany, 31 March–1 April 2011; Volume 31. [Google Scholar]
- Gatti, A.; Reguzzoni, M.; Migliaccio, F.; Sanso, F. Space-wise grids of gravity gradients from GOCE data at nominal satellite altitude. In Proceedings of the 5th International GOCE User Workshop, Paris, France, 25–28 November 2014; pp. 25–28. [Google Scholar]
- Gatti, A.; Reguzzoni, M.; Migliaccio, F.; Sansò, F. Computation and assessment of the fifth release of the GOCE-only space-wise solution. In Proceedings of the 1st Joint Commission 2 and IGFS Meeting, Thessaloníki, Greece, 19–23 September 2016; pp. 19–23. [Google Scholar]
- Goiginger, H.; Rieser, D.; Mayer-guerr, T.; Pail, R.; Schuh, W.d. The combined satellite-only global gravity field model GOCO02S. In Proceedings of the European Geophysical Research Abstracts, Vienna, Austria, 12–17 April 2011; Volume 13, p. 10571. [Google Scholar]
- Mayer-Gürr, T. The new combined satellite only model GOCO03s. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems 2012, Venice, Italy, 9–12 October 2012. [Google Scholar]
- Mayer-Guerr, T. The combined satellite gravity field model GOCO05s. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 12–17 April 2015; Volume 18, p. EGU2016–7696. [Google Scholar]
- Kvas, A.; Brockmann, J.M.; Krauss, S.; Schubert, T.; Gruber, T.; Meyer, U.; Mayer-Gürr, T.; Schuh, W.D.; Jäggi, A.; Pail, R. GOCO06s—A satellite-only global gravity field model. Earth Syst. Sci. Data 2021, 13, 99–118. [Google Scholar] [CrossRef]
- Arslan, S. Geophysical regional gravity maps of Turkey and its general assessment. Bull. Miner. Res. Explor. 2016, 2016, 203–222. [Google Scholar] [CrossRef]
- Hammer, S. Terrain Corrections for Gravimeter Stations. Geophysics 1939, 4, 184–194. [Google Scholar] [CrossRef]
- Ayhan, M.E.; Demir, C.; Lenk, O.; Kılıçoğlu, A.; Aktuğ, B.; Açıkgöz, M.; Fırat, O.; Şengün, Y.; Cingöz, A.; Gürdal, M.; et al. Türkiye Ulusal Temel GPS Ağı-1999 (TUTGA-99A). Harit. Derg. 2002, 145, 1–14. [Google Scholar]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. Available from the CGIAR-CSI SRTM 90 m Database. 2008. Available online: http://srtm.csi.cgiar.org/ (accessed on 1 September 2022).
- Ekman, M. Impacts of geodynamic phenomena on systems for height and gravity. Bull. Géod. 1989, 63, 281–296. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: Vienna, Austria, 2006; pp. 1–403. [Google Scholar] [CrossRef]
- Sánchez, L.; Sideris, M.G. Vertical datum unification for the International Height Reference System (IHRS). Geophys. J. Int. 2017, 209, 570–586. [Google Scholar] [CrossRef]
- Sánchez, L.; Čunderlík, R.; Dayoub, N.; Mikula, K.; Minarechová, Z.; Šíma, Z.; Vatrt, V.; Vojtíšková, M. A conventional value for the geoid reference potential W0. J. Geod. 2016, 90, 815–835. [Google Scholar] [CrossRef]
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Technical Report 355; Department of Geodetic Science and Surveying, Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Molodenskii, M.S.; Eremeev, V.F.; Yurkina, M.I. Methods for Study of the External Gravitational Field and Figure of the Earth; Israel Program for Scientific Translations: Jerusalem, Israel, 1962; Available online: http://www.helmut-moritz.at/SciencePage/Molodensky.pdf (accessed on 10 July 2022). (In Russian)
- Ellmann, A. Two deterministic and three stochastic modifications of Stokes’s formula: A case study for the Baltic countries. J. Geod. 2005, 79, 11–23. [Google Scholar] [CrossRef]
- Sjöberg, L. Topographic Effects in Geoid Determinations. Geosciences 2018, 8, 143. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A solution to the downward continuation effect on the geoid determined by Stokes’ formula. J. Geod. 2003, 77, 94–100. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Nahavandchi, H. The atmospheric geoid effects in Stokes’ formula. Geophys. J. Int. 2000, 140, 95–100. [Google Scholar] [CrossRef]
- Sjöberg, L.E. The ellipsoidal corrections to the topographic geoid effects. J. Geod. 2004, 77, 804–808. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.V.; Einarsson, I.; Manandhar, N.; Shreshta, K. Geoid of Nepal from Airborne Gravity Survey. In Earth on the Edge: Science for a Sustainable Planet. International Association of Geodesy Symposia; Rizos, C., Willis, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 521–527. [Google Scholar] [CrossRef]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S. A high-resolution gravimetric quasigeoid model for Vietnam. Earth Planets Space 2019, 71, 65. [Google Scholar] [CrossRef]
- Fotopoulos, G. Combination of Heights. In Geoid Determination: Theory and Methods; Sansò, F., Sideris, M.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 517–544. [Google Scholar] [CrossRef]
- Isik, M.S.; Erol, B.; Çevikalp, M.R.; Erol, S. Geoid modeling with least squares modification of Hotine’s integral using gravity disturbances in Turkey. Earth Sci. Inform. 2022. [Google Scholar] [CrossRef]
- Silver, P.G.; Carlson, R.W.; Olson, P. Deep Slabs, Geochemical Heterogeneity, and the Large-Scale Structure of Mantle Convection: Investigation of an Enduring Paradox. Annu. Rev. Earth Planet. Sci. 1988, 16, 477–541. [Google Scholar] [CrossRef]
- Featherstone, W. On the Use of the Geoid in Geophysics: A Case Study Over the North West Shelf of Australia. Explor. Geophys. 1997, 28, 52–57. [Google Scholar] [CrossRef]
- Kiamehr, R.; Sjöberg, L. Impact of a precise geoid model in studying tectonic structures—A case study in Iran. J. Geodyn. 2006, 42, 1–11. [Google Scholar] [CrossRef]
- Styron, R.; Pagani, M. The GEM Global Active Faults Database. Earthq. Spectra 2020, 36, 160–180. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 2019, 20, 5556–5564. [Google Scholar] [CrossRef]



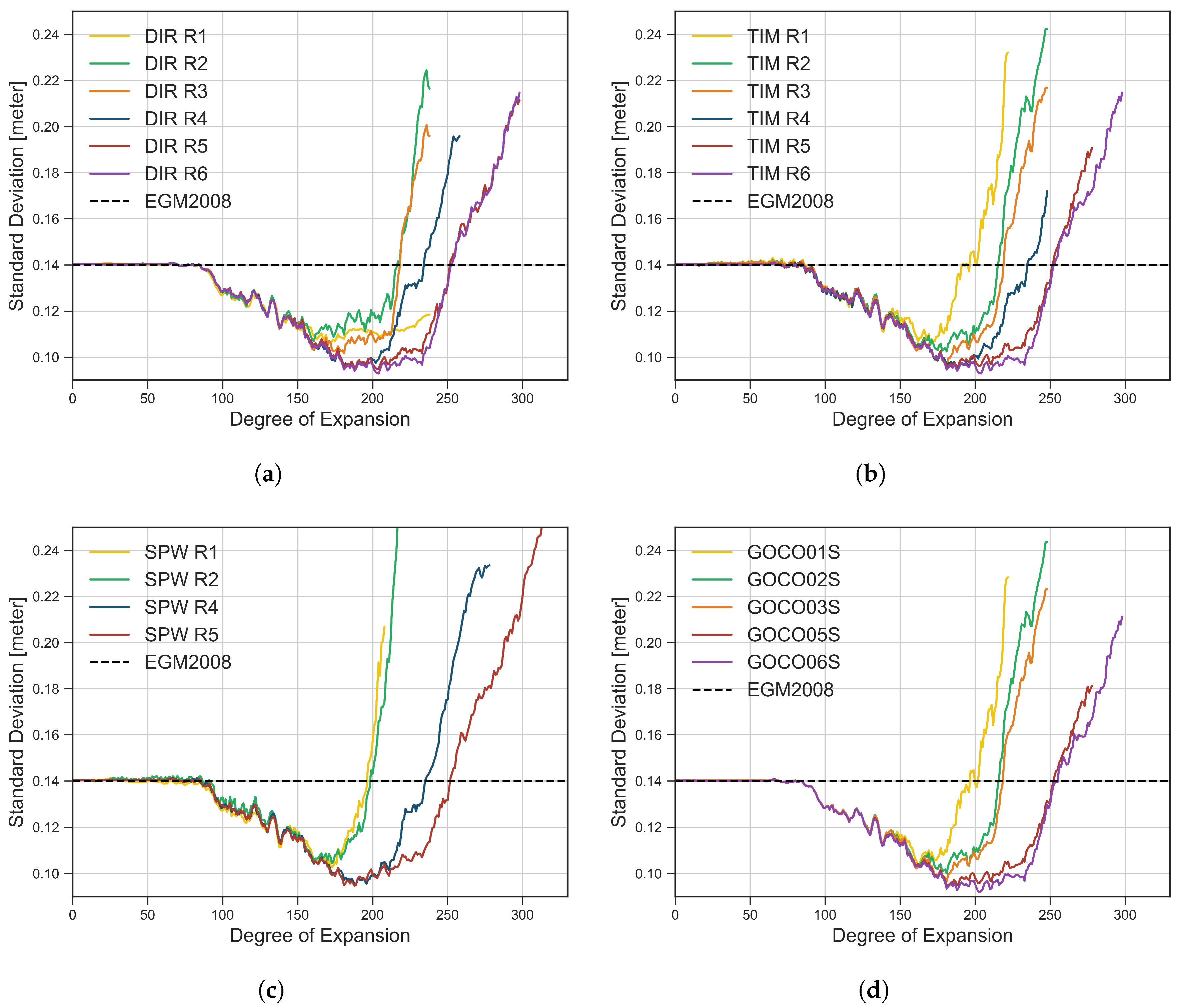
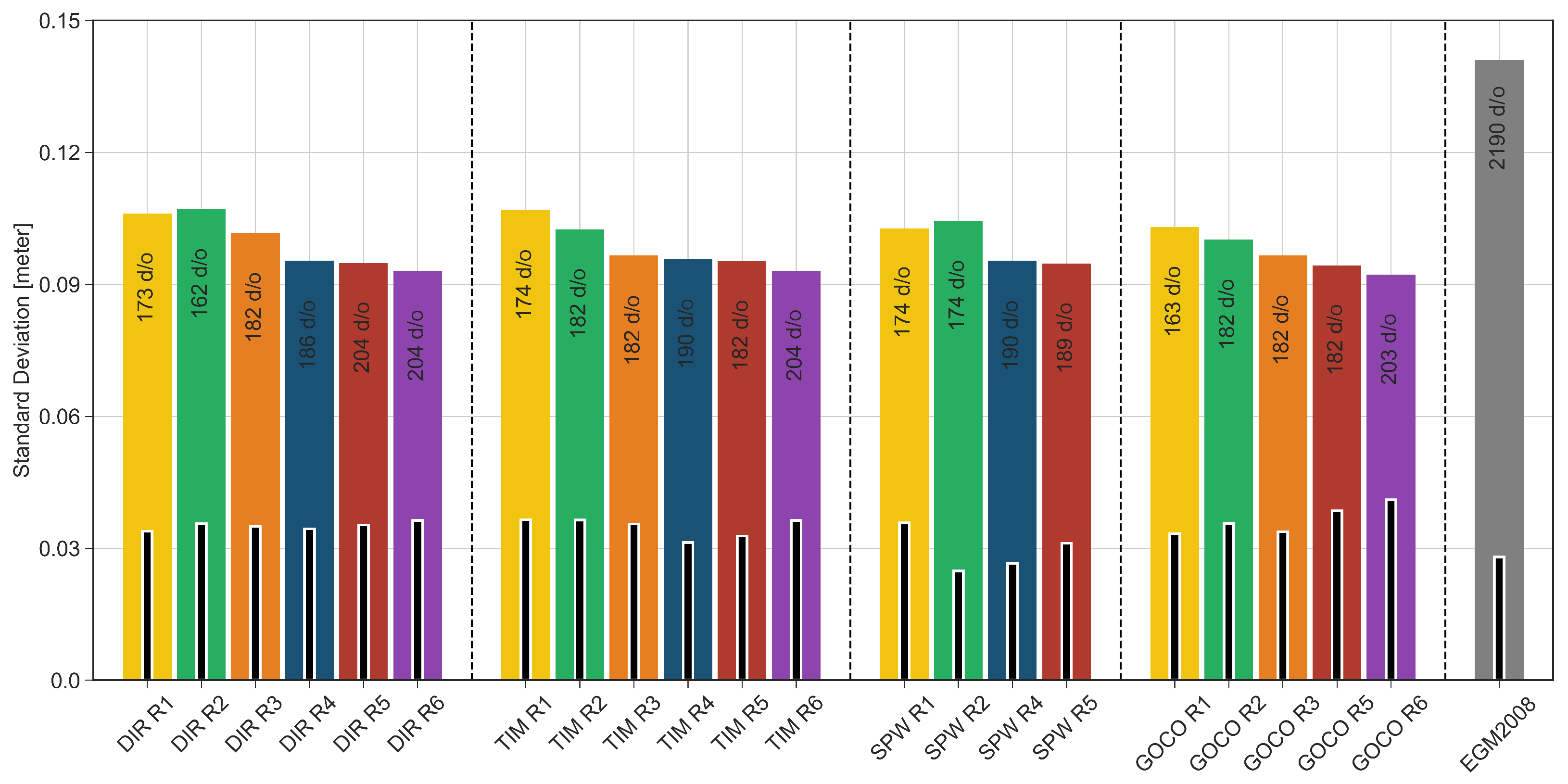
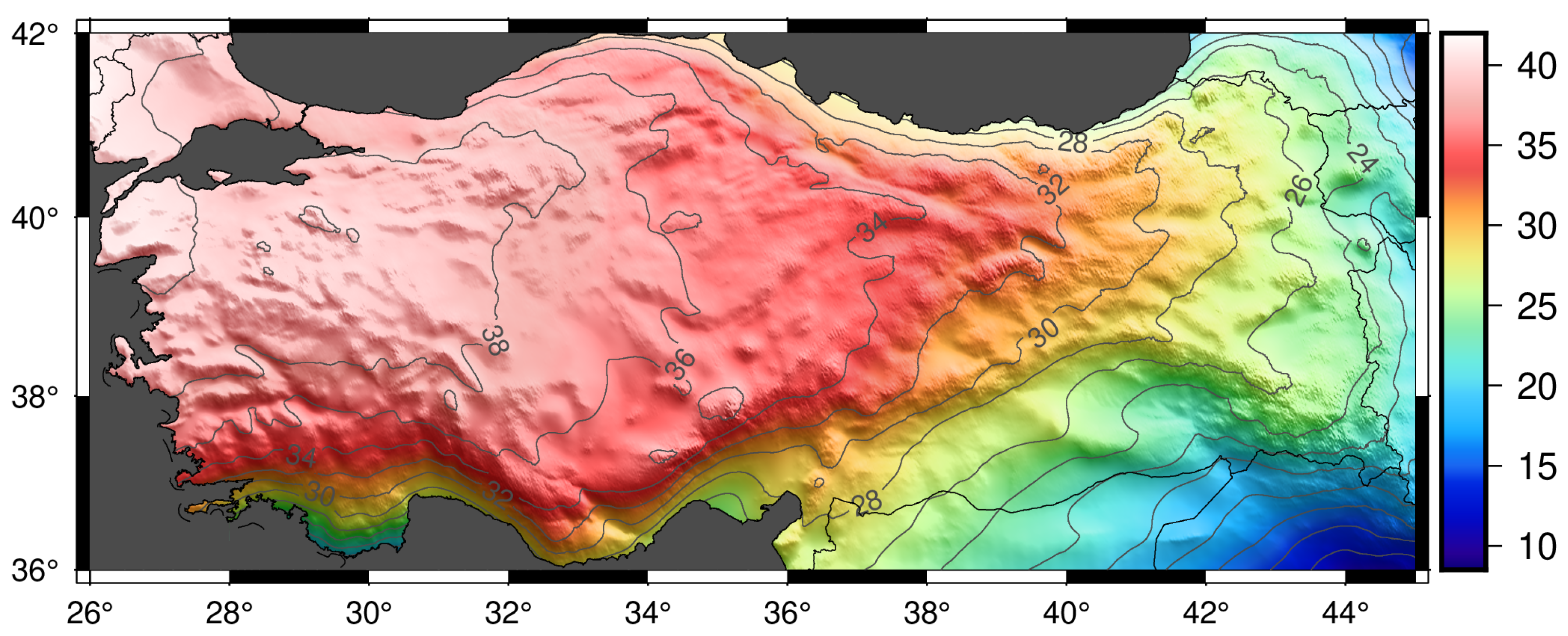
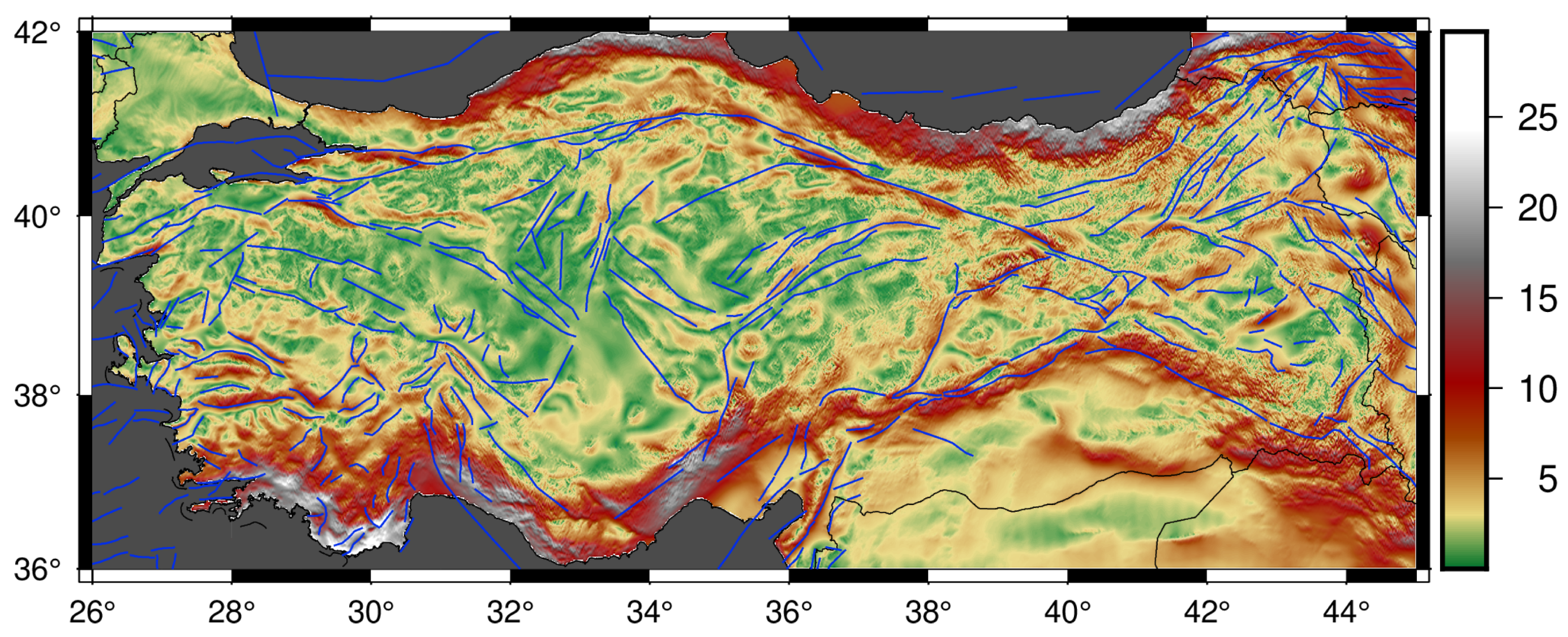
| Model | Max Degree | Data |
|---|---|---|
| DIR R1 | 240 | GOCE (2 m) |
| DIR R2 | 240 | GOCE (8 m) |
| DIR R3 | 240 | GOCE (18 m), GRACE (6.5 y), SLR (6.5 y) |
| DIR R4 | 260 | GOCE (33 m), GRACE (9 y), SLR (>10 y) |
| DIR R5 | 300 | GOCE (48 m), GRACE (>10 y), SLR (>10 y) |
| DIR R6 | 300 | GOCE (48 m), GRACE (>10 y), SLR (>10 y) |
| TIM R1 | 224 | GOCE (2 m) |
| TIM R2 | 250 | GOCE (8 m) |
| TIM R3 | 250 | GOCE (18 m) |
| TIM R4 | 250 | GOCE (33 m) |
| TIM R5 | 250 | GOCE (48 m) |
| TIM R6 | 300 | GOCE (48 m) |
| SPW R1 | 210 | GOCE (2 m) |
| SPW R2 | 240 | GOCE (8 m) |
| SPW R4 | 280 | GOCE (33 m) |
| SPW R5 | 330 | GOCE (48 m) |
| GOCO0S R1 | 224 | GOCE (2 m), GRACE (7.5 y) |
| GOCO0S R2 | 250 | GOCE (8 m), GRACE (7.5 y), SLR (5 y) |
| GOCO0S R3 | 250 | GOCE (18 m), GRACE (7.5 y), SLR (5 y) |
| GOCO0S R5 | 280 | GOCE (48 m), GRACE (10.5 y), CHAMP (6 y), SLR (>10 y) |
| GOCO0S R6 | 300 | GOCE (48 m), GRACE (15.5 y), CHAMP (6 y), SLR (>10 y) |
| GGM | Degree | Min | Max | Mean | SD |
|---|---|---|---|---|---|
| DIR-R6 | 204 * | −22.2 | 28.7 | 3.7 | 9.3 |
| TIM-R6 | 204 * | −22.4 | 28.4 | 3.7 | 9.3 |
| SPW-R5 | 189 * | −18.2 | 25.7 | 3.1 | 9.5 |
| GOCO06S | 203 * | −22.0 | 30.8 | 4.2 | 9.3 |
| EGM2008 | 2190 | −27.7 | 42.0 | 2.9 | 14.1 |
| Geoid Model | Reference GGM | Min | Max | Mean | SD | |
|---|---|---|---|---|---|---|
| expGeoid-1 | EGM2008 () | Before fit | −62.7 | 56.6 | −1.2 | 20.5 |
| After fit | −50.5 | 59.7 | 0.0 | 19.3 | ||
| expGeoid-2 | EIGEN-6C4 () | Before fit | −60.1 | 53.7 | −0.7 | 20.0 |
| After fit | −50.3 | 46.6 | 0.0 | 18.1 | ||
| expGeoid-3 | TIM-R6 () | Before fit | −58.5 | 53.2 | −0.2 | 20.1 |
| After fit | −50.0 | 42.0 | 0.0 | 18.4 | ||
| expGeoid-4 | EGM2008 () | Before fit | −37.0 | 29.7 | −0.3 | 11.5 |
| After fit | −33.9 | 35.6 | 0.0 | 10.3 | ||
| expGeoid-5 | EIGEN-6C4 () | Before fit | −25.6 | 20.2 | −1.6 | 9.2 |
| After fit | −20.5 | 20.6 | 0.0 | 7.9 | ||
| expGeoid-6 | TIM-R6 + EGM2008 | Before fit | −24.6 | 23.5 | 0.7 | 8.9 |
| (mixed model − ) | After fit | −20.2 | 17.5 | 0.0 | 7.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isik, M.S.; Çevikalp, M.R.; Erol, B.; Erol, S. Improvement of GOCE-Based Global Geopotential Models for Gravimetric Geoid Modeling in Turkey. Geosciences 2022, 12, 432. https://doi.org/10.3390/geosciences12120432
Isik MS, Çevikalp MR, Erol B, Erol S. Improvement of GOCE-Based Global Geopotential Models for Gravimetric Geoid Modeling in Turkey. Geosciences. 2022; 12(12):432. https://doi.org/10.3390/geosciences12120432
Chicago/Turabian StyleIsik, Mustafa Serkan, Muhammed Raşit Çevikalp, Bihter Erol, and Serdar Erol. 2022. "Improvement of GOCE-Based Global Geopotential Models for Gravimetric Geoid Modeling in Turkey" Geosciences 12, no. 12: 432. https://doi.org/10.3390/geosciences12120432
APA StyleIsik, M. S., Çevikalp, M. R., Erol, B., & Erol, S. (2022). Improvement of GOCE-Based Global Geopotential Models for Gravimetric Geoid Modeling in Turkey. Geosciences, 12(12), 432. https://doi.org/10.3390/geosciences12120432









