Assessing Antithetic Sampling for Approximating Shapley, Banzhaf, and Owen Values
Abstract
:1. Introduction
2. Preliminaries
2.1. Cooperative Game with Transferable Utility
2.2. Monte Carlo Methods
3. Antithetic Sampling for the Shapley and Banzhaf Values
3.1. Antithetic Subset Generation
3.2. Computing Shapley Values Using Antithetic Sampling
| Algorithm 1 Antithetic sampling for Shapley value approximation |
for do Take a random order for do end for end for |
3.3. Computing Shapley Values Using a Combination of Stratified and Antithetic Sampling
| Algorithm 2 Stratified antithetic sampling for Shapley value approximation |
for do for do Take a random subset of size end for if () then else end if end for |
| Algorithm 3 Sample allocation for stratified antithetic sampling for Shapley value approximation |
if then end if |
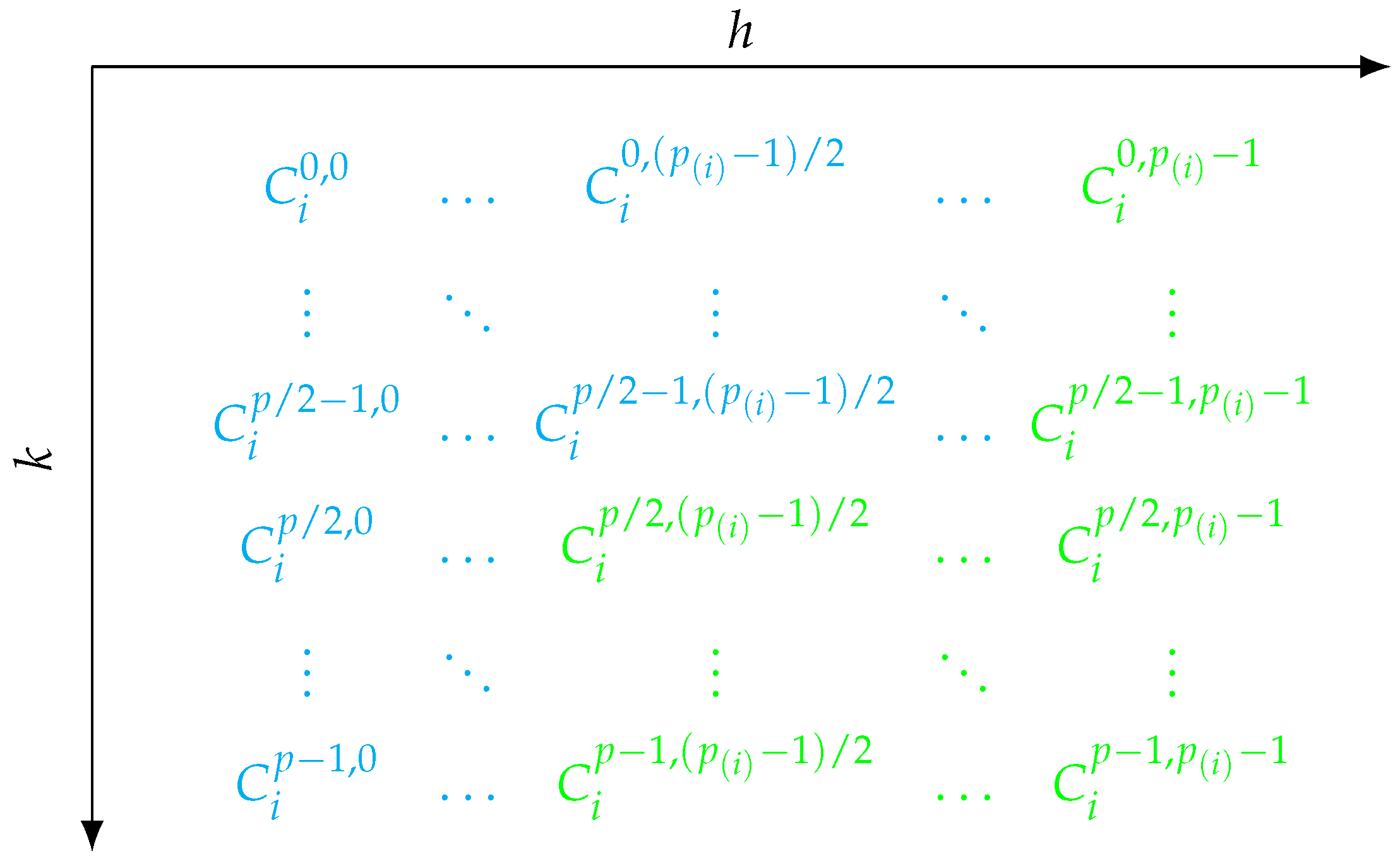
3.4. Computing Shapley Values Using Two-Stage-Stratification and Antithetic Samples
| Algorithm 4 Adapted optimum sample allocation for stratified antithetic sampling for Shapley value approximation |
while there are any negative do for and do if then end if end for for and do if then end if end for end while |
| Algorithm 5 Defining for a given position of player i |
function get_antithetic_S_for_same_position(N, S, i) if then Take a random subset of size else if then Take a random subset of size s end if return end function |
| Algorithm 6 Stratified antithetic sampling for Shapley value approximation with optimum sample allocation |
for and do for do Choose random subset of size h get_antithetic_S_for_same_position(N, S, i) end for end for Obtain according to Algorithm 4 or Castro et al. (2017) [22] for and do for do Choose random subset of size h get_antithetic_S_for_same_position(N, S, i) end for end for |
3.5. Computing Banzhaf Values Using Antithetic Sampling
| Algorithm 7 Antithetic sampling for Banzhaf value approximation |
for do Take a random subset end for |
4. Antithetic Sampling for the Owen Value
4.1. Antithetic Subset Generation for Games with Precoalitions
4.2. Computing Owen Values Using Antithetic Sampling
| Algorithm 8 Antithetic sampling for Owen value approximation |
for do Take a random order , i.e., a permutation compatible with the partition P for do end for end for |
4.3. Computing Owen Values Using a Combination of Stratified and Antithetic Sampling
| Algorithm 9 Stratified antithetic sampling for Owen value approximation |
for do for do if then continue end if for do Choose a random subset of size k Choose a random subset of size end for if ( then else end if end for end for |
| Algorithm 10 Sample allocation for stratified antithetic sampling for Owen value approximation |
for do for do if then continue end if end for end for if then end if |
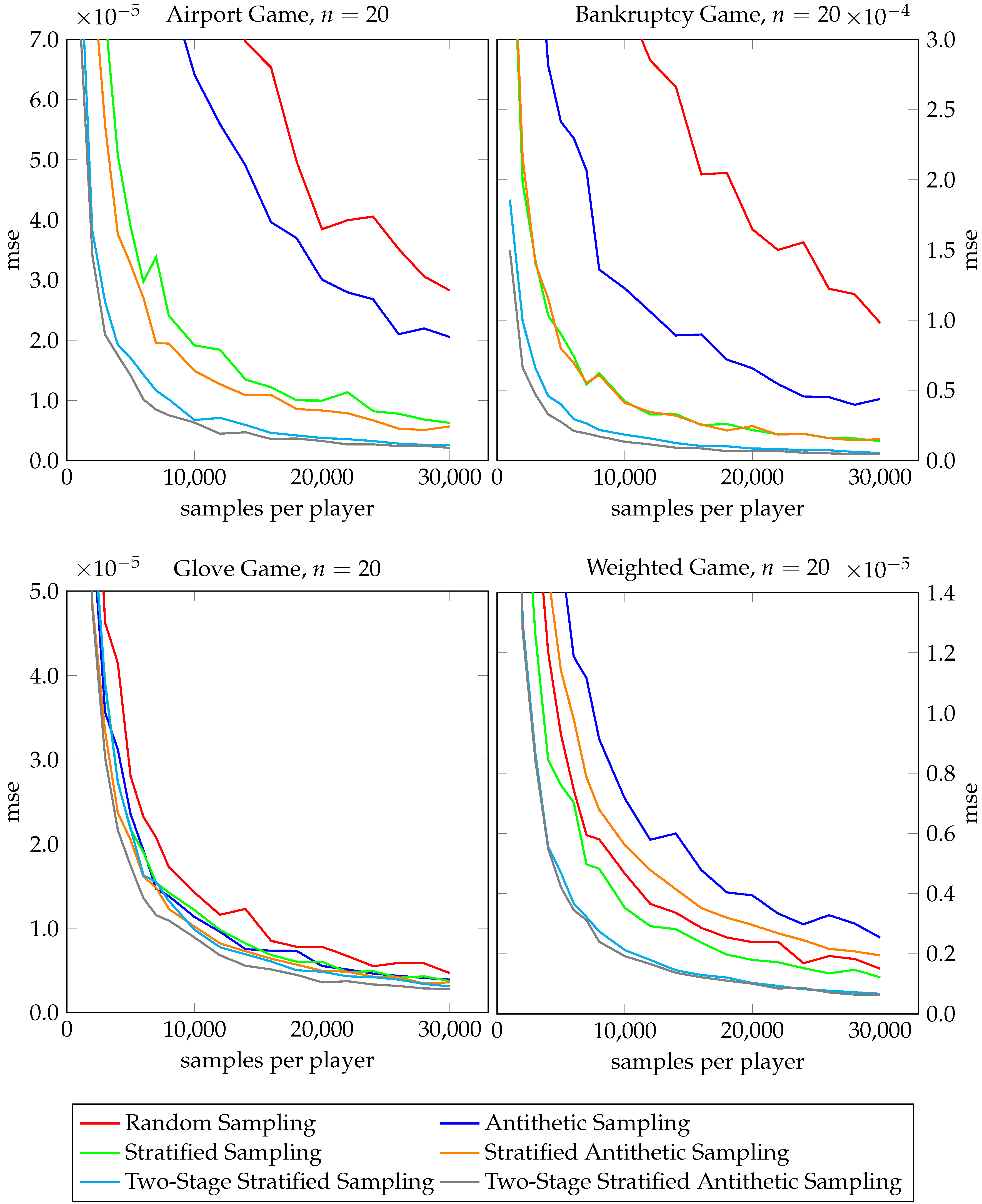
5. Results
5.1. Test Games with Known Solutions
5.2. Numerical Results
5.3. Comparison with the Ergodic Sampling Approach by Illés and Kerényi
5.4. Critical Appraisal of Antithetic Sampling
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Branzei, R.; Dimitrov, D.; Tijs, S. Models in Cooperative Game Theory; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Peleg, B.; Sudhölter, P. Introduction to the Theory of Cooperative Games, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Algaba, E.; Bilbao, J.M.; Fernández-García, J.R. The distribution of power in the European Constitution. Eur. J. Oper. Res. 2007, 176, 1752–1766. [Google Scholar] [CrossRef]
- Kóczy, L.A. Beyond Lisbon. Demographic trends and voting power in the European Union Council of Ministers. Math. Soc. Sci. 2012, 63, 152–158. [Google Scholar] [CrossRef]
- Kóczy, L.A. Brexit and Power in the Council of the European Union. Games 2021, 12, 51. [Google Scholar] [CrossRef]
- Moretti, S.; Patrone, F.; Bonassi, S. The class of microarray games and the relevance index for genes. Top 2007, 15, 256–280. [Google Scholar] [CrossRef]
- Lucchetti, R.; Radrizzani, P. Microarray Data Analysis via Weighted Indices and Weighted Majority Games. In Computational Intelligence Methods for Bioinformatics and Biostatistics. CIBB 2009. Lecture Notes in Computer Science; Masulli, F., Peterson, L.E., Tagliaferri, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 6160, pp. 179–190. [Google Scholar] [CrossRef]
- Algaba, E.; Prieto, A.; Saavedra-Nieves, A.; Hamers, H. Analyzing the Zerkani Network with the Owen Value. In Advances in Collective Decision Making. Studies in Choice and Welfare; Kurz, S., Maaser, N., Mayer, A., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Algaba, E.; Prieto, A.; Saavedra-Nieves, A. Risk analysis sampling methods in terrorist networks based on the Banzhaf value. Risk Anal. 2023, 1–16. [Google Scholar] [CrossRef] [PubMed]
- van Campen, T.; Hamers, H.; Husslage, B.; Lindelauf, R. A new approximation method for the Shapley value applied to the WTC 9/11 terrorist attack. Soc. Netw. Anal. Min. 2018, 8, 3. [Google Scholar] [CrossRef]
- Staudacher, J.; Olsson, L.; Stach, I. Implicit power indices for measuring indirect control in corporate structures. In Transactions on Computational Collective Intelligence XXXVI. Lecture Notes in Computer Science; Nguyen, N., Kowalczyk, R., Mercik, J., Motylska-Kuźma, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 13010, pp. 73–93. [Google Scholar] [CrossRef]
- Staudacher, J.; Olsson, L.; Stach, I. Algorithms for measuring indirect control in corporate networks and effects of divestment. In Transactions on Computational Collective Intelligence XXXVII, Lecture Notes in Computer Science; Nguyen, N.T., Kowalczyk, R., Mercik, J., Motylska-Kuźma, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 13750, pp. 53–74. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. Contrib. Theory Games 1953, 28, 307–317. [Google Scholar]
- Fernández, J.R.; Algaba, E.; Bilbao, J.M.; Jiménez, A.; Jiménez, N.; López, J.J. Generating functions for computing the Myerson value. Ann. Oper. Res. 2002, 9, 143–158. [Google Scholar] [CrossRef]
- Deng, X.; Papadimitriou, C.H. On the complexity of cooperative solution concepts. Math. Oper. Res. 1994, 19, 257–266. [Google Scholar] [CrossRef]
- Faigle, U.; Kern, W. The Shapley value for cooperative games under precedence constraints. Int. J. Game Theory 1992, 21, 249–266. [Google Scholar] [CrossRef]
- Rozemberczki, B.; Watson, L.; Bayer, P.; Yang, H.; Kiss, O.; Nilsson, S.; Sarkar, R. The Shapley value in machine learning. In Proceedings of the 31st International Joint Conference on Artificial Intelligence, Vienna, Austria, 23–29 July 2022; de Raedt, L., Ed.; International Joint Conferences on Artificial Intelligence Organization: Vienna, Austria, 2022; pp. 5572–5579. [Google Scholar] [CrossRef]
- Chen, H.; Covert, I.C.; Lundberg, S.M.; Lee, S. Algorithms to estimate Shapley value feature attributions. Nat. Mach. Intell. 2023, 5, 590–601. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Molnar, C. Interpreting Machine Learning Models with SHAP; LeanPub: Victoria, BC, Canada, 2023; Available online: https://leanpub.com/shap (accessed on 4 October 2023).
- Castro, J.; Gómez, D.; Tejada, J. Polynomial calculation of the Shapley value based on sampling. Comput. Oper. Res. 2009, 36, 1726–1730. [Google Scholar] [CrossRef]
- Castro, J.; Gómez, D.; Molina, E.; Tejada, J. Improving polynomial estimation of the Shapley value by stratified random sampling with optimum allocation. Comput. Oper. Res. 2017, 82, 180–188. [Google Scholar] [CrossRef]
- Mitchell, R.; Cooper, J.; Frank, E.; Holmes, G. Sampling permutations for Shapley value estimation. J. Mach. Learn. Res. 2022, 23, 2082–2127. Available online: http://jmlr.org/papers/v23/21-0439.html (accessed on 4 October 2023).
- Ballester-Ripoll, R. Tensor approximation of cooperative games and their semivalues. Int. J. Approx. Reason. 2022, 142, 94–108. [Google Scholar] [CrossRef]
- Banzhaf, J.F., III. Weighted voting doesn’t work: A mathematical analysis. Rutgers L. Rev. 1964, 19, 317. [Google Scholar]
- Owen, G. Multilinear extensions and the Banzhaf value. Nav. Res. Logist. Q. 1975, 22, 741–750. [Google Scholar] [CrossRef]
- Wang, J.T.; Jia, R. DataBanzhaf: A robust data valuation framework for machine learning. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 25–27 April 2023; Camps-Valls, G., Ruiz, F., Valera, I., Eds.; PMLR: London, UK, 2023; Volume 151, pp. 6388–6421. Available online: https://proceedings.mlr.press/v206/wang23e/wang23e.pdf (accessed on 4 October 2023).
- Owen, G. Values of Games with a Priori Unions. In Mathematical Economics and Game Theory. Lecture Notes in Economics and Mathematical Systems; Henn, R., Moeschlin, O., Eds.; Springer: Berlin/Heidelberg, Germany, 1977; Volume 141, pp. 76–88. [Google Scholar] [CrossRef]
- Saavedra-Nieves, A. On stratified sampling for estimating coalitional values. Ann. Oper. Res. 2023, 320, 325–353. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Sharp, A.; Wexler, T.; Woods, K. Computing shapley value in supermodular coalitional games. In Computing and Combinatorics. COCOON 2012. Lecture Notes in Computer Science; Gudmundsson, J., Mestre, J., Viglas, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7434, pp. 568–579. [Google Scholar] [CrossRef]
- Burgess, M.A.; Chapman, A.C. Stratied Finite Empirical Bernstein Sampling. Preprints 2019, 1–30. [Google Scholar] [CrossRef]
- Burgess, M.A.; Chapman, A.C. Approximating the Shapley Value Using Stratified Empirical Bernstein Sampling. In Proceedings of the IJCAI, Montreal, QC, Canada, 19–27 August 2021; pp. 73–81. [Google Scholar]
- Owen, G. Multilinear extensions of games. Manag. Sci. 1972, 18, 64–79. [Google Scholar] [CrossRef]
- Okhrati, R.; Lipani, A. A Multilinear Sampling Algorithm to Estimate Shapley Values. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 7992–7999. [Google Scholar] [CrossRef]
- Soufiani, H.A.; Charles, D.X.; Chickering, D.M.; Parkes, D.C. Approximating the shapley value via multi-issue decomposition. In Proceedings of the International Foundation for Autonomous Agents and Multiagent Systems, Paris, France, 5–9 May 2014; pp. 1209–1216. [Google Scholar]
- Corder, K.; Decker, K. Shapley value approximation with divisive clustering. In Proceedings of the 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 234–239. [Google Scholar] [CrossRef]
- Jethani, N.; Sudarsan, M.; Covert, I.C.; Lee, S. Fastshap: Real-time shapley value estimation. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Saavedra-Nieves, A.; García-Jurado, I.; Fiestras-Janeiro, M.G. Estimation of the Owen value based on sampling. In The Mathematics of the Uncertain: A Tribute to Pedro Gil. Studies in Systems, Decision and Control; Gil, E., Gil, E., Gil, J., Gil, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 142, pp. 347–356. [Google Scholar] [CrossRef]
- Botev, Z.; Ridder, A. Variance reduction. In Wiley statsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Rubinstein, R.; Kroese, D. Monte Carlo methods. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 48–58. [Google Scholar] [CrossRef]
- Lomeli, M.; Rowland, M.; Gretton, A.; Ghahramani, Z. Antithetic and Monte Carlo kernel estimators for partial rankings. Stat. Comput. 2019, 29, 1127–1147. [Google Scholar] [CrossRef]
- Maleki, S.; Tran-Thanh, L.; Hines, G.; Rahwan, T.; Rogers, A. Bounding the estimation error of sampling-based Shapley value approximation. arXiv 2013, arXiv:1306.4265. [Google Scholar]
- Neyman, J. On the Two Different Aspects of the Representative Method: The Method of Stratified Sampling and the Method of Purposive Selection. J. R. Stat. 1934, 97, 558–625. [Google Scholar] [CrossRef]
- Saavedra-Nieves, A. Statistics and game theory: Estimating coalitional values in R software. Oper. Res. Lett. 2021, 49, 129–135. [Google Scholar] [CrossRef]
- Littlechild, S.C.; Thompson, G.F. Aircraft landing fees: A game theory approach. Bell J. Econ. 1977, 8, 186–204. [Google Scholar] [CrossRef]
- Borm, P.; Hamers, H.; Hendrickx, R. Operations research games: A survey. Top 2001, 9, 139–199. [Google Scholar] [CrossRef]
- Vázquez-Brage, M.; van den Nouweland, A.; García-Jurado, I. Owen’s coalitional value and aircraft landing fees. Math. Soc. Sci. 1997, 34, 273–286. [Google Scholar] [CrossRef]
- Staudacher, J.; Anwander, J. Using the R Package CoopGame for the Analysis, Solution and Visualization of Cooperative Games with Transferable Utility. R Vignette for Package Version 0.2.2. 2021. Available online: https://cran.r-project.org/package=CoopGame (accessed on 20 October 2023).
- O’Neill, B. A problem of rights arbitration from the Talmud. Math. Soc. Sci. 1982, 2, 345–371. [Google Scholar] [CrossRef]
- Peters, H. Game Theory: A Multi-Leveled Approach, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Staudacher, J.; Kóczy, L.Á.; Stach, I.; Filipp, J.; Kramer, M.; Noffke, T.; Olsson, L.; Pichler, J.; Singer, T. Computing power indices for weighted voting games via dynamic programming. Oper. Res. Dec. 2021, 31, 123–145. [Google Scholar] [CrossRef]
- Staudacher, J.; Wagner, F.; Filipp, J. Dynamic Programming for Computing Power Indices for Weighted Voting Games with Precoalitions. Games 2021, 13, 6. [Google Scholar] [CrossRef]
- Staudacher, J. Computing the Public Good index for weighted voting games with precoalitions using dynamic programming. In Power and Responsibility: Interdisciplinary Perspectives for the 21st Century in Honor of Manfred J. Holler; Leroch, M.A., Rupp, F., Eds.; Springer: Cham, Switzerland, 2023; pp. 107–124. [Google Scholar] [CrossRef]
- R Core Team, R. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 4 October 2023).
- Illés, F.; Kerényi, P. Estimation of the Shapley value by ergodic sampling. arXiv 2022, arXiv:1906.05224v2. [Google Scholar]
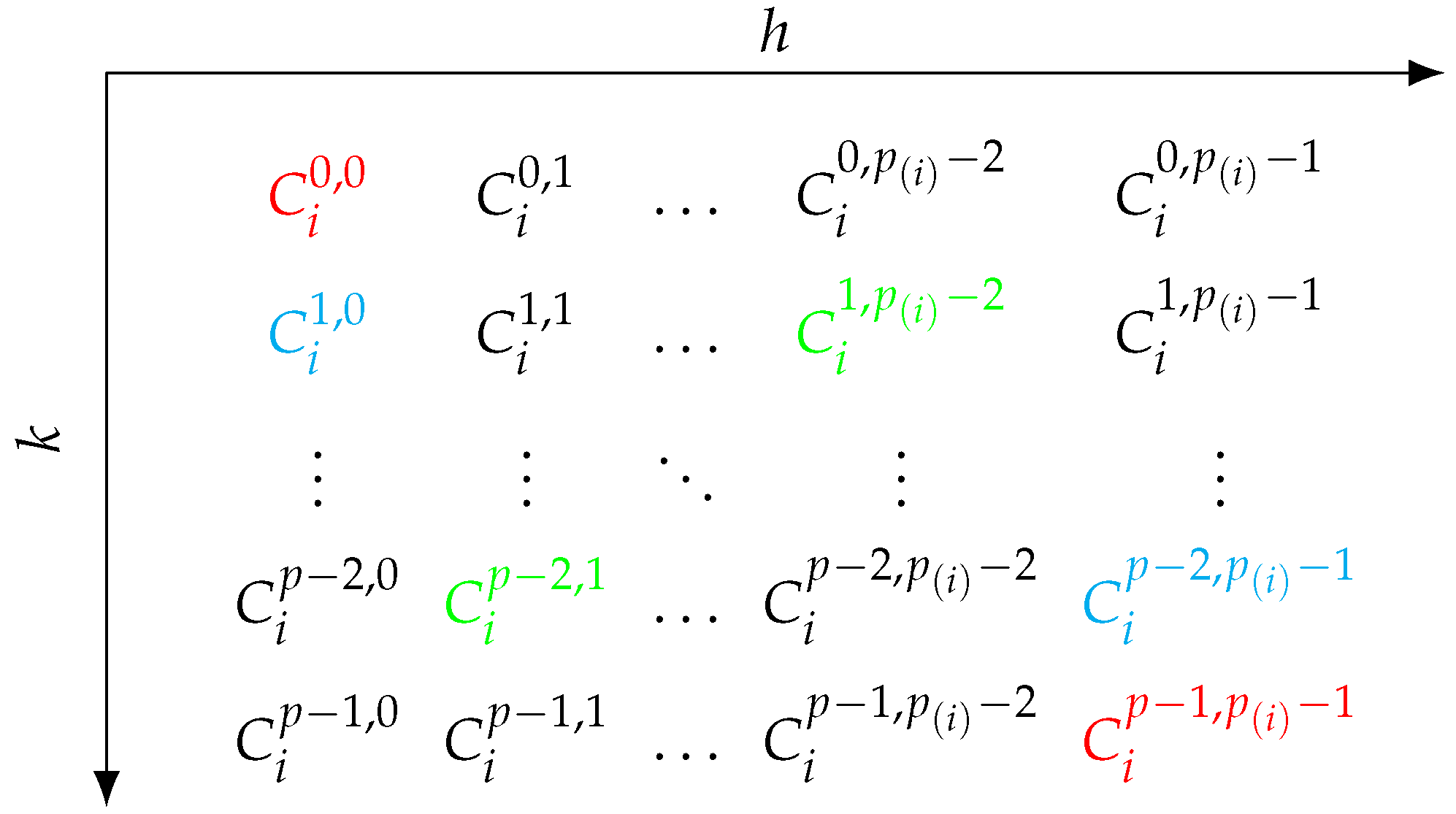
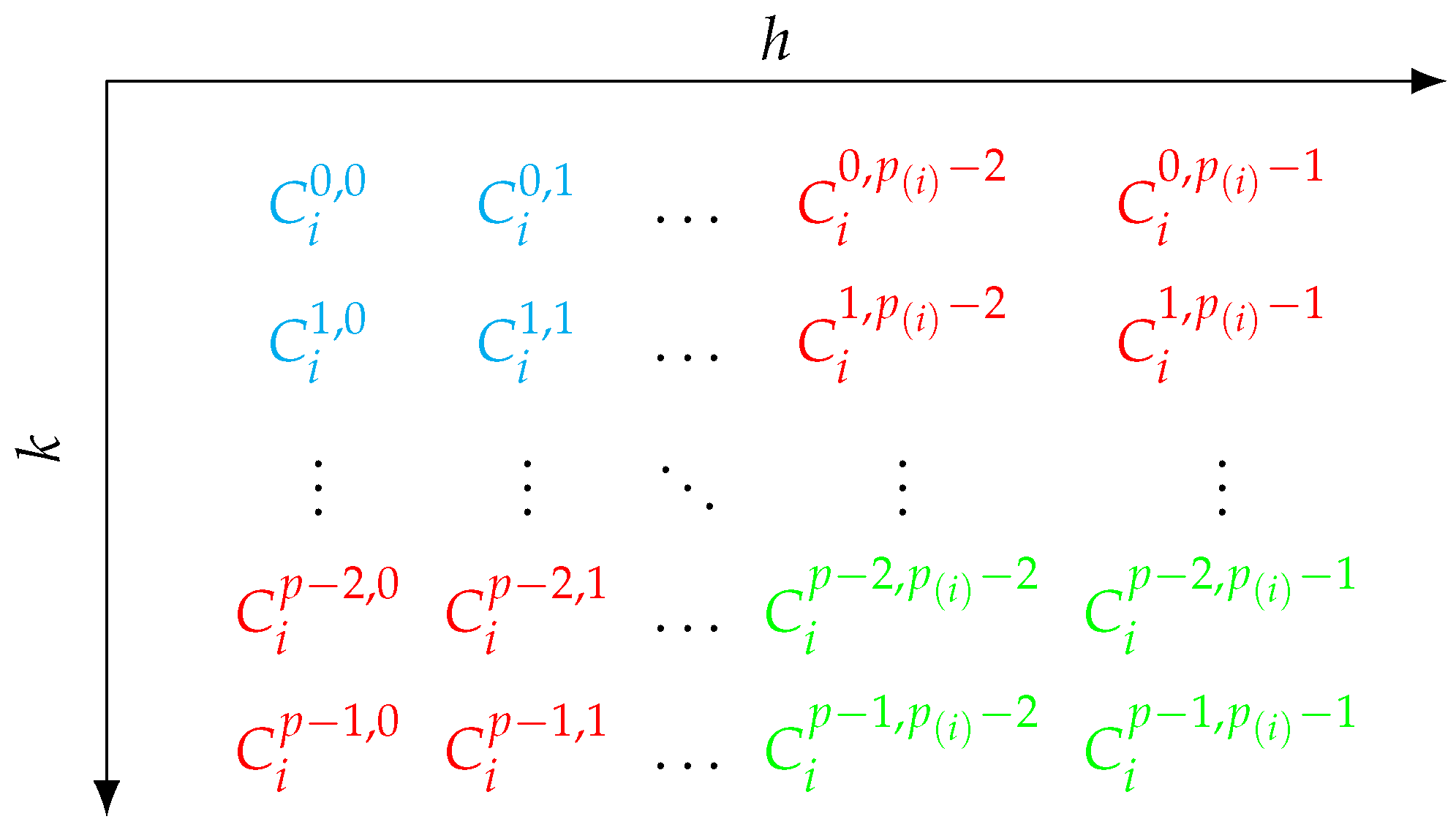




| Game | Algorithm | Exec Time | MSE |
|---|---|---|---|
| Random Sampling | 17.6 s | ||
| Airport Game, | Random Antithetic Sampling | 21.8 s | |
| players, | Stratified Sampling | 30.7 s | |
| Medium variance (17) | Stratified Antithetic Sampling | 24.2 s | |
| Two-Stage Stratified Sampling | 29.6 s | ||
| Two-Stage Stratified Antithetic Sampling | 37.4 s | ||
| Random Sampling | 25.5 s | ||
| Airport Game, | Random Antithetic Sampling | 32.6 s | |
| players, | Stratified Sampling | 45.7 s | |
| Low variance (16) | Stratified Antithetic Sampling | 36.0 s | |
| Two-Stage Stratified Sampling | 42.4 s | ||
| Two-Stage Stratified Antithetic Sampling | 53.9 s | ||
| Random Sampling | 32.6 s | ||
| Airport Game, | Random Antithetic Sampling | 42.2 s | |
| players, | Stratified Sampling | 59.4 s | |
| High variance (18) | Stratified Antithetic Sampling | 47.2 s | |
| Two-Stage Stratified Sampling | 53.3 s | ||
| Two-Stage Stratified Antithetic Sampling | 69.4 s | ||
| Random Sampling | 39.2 s | ||
| Airport Game | Random Antithetic Sampling | 51.8 s | |
| players, | Stratified Sampling | 72.4 s | |
| Medium variance (17) | Stratified Antithetic Sampling | 56.8 s | |
| Two-Stage Stratified Sampling | 63.5 s | ||
| Two-Stage Stratified Antithetic Sampling | 81.8 s |
| Algorithm | Exec Time | MSE |
|---|---|---|
| Random Sampling | 28.8 s | |
| Random Antithetic Sampling | 30.6 s | |
| Stratified Sampling | 40.6 s | |
| Stratified Antithetic Sampling | 34.2 s | |
| Two-Stage Stratified Sampling | 41.4 s | |
| Two-Stage Stratified Antithetic Sampling | 48.7 s | |
| Ergodic Sampling, | 43.4 s | |
| Ergodic Sampling, | 43.6 s | |
| Ergodic Sampling, | 45.3 s | |
| Ergodic Sampling, | 47.5 s | |
| Ergodic Sampling, | 51.1 s | |
| Ergodic Sampling, | 59.3 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staudacher, J.; Pollmann, T. Assessing Antithetic Sampling for Approximating Shapley, Banzhaf, and Owen Values. AppliedMath 2023, 3, 957-988. https://doi.org/10.3390/appliedmath3040049
Staudacher J, Pollmann T. Assessing Antithetic Sampling for Approximating Shapley, Banzhaf, and Owen Values. AppliedMath. 2023; 3(4):957-988. https://doi.org/10.3390/appliedmath3040049
Chicago/Turabian StyleStaudacher, Jochen, and Tim Pollmann. 2023. "Assessing Antithetic Sampling for Approximating Shapley, Banzhaf, and Owen Values" AppliedMath 3, no. 4: 957-988. https://doi.org/10.3390/appliedmath3040049
APA StyleStaudacher, J., & Pollmann, T. (2023). Assessing Antithetic Sampling for Approximating Shapley, Banzhaf, and Owen Values. AppliedMath, 3(4), 957-988. https://doi.org/10.3390/appliedmath3040049







