Semi-Active Vibration Control for High-Speed Elevator Using Magnetorheological Damper

Abstract

This paper presents the results of investigating the application of magnetorheological fluids in controlling the lateral and angular vibrations of a high-speed elevator. Numerical simulations are performed for a mathematical model with two degrees of freedom. The lateral and rotational accelerations are analyzed for different travel speeds to determine passenger comfort levels. To attenuate the elevator vibrations, the introduction of a magnetorheological damper in parallel with the passive damper of the elevator rollers is considered. To semi-actively control the dissipative forces of the magnetorheological fluids, a State-Dependent Riccati Equation (SDRE control) is proposed. The numerical results demonstrate that using an MR damper makes it possible to reduce the acceleration levels of the elevator cabin, thus improving passenger comfort and reducing the elevator’s vibration levels and wear on the mechanical and electronic components of the elevator. In addition to the results, a detailed sensitivity analysis is presented.

1. Introduction

With the construction of increasingly tall buildings, the need for elevators with increasingly higher vertical displacement capacity has arisen. However, the upward and downward movements in the elevator shaft generate vibrations, discomfort for passengers, and wear on elevator components [1,2,3,4,5,6]. The elevator travel speed, deviations in the guide rail profile, and the dynamic parameters of the rolling guide shoe are the primary sources of vibration in the elevator cabin [1,2,3,4,5,6,7]. In [7], the influence of the operating speed of a high-speed elevator, the deviation of the guide rail profile, and the dynamic parameters of the rolling guide shoe on the horizontal vibration of the car and passenger comfort is presented [1,2,7].

With the need to reduce the vibration levels of the elevator cabin and increase its travel speed, research on control systems and actuators applied to lateral and angular acceleration control has grown recently [1,2,3]. In [8], a sliding mode controller is considered to reduce the horizontal vibrations of the elevator cabin caused by irregularities in the guide rail. In [9], the horizontal vibrations caused by guide “casters” in the high-speed elevator car are examined. In [10], the vibrations of the elevator car generated by the irregularity of the guide rail, uncertainty in the modeling of the guide shoe, wear, and the aging of the spring between the guide shoe bearing and the guide rail are investigated. Based on this, an H2/H∞ control system is proposed to reduce the vibrations. In [11,12], the vibrations originating from the elevator lifting cables are investigated.

This paper proposes the control of the lateral and angular vibrations of an elevator with two degrees of freedom using a magnetorheological (MR) damper. The MR damper force is regulated by controlling the electrical voltage applied to the damper coil, thus acting on the magnetorheological fluid in the damper. To determine the relationship between electrical voltage and damper force, the LuGre friction model is used, and an SDRE (State-Dependent Riccati Equation) control is used to determine the ideal force to be applied in the control. Unlike in the works [1,3,6,7,13], in which only lateral displacements are considered, this paper assesses lateral and angular displacements and the control of their displacements. To control lateral and angular vibrations, an MR damper is included parallel to the roller damper of the elevator damping system. Control through the use of the MR damper builds on the works [2,4,8,9,10,11], which consider only the lateral and angular vibrations of the elevator without considering the MR damper. The use of the MR damper in this paper is due to its importance and relevance to research in the area of smart magnetic materials and vibration control, as well as its versatility. The number of research studies on applying MR dampers has increased annually, with them being used in vehicle suspension systems [14,15,16,17], in the semi-active damping control of aircraft landing gear [18,19,20], in transverse suspension systems for railway vehicles [21,22,23], in smart prosthetic knee joints [24], and in Earthquake-resistant building protection [25,26].

Magnetorheological (MR) fluids are smart materials considered semi-active devices and belong to the class of controllable fluids. They comprise significant amounts of micrometric-sized, highly magnetizable solid particles (up to 50% vol) in a non-magnetizable liquid, such as mineral and silicone oils, polyesters, polyethers, synthetic hydrocarbons, and water. Typically, the solid particles are carbonyl iron particles, and they are used due to their high saturation magnetization. The main characteristic of MR fluids is their ability to change from viscous liquids to semi-solids in milliseconds when exposed to a magnetic field. This characteristic gives them a simple architecture and a fast response when interfacing electronic controllers and mechanical systems, thus enabling their use in mechanical systems requiring semi-active vibration control or torque transmission [27,28,29,30]. Valve mode, direct cut mode, and squeezed film mode are the three basic design forms of equipment that uses MR fluids as actuators. In valve mode, the magnetic poles are fixed, and the fluid is forced to pass between these poles, as illustrated in Figure 1.

Valve mode can be used in hydraulically controlled valve dampers since the poles perform the valve function as the magnetic field strength varies, altering the viscosity of the fluid passing between the poles. This variable resistance to fluid flow allows the use of MR fluid in viscous dampers and other electrically controllable devices [27].

In [31], an MR damper was used to control the vibrations of the wheel motor of an electric vehicle. Damper force control was performed by adjusting the electrical voltage estimated by the Bouc-Wen mode and using a PID controller. Numerical results considering MATLAB/Simulink software were presented to demonstrate the effectiveness of the proposed control. In [32], an MR damper in vehicle seat suspension is considered. A narrowband-frequency semi-active control (NFSSC) algorithm is proposed to optimize vibration suppression. Experimental results demonstrate the effectiveness of the MR damper as a semi-active vibration control. In [33], the damping performance of MR dampers is investigated in vehicle vibration control to improve vehicle ride quality. MR damper force is controlled by regulating the electrical current applied to the damper coil. In [34], the control of the electrical current of the MR damper is proposed, considering the damper in a semi-active suspension system applied to vehicle suspension. Numerical results demonstrated the proposed control’s effectiveness and performance in the semi-active suspension system based on the MR feedback damper. In [7], fuzzy control is considered for the electric current control of a magnetorheological damper used in the vibration control of a high-speed elevator.

2. Materials and Methods

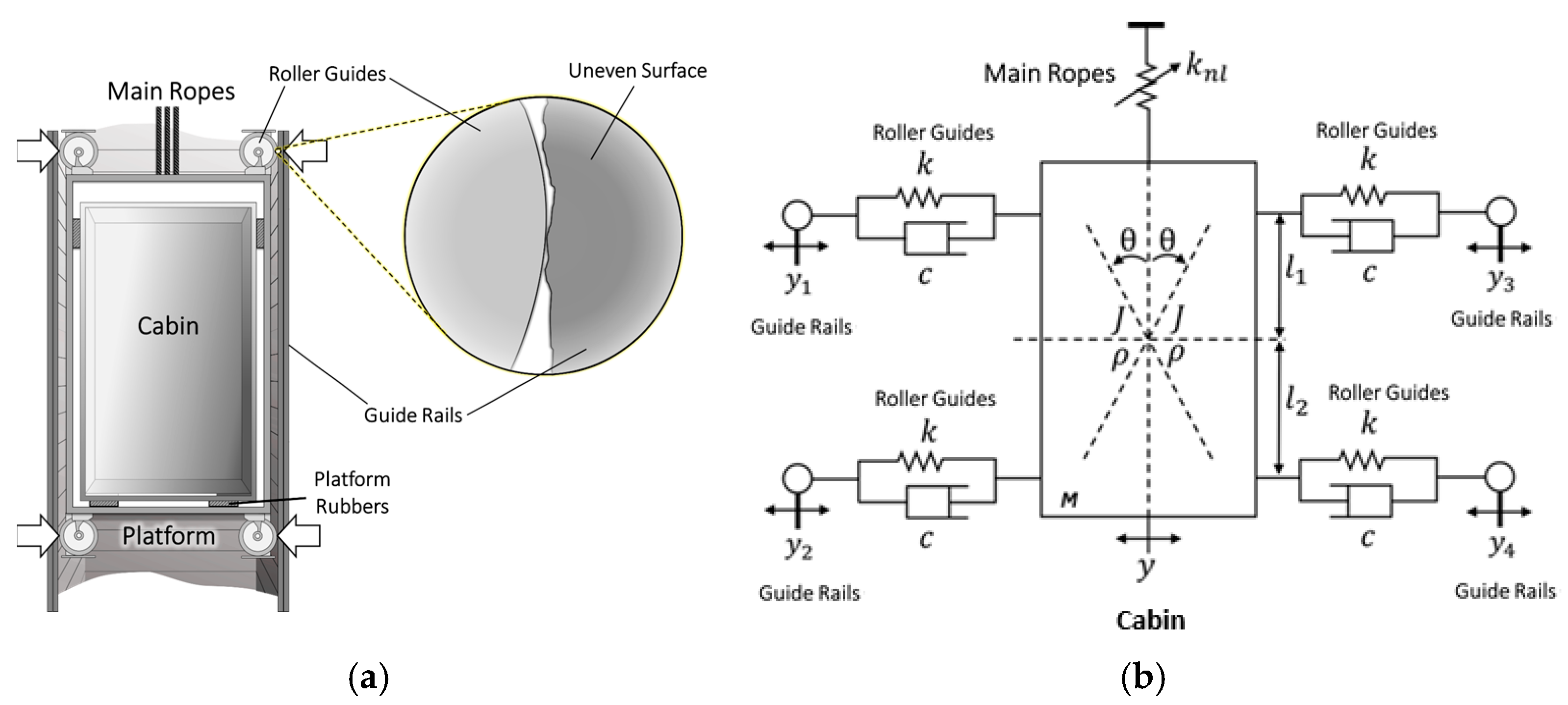
2.1. Mathematical Model of the Elevator

Figure 2 presents a dynamic representation of the elevator movements, with two degrees of freedom considered in this model. In Figure 2b, (y) is the translation of the cabin in the horizontal direction, and (θ) is its rotation around the centroid. Guide shoes and their rollers correspond to the contact of the elevator cabin with the guide rails. In vertical movement, the steel cable’s rigidity is considered an elastic spring with a cubic stiffness coefficient [2,4,8,9,10,11].

The roller guide shoes are composed of a spring and a shock absorber in parallel, as can be seen in Figure 1, where y₁, y₂, y₃, and y₄ are the displacements of the four guide shoes in the horizontal direction, excited by the unevenness of the guide rails; k_nl represents the coefficient of stiffness of the elevator cables with reference to the tilting movement of the cabin.

Considering Figure 2, we can determine the horizontal displacement of the four guide shoes by the following equation [2]:

$$\begin{array}{l}{y^{\prime }}_1={y^{\prime }}_3=y-l_1\theta \\ {y^{\prime }}_2={y^{\prime }}_4=y-l_2\theta \end{array}$$

(1)

The deformation of the springs and shock absorbers of the shoes can be determined by the following equations [21]:

$$\begin{array}{l}{q}_1={y^{\prime }}_1-y_1=y-l_1\theta -y_1\\ q_2={y^{\prime }}_2-y_2=y+l_2\theta -y_2\\ q_3={y^{\prime }}_3-y_3=y-l_1\theta -y_3\\ q_4={y^{\prime }}_4-y_4=y+l_2\theta -y_4\end{array}$$

(2)

The mathematical modeling of the lateral and angular vibrations of the elevator can be obtained considering the dynamic characteristics of the elastic and damping elements and the D’Alembert principle [2], including the influence of the elevator hoisting cable [3].

$$\left\{\begin{array}{l}\ddot{y}=-{\alpha }_1\dot{y}-{\alpha }_{2}y-{\alpha }_3{y}^3+{\alpha }_4\dot{\theta }+{\alpha }_5\theta +{\alpha }_6{\theta }^3+{\alpha }_7{\dot{y}}_1-{\alpha }_8{y}_1+{\alpha }_9{\dot{y}}_2-{\alpha }_{10}{y}_2\\ +{\alpha }_{11}{\dot{y}}_3-{\alpha }_{12}{y}_3+{\alpha }_{13}{\dot{y}}_4-{\alpha }_{14}{y}_4\\ \ddot{\theta }={\beta }_{1}y+{\beta }_2\theta +{\beta }_3{y}^3+{\beta }_4{\theta }^3+{\beta }_3\dot{y}+{\beta }_4\dot{\theta }-{\beta }_5{y}_1+{\beta }_6{y}_2-{\beta }_7{y}_3\\ +{\beta }_8{y}_4-{\beta }_9{\dot{y}}_1+{\beta }_{10}{\dot{y}}_2-{\beta }_{11}{\dot{y}}_3+{\beta }_{12}{\dot{y}}_4\end{array}\right.$$

(3)

where ${\alpha }_1={\displaystyle \frac{\left(c_1+c_2+c_3+c_4\right)}{M}}$, ${\alpha }_2={\displaystyle \frac{\left(k_1+k_2+k_3+k_4\right)}{M}}$, ${\alpha }_3={\displaystyle \frac{k_{nl}}{M}}$, ${\beta }_7={\displaystyle \frac{l_1{k}_3}{J}}$, ${\beta }_8={\displaystyle \frac{l_2{k}_4}{J}}$, ${\alpha }_4={\displaystyle \frac{\left(c_1{l}_1-c_2{l}_2+c_3{l}_1-c_4{l}_2\right)}{M}}$, ${\alpha }_5={\displaystyle \frac{\left(k_1{l}_1-k_2{l}_2+k_3{l}_1-k_4{l}_2\right)}{M}}$, ${\alpha }_6={\displaystyle \frac{\left(k_{nl}{l}_1\right)}{M}}$, ${\alpha }_7={\displaystyle \frac{c_1}{M}}$, ${\alpha }_8={\displaystyle \frac{k_1}{M}}$, ${\alpha }_9={\displaystyle \frac{c_2}{M}}$, ${\alpha }_{10}={\displaystyle \frac{k_2}{M}}$, ${\alpha }_{11}={\displaystyle \frac{c_3}{M}}$, ${\alpha }_{12}={\displaystyle \frac{k_3}{M}}$, ${\alpha }_{13}={\displaystyle \frac{c_4}{M}}$, ${\alpha }_{14}={\displaystyle \frac{k_4}{M}}$, ${\beta }_1={\displaystyle \frac{\left(-l_2\left(k_2+k_4\right)+l_1\left(k_1+k_3\right)\right)}{J}}$, ${\beta }_2={\displaystyle \frac{\left(-l_2\left(k_2+k_4\right)-l_1^2\left(k_1+k_3\right)\right)}{J}}$, ${\beta }_3={\displaystyle \frac{k_{nl}{l}_1}{J}}$, ${\beta }_4={\displaystyle \frac{-k_{nl}{l}_1^2}{J}}$, ${\beta }_5{\displaystyle \frac{\left(-l_2\left(c_2+c_4\right)+l_1\left(c_1+c_3\right)\right)}{J}}$, ${\beta }_6{\displaystyle \frac{\left(-l_2^2\left(c_2+c_4\right)-l_1^2\left(c_1+c_3\right)\right)}{J}}$, ${\beta }_7={\displaystyle \frac{l_1{k}_1}{J}}$, ${\beta }_8={\displaystyle \frac{l_2{k}_2}{J}}$, ${\beta }_9={\displaystyle \frac{l_1{k}_3}{J}}$, ${\beta }_{10}={\displaystyle \frac{l_2{k}_4}{J}}$, ${\beta }_{11}={\displaystyle \frac{l_1{c}_1}{J}}$, ${\beta }_{12}={\displaystyle \frac{l_2{c}_2}{J}}$, ${\beta }_{13}={\displaystyle \frac{l_1{c}_3}{J}}$, and ${\beta }_{14}={\displaystyle \frac{l_2{c}_4}{J}}$.

c₁, c₂, c₃, and c₄ are the equivalent dampings of the guide shoe (Ns/m), J the moment of inertia of the car (kgm²), k₁, k₂, k₃, and k₄ the equivalent stiffness of the guide shoe (N/m), l₁ the distance between the car system mass center and the upper guide shoe (m), l₂ the distance between the car system mass center and the lower guide shoe (m), “M” the mass of the car system (kg), Δ_m the rated load of the car (kg), v the vertical velocity of the elevator (m/s), y the horizontal displacement (m), θ the angular displacement around the centroid (rad), and k_nl the coefficient of stiffness of the elevator cables with reference to the tilting movement of the cabin (N/m). The external vibrations associated with the elevator’s travel speed are represented by $y_1$, $y_2$, $y_3$, $y_4$, ${\dot{y}}_1$, ${\dot{y}}_2$, ${\dot{y}}_3$, and ${\dot{y}}_4$.

Equation (3) can be represented in a system of first-order differential equations:

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=-{\alpha }_1{x}_2-{\alpha }_2{x}_1-{\alpha }_3{x_1}^3+{\alpha }_4{x}_4+{\alpha }_5{x}_3+{\alpha }_6{x_3}^3+{\alpha }_7{\dot{y}}_1-{\alpha }_8{y}_1+{\alpha }_9{\dot{y}}_2-{\alpha }_{10}{y}_2\\ +{\alpha }_{11}{\dot{y}}_3-{\alpha }_{12}{y}_3+{\alpha }_{13}{\dot{y}}_4-{\alpha }_{14}{y}_4\\ {\dot{x}}_4=x_4\\ {\dot{x}}_4={\beta }_1{x}_1+{\beta }_2{x}_3+{\beta }_3{x_1}^3+{\beta }_4{x_3}^3+{\beta }_3{x}_2+{\beta }_4{x}_4-{\beta }_5{y}_1+{\beta }_6{y}_2-{\beta }_7{y}_3\\ +{\beta }_8{y}_4-{\beta }_9{\dot{y}}_1+{\beta }_{10}{\dot{y}}_2-{\beta }_{11}{\dot{y}}_3+{\beta }_{12}{\dot{y}}_4\end{array}\right.$$

(4)

where $x_1=y$, $x_2=\dot{y}$, $x_3=\theta$, and $x_4=\dot{\theta }$.

Alternatively, it can be expressed in the following matrix form:

$$\begin{array}{c}\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ -{\alpha }_2-{\alpha }_3{x_1}^2& -{\alpha }_1& {\alpha }_5+{\alpha }_6{x_3}^2& {\alpha }_4\\ 0& 0& 0& 1\\ {\beta }_1+{\beta }_3{x_1}^2& {\beta }_3& {\beta }_4{x_3}^2+{\beta }_2& {\beta }_4\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]+\\ \left[\begin{array}{c}0\\ {\alpha }_6{\dot{y}}_1-{\alpha }_7{y}_1+{\alpha }_8{\dot{y}}_2-{\alpha }_9{y}_2+{\alpha }_{10}{\dot{y}}_3-{\alpha }_{11}{y}_3+{\alpha }_{12}{\dot{y}}_4-{\alpha }_{13}{y}_4\\ 0\\ -{\beta }_5{y}_1+{\beta }_6{y}_2-{\beta }_7{y}_3+{\beta }_8{y}_4-{\beta }_9{\dot{y}}_1+{\beta }_{10}{\dot{y}}_2-{\beta }_{11}{\dot{y}}_3+{\beta }_{12}{\dot{y}}_4\end{array}\right]\end{array}$$

(5)

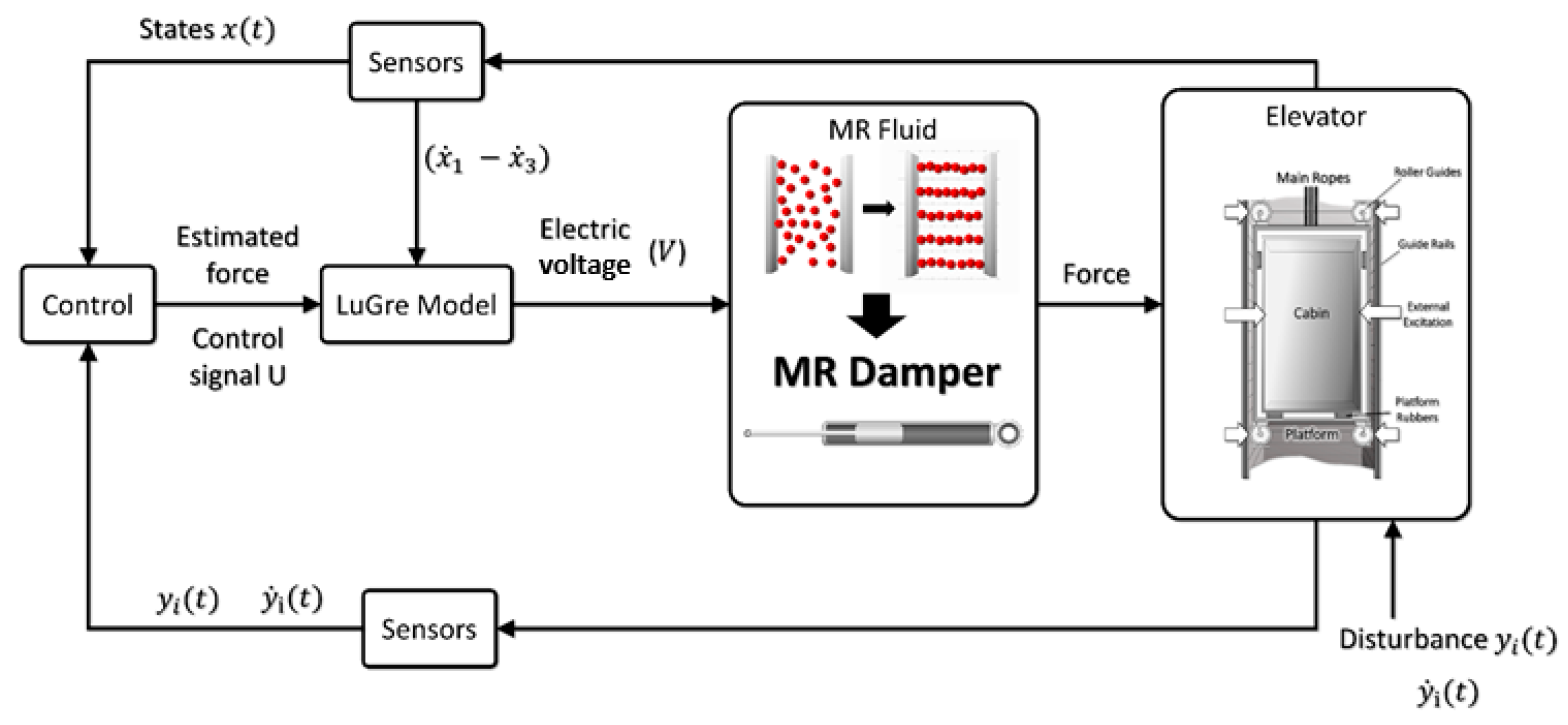
2.2. Proposed Elevator Vibration Control System

To reduce the vibration levels of the elevator cabin, the introduction of magnetorheological dampers in parallel with the passive roller dampers will be considered, as shown in Figure 3.

Considering the costs of the MR damper control system, the control proposal presented in Figure 3 aims to reduce control costs and enable the best reductions in elevator vibration levels in the case of using only one MR damper.

In Equation (6), we present the system with the proposed control.

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=-{\alpha }_1{x}_2-{\alpha }_2{x}_1-{\alpha }_3{x_1}^3+{\alpha }_4{x}_4+{\alpha }_5{x}_3+{\alpha }_6{x_3}^3+{\alpha }_7{\dot{y}}_1-{\alpha }_8{y}_1+{\alpha }_9{\dot{y}}_2-{\alpha }_{10}{y}_2\\ +{\alpha }_{11}{\dot{y}}_3-{\alpha }_{12}{y}_3+{\alpha }_{13}{\dot{y}}_4-{\alpha }_{14}{y}_4-{\alpha }_{14}{F}_{mr}\\ {\dot{x}}_4=x_4\\ {\dot{x}}_4={\beta }_1{x}_1+{\beta }_2{x}_3+{\beta }_3{x_1}^3+{\beta }_4{x_3}^3+{\beta }_3{x}_2+{\beta }_4{x}_4-{\beta }_5{y}_1+{\beta }_6{y}_2-{\beta }_7{y}_3\\ +{\beta }_8{y}_4-{\beta }_9{\dot{y}}_1+{\beta }_{10}{\dot{y}}_2-{\beta }_{11}{\dot{y}}_3+{\beta }_{12}{\dot{y}}_4+{\beta }_{13}{F}_{mr}\end{array}\right.$$

(6)

where ${\alpha }_{14}={\displaystyle \frac{1}{M}}$ and ${\beta }_{13}={\displaystyle \frac{l_1}{J}}$.

2.3. Mathematical Model for MR Damper

The LuGre friction model was considered in this paper because it more accurately describes the characteristics of viscous sliding motion, friction hysteresis, pre-sliding displacement, and variable maximum static friction force in the friction process, features observed in MR fluids, where shear stress is generated by the deflection of particle chains [35,36,37]. To include the nonlinear friction phenomena of magnetorheological dampers and their hysteresis effects, this paper will consider the LuGre friction model, as presented in Equation (7) [36,38]:

$$\begin{array}{l}{F}_{mrd}={\sigma }_{a}z+{\sigma }_{0}zV+{\sigma }_1\dot{z}+{\sigma }_2\dot{y}+{\sigma }_b\dot{y}V\\ \dot{z}=\dot{y}-{\sigma }_0{a}_0\left|\dot{y}\right|z\end{array}$$

(7)

where F_mrd is the damping force, $V$ is the input voltage, $z$ is the internal state variable, and $\dot{y}$ is the velocity of the damper piston, with ${\sigma }_0$, ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_a$, ${\sigma }_b$, and $a_0$ being constant values.

Considering Equation (7), we can determine the electrical voltage dependent on the desired force $F_{mrd}$ by isolating the variable $V$:

$$V={\displaystyle \frac{F_{mrd}-{\sigma }_{a}z-{\sigma }_1\dot{z}-{\sigma }_2\dot{y}}{{\sigma }_{0}z+{\sigma }_b\dot{y}}}$$

(8)

Considering the case of a control strategy, to determine the desired force, $F_{mrd}$, we have a maximum limit for the electrical voltage ($V_{\max }$), $F_{mrd}=U$, and negative electrical voltages are not used. In this case, the rule for obtaining the electrical voltage is given by the following equation:

$$\nu =\left\{\begin{array}{cc}if\begin{array}{c}\end{array}V<0 \to & V=0\\ if\begin{array}{c}\end{array}0<V<V_{\max } \to & V={\displaystyle \frac{U-{\sigma }_{a}z-{\sigma }_1\dot{z}-{\sigma }_2\dot{y}}{{\sigma }_{0}z+{\sigma }_b\dot{y}}}\\ if\begin{array}{c}\end{array}V>V_{\max } \to & V=V_{\max }\end{array}\right.$$

(9)

2.4. Electrical Voltage Control Project by SDRE Control

Consider system (6) in the following form:

$$\dot{X}=AX+BU+G$$

(10)

where $X$ is the states of the system, A(X) is the state matrix, B is the control matrix, $U$ is the feedback control, and $G$ is the terms that do not contain the states.

For system (6), we have the following matrices:

$X=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]$, $A=\left[\begin{array}{cccc}0& 1& 0& 0\\ -{\alpha }_2-{\alpha }_3{x_1}^2& -{\alpha }_1& {\alpha }_5+{\alpha }_6{x_3}^2& {\alpha }_4\\ 0& 0& 0& 1\\ {\beta }_1+{\beta }_3{x_1}^2& {\beta }_3& {\beta }_4{x_3}^2+{\beta }_2& {\beta }_4\end{array}\right]$, $B=\left[\begin{array}{cc}0& 0\\ -{\alpha }_{14}& 0\\ 0& 0\\ 0& {\beta }_{13}\end{array}\right]$, and $G(t)=\left[\begin{array}{c}0\\ {\alpha }_6{\dot{y}}_1-{\alpha }_7{y}_1+{\alpha }_8{\dot{y}}_2-{\alpha }_9{y}_2+{\alpha }_{10}{\dot{y}}_3-{\alpha }_{11}{y}_3+{\alpha }_{12}{\dot{y}}_4-{\alpha }_{13}{y}_4\\ 0\\ -{\beta }_5{y}_1+{\beta }_6{y}_2-{\beta }_7{y}_3+{\beta }_8{y}_4-{\beta }_9{\dot{y}}_1+{\beta }_{10}{\dot{y}}_2-{\beta }_{11}{\dot{y}}_3+{\beta }_{12}{\dot{y}}_4\end{array}\right]$.

The feedback control is obtained from the following [39]:

$$U=-R^{-1}{B}^{\mathrm{T}}Pe$$

(11)

where $e=[X-X^{*}]$, $X$ is the states of the system, and $X^{*}$ is the desired states.

The matrix $P$ is obtained from the following [39]:

$$A^{T}P+PA-PB{R}^{-1}{B}^{T}P+Q=0$$

(12)

The functional cost considered for $U$ is given by the following [40]:

$$J={\displaystyle \frac{1}{2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}(e^{T}Qe+U^{T}RU)}dt$$

(13)

where Q and R are positive definite matrices.

In this paper, Q and R, diagonal matrices, will be considered, with each term of the diagonal determining the weight of the gain for each state of the system.

The proposed control strategy can be observed in Figure 4.

3. Results

This section presents the results of numerical simulations for the system without an MR damper and the system with an MR damper controlled through LQR control, as shown in Figure 4.

Most of the vibrations in high-speed elevators are caused by irregularities in the guide rails [40]. In this paper, for computational simulations, a slight deformation in the guide rail will be considered using the following equation:

$$\begin{array}{l}{y}_1=A_d\sin (\omega (t+t_0))\\ y_2=A_d\sin (\omega t)\\ y_3=y_4=0\end{array}$$

(14)

Equation (14) represents the vibrations originating from the guide rail connections [21], where $\omega ={\displaystyle \frac{2\pi \nu }{\lambda }}$, $\lambda$ is the length of the excitation wave signal, $\nu$ is the elevator travel speed, and $A_d$ is the displacement amplitude.

The fourth-order Runge–Kutta method with an integration step h = 0.01 is used for the numerical integrations, and the following parameters are used for the simulations: $k_1={10}^5$ (N/m), $k_2={10}^5$ (N/m), $k_3={10}^5$ (N/m), $k_4={10}^5$ (N/m), $c_1={10}^3$ (Ns/m), $c_2={10}^3$ (Ns/m), $c_3={10}^3$ (Ns/m), $c_4={10}^3$ (Ns/m), $l_1=2.8$ (m), $l_2=3.7$ (m), $M=[1500:2000]$ (kg), $J=8090$ (kgm²), $k_{nl}=219027*{10}^2$ (N/m), $v=[1:10]$ (m/s), $A_d=0.01$ (m), $\lambda =5$ (m), $t_0=(l1+l2)/v$ (s), ${\sigma }_0=533333.33$ (N/(mV)), ${\sigma }_1=1066.66$ (Ns/m), ${\sigma }_2=100$ (Ns/m), ${\sigma }_a=266666.66$ (N/m), ${\sigma }_b=533.33$ (Ns/(mV)), and $a_0=0.00003$ (V/N) [1,2,36].

c₁, c₂, c₃, and c₄ are the equivalent dampings of the guide shoe (Ns/m), J the moment of inertia of the car (kgm²), k₁, k₂, k₃, and k₄ the equivalent stiffness of the guide shoe (N/m), l₁ the distance between the car system mass center and the upper guide shoe (m), l₂ the distance between the car system mass center and the lower guide shoe (m), “M” the mass of the car system (kg), Δ_m the rated load of the car (kg), v the vertical velocity of the elevator (m/s), y the horizontal displacement (m), θ the angular displacement around the centroid (rad), and k_nl the coefficient of stiffness of the elevator cables with reference to the tilting movement of the cabin (N/m).

3.1. Numerical Simulations for the Passive System

Considering the importance of passenger comfort, acceleration levels will be considered as the variable to be analyzed in computer simulations and for reduction in the control design. In this research, acceleration in RMS will be considered, as it is commonly used as a parameter to measure passenger comfort. A variation in deformity $A_d=0.01$ was considered in this research to extrapolate the deformation levels of the guide rails.

Figure 5 shows the variations in lateral and angular accelerations, considering the variation in elevator mass (variation in the number of passengers) and elevator velocity, considering $M=[1500:2000]$ and $v=[1:10]$.

As shown in the results in Figure 5, the elevator mass (M) variation does not significantly affect the cabin acceleration levels. However, the travel speed is highly relevant to the increase in cabin acceleration and, thus, the discomfort of passengers.

Figure 6 shows the variation in accelerations for the case of M = 1600 kg.

As we can see, the accelerations increase significantly as we increase the elevator’s travel speed. To reduce the vibrations that cause these high levels of acceleration, in the following sections, the inclusion of control in the elevator damping system will be considered, considering the elevator at a high speed of $v=10$ (m/s) and M = 1600 kg.

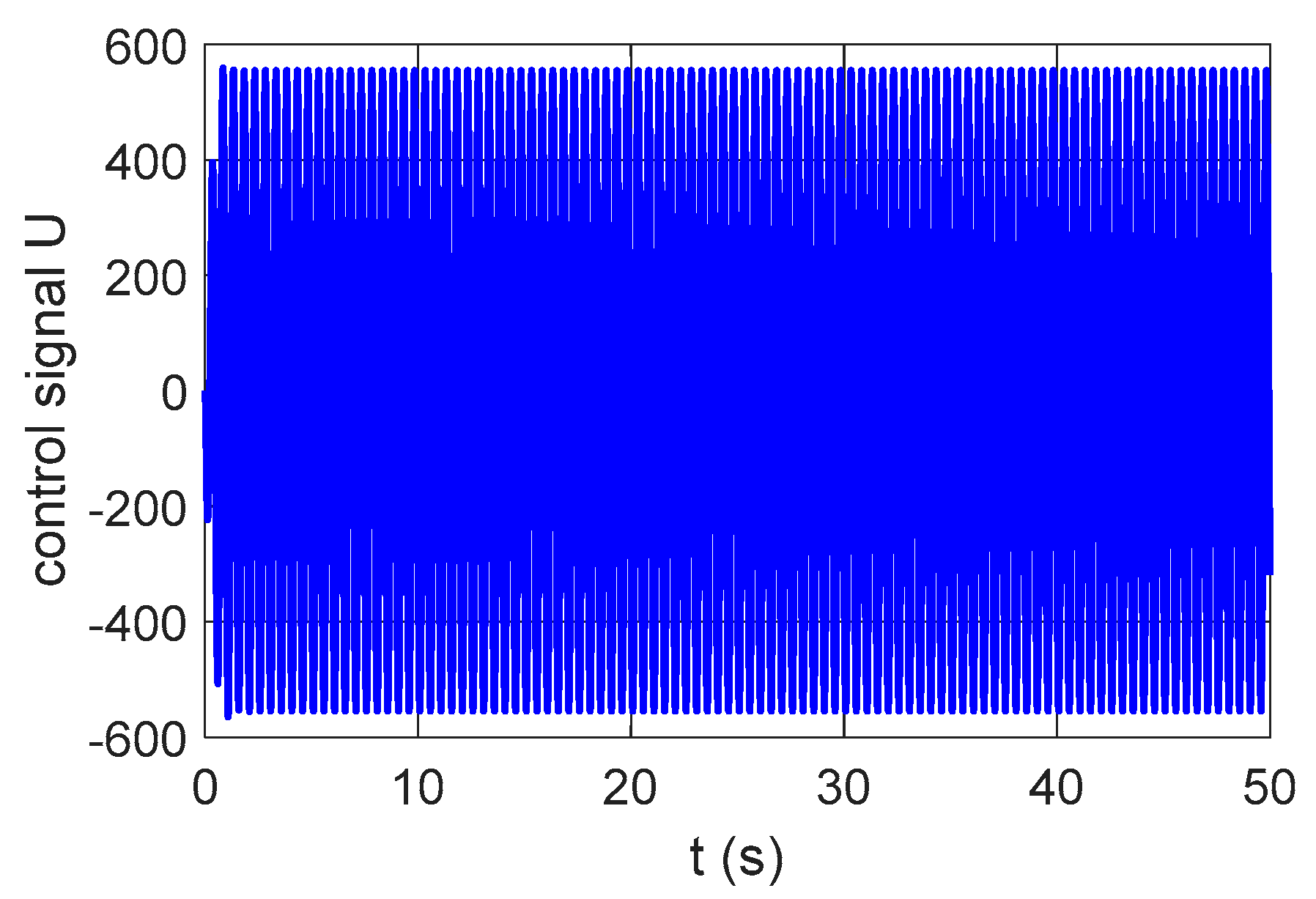
3.2. Numerical Simulations for the System with Active Control

Considering the system with control (11), and to obtain the gains of the SDRE control, the following matrices will be considered:

$$Q=\left[\begin{array}{cccc}{10}^6& 0& 0& 0\\ 0& {10}^6& 0& 0\\ 0& 0& {10}^6& 0\\ 0& 0& 0& {10}^6\end{array}\right]\mathrm{and}R=\left[{10}^{-2}\right]$$

(15)

Figure 7 shows the lateral and angular displacements and their velocities for systems with active control.

As we can see in Figure 7, with the control, it was possible to significantly reduce the elevator’s vibrations, thus contributing to preserving its mechanical and electronic components.

In Figure 8, we can observe the variation in the lateral and angular acceleration of the cabin.

Analyzing the results presented in Figure 8, we can observe that the control also reduced the cabin accelerations. Considering the RMS, we observe that the lateral acceleration for the system without control was 1.2106 (m/s²), and for the system with control, the acceleration was 0.6103 (m/s²), a reduction of 42% in lateral acceleration. In the case of angular acceleration, we have an angular acceleration of 0.6947 (rad/s²) for the passive system and an acceleration of 0.5429 (rad/s²) for the active system, which indicates a reduction of 9.96% in angular acceleration.

Figure 9 shows the values of the variation in the control signal U, according to the elevator displacement.

The results presented in Figure 9 represent the force required for an active or semi-active damper, which was considered to be included parallel to the damper c₁.

As can be seen, the control effectively reduced the elevator vibrations; however, a specific actuator was not considered, which is why the results presented also apply to actuation systems other than an MR damper.

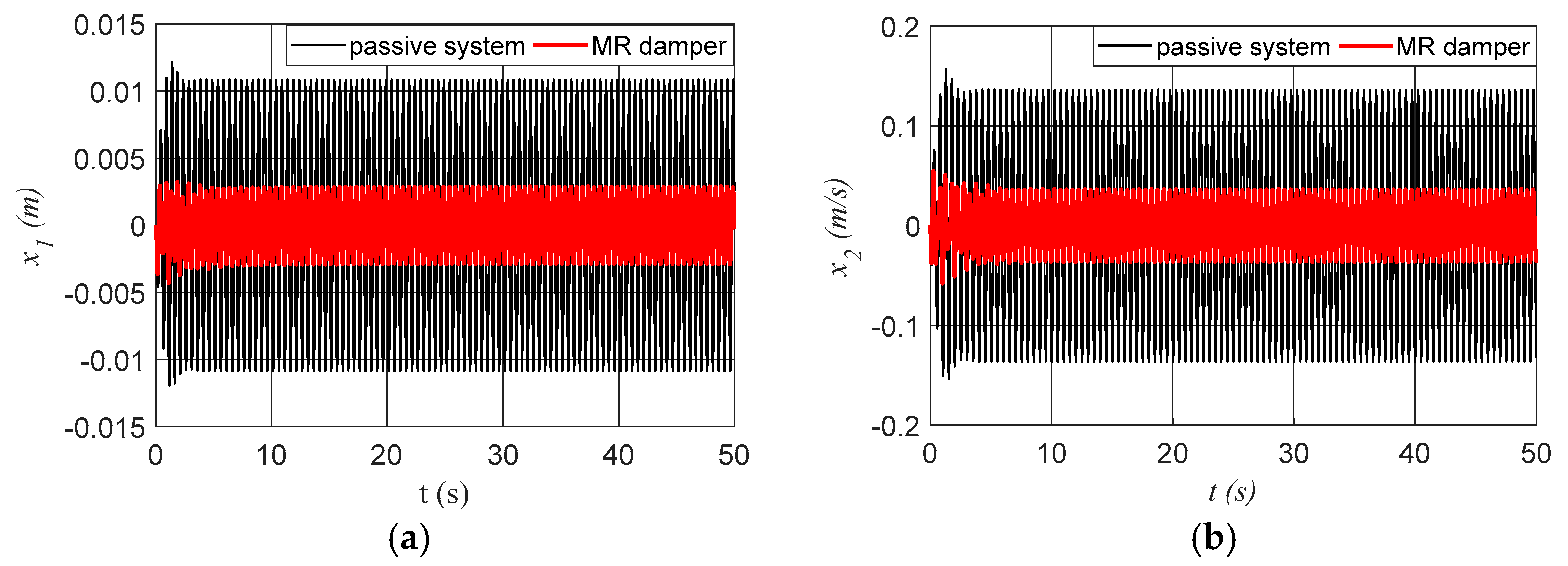
3.3. Numerical Simulations for the System with Semi-Active Control by an MR Damper

Considering the application of the MR damper, it is necessary to determine the electrical voltage to be applied to the damper coil and consider only the dissipative force in the control. Thus, it is necessary to take Equation (7) into consideration in the control signal. In this case, we have a semi-active control system.

Figure 10 shows the lateral and angular displacements and their velocities for systems with a controlled MR damper.

The results demonstrate that the use of an MR damper as a semi-active control effectively reduces elevator cabin vibrations.

In Figure 11, we can observe the variation in the lateral and angular acceleration of the cabin.

Analyzing the results presented in Figure 11, we can observe that the use of the MR damper also reduced cabin accelerations. In RMS, we have a lateral acceleration of 0.3308 (m/s²), representing a reduction of 72.67% in lateral acceleration. The angular acceleration is 0.3919 (rad/s²), representing a reduction of 35.00% in angular acceleration.

Figure 12 shows the variation in the control signal U and the electrical voltage V (volts).

Analyzing the results presented in Figure 11, we can observe that the control with the MR damper provided a greater reduction in lateral and angular accelerations compared to the active control U shown in Figure 8. Analyzing Equation (7), we can observe that even for zero voltage (V = 0), the damper maintains a damping force, which contributes to the additional reduction in vibration, also reducing acceleration levels when compared with the results of the active system, which did not have the additional damping of the passive MR. The contribution of the U control is in estimating the best force to be applied for the cases V > 0, considering saturation at 2.5 volts ($V_{\max }=2.5$), the voltage available in [41].

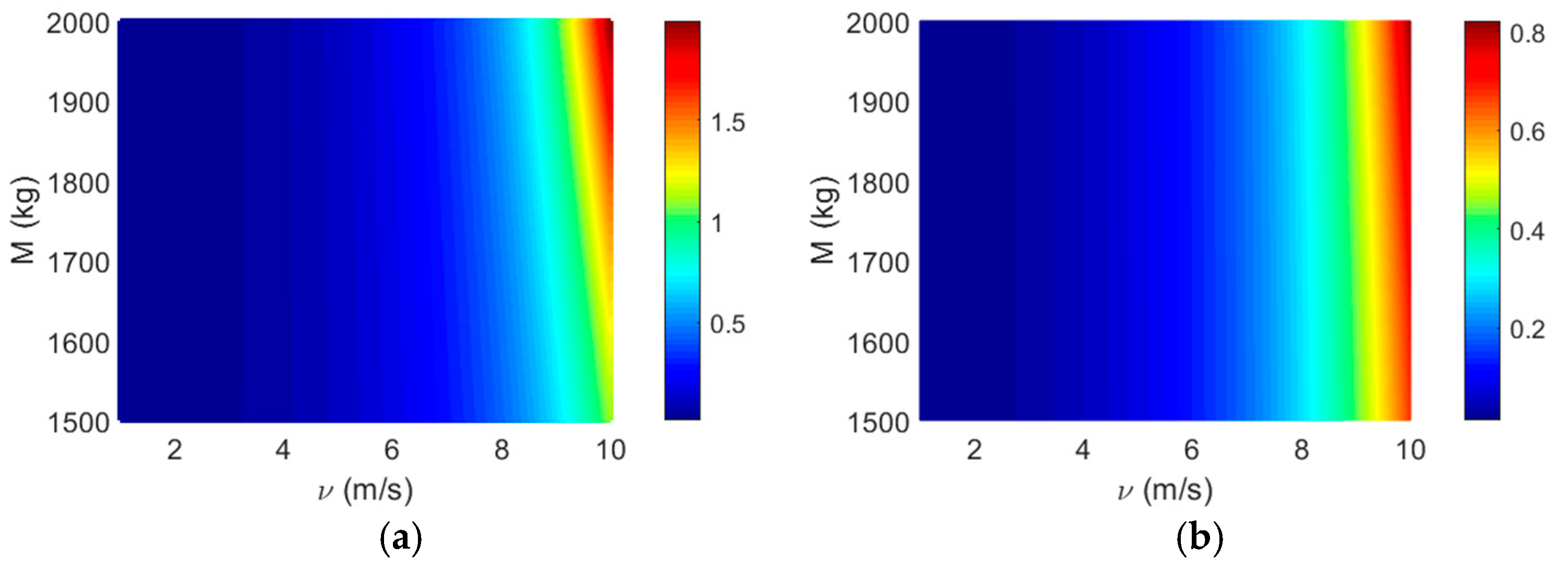
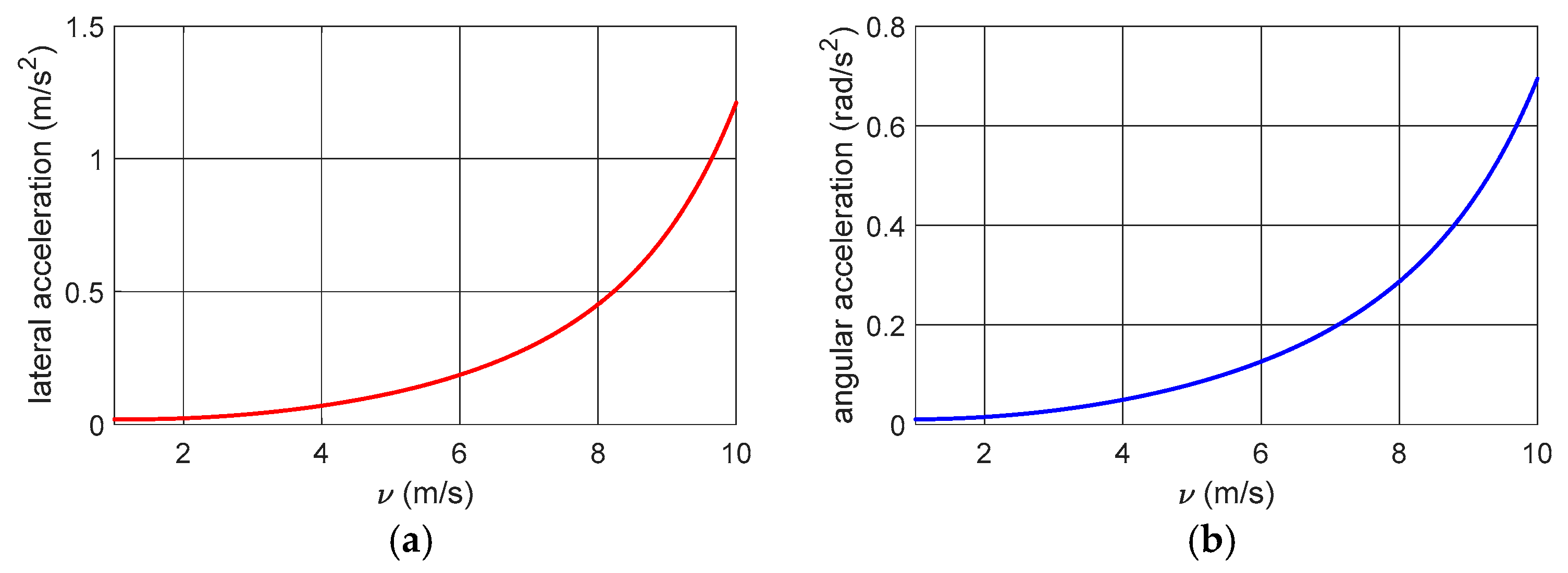
3.4. System Sensitivity in the Case of Parametric Variations

To consider the effect of parameter variations on system dynamics and controller performance, it will be assumed that the parameters can vary by ± 10%, thus including a random variation of 10% in the parameters.

In this work, two situations are considered. The first one considers variations in the following elevator parameters: k₁ = 10⁵(0.9 + 0.2r(t)), c₁ = 10³(0.9 + 0.2r(t)), M = 1600(0.9 + 0.2r(t)), and J = 8090(0.9 + 0.2r(t)). In the second case, variations in the vibration source are considered, with the following parameters: $A_d=0.01(0.9+0.2r(t))$ and $\lambda =5(0.9+0.2r(t))$.

Figure 13, Figure 14 and Figure 15 show the lateral and angular variations, force, and electrical voltage for the case of variations only in k₁, c₁, M, and J.

Figure 14 shows the variation in lateral and angular accelerations.

Figure 15 shows the variation in force and electrical voltage.

Figure 16, Figure 17 and Figure 18 show the lateral and angular variations, force, and electrical voltage for the case of variations only in A_d and λ.

Figure 16 shows the lateral and angular displacements and velocities.

Figure 17 shows the lateral and angular accelerations.

Figure 17 shows the variations in the force of the MR damper and the electrical voltage.

As can be seen in the results presented, both the passive system and the system with control are sensitive to parametric variations for both the elevator parameters and the vibration source.

In

Table 1. Sensitivity of the passive system to parametric variations.

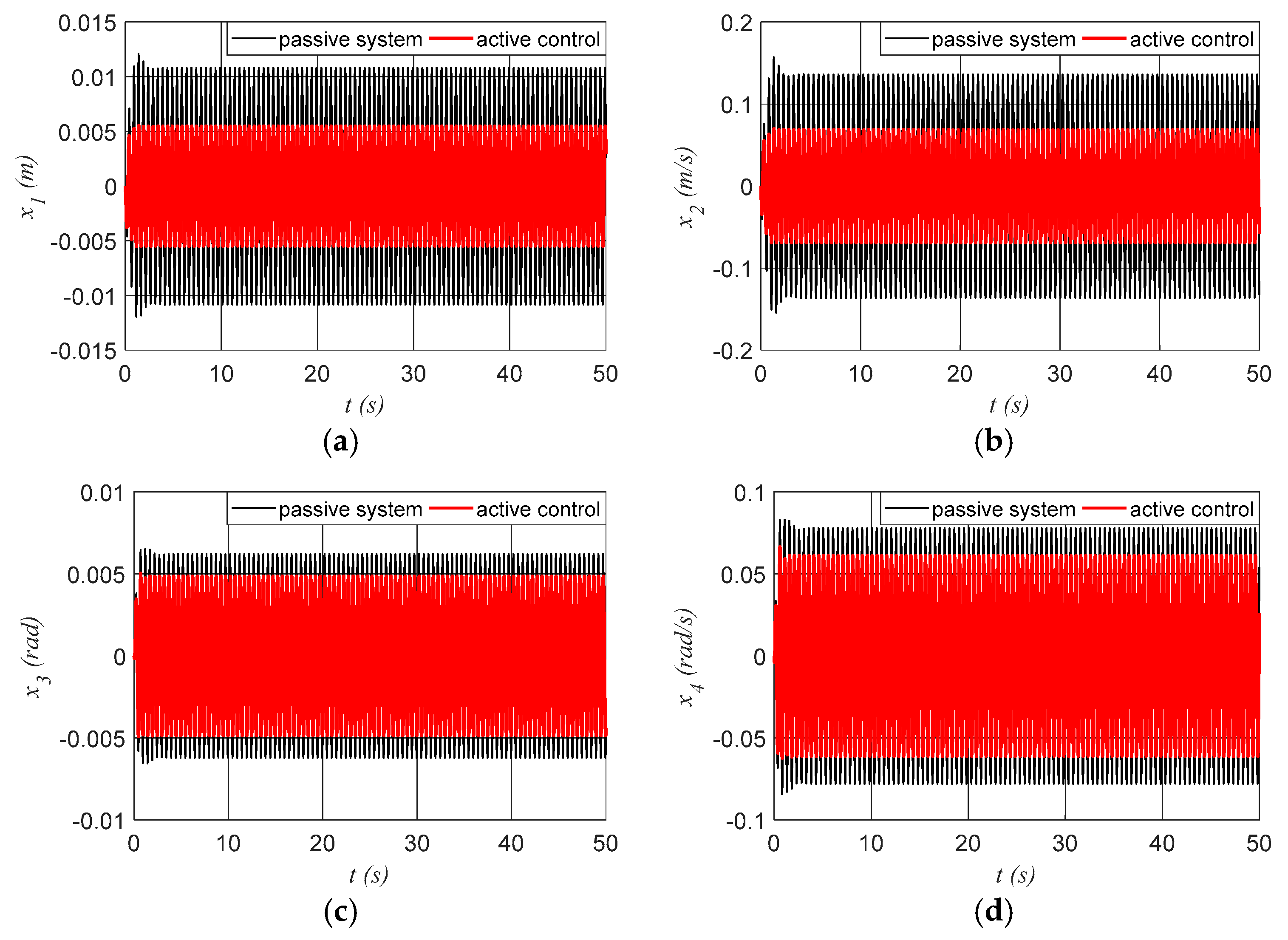
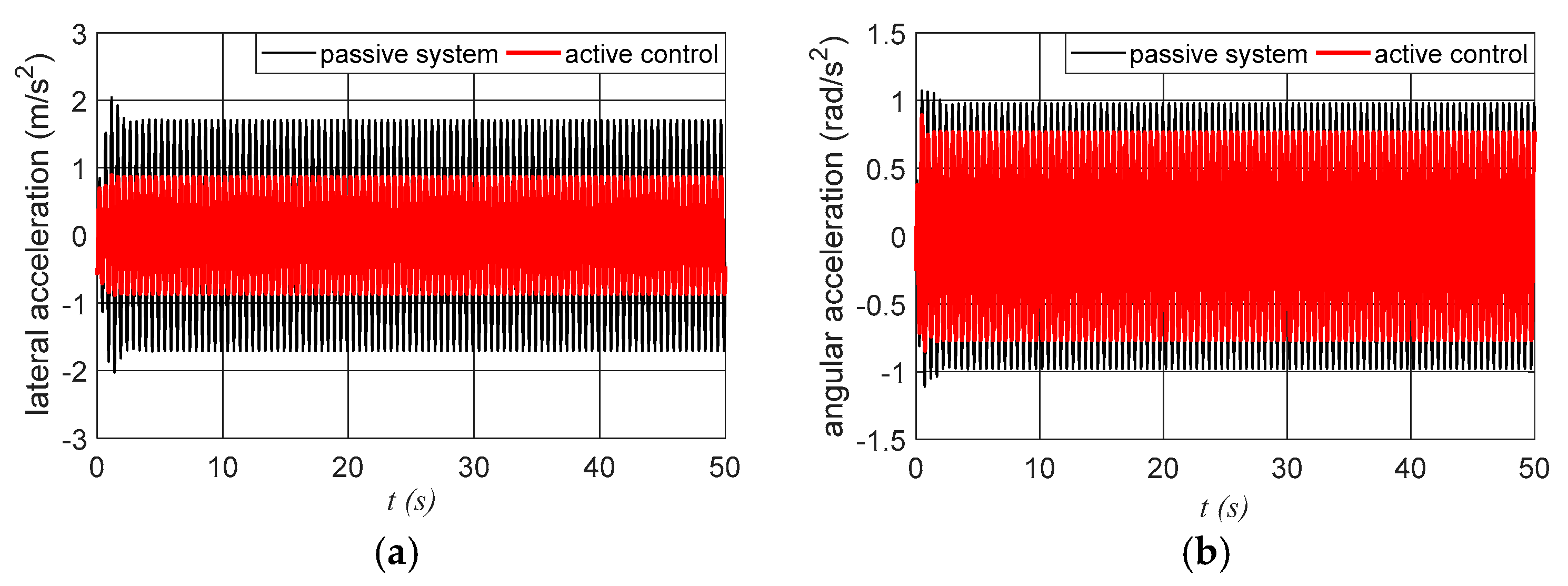
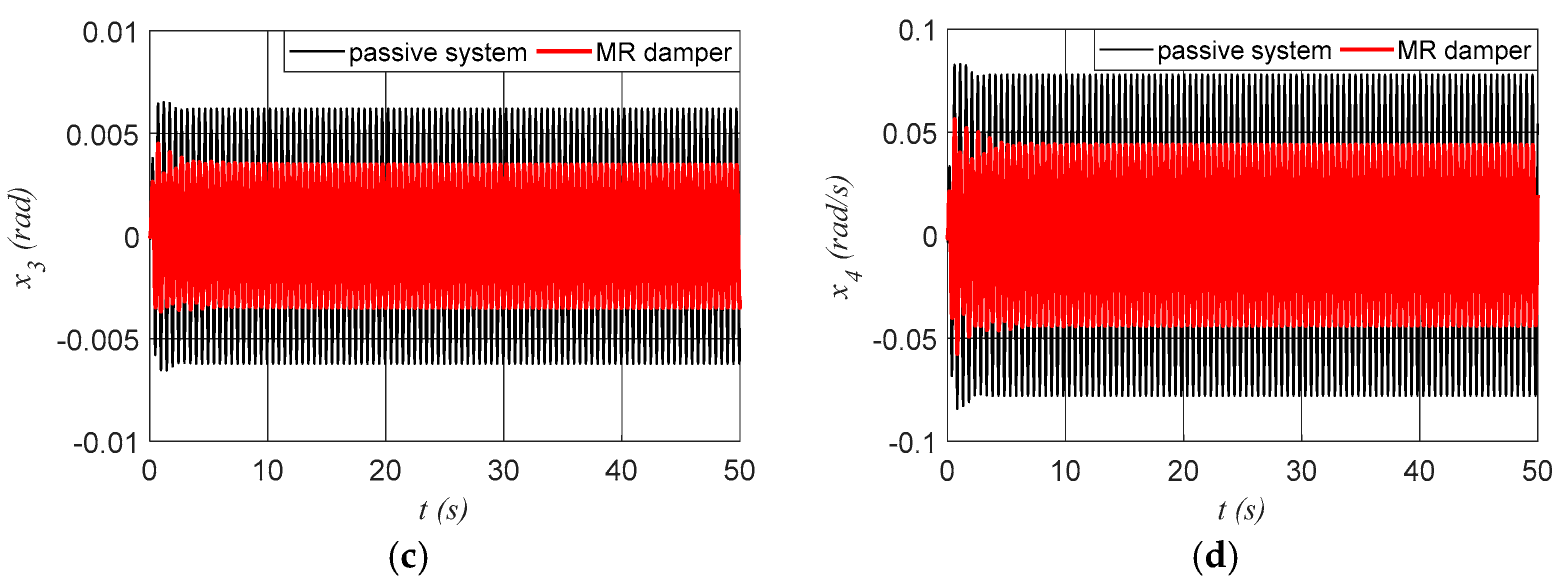
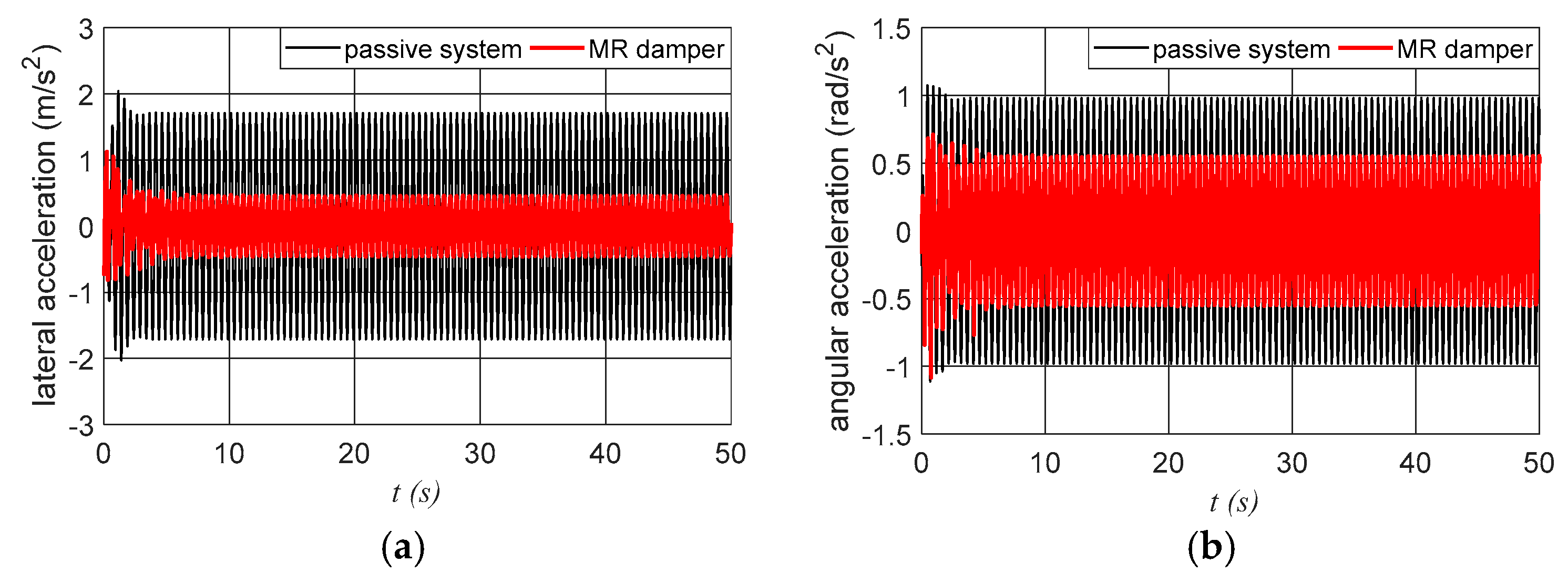
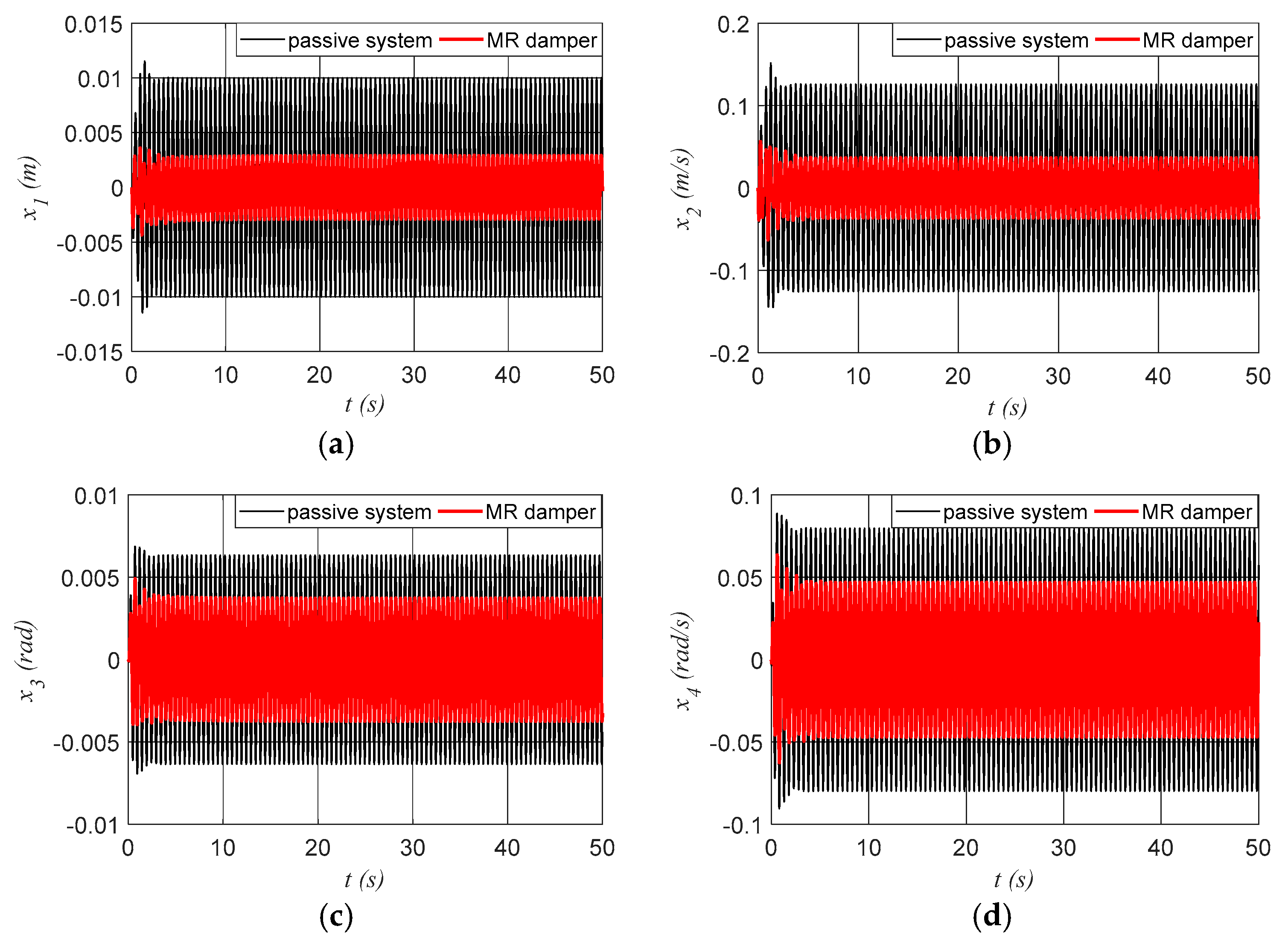
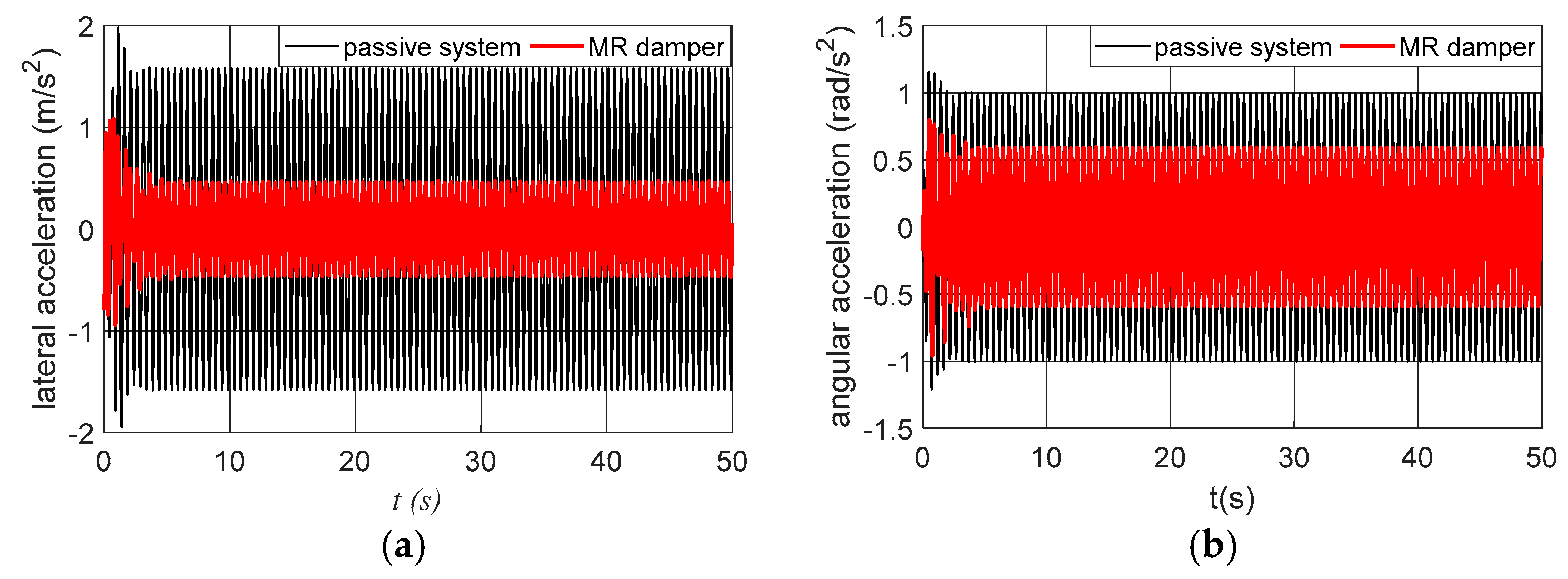
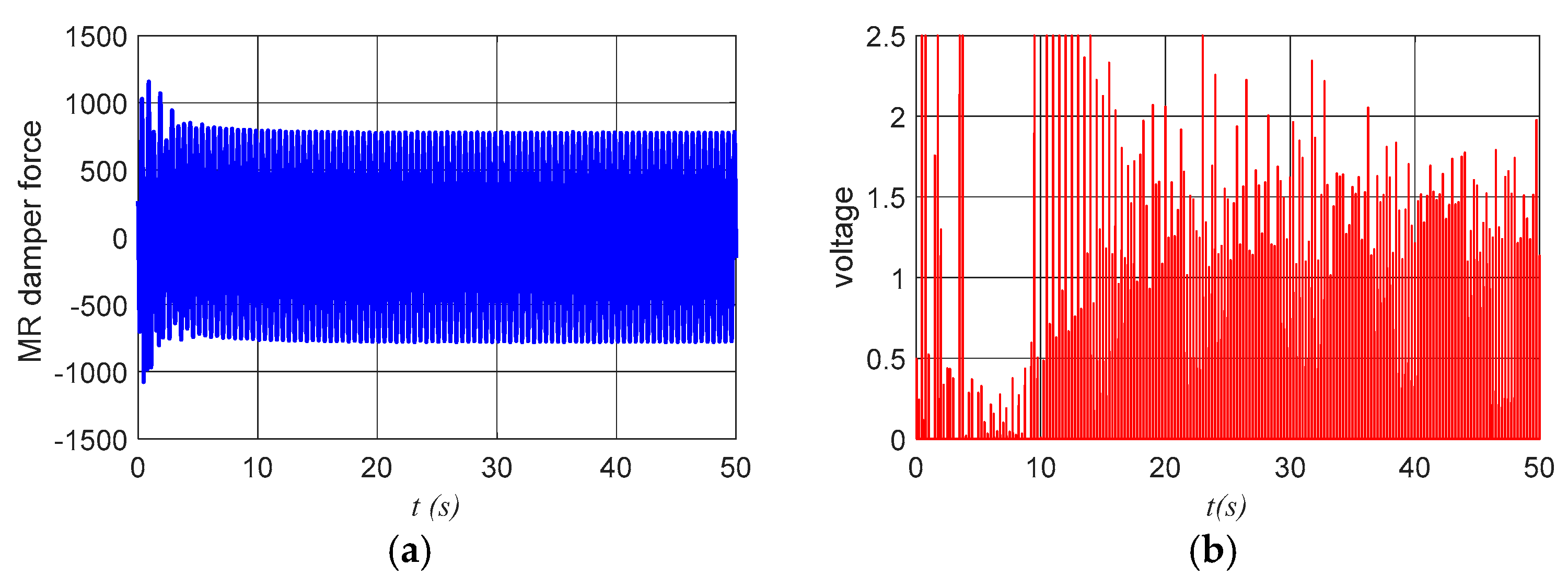
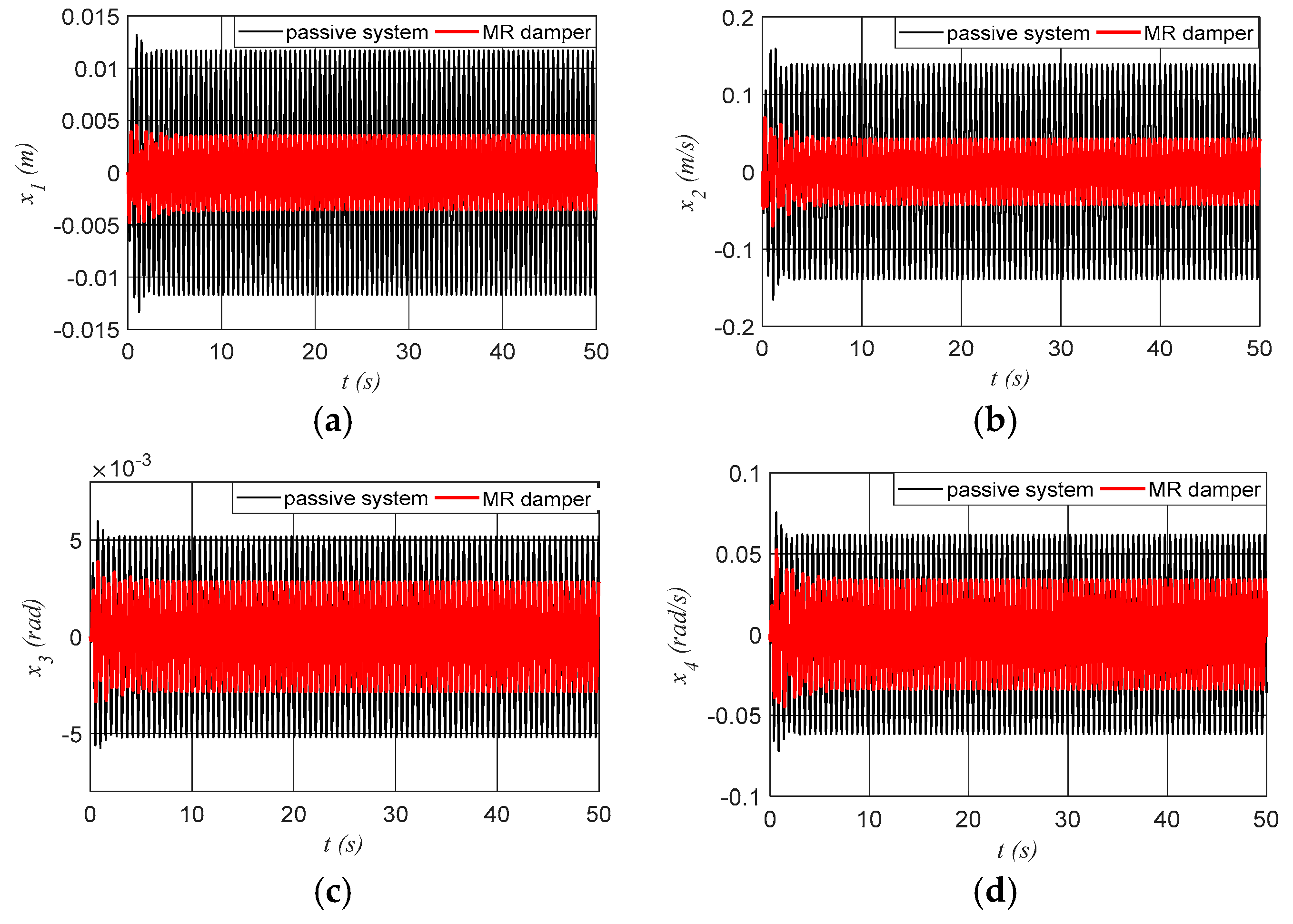
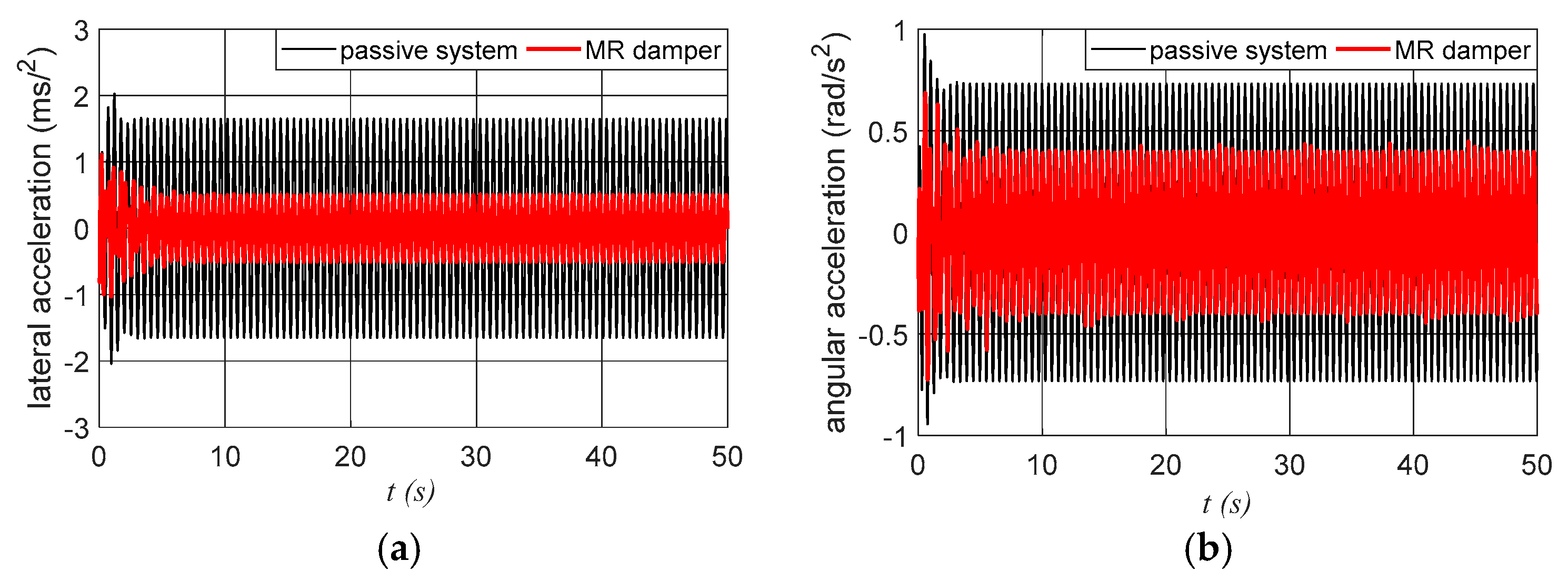
	x1 (m)	x2 (m/s)	x3 (rad)	x4 (rad/s)	al (m/s2)	aa (rad/s2)
without parametric variations	0.01084	0.1364	0.0062	0.07799	1.2106	0.603
elevator parametric variations	0.01	0.1257	0.0063	0.07973	1.1169	0.7098
parametric variations in vibration source	0.01171	0.139	0.005192	0.06163	1.1684	0.5201

, we present the maximum value of displacement, speed, considering the passive system, for the steady-state system. The accelerations are considered in RMS.

Table 2. Sensitivity of the controlled system to parametric variations.

	x1 (m)	x2 (m/s)	x3 (rad)	x4 (rad/s)	al (m/s2)	aa (rad/s2)	$F_{mrd}$ (N)
without parametric variations	0.0028	0.3569	0.0034	0.4375	0.3308	0.3919	763.1
elevator parametric variations	0.0029	0.03671	0.0037	0.04689	0.3347	0.4198	775.6
parametric variations in vibration source	0.003575	0.04202	0.002828	0.03339	0.3653	0.2860	945.2

presents the maximum value of displacement, velocity, and variation in the MR damper force for the system with the MR damper. Accelerations are also considered in RMS.

An analysis of the data presented in Table 1 and Table 2 shows how sensitive the passive and controlled systems are to parameter variations. We can also observe that the control efficiently reduces the acceleration levels for different parametric variations.

4. Conclusions

In an analysis of the numerical results presented, it is evident that high speed greatly influences vibration levels, thus justifying the application of vibration control systems for high-speed elevators. Regarding the use of the MR damper, its versatility in changing its viscosity by varying the electrical voltage applied to the damper coil is also evident, a feature that allows its use in semi-active vibration control. In an analysis of the results obtained with the proposed control and the results obtained with the passive system, the reduction in lateral and angular acceleration levels is evident. This reduction is related to the increase in the viscosity of the MR damper.

The use of only one MR damper proved to be sufficient to effectively reduce elevator vibration levels at the lowest cost. In continuations of this work, more MR dampers can be included, as well as an optimization analysis to determine the best performance achievable at the lowest cost. Regarding the control strategy using the SDRE control, it was possible to verify that the control is efficient in estimating the necessary forces. However, it was also possible to observe sensitivity to parametric variations, with results encouraging continued research in comparing different control strategies in conjunction with the MR damper.