Ab Initio Investigation on the Magnetic Moments, Magnetocrystalline Anisotropy and Curie Temperature of Fe2P-Based Magnets
Abstract
1. Introduction
2. Computational Details and Methods
3. Results
3.1. Physical and Magnetic Properties of the Binary Parent Fe2P
3.2. Evolution of Magnetic Moment, Polarization and
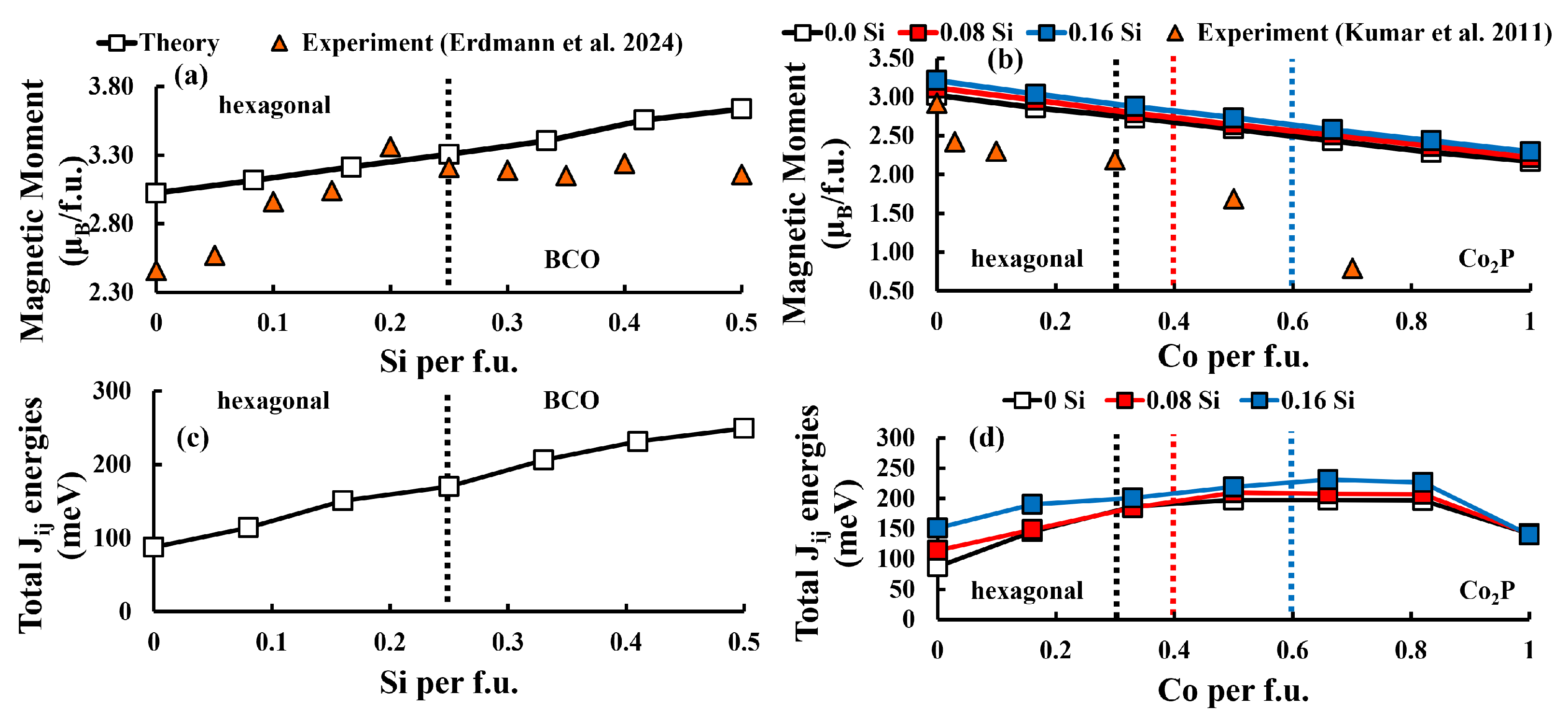

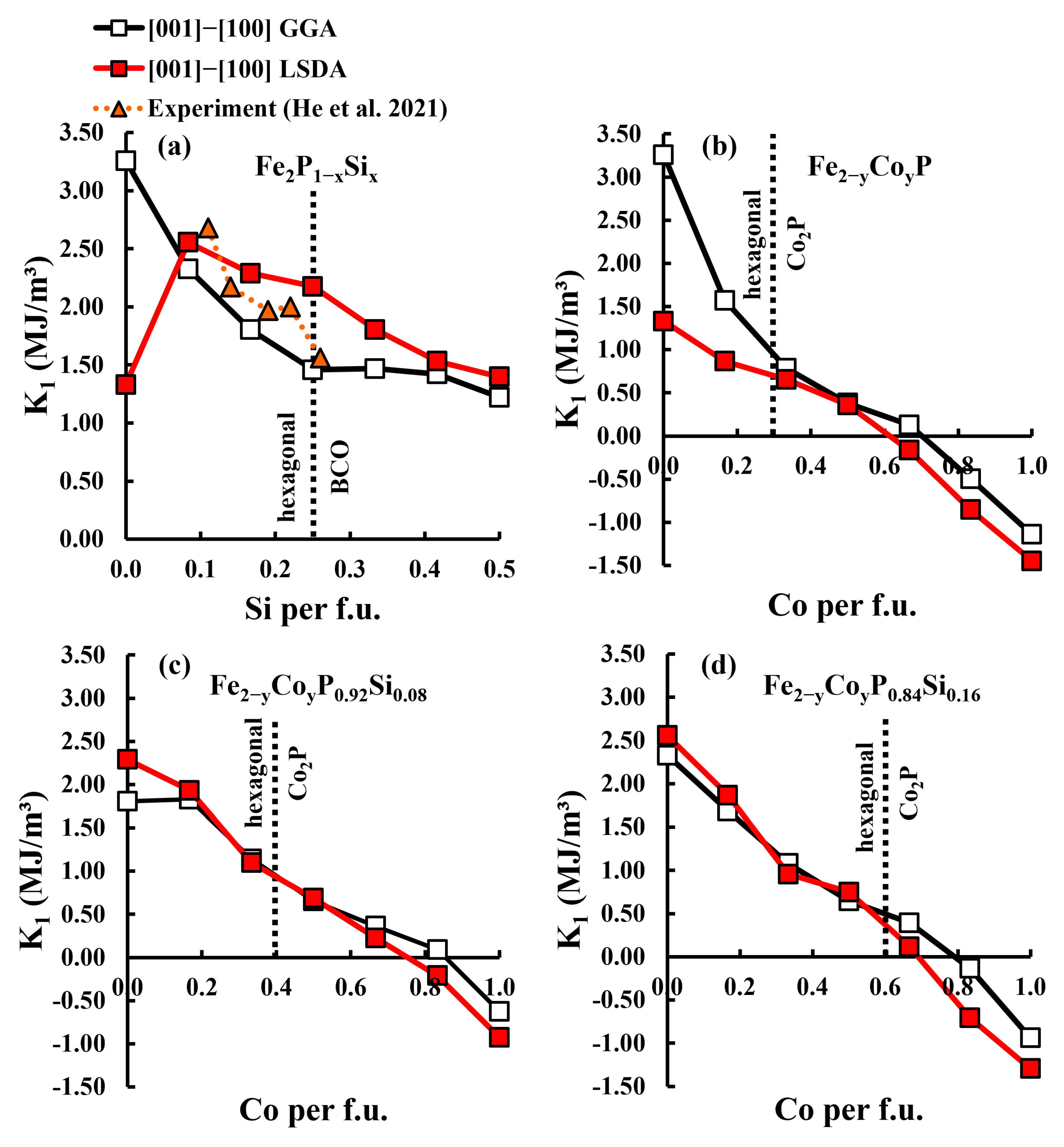
3.3. Magnetocrystalline Anisotropy Energy
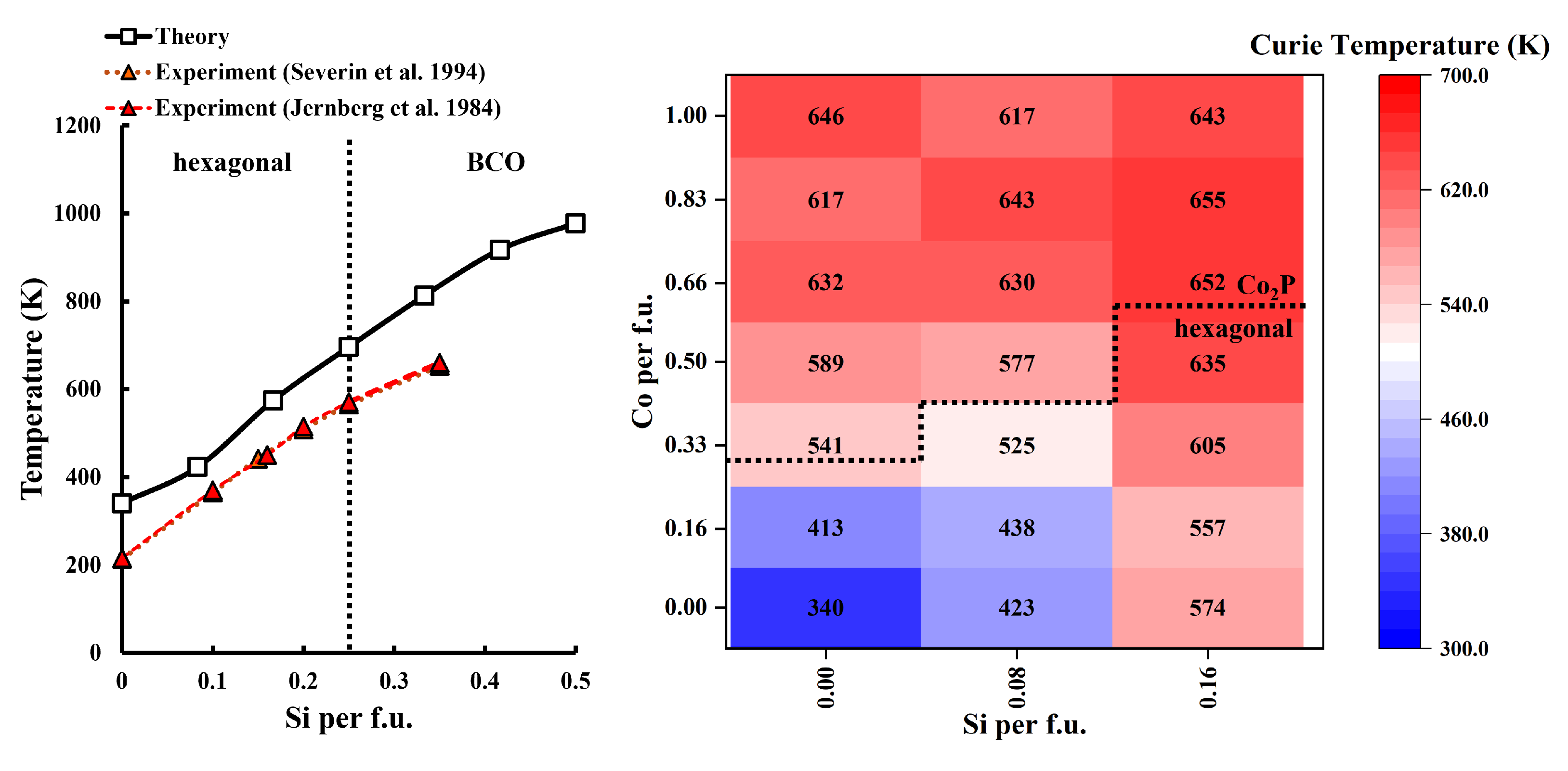
3.4. Curie Temperature
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| MAE | Magnetocrystalline anisotropy energy |
| Curie temperature | |
| RE | Rare-earth |
| TM | Transition metal |
| VASP | Vienna ab initio Simulation Package |
| PAW | Projector-augmented wave |
| GGA | Generalzized gradient approximation |
| PBE | Perdew–Burke–Ernzerhof |
| SCF | Self-consistent field |
| LSDA | Local Spin Density approximation |
| Exchange interaction energies | |
| KKR | Korringa–Kohn–Rostoker |
| FM | Ferromagnetic |
| CPA | Coherent potential approximation |
| BCO | Body-centered orthorhombic |
| Total magnetic moment | |
| Polarization Saturation | |
| Maximum energy product | |
| Anisotropy constant | |
| Anisotropy field | |
| HPC | High-performance computing |
| DFG | Deutsche Forschungsgemeinschaft |
| MWK | Ministry of Science and Culture |
References
- Erdmann, S.; Klüner, T.; İbrahim Sözen, H. Magnetic properties of rare-earth-lean ThMn12-type (Nd,X)Fe11Ti (X: Y and Ce) compounds: A DFT study. J. Magn. Magn. Mater. 2023, 572, 170645. [Google Scholar] [CrossRef]
- Sözen, H.I.; Klüner, T. Ab initio phase stabilities of rare-earth lean Nd-based hard magnets. J. Magn. Magn. Mater. 2022, 559, 169529. [Google Scholar] [CrossRef]
- Sözen, H.I. Ab initio Phase Stabilities of Ce-Based Hard Magnetic Materials. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2019. [Google Scholar]
- Sözen, H.I.; Ener, S.; Maccari, F.; Fayyazi, B.; Gutfleisch, O.; Neugebauer, J.; Hickel, T. Combined ab initio and experimental screening of phase stabilities in the Ce-Fe-Ti- X system (X = 3 d and 4 d metals). Phys. Rev. Mater. 2023, 7, 014410. [Google Scholar] [CrossRef]
- Wittemann, T.; Sözen, H.I.; Oezaslan, M.; Klüner, T. Ab initio calculations of the chemisorption of atomic H and O on Pt and Ir metal and on bimetallic PtxIry surfaces. Z. Fur Naturforschung Sect. B J. Chem. Sci. 2024, 79, 177–190. [Google Scholar] [CrossRef]
- Erdmann, S.; Sozen, H.I.; Guillou, F.; Yibole, H.; Kluner, T. Theoretical and experimental investigations on Fe2P -type magnets: Effects of Si and Co substitution on physical and magnetic properties. Phys. Rev. Mater. 2024, 8, 094401. [Google Scholar] [CrossRef]
- Coey, J.M. Perspective and Prospects for Rare Earth Permanent Magnets. Engineering 2020, 6, 119–131. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Willard, M.A.; Brück, E.; Chen, C.H.; Sankar, S.G.; Liu, J.P. Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Adv. Mater. 2011, 23, 821–842. [Google Scholar] [CrossRef]
- Coey, J.M. Permanent magnets: Plugging the gap. Scr. Mater. 2012, 67, 524–529. [Google Scholar] [CrossRef]
- Woodcock, T.G.; Zhang, Y.; Hrkac, G.; Ciuta, G.; Dempsey, N.M.; Schrefl, T.; Gutfleisch, O.; Givord, D. Understanding the microstructure and coercivity of high performance NdFeB-based magnets. Scr. Mater. 2012, 67, 536–541. [Google Scholar] [CrossRef]
- Bauer, D.; Diamond, D.; Li, J.; McKittrick, M.; Sandalow, D.; Telleen, P. Critical Materials Strategy for Clean Energy Technologies; US Department of Energy Office of Policy and International Affairs (PI): Washington, DC, USA, 2011; pp. 1–170.
- Directorate-General for Internal Market, Industry, E.; Commission, S.E.; Grohol, M.; Veeh, C. Study on the Critical Raw Materials for the EU 2023—Final Report; Technical report; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar] [CrossRef]
- He, Y.; Adler, P.; Schneider, S.; Soldatov, I.; Mu, Q.; Borrmann, H.; Schnelle, W.; Schaefer, R.; Rellinghaus, B.; Fecher, G.H.; et al. Intrinsic Magnetic Properties of a Highly Anisotropic Rare-Earth-Free Fe2P-Based Magnet. Adv. Funct. Mater. 2022, 32. [Google Scholar] [CrossRef]
- Surilemu, Z.; Bao, L.L.; Yibole, H.; Erdmann, S.; Sözen, H.; Klüner, T.; Guillou, F. Structure, phase transitions and hard magnetic properties of ternary Fe1.93(P1−xSix) compounds with x ≤ 0.5. Acta Mater. 2025, 291. [Google Scholar] [CrossRef]
- Bao, L.L.; Yibole, H.; Xu, J.Y.; Ou, Z.Q.; Haschuluu, O.; Tegus, O.; van Dijk, N.H.; Brück, E.; Guillou, F. Crystal structures and magnetic properties of Fe1.93−xCoxP1−ySiy compounds. J. Alloys Compd. 2022, 903. [Google Scholar] [CrossRef]
- Tobola, J.; Koumina, M.D.B.F.S.K.A.; Soubeyroux, S.N.J.L.; Zach, R. Magnetism of Fe2P investigated by neutron experiments and band structure calculations. J. Magn. Magn. Mater. 1996, 157–158, 708–710. [Google Scholar] [CrossRef]
- Fujii, H.; Hokabe, T.; Kamigaichi, T.; Okamoto, T. Magnetic Properties of Fe2P Single Crystal. J. Phys. Soc. Jpn. 1977, 43, 41–46. [Google Scholar] [CrossRef]
- Häggström, L.; Severin, L.; Andersson, Y. Experimental and theoretical studies of Si/P substituted orthorhombic Fe2P. Hyperfine Interact. 1994, 94, 2075–2079. [Google Scholar] [CrossRef]
- Caron, L.; Hudl, M.; Höglin, V.; Dung, N.H.; Gomez, C.P.; Sahlberg, M.; Brück, E.; Andersson, Y.; Nordblad, P. Magnetocrystalline anisotropy and the magnetocaloric effect in Fe2P. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88. [Google Scholar] [CrossRef]
- Vos, K.J.D.; Velge, W.A.; Steeg, M.G.V.D.; Zijlstra, H. Permanent magnetic properties of iron-cobalt-phosphides. J. Appl. Phys. 1962, 33, 1320–1322. [Google Scholar] [CrossRef]
- Wäppling, R.; Häggström, L.; Ericsson, T.; Devanarayanan, S.; Karlsson, E.; Carlsson, B.; Rundqvist, S. First Order Magnetic Transition, Magnetic Structure, and Vacancy Distribution in Fe2P. J. Solid State Chem. 1975, 13, 258–271. [Google Scholar] [CrossRef]
- Lundgren, L.; Tarmohamed, G.; Beckman, O.; Carlsson’, B.; Rundqvist’, S. First Order Magnetic Phase Transition in Fe2P. Phys. Scr. 1978, 17, 39–48. [Google Scholar] [CrossRef]
- Fruchart, R.; Roger, A.; Senateur, J.P. Crystallographic and magnetic properties of solid solutions of the phosphides M2P, M = Cr, Mn, Fe, Co, and Ni. J. Appl. Phys. 1969, 40, 1250–1257. [Google Scholar] [CrossRef]
- Xu, J.Y.; Bao, L.; Yibole, H.; Guillou, F. Structure and magnetic properties of Fe1.95−xNixP1−ySiy alloys. Solid State Commun. 2020, 319, 113996. [Google Scholar] [CrossRef]
- Guillou, F.; Liting, S.; Haschuluu, O.; Ou, Z.Q.; Brück, E.; Tegus, O.; Yibole, H. Room temperature magnetic anisotropy in Fe2P-type transition metal based alloys. J. Alloys Compd. 2019, 800, 403–411. [Google Scholar] [CrossRef]
- Zhuravlev, I.A.; Antropov, V.P.; Vishina, A.; Schilfgaarde, M.V.; Belashchenko, K.D. Tunable dimensional crossover and magnetocrystalline anisotropy in Fe2P-based alloys. Phys. Rev. Mater. 2017, 1. [Google Scholar] [CrossRef]
- Severin, L.; Häggström, L.; Nordström, L.; Andersson, Y.; Johansson, B. Magnetism and crystal structure in orthorhombic Fe2P: A theoretical and experimental study. J. Phys. Condens. Matter 1995, 7, 185–198. [Google Scholar] [CrossRef]
- Yibole, H.; Lingling-Bao, B.; Xu, J.Y.; Alata, H.; Tegus, O.; Hanggai, W.; van Dijk, N.H.; Brück, E.; Guillou, F. (Fe,Co)2(P,Si) rare-earth free permanent magnets: From macroscopic single crystals to submicron-sized particles. Acta Mater. 2021, 221, 117388. [Google Scholar] [CrossRef]
- Jernberg, P.; Yousif, A.A.; Häggström, L.; Andersson, Y. A Mössbauer Study of Fe2P1−xSix, (x ≤ 0.35). J. Solid State Chem. 1984, 53, 313–322. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Nikitin, S.A.; Tereshina, I.S.; Verbetsky, V.N.; Salamova, A.A. Magnetic anisotropy of YFe11Ti single crystal and its hydride. Int. J. Hydrogen Energy 1999, 24, 217–219. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: Oxford, UK, 1984; Volume 8. [Google Scholar]
- Merkt, N.Y.; Erdmann, S.; Klüner, T.; İbrahim Sözen, H. Effect of Zr Substitution on the Nd-based Magnets: Theoretical Investigation of (Zr,Nd)(Fe,Ti)12 Compounds. J. Magn. Soc. Jpn. 2024, 48, 60–74. [Google Scholar] [CrossRef]
- Herper, H.C.; Skokov, K.; Ener, S.; Thunström, P.; Diop, L.V.B.; Gutfleisch, O.; Eriksson, O. Magnetic Properties of NdFe11Ti and YFe11Ti, from Experiment and Theory. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Ke, L.; Johnson, D.D. Intrinsic magnetic properties in R(Fe1−xCox)11TiZ (R = Yand Ce; Z = H, C, and N). Phys. Rev. B 2016, 94, 024423. [Google Scholar] [CrossRef]
- Liechtenstein, A.; Katsnelson, M.; Antropov, V.; Gubanov, V. Local Spin Density Functional Approach to the Theory of Exchange Interactions in Ferromagnetic Metals and Alloys. J. Magn. Magn. Mater. 1987, 67, 65–74. [Google Scholar] [CrossRef]
- Korringa, J. On the Calculation of the Energy of a Bloch Wave in a Metal. Physica 1947, 13, 392–400. [Google Scholar] [CrossRef]
- Kohn, W.; Rostoker, N. Solution of the schrödinger equation in periodic lattices with an application to metallic lithium. Phys. Rev. 1954, 94, 1111–1120. [Google Scholar] [CrossRef]
- Akai, H. Available online: http://kkr.issp.u-tokyo.ac.jp (accessed on 25 April 2025).
- Shiba, H. A Reformulation of the Coherent Potential Approximation and Its Applications. Prog. Theor. Phys. 1971, 46, 77–94. [Google Scholar] [CrossRef]
- Akai, H. Residual resistivity of Ni-Fe, Ni-Cr and other ferromagnetic alloys. Physica B+C 1977, 86-88, 539–540. [Google Scholar] [CrossRef]
- Slater, J.C. Atomic radii in crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Janak, J.F.; Williams, A.R. Calculated Properties of Metals; Pergamon Press: New York, NY, USA, 1978. [Google Scholar]
- Khongorzul, B.; Ochirkhuyag, T.; Taivansaikhan, P.; Odbadrakh, K.; Odkhuu, D. First-principles study on enhanced magnetocrystalline anisotropy of Fe2P-type alloys. AIP Adv. 2025, 15, 035015. [Google Scholar] [CrossRef]
- Dera, P.; Lavina, B.; Borkowski, L.A.; Prakapenka, V.B.; Sutton, S.R.; Rivers, M.L.; Downs, R.T.; Boctor, N.Z.; Prewitt, C.T. High-pressure polymorphism of Fe2P and its implications for meteorites and Earth’s core. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef]
- Gercsi, Z.; Delczeg-Czirjak, E.K.; Vitos, L.; Wills, A.S.; Daoud-Aladine, A.; Sandeman, K.G. Magnetoelastic effects in doped Fe2P. Phys. Rev. B 2013, 88, 024417. [Google Scholar] [CrossRef]
- Nylund, A.; Roger, A.; Sénateur, J.P.; Fruchard, R. Evolution Structurale des Phosphures, Arséniures et Arséniophosphures M2O, M2As et M2(O1−xAsx). J. Solid State Chem. 1972, 4, 115–122. [Google Scholar] [CrossRef]
- Miao, X.F.; Caron, L.; Roy, P.; Dung, N.H.; Zhang, L.; Kockelmann, W.A.; deGroot, R.A.; Dijk, N.H.V.; Brück, E. Tuning the phase transition in transition-metal-based magnetocaloric compounds. Phys. Rev. B 2014, 89, 174429. [Google Scholar] [CrossRef]
- Bacmann, M.; Soubeyroux, J.L.; Barrett, R.; Fruchart, D.; Zach, R.; Niziol, S.; Fruchart, R. Magnetoelastic transition and antiferro-ferromagnetic ordering in the system MnFeP1−yAsy. J. Magn. Magn. Mater. 1994, 134, 59–67. [Google Scholar] [CrossRef]
- Dung, N.H.; Zhang, L.; Ou, Z.Q.; Zhao, L.; Eijck, L.V.; Mulders, A.M.; Avdeev, M.; Suard, E.; Dijk, N.H.V.; Brück, E. High/low-moment phase transition in hexagonal Mn-Fe-P-Si compounds. Phys. Rev. B 2012, 86, 045134. [Google Scholar] [CrossRef]
- Berak, J. Das System Eisen-Phosphor-Kobalt. Arch. Das Eisenhüttenwesen 1951, 22, 131–135. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, T.; Sun, Q.; Shao, B. Tuning magnetic property of Si-doped Fe2P alloys via strain engineering. J. Magn. Magn. Mater. 2023, 587. [Google Scholar] [CrossRef]
- Delczeg-Czirjak, E.K.; Bergqvist, L.; Eriksson, O.; Gercsi, Z.; Nordblad, P.; Szunyogh, L.; Johansson, B.; Vitos, L. Microscopic theory of magnetism in the magnetocaloric material Fe2P1−xTx (T=B and Si). Phys. Rev. B 2012, 86, 045126. [Google Scholar] [CrossRef]
- Delczeg-Czirjak, E.K.; Delczeg, L.; Punkkinen, M.P.; Johansson, B.; Eriksson, O.; Vitos, L. Ab initio study of structural and magnetic properties of Si-doped Fe2P. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
- Kumar, S.; Krishnamurthy, A.; Srivastava, B.K. On nature of magnetism in ferromagnetic alloys (Fe1−xCox)2P. J. Phys. D Appl. Phys. 2008, 41. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Gignoux, D.; Tobola, J.; Hlil, E.K.; Wolfers, P.; Zach, R. Magnetocaloric effect in ternary metal phosphides (Fe1−xNix)2P. J. Magn. Magn. Mater. 2007, 316, 358–360. [Google Scholar] [CrossRef]
- Zach, R.; Toboła, J.; Średniawa, B.; Kaprzyk, S.; Casado, C.; Bacmann, M.; Fruchart, D. Magneto-elastic properties and electronic structure analysis of the (Fe1−xNix)2P system. J. Alloys Compd. 2004, 383, 322–327. [Google Scholar] [CrossRef]
- Kumar, S.; Krishnamurthy, A.; Srivastava, B.K. Influence of Co doping on structural and magnetic properties of Fe2P. Solid State Phenom. 2011, 171, 93–106. [Google Scholar] [CrossRef]
- Lewis, L.H.; Jiménez-Villacorta, F. Perspectives on permanent magnetic materials for energy conversion and power generation. Metall. Mater. Trans. A 2013, 44. [Google Scholar] [CrossRef]
- Coey, J.M. Hard magnetic materials: A perspective. IEEE Trans. Magn. 2011, 47, 4671–4681. [Google Scholar] [CrossRef]
- Tujii, H.; Kamigaichi, T.; Tsuneo, H.; Tetsuhiko, O. Magnetocrystalline Anisotropy of Fe2P and (Fe1−xNix)2P Compounds. J. Phys. Soc. Jpn. 1974, 37, 1712. [Google Scholar] [CrossRef]
- Fujii, H.; Hokabe, T.; Fujiwara, H.; Okamoto, T. Magnetic Properties of Single Crystals of the System (Fe1−xNix)2P. J. Phys. Soc. Jpn. 1977, 44. [Google Scholar] [CrossRef]
- Long, N.H.; Akai, H. First-principles KKR-CPA calculation of interactions between concentration fluctuations. J. Phys. Condens. Matter 2007, 19, 365232. [Google Scholar] [CrossRef] [PubMed]
- Köhler, S.; Ruocco, G.; Schirmacher, W. Coherent potential approximation for diffusion and wave propagation in topologically disordered systems. Phys. Rev. B 2013, 88, 064203. [Google Scholar] [CrossRef]
- Rowlands, D.A. Short-range correlations in disordered systems: Nonlocal coherent-potential approximation. Rep. Prog. Phys. 2009, 72, 086501. [Google Scholar] [CrossRef]
- Delczeg-Czirjak, E.K.; Gercsi, Z.; Bergqvist, L.; Eriksson, O.; Szunyogh, L.; Nordblad, P.; Johansson, B.; Vitos, L. Magnetic exchange interactions in B-, Si-, and As-doped Fe2P from first-principles theory. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 179903. [Google Scholar] [CrossRef]
- Liu, X.B.; Liu, J.P.; Zhang, Q.; Altounian, Z. Fe magnetic moment formation and exchange interaction in Fe2P: A first-principles study. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2013, 377, 731–735. [Google Scholar] [CrossRef]

| Lattice Constant (Å) | Volume (Å3) | (/f.u.) | (T) | Bulk Modulus (GPa) | |||||
|---|---|---|---|---|---|---|---|---|---|
| This work | 5.808 | 3.425 | 100.09 | 3.02 | 1.06 | 221.8 | GGA 3.26 1 LSDA 1.33 2 | 6.17 2.52 | 214 |
| Theory | 5.809 3 | 3.425 3 | 100.07 3 | 3.01 3 | 1.04 3 | 3.0 3 | 5.77 3 | ||
| Experiment | 5.872 4 | 3.460 4 | 2.94 5 | 1.03 6 | 2.68 6,7 2.32 5,8 | 6.5 6,7 | 223 9 | ||
| Si Subst. | Co-Free | Co subst. | x = 0.0 Si | x = 0.08 Si | x = 0.16 Si | ||||
|---|---|---|---|---|---|---|---|---|---|
| (T) | (T) | (T) | (T) | ||||||
| Fe2P | 3.26 (1.33) | 6.17 (2.52) | Fe2P1−x | 3.26 (1.33) | 6.17 (2.52) | 2.33 (2.55) | 4.30 (4.72) | 1.80 (2.29) | 3.25 (4.12) |
| Fe2P0.92Si0.08 | 2.33 (2.55) | 4.30 (4.72) | Fe1.84Co0.16P1−xSix | 1.57 (0.87) | 3.13 (1.72) | 1.68 (1.87) | 3.27 (3.62) | 1.83 (1.93) | 3.47 (4.12) |
| Fe2P0.84Si0.16 | 1.80 (2.29) | 3.25 (4.12) | Fe1.67Co0.33P1−xSix | 0.78 (0.66) | 1.64 (1.37) | 1.08 (0.96) | 2.20 (1.95) | 1.14 (1.10) | 2.27 (2.19) |
| Fe2P0.75Si0.25 | 1.46 (2.18) | 2.57 (3.83) | Fe1.5Co0.5P1−xSix | 0.38 (0.36) | 0.83 (0.79) | 0.65 (0.75) | 1.39 (1.61) | 0.66 (0.69) | 1.37 (1.44) |
| Fe2P0.67Si0.33 | 1.47 (1.80) | 2.51 (3.09) | Fe1.34Co0.66P1−xSix | 0.13 (−0.16) | 0.30 (−0.38) | 0.39 (0.12) | 0.89 (0.26) | 0.36 (0.23) | 0.80 (0.50) |
| Fe2P0.59Si0.41 | 1.42 (1.53) | 2.33 (2.51) | Fe1.17Co0.83P1−xSix | −0.50 (−0.85) | −1.22 (−2.10) | −0.14 (−0.71) | −0.32 (−1.68) | 0.09 (−0.21) | 0.21 (−0.49) |
| Fe2P0.5Si0.5 | 1.22 (1.40) | 1.96 (2.25) | FeCoP1−xSix | −1.14 (−1.45) | −2.96 (−3.75) | −0.94 (−1.29) | −2.38 (−3.29) | −0.63 (−0.93) | −1.54 (−2.29) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erdmann, S.; Sözen, H.İ.; Klüner, T. Ab Initio Investigation on the Magnetic Moments, Magnetocrystalline Anisotropy and Curie Temperature of Fe2P-Based Magnets. Magnetism 2025, 5, 14. https://doi.org/10.3390/magnetism5020014
Erdmann S, Sözen Hİ, Klüner T. Ab Initio Investigation on the Magnetic Moments, Magnetocrystalline Anisotropy and Curie Temperature of Fe2P-Based Magnets. Magnetism. 2025; 5(2):14. https://doi.org/10.3390/magnetism5020014
Chicago/Turabian StyleErdmann, Stephan, Halil İbrahim Sözen, and Thorsten Klüner. 2025. "Ab Initio Investigation on the Magnetic Moments, Magnetocrystalline Anisotropy and Curie Temperature of Fe2P-Based Magnets" Magnetism 5, no. 2: 14. https://doi.org/10.3390/magnetism5020014
APA StyleErdmann, S., Sözen, H. İ., & Klüner, T. (2025). Ab Initio Investigation on the Magnetic Moments, Magnetocrystalline Anisotropy and Curie Temperature of Fe2P-Based Magnets. Magnetism, 5(2), 14. https://doi.org/10.3390/magnetism5020014








