Abstract
We investigate the role of high-harmonic wave-vector interactions, which affect the stability of the single-Q spiral state and often result in the formation of multiple-Q states. By performing simulated annealing for an effective spin model on a two-dimensional square lattice, we examine the modulation of the single-Q spiral spin configuration by the high-harmonic wave-vector interaction. As a result, we find that the interactions at particular high-harmonic wave vectors affect the stability of the single-Q spiral state. In particular, the incorporation of interactions at high-harmonic wave vectors formed by the sum of two mutually perpendicular ordering wave vectors can lead to the emergence of three double-Q states and a square skyrmion crystal. The present study unveils the importance of high-harmonic wave-vector interactions in order to realize complicated noncoplanar spin textures.
1. Introduction
Noncollinear magnetic textures have attracted considerable attention in recent years owing to their rich physical properties like the anomalous Hall effect [1,2,3,4,5,6,7] and potential applications in spintronic devices [8,9,10,11,12]. Among them, a spiral (helical) magnetic state, in which spin moments rotate periodically in real space, represents a prototypical system that exhibits various spin-order-driven physical phenomena. For example, reflecting the breaking of spatial inversion symmetry by the spiral spin texture, the system exhibits an emergent electric polarization [13,14,15,16,17,18] and antisymmetric spin-split band structures without relying on the relativistic spin-orbit coupling [19,20,21], which results in the Edelstein effect [22,23,24,25,26], the spin Hall effect [27,28,29,30,31], and unconventional spin-orbital coupling [32,33,34,35].
From the viewpoint of theoretical modeling, there are three main stabilization mechanisms for the spiral state. The first is the competition between the ferromagnetic exchange interaction and the Dzyaloshinskii–Moriya interaction [36,37], the latter of which arises from the relativistic spin-orbit coupling under the breaking of the spatial inversion symmetry. The second is the competition between the ferromagnetic exchange interaction and further-neighbor antiferromagnetic exchange interactions [38,39,40,41,42]. The third is the long-range interaction in itinerant magnets [43,44,45], which is the so-called Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction [46,47,48]. Although the first mechanism relies on a noncentrosymmetric lattice structure, the other two are effective irrespective of the lattice symmetry.
Since the spin configuration of the spiral state is characterized by a single dominant ordering wave vector Q in momentum space, this can be referred to as a single-Q state. In contrast, the superposition of the single-Q spin configuration at different ordering wave vectors gives rise to more complex spin configurations, which is denoted as a multiple-Q state; we refer to the spin state as the double-Q (triple-Q) state when a double-Q (triple-Q) superposition of the single-Q spiral state occurs [49,50,51,52]. Such multiple-Q states are of great interest due to their potential to host topologically nontrivial magnetic textures, including skyrmion crystals (SkXs) [53,54,55,56,57,58,59,60,61]. For example, the superposition of two orthogonal spiral waves leads to the square skyrmion crystal (SkX), and the superposition of three spiral waves leads to the triangular SkX, both of which accompany nonzero topological charges. Depending on the relative phases among the constituent waves, one can construct topologically distinct multiple-Q states, such as meron–antimeron crystals consisting of merons with the topological number of () and antimerons with the topological number of (), leading to a cancellation of the net topological charge [62,63,64,65,66], which differs from another topologically nontrivial multiple-Q state, bimeron crystal with a nonzero topological number [67,68,69,70,71]. In order to stabilize such multiple-Q states, including SkXs, one needs to take into account other effects in addition to the interactions inducing the single-Q spiral state [72], such as thermal fluctuations [73,74,75], the bond-dependent symmetric anisotropic exchange interaction [76,77,78,79,80,81,82,83,84,85,86], multiple-spin interactions [87,88,89,90,91,92], and nonmagnetic impurities [93] in addition to an external magnetic field [55,60,94,95].
In the present study, we investigate the stability of single-Q and multiple-Q states by focusing on a mechanism that induces multiple-Q instabilities: interactions at high-harmonic wave vectors in momentum space. While the primary contributions to the stabilization of single-Q and multiple-Q states are typically governed by interactions at the fundamental ordering wave vectors, recent studies have demonstrated that interactions at higher-harmonic wave vectors can also play an important role in stabilizing multiple-Q states [96,97]. For example, the high-harmonic wave-vector interaction at wave vectors given by the sum of two ordering wave vectors serves as the microscopic origin of multiple SkX phases observed in GdRu2Ge2 [98]. Here, we examine the effect of high-harmonic wave-vector interactions on the stability of the single-Q spiral state, identifying the specific interaction channels that can trigger multiple-Q instabilities. To this end, we analyze an effective spin model with momentum-resolved interactions on a two-dimensional square lattice by employing simulated annealing. As a result, we find that interactions at second-harmonic wave vectors affect the stability of the single-Q spiral state, whereas those at third-harmonic wave vectors have negligible influence, although neither interaction leads to the emergence of multiple-Q states. Furthermore, we show that four distinct multiple-Q states, including the SkX, are stabilized when interactions are introduced at specific high-harmonic wave vectors formed by linear combinations of two ordering wave vectors. These findings provide another guideline for engineering multiple-Q states and SkXs through the design of microscopic interaction models.
The rest of this paper is organized as follows: In Section 2, we introduce an effective spin model with momentum-resolved interactions on the square lattice. We also outline the numerical method based on simulated annealing. In Section 3, we show the results obtained by the simulated annealing. After presenting the result without high-harmonic wave-vector interactions, where only the single-Q spiral state appears, we discuss the effect of five-type high-harmonic wave-vector interactions on the single-Q spiral state. We show that only one of the high-harmonic wave-vector interactions results in the instabilities toward double-Q states. Finally, we conclude our results in Section 4.
2. Model and Method
As a starting point, we consider a localized spin model on a centrosymmetric square lattice in two dimensions; we set the lattice constant of the square lattice as unity. The classical spin model is given by
where denotes the classical localized spin at site i, with its magnitude set to unity. The Hamiltonian consists of the exchange interactions in the first term and the Zeeman coupling in the second term. In the first term, we consider the -type exchange interaction between ith and jth spins, since such an Ising-type interaction often leads to multiple-Q and SkX instabilities [94,95,99,100,101,102,103]. We consider competing exchange interactions by taking the ferromagnetic exchange interaction between the nearest-neighbor spins and the antiferromagnetic exchange interactions between the further-neighbor spins so that the Fourier transform of and shows the energy minima at and for the isotropic case, i.e., ; the interactions at and are equivalent owing to the fourfold rotational symmetry of the square lattice. As an example, such peak structures at and can be realized when the parameters are chosen as , , and so on, for the first-, second-, and third-neighbor interactions, , , and .
Since the internal energy in the ground-state spin configuration is largely determined by the dominant ordering wave vectors, we simplify the interaction term accordingly:
where is the component of localized spins , which is derived by the Fourier transformation. The first term represents the contribution from the dominant ordering wave vectors, where is the label of the dominant ordering wave vectors: and . The prefactor 2 means the contributions at and . The second term represents the contribution from the other wave vectors, where is the label of the corresponding wave vectors. In order to clarify the role of the high-harmonic wave-vector interactions, we consider the following five situations:
- (i)
- and
- (ii)
- and
- (iii)
- and
- (iv)
- and
- (v)
- , , , and .
We set the magnitude of the high-harmonic wave-vector interactions as for case (i), for case (ii), for case (iii), for case (iv), and for case (v). Among (i)–(v), the contributions at (i) and (ii) play an important role when the effect of is considered, whereas the contributions at (iii), (iv), and (v) are important in discussing multiple-Q instabilities consisting of and . We ignore the -type anisotropic effect for the high-harmonic wave-vector interaction for simplicity. We also neglect the interactions for other wave vectors, since they have a negligible effect on the ground-state energy when the spin configuration is characterized by and . In other words, a superposition of wave vectors at symmetry-unrelated positions usually leads to energy loss compared to the single-Q spiral state [104]. Meanwhile, the above high-harmonic wave vectors of and sometimes assist the formation of multiple-Q states. In the following, we set as the energy unit of the model in Equation (1), and we fix , which favors the easy-axis spin configuration; we confirm that the following results are not altered qualitatively for . The second term in Equation (1) denotes the effect of the out-of-plane magnetic field with the strength H.
To explore the ground-state spin configurations as functions of and H, we employ the simulated annealing combined with the Metropolis algorithm for updating localized spins in real space. Each simulation begins with a randomly generated spin configuration at a high initial temperature . The system is then gradually cooled down to a final temperature using an exponential annealing schedule defined by in each Monte Carlo step, where the annealing rate ranges from to . After reaching T, we perform – Monte Carlo sweeps to calculate thermal averages. This procedure is repeated independently for each set of model parameters to ensure proper sampling. The system size is taken at , chosen to be commensurate with the ordering wave vectors ; the system size is also taken at , where we confirmed that the obtained magnetic phases are the same.
To characterize the spin textures obtained in the simulations, we evaluate the magnetic moment resolved by wave vector and spin component , denoted by . It is computed via the spin structure factor as
where denotes the Monte Carlo average over thermalized spin configurations, and N is the total number of lattice sites; represents the position vector at site i. From the rotational symmetry around the z-axis in spin space, the components of the magnetic moments and spin structure factor are calculated. In addition, the uniform magnetization along the z-axis is calculated as .
3. Result
In this section, we show the results obtained by the simulated annealing. First, we discuss the magnetic phases appearing in the absence of high-harmonic wave-vector interactions in Section 3.1. Then, we discuss the effect of high-harmonic wave-vector interactions, which can be a source of multiple-Q states, in Section 3.2.
3.1. Without High-Harmonic Wave-Vector Interaction
Figure 1a shows the H dependence of the uniform magnetization for the model in Equation (1), where the effect of high-harmonic wave-vector interactions is neglected, i.e., . There are three magnetic phases, which are distinguished by the behavior of the -H curve: the single-Q vertical spiral (1Q VS) state, the single-Q conical spiral (1Q CS) state, and the fully polarized (FP) state. The 1Q VS state stabilized in the low-field regions has the single-Q spiral spin configuration at or , as shown in Figure 1b. Owing to the presence of the -type easy-axis anisotropy , the z component of magnetic moments, is larger than the component, . When the magnetic field H increases, is slightly suppressed so as to gain the Zeeman energy. The real-space spin configuration of the 1Q VS state is given by , where a, b, and stand for the variational parameters depending on , and represents the normalization factor; the spiral plane lies on the plane and its shape is elliptical. It is noted that the 1Q VS state with the spiral plane on the plane has the same energy owing to the presence of the spin rotational symmetry around the z-axis.
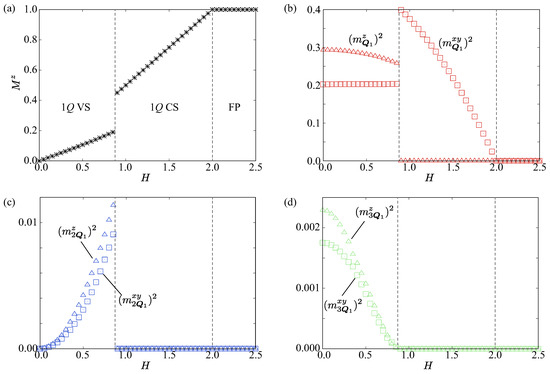
Figure 1.
H dependence of (a) the magnetization along the z direction, , (b) the in-plane and out-of-plane components of squared magnetic moments at , and , (c) those at , , and , and (d) those at , , and without the high-harmonic wave-vector interactions. 1Q CS, 1Q VS, and FP represent the single-Q conical spiral state, the single-Q vertical spiral state, and the fully polarized state, respectively.
For , the 1Q VS state shows a phase transition to the 1Q CS state with a jump in the magnetization, as shown in Figure 1a. Accordingly, the magnetic structure of the 1Q CS state is modulated so as to vanish , as shown in Figure 1b. Thus, this transition is regarded as the spin-flop transition, where the spiral plane changes from the plane to the plane. Indeed, the real-space spin configuration is characterized by the circular spiral spin configuration on the plane expressed as . The 1Q VS state continuously turns into the FP state with .
Owing to the local spin length constraint, there is a finite intensity of the spin moment at high-harmonic wave vectors. Figure 1c,d show the H dependence of the magnetic moments at the second-harmonic wave vector and the third-harmonic wave vector , respectively. The data show that both and become nonzero in the 1Q VS state, while they vanish in the 1Q CS state. The appearance of the intensities at high-harmonic wave vectors is attributed to the elliptical spiral plane in the 1Q VS state under the local spin length constraint. The behaviors of and against H are different from each other; tend to be enhanced for larger H, while tend to be suppressed for larger H. In particular, the intensity at the second-harmonic wave vector is due to the presence of the magnetic field [105,106]. Such a different behavior affects the stability of the 1Q VS state, as will be discussed in the subsequent section.
3.2. With High-Harmonic Wave-Vector Interaction
We discuss the effect of high-harmonic wave-vector interactions on the stability of the single-Q spiral state. We show the results under the five types of high-harmonic wave-vector interactions introduced in Section 2 one by one below.
3.2.1. Case (i)
We consider the case of the interaction at the second-harmonic wave vectors, i.e., and . Figure 2a shows the phase diagram in the plane of and H constructed by performing the simulated annealing. Although no additional phases appear in the phase diagram for , the phase boundary between the 1Q VS and 1Q CS states shifts upward as increases. This shift in the phase boundary is due to the second-harmonic wave-vector interaction, which is understood from the results in Figure 1c. In other words, nonzero intensity at can contribute to the internal energy when the corresponding interaction is considered, which enlarges the region of the 1Q VS state with the intensity at in the spin structure factor. Thus, the second-harmonic wave-vector interaction tends to favor the 1Q VS state rather than the 1Q CS state.
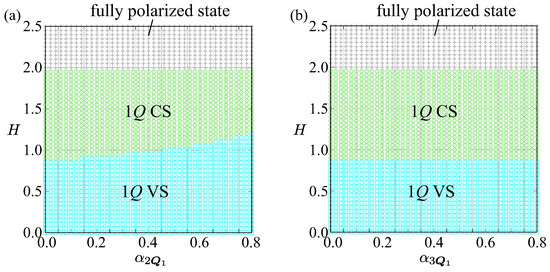
Figure 2.
Magnetic phase diagrams of the model in Equation (1) in the presence of the high-harmonic wave-vector interaction at (a) and and (b) and . 1Q CS and 1Q VS stand for the single-Q conical spiral and single-Q vertical spiral states, respectively.
3.2.2. Case (ii)
We show the phase diagram in Figure 2b when the third-harmonic wave-vector interaction with and is included. In contrast to the second-harmonic wave-vector interaction in Figure 2a, there is no change in the phase boundary, which means that the third-harmonic wave-vector interaction has little effect on the stability of the single-Q spiral state. Such a behavior is also understood from the H dependence of in Figure 1d. Both and become smaller in the vicinity of the phase boundary, which indicates that there is almost no energy gain by . Thus, we can neglect the contribution of the third-harmonic wave-vector interaction in the effective spin model with the momentum-resolved interaction.
3.2.3. Case (iii)
We consider the effect of the high-harmonic wave-vector interaction of and , i.e., and [107]. As shown in the phase diagram in Figure 3, four additional phases appear in the phase diagram in the intermediate-field regions, which are denoted as SkX, 2Q I, 2Q II, and 2Q III. Among them, the most notable phase is the SkX, which consists of the periodic alignment of the skyrmions, as shown by the real-space spin configuration in Figure 4a. The SkX is characterized by a superposition of two vertical spiral waves at and . As shown in the spin structure factor in Figure 4e,i, both and z components show the fourfold symmetric peak structures at and with the same intensity. Owing to the vortex-type spin configuration, this state exhibits a nonzero quantized skyrmion number calculated by the solid angle among three neighboring spins [108]; it is noted that the spin configuration with the skyrmion number of [Figure 4a] has the same energy as that with the skyrmion number of owing to the spin rotational symmetry around the z-axis. The appearance of the SkX with the skyrmion number of in Figure 4a is due to initial spin configurations; we also obtain the spin configuration with the skyrmion number of in the simulations for different initial spin configurations. Such a degeneracy can be lifted by considering the bond-dependent magnetic anisotropy arising from the discrete fourfold rotational symmetry of the square lattice [109]. The SkX is stabilized for large , which indicates that the high-harmonic wave-vector interaction at becomes the essence to induce the SkX [107]. Since the present SkX in centrosymmetric magnets shares the same real-space topological properties as the SkX stabilized by the Dzyaloshinskii–Moriya interaction, the spin waves in the present SkX are supposed to be topological [110,111]. In contrast to the previous study, we do not obtain the instability toward the rectangular SkX characterized by different intensities of magnetic moments at and [107].
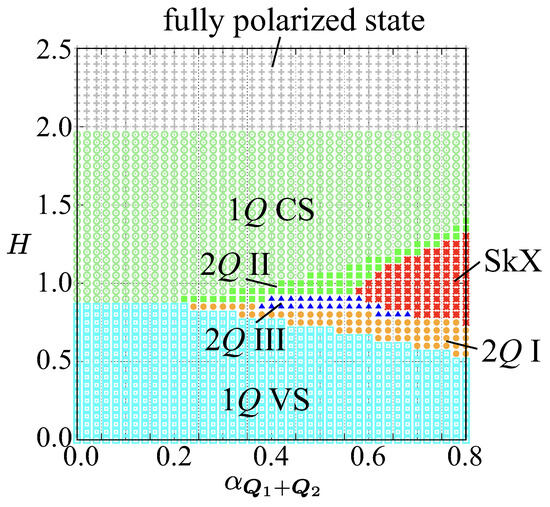
Figure 3.
Magnetic phase diagrams of the model in Equation (1) in the presence of the high-harmonic wave-vector interaction at . 2Q I, 2Q II, and 2Q III represent the double-Q states characterized by different spin configurations. SkX stands for the skyrmion crystal.
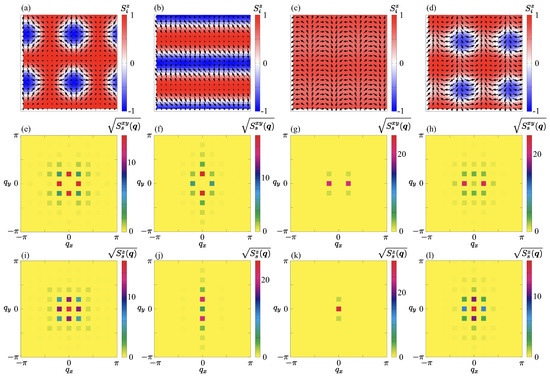
Figure 4.
(a–d) Real-space spin configurations of (a) the SkX at and , (b) the 2Q I state at and , (c) the 2Q II state at and , and (d) the 2Q III state at and . The arrows represent the direction of spins, and the color represents the z component of spins. (e–h) Square root of the spin structure factor for the in-plane component, which corresponds to (a–d). (i–l) Square root of the spin structure factor for the out-of-plane component, which corresponds to (a–d). The data in this figure are obtained for the system with the spins.
We describe the spin configurations for the other three double-Q states stabilized for nonzero , all of which are topologically trivial. The 2Q I state emerges when the magnetic field increases in the 1Q VS region. As shown by the real-space spin configuration in Figure 4b, the single-Q spiral modulation at seems to be dominant. Indeed, the data in terms of the spin structure factor show that the 2Q I state is characterized by the dominant peak at and the subdominant peak at , as shown in Figure 4f,j. Since there is no intensity of , this state is described by the superposition of the vertical spiral wave at and the sinusoidal wave at , where the sinusoidal-wave direction is perpendicular to the spiral plane.
The 2Q II state is stabilized in the region adjacent to the 1Q CS state upon decreasing H. This spin configuration resembles the 1Q CS state, as shown by the real-space spin configuration in Figure 4c. By closely looking at the spin configuration, one finds that there is an oscillation in the z-spin component, as shown by the component of the z-spin structure factor in Figure 4k. On the other hand, the spin component is almost characterized by the component, as shown in Figure 4g, which indicates the presence of the conical spiral configuration at . Thus, the spin configuration of the 2Q II state is represented by a superposition of the conical spiral wave at and the sinusoidal wave at . Additionally in this case, the sinusoidal-wave direction is perpendicular to the spiral plane. The phase sequence at is shown by the H– plot in Figure 5.
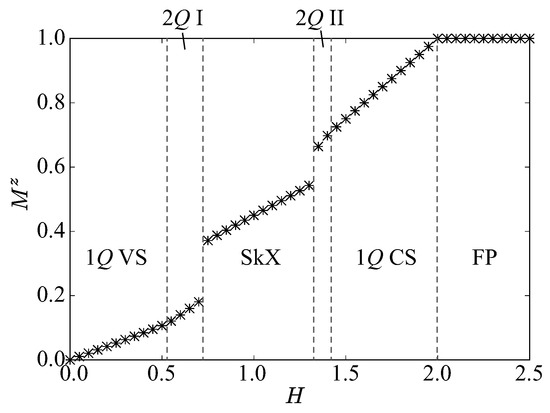
Figure 5.
H dependence of the magnetization along the z direction at . The vertical dashed lines denote the phase boundaries between different magnetic phases.
The 2Q III state appears in the narrow region sandwiched by the 2Q I and 2Q II states, as shown in the phase diagram in Figure 3. The real-space spin configuration of the 2Q III state is shown in Figure 4d; the -spin configuration resembles the conical spiral state, while the z-spin configuration resembles the SkX. In the spin structure factor, both and z components show the anisotropic peak structures at and , as shown in Figure 4h and Figure 4l, respectively.
Common to all the double-Q states and SkX, the double-Q superposition occurs so as to have the intensity at and in Figure 4e–l. This is due to the energy gain by the high-harmonic wave-vector interactions. In other words, the high-harmonic wave-vector interactions at lead to double-Q instabilities, which play an essential role in stabilizing the SkX.
3.2.4. Case (iv)
We consider a different type of high-harmonic wave-vector interaction at and . Figure 6a shows the magnetic phase diagram against and H. The results show no change in the phase boundaries while is varied, which indicates that the high-harmonic wave-vector interaction at plays a less significant role in inducing multiple-Q states.
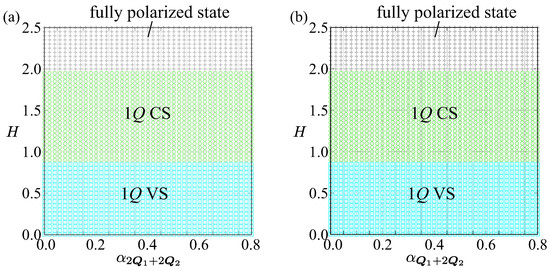
Figure 6.
Magnetic phase diagrams of the model in Equation (1) in the presence of the high-harmonic wave-vector interaction at (a) and (b) and .
3.2.5. Case (v)
The last case is the inclusion of the high-harmonic wave-vector interaction at , , , and . Similarly to the result in Figure 6a, the phase boundary in Figure 6b shows no dependence of . Thus, the high-harmonic wave-vector interaction at also plays a less significant role in inducing multiple-Q states.
4. Conclusions
In conclusion, we have examined the role of the high-harmonic wave-vector interaction on the stability of single-Q and multiple-Q states in a tetragonal crystalline system. Using simulated annealing applied to an effective spin model on the two-dimensional centrosymmetric square lattice, we have investigated how these interactions modulate the single-Q spiral spin configurations. Our findings revealed that specific high-harmonic wave-vector components play a stabilizing role in maintaining the single-Q vertical spiral state. More importantly, when the interactions involve wave vectors corresponding to the sum of two orthogonal ordering wave vectors, the system exhibits a rich variety of multiple-Q phases, including three distinct double-Q states and a square SkX. These results highlight the essential role of high-harmonic wave-vector interactions in generating complex noncollinear spin textures, which provide a new microscopic pathway toward engineering exotic magnetic phases in centrosymmetric systems. One of the important consequence is that the interactions at and can be a source of various multiple-Q phases rather than those at other high-harmonic wave vectors. Therefore, when applying the model to real materials, it is desirable to evaluate the effective interactions not only at and , but also at and , based on first-principles calculations. Furthermore, recent studies have demonstrated that topological spin textures such as hedgehogs and hopfions can be represented by superpositions of spin density waves [112]. Given that such superpositions give rise to intensities in the high-harmonic wave-vector components of the spin structure factor, the interaction explored in this work may play a role in stabilizing these exotic spin phases.
Funding
This research was supported by JSPS KAKENHI grant numbers JP21H01037, JP22H00101, JP22H01183, JP23H04869, JP23K03288, and JP23K20827, and by JST CREST (JPMJCR23O4) and JST FOREST (JPMJFR2366). Parts of the numerical calculations were performed on the supercomputing systems at ISSP, the University of Tokyo.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Tomizawa, T.; Kontani, H. Anomalous Hall effect in the t2g orbital kagome lattice due to noncollinearity: Significance of the orbital Aharonov-Bohm effect. Phys. Rev. B 2009, 80, 100401. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Q.; MacDonald, A.H. Anomalous Hall Effect Arising from Noncollinear Antiferromagnetism. Phys. Rev. Lett. 2014, 112, 017205. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.C.; Xiao, D.; Guo, G.Y.; Niu, Q.; MacDonald, A.H. Manipulating anomalous Hall antiferromagnets with magnetic fields. Phys. Rev. B 2020, 101, 104418. [Google Scholar] [CrossRef]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef]
- Jungwirth, T.; Sinova, J.; Manchon, A.; Marti, X.; Wunderlich, J.; Felser, C. The multiple directions of antiferromagnetic spintronics. Nat. Phys. 2018, 14, 200–203. [Google Scholar] [CrossRef]
- Fukami, S.; Lorenz, V.O.; Gomonay, O. Antiferromagnetic spintronics. J. Appl. Phys. 2020, 128, 070401. [Google Scholar] [CrossRef]
- Dal Din, A.; Amin, O.; Wadley, P.; Edmonds, K. Antiferromagnetic spintronics and beyond. npj Spintron. 2024, 2, 25. [Google Scholar] [CrossRef]
- Rimmler, B.H.; Pal, B.; Parkin, S.S. Non-collinear antiferromagnetic spintronics. Nat. Rev. Mater. 2025, 10, 109–127. [Google Scholar] [CrossRef]
- Katsura, H.; Nagaosa, N.; Balatsky, A.V. Spin Current and Magnetoelectric Effect in Noncollinear Magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef] [PubMed]
- Mostovoy, M. Ferroelectricity in Spiral Magnets. Phys. Rev. Lett. 2006, 96, 067601. [Google Scholar] [CrossRef]
- Sergienko, I.A.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef]
- Harris, A.B.; Yildirim, T.; Aharony, A.; Entin-Wohlman, O. Towards a microscopic model of magnetoelectric interactions in Ni3V2O8. Phys. Rev. B 2006, 73, 184433. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef]
- Cardias, R.; Szilva, A.; Bezerra-Neto, M.; Ribeiro, M.; Bergman, A.; Kvashnin, Y.O.; Fransson, J.; Klautau, A.; Eriksson, O.; Nordström, L. First-principles Dzyaloshinskii–Moriya interaction in a non-collinear framework. Sci. Rep. 2020, 10, 20339. [Google Scholar] [CrossRef]
- Hayami, S. Mechanism of antisymmetric spin polarization in centrosymmetric multiple-Q magnets based on effective chiral bilinear and biquadratic spin cross products. Phys. Rev. B 2022, 105, 024413. [Google Scholar] [CrossRef]
- Sukhachov, P.; Linder, J. Impurity-induced Friedel oscillations in altermagnets and p-wave magnets. Phys. Rev. B 2024, 110, 205114. [Google Scholar] [CrossRef]
- Brekke, B.; Sukhachov, P.; Giil, H.G.; Brataas, A.; Linder, J. Minimal Models and Transport Properties of Unconventional p-Wave Magnets. Phys. Rev. Lett. 2024, 133, 236703. [Google Scholar] [CrossRef] [PubMed]
- Edelstein, V.M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. [Google Scholar] [CrossRef]
- Yip, S.K. Two-dimensional superconductivity with strong spin-orbit interaction. Phys. Rev. B 2002, 65, 144508. [Google Scholar] [CrossRef]
- Fujimoto, S. Magnetoelectric effects in heavy-fermion superconductors without inversion symmetry. Phys. Rev. B 2005, 72, 024515. [Google Scholar] [CrossRef]
- Yoda, T.; Yokoyama, T.; Murakami, S. Orbital Edelstein Effect as a Condensed-Matter Analog of Solenoids. Nano Lett. 2018, 18, 916–920. [Google Scholar] [CrossRef] [PubMed]
- Massarelli, G.; Wu, B.; Paramekanti, A. Orbital Edelstein effect from density-wave order. Phys. Rev. B 2019, 100, 075136. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Dissipationless quantum spin current at room temperature. Science 2003, 301, 1348–1351. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Spin-Hall Insulator. Phys. Rev. Lett. 2004, 93, 156804. [Google Scholar] [CrossRef]
- Sinova, J.; Culcer, D.; Niu, Q.; Sinitsyn, N.A.; Jungwirth, T.; MacDonald, A.H. Universal Intrinsic Spin Hall Effect. Phys. Rev. Lett. 2004, 92, 126603. [Google Scholar] [CrossRef]
- Fujimoto, S. Emergent Nodal Excitations due to Coexistence of Superconductivity and Antiferromagnetism: Cases with and without Inversion Symmetry. J. Phys. Soc. Jpn. 2006, 75, 083704. [Google Scholar] [CrossRef]
- Fujimoto, S. Fermi liquid theory for heavy fermion superconductors without inversion symmetry: Magnetism and transport coefficients. J. Phys. Soc. Jpn. 2007, 76, 034712. [Google Scholar] [CrossRef]
- Fu, L. Parity-Breaking Phases of Spin-Orbit-Coupled Metals with Gyrotropic, Ferroelectric, and Multipolar Orders. Phys. Rev. Lett. 2015, 115, 026401. [Google Scholar] [CrossRef]
- Kozii, V.; Fu, L. Odd-Parity Superconductivity in the Vicinity of Inversion Symmetry Breaking in Spin-Orbit-Coupled Systems. Phys. Rev. Lett. 2015, 115, 207002. [Google Scholar] [CrossRef]
- Venderbos, J.W.F.; Kozii, V.; Fu, L. Odd-parity superconductors with two-component order parameters: Nematic and chiral, full gap, and Majorana node. Phys. Rev. B 2016, 94, 180504(R). [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H.; Motome, Y. Electric Toroidal Quadrupoles in the Spin-Orbit-Coupled Metal Cd2Re2O7. Phys. Rev. Lett. 2019, 122, 147602. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Nambu, Y.; Tonomura, H.; Sakai, O.; Jonas, S.; Broholm, C.; Tsunetsugu, H.; Qiu, Y.; Maeno, Y. Spin disorder on a triangular lattice. Science 2005, 309, 1697–1700. [Google Scholar] [CrossRef] [PubMed]
- Day, P.; Moore, M.W.; Wilkinson, C.; Ziebeck, K.R.A. Neutron diffraction study of the incommensurate magnetic phase of Ni0.92Zn0.08Br2. J. Phys. C Solid State Phys. 1981, 14, 3423. [Google Scholar] [CrossRef]
- Regnault, L.; Rossat-Mignod, J.; Adam, A.; Billerey, D.; Terrier, C. Inelastic neutron scattering investigation of the magnetic excitations in the helimagnetic state of NiBr2. J. Phys. 1982, 43, 1283–1290. [Google Scholar] [CrossRef]
- Ghimire, N.; Ronning, F.; Williams, D.; Scott, B.; Luo, Y.; Thompson, J.; Bauer, E. Investigation of the physical properties of the tetragonal CeMAl4Si2 (M = Rh, Ir, Pt) compounds. J. Phys. Condens. Matter 2014, 27, 025601. [Google Scholar] [CrossRef]
- Gunasekera, J.; Harriger, L.; Dahal, A.; Maurya, A.; Heitmann, T.; Disseler, S.M.; Thamizhavel, A.; Dhar, S.; Singh, D.J.; Singh, D.K. Electronic nature of the lock-in magnetic transition in CeXAl4Si2. Phys. Rev. B 2016, 93, 155151. [Google Scholar] [CrossRef]
- Yoshimori, A. A new type of antiferromagnetic structure in the rutile type crystal. J. Phys. Soc. Jpn. 1959, 14, 807–821. [Google Scholar] [CrossRef]
- Kaplan, T.A. Some Effects of Anisotropy on Spiral Spin-Configurations with Application to Rare-Earth Metals. Phys. Rev. 1961, 124, 329–339. [Google Scholar] [CrossRef]
- Elliott, R.J. Phenomenological Discussion of Magnetic Ordering in the Heavy Rare-Earth Metals. Phys. Rev. 1961, 124, 346–353. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Bak, P.; Lebech, B. “Triple-” Modulated Magnetic Structure and Critical Behavior of Neodymium. Phys. Rev. Lett. 1978, 40, 800–803. [Google Scholar] [CrossRef]
- Shapiro, S.M.; Gurewitz, E.; Parks, R.D.; Kupferberg, L.C. Multiple-q Magnetic Structure in CeAl2. Phys. Rev. Lett. 1979, 43, 1748–1751. [Google Scholar] [CrossRef]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 13, L881. [Google Scholar] [CrossRef]
- Forgan, E.M.; Gibbons, E.P.; McEwen, K.A.; Fort, D. Observation of a Quadruple-q Magnetic Structure in Neodymium. Phys. Rev. Lett. 1989, 62, 470–473. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Koshibae, W.; Tokunaga, Y.; Shibata, K.; Taguchi, Y.; Nagaosa, N.; Tokura, Y. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 2018, 564, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.h.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef]
- Chen, K.; Luo, Q.; Zhou, Z.; He, S.; Xi, B.; Jia, C.; Luo, H.G.; Zhao, J. Triple-meron crystal in high-spin Kitaev magnets. New J. Phys. 2023, 25, 023006. [Google Scholar] [CrossRef]
- Xie, Y.M.; Nagaosa, N. Phase shifts, band geometry, and responses in triple-Q charge and spin density waves. Phys. Rev. B 2024, 110, L241108. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I.; Tretiakov, O.A. Magnetic bimerons as skyrmion analogues in in-plane magnets. Phys. Rev. B 2019, 99, 060407(R). [Google Scholar] [CrossRef]
- Kim, S.K. Dynamics of bimeron skyrmions in easy-plane magnets induced by a spin supercurrent. Phys. Rev. B 2019, 99, 224406. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, J.; Shen, L.; Ezawa, M.; Tretiakov, O.A.; Zhao, G.; Liu, X.; Zhou, Y. Static and dynamic properties of bimerons in a frustrated ferromagnetic monolayer. Phys. Rev. B 2020, 101, 144435. [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Shen, L.; Xia, J.; Chen, Z.; Li, X.; Zhang, X.; Tretiakov, O.A.; Shao, Q.; Zhao, G.; Liu, X.; Ezawa, M.; et al. Nonreciprocal dynamics of ferrimagnetic bimerons. Phys. Rev. B 2022, 105, 014422. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef] [PubMed]
- Laliena, V.; Campo, J. Stability of skyrmion textures and the role of thermal fluctuations in cubic helimagnets: A new intermediate phase at low temperature. Phys. Rev. B 2017, 96, 134420. [Google Scholar] [CrossRef]
- Laliena, V.; Albalate, G.; Campo, J. Stability of the skyrmion lattice near the critical temperature in cubic helimagnets. Phys. Rev. B 2018, 98, 224407. [Google Scholar] [CrossRef]
- Becker, M.; Hermanns, M.; Bauer, B.; Garst, M.; Trebst, S. Spin-orbit physics of j = Mott insulators on the triangular lattice. Phys. Rev. B 2015, 91, 155135. [Google Scholar] [CrossRef]
- Lee, E.K.H.; Kim, Y.B. Theory of magnetic phase diagrams in hyperhoneycomb and harmonic-honeycomb iridates. Phys. Rev. B 2015, 91, 064407. [Google Scholar] [CrossRef]
- Janssen, L.; Andrade, E.C.; Vojta, M. Honeycomb-Lattice Heisenberg-Kitaev Model in a Magnetic Field: Spin Canting, Metamagnetism, and Vortex Crystals. Phys. Rev. Lett. 2016, 117, 277202. [Google Scholar] [CrossRef]
- Rousochatzakis, I.; Rössler, U.K.; van den Brink, J.; Daghofer, M. Kitaev anisotropy induces mesoscopic Z2 vortex crystals in frustrated hexagonal antiferromagnets. Phys. Rev. B 2016, 93, 104417. [Google Scholar] [CrossRef]
- Yao, X.; Dong, S. Topological triple-vortex lattice stabilized by mixed frustration in expanded honeycomb Kitaev-Heisenberg model. Sci. Rep. 2016, 6, 26750. [Google Scholar] [CrossRef]
- Chern, G.W.; Sizyuk, Y.; Price, C.; Perkins, N.B. Kitaev-Heisenberg model in a magnetic field: Order-by-disorder and commensurate-incommensurate transitions. Phys. Rev. B 2017, 95, 144427. [Google Scholar] [CrossRef]
- Maksimov, P.A.; Zhu, Z.; White, S.R.; Chernyshev, A.L. Anisotropic-Exchange Magnets on a Triangular Lattice: Spin Waves, Accidental Degeneracies, and Dual Spin Liquids. Phys. Rev. X 2019, 9, 021017. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Helicity locking of a square skyrmion crystal in a centrosymmetric lattice system without vertical mirror symmetry. Phys. Rev. B 2022, 105, 104428. [Google Scholar] [CrossRef]
- Momoi, T.; Kubo, K.; Niki, K. Possible Chiral Phase Transition in Two-Dimensional Solid 3He. Phys. Rev. Lett. 1997, 79, 2081–2084. [Google Scholar] [CrossRef]
- Kurz, P.; Bihlmayer, G.; Hirai, K.; Blügel, S. Three-Dimensional Spin Structure on a Two-Dimensional Lattice: Mn/Cu(111). Phys. Rev. Lett. 2001, 86, 1106–1109. [Google Scholar] [CrossRef]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Ueland, B.; Miclea, C.; Kato, Y.; Ayala-Valenzuela, O.; McDonald, R.; Okazaki, R.; Tobash, P.; Torrez, M.; Ronning, F.; Movshovich, R.; et al. Controllable chirality-induced geometrical Hall effect in a frustrated highly correlated metal. Nat. Commun. 2012, 3, 1067. [Google Scholar] [CrossRef]
- Akagi, Y.; Udagawa, M.; Motome, Y. Hidden Multiple-Spin Interactions as an Origin of Spin Scalar Chiral Order in Frustrated Kondo Lattice Models. Phys. Rev. Lett. 2012, 108, 096401. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Multiple-Q instability by (d-2)-dimensional connections of Fermi surfaces. Phys. Rev. B 2014, 90, 060402(R). [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]
- Butenko, A.B.; Leonov, A.A.; Rößler, U.K.; Bogdanov, A.N. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Hayami, S.; Kato, Y. Widely-sweeping magnetic field–temperature phase diagrams for skyrmion-hosting centrosymmetric tetragonal magnets. J. Magn. Magn. Mater. 2023, 571, 170547. [Google Scholar] [CrossRef]
- Yoshimochi, H.; Takagi, R.; Ju, J.; Khanh, N.; Saito, H.; Sagayama, H.; Nakao, H.; Itoh, S.; Tokura, Y.; Arima, T.; et al. Multistep topological transitions among meron and skyrmion crystals in a centrosymmetric magnet. Nat. Phys. 2024, 20, 1001. [Google Scholar] [CrossRef]
- Lin, S.Z.; Saxena, A.; Batista, C.D. Skyrmion fractionalization and merons in chiral magnets with easy-plane anisotropy. Phys. Rev. B 2015, 91, 224407. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Leonov, A.O.; Kézsmárki, I. Asymmetric isolated skyrmions in polar magnets with easy-plane anisotropy. Phys. Rev. B 2017, 96, 014423. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Kosugi, T.; Kawano, S.; Achiwa, N.; Onodera, A.; Nakai, Y.; Yamamoto, N. Direct evidence of helifan structures in holmium by single crystal neutron diffraction. Phys. B Condens. Matter 2003, 334, 365–368. [Google Scholar] [CrossRef]
- Ghimire, N.J.; Dally, R.L.; Poudel, L.; Jones, D.; Michel, D.; Magar, N.T.; Bleuel, M.; McGuire, M.A.; Jiang, J.; Mitchell, J.; et al. Competing magnetic phases and fluctuation-driven scalar spin chirality in the kagome metal YMn6Sn6. Sci. Adv. 2020, 6, eabe2680. [Google Scholar] [CrossRef]
- Hayami, S. Rectangular and square skyrmion crystals on a centrosymmetric square lattice with easy-axis anisotropy. Phys. Rev. B 2022, 105, 174437. [Google Scholar] [CrossRef]
- Berg, B.; Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Roldán-Molina, A.; Nunez, A.; Fernández-Rossier, J. Topological spin waves in the atomic-scale magnetic skyrmion crystal. New J. Phys. 2016, 18, 045015. [Google Scholar] [CrossRef]
- Aguilera, E.; Jaeschke-Ubiergo, R.; Vidal-Silva, N.; Torres, L.E.F.F.; Nunez, A.S. Topological magnonics in the two-dimensional van der Waals magnet CrI3. Phys. Rev. B 2020, 102, 024409. [Google Scholar] [CrossRef]
- Hou, W.T.; Xiang, Z.; Liu, Y.; Zang, J. Construction of Hopfion Crystals. arXiv 2025, arXiv:2504.03981. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).