Lorenz’s View on the Predictability Limit of the Atmosphere
Definition
1. Introduction
The intrinsic predictability limit of two weeks was reported in Lorenz (1969) [10].
2. A Review of Lorenz’s View and the 1969 Model
2.1. Lorenz’s View of the Predictability Limit
I was hoping to get a better idea what the limits were because “this simple model” said there were limits but it didn’t tell you whether they were a week or year or what.
The lack of complete periodicity in the atmosphere’s behavior is sufficient evidence for instability (Lorenz, 1963b) [4], but it does not reveal the range at which the uncertainty in prediction must become large.
What is the basis for choosing two weeks as a time after which the forecasts might differ significantly?
We may summarize our results in the statement that, based on the most realistic of the general circulation models available, the limit of deterministic predictability for the atmosphere is about two weeks in the winter and somewhat longer in the summer.
Predictability experiments were soon made with the few large global circulation models then in existence (Smagorinsky 1963 [38], Mintz 1964 [39], Leith 1965 [40]); ……. As might have been anticipated, the models were sufficiently dissimilar to one another for the predictability studies performed with them to give contradicting results. Leith’s model indicated no growth of errors at all; Smagorinsky’s indicated a 10-day doubling time, while Mintz’s showed a 5-day doubling time. For various reasons Mintz’s result came to be the most generally accepted one (see Charney et al., 1966) [5].
Now it begins to look as if the upper limit may be somewhere around two weeks, and I get the feeling that another 20 years or so we may actually be making useful day-to-day forecasts up to the two-week range, though I don’t think we are doing it now. But we got up to one week, which I didn’t really expect at the time.
I have confined my quantitative discussions to results deduced from pairs or ensembles of numerical solutions of mathematical models with various degrees of sophistication, but alternative approaches have also been exploited. Some studies have been based on equations whose variables are ensemble averages of error magnitudes. These equations have been derived from conventional atmospheric models, but, to close the equations, i.e., to limit the number of variables to the number of equations, it has been necessary to introduce auxiliary assumptions of questionable validity (see, for example, Thompson, 1957 [1]; Lorenz, 1969 [10]). Results agree reasonably well with those yielded by more conventional approaches.
2.2. Major Features of the Lorenz 1969 Model
3. Discussion
4. Summary
- A.
- The Lorenz 1963 model qualitatively revealed the essence of a finite predictability within a chaotic system such as the atmosphere. However, it did not determine a precise limit for the predictability of the atmosphere.
- B.
- In the 1960s, the two-week predictability limit was originally estimated based on a doubling time of five days in real-world models. Since then, this finding has been documented in Charney et al. (1966 [5]) and has become a consensus.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thompson, P.D. Uncertainty of initial state as a factor in the predictability of large-scale atmospheric flow patterns. Tellus 1957, 9, 275–295. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of hydrodynamic flow. Trans. N. Y. Acad. Sci. 1963, 25, 409–432. [Google Scholar] [CrossRef]
- Lorenz, E.N. Atmospheric predictability experiments with a large numerical model. Tellus 1982, 34, 505–513. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Charney, J.G.; Fleagle, R.G.; Lally, V.E.; Riehl, H.; Wark, D.Q. The feasibility of a global observation and analysis experiment. Bull. Amer. Meteor. Soc. 1966, 47, 200–220. [Google Scholar]
- Lorenz, E.N. Predictability—A problem partly solved. In Proceedings of the Seminar on Predictability, Reading, UK, 4–8 September 1995; ECMWF: Reading, UK, 1996; Volume 1. [Google Scholar]
- Lorenz, E.N. Predictability—A problem partly solved. In Predictability of Weather and Climate; Palmer, T., Hagedorn, R., Eds.; Cambridge University Press: Cambridge, UK, 2006; pp. 40–58. [Google Scholar] [CrossRef]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993; p. 227. [Google Scholar]
- Reeves, R.W. Edward Lorenz Revisiting the Limits of Predictability and Their Implications: An Interview From 2007. Bull. Am. Meteorol. Soc. 2014, 95, 681–687. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Lilly, D.K. Numerical simulation studies of two-dimensional turbulence: II. Stability and predictability studies. Geophys. Fluid Dyn. 1972, 4, 1–28. [Google Scholar] [CrossRef]
- Tribbia, J.J.; Baumhefner, D.P. Scale Interactions and Atmospheric Predictability: An Updated Perspective. Mon. Weather. Rev. 2004, 132, 703–713. [Google Scholar] [CrossRef]
- Lorenz, E.N. Some aspects of atmospheric predictability. European Centre for Medium Range Weather Forecasts, Seminar 1981. In Proceedings of the Problems and Prospects in Long and Medium Range Weather Forecasting, Reading, UK, 14–18 September 1984; pp. 1–20, (BWS: this study was presented in 1981 and cited as 1982 by Lorenz in his web site. However, it was published in 1984.). [Google Scholar]
- Leith, C.E. Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 1971, 28, 145–161. [Google Scholar] [CrossRef]
- Leith, C.E.; Kraichnan, R.H. Predictability of turbulent flows. J. Atmos. Sci. 1972, 29, 1041–1058. [Google Scholar] [CrossRef]
- Li, T.-Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Shen, B.-W. Nonlinear Feedback in a Five-Dimensional Lorenz Model. J. Atmospheric Sci. 2014, 71, 1701–1723. [Google Scholar] [CrossRef]
- Shen, B.-W. Aggregated Negative Feedback in a Generalized Lorenz Model. Int. J. Bifurc. Chaos 2019, 29, 1950037. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, S.R.A.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is weather chaotic? Coexistence of chaos and order within a generalized lorenz model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. Available online: https://journals.ametsoc.org/view/journals/bams/102/1/BAMS-D-19-0165.1.xml (accessed on 29 January 2021). [CrossRef]
- Shen, B.-W.; Pielke, R.A.; Zeng, X. One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models. Atmosphere 2022, 13, 753. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Kesarkar, A.; Zeng, X.; Atlas, R. The Dual Nature of Chaos and Order in the Atmosphere. Atmosphere 2022, 13, 1892. [Google Scholar] [CrossRef]
- Lilly, K.D. Lectures in Sub-Synoptic Scales of Motions and Two-Dimensional Turbulence Dynamic Meteorology; Morel, P., Ed.; Reidel: Boston, MA, USA, 1973; pp. 353–418. [Google Scholar]
- Lilly, K.D. Numerical prediction of thunderstorms-has its time come? J. R. Meteorol. Soc. 1990, 116, 779–798. [Google Scholar]
- Rotunno, R.; Snyder, C. A Generalization of Lorenz’s Model for the Predictability of Flows with Many Scales of Motion. J. Atmospheric Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Palmer, T.N.; Döring, A.; Seregin, G. The real butterfly effect. Nonlinearity 2014, 27, R123–R141. [Google Scholar] [CrossRef]
- Durran, D.R.; Gingrich, M. Tmospheric predictability: Why atmospheric butterflies are not of practical importance. J. Atmos. Sci. 2014, 71, 2476–2478. [Google Scholar] [CrossRef]
- Lloveras, D.J.; Tierney, L.H.; Durran, D.R. Mesoscale Predictability in Moist Midlatitude Cyclones Is Not Sensitive to the Slope of the Background Kinetic Energy Spectrum. J. Atmospheric Sci. 2022, 79, 119–139. [Google Scholar] [CrossRef]
- Turing, A.M. The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. Lond. 1952, 237, 37–72. [Google Scholar]
- Shen, B.-W.; Tao, W.-K.; Wu, M.-L.C. African easterly waves in 30-day high-resolution global simulations: A case study during the 2006 NAMMA period. Geophys. Res. Lett. 2010, 37, L18803. [Google Scholar] [CrossRef]
- Shen, B.-W.; Tao, W.-K.; Green, B. Coupling Advanced Modeling and Visualization to Improve High-Impact Tropical Weather Prediction (CAMVis). IEEE Comput. Sci. Eng. 2011, 13, 56–67. [Google Scholar] [CrossRef]
- Lighthill, J.M. The recently recognized failure of predictability in Newtonian dynamics. Proc. R. Soc. Lond. A 1986, 407, 35–50. [Google Scholar] [CrossRef]
- Zeng, X.; Pielke, R.A.; Eykholt, R. Chaos Theory and Its Applications to the Atmosphere. Bull. Am. Meteorol. Soc. 1993, 74, 631–644. [Google Scholar] [CrossRef]
- Ghil, M.; Read, P.; Smith, L. Geophysical flows as dynamical systems: The influence of Hide’s experiments. Astron. Geophys. 2010, 51, 4.28–4.35. [Google Scholar] [CrossRef]
- Read, P. Application of Chaos to Meteorology and Climate. In The Nature of Chaos; Mullin, T., Ed.; Clarendo Press: Oxford, UK, 1993; pp. 222–260. [Google Scholar]
- Legras, B.; Ghil, M. Persistent anomalies, blocking, and variations in atmospheric predictability. J. Atmos. Sci. 1985, 42, 433–471. [Google Scholar] [CrossRef]
- Washington, R. Quantifying Chaos in the Atmosphere. Prog. Phys. Geogr. 2000, 24, 499–514. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Atlas, R. Three Kinds of Butterfly Effects within Lorenz Models. Encyclopedia 2022, 2, 1250–1259. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. I. The basic experiment. Mon. Wea. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Mintz, Y. Very long-term global integrations of the primitive equations of atmospheric motion. In WMO-IUGG Symposium on Research and Development Aspects of Long-Range Forecasting; Technical Note, No. 66; World Meteorological Organization: Geneva, Switzerland, 1964; pp. 141–155. [Google Scholar]
- Leith, C.E. Numerical simulation of the Earth’s atmosphere. In Methods in Computational Physics; Academic Press: New York, NY, USA, 1965; Volume 4, pp. 1–28. [Google Scholar]
- Judt, F. Insights into Atmospheric Predictability through Global Convection-Permitting Model Simulations. J. Atmospheric Sci. 2018, 75, 1477–1497. [Google Scholar] [CrossRef]
- Judt, F. Atmospheric Predictability of the Tropics, Middle Latitudes, and Polar Regions Explored through Global Storm-Resolving Simulations. J. Atmospheric Sci. 2020, 77, 257–276. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, Y.Q.; Magnusson, L.; Buizza, R.; Lin, S.J.; Chen, J.H.; Emanuel, K. What is the predictability limit of midlatitude weather? J. Atmos. Sci. 2019, 76, 1077–1091. [Google Scholar] [CrossRef]
- Orszag, S.A. Fluid Dynamics; Balian, R., Peuble, J.L., Eds.; Gordon and Breach: London, UK, 1977. [Google Scholar]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in systems with many characteristic times: The case of turbulence. Phys. Rev. E 1996, 53, 2337–2349. [Google Scholar] [CrossRef]
- Lorenz, E.N. Estimates of atmospheric predictability at medium range. In Predictability of Fluid Motions; Holloway, G., West, B., Eds.; American Institute of Physics: New York, NY, USA, 1984; pp. 133–139. [Google Scholar]
- Shen, B.-W. Solitary Waves, Homoclinic Orbits, and Nonlinear Oscillations within the non-dissipative Lorenz Model, the inviscid Pedlosky Model, and the KdV Equation. In Proceedings of the 13th Chaos International Conference CHAOS 2020, Florence, Italy, 9–12 June 2020; Skiadas, C.H., Dimotikalis, Y., Eds.; Springer Proceedings in Complexity, Springer: Cham, Switzerland, 2021. [Google Scholar]
- Pedlosky, J. Finite-Amplitude Baroclinic Waves with Small Dissipation. J. Atmospheric Sci. 1971, 28, 587–597. [Google Scholar] [CrossRef]
- Pedlosky, J. Limit Cycles and Unstable Baroclinic Waves. J. Atmospheric Sci. 1972, 29, 53–63. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: New York, NY, USA, 1987; 710p. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Jordan, D.W.; Smith, S. Nonlinear Ordinary Differential Equations. In An Introduction for Scientists and Engineers, 4th ed.; Oxford University Press: New York, NY, USA, 2007; 560p. [Google Scholar]
- Tucker, W. A rigorous ODE solver and Smale’s 14th problem. Found. Comput. Math. 2002, 2, 53–117. [Google Scholar] [CrossRef]
- Stewart, I. The Lorenz attractor exists. Nature 2000, 406, 948–949. [Google Scholar] [CrossRef]
- Lorenz, E.N. Designing chaotic models. J. Atmos. Sci. 2005, 62, 1574–1587. [Google Scholar] [CrossRef]
- Lorenz, E.N. Investigating the predictability of turbulent motion. Statistical Models and Turbulence. In Proceedings of the Symposium Held at the University of California, San Diego, CA, USA, 15–21 July 1971; Springer: Berlin/Heidelberg, Germany, 1972; pp. 195–204. Available online: https://eapsweb.mit.edu/sites/default/files/Investigating_predictability_1972.pdf (accessed on 6 July 2023).
- Lorenz, E. Low-order models representing realizations of turbulence. J. Fluid Mech. 1972, 55, 545–563. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A.; Zeng, X. 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Special Issue on Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. Atmosphere, 2023; submitted. [Google Scholar] [CrossRef]
- Lorenz, E.N. Progress Report on Atmospheric Predictability. Never Printed. 1970. Available online: https://eapsweb.mit.edu/sites/default/files/Progress_Report_on_Atmospheric_Predictability_1970.pdf (accessed on 6 July 2023).
- Lorenz, E. Limits of Meteorological Predictability. Prepared for the American Meteorological Society, February. 1972 (Unpublished). Available online: https://eapsweb.mit.edu/sites/default/files/Limits_of_Meteorological_Predictability_Feb1972.pdf (accessed on 6 July 2023).
- Lorenz, E.N. The growth of errors in prediction. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Social Italiana di Fisica: Bologna, Italy, 1985; pp. 243–265. [Google Scholar]
- Zeng, X. Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere 2023, 14, 433. [Google Scholar] [CrossRef]
- Smagorinsky, J. problems and promises of deterministic extended range forecasting1. Bull. Am. Meteorol. Soc. 1969, 50, 286–312. [Google Scholar] [CrossRef]
- Sonechkin, D.M.; Samrov, V.P.; Zimin, N.E. The Model Averaged with Respect to Planetary Wave Phases Reveals the Ability to Overcome the Weekly Predictability Limit. MWR 1995, 123, 2461–2473. [Google Scholar] [CrossRef]
- Mukougawa, H.; Sakai, H.; Hirooka, T. High Sensitivty to the Initial Condition for the Prediction of Stratospheric Sudden Warming. GRL 2005, 32, L17806. [Google Scholar] [CrossRef]
- Liu, H.-L.; Sassi, F.; Garcia, R.R. Error Growth in a Whole Atmosphere Climate Model. J. Atmospheric Sci. 2009, 66, 173–186. [Google Scholar] [CrossRef]
- Krishnamurthy, V.; Sharma, A.S. Predictability at intraseasonal time scale. Geophys. Res. Lett. 2017, 44, 8530–8537. [Google Scholar] [CrossRef]
- Krishnamurthy, V. Predictability of Weather and Climate. Earth Space Sci. 2019, 6, 1043–1056. [Google Scholar] [CrossRef]
- Mishra, A.K.; Dwivedi, S.; Di Sante, F. Performance of the RegCM-MITgcm Coupled Regional Model in Simulating the Indian Summer Monsoon Rainfall. Pure Appl. Geophys. 2021, 178, 603–617. [Google Scholar] [CrossRef]
- Mukougawa, H.; Hirooka, T. Predictability of stratospheric sudden warming: A case study for 1998/99 winter. Mon. Weather Rev. 2004, 132, 1764–1776. [Google Scholar] [CrossRef]
- Quiroz, R.S. The association of stratospheric warmings with troposphericblocking. J. Geophys. Res. 1986, 91, 5277–5285. [Google Scholar] [CrossRef]
- Dwivedi, S. Quantifying predictability of Indian summer monsoon intraseasonal oscillations using nonlinear time series analysis. Meteorol. Z. 2012, 21, 413–419. [Google Scholar] [CrossRef]
- Magnusson, L.; Källén, E. Factors Influencing Skill Improvements in the ECMWF Forecasting System. Mon. Weather. Rev. 2013, 141, 3142–3153. [Google Scholar] [CrossRef]
- Žagar, N.; Szunyogh, I. Comments on “What Is the Predictability Limit of Midlatitude Weather?”. J. Atmospheric Sci. 2020, 77, 781–785. [Google Scholar] [CrossRef]
- Lorenz, E.N. A study of the predictability of a 28-variable atmospheric model. Tellus 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Sheshadri, A.; Borrus, M.; Yoder, M.; Robinson, T. Midlatitude Error Growth in Atmospheric GCMs: The Role of Eddy Growth Rate. Geophys. Res. Lett. 2021, 48, e2021GL096126. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Can Machines Learn to Predict Weather? Using Deep Learning to Predict Gridded 500-hPa Geopotential Height from Historical Weather Data. J. Adv. Model. Earth Syst. 2019, 11, 2680–2693. [Google Scholar] [CrossRef]
- Weyn, J.A.; Durran, D.R.; Caruana, R. Improving data-driven global weather prediction using deep convolutional neural networks on a cubed sphere. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002109. [Google Scholar] [CrossRef]
- Weyn, J.; Durran, D.; Caruana, R.; Cresswell-Clay, N. Sub-seasonal forecasting with a large ensemble of deeplearning weather prediction models. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002502. [Google Scholar] [CrossRef]
- Pathak, J.; Lu, Z.; Hunt, B.R.; Girvan, M.; Ott, E. Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos 2017, 27, 121102. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Hunt, B.R.; Ott, E. Attractor reconstruction by machine learning. Chaos 2018, 28, 061104. [Google Scholar] [CrossRef]
- Tomizawa, F.; Sawada, Y. Combining Ensemble Kalman Filter and Reservoir Computing to Predict Spatiotemporal Chaotic Systems from Imperfect Observations and Models. Geosci. Model Dev. 2021, 14, 5623–5635. [Google Scholar] [CrossRef]
- Walleshauser, B.; Bollt, E. Predicting sea surface temperatures with coupled reservoir computers. Nonlinear Process. Geophys. 2022, 29, 255–264. [Google Scholar] [CrossRef]
- Buizza, R.; Leutbecher, M. The forecast skill horizon. Q. J. R. Meteorol. Soc. 2015, 141, 3366–3382. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Khairoutdinov, M.F. Convective self-aggregation feedbacks in near-global cloud-resolving simulations of an aquaplanet. J. Adv. Model. Earth Syst. 2015, 7, 1765–1787. [Google Scholar] [CrossRef]
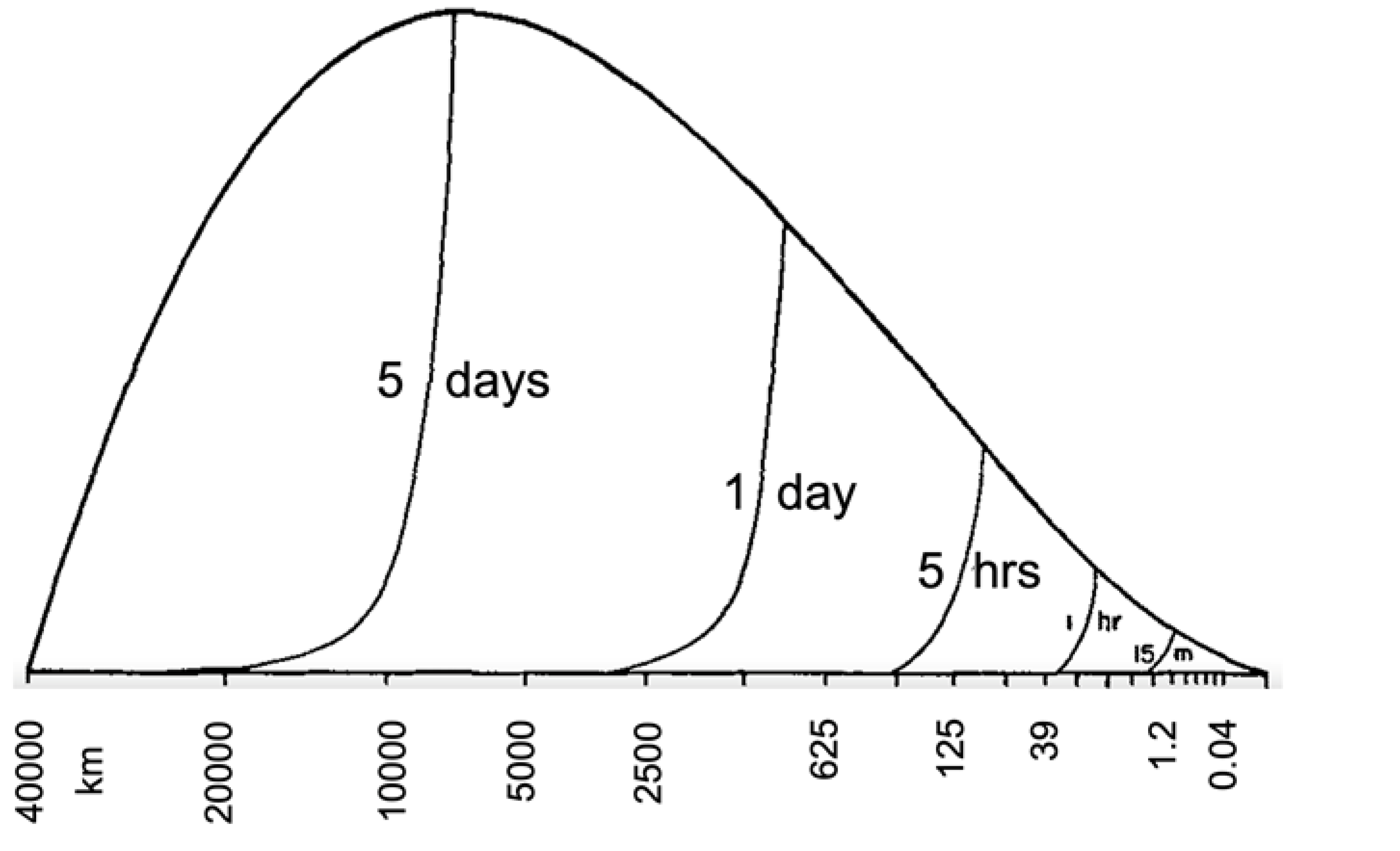

| n | tn | |
|---|---|---|
| 21 | 38 m | 2.9 min |
| 20 | 76 | 3.1 |
| 19 | 153 | 4 |
| 18 | 305 | 5.7 |
| 17 | 610 | 8.4 |
| 16 | 1221 | 13 |
| 15 | 2441 | 20.3 |
| 14 | 4883 | 32.1 |
| 13 | 9766 | 51.1 |
| 12 | 19,531 | 1.3 h |
| 11 | 39 km | 2.2 |
| 10 | 78 | 3.6 |
| 9 | 156 | 5.8 |
| 8 | 312 | 9.5 |
| 7 | 625 | 15.7 |
| 6 | 1250 | 1.1 day |
| 5 | 2500 | 1.8 |
| 4 | 5000 | 3.2 |
| 3 | 10,000 | 5.6 |
| 2 | 20,000 | 10.1 |
| 1 | 40,000 | 16.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Zeng, X. Lorenz’s View on the Predictability Limit of the Atmosphere. Encyclopedia 2023, 3, 887-899. https://doi.org/10.3390/encyclopedia3030063
Shen B-W, Pielke RA Sr., Zeng X, Zeng X. Lorenz’s View on the Predictability Limit of the Atmosphere. Encyclopedia. 2023; 3(3):887-899. https://doi.org/10.3390/encyclopedia3030063
Chicago/Turabian StyleShen, Bo-Wen, Roger A. Pielke, Sr., Xubin Zeng, and Xiping Zeng. 2023. "Lorenz’s View on the Predictability Limit of the Atmosphere" Encyclopedia 3, no. 3: 887-899. https://doi.org/10.3390/encyclopedia3030063
APA StyleShen, B.-W., Pielke, R. A., Sr., Zeng, X., & Zeng, X. (2023). Lorenz’s View on the Predictability Limit of the Atmosphere. Encyclopedia, 3(3), 887-899. https://doi.org/10.3390/encyclopedia3030063










