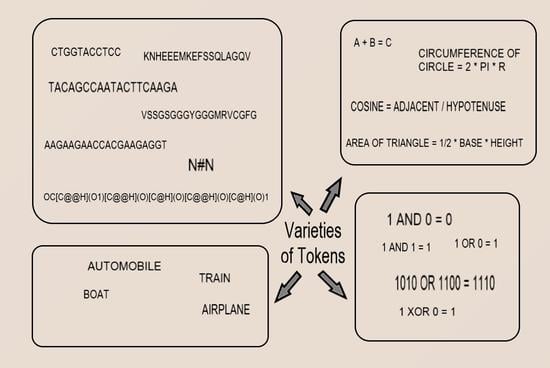
Tokenization in the Theory of Knowledge

Definition

Tokenization is a procedure for recovering the elements of interest in a sequence of data. This term is commonly used to describe an initial step in the processing of programming languages, and also for the preparation of input data in the case of artificial neural networks; however, it is a generalizable concept that applies to reducing a complex form to its basic elements, whether in the context of computer science or in natural processes. In this entry, the general concept of a token and its attributes are defined, along with its role in different contexts, such as deep learning methods. Included here are suggestions for further theoretical and empirical analysis of tokenization, particularly regarding its use in deep learning, as it is a rate-limiting step and a possible bottleneck when the results do not meet expectations.

1. Tokens and Their Properties

In computer science, a token is an element of a programming language, such as the expression of a multiplication operation or a reserved keyword to exit a block of code. In a more general context, including from other areas of study, tokenization and tokens are useful to represent objects in general. In the case of a common computer program, tokenization is a procedure that creates tokens from a data source that consists of human readable text in the form of instructions (computer code). Given that the source code is a target to be compiled as a program, the idealized procedure is to begin with a tokenizer that transforms the text to a sequence of tokens, followed by delivery of the individual tokens to the subsequent step. Next, a parsing procedure transforms the tokenized sequence to a hierarchical data structure, along with validation and further processing of the code. Lastly, the machine code, a set of instructions as expected by a computer processing unit, is generated [1].

In an artificial environment, such as machine learning, there are other examples of tokenization apart from the idealized computer compiler, including the multi-layer artificial neural network and its weighted connections, in itself a type of computer program [2,3]. This network and its input data are likewise dependent on tokenization to create a sequence of tokens. As a neural network is expanded by adding layers of artificial neurons, this architecture may be referred to as deep learning.

In Nature, such as in the case of human speech, words are also divisible into a set of smaller elements, the phonemes, which are a type of set of tokens [4]. These phonemes are categorized by their occurrence along the natural boundaries of spoken words, emerging from the mechanics of speech and the cognitive processes. These elements, the phonemes, are further transformed, processed, and potentially routed to the other pathways of cognition. From an abstract perspective, these corresponding pathways encapsulate the internal representational forms, a type of intermediate language that originates with the tokenization process; these forms are expected to emerge from the cognitive processing of the phonemes. Otherwise, there is an expectation that the phonemes are unprocessed and uninterpretable along the downstream pathways of cognition.

Tokens are also the essential elements of text as observed in common documents. In this case, tokens are typically constrained in number, presumably a limitation of any human readable source that relies on the limits of human thought. However, in all cases, there is a potential for the generation of combinations and recombinations of tokens, and therefore the formation of new objects based on prior information, a process that corresponds to the mechanics of building knowledge. In deep learning, such as that implemented by the transformer architecture [5], the power is in collecting a large number of tokens as the essential elements for training a neural network [6,7,8]—a graph composed of artificial neurons (nodes) and their interconnections (edges) with weight value assignments [2,3].

2. Tokens as Elements of Nature

The basis of forming higher order objects from a set of constituent elements (atomism) has its origins in antiquity, including in the theories of Leucippus and Democritus [9,10]. Their theories of the natural world suggest the existence of a variety of elemental substances; each variant is associated with a unique set of properties, and the variants may combine and recombine into the more complex forms. From a modern perspective, observations in the natural world are consistent with these ideas of atomism, including atoms and molecules as the constituents of matter, the biological molecules of cells, the genetic elements of living organisms, and the protein receptors of vertebrate immunity [11].

The tokens of deep learning also represent a set of elements, the discretized units of information. Therefore, the representational forms of the natural world and those of cognition and neural networks are expected to originate from the most basic of elemental forms; the open question, at least in Nature, is whether any set of elements is truly indivisible into a set of smaller forms. A modern corollary to atomism is that natural processes are non-deterministic, and the divisibility of any hypothesized elemental form is indefinite, a problem that may extend beyond the limits of knowledge [12].

Nature provides examples on the limits of the potentiality of elements to combine into the more complex forms. An example from biological evolution shows limits in the exploration of all possible genetic variants, as originating by mutation and recombination, where these processes are restricted in practice by the high probability of lower fitness with the occurrence of each genetic change [13]. Therefore, the evolutionary search space of all possible life forms is largely unexplored. Another example is in the chemistry of biological processes. The molecules of cells are a highly restricted subset of arrangements as compared to the world of all possible molecules; this is partly a result of the evolutionary process and the unexplored space of novelty in molecular processes. These observations support the dictates of probabilism in Nature and its potential for construction of new forms, including restriction by spatial and temporal factors. In other words, Nature is highly dynamic at all scales as measured by spatial extent and time.

Likewise, in an artificial setting, a computer compiler is dependent on a restricted number of tokens, although this observation may be considered a limitation of the programmer’s capability to memorize a very large number of tokens that correspond to the keywords, expressions, and other elements of a computer language. The artificial neural network is less or not necessarily restricted by biological constraints, so it may include a very large number of tokens. As an example, the transformer-based GPT-2 model of natural language [14], as implemented by Huggingface [15], is dependent on approximately fifty thousand tokens. In the case of a natural language corpus, the natural language model is instead restricted by a multitude of transcriptional and spoken forms [4], a phenomenon best sampled at the population level, so the number of tokens in the GPT-2 model may be compared against a survey of a common dictionary of words, such as in the English language [16,17]. This survey results in a half-million words. However, in the context of tokenization, a word may be classified as overlapping with other words if they share a major component. Another issue in tokenization is common versus rare words, where their distribution affects the reliability of a neural network trained on a number of tokens. For example, if a word appears just a few times in a corpus, then its absence during tokenization and training may expectedly have little effect on the robustness of the model.

3. Tokens as Scientific Data

However, the many types of scientific data expressed in sequence format, an expression typically incompatible with the natural languages, are commonly encoded for the attributes of precision, reliability, and machine readability, such as available in the one letter amino acid code of proteins [18] and in the text-based SMILES code (simplified molecular input line entry system) that represents the two dimensional arrangement of atoms of a molecule [19,20,21,22,23]. The SMILES code is also used to represent the pathways of chemical reactions [20,22]. In these cases, there are limits on the atoms for forming chemical compounds, and, in the case of biology, the arrangement of amino acids that can form proteins. Therefore, tokenization based on the individual elements of these sequences results in a smaller number of tokens than can potentially occur [20,24]. However, if there is a generation of tokens in which the tokens may consist of more than one element, such as in the case of an amino acid sequence [25], then the token count may exceed, even significantly exceed, that observed in the natural languages, as the latter are further constrained by phoneme variety, a product of speech and its perception, and human memory.

Furthermore, as tokenization in deep learning affects the subsequent steps of the methodology, the distribution of potential tokens is a bottleneck for the performance of a model, and is a crucial area of study in theoretical and empirical contexts. This practice would lead to a better expectation in the design of a deep learning system that blends natural language with the many types of scientific data [23,26]. Another possible constraint in deep learning (for example, when using the highly efficient transformer architecture) is modeling the long-range associations of tokens along a sequence, particularly in a very large document where associations between words or symbols are distant.

As the sequence databases of biology and chemistry are vast, along with their appended descriptions in human readable format, deep learning methods are highly competitive with traditional search methods for the retrieval of scientific data and journal articles [26]. The Galactica model by Meta [26] further captures the information of mathematical expressions (LaTex) and computer code. Moreover, Taylor and others [26] include a detailed discussion of the importance of tokenization in achieving their promising results, which shows improvement over prior work.

It is possible to further explore the many varieties and combinations of tokens of scientific data and the expectation on prediction of the higher order structures, such as those observed in the correspondence between a protein sequence and its tertiary structure [27,28,29]. Where the algorithms of Nature are not amenable to these approaches, then other methods of reinforcement learning [30] and use of a decision transformer [31] are powerful tools for the discovery of the higher order forms from the low dimensional information in scientific data.

These methods of curating and identifying syntactical structure within data, particularly in the case of automatic curation, as in the use of keyword tagging in a corpus for the identification and processing of the data types, is a synergistic approach for extending the foundational language models [32]. There is also an important distinction between natural language and scientific data. The latter are not a product of persuasive speech, at least not ordinarily, so the data quality is more verifiable. However, as expected, the natural language corpus is replete with examples of mere opinion and persuasion [33,34], so it is difficult, at best, and arguably not possible, to truly verify the validity of statements in common samples of natural language.

4. Tokens as Elements of Logic

The constraints on validating samples in the corpus as coded by natural language are partly a byproduct of phylogenetic dependence [35,36] on this form of communication, a descendant of similar forms of animal communication, including their underlying physical mechanisms, as observed in the morphological characters that relate to aural communication. These include the mechanical and anatomical features of the larynx and also the bones of the middle ear. Furthermore, they contribute as drivers for the intermediate steps in the pathways of speech and its perception, along with their downstream influence on other cognitive pathways involved in the construction and interpretation of sensory data. This imperfect process of knowledge transfer has led to the ancient and modern human pursuit of rhetoric as an art form in itself, along with the support of vast academic and public enterprises of titled interpreters and associated publications based on opinion, and corresponding interpretation and reinterpretation of current and past written knowledge [33,34,37,38]. Altogether, this is presumed a byproduct of an evolutionary design for animal communication and behavior, as opposed to any engineered design purposed for the idealized flow of information and knowledge [39].

The lack of consistency and permanence in conveying an idea in any natural language, and that natural languages are not purposed for the construction of knowledge, led philosophers to pursue logic as a reliable method of communication of concepts [33,34,39,40]. This pursuit has been essentially a reference to a set of logical primitives that describe objects and their interrelationships as perceived in the world, a type of tokenizing of material and abstract entities, regardless of whether the origin of the object is in Nature or the Mind [33]. Further, for this conjecture, these basic primitives are considered the elemental constituents of any of these objects, the idealized forms. These forms are expectedly robust, precise, and low in dimensionality, properties that lend themselves to efficiency in computation (Figure 1). These properties are also ideal in the formation of reliable knowledge with resistance to perceptual perturbation, such as those observed across the various visual perspectives or the variation of percepts as constructed among individuals. The philosophers of antiquity [33] theorized about the permanence and indivisibility of these primitives (the elemental forms of logic), a general concept revisited and diminished by modern theorists and empiricists [12,39,40].

The world of mathematics and of computer code are more closely related to the above formal systems than to natural language. Computer code and mathematics both consist of a formal syntax of keywords, symbols, and rules, and an adaptation for transformation to machine level code, such as by a computer compiler or interpreter. Use of an intermediate language for representing math or computer problems, such as LaTeX, or in the code of Python, has led to successes in deep learning and inference on advanced math, such as math questions as posed in a natural language format [26]. This is a concrete example of the importance of data, their tokenization, and signal processing [42] in the expectations regarding building a robust model and recovery of the basic elements (primitives) from a data source.

As it is possible to acquire general knowledge of an academic topic with dependence on a structured and formalized language, such as in the mathematics of trigonometry or in the discipline of classical mechanics, these languages result in information that is hypothetically very compressible and adapted to the processes of learning and cognition. These languages are correspondingly distinct in their operations, syntax, and definitions. If this hypothesis is not true, then knowledge would not be generalizable (an extreme form of an hypothesis, as proposed in antiquity by Heraclitus, in which change is rendering all or nearly all forms as distinct and unique). The natural world instead has narrow paths of change that are mapped along physical pathways, at least within the confines of human experience and measurement, so a categorization of forms and its associated knowledge are favored against the product of miscategorization and a lack of commonality in Nature. This is another limit to knowledge of the natural world, as specifically documented in the evolutionary sciences, a discipline firmly based on an essential and formalized language for discerning the true and false categories of characters and their states [35,36].

5. Conclusions

In summary, there are a variety of ways to study a deep learning system, including the data collection step, the neural network architecture, and the dependence of these systems on a tokenization procedure for achieving robust results. Of these parts of a system, tokenization, is as crucial a factor as the design of the deep learning architecture (

Table 1. Summary of concepts in this entry.

Concept	Description
Tokens in general	A token can be considered the elementary unit of a text document, speech, computer code, or another form of sequence information.
Tokens in Nature	In natural processes, a token can represent the elemental forms that matter are composed of, such as a chemical compound or the genetic material of a living organism.
Tokens as scientific data	In scientific data, a token can represent the smallest unit of information in a machine readable description of a chemical compound or a genetic sequence.
Tokens in math & logic	In the structured and precise languages of math and logic, a token can represent the elementary instructions that are read and processed, as in the case of an arithmetical expression, a keyword in a computer language, or a logical operator that connects logical statements.

), although the architecture is often displayed as the main feature of deep learning. Moreover, ensuring the quality and curation of source data introduces efficiency and robustness in the training and inference stages of deep learning [26].

Apart from data quality, it may be possible to increase the extraction of salient information, particularly in a scientific data set, by training the neural network on tokens as formed from different perspectives. As an example, biological data which has information as extracted from the individual amino acids of a sequence also has information at the subsequence level as reflected by the structural and functional elements of a protein. This possibility emerges from the observation that natural processes are influenced at various scales, as in the combinatorics of natural language with its definite biological limits, as observed by the dictionary of available phonemes and constraints in the associated cognitive processes. To capture the higher order information in protein sequence data, AlphaFold [27] appended tokens from other sources; however, it is ideal to capture these rules of Nature as they emerge from the sequence data itself and their associated tokens [28].

Furthermore, tokens, as the representative elements of knowledge, are not likely uniform in status, but instead are expected to have an uneven distribution in their applicability as descriptors (Figure 1). The commonality of forms and objects that lead to knowledge are sometimes frequent in occurrence, but it can be conjectured that these commonalities are often rare. This hypothesis, even if proposed in posterior to recent findings from the study of large language models, supports an expansive search for data in the construction of deep learning models, even if to merely validate the importance of rare patterns that have not yet been sampled from the overall population of patterns in the world of data.

As a final comment, overall deep learning methodology may be considered a variant of the computer compiler and its architecture, with tokenization of input data (tokens) and transformation of tokens into a graph data structure, along with a final generation of code to form a program (neural network and weight values). Each step of this process is ideally subjected to hypothesis testing for better expectations and designs in the practice of the science of deep learning.