Definition
The suggested methodology for the characterization of temperature extrema presents a multistep preprocessing procedure intended to derive extrema time series of correctly identified and thermally defined daily air temperature extrema pairs. The underlying conceptual framework for this approach was developed in response to the existing gaps in the current state of daily extrema identification and the development of extrema-based synthetic air temperature time series. A code consisting of a series of algorithms was developed to establish four-parameter criteria for a more accurate representation of daily variability that allows easy replication of temperature distribution based on the correct characterization of daily temperature patterns. The first preprocessing step consists of subjecting the high-frequency temperature time series to a theoretical diurnal observing window that imposes latitudinally and seasonally crafted limits for the individual identification of daily minima and maxima. The following pre-processing step involves the supplementation of air temperature extrema with the information on the occurrence of extrema timing deemed as vital information for the reconstruction of the temperature time series. The subsequent step involves the application of an innovative temperature pattern recognition algorithm that identifies physically homogeneous air temperature populations based on the information obtained in previous steps. The last step involves the use of a metric for the assessment of extrema temperature and timing parameters’ susceptibility to climate change. The application of the presented procedure to high-frequency temperature data yields two strains of physically homogeneous extrema time series with the preserved characteristics of the overall temperature variability. In the present form, individual elements of this methodology are applicable for correcting historical sampling and air temperature averaging biases, improving the reproducibility of daily air temperature variation, and enhancing the performance of temperature index formulae based on daily temperature extrema. The objective of this analysis is the eventual implementation of the presented methodology into the practice of systematic temperature extrema identification and preprocessing of temperature time series for the configuration of physically homogeneous air temperature subpopulations.
1. Introduction
The accurate identification of air temperature and the abundance of sources of error in daily observation practices remain a current subject in the scientific literature [1,2,3,4,5,6,7,8,9]. In addition, the common scarcity of high-resolution temperature data naturally transfers the reliance on daily minima and maxima for the variety of scientific evaluations. Furthermore, the extensive scope of climatological analyses, climate change impact assessments, and future climate projections rely upon rigor in the identification of daily temperature extrema. With this in mind, it would be expected that the determination of daily extrema from high-frequency data sets is straightforward. However, the long-term comparative analysis of continuous temperature measurements with derived daily extrema reveals a lack of agreement resulting in a large negative temperature bias in daily minima [10]. The ultimate goal of identifying daily extrema is the summarization of temperature variability into the smallest number of representative data points. However, the assumption that daily minima and maxima contain sufficient information to correctly characterize diurnal air temperature variability is not always justifiable [5]. The systematic application of a discrete extrema search, or the use of MIN/MAX functions to identify the lowest and the highest values for a specified range, entails a number of pitfalls associated with selecting the initial point and the length of the search interval [10]. The same principle extends to daily extrema observations given below.
The definition of the starting point of the observational window for daily extrema identification has been a constant source of uncertainty throughout Canadian temperature recording history. The common mischaracterization of diurnal minima, caused by the old observational window, initiated a Canada-wide redefinition of the observing time for temperature recording. On 1 July, 1961, the climatological day was redefined at all Canadian synoptic stations to end at 6:00 UTC. However, the change in the observing window did not result in the anticipated alleviation of the observational bias. The shifting of the initial point instead introduced a cold bias to the observations, by affecting 15% to 38% of days in Canada annually by increasing the potential for recording minimal temperatures on two consecutive days. The bias in daily minima was observed to be more pronounced in the eastern regions of Canada [11,12,13]. Variations in the time limits of the day, i.e., the differences in the definition of a beginning and the end of the “day”, have been known to affect the quality of recording of a daily air temperature minimum in general [14,15].
The need for the development of the new methodology first became apparent through the examination of the relationship between diurnal air temperature variability and the degree-day snowmelt volume estimation [16]. The unavailability of continuous air temperature data and frequent encounters with missing data, affecting the quality of daily snowmelt water equivalent estimation, raised the need for the development of air temperature approximating methods for the improvement of the degree-day formula. The search for an analytical solution for the reproduction of the temperature–time dependence curve identified the need for an accurate sequence of extrema as the key input for a successful air temperature approximation. However, the attempt to identify chronologically ordered extrema using discretized methods has proven to be a surprisingly complex task, yielding frequently mischaracterized and ‘reverse-ordered’ extrema. More specifically, the sequence of minima and maxima, necessary for the reproduction of air temperature, is often reversed due to the omission of a local minimum which the traditional method of extrema identification misses because it does not represent the lowest temperature of the day. The implications of mischaracterized extrema and ensuing extrema sequence result in low performance of the degree-day formula commonly used in various climatological, hydrological, agricultural, and civil engineering applications [17,18,19,20,21,22,23,24,25,26]. The comparison of measured and reproduced temperature series, based on the correct extrema sequence, cast doubt on the accuracy of identified diurnal extrema using the current observing window and pointed to the knowledge gap in discrete extrema identification. These findings led to the conceptualization of the Climatological Observing Window (COW) and the creation of a code for the automated processing of high-frequency temperature time series into accurate chronologically ordered extrema time series [10].
A related observation that led to the further development of this methodology was the recognition of the role of the timing of daily extrema occurrence in the improvement of the accuracy of daily temperature replication with analytical approximations. It became apparent that the ongoing search for the improvement of the reproduction of the diurnal temperature variability in fact represented an indirect pursuit for the missing element in daily temperature reporting, i.e., the exact timing of diurnal extrema occurrence [27,28,29,30,31,32,33,34]. This consideration further unraveled the abundance of information in the turning points of the daily temperature–time curve and led to the attribution of a parameter status to the Diurnal Extrema Timing (DET) of a daily minimum and maximum temperature [35].
The third element of our methodology emerged from the platform developed for the establishment of the first two elements. The algorithms developed in the R programming language [36] in previous stages represented the basis for the detection of the physically heterogeneous nature of the air temperature extrema population. The development of the Linear Pattern Discrimination (LPD) algorithm enabled the separation of the complete temperature–time series into two homogeneous extrema temperature populations. The separation of the chronologically ordered daily extrema sequence into two homogeneous extrema populations uses the criterion derived from the timing of the extrema parameter. This criterion enabled the algorithmic recognition of the Diurnal Temperature Pattern, a concept conceived from the unique difference in the timing between two consecutive daily turning points on the temperature–time curve [37]. The extension of this concept into the seasonal analysis of radiative and advective temperature trends reveals specific indicators of temperature changes and thermal regimes of individual homogeneous temperature subpopulations [38].
The last element of the theoretical framework for extrema characterization represents the Climate Parameter Sensitivity Index (CPSI) devised to assess the warming trends in temperature and timing parameters of derived indices obtained from the previous three stages of the analysis [35]. A vulnerability assessment of temperature and timing indices uncovers a greater susceptibility of the timing parameter than temperature to climate change.
It is important to note that while this new methodology for extrema characterization remains open to additional advances in research development, the current state of its all elements is fully operational.
2. Elements of the Methodology for Temperature Extrema Characterization
The basic task of correctly identifying the daily minimum and maximum has turned out to be a critically important basis for the variety of applications involving the use of daily extrema. Otherwise, the introduction of systematic bias at the level of the basic time unit of air temperature recording (24 h) involves the mischaracterization of temperature variability reflected in erroneous daily averages, with the implication of bias propagation to all larger time steps. Moreover, mischaracterized daily extrema do not reflect any of the physical characteristics of the climate system otherwise represented in achieved extremes (peaks or lows) of the daily temperature function.
2.1. Definition of Problem Areas Surrounding the Subject of Extrema Identification
The description of the main problem areas is presented in Section 2.1.1 to Section 2.1.4 which provide the terminology and the background necessary to describe the sources of error and misinterpretation in the field of extrema identification.
2.1.1. The Calendar and the Climatological Day for Temperature Extrema Observations
Observations taken based on a calendar day often miss the actual minimums and maximums or the points on a temperature curve that are truly reflective of a change in a daily air temperature trend. Capturing the coldest period of the day just before sunrise and the warmest period after the sun reaches its zenith in the afternoon is conditioned by the regularity of daily temperature variation as well as by the length of the observational window [10]. For taking the official weather observations in Canada, the calendar day was replaced with the climatological day to ensure the capturing of true “peaks and lows” of air temperature variation [39]. At Canadian meteorological sites reporting temperature extrema twice daily, the operational definition of a temperature minimum and maximum differs from the calendar day definition that refers only to sites reporting extrema once per day. The climatological day frequently omits the true extrema points and often reaches out of the bounds of a 24 h calendar day to identify the true daily minimum.
2.1.2. Nonconformity of Daily Extrema with Mathematical Extrema Definition
The daily air temperature minimum (Tn) and, maximum (Tx) observed over a 24 h interval often do not conform with the mathematical definition of an extremum point. Mathematical temperature extrema are defined as the points on the air temperature–time curve in which the daily temperature trend changes its sign from positive to negative or negative to positive and the derivative of the air temperature function equals zero.
2.1.3. The Mischaracterization of Temperature Minima Due to the Observation Interval
The systematic discrete identification of daily temperature extrema, as a rule, implies the selection of the highest and lowest temperatures using a common 24 h long search interval for the identification of daily minima and maxima. Due to the vagueness of the extrema definition in climatological practice, various mischaracterizations of primarily the daily minimum occur. Systematic biases in long-term records of daily minima stem from the common omission of warmer minima, the identification of endpoint minima, and the double counting of minima [10]. The rigidity of the starting point of the observing window and the lack of consideration for the geographical location of the observation site presents the root cause for the erroneous identification of minima. Additionally, the discrete air temperature extrema identification is strongly conditioned by the selection of the length of the extrema search window. While in standard practice both extrema are identified across a common 24 h interval, in this methodology a minimum is identified during the location and season-specific nighttime. Likewise, the daily maximum is identified during the latitudinally and seasonally dependent daytime.
2.1.4. The Effect of Minima Mischaracterization on the Sequence of Temperature Extrema
Several seemingly unrelated climatological obstacles, frequently encountered in air temperature analysis, stem from a lack of a correctly identified succession of daily minima and maxima. The common mischaracterization of extrema, using a standard identification approach, arises from the position of the divide between days, i.e., the limit of the day. Due to the fragmentation of nighttime into a section that precedes daytime and another section that extends until the end of a 24 h period, the identification of a daily minimum is frequently erroneous, resulting in a significant negative bias in annual minima [10]. The misidentified minima consequently disarrange the extrema succession, placing a large number of daily minima in reverse order and creating an inadequate extrema sequence for the approximation of daily temperature distribution or the estimation of temperature-related quantities. Alternatively, the identification of minima during the nighttime and maxima during the daytime results in a chronologically ordered extrema sequence.
2.2. Preprocessing Steps of the Procedure for Temperature Extrema Characterization
The major elements of the proposed methodology for daily extrema characterization are discussed in Section 2.2.1 to Section 2.2.4 and illustrated in Figure 1.
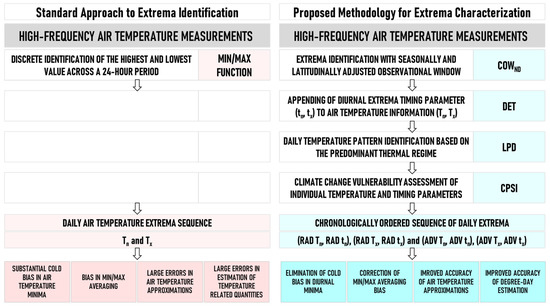
Figure 1.
Comparison of the standard approach for extrema identification with the new multi-step methodology for extrema characterization.
2.2.1. Step 1—Climatological Observing Window (COWND) Night–Day
The basic 24 h long temperature observing unit is subdivided into nighttime and daytime periods representative of the positive and negative heat exchange periods. Based on the premise that nighttime and daytime are physically unique climatological periods, the improvement with regard to the observational day consists of the adjustment of the starting point and duration of daytime and nighttime length according to the location and season. The newly introduced Climatological Observing Window Night–Day (COWND) concept was validated using multiple Canadian long-term (65 yrs.) high-frequency (hourly) temperature measurements. The performance of the COWND method was proven superior to the standard approach of diurnal extrema identification in the ‘air temperature tracking’ mode of validation that calculates errors between the measured and identified daily temperature extrema. The air temperature tracking procedure revealed a larger error in the identification of extrema using the standard MIN/MAX function and a significant ‘cold bias’ in daily minima. The average cold bias in Canadian long-term minima using a standard extrema identification procedure is estimated to be ~0.7 °C [10].
2.2.2. Step 2—Diurnal Extrema Timing (DET) Parameter
The second missing element in the proper characterization of daily extrema is the information on their minima and maxima timing occurrence. Despite the imprecision of the timing information derived from the hourly temperature data that associate the time of minimum or maximum occurrence with the exact hour, the advantage of the definition of an extremum temperature point with two spatial coordinates cannot be overstated [35]. The succession of heating and cooling periods takes place at the turning points of the air temperature function, i.e., at the daily minimum and maximum temperatures. In order to spatially characterize turning points, it is necessary to obtain the abscissa and the ordinate information. Thus far, in meteorological practice, the discrete identification of extrema implies only the attribution of the lowest and the highest values in reference to the y-axis. Such a one-dimensional characterization of daily extrema disregards the nature of the temperature turning point by depriving it of crucially important information on the exact timing of diurnal temperature trend changes. The DET concept was validated using twenty-four long-term (1953–2018) Canadian hourly temperature records. Detailed DET analysis revealed substantial changes in the Canadian average of extrema timing accrued over the study period ranging between 29 min/65 yrs. for air temperature minima and 31 min/65 yrs. for maxima [35].
2.2.3. Step 3—Linear Pattern Discrimination (LPD) Algorithm
A midlatitude high-frequency air temperature distribution reveals a predominantly quasi-oscillatory variation with alternating daily heating and cooling periods. Occasional deviation from the usual diurnal cycle to a quasi-linear distribution commonly results from weather front-associated temperature changes. In simple terms, the identification of air temperature patterns is achieved through the identification of the time span between the occurrence of a daily air temperature minimum and maximum. The Linear Pattern Discrimination algorithm identifies daily temperature patterns and separates the total temperature population into two physically homogeneous extrema time series [37,38]. The LPD concept was applied to twenty-five Canadian hourly temperature time series to separate radiatively driven days from advectively driven days. Radiative Temperature Population (RTP), consisting of radiatively characterized days, makes up the majority of the Canadian temperature time series (82%) and varies geographically and seasonally. The Advective Temperature Population (ATP) represents the remaining 18% of the typical mid-latitudinal temperature time series [37,38].
2.2.4. Step 4—Climate Parameter Sensitivity Index (CPSI) Metrics
The assessment of the vulnerability of temperature and timing parameters to climate change allows insights into the direction of changes in these parameters caused by the retention of heat in the atmosphere. Long-term sensitivity testing specifies the degree and the direction of change in a two-dimensional temperature–time space. The CPSI metric quantifies the change in a parameter by evaluating the ratio of the parameter’s variability due to climate change against the overall parameter’s variability span during the study period. An analysis of twenty-four long-term Canadian hourly temperature time series examined the individual changes in before-midnight and after-midnight temperature and timing indices as well as before-noon and after-noon temperature and timing indices. Temperature and timing samples were split into midnight and noon subpopulations to evaluate their displacement across midnight and noon delineation points. The outcome of the CPSI assessment of extrema temperature and timing indices reveals the timing of the After Noon Maxima (ANM) as the most vulnerable variable to climate change, followed by the timing of the After Midnight Minima (AMM) [35].
3. Advantages and Disadvantages of the Methodology for Extrema Characterization
The main advantages of physically meaningful extrema characterization transpire due to the following elements achieved through the application of the presented methodology:
- The improved accuracy of daily extrema identification demonstrated by point-to-point linear temperature tracking. The synthetic hourly temperature data, obtained by the linear approximation of temperature curves connected in daily extrema points, were compared with true hourly temperature measurements for the estimation of errors. Error distributions, resulting from the approximated and corresponding measured temperature were compared between the standard method and the new methodology. Linear interpolation between the preprocessed extrema has proven more accurate due to the correct characterization of daily minima [10,35].
- Removal of algorithmic biases in processed daily extrema. Retroactive analysis of historical data sets and the correction of long-term biases is achievable using high-frequency temperature records. An average cold bias of ~0.7 °C was detected in the Canadian annual minima calculated over the 60-year range [10].
- Inclusion of extrema timing as a new parameter that is potentially indicative of climate change. The supplementation of temperature extrema information with a time coordinate results in the spatial definition of a daily minimum and maximum. The relevance of the inclusion of the diurnal extrema timing parameter is seen in the benefit of examining the time evolution of the nighttime and daytime extrema timing and assessing changes in their historical trends due to climate change [35].
- Establishment of a criterion for the identification of common daily temperature patterns. The time span between the occurrence of a daily temperature minimum and maximum exposes the characteristics of a diurnal temperature pattern [37].
- Identification of physically caused heterogeneity in populations of daily extrema. The recognition of daily temperature patterns based on the timing criterion reveals the prevailing atmospheric conditions that control diurnal temperature variation. A diurnal temperature pattern presents a visual outline of daily temperature variation. The majority of spring and summertime days exhibit a radiatively driven diurnal temperature pattern that is quasi-sinusoidal and compliant with the daily solar cycle. On the other hand, the incidences of air temperature pattern distortion caused by atmospheric advection are common during the fall and winter seasons. Prolonged, quasi-linear patterns are often indicative of abrupt shifts in the atmospheric thermal regime. The advantage of applying the recommended preprocessing steps is in the detection of physical heterogeneity of temperature series that consist of radiatively driven and advectively driven temperature populations [37,38].
- Algorithmic separation of temperature arrays based on the differences in diurnal extrema timing. The application of the LPD algorithm to air temperature time series successfully separates annual portions of radiative and advective air temperature populations. The subsequent adjustment of the LPD algorithm to the astronomical calendar for the identification of radiative and advective populations on the equinox to equinox time scale yields eight physically homogeneous temperature populations. The advantage of the use of the suggested methodology is in the identification of seasonal thermal regimes based on air temperature records alone. This aspect of air temperature analysis demonstrates the existence of predominant thermal regimes: a stable spring–summer period, dominated by radiative days, and an unstable fall–winter period characterized by a rapidly decreasing advective population [37,38].
- Introduction of a quantitative measure of parameter sensitivity to climate change. The benefits of the application of the Climate Parameter Sensitivity Index (CPSI) to high-frequency temperature time series include the quantification of the parameter’s sensitivity to climate change and the quantitative comparison of various parameters, including the ranking of their sensitivity to climate change. The advantage of this particular step in extrema characterization is the ability to identify the changes in diurnal extrema timing and obtain evidence of the related time shifts occurring in this parameter throughout the observational history [35].
The major disadvantages of the new methodology for extrema characterization are:
- Suggested data preprocessing presents a more complex process than the discrete air temperature extrema search using simple MIN/MAX functions.
- The present benefit of extrema characterization is applicable only to existing high-frequency data sets that allow a historical correction of temperature biases. However, the greatest benefit of this new methodology would be the implementation of diurnal extrema and timing identification procedures based on location and season-specific climatological observing windows.
4. Conclusions and Prospects
Specific areas of oversight in the identification of daily air temperature extrema are presented along with a multistep theoretical approach suitable for preserving physically meaningful information in points of daily air temperature trend changes.
The chronologically ordered sequence of mathematical extrema with known times of their occurrence identified using this methodology encapsulates critical physical features of the succession of true daily extrema essential for accurate temperature reproducibility.
This entry proposes the implementation of the elements of new methodology into the practice of the systematic identification of daily extrema from large temperature data sets. Secondly, it suggests the re-evaluation of temperature observational practices with the goal of adopting the idea of the systematic acquisition of daily extrema timing along with air temperature recording.
Author Contributions
Conceptualization, methodology, formal analysis, writing—original draft preparation, A.Ž.-Ć.; writing—review and editing, W.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed. Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schaal, L.A.; Dale, R.F. Time of observation temperature bias and “climatic change”. J. Appl. Meteorol. 1977, 16, 215–222. [Google Scholar] [CrossRef]
- Lin, X.; Hubbard, K.G. What are daily maximum and minimum temperatures in observed climatology? Int. J. Climatol. 2008, 28, 283–294. [Google Scholar] [CrossRef]
- Bonacci, O.; Željković, I.; Šakić Trogrlić, R.; Milković, J. Differences between true mean, daily, monthly and annual air temperatures and air temperatures calculated with three equations: A case from three Croatian stations. Theor. Appl. Climatol. 2013, 114, 271–279. [Google Scholar] [CrossRef]
- Wang, K.C. Sampling biases in datasets of historical mean air temperature over land. Sci. Rep. 2014, 4, 4637. [Google Scholar] [CrossRef]
- Gough, W.A.; Žaknić-Ćatović, A.; Zajch, A. Sampling frequency of climate data for the determination of daily temperature and daily temperature extrema. Int. J. Climatol. 2020, 40, 5451–5463. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Vincent, L.A.; Milewska, E.J.; Xiolan, L.W.; Hartwell, M.M. Uncertainty in homogenized daily temperatures and derived indices of Extrema illustrated using parallel observations in Canada. Int. J. Climatol. 2018, 38, 692–707. [Google Scholar] [CrossRef]
- Collison, P.; Tabony, R.C. The estimation of mean temperature from daily minima and maxima. Meteorol. Mag. 1984, 113, 329–337. [Google Scholar]
- Trewin, B. Effects of changes in algorithms used for the calculation of Australian mean temperature. Aust. Meteorol. Mag. 2004, 53, 1–11. [Google Scholar]
- Žaknić-Ćatović, A.; Gough, W.A. A comparison of climatological observing windows and their impact on detecting daily temperature extrema. Theor. Appl. Climatol. 2018, 132, 41–54. [Google Scholar] [CrossRef]
- Vincent, L.A.; Milewska, E.J.; Hopkinson, R.; Malone, L. Bias in minimum temperature introduced by a redefinition of the climatological day at the Canadian synoptic stations. J. Appl. Meteorol. Climatol. 2009, 48, 2160–2168. [Google Scholar] [CrossRef]
- Vincent, L.A.; Wang, X.L.; Milewska, E.J.; Wan, H.; Yang, F.; Swail, V. A second generation of homogenized Canadian monthly surface air temperature for climate trend analysis. J. Geophys. Res. 2012, 117, D18110. [Google Scholar] [CrossRef]
- Hopkinson, R.F.; McKenney, D.W.; Daniel, W.; Milewska, E.J.; Hutchinson, M.F.; Papadopol, P.; Vincent, L.A. Impact of aligning climatological day on gridding daily maximum-minimum temperatures and precipitation over Canada. J. Appl. Meteorol. Climatol. 2011, 50, 1654–1665. [Google Scholar] [CrossRef]
- Nichols, E.S. Time limits of the day affecting records of minimum temperature. Mon. Weather. Rev. 1934, 62, 337–343. [Google Scholar] [CrossRef]
- Janis, M.J. Observation-time-dependent biases and departures for daily minimum and maximum air temperatures. J. Appl. Meteorol. 2001, 41, 588–603. [Google Scholar] [CrossRef]
- Žaknić-Ćatović, A.; Howard, K.W.F.; Ćatović, Z. Modification of the degree-day formula for diurnal meltwater generation and refreezing. Theor. Appl. Climatol. 2018, 131, 1157–1171. [Google Scholar] [CrossRef]
- Weiss, A.; Hays, C.J. Calculating daily mean temperature by different methods: Implications from a non-linear algorithm. Agric. For. Meteorol. 2005, 128, 57–65. [Google Scholar] [CrossRef]
- Bilbao, J.; Kambezidis, H.D. Air temperature model evaluation in the North Mediterranean Belt area. J. Appl. Meteorol. 2002, 41, 872–884. [Google Scholar] [CrossRef]
- Linvill, D.E. Calculating chilling hours and chill units from daily maximum and minimum temperature observations. Hort. Science 1990, 25, 14–16. [Google Scholar] [CrossRef]
- Parton, W.J.; Logan, J.A. A model for variation in soil and air temperature. Agric. Meteorol. 1981, 23, 205–216. [Google Scholar] [CrossRef]
- Reicosky, D.C.; Winkelman, L.J.; Baker, J.M.; Baker, D.G. Accuracy of hourly air temperatures calculated from daily minima and maxima. Agric. For. Meteorol. 1989, 46, 193–209. [Google Scholar] [CrossRef]
- Chow, D.H.C.; Levermore, G.J. New algorithm for generating hourly temperature values using daily maximum, minimum and average values from climate models. Build. Serv. Eng. Res. Technol. 2007, 28, 237–248. [Google Scholar] [CrossRef]
- Watanabe, N. An improved method for computing heat accumulation from daily maximum and minimum temperatures. Appl. Entomol. Zool. 1978, 13, 44–46. [Google Scholar] [CrossRef]
- Pandzic, K.; Likso, T.; Bonacci, O. A review of extreme air temperature analysis in Croatia. Atmosphere 2022, 19, 1893. [Google Scholar] [CrossRef]
- Schaub, W.R., Jr. A Method for Estimating Missing Hourly Temperatures Using Daily Maximum and Minimum Temperatures; USAF Environmental Technical Applications Center, Scott Air Force Base: St. Louis, IL, USA, 1991; USAFETAC/PR-91/017. [Google Scholar]
- Hartzell, F.Z. Comparison of methods for computing daily mean temperatures: Effect of discrepancies upon investigations of climatologists and biologists. Mon. Weather Rev. 1919, 47, 799–801. [Google Scholar] [CrossRef]
- Floyd, R.B.; Braddock, R.D. A simple method for fitting average diurnal temperature curves. Agric. For. Meteorol. 1984, 32, 107–119. [Google Scholar] [CrossRef]
- Magnano, L.; Boland, J.W.; Hyndman, R.J. Generation of synthetic sequences of half-hourly temperatures. Environmetrics 2008, 19, 818–835. [Google Scholar] [CrossRef]
- Hansen, J.E. A mathematical model for the generation of hourly temperatures. J. Appl. Meteorol. 1962, 16, 935–994. [Google Scholar] [CrossRef]
- Sadler, J.E.; Schroll, R.E. An empirical model of diurnal temperature patterns. Agron. J. 1997, 89, 542–548. [Google Scholar] [CrossRef]
- Dall’Amico, M.; Hornsteiner, M. A simple method for estimating daily and monthly mean temperatures from daily minima and maxima. Int. J. Clim. 2006, 26, 1929–1936. [Google Scholar] [CrossRef]
- Besson, F.; Bazile, E.; Soci, C.; Soubeyroux, J.-M.; Ouzeau, G.; Perrin, M. Diurnal temperature cycle deduced from extreme daily temperatures and impact over a surface reanalysis system. Adv. Sci. Res. 2015, 12, 137–140. [Google Scholar] [CrossRef]
- Wann, M.; Yen, D.; Gold, H.J. Evaluation and calibration of three models for daily cycle of air temperature. Agric. For. Meteorol. 1985, 34, 121–128. [Google Scholar] [CrossRef]
- Deshani, K.; Attygalle, D.; Hansen, L. Incorporating Influential Factors in Diurnal Temperature Estimation with Sparse Data. GSTF J. Math. Stat. Oper. Res. 2016, 4, 10. [Google Scholar] [CrossRef]
- Žaknić-Ćatović, A.; Gough, W.A. Diurnal Extrema Timing—A New Climatological Parameter? Climate 2022, 10, 5. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Žaknić-Ćatović, A.; Gough, W.A. Identification of radiative and advective populations in Canadian temperature time series using the Linear Pattern Discrimination algorithm. Int. J. Climatol. 2021, 41, 5100–5124. [Google Scholar] [CrossRef]
- Žaknić-Ćatović, A.; Gough, W.A. Seasonal Aspects of Radiative and Advective Air Temperature Populations: A Canadian Perspective. Atmosphere 2022, 13, 1017. [Google Scholar] [CrossRef]
- Government of Canada. About the Data. Available online: Climate.weather.gc.ca (accessed on 1 November 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).