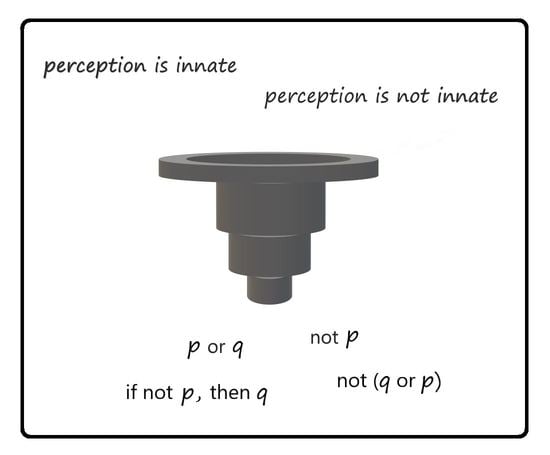
Large Language Models and Logical Reasoning
Definition
1. Background
2. Construction of Logical Statements
2.1. Deep Learning Models
2.2. Models of Tokenization
2.3. Prompt-Based Methods in Deep Learning
2.4. Validation of Models
3. Problems in Logic and Language
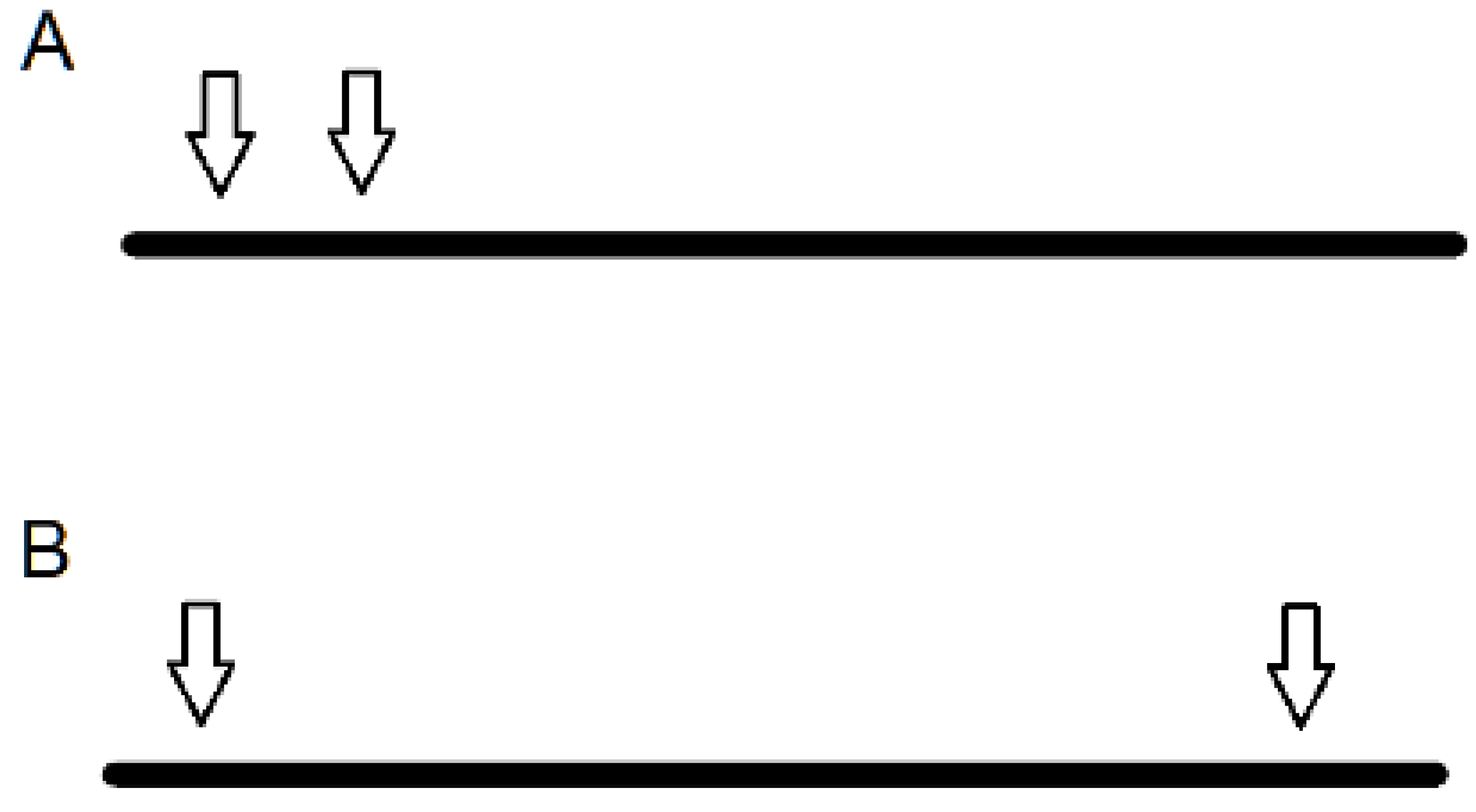
3.1. Internal Representations of Logic
3.2. Potential Limitations of Logical Systems
4. Large Language Models and Society
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brants, T.; Popat, A.C.; Xu, P.; Och, F.J.; Dean, J. Large Language Models in Machine Translation. In Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28–30 June 2007; pp. 858–867. [Google Scholar]
- Hennig, W. Phylogenetic Systematics. Annu. Rev. Entomol. 1965, 10, 97–116. [Google Scholar] [CrossRef]
- Scott-Phillips, T.C.; Kirby, S. Language evolution in the laboratory. Trends Cogn. Sci. 2010, 14, 411–417. [Google Scholar] [CrossRef] [PubMed]
- Pinker, S.; Bloom, P. Natural language and natural selection. Behav. Brain Sci. 1990, 13, 707–727. [Google Scholar] [CrossRef]
- Friedman, R. Tokenization in the Theory of Knowledge. Encyclopedia 2023, 3, 380–386. [Google Scholar] [CrossRef]
- Waddell, W.W. The Parmenides of Plato; James Maclehose and Sons: Glasgow, UK, 1894. [Google Scholar]
- Owen, G.E.L. Eleatic Questions. Class. Q. 1960, 10, 84–102. [Google Scholar] [CrossRef]
- Merriam-Webster Dictionary. Available online: https://www.merriam-webster.com/dictionary/rhetoric (accessed on 6 April 2023).
- The Britannica Dictionary. Available online: https://www.britannica.com/dictionary/rhetoric (accessed on 11 April 2023).
- Rae, J.W.; Borgeaud, S.; Cai, T.; Millican, K.; Hoffmann, J.; Song, F.; Aslanides, J.; Henderson, S.; Ring, R.; Young, S.; et al. Scaling Language Models: Methods, Analysis & Insights from Training Gopher. arXiv 2021, arXiv:2112.11446. [Google Scholar]
- Traylor, A.; Feiman, R.; Pavlick, E. Can Neural Networks Learn Implicit Logic from Physical Reasoning? In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023; (in review). Available online: https://openreview.net/forum?id=HVoJCRLByVk (accessed on 12 May 2023).
- Evans, R.; Saxton, D.; Amos, D.; Kohli, P.; Grefenstette, E. Can Neural Networks Understand Logical Entailment? arXiv 2018, arXiv:1802.08535. [Google Scholar]
- Shi, S.; Chen, H.; Ma, W.; Mao, J.; Zhang, M.; Zhang, Y. Neural Logic Reasoning. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Online, 19–23 October 2020; pp. 1365–1374. [Google Scholar]
- Horn, L.R.; Wansing, H. Negation. In The Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2015; Available online: https://plato.stanford.edu/entries/negation (accessed on 11 May 2023).
- Aloni, M. Disjunction. In The Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2016; Available online: https://plato.stanford.edu/entries/disjunction (accessed on 11 May 2023).
- Boole, G. The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning; Macmillan, Barclay, & Macmillan: London, UK, 1847. [Google Scholar]
- Leibniz, G.W. De Progressione Dyadica Pars I. 1679. In Herrn von Leibniz’ Rechnung mit Null und Einz; Hochstetter, E., Greve, H.-J., Eds.; Siemens Aktiengesellschaft: Berlin, Germany, 1966. [Google Scholar]
- Klement, K.C. Propositional Logic. Internet Encyclopedia of Philosophy. Available online: https://iep.utm.edu/propositional-logic-sentential-logic (accessed on 12 April 2023).
- Russell, S. Unifying Logic and Probability. Commun. ACM 2015, 58, 88–97. [Google Scholar] [CrossRef]
- Braine, M.D.; Reiser, B.J.; Rumain, B. Some Empirical Justification for a Theory of Natural Propositional Logic. Psychol. Learn. Motiv. 1984, 18, 313–371. [Google Scholar]
- Garcez, A.D.A.; Gori, M.; Lamb, L.C.; Serafini, L.; Spranger, M.; Tran, S.N. Neural-Symbolic Computing: An Effective Methodology for Principled Integration of Machine Learning and Reasoning. arXiv 2019, arXiv:1905.06088. [Google Scholar]
- Yang, Y.; Zhuang, Y.; Pan, Y. Multiple knowledge representation for big data artificial intelligence: Framework, applications, and case studies. Front. Inf. Technol. Electron. Eng. 2021, 22, 1551–1558. [Google Scholar] [CrossRef]
- Liang, P.; Potts, C. Bringing machine learning and compositional semantics together. Annu. Rev. Linguist. 2015, 1, 355–376. [Google Scholar] [CrossRef]
- Hitzler, P.; Eberhart, A.; Ebrahimi, M.; Sarker, M.K.; Zhou, L. Neuro-symbolic approaches in artificial intelligence. Natl. Sci. Rev. 2022, 9, nwac035. [Google Scholar] [CrossRef]
- De Raedt, L.; Dumancic, S.; Manhaeve, R.; Marra, G. From Statistical Relational to Neuro-Symbolic Artificial Intelligence. arXiv 2020, arXiv:2003.08316. [Google Scholar]
- Kant, I. Critique of Pure Reason; Weigelt, M., Translator; Penguin Classics: London, UK, 2003. [Google Scholar]
- Friedman, R. A Perspective on Information Optimality in a Neural Circuit and Other Biological Systems. Signals 2022, 3, 410–427. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Bubeck, S.; Chandrasekaran, V.; Eldan, R.; Gehrke, J.; Horvitz, E.; Kamar, E.; Lee, P.; Lee, Y.T.; Li, Y.; Lundberg, S.; et al. Sparks of Artificial General Intelligence: Early experiments with GPT-4. arXiv 2023, arXiv:2303.12712. [Google Scholar]
- Wei, J.; Tay, Y.; Bommasani, R.; Raffel, C.; Zoph, B.; Borgeaud, S.; Yogatama, D.; Bosma, M.; Zhou, D.; Metzler, D.; et al. Emergent Abilities of Large Language Models. arXiv 2022, arXiv:2206.07682. [Google Scholar]
- Schick, T.; Dwivedi-Yu, J.; Dessì, R.; Raileanu, R.; Lomeli, M.; Zettlemoyer, L.; Cancedda, N.; Scialom, T. Toolformer: Language models can teach themselves to use tools. arXiv 2023, arXiv:2302.04761. [Google Scholar]
- Efstathiou, V.; Hunter, A. Algorithms for generating arguments and counterarguments in propositional logic. Int. J. Approx. Reason. 2011, 52, 672–704. [Google Scholar] [CrossRef]
- Lukins, S.; Levicki, A.; Burg, J. A Tutorial Program for Propositional Logic with Human/Computer Interactive Learning. ACM SIGCSE Bull. 2002, 34, 381–385. [Google Scholar] [CrossRef]
- Ni, J.; Young, T.; Pandelea, V.; Xue, F.; Cambria, E. Recent Advances in Deep Learning Based Dialogue Systems: A Systematic Survey. Artif. Intell. Rev. 2022, 56, 3055–3155. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Zidek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Lin, Z.; Akin, H.; Rao, R.; Hie, B.; Zhu, Z.; Lu, W.; Smetanin, N.; Verkuil, R.; Kabeli, O.; Shmueli, Y.; et al. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science 2023, 379, 1123–1130. [Google Scholar] [CrossRef]
- Creswell, A.; Shanahan, M.; Higgins, I. Selection-Inference: Exploiting Large Language Models for Interpretable Logical Reasoning. arXiv 2022, arXiv:2205.09712. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Chan, S.; Santoro, A.; Lampinen, A.; Wang, J.; Singh, A.; Richemond, P.; McClelland, J.; Hill, F. Data Distributional Properties Drive Emergent In-Context Learning in Transformers. Adv. Neural Inf. Process. Syst. 2022, 35, 18878–18891. [Google Scholar]
- Beurer-Kellner, L.; Fischer, M.; Vechev, M. Prompting Is Programming: A Query Language for Large Language Models. arXiv 2022, arXiv:2212.06094. [Google Scholar]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Chi, E.; Le, Q.; Zhou, D. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. arXiv 2022, arXiv:2201.11903. [Google Scholar]
- Taylor, R.; Kardas, M.; Cucurull, G.; Scialom, T.; Hartshorn, A.; Saravia, E.; Poulton, A.; Kerkez, V.; Stojnic, R. Galactica: A Large Language Model for Science. arXiv 2022, arXiv:2211.09085. [Google Scholar]
- Friedman, R. Themes of advanced information processing in the primate brain. AIMS Neurosci. 2020, 7, 373. [Google Scholar] [CrossRef]
- Saharia, C.; Chan, W.; Saxena, S.; Li, L.; Whang, J.; Denton, E.L.; Ghasemipour, K.; Gontijo Lopes, R.; Karagol Ayan, B.; Salimans, T.; et al. Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding. Adv. Neural Inf. Process. Syst. 2022, 35, 36479–36494. [Google Scholar]
- Floyd, J. Wittgenstein on Philosophy of Logic and Mathematics. Grad. Fac. Philos. J. 2004, 25, 227–287. [Google Scholar]
- Hinton, G.E. Connectionist learning procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Srivastava, A.; Rastogi, A.; Rao, A.; Shoeb, A.A.M.; Abid, A.; Fisch, A.; Brown, A.R.; Santoro, A.; Gupta, A.; Garriga-Alonso, A.; et al. Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models. arXiv 2022, arXiv:2206.04615. [Google Scholar]
- Fusi, S.; Miller, E.K.; Rigotti, M. Why neurons mix: High dimensionality for higher cognition. Curr. Opin. Neurobiol. 2016, 37, 66–74. [Google Scholar] [CrossRef]
- Demortier, G. Revisiting the construction of the Egyptian pyramids. Europhys. News 2009, 40, 27–31. [Google Scholar] [CrossRef]
- Tamkin, A.; Brundage, M.; Clark, J.; Ganguli, D. Understanding the Capabilities, Limitations, and Societal Impact of Large Language Models. arXiv 2021, arXiv:2102.02503. [Google Scholar]
- Porter, M.E. The Competitive Advantage of Nations. Harv. Bus. Rev. 1990, 68, 73–93. [Google Scholar]
- Lippmann, W. Public Opinion; Harcourt, Brace and Company: New York, NY, USA, 1922. [Google Scholar]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.; et al. Recent advances and applications of deep learning methods in materials science. NPJ Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Meher, S.K.; Panda, G. Deep learning in astronomy: A tutorial perspective. Eur. Phys. J. Spec. Top. 2021, 230, 2285–2317. [Google Scholar]
- Liu, Y.; Han, T.; Ma, S.; Zhang, J.; Yang, Y.; Tian, J.; He, H.; Li, A.; He, M.; Liu, Z.; et al. Summary of ChatGPT/GPT-4 Research and Perspective Towards the Future of Large Language Models. arXiv 2023, arXiv:2304.01852. [Google Scholar]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.A.; Lacroix, T.; Roziere, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. LLaMA: Open and Efficient Foundation Language Models. arXiv 2023, arXiv:2302.13971. [Google Scholar]
- Newton, A.; Dhole, K. Is AI Art Another Industrial Revolution in the Making? arXiv 2023, arXiv:2301.05133. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friedman, R. Large Language Models and Logical Reasoning. Encyclopedia 2023, 3, 687-697. https://doi.org/10.3390/encyclopedia3020049
Friedman R. Large Language Models and Logical Reasoning. Encyclopedia. 2023; 3(2):687-697. https://doi.org/10.3390/encyclopedia3020049
Chicago/Turabian StyleFriedman, Robert. 2023. "Large Language Models and Logical Reasoning" Encyclopedia 3, no. 2: 687-697. https://doi.org/10.3390/encyclopedia3020049
APA StyleFriedman, R. (2023). Large Language Models and Logical Reasoning. Encyclopedia, 3(2), 687-697. https://doi.org/10.3390/encyclopedia3020049