Conductive Heat Transfer in Thermal Bridges
Definition
:1. Introduction
2. Definition of Important Terms and Quantities
2.1. Thermal Bridge
2.2. Types of Heat Transfer and Their Impact on Thermal Bridge Modeling
2.3. The Main Problem
2.4. Essential Physical Quantities
2.4.1. Temperature Gradient
2.4.2. Thermal Conductivity
2.4.3. Thermal Flux
2.4.4. Thermal Dissipation
2.4.5. Thermal Transmittance or U-Value and Thermal Resistance
2.4.6. Thermal Conductance
3. Physical Background
3.1. The Physics of Heat Transfer
3.2. Relationship with the “Heat Equation” from PDE Literature
3.3. The Steady State Heat Equation
3.4. Simple Analytical and Computational Examples
3.4.1. In One Dimension
3.4.2. In Two Dimensions
3.4.3. In Three Dimensions
3.5. Existence and Uniqueness of Solutions
4. Finite Elements—The Numerical and Computational Fundamentals
4.1. Boundary Conditions
4.1.1. Exterior and Interior Facing Surfaces—Dirichlet Boundary Conditions
4.1.2. Structure Facing Surfaces—Neumann Boundary Conditions
4.2. Tetrahedral Meshes
- a collection of vertices—points in three-dimensional space, together with
- a collection of tetrahedra—quadruples of indices into the vertex list, together with
- a way of associating each tetrahedron with one and only one material.
- 1.
- The union of all tetrahedra covers the entire thermal bridge but no other volumes.
- 2.
- Each material corresponds uniquely to a subset of all tetrahedra.
- 3.
- The surfaces constituting the material boundaries are surface sub-meshes in the sense that faces that lie on the boundary are a surface mesh without topological defects. These surfaces appear as the “constraints” of the Delaunay triangulation.
- 4.
- Each tetrahedron should be “as equilateral as possible” in the sense that no interior edge angle among all vertices is less than a typical threshold of about .
4.3. Derivation of Algorithm for the Temperature Coefficients
- Compute the lower right block of the stiffness matrix A as well as an appropriate sparse matrix factorization.
- Compute the lower left block —a rectangular sub-matrix with q rows and p columns.
- Assemble the vector of Dirichlet boundary components b; this is a vector of size p; solve the linear system of equations , resulting in the desired coefficients .
4.4. Extraction of Dissipation and U-Value from the Discretized Temperature
4.5. Norms and Standards
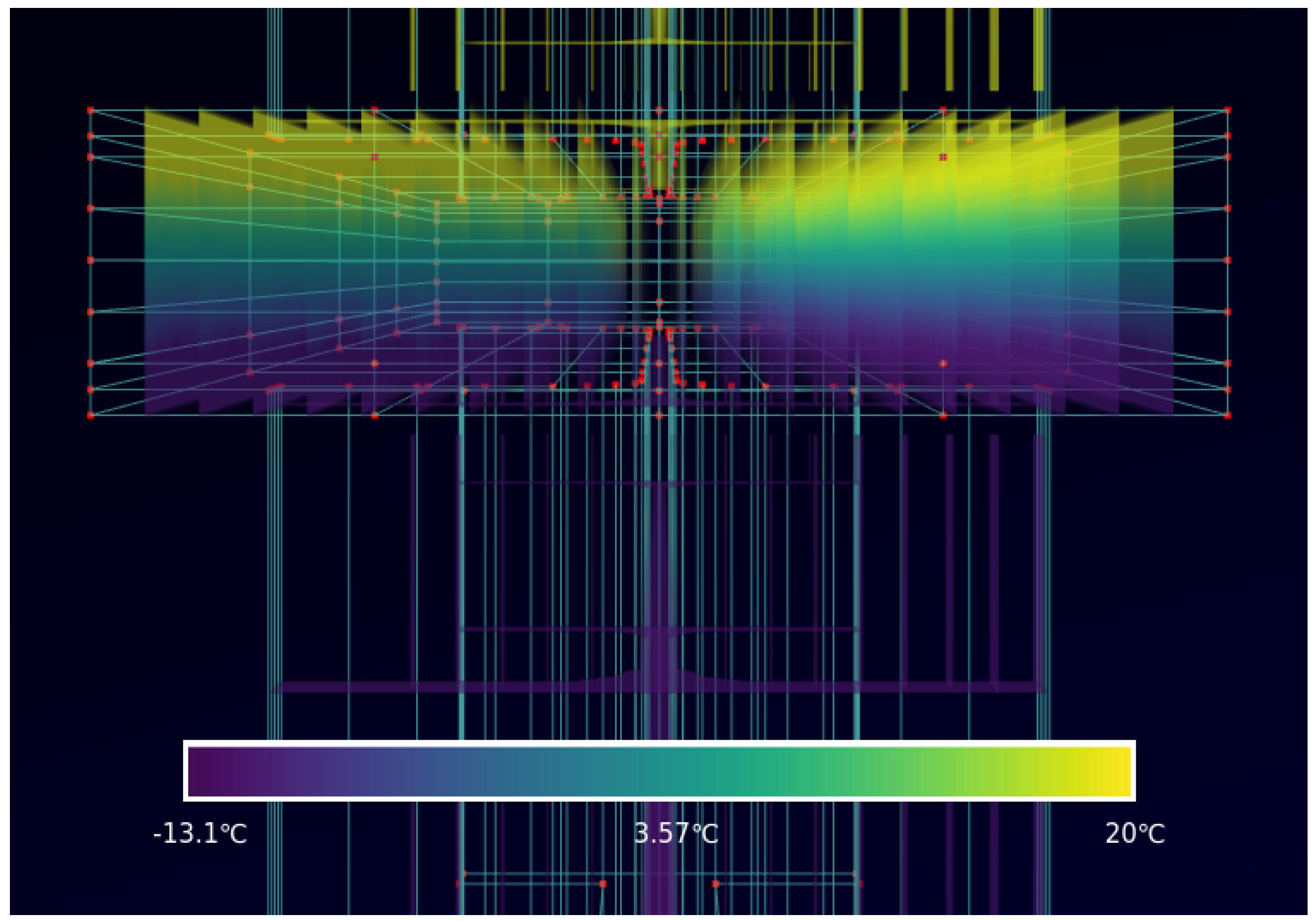
5. I-Beam
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | finite element method |
| PDE | Partial differential equation |
| thermal dissiplation | thermal energy loss per unit duration |
| Laplacian | the operator |
| scalar field | the assignment of a real number to each point |
| vector field | the assignment of a vector (three real numbers) to each point |
| time derivative of a scalar field | |
| ∇ | on a scalar field, its gradient; on a vector field, its divergence |
| gradient | the vector field given by the three partial derivatives of a scalar field |
| divergence | the scalar field given by the sum of the three |
| separate partial derivatives of a vector field | |
| stationary heat equation | the heat equation with ; synonym with steady state |
References
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Elsevier/Butterworth Heinemann: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Wilson, E.L.; Nickell, R.E. Application of the finite element method to heat conduction analysis. Nucl. Eng. Des. 1966, 4, 276–286. [Google Scholar] [CrossRef]
- Lewis, R.W.; Morgan, K.; Thomas, H.; Seetharamu, K.N. The Finite Element Method in Heat Transfer Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Häupl, P.; Homann, M.; Kölzow, C.; Riese, O.; Maas, A.; Höfker, G.; Christian, N. Lehrbuch der Bauphysik: Schall-Wärme-Feuchte-Licht-Brand-Klima; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Cody, B. Form Follows Energy: Using Natural Forces to Maximize Performance; Birkhäuser: Basel, Switzerland, 2017. [Google Scholar]
- Asdrubali, F.; Baldinelli, G.; Bianchi, F. A quantitative methodology to evaluate thermal bridges in buildings. Appl. Energy 2012, 97, 365–373. [Google Scholar] [CrossRef]
- Zalewski, L.; Lassue, S.; Rousse, D.; Boukhalfa, K. Experimental and numerical characterization of thermal bridges in prefabricated building walls. Energy Convers. Manag. 2010, 51, 2869–2877. [Google Scholar] [CrossRef]
- Arto, I.; Capellán-Pérez, I.; Lago, R.; Bueno, G.; Bermejo, R. The energy requirements of a developed world. Energy Sustain. Dev. 2016, 33, 1–13. [Google Scholar] [CrossRef]
- Kleinhückelkotten, S.; Neitzke, H.; Moser, S. Repräsentative Erhebung von Pro-Kopf-Verbräuchen natürlicher Ressourcen in Deutschland (nach Bevölkerungsgruppen); Umweltbundesamt: Dessau-Roßlau, Germany, 2016. [Google Scholar]
- Khazal, A.; Sønstebø, O.J. Valuation of energy performance certificates in the rental market—Professionals vs. nonprofessionals. Energy Policy 2020, 147, 111830. [Google Scholar] [CrossRef]
- Terms and Conditions; Ansys Fluent; Ansys: Canonsburg, PA, USA, 2015; Available online: https://www.ansys.com/academic/terms-and-conditions (accessed on 1 April 2022).
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]
- Déqué, F.; Ollivier, F.; Roux, J. Effect of 2D modelling of thermal bridges on the energy performance of buildings: Numerical application on the Matisse apartment. Energy Build. 2001, 33, 583–587. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Sawhney, R.; Crane, K. Monte Carlo Geometry Processing: A Grid-Free Approach to PDE-Based Methods on Volumetric Domains. ACM Trans. Graph. 2020, 39, 123. [Google Scholar] [CrossRef]
- Grossmann, C.; Roos, H.G.; Stynes, M. Numerical Treatment of Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007; Volume 154. [Google Scholar]
- Din Norm. DIN Norm 4180-2: Thermal Protection and Energy Economy in Buildings—Part 2: Minimum Requirements to Thermal Insulation; Din Norm: Berlin, Germany, 2012. [Google Scholar]
- Taylor, B.J.; Cawthorne, D.; Imbabi, M.S. Analytical investigation of the steady-state behaviour of dynamic and diffusive building envelopes. Build. Environ. 1996, 31, 519–525. [Google Scholar] [CrossRef]
- Gasparin, S.; Berger, J.; Dutykh, D.; Mendes, N. Solving nonlinear diffusive problems in buildings by means of a Spectral reduced-order model. J. Build. Perform. Simul. 2019, 12, 17–36. [Google Scholar] [CrossRef]
- ISO. Norm 10211: Thermal Bridges in Building Construction–Heat Flows and Surface Temperatures–Detailed Calculations; ISO Norm, Vernier: Geneva, Switzerland, 2017. [Google Scholar]
- Gerthsen, C.; Vogel, H. Physik, 17. Auflage; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Walter, W. Gewöhnliche Differentialgleichungen. Eine Einführung; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Glaser, H. Vereinfachte Berechnung der Dampfdiffusion durch geschichtete Wände bei Ausscheidung von Wasser und Eis. Kältetechnik 1958, 10, 358–364. [Google Scholar]
- Nirenberg, L. Remarks on strongly elliptic partial differential equations. Commun. Pure Appl. Math. 1955, 8, 649–675. [Google Scholar] [CrossRef]
- Shewchuk, J.R.; Brown, B.C. Fast segment insertion and incremental construction of constrained Delaunay triangulations. Comput. Geom. 2015, 48, 554–574. [Google Scholar] [CrossRef]
- Hang, S. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Trans. Math. Softw. 2015, 41, 11. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D Finite Element Mesh Generator with built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Mancinelli, C.; Livesu, M.; Puppo, E. A comparison of methods for gradient field estimation on simplicial meshes. Comput. Graph. 2019, 80, 37–50. [Google Scholar] [CrossRef]
- ISO. Norm 7345: Thermal Performance of Buildings and Building Components—Physical Quantities and Definitions; ISO Norm, Vernier: Geneva, Switzerland, 2018. [Google Scholar]
- ISO. Norm 6946: Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods; ISO Norm, Vernier: Geneva, Switzerland, 2017. [Google Scholar]
- ISO. Norm 10077-1: Thermal Performance of Windows, Doors and Shutters—Calculation of Thermal Transmittance—Part 1: General; ISO Norm, Vernier: Geneva, Switzerland, 2017. [Google Scholar]
- ISO. Norm 10077-2: Thermal Performance of Windows, Doors and Shutters—Calculation of Thermal Transmittance—Part 2: Numerical Method for Frames; ISO Norm, Vernier: Geneva, Switzerland, 2017. [Google Scholar]
- ISO. Norm 13786:Thermal Performance of Building Components—Dynamic Thermal Characteristics—Calculation Methods; ISO Norm, Vernier: Geneva, Switzerland, 2017. [Google Scholar]
- ISO. Norm 13787: Thermal Insulation Products for Building Equipment and Industrial Installations—Determination of Declared Thermal Conductivity; ISO Norm, Vernier: Geneva, Switzerland, 2003. [Google Scholar]
- ISO. Norm 13788: Hygrothermal Performance of Building Components and Building Elements—Internal Surface Temperature to Avoid Critical Surface Humidity and Interstitial Condensation—Calculation Methods; ISO Norm, Vernier: Geneva, Switzerland, 2012. [Google Scholar]
- ISO. Norm 13789: Thermal Performance of Buildings — Transmission and Ventilation Heat Transfer Coefficients — Calculation Method; ISO Norm, Vernier: Geneva, Switzerland, 2017. [Google Scholar]
- ISO. Norm CSA Z5010: Thermal Bridging Calculation Methodology; ISO Norm: Toronto, ON, Canada, 2021. [Google Scholar]
- Müller, M.; Li, Z.; Standeker, J. Schöck Isokorb®–Gebrauchstauglichkeit unter Berücksichtigung der Langzeiteigenschaften. Beton-Und Stahlbetonbau 2020, 115, 35–43. [Google Scholar] [CrossRef]
- Fuchs, M. I Beam Thermal Break Visualization. Available online: https://mathiasfuchs.com/rawtetgen.html (accessed on 31 March 2022).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuchs, M. Conductive Heat Transfer in Thermal Bridges. Encyclopedia 2022, 2, 1019-1035. https://doi.org/10.3390/encyclopedia2020067
Fuchs M. Conductive Heat Transfer in Thermal Bridges. Encyclopedia. 2022; 2(2):1019-1035. https://doi.org/10.3390/encyclopedia2020067
Chicago/Turabian StyleFuchs, Mathias. 2022. "Conductive Heat Transfer in Thermal Bridges" Encyclopedia 2, no. 2: 1019-1035. https://doi.org/10.3390/encyclopedia2020067
APA StyleFuchs, M. (2022). Conductive Heat Transfer in Thermal Bridges. Encyclopedia, 2(2), 1019-1035. https://doi.org/10.3390/encyclopedia2020067





