Numerical Solution of Desiccation Cracks in Clayey Soils
Definition
:1. Introduction
2. Mathematical Formulation and Numerical Solution for Desiccation Cracks in Clayey Soils
2.1. Mathematical Formulation
2.1.1. Mechanical and Hydraulic Constitutive Relations
- Stress state variables.
- Stress–strain–suction relations.
- Stress–strain relation.
- Generalized Darcy’s law for unsaturated soils and permeability tensor.
- Water retention curve.
Stress State Variables
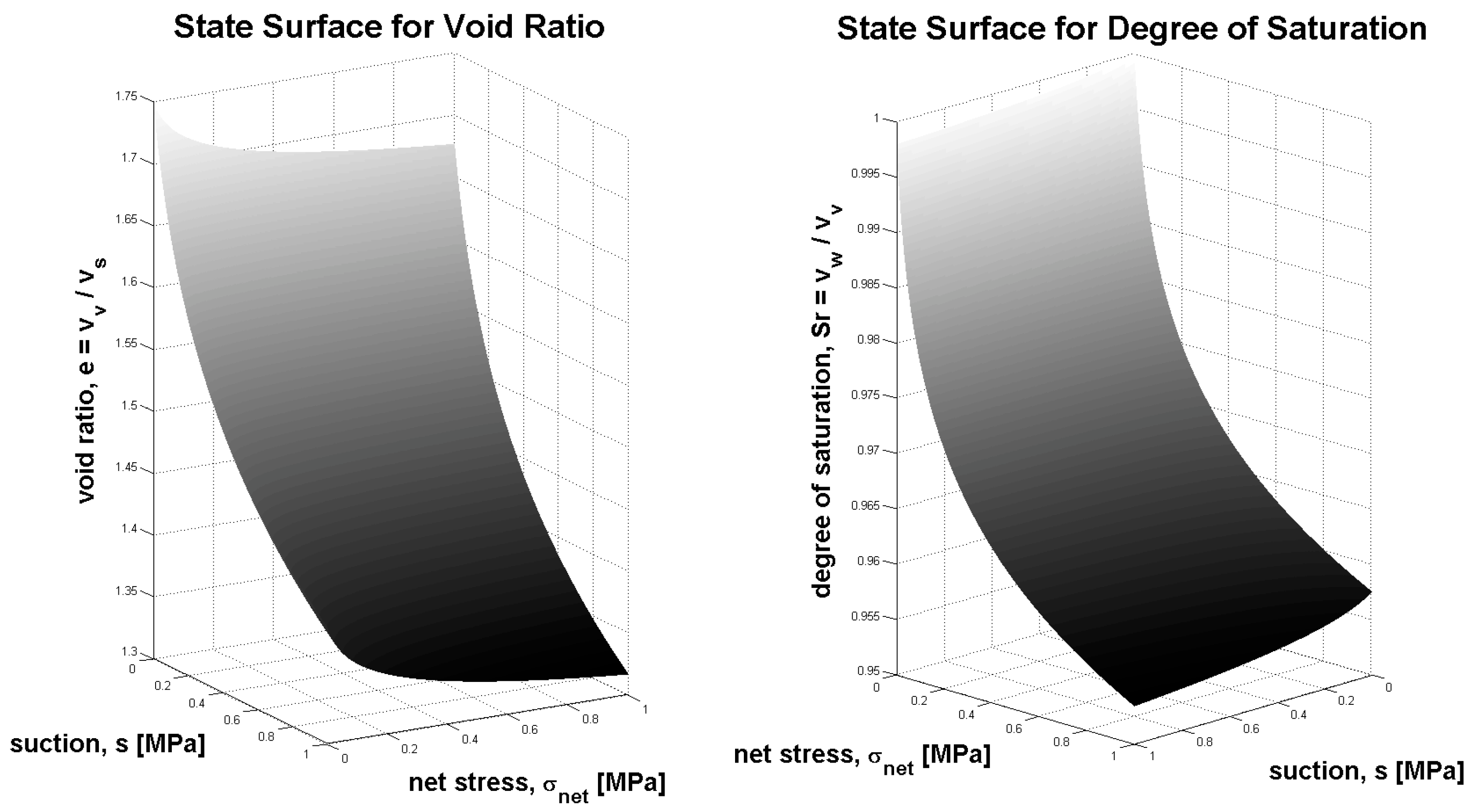
Stress–Strain–Suction Relations
Stress–Strain Constitutive Law
Generalized Darcy’s Law for Unsaturated Soils and Permeability Tensor
Water Retention Curve
2.1.2. Governing Equations
- Equilibrium equation of the solid particles.
- Balance equation of water.
Equilibrium Equations
Balance Equations
2.2. Numerical Approach
2.2.1. Finite Element Approximation
The u–p Formulation
Time Integration of the Coupled Problem
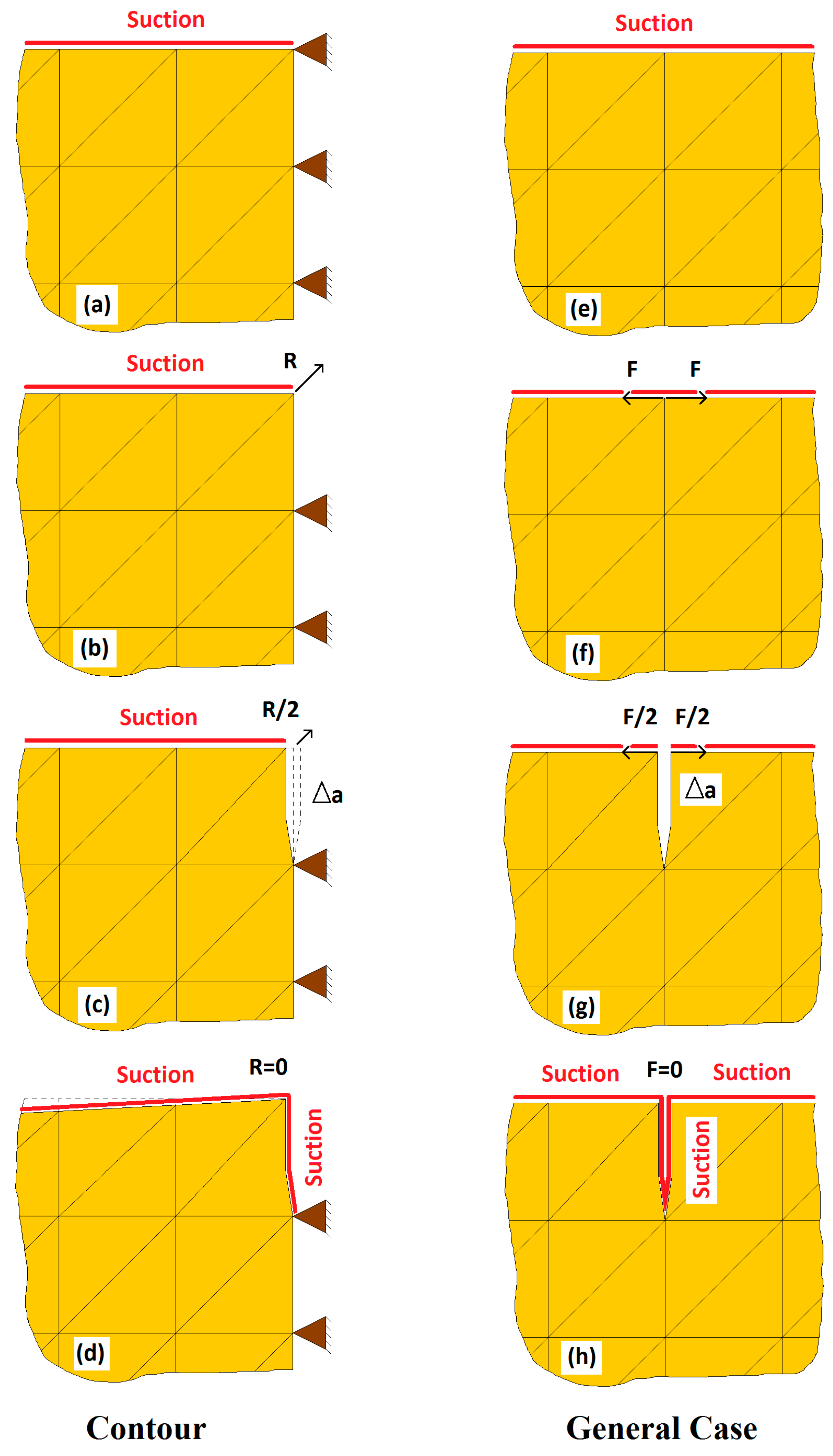
2.2.2. Release Node Algorithm
Release Node Algorithm
- Fracture criterion is reached at a point in the soil matrix.
- Keep the external loads constant (suction profile for desiccation problems).
- Calculate reactions at the boundary, , or calculate equivalent forces that keep the split nodes together, .
- Delete the nodal restriction in the contour or split the nodes in the surface of the soil where the tensile strength was reached.
- Add reaction R at the released node (reaction in the contour) or forces in the node that was split.
- Reduce the force or F step by step to zero.
- Add suction on the new surface created by the crack and exposed to the environment.
- Once the model is in equilibrium, check whether the fracture criterion is reached at any other point of the geometry.
- If yes, go to step 3 to initiate again the release node algorithm.
- If no, continue the hydromechanical analysis.
Limitations of the Model
3. Conclusions and Prospects
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Set of Parameters for a Numerical Model for Barcelona Silty Clay
| Void Ratio (e) | Porosity (n) | Dried Unit Weight γd (g/cm3) | fn = exp[−η(n − n0)] | λ | 1/(1 − λ) |
|---|---|---|---|---|---|
| 0.87 | 0.47 | 1.45 | 1.04 | 0.27 | 1.37 |
| 0.75 | 0.43 | 1.55 | 1.07 | 0.25 | 1.33 |
| 0.64 | 0.39 | 1.65 | 1.12 | 0.23 | 1.30 |
| 0.55 | 0.35 | 1.75 | 1.16 | 0.20 | 1.25 |
| Mechanical Parameters | ||||||
|---|---|---|---|---|---|---|
| State surface parameters | (MPa) | Poisson Ratio | Tensile strength (MPa) | |||
(MPa) | ||||||
| −0.02 | −0.0025 | −0.000039 | 0.023 | 0.1 | 0.4 | 0.0035 |
| Hydraulic Parameters | ||||||
| Initial permeability (m/s) | Material parameter | Initial porosity | Material parameter | |||
| 9.27 × 10−10 | 25 | 0.6 | 3 | |||
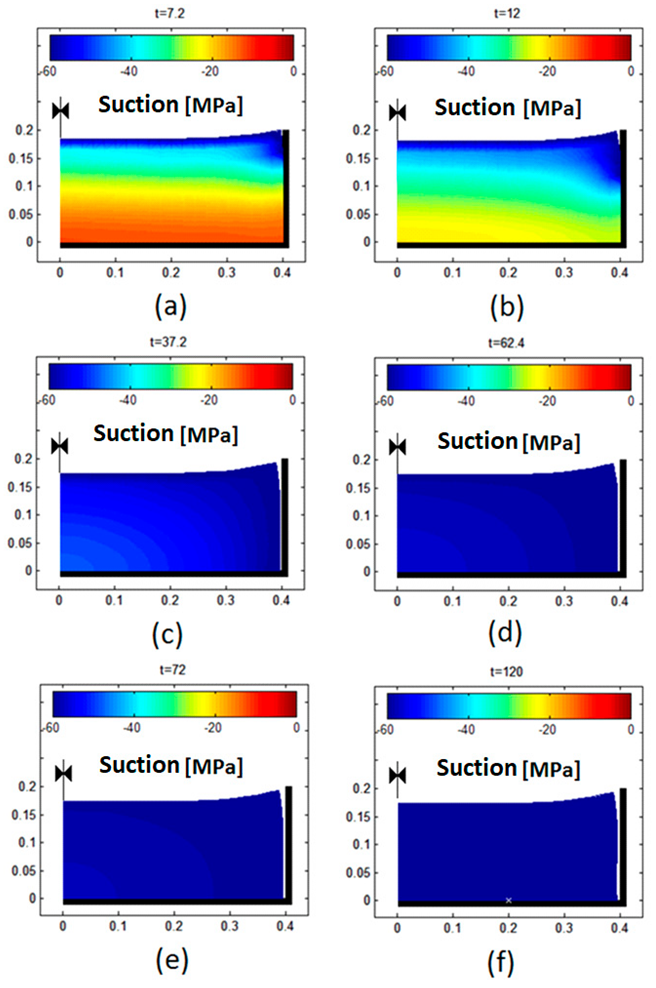
Appendix B. Numerical Results of the Model for Barcelona Silty Clay
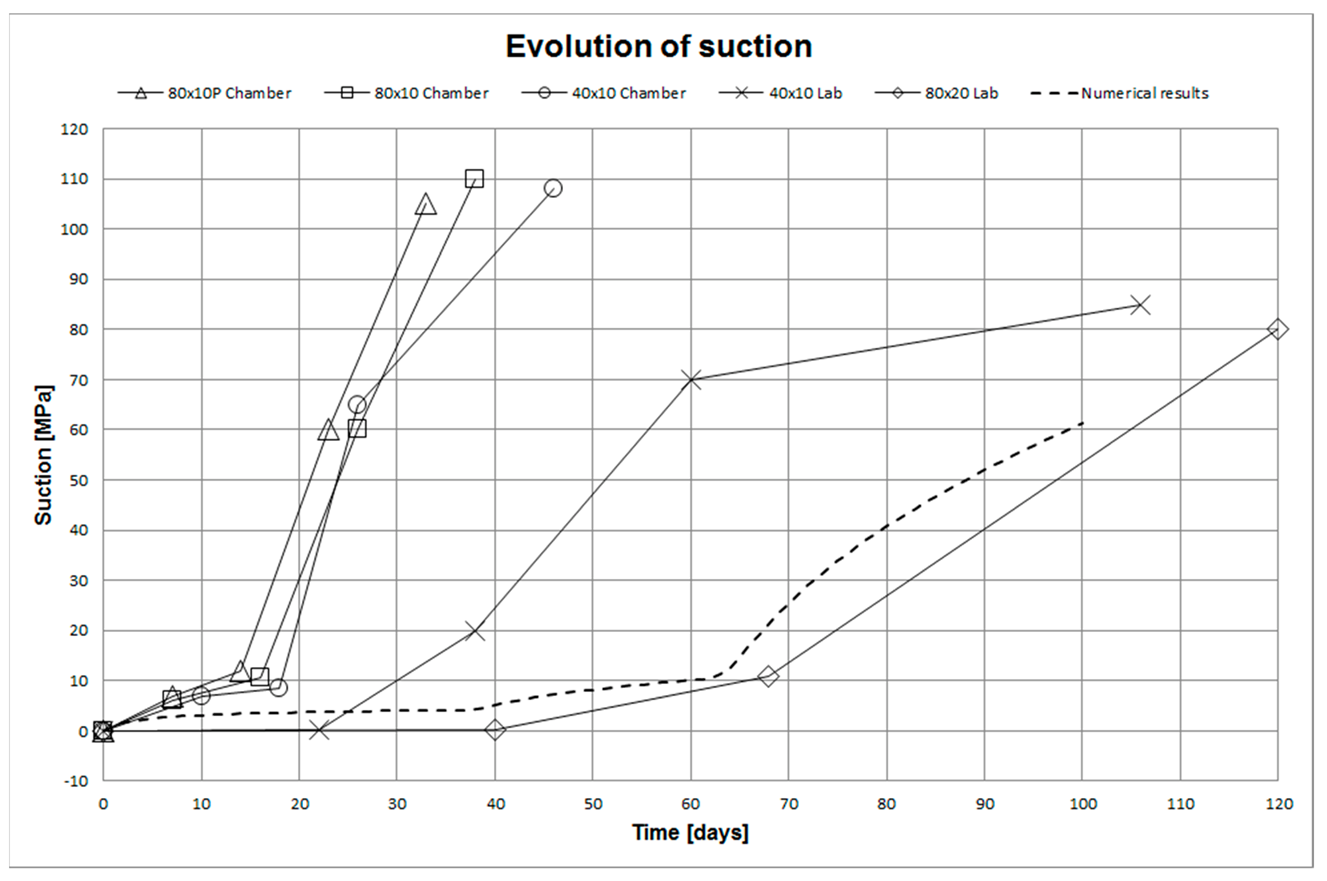
Appendix C. Comparison of Experimental and Numerical Results of the Model
References
- Rodríguez, R.L. Estudio Experimental de Flujo y Transporte de Cromo, Níquel Y Manganeso en Residuos de la Zona Minera de Moa (Cuba): Influencia del Comportamiento Hidromecánico. Ph.D. Thesis, UPC-BarcelonaTech, Barcelona, Spain, 2002. [Google Scholar]
- Rodríguez, R.L.; Sánchez, M.J.; Ledesma, A.; Lloret, A. Experimental and numerical analysis of a mining waste desiccation. Can. Geotech. J. 2007, 44, 644–658. [Google Scholar] [CrossRef]
- Tang, C.-S.; Shi, B.; Liu, C.; Zhao, L.; Wang, B. Influencing factors of geometrical structure of surface shrinkage cracks in clayey soils. Eng. Geol. 2008, 101, 204–217. [Google Scholar] [CrossRef]
- Justo, J.L.; Vázquez, N.J.; Justo, E. Subsidence in saturated-unsaturated soils: Application to Murcia (Spain). In Third International Conference on Unsaturated Soils; Jucá, J.F.T., de Campos, T.M.P., Marinho, F.A.M., Eds.; Balkema: Rotterdam, The Netherlands, 2002; pp. 845–850. [Google Scholar]
- Bronswijk, J.J.B. Modeling of water balance, cracking and subsidence in clay soils. J. Hydrol. 1988, 97, 199–212. [Google Scholar] [CrossRef]
- Kodikara, J.; Barbour, S.L.; Fredlund, D.G. Desiccation cracking of soil layers. In Unsaturated Soils for Asia; Rahardjo, H., Toll, D.G., Leong, E.C., Eds.; Balkema: Rotterdam, The Netherlands, 2000; pp. 693–698. [Google Scholar]
- Ávila, G. Estudio de la Retracción Y el Agrietamiento de Arcillas. Aplicación a la Arcilla de Bogotá. Ph.D. Thesis, UPC-BarcelonaTech, Barcelona, Spain, 2004. [Google Scholar]
- Chertkov, V.Y. Modelling cracking stages of saturated soils as they dry and shrink. Eur. J. Soil Sci. 2002, 53, 105–118. [Google Scholar] [CrossRef]
- Corte, A.; Higashi, A. Experimental Research on Desiccation Cracks in Soil; U.S. Army Materiel Command Cold Regions Research & Engineering Laboratory: Wilmette, IL, USA, 1960. [Google Scholar]
- Hu, L.B.; Hueckel, T.; Péron, H.; Laloui, L. Modeling Evaporation, Shrinkage and Cracking of Desiccating Soils. In Proceedings of the International Association for Computer Methods and Advances in Geomechanics (IACMAG), Goa, India, 1–6 October 2008; pp. 1083–1090. [Google Scholar]
- Kodikara, J.K.; Nahlawi, H.; Bouazza, A. Modelling of curling in desiccation clay. Can. Geotech. J. 2004, 41, 560–566. [Google Scholar] [CrossRef]
- Lakshmikantha, M.R. Experimental and Theoretical Analysis of Cracking in Drying Soils. Ph.D. Thesis, UPC-BarcelonaTech, Barcelona, Spain, 2009. [Google Scholar]
- Lakshmikantha, M.R.; Prat, P.C.; Ledesma, A. Characterization of crack networks in desiccating soils using image analysis techniques. In Numerical Models in Geomechanics X; Pande, G.N., Pietruszczak, S., Eds.; Balkema: Rotterdam, The Netherlands, 2007; pp. 167–176. [Google Scholar]
- Lakshmikantha, M.R.; Prat, P.C.; Ledesma, A. Image analysis for the quantification of a developing crack network on a drying soil. Geotech. Test. J. 2009, 32, 505–515. [Google Scholar]
- Lakshmikantha, M.R.; Prat, P.C.; Ledesma, A. Experimental evidences of size-effect in soil cracking. Can. Geotech. J. 2012, 49, 264–284. [Google Scholar] [CrossRef]
- Lakshmikantha, M.R.; Prat, P.C.; Ledesma, A. Evidences of hierarchy in cracking of drying soils. ASCE Geotech. Spec. Publ. 2013, 231, 782–789. [Google Scholar]
- Lau, J.T.K. Desiccation Cracking of Clay Soils. M.S. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 1987. [Google Scholar]
- Morris, P.H.; Graham, J.; Williams, D.J. Cracking in drying soils. Can. Geotech. J. 1992, 29, 263–277. [Google Scholar] [CrossRef]
- Nahlawi, H.; Kodikara, J. Laboratory experiments on desiccation cracking of thin soil layers. Geotech. Geol. Eng. 2006, 24, 1641–1664. [Google Scholar] [CrossRef]
- Péron, H.; Hueckel, T.; Laloui, L.; Hu, L.B. Fundamentals of desiccation cracking of fine-grained soils: Experimental characterisation and mechanisms identification. Can. Geotech. J. 2009, 46, 1177–1201. [Google Scholar] [CrossRef]
- Tang, C.-S.; Shi, B.; Liu, C.; Gao, L.; Inyang, H. Experimental Investigation of the Desiccation Cracking Behavior of Soil Layers during Drying. J. Mater. Civ. Eng. 2011, 23, 873–878. [Google Scholar] [CrossRef]
- Tang, C.-S.; Shi, B.; Liu, C.; Suo, W.-B.; Gao, L. Experimental characterization of shrinkage and desiccation cracking in thin clay layer. Appl. Clay Sci. 2011, 52, 69–77. [Google Scholar] [CrossRef]
- Vogel, H.J.; Hoffmann, H.; Roth, K. Studies of crack dynamics in clay soil. I: Experimental methods, results, and morphological quantification. Geoderma 2005, 125, 203–211. [Google Scholar] [CrossRef]
- Levatti, H.U. Estudio Experimental Y Análisis Numérico de la Desecación en Suelos Arcillosos. Ph.D. Thesis, UPC-BarcelonaTech, Barcelona, Spain, 2015. Available online: https://www.tdx.cat/handle/10803/299202#page=1 (accessed on 12 January 2022).
- Trabelsi, H.; Jamei, M.; Zenzri, H.; Olivella, S. Crack patterns in clayey soils: Experiments and modelling. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 1410–1433. [Google Scholar] [CrossRef]
- Sima, J.; Jiang, M.; Zhou, C. Modeling desiccation cracking in thin clay layer using three-dimensional discrete element method. Proc. Am. Inst. Phys. 2013, 1542, 245–248. [Google Scholar]
- Amarasiri, A.L.; Kodikara, J.; Costa, S. Numerical modelling of desiccation cracking. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 82–96. [Google Scholar] [CrossRef]
- Sánchez, M.; Manzoli, O.L.; Guimarães, L.N. Modeling 3-D desiccation soil crack networks using a mesh fragmentation technique. Comput. Geotech. 2014, 62, 27–39. [Google Scholar] [CrossRef]
- Gui, Y.; Zhao, G.F. Modelling of laboratory soil desiccation cracking using DLSM with a two-phase bond model. Comput. Geotech. 2015, 69, 578–587. [Google Scholar] [CrossRef]
- Yan, C.; Luo, Z.; Zheng, Y.; Ke, W. A 2D discrete moisture diffusion model for simulating desiccation fracturing of soil. Eng. Anal. Bound. Elem. 2022, 138, 42–64. [Google Scholar] [CrossRef]
- Nikolic, M. Discrete element model for the failure analysis of partially saturated porous media with propagating cracks represented with embedded strong discontinuities. Comput. Methods Appl. Mech. Eng. 2022, 390, 27. [Google Scholar] [CrossRef]
- Lee, F.H.; Lo, K.W.; Lee, S.L. Tension crack development in soils. J. Geotech. Eng. ASCE 1988, 114, 915–929. [Google Scholar] [CrossRef]
- ITASCA. FLAC3D: Fast Lagrangian Analysis of Continua in Three Dimensions; Version 2.0 Manual; Itasca Consulting Group: Minneapolis, MN, USA, 1997. [Google Scholar]
- ITASCA. UDEC: Distinct-Element Modeling of Jointed and Blocky Material in 2D; Itasca Consulting Group: Minneapolis, MN, USA, 2017. [Google Scholar]
- ITASCA. PFC3D: Particle Flow Code in Three Dimensions; Version 3.0 Manual; Itasca Consulting Group: Minneapolis, MN, USA, 2003. [Google Scholar]
- Musielak, G.; Sliwa, T. Modeling and Numerical Simulation of Clays Cracking During Drying. Dry. Technol. 2015, 33, 1758–1767. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Chan, A.H.C.; Pastor, M.; Paul, D.K.; Shiomi, T. Static and Dynamic Behaviour of Soils: A Rational Approach to Quantitative Solutions. I. Fully Saturated Problems. Proceedings of the Royal Society of London Series A. Math. Phys. Sci. 1990, 429, 285–309. [Google Scholar]
- Levatti, H.U.; Prat, P.C.; Ledesma, A. Numerical and experimental study of initiation and propagation of desiccation cracks in clayey soils. Comput. Geotech. 2019, 105, 155–167. Available online: https://openresearch.lsbu.ac.uk/item/865wv (accessed on 12 January 2022). [CrossRef]
- Platten, J.K. The Soret Effect: A Review of Recent Experimental Results. J. Appl. Mech. 2006, 73, 5–15. [Google Scholar] [CrossRef]
- Ludwig, C. Diffusion zwischen ungleich erwwa”rmten orten gleich zusammengestzter lo”sungen. Sitz Ber. Akad. Wiss. Wien. Math.-Naturw. Kl. 1856, 20, 539. [Google Scholar]
- Soret, C. Sur l’état d’équilibre que prend au point de vue de sa concentration une dissolution saline primitivement homohéne dont deux parties sont portées à des températures différentes. Ann. Chim. Phys. 1881, 22, 293–297. [Google Scholar]
- Mitrovic, J. Josef Stefan and his evaporation–diffusion tube—the Stefan diffusion problem. Chem. Eng. Sci. 2012, 75, 279–281. [Google Scholar] [CrossRef]
- Varsei, M.; Miller, G.A.; Hassanikhah, A. Novel approach to measuring tensile strength of compacted clayey soil during desiccation. Int. J. Geomech. 2016, 16, D4016011. [Google Scholar] [CrossRef]
- Lakshmikantha, M.R.; Prat, P.C.; Tapia, J.; Ledesma, A. Effect of moisture content on tensile strength and fracture toughness of a silty soil. In Unsaturated Soils: Advances in Geo-Engineering; Toll, D.G., Augarde, C.E., Gallipoli, D., Wheeler, S.J., Eds.; CRC Press/Balkema: Leiden, The Netherlands, 2008; pp. 405–409. [Google Scholar]
- Hueckel, T. On effective stress concept and deformation in clays subjected to environmental loads: Discussion. Can. Geotech. J. 1992, 29, 1120–1125. [Google Scholar] [CrossRef]
- Sheng, D. Review of fundamental principles in modelling unsaturated soil behaviour. Comput. Geotech. 2011, 38, 757–776. [Google Scholar] [CrossRef]
- Matyas, E.L.; Radhakrishna, H.S. Volume change characteristics of partially saturated soils. Géotechnique 1968, 18, 432–448. [Google Scholar] [CrossRef]
- Lloret, A.; Alonso, E.E. State surfaces for partially saturated soils. In Proceedings of the XI International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985; pp. 557–562. [Google Scholar]
- Barrera, M. Estudio Experimental del Comportamiento Hidro-Mecánico de Suelos Colapsables. Ph.D. Thesis, UPC-BarcelonaTech, Barcelona, Spain, 2002. [Google Scholar]
- Konrad, J.-M.; Ayad, R. An idealized framework for the analysis of cohesive soils undergoing desiccation. Can. Geotech. J. 1997, 34, 477–488. [Google Scholar] [CrossRef]
- Gens, A.; Sánchez, M.; Sheng, D. On constitutive modelling of unsaturated soils. Acta Geotech. 2006, 1, 137–147. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. Closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Bishop, A.W. The principles of effective stress. Tek. Ukebl. 1959, 106, 859–863. [Google Scholar]
- Burland, J.B. Some aspects of the mechanical behaviour of partly saturated soil. In Moisture Equilibrium and Moisture Changes in Soils Beneath Covered Areas; Butterworths: Sydney, Australia, 1965; pp. 270–278. [Google Scholar]
- Bishop, A.W.; Blight, G.E. Some aspects of effective stress in saturated and partly saturated soils. Géotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Blight, G.E. A study of effective stresses for volume change. In Moisture Equilibrium and Moisture Changes in Soils Beneath Covered Areas; Butterworths: Sydney, Australia, 1965; pp. 259–269. [Google Scholar]
- Aitchison, G.D. Soil properties. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, SMFE, Montreal, QC, Canada, 8–15 September 1965; pp. 319–321. [Google Scholar]
- Jennings, J.; Burland, J.B. Limitations to the use of effective stress in partly saturated soils. Géotechnique 1962, 12, 125–144. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomenon of rupture and flow in solids. Philos. Trans. Roy. Soc. Lond. 1921, 221, 163–198. [Google Scholar]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media, 2nd ed.; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Schrefler, B.A.; Simoni, L.; Majorana, C.E. A general model for the mechanics of saturated-unsaturated porous materials. Mater. Struct. 1989, 22, 323–334. [Google Scholar] [CrossRef]
- Nahlawi, H.; Kodikara, J. Experimental observations on curling of desiccating clay. In Third International Conference on Unsaturated Soils; Jucá, J.F.T., de Campos, T.M.P., Marinho, F.A.M., Eds.; Balkema: Rotterdam, The Netherlands, 2004; pp. 553–556. [Google Scholar]
- Ledesma, A. Cracking in desiccating soils. In Proceedings of the 3rd European Conference on Unsaturated Soils, E-UNSAT, Paris, France, 12–14 September 2016. [Google Scholar]
- Cui, Y. Soil-atmosphere interaction in earth structures. J. Rock Mech. Geotech. Eng. 2022, 14, 35–49. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhu, C.; Tang, C.S.; Xu, H.; Shi, X.; Mark, V. 3D characterization of desiccation cracking in clayey soils using a structured light scanner. Eng. Geol. 2022, 299, 106566. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levatti, H.U. Numerical Solution of Desiccation Cracks in Clayey Soils. Encyclopedia 2022, 2, 1036-1058. https://doi.org/10.3390/encyclopedia2020068
Levatti HU. Numerical Solution of Desiccation Cracks in Clayey Soils. Encyclopedia. 2022; 2(2):1036-1058. https://doi.org/10.3390/encyclopedia2020068
Chicago/Turabian StyleLevatti, Hector U. 2022. "Numerical Solution of Desiccation Cracks in Clayey Soils" Encyclopedia 2, no. 2: 1036-1058. https://doi.org/10.3390/encyclopedia2020068
APA StyleLevatti, H. U. (2022). Numerical Solution of Desiccation Cracks in Clayey Soils. Encyclopedia, 2(2), 1036-1058. https://doi.org/10.3390/encyclopedia2020068






