Next-Generation Interferometry with Gauge-Invariant Linear Optical Scatterers
Abstract
1. Introduction
2. Optical Interference and Linear Optical Scatterers
2.1. Background
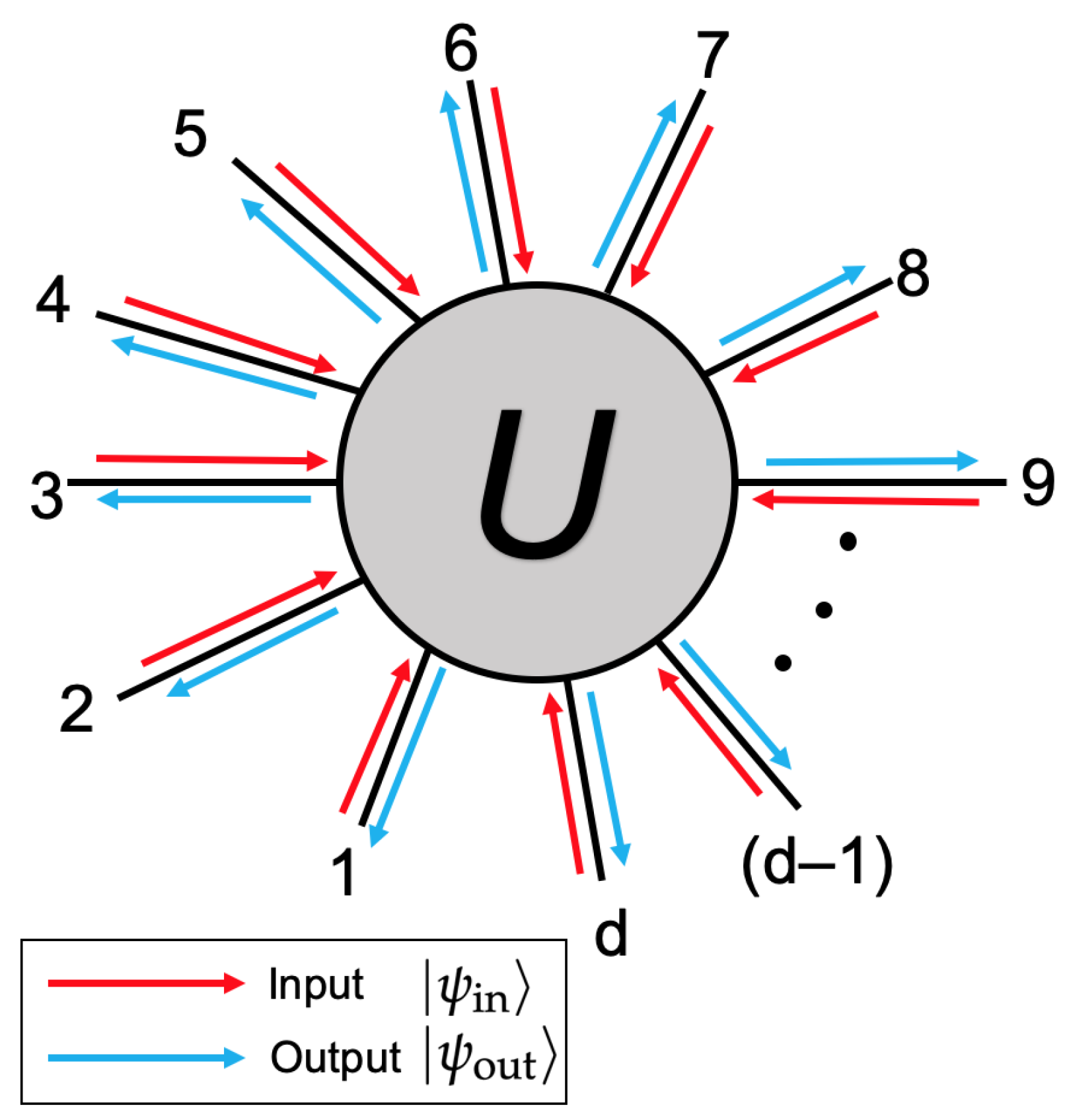
2.2. Matrix Formalism of Linear Optical Scattering
2.3. Scattering Process Gauge Symmetries
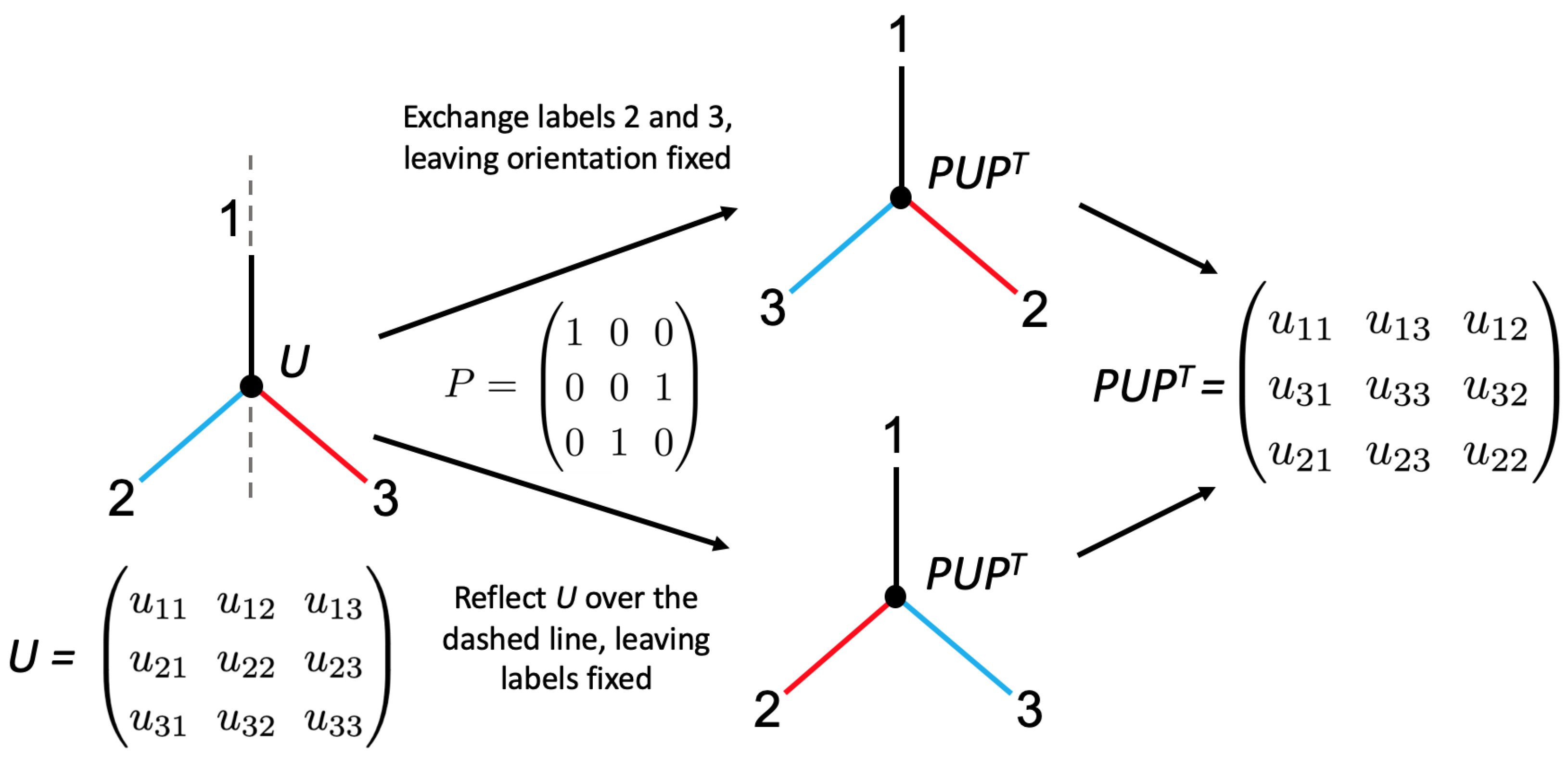
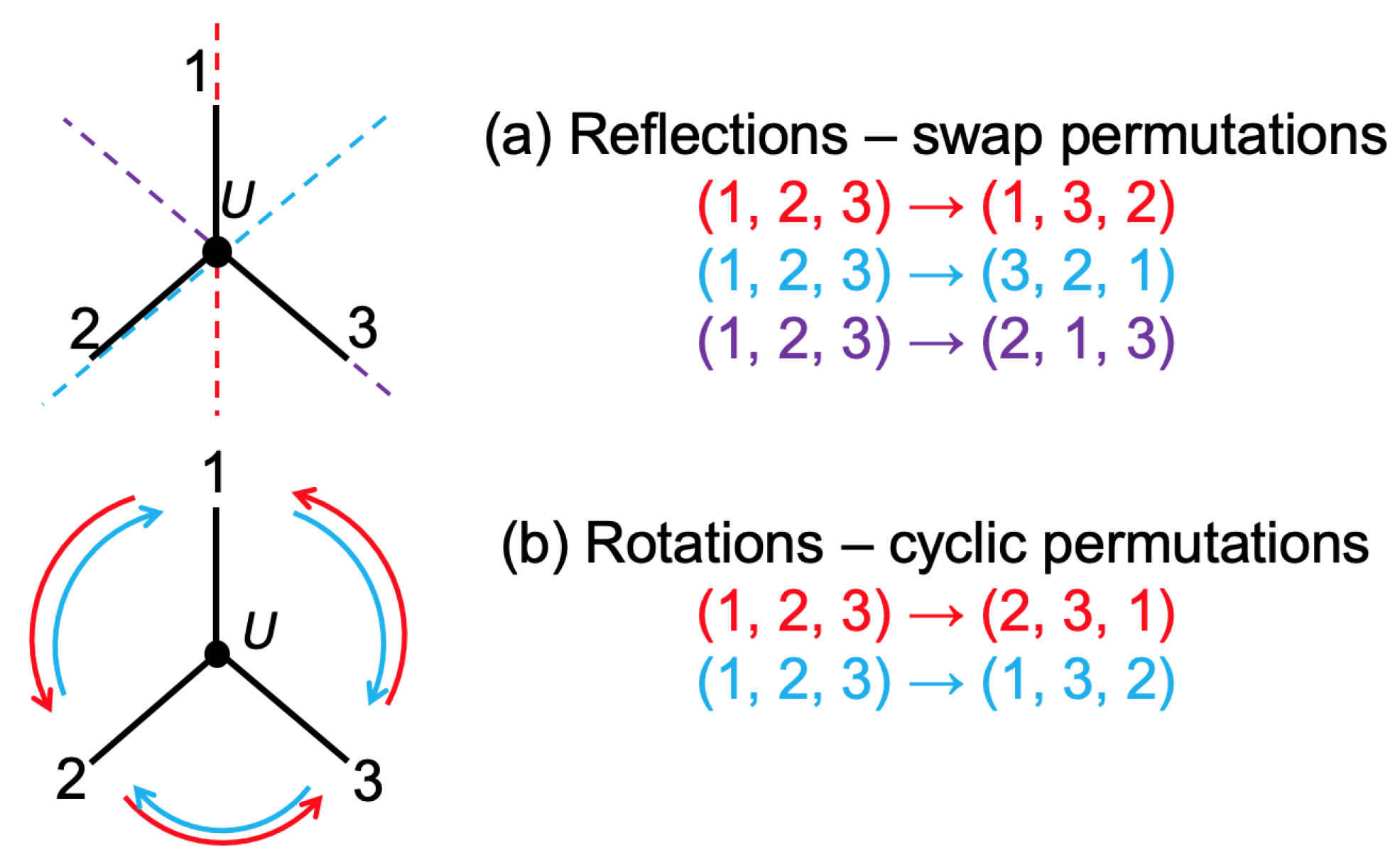
2.3.1. Geometric Scattering Transformations
2.3.2. External Phase Shifts
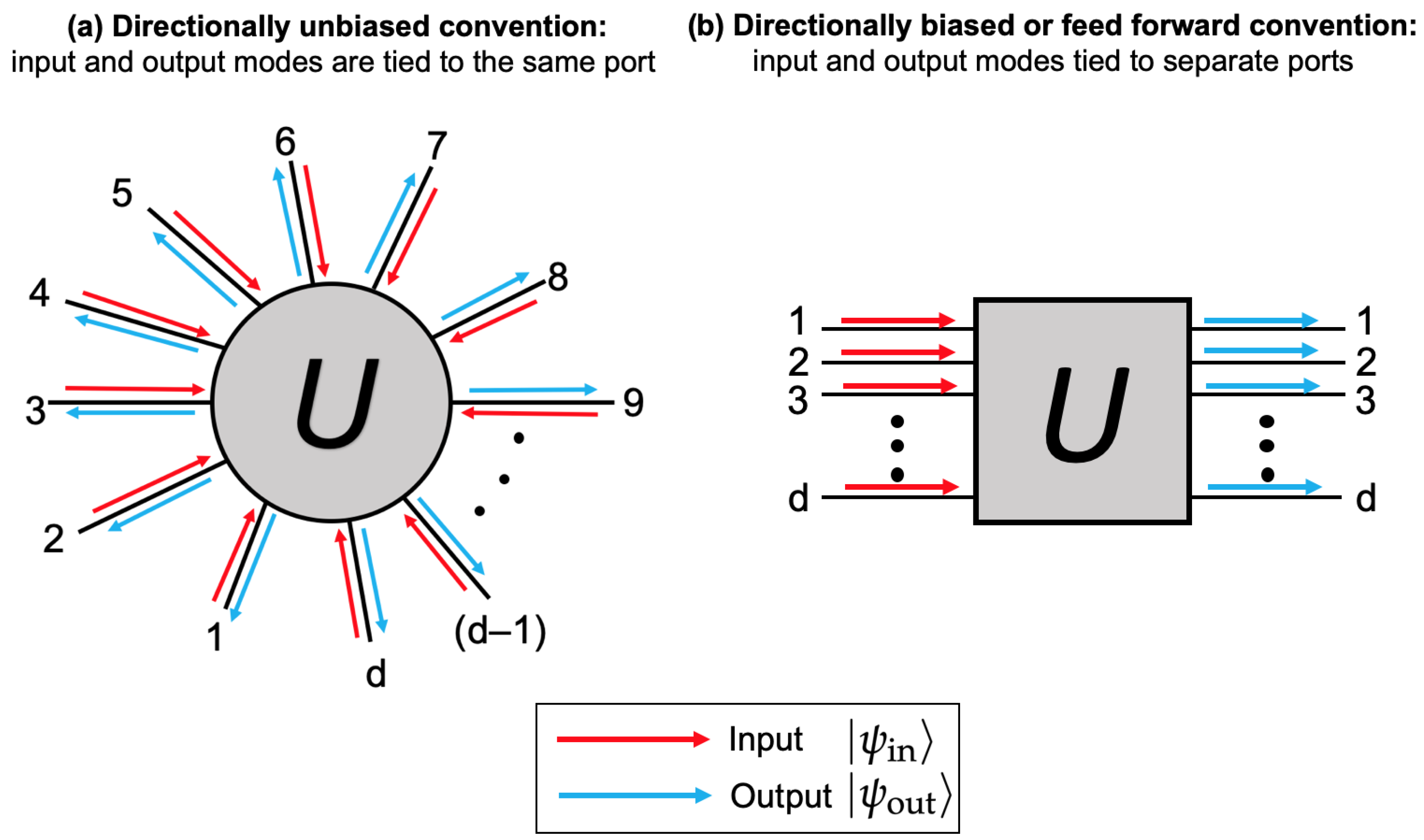
2.4. Directionally Biased and Unbiased Devices
2.5. U(1) Scattering Processes
2.6. U(2) Scattering Processes
2.7. Gauge-Invariant U(3) Scatterers
2.7.1. Generalized Three-Port Circulators
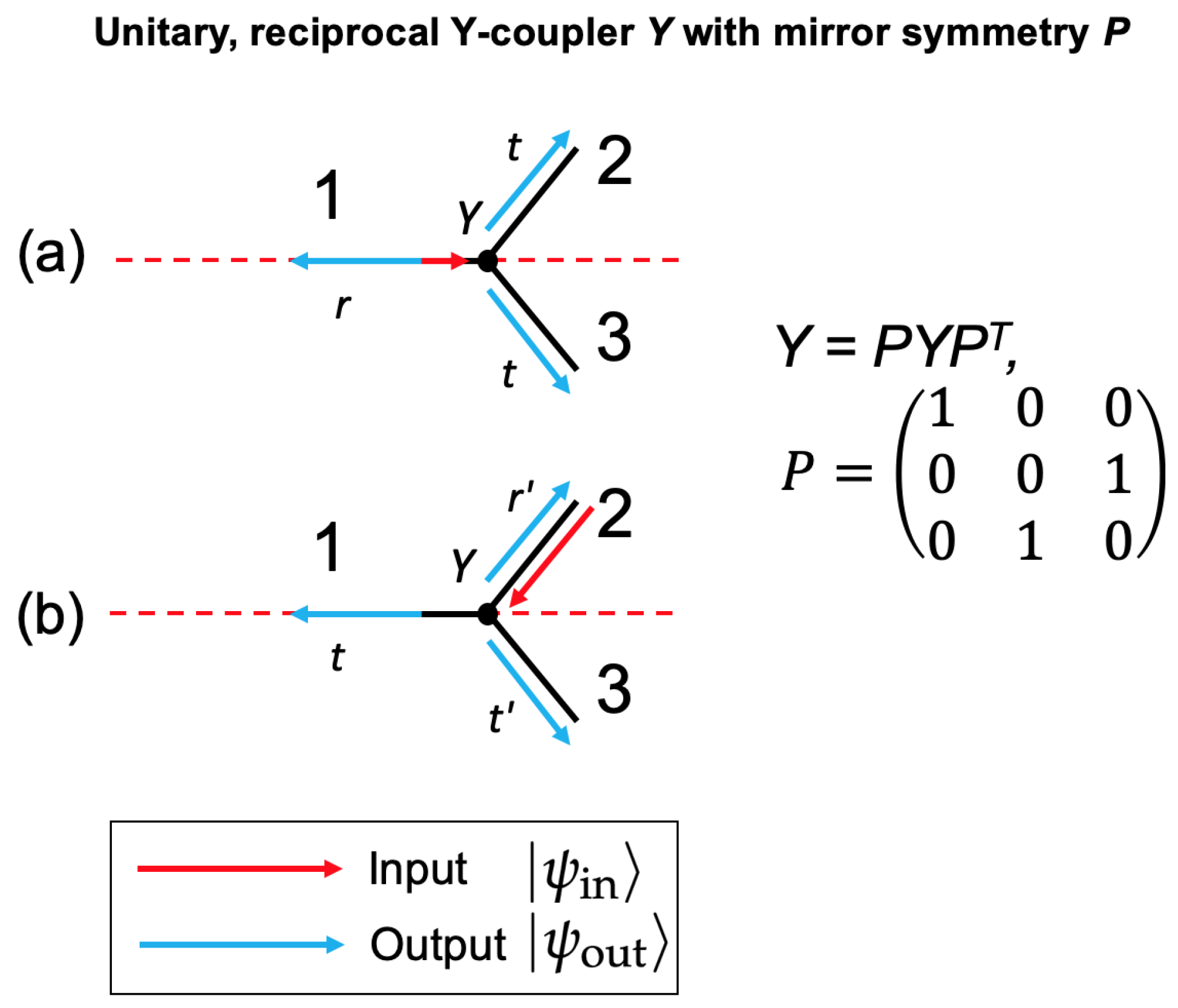
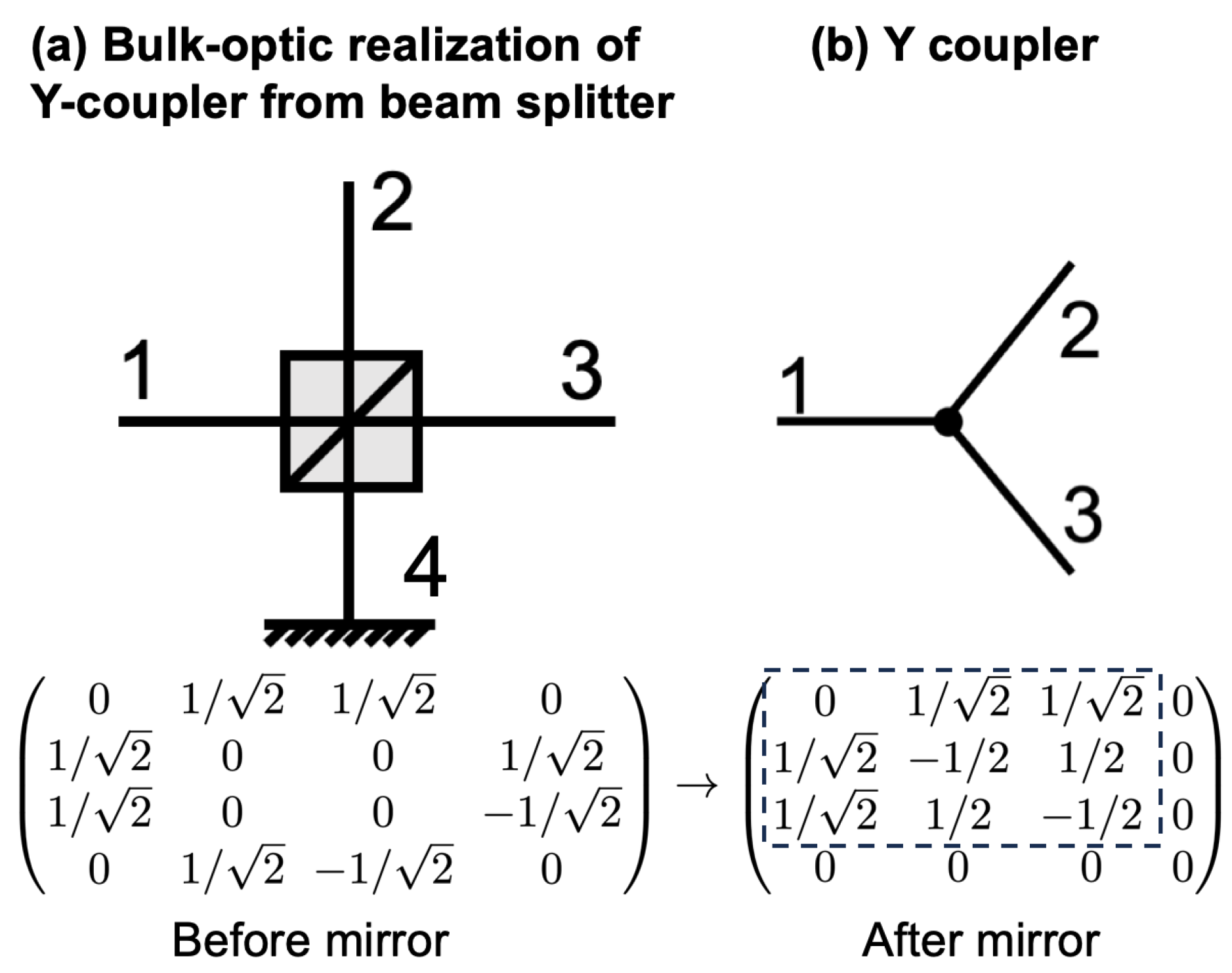
2.7.2. Y-Couplers
2.8. Gauge-Invariant U(4) Scatterers
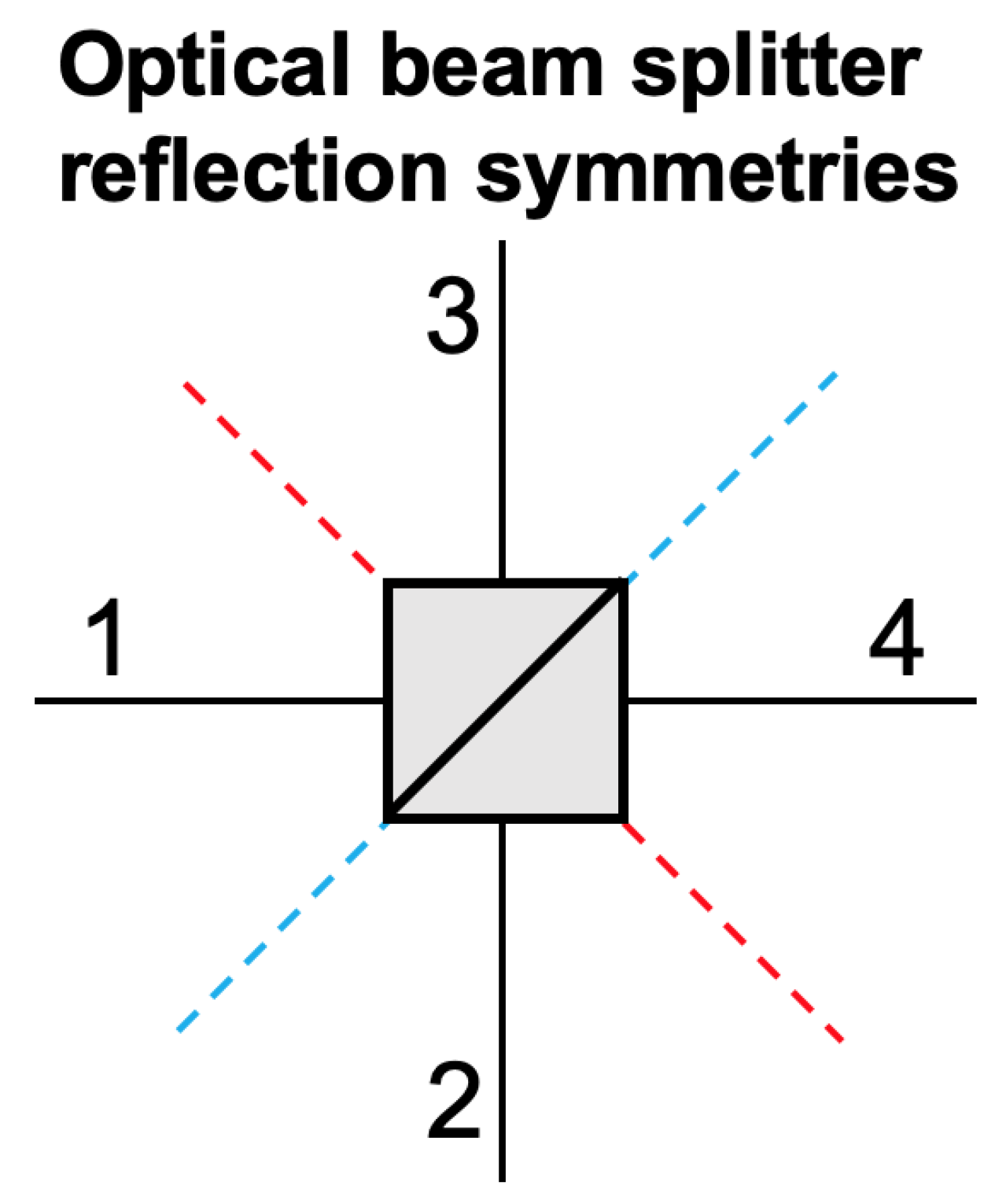
2.8.1. Beam Splitters
2.8.2. Grover Four-Ports
3. Optical Interferometry
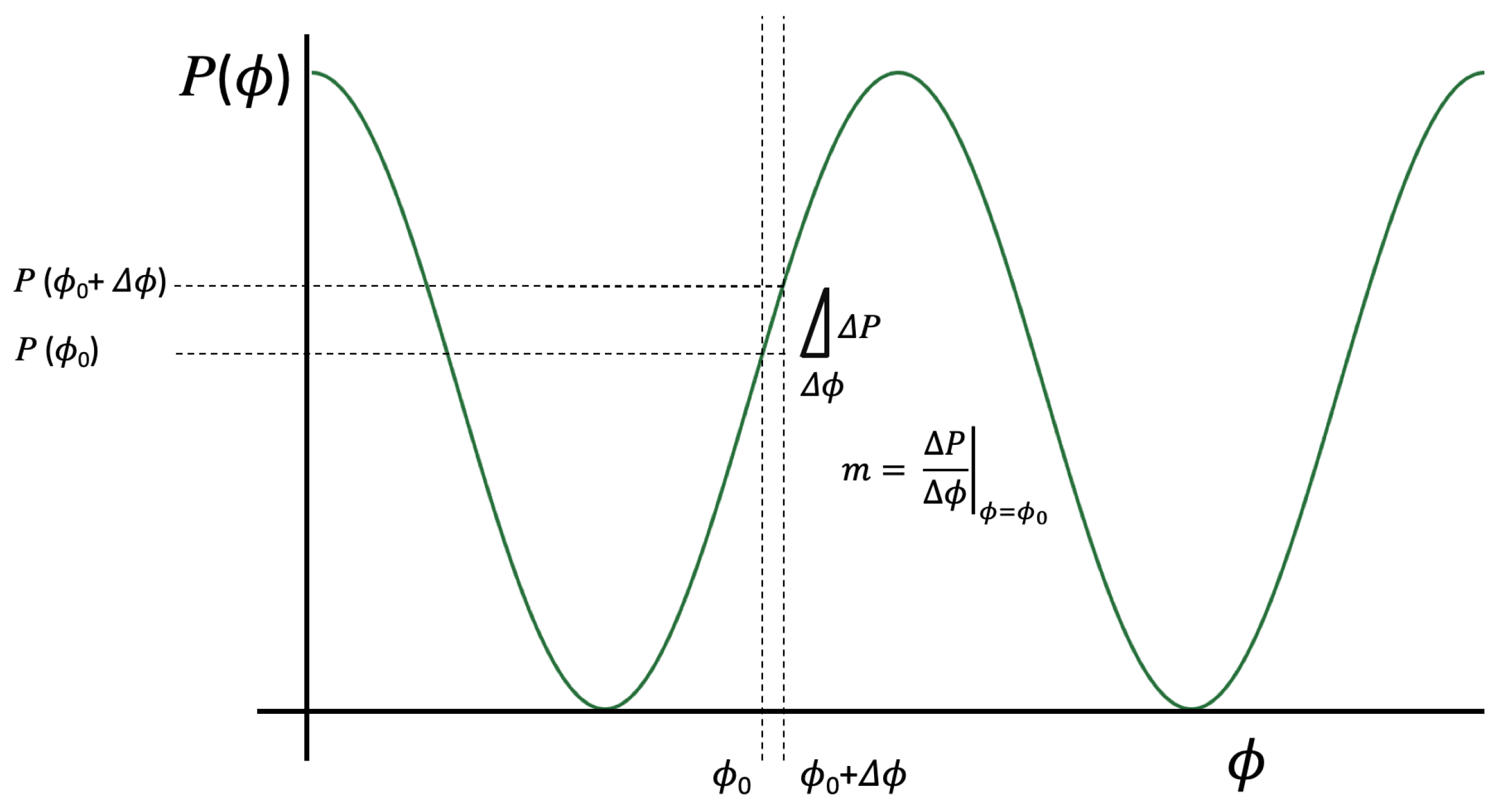
3.1. Interferometric Gauge Freedoms
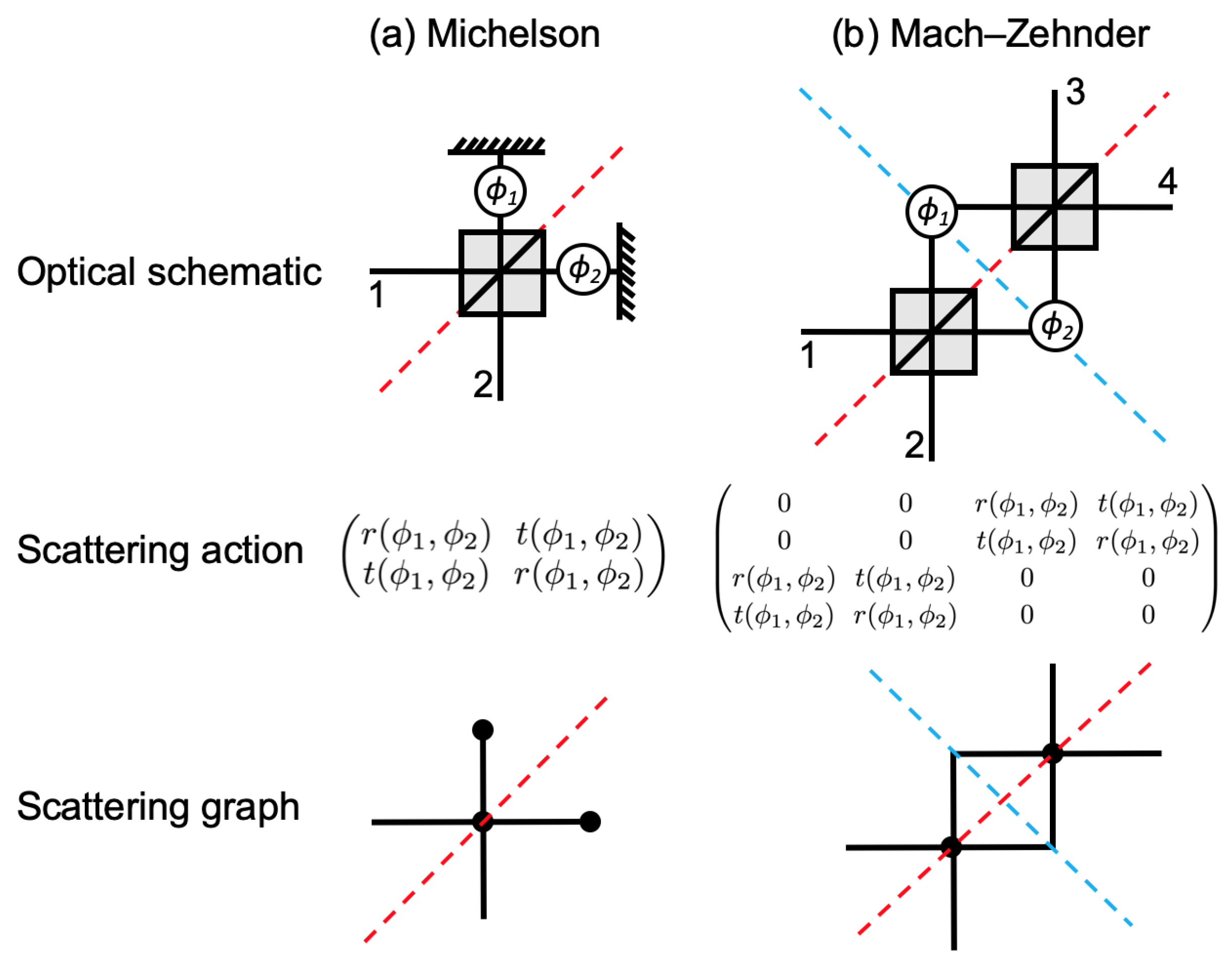
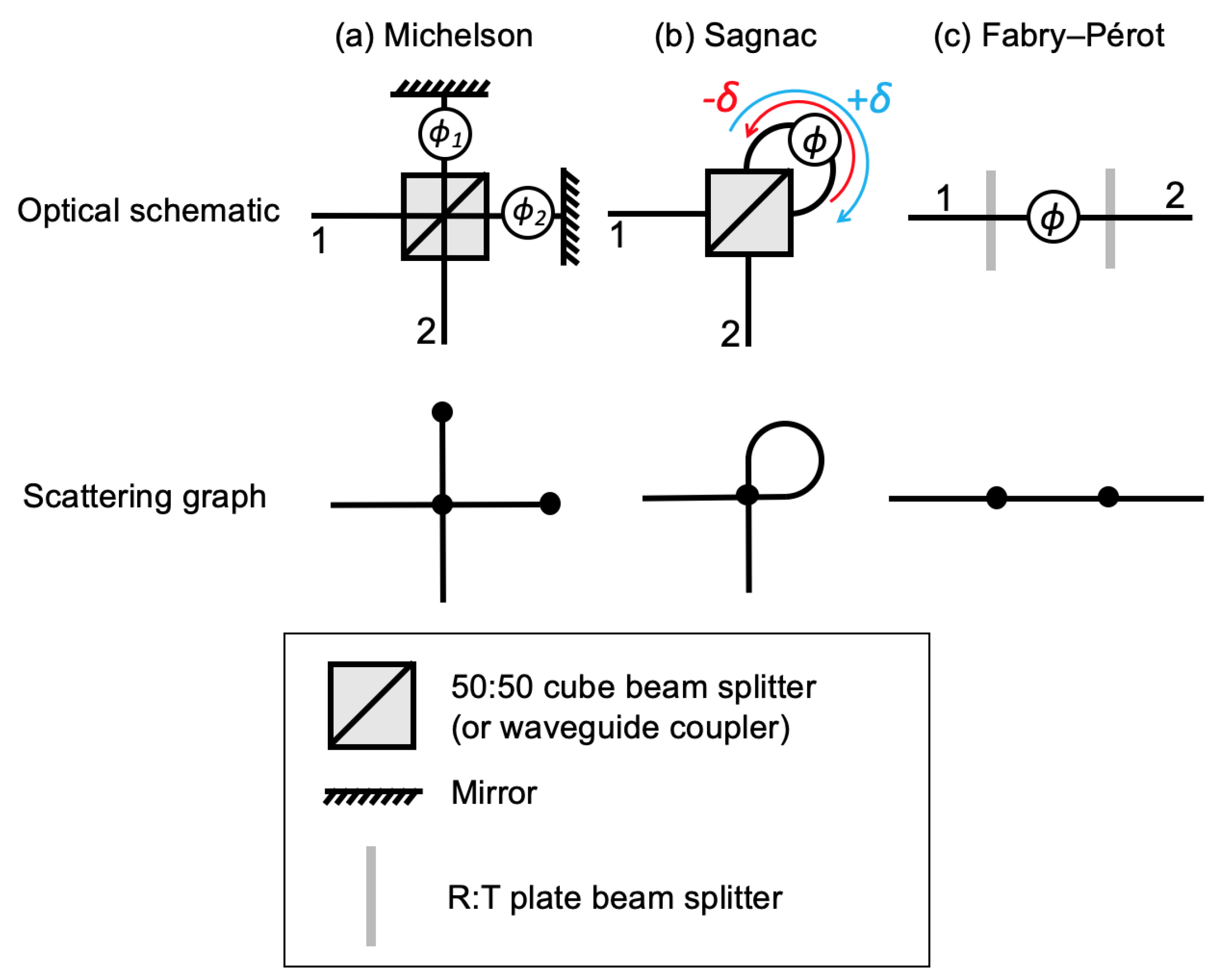
3.2. Traditional Interferometric Sensing Systems
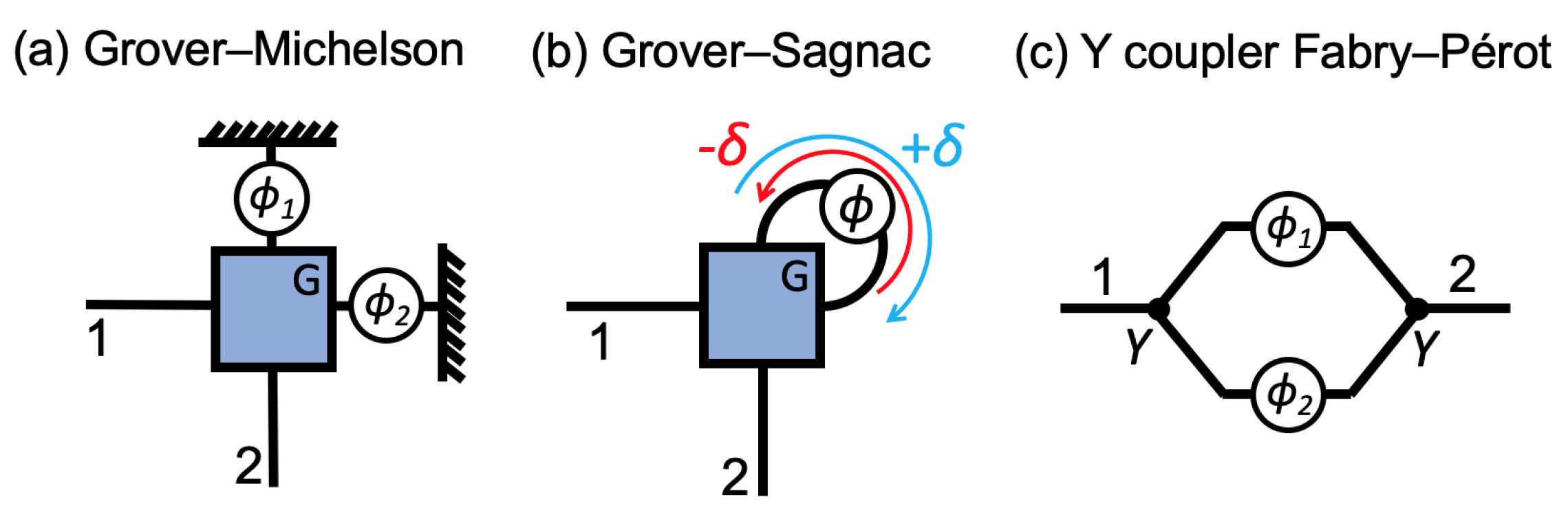
3.3. Novel Higher-Dimensional Interferometric Sensors
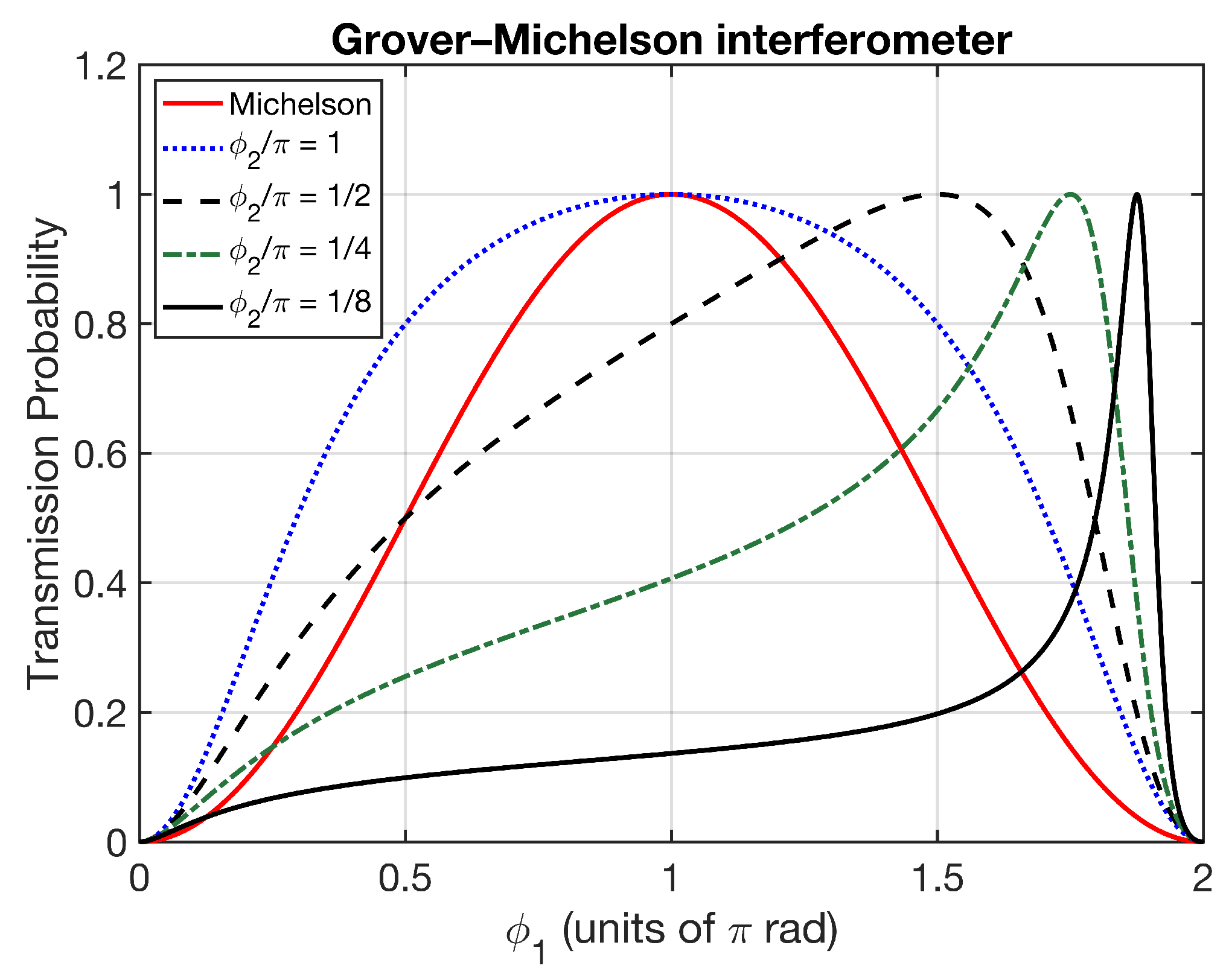
3.3.1. Experimental Demonstration of the Grover–Michelson Interferometer
3.3.2. Grover–Sagnac Interferometer
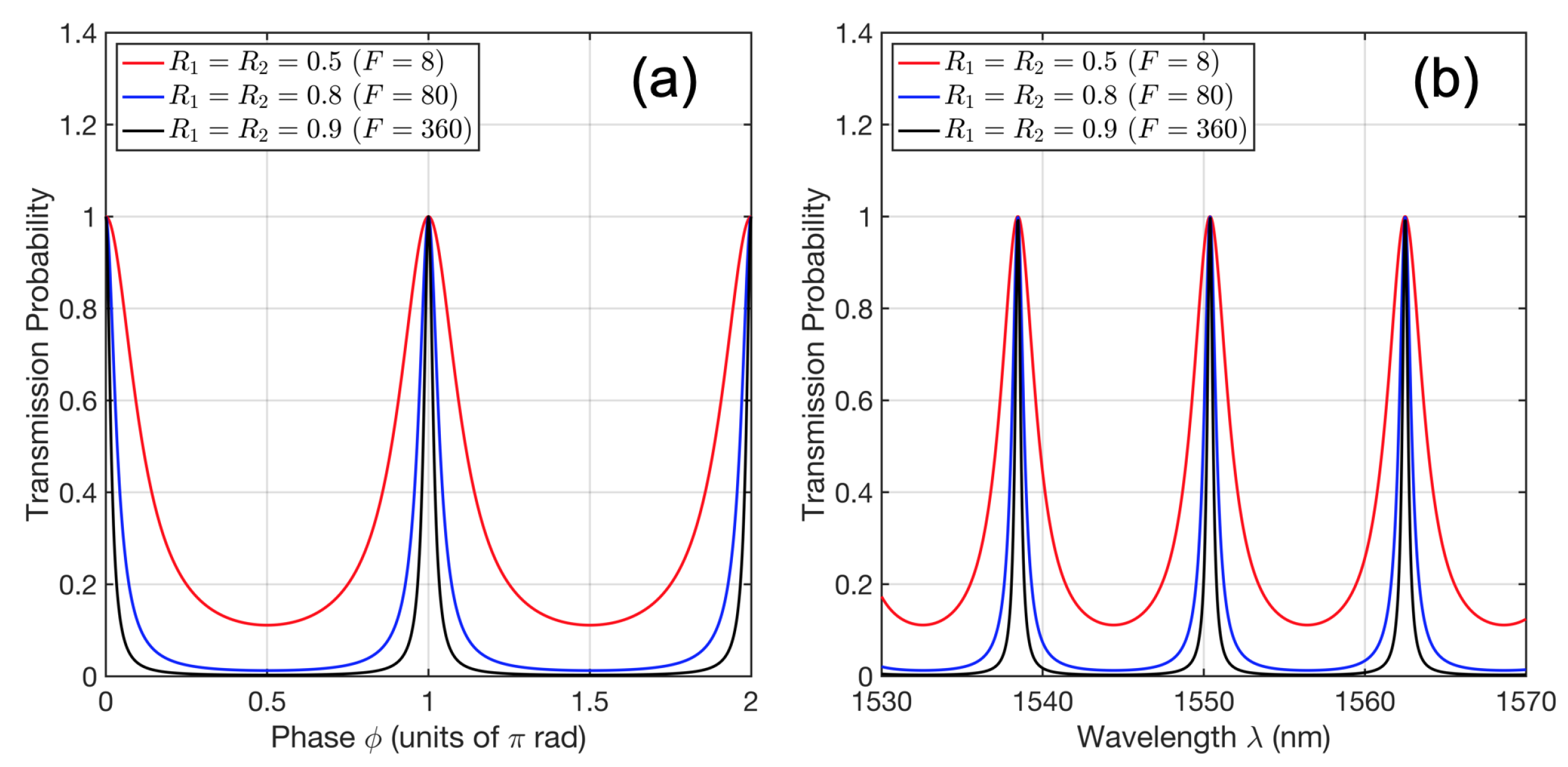
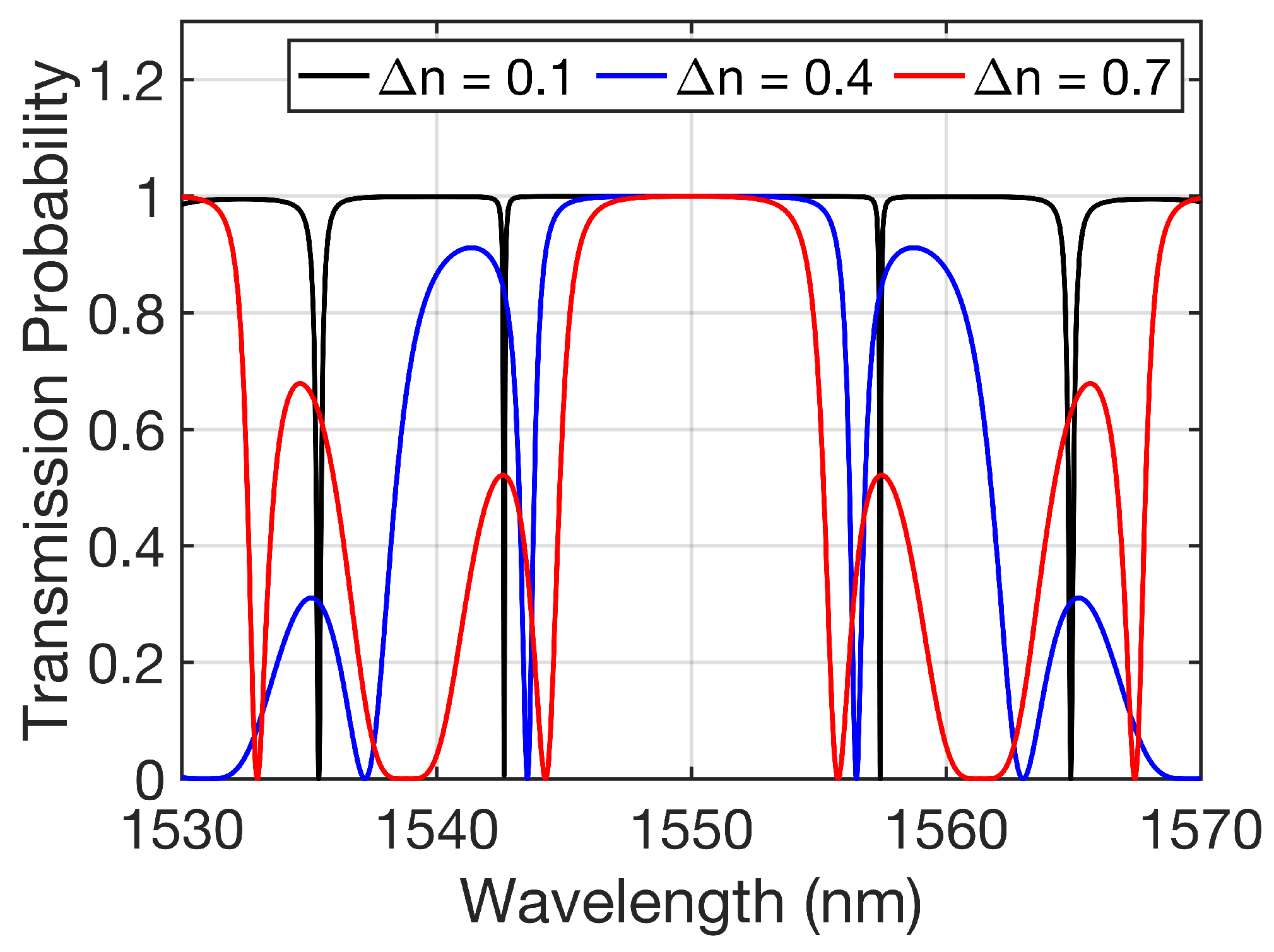
3.3.3. Higher-Dimensional Fabry–Pérot Interferometer
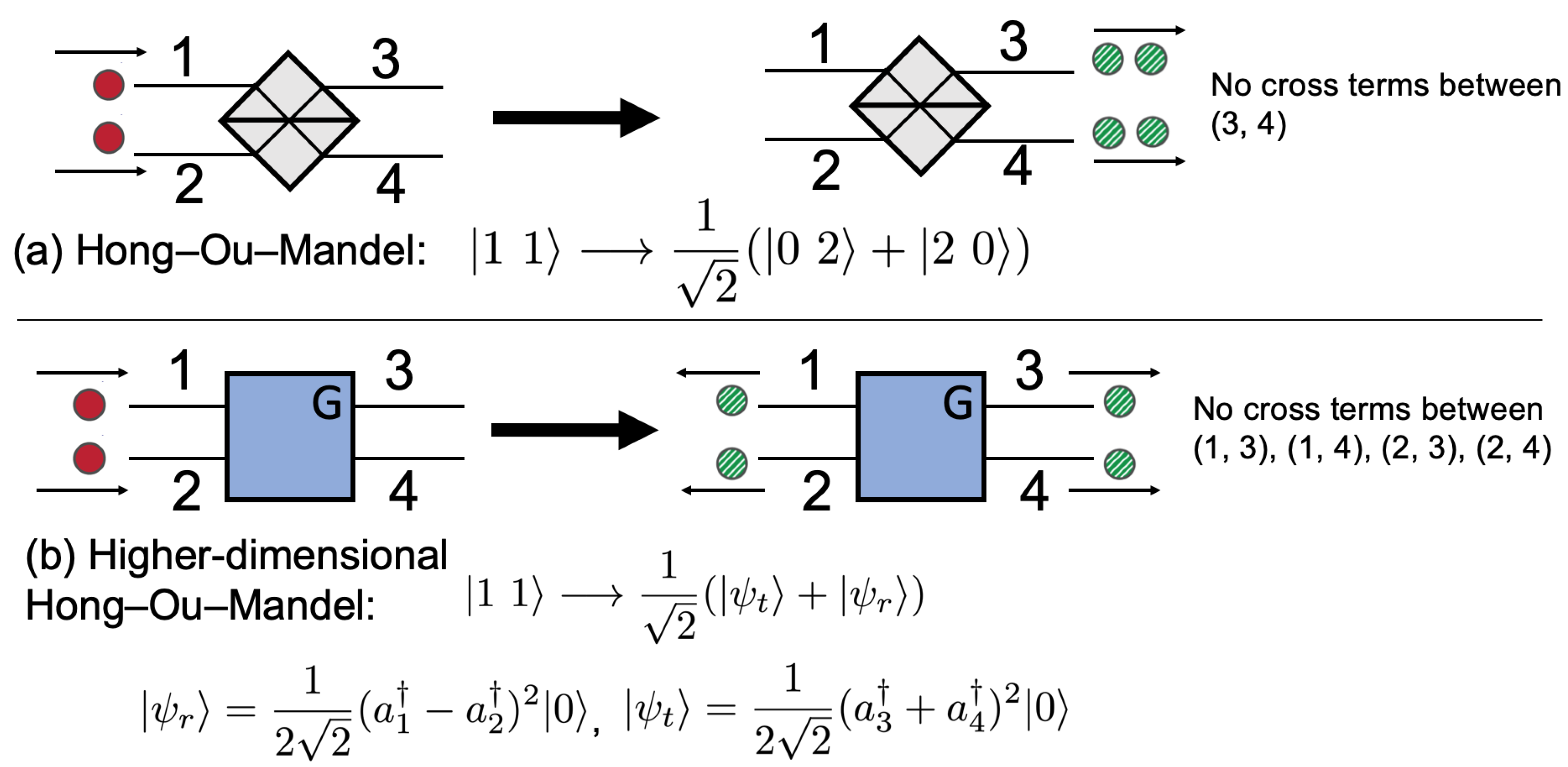
3.4. Hong–Ou–Mandel Two-Photon Interference
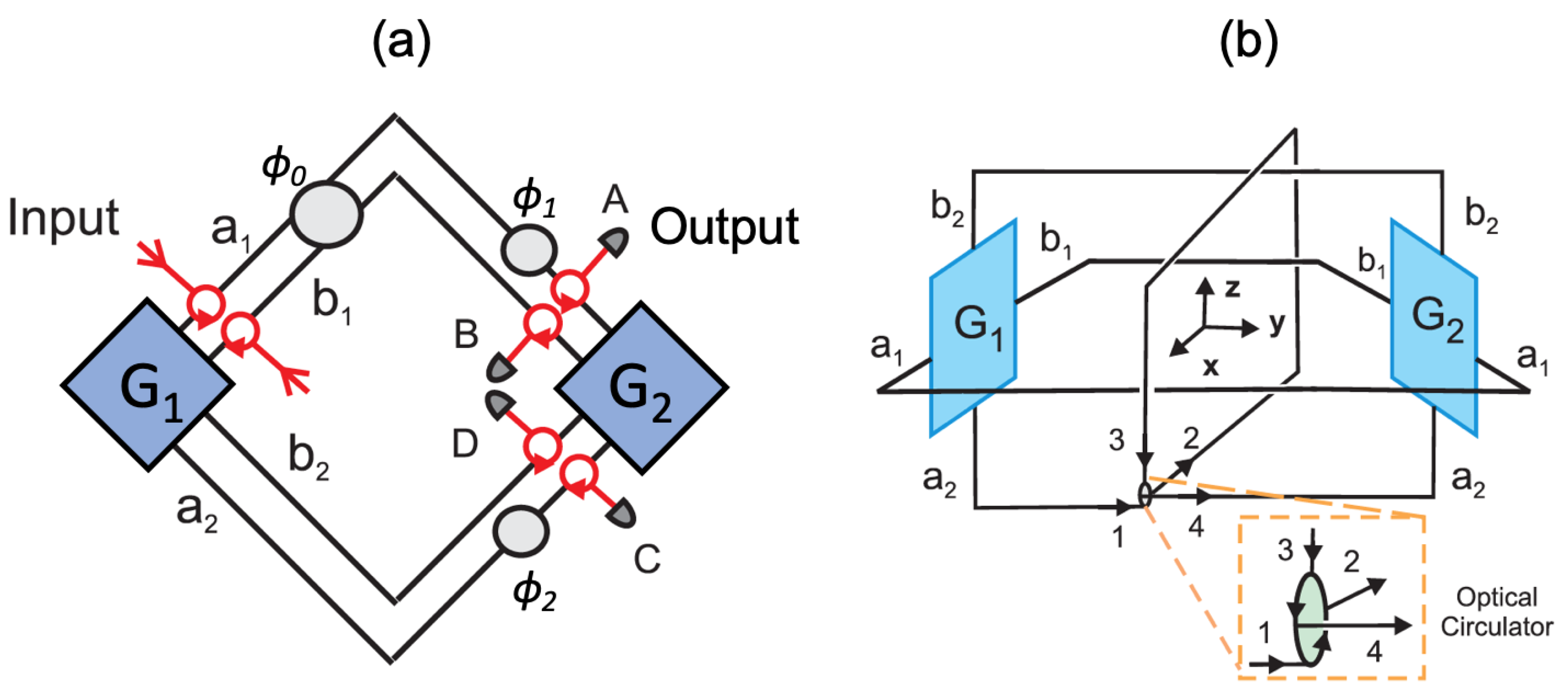
3.5. Two-Photon Grover–Mach–Zehnder Interferometry
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fearn, H.; Loudon, R. Quantum theory of the lossless beam splitter. Opt. Commun. 1987, 64, 485–490. [Google Scholar] [CrossRef]
- Campos, R.A.; Saleh, B.E.A.; Teich, M.C. Quantum-mechanical lossless beam splitter: SU(2) symmetry and photon statistics. Phys. Rev. A 1989, 40, 1371–1384. [Google Scholar] [CrossRef] [PubMed]
- Rubano, A.; Cardano, F.; Piccirillo, B.; Marrucci, L. Q-plate technology: A progress review [Invited]. J. Opt. Soc. Am. B 2019, 36, D70–D87. [Google Scholar] [CrossRef]
- Lim, A.E.J.; Song, J.; Fang, Q.; Li, C.; Tu, X.; Duan, N.; Chen, K.K.; Tern, R.P.C.; Liow, T.Y. Review of Silicon Photonics Foundry Efforts. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 405–416. [Google Scholar] [CrossRef]
- Smith, J.A.; Francis, H.; Navickaite, G.; Strain, M.J. SiN foundry platform for high performance visible light integrated photonics. Opt. Mater. Express 2023, 13, 458–468. [Google Scholar] [CrossRef]
- Simon, D.S.; Fitzpatrick, C.A.; Sergienko, A.V. Group transformations and entangled-state quantum gates with directionally unbiased linear-optical multiports. Phys. Rev. A 2016, 93, 043845. [Google Scholar] [CrossRef]
- Weihs, G.; Reck, M.; Weinfurter, H.; Zeilinger, A. All-fiber three-path Mach–Zehnder interferometer. Opt. Lett. 1996, 21, 302–304. [Google Scholar] [CrossRef]
- Saleh, A.; Kogelnik, H. Reflective single-mode fiber-optic passive star couplers. J. Light. Technol. 1988, 6, 392–398. [Google Scholar] [CrossRef]
- Metcalf, B.J.; Thomas-Peter, N.; Spring, J.B.; Kundys, D.; Broome, M.A.; Humphreys, P.C.; Jin, X.M.; Barbieri, M.; Steven Kolthammer, W.; Gates, J.C.; et al. Multiphoton quantum interference in a multiport integrated photonic device. Nat. Commun. 2013, 4, 1356. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, N.; Vitelli, C.; Aparo, L.; Mataloni, P.; Sciarrino, F.; Crespi, A.; Ramponi, R.; Osellame, R. Three-photon bosonic coalescence in an integrated tritter. Nat. Commun. 2013, 4, 1606. [Google Scholar] [CrossRef]
- Osawa, S.; Simon, D.S.; Sergienko, A.V. Experimental demonstration of a directionally-unbiased linear-optical multiport. Opt. Express 2018, 26, 27201–27211. [Google Scholar] [CrossRef]
- Kim, I.; Lee, D.; Hong, S.; Cho, Y.W.; Lee, K.J.; Kim, Y.S.; Lim, H.T. Implementation of a 3 x 3 directionally-unbiased linear optical multiport. Opt. Express 2021, 29, 29527–29540. [Google Scholar] [CrossRef]
- Schwarze, C.R.; Simon, D.S.; Manni, A.D.; Ndao, A.; Sergienko, A.V. Experimental demonstration of a Grover-Michelson interferometer. Opt. Express 2024, 32, 34116–34127. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys. Rev. Lett. 1997, 79, 325–328. [Google Scholar] [CrossRef]
- Gerrard, A.; Burch, J. Introduction to Matrix Methods in Optics; Dover Books on Physics: Dover, UK, 1994. [Google Scholar]
- Kim, H.; Park, J.; Lee, B. Fourier Modal Method and Its Applications in Computational Nanophotonics; Taylor & Francis: Abingdon, UK, 2012. [Google Scholar]
- Barnett, S.M. On single-photon and classical interference. Phys. Scr. 2022, 97, 114004. [Google Scholar] [CrossRef]
- Guo, C.; Zhao, Z.; Fan, S. Internal transformations and internal symmetries in linear photonic systems. Phys. Rev. A 2022, 105, 023509. [Google Scholar] [CrossRef]
- Deák, L.; Fülöp, T. Reciprocity in quantum, electromagnetic and other wave scattering. Ann. Phys. 2012, 327, 1050–1077. [Google Scholar] [CrossRef]
- Post, E.J. Sagnac Effect. Rev. Mod. Phys. 1967, 39, 475–493. [Google Scholar] [CrossRef]
- Törmä, P.; Stenholm, S.; Jex, I. Hamiltonian theory of symmetric optical network transforms. Phys. Rev. A 1995, 52, 4853–4860. [Google Scholar] [CrossRef] [PubMed]
- Pinter, C. A Book of Abstract Algebra; International series in pure and applied mathematics; McGraw-Hill: Columbus, OH, USA, 1990. [Google Scholar]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Clements, W.R.; Humphreys, P.C.; Metcalf, B.J.; Kolthammer, W.S.; Walmsley, I.A. Optimal design for universal multiport interferometers. Optica 2016, 3, 1460–1465. [Google Scholar] [CrossRef]
- Suzuki, K.; Sharma, V.; Fujimoto, J.G.; Ippen, E.P.; Nasu, Y. Characterization of symmetric 3 x 3 directional couplers fabricated by direct writing with a femtosecond laser oscillator. Opt. Express 2006, 14, 2335–2343. [Google Scholar] [CrossRef]
- Schwarze, C.R.; Manni, A.D.; Simon, D.S.; Sergienko, A.V. Single-photon description of the lossless optical Y coupler. Phys. Rev. A 2024, 110, 023527. [Google Scholar] [CrossRef]
- Kumar, S.P.; Dhand, I. Unitary matrix decompositions for optimal and modular linear optics architectures. J. Phys. Math. Theor. 2021, 54, 045301. [Google Scholar] [CrossRef]
- Yasir, P.A.A.; van Loock, P. Compactifying linear optical unitaries using multiport beamsplitters. arXiv 2025, arXiv:2505.11371. [Google Scholar] [CrossRef]
- Taballione, C.; Anguita, M.C.; de Goede, M.; Venderbosch, P.; Kassenberg, B.; Snijders, H.; Kannan, N.; Vleeshouwers, W.L.; Smith, D.; Epping, J.P.; et al. 20-Mode Universal Quantum Photonic Processor. Quantum 2023, 7, 1071. [Google Scholar] [CrossRef]
- Maring, N.; Fyrillas, A.; Pont, M.; Ivanov, E.; Stepanov, P.; Margaria, N.; Hease, W.; Pishchagin, A.; Lemaître, A.; Sagnes, I.; et al. A versatile single-photon-based quantum computing platform. Nat. Photonics 2024, 18, 603–609. [Google Scholar] [CrossRef]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Schwarze, C.R.; Simon, D.S.; Sergienko, A.V. Enhanced-sensitivity interferometry with phase-sensitive unbiased multiports. Phys. Rev. A 2023, 107, 052615. [Google Scholar] [CrossRef]
- Mizutani, Y.; Horikiri, T.; Matsuoka, L.; Higuchi, Y.; Segawa, E. Implementation of a discrete-time quantum walk with a circulant matrix on a graph by optical polarizing elements. Phys. Rev. A 2022, 106, 022402. [Google Scholar] [CrossRef]
- Childs, A.M. Universal Computation by Quantum Walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef] [PubMed]
- Lovett, N.B.; Cooper, S.; Everitt, M.; Trevers, M.; Kendon, V. Universal quantum computation using the discrete-time quantum walk. Phys. Rev. 2010, 81, 042330. [Google Scholar] [CrossRef]
- Childs, A.M.; Goldstone, J. Spatial search by quantum walk. Phys. Rev. A 2004, 70, 022314. [Google Scholar] [CrossRef]
- Apers, S.; Chakraborty, S.; Novo, L.; Roland, J. Quadratic Speedup for Spatial Search by Continuous-Time Quantum Walk. Phys. Rev. Lett. 2022, 129, 160502. [Google Scholar] [CrossRef]
- Kendon, V.; Maloyer, O. Optimal computation with non-unitary quantum walks. Theor. Comput. Sci. 2008, 394, 187–196. [Google Scholar] [CrossRef]
- Schwarze, C.R.; Simon, D.S.; Manni, A.D.; Ndao, A.; Sergienko, A.V. Finite-element assembly approach of optical quantum walk networks. J. Opt. Soc. Am. B 2024, 41, 1304–1316. [Google Scholar] [CrossRef]
- Redheffer, R. On the Relation of Transmission-Line Theory to Scattering and Transfer. J. Math. Phys. 1962, 41, 1–41. [Google Scholar] [CrossRef]
- Michelson, A.A.; Gale, H.G. The Effect of the Earth’s Rotation on the Velocity of Light. Nature 1925, 115, 566. [Google Scholar] [CrossRef]
- Chow, W.W.; Gea-Banacloche, J.; Pedrotti, L.M.; Sanders, V.E.; Schleich, W.; Scully, M.O. The ring laser gyro. Rev. Mod. Phys. 1985, 57, 61–104. [Google Scholar] [CrossRef]
- Ashtekar, A.; Magnon, A. The Sagnac effect in general relativity. J. Math. Phys. 1975, 16, 341–344. [Google Scholar] [CrossRef]
- Wang, R.; Zheng, Y.; Yao, A. Generalized Sagnac Effect. Phys. Rev. Lett. 2004, 93, 143901. [Google Scholar] [CrossRef]
- Shanavas, T.; Krueper, G.; Zhu, J.; Park, W.; Gopinath, J.T. Nonlinear Symmetry Breaking to Enhance the Sagnac Effect in a Microresonator Gyroscope. arXiv 2025, arXiv:2508.09132. [Google Scholar] [CrossRef]
- Wei, C.P.; Xu, C.G.; Liu, Q. Phase sensitivity of a modified Grover-Michelson interferometer. Opt. Contin. 2025, 4, 1266–1278. [Google Scholar] [CrossRef]
- Schwarze, C.R.; Manni, A.D.; Simon, D.S.; Ndao, A.; Sergienko, A.V. Grover-Sagnac interferometer. J. Opt. Soc. Am. A 2025, 42, 290–297. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044–2046. [Google Scholar] [CrossRef] [PubMed]
- Drago, C.; Brańczyk, A.M. Hong–Ou–Mandel interference: A spectral–temporal analysis. Can. J. Phys. 2024, 102, 411–421. [Google Scholar] [CrossRef]
- Osawa, S.; Simon, D.S.; Sergienko, A.V. Higher-dimensional Hong-Ou-Mandel effect and state redistribution with linear-optical multiports. Phys. Rev. A 2020, 102, 063712. [Google Scholar] [CrossRef]
- Osawa, S.; Simon, D.S.; Malinovsky, V.S.; Sergienko, A.V. Controllable entangled-state distribution in a dual-rail reconfigurable optical network. Phys. Rev. A 2021, 104, 012617. [Google Scholar] [CrossRef]
- Meany, T.; Delanty, M.; Gross, S.; Marshall, G.D.; Steel, M.J.; Withford, M.J. Non-classical interference in integrated 3D multiports. Opt. Express 2012, 20, 26895–26905. [Google Scholar] [CrossRef]
- Tabia, G.N.M. Recursive multiport schemes for implementing quantum algorithms with photonic integrated circuits. Phys. Rev. A 2016, 93, 012323. [Google Scholar] [CrossRef]
- Simon, D.S.; Schwarze, C.R.; Sergienko, A.V. Interferometry and higher-dimensional phase measurements using directionally unbiased linear optics. Phys. Rev. A 2022, 106, 033706. [Google Scholar] [CrossRef]
- Guo, C.; Miller, D.A.B.; Fan, S. Unitary control of multiport wave transmission. Phys. Rev. A 2025, 111, 023507. [Google Scholar] [CrossRef]
- Guo, C.; Fan, S. Unitary control of partially coherent waves. I. Absorption. Phys. Rev. B 2024, 110, 035430. [Google Scholar] [CrossRef]
- Guo, C.; Fan, S. Unitary control of partially coherent waves. II. Transmission or reflection. Phys. Rev. B 2024, 110, 035431. [Google Scholar] [CrossRef]
- Ma, W.; Pestourie, R.; Johnson, S.G. Time-reversal-symmetry bounds on electromagnetic fields. Phys. Rev. A 2025, 111, 063518. [Google Scholar] [CrossRef]
- Guo, C.; Fan, S. Reciprocity Constraints on Reflection. Phys. Rev. Lett. 2022, 128, 256101. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chen, J.; Wang, Y.; Yuan, Z.; Huang, C.; Sun, J.; Feng, C.; Li, M.; Qiu, K.; Zhu, S.; et al. Tbps wide-field parallel optical wireless communications based on a metasurface beam splitter. Nat. Commun. 2024, 15, 7744. [Google Scholar] [CrossRef] [PubMed]
- Hemayat, S.; Hsu, L.; Ha, J.; Ndao, A. Near-unity uniformity and efficiency broadband meta-beam-splitter/combiner. Opt. Express 2023, 31, 3984–3997. [Google Scholar] [CrossRef]
- Shen, Z.; Huang, D. A Review on Metasurface Beam Splitters. Nanomanufacturing 2022, 2, 194–228. [Google Scholar] [CrossRef]
- Pei, X.Z.; Bao, L.; Wang, Q.H.; Wu, B.; Fu, P.; Zhou, H.J.; Deng, J.; Ni, P.N.; Kan, Q.; Chen, P.P.; et al. On-chip Integration of Metasurface-Based Beam Splitter with Variable Split Ratio. Laser Photonics Rev. 2025, 19, 2500140. [Google Scholar] [CrossRef]
- Park, J.; Yang, Y.; Park, Y.; Kang, H.; Shin, J.; Keawmuang, H.; Kim, W.S.; Badloe, T.; Kim, Y.K.; Rho, J. Electrically Tunable Metasurfaces for Broadband Beam Splitting Across the Visible Spectrum. Adv. Opt. Mater. 2025, 13, 2403413. [Google Scholar] [CrossRef]
- Soldano, L.; Pennings, E. Optical multi-mode interference devices based on self-imaging: Principles and applications. J. Light. Technol. 1995, 13, 615–627. [Google Scholar] [CrossRef]
- Heaton, J.; Jenkins, R. General matrix theory of self-imaging in multimode interference (MMI) couplers. IEEE Photonics Technol. Lett. 1999, 11, 212–214. [Google Scholar] [CrossRef]
- Pennings, E.; van Roijen, R.; van Stralen, M.; de Waard, P.; Koumans, R.; Verbeck, B. Reflection properties of multimode interference devices. IEEE Photonics Technol. Lett. 1994, 6, 715–718. [Google Scholar] [CrossRef]
- Maese-Novo, A.; Halir, R.; Romero-García, S.; Pérez-Galacho, D.; Zavargo-Peche, L.; Ortega-Moñux, A.; Molina-Fernández, I.; Wangüemert-Pérez, J.G.; Cheben, P. Wavelength independent multimode interference coupler. Opt. Express 2013, 21, 7033–7040. [Google Scholar] [CrossRef]
- Bachmann, M.; Besse, P.A.; Melchior, H. General self-imaging properties in N × N multimode interference couplers including phase relations. Appl. Opt. 1994, 33, 3905–3911. [Google Scholar] [CrossRef] [PubMed]
- Cooney, K.; Peters, F.H. Analysis of multimode interferometers. Opt. Express 2016, 24, 22481–22515. [Google Scholar] [CrossRef] [PubMed]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef]
- Kang, C.; Park, C.; Lee, M.; Kang, J.; Jang, M.S.; Chung, H. Large-scale photonic inverse design: Computational challenges and breakthroughs. Nanophotonics 2024, 13, 3765–3792. [Google Scholar] [CrossRef]
- Huang, S.Y.; Kumar, S.; Huster, J.; Augenstein, Y.; Rockstuhl, C.; Barz, S. Multiphoton Quantum Interference at Ultracompact Inverse-Designed Multiport Beam Splitter. arXiv 2025, arXiv:2504.00114. [Google Scholar] [CrossRef]
- De Carlo, M.; De Leonardis, F.; Soref, R.A.; Colatorti, L.; Passaro, V.M.N. Non-Hermitian Sensing in Photonics and Electronics: A Review. Sensors 2022, 22, 3977. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, H.; Gupta, S.K.; Zhang, H.; Xie, B.; Lu, M.; Chen, Y. Photonic non-Hermitian skin effect and non-Bloch bulk-boundary correspondence. Phys. Rev. Res. 2020, 2, 013280. [Google Scholar] [CrossRef]
- Yan, Q.; Zhao, B.; Zhou, R.; Ma, R.; Lyu, Q.; Chu, S.; Hu, X.; Gong, Q. Advances and applications on non-Hermitian topological photonics. Nanophotonics 2023, 12, 2247–2271. [Google Scholar] [CrossRef]
- Parto, M.; Liu, Y.G.N.; Bahari, B.; Khajavikhan, M.; Christodoulides, D.N. Non-Hermitian and topological photonics: Optics at an exceptional point. Nanophotonics 2021, 10, 403–423. [Google Scholar] [CrossRef]
- Longhi, S.; Gatti, D.; Valle, G.D. Robust light transport in non-Hermitian photonic lattices. Sci. Rep. 2015, 5, 13376. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Wei, H.; Cotrufo, M.; Chen, W.; Mann, S.; Ni, X.; Xu, B.; Chen, J.; Wang, J.; Fan, S.; et al. Exceptional points and non-Hermitian photonics at the nanoscale. Nat. Nanotechnol. 2023, 18, 706–720. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwarze, C.R.; Manni, A.D.; Simon, D.S.; Ndao, A.; Sergienko, A.V. Next-Generation Interferometry with Gauge-Invariant Linear Optical Scatterers. Metrology 2025, 5, 65. https://doi.org/10.3390/metrology5040065
Schwarze CR, Manni AD, Simon DS, Ndao A, Sergienko AV. Next-Generation Interferometry with Gauge-Invariant Linear Optical Scatterers. Metrology. 2025; 5(4):65. https://doi.org/10.3390/metrology5040065
Chicago/Turabian StyleSchwarze, Christopher R., Anthony D. Manni, David S. Simon, Abdoulaye Ndao, and Alexander V. Sergienko. 2025. "Next-Generation Interferometry with Gauge-Invariant Linear Optical Scatterers" Metrology 5, no. 4: 65. https://doi.org/10.3390/metrology5040065
APA StyleSchwarze, C. R., Manni, A. D., Simon, D. S., Ndao, A., & Sergienko, A. V. (2025). Next-Generation Interferometry with Gauge-Invariant Linear Optical Scatterers. Metrology, 5(4), 65. https://doi.org/10.3390/metrology5040065







