Abstract
Optical fringe projection is an outstanding technology that significantly enhances three-dimensional (3D) metrology in numerous applications in science and engineering. Although the complexity of fringe projection systems may be overwhelming, current scientific advances bring improved models and methods that simplify the design and calibration of these systems, making 3D metrology less complicated. This paper provides an overview of the fundamentals of fringe projection profilometry, including imaging, stereo systems, phase demodulation, triangulation, and calibration. Some applications are described to highlight the usefulness and accuracy of modern optical fringe projection profilometers, impacting 3D metrology in different fields of science and engineering.
1. Introduction
Optical fringe projection is an essential technology driving important applications in science, engineering, medicine, entertainment, and many other fields [1,2,3]. The effectiveness of this technology stems from several valuable features, including contactless operation, high accuracy, high resolution, and easy-to-operate equipment [4,5]. Moreover, modern digital cameras, projectors, and high-performance embedded computers enable fringe projection systems to operate at high rates [6,7], allowing the sensing of fast shape changes in dynamic phenomena [8,9]. The development of portable profilometers [10,11] has expanded the usefulness of fringe projection systems for in situ studies in archaeological [12] and forensic applications [13].
Despite progress in hardware and theoretical models, fringe projection profilometry remains an active research area within the scientific community worldwide [14,15]. Researchers are working to overcome new challenges in fringe projection technology [16]. Current investigations include miniaturization of electronic devices [17], multi-dimensional information sensing [18], multimodal imaging [19,20], self-calibration [21,22,23], motion-induced error suppression [24,25,26,27], setup optimization for full-view object reconstruction [28,29,30,31], dynamic range improvement for reconstructing reflective objects [32,33], and enabling automatic and adaptive operation [34,35,36]. For this reason, the specialization of students and professionals in this research area is crucial.
The research on fringe projection profilometry has produced extensive results in optical designs, mathematical models, data processing algorithms, and calibration methods [37,38,39]. Inexperienced readers may feel overwhelmed by the abundance of specialized literature in books and scientific articles available today [40,41,42,43]. Frustrating months of reading literature could pass without acquiring enough background to construct and operate an optical fringe projection profilometer. Given this situation, this paper aims to provide the fundamental knowledge for setting up and operating a fringe projection system, offering practical learning for engaging effectively with specialized literature and research projects.
In this paper, a concise overview of representative optical fringe projection techniques for 3D metrology is provided in Section 2. Then, the five constituent blocks comprising a fringe projection system are examined in Section 3. Next, essential concepts and helpful insights into the working principles of optical fringe projection are presented in Section 4, Section 5 and Section 6. Illustrative applications where this technology has been implemented are described in Section 7. The concluding remarks for this review are provided in Section 8. This study offers a concise guide through the fundamentals of fringe projection profilometry, making this technology a straightforward tool for driving 3D metrology toward new frontiers.
2. Fringe Projection Profilometry
Fringe projection profilometry has evolved from optical testing techniques that utilize lasers and other light sources [44,45], along with gratings and other reference masks [46,47], designed to capture the topography of surfaces and optical wavefronts [48,49]. Currently, fringe projection refers to numerous 3D reconstruction techniques that have emerged from diverse fringe-pattern analysis methods and the numerous options available for producing high-quality gratings, as outlined below.
A typical fringe projection profilometer is an apparatus comprising three elements: a camera, a projector, and a computer, as shown in Figure 1a. The operation of a fringe projection profilometer can be described in simple terms as follows. First, the projector illuminates the object being tested with straight fringes, as shown in Figure 1b. The shape of the object alters the straightness of the displayed fringes. Then, the camera captures one or more images of the deformed fringes, as shown in Figure 1c. Finally, the computer analyzes the captured fringe patterns to determine the object’s shape and returns a 3D point cloud, as shown in Figure 1d. The fringe patterns used for shape extraction are two-dimensional sinusoidal signals characterized by the following [50,51]:
- A bias term (background light);
- Fringe amplitude;
- A fringe phase map.

Figure 1.
(a) Typical fringe projection profilometer setup. (b) Grating with straight fringes sent to the projector as a slide to illuminate the object being tested. (c) Fringe pattern captured by the camera, observing fringes deformed by the object. (d) Resulting 3D point cloud reconstruction.
The deformation from straight to curved fringes corresponds to an alteration in the fringe phase. Therefore, shape extraction is performed through a phase-demodulation process [52]. It is worth mentioning that typical noise sources (e.g., variations in object color and ambient light) affect the bias and amplitude of fringe patterns but have a negligible effect on the phase (curvature of the fringes). Consequently, the phase-based shape extraction approach makes fringe projection profilometry a robust and accurate tool for optical 3D metrology.
Moiré topography (MT) is considered a predecessor of modern fringe projection profilometry techniques [53]. MT produces fringe patterns that are directly related to depth/height contour maps [54,55], as depicted in Figure 2a,b. However, depressions and elevations (hills and valleys) cannot be distinguished [56], as shown in Figure 2c–f. In contrast, Fourier transform profilometry (FTP) employs a carrier frequency to automatically distinguish between surface depressions and elevations [57], as shown in Figure 2g–i. This technique enables real-time applications by requiring only a single fringe pattern for phase demodulation using the Fourier transform method [58]. However, its usability depends on satisfying the continuous surface condition (object surfaces without holes or steps). Unlike FTP, which carries out a filtering process in the frequency domain, alternative techniques such as spatial phase detection (SPD) [59], phase-locked loop profilometry [60], and regularized filters [61] apply the filtering process in the spatial domain [62]. However, the performance of the FTP and SPD techniques depends significantly on the user’s ability to design and tune the filters correctly [63].
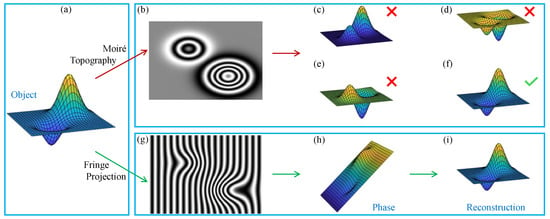
Figure 2.
Object reconstruction using Moiré topography and Fourier transform profilometry. (a) Object to be recovered. (b) Moiré pattern. (c–f) Possible reconstructions from the given Moiré pattern. (g) Fourier fringe pattern. (h) Demodulated phase with carrier. (i) Reconstructed object.
Phase-shifting profilometry (PSP) successfully avoids the surface continuity constraint [64,65]. Moreover, this technique achieves maximum spatial resolution and robustness by processing multiple fringe patterns using the phase-shifting method [66]. However, the need for multiple fringe patterns makes PSP challenging to implement in real-time applications. Several approaches have been proposed to combine the advantages of FTP and PSP, such as -shifted FTP [67] and multi-demodulation phase-shifting [68]. However, a trade-off must be established between the advantages of FTP and PSP for each specific application. Other approaches have been developed to enhance the original FTP and PSP techniques, including windowed FTP [69], fringe-normalized FTP [70], two-step phase-shifting [71,72], and phase-differencing profilometry [73]. However, their implementation is more complex and requires greater computational resources [74].
Alternatively, modulation measurement profilometry (MMP) differs from the previous methods in that the object shape is obtained from the fringe amplitude rather than the phase [75]. This technique exploits the defocus that occurs when observed points move away from the focal plane. The defocus level is estimated through the fringe amplitude, which decreases as the defocus increases. Then, the depth/height is quantified as a function of the defocus. An additional advantage of MMP is that shadows and occlusions are absent because the camera and projector are arranged to share the same optical axis [76]. However, MMP (amplitude-based) is more sensitive to external noise sources than FTP and PSP (phase-based) techniques.
Fringe projection techniques also differ in the hardware and methods used to generate straight fringes for illuminating the test object [77,78], as well as the implemented fringe analysis approach [79,80], which is discussed in Section 3. Complementary surveys about the different fringe projection techniques can be found in [81,82,83]. For a more comprehensive study of fringe projection profilometry, the reader is referred to [84,85,86]. The rest of this paper reviews the fundamental concepts of setting up and operating a fringe projection profilometer.
3. Fringe Projection System
The operation of an optical fringe projection profilometer can be analyzed through its five main components, as depicted in Figure 3. The following subsections provide a brief description of each of these components.
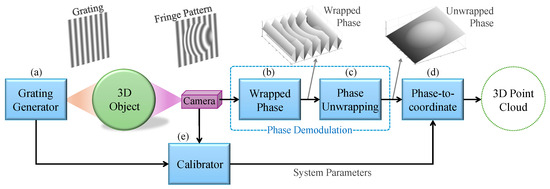
Figure 3.
Main components of an optical fringe projection system: (a) grating generator, (b) wrapped phase extraction, (c) phase unwrapping, (d) phase-to-coordinate conversion, and (e) calibrator.
3.1. Grating Generator
The primary component of an optical fringe projection system is the grating generator [87], as shown in Figure 3a. This component illuminates the object being examined with two-dimensional (2D) cosine signals called gratings. The grating generator can control the properties of gratings, such as the phase shift, frequency, and angle [88,89], as well as the properties of the light source, including the wavelength (color) [90,91,92], intensity [93], and polarization [94]. As a result, the camera captures one or more 2D cosine signals known as fringe patterns, which are deformed by the shape of the object being examined.
A grating generator can be constructed using interferometric techniques [95,96,97]. Although interferometers produce high-quality gratings [98], the equipment is expensive, difficult to use, and sensitive to environmental perturbations [99,100]. Other alternatives to set up grating generators are the Moiré effect [101,102], defocused rulings [103,104,105], pulse-width modulation (PWM) [106], colored PWM [107], color-encoded projection [108,109], binary dithering [110], filled binary sinusoidal patterns [111], linear light-emitting diode array [112], and rotating slides [113,114,115]. The advent of digital projectors has simplified the grating generator component to a compact electronic unit [116]. Digital projectors allow easy and precise control of important grating properties such as the phase shift, frequency, and color. Additionally, the polarized light emitted by liquid crystal display-based projectors can be exploited to reconstruct shiny objects such as metallic workpieces and ceramic pottery [117,118]. As discussed in a recent study, the optical fringe projection technique that uses a computer-controlled projector is known as digital fringe projection [119].
3.2. Wrapped Phase Extraction
Optical fringe projection systems encode 3D shapes in the phase of the captured fringe patterns. For this reason, the phase recovery process, known as phase demodulation, is essential [52]. In practice, phase demodulation is performed through two components: wrapped phase extraction and phase unwrapping. Wrapped phase extraction requires one or more fringe patterns and returns a wrapped phase map, as shown in Figure 3b. Depending on the number of fringe patterns available, wrapped phase extraction can be performed using either the spatial or temporal approach [120].
3.2.1. Spatial Wrapped Phase Extraction and Fourier Fringe Analysis
Spatial wrapped phase extraction methods operate with a single fringe pattern [121]. In general terms, the phase at any pixel of the fringe pattern is computed based on the information from neighboring pixels, as depicted in Figure 4a. The most common approach consists of applying the Fourier transform to the given fringe pattern and exploiting the fact that the spectrum of the encoded phase is isolated around the carrier frequency, distinguishing it from other spectra in the Fourier domain [58]. A filter is used to isolate the spectrum of interest, and the required phase is recovered by applying the inverse Fourier transform [122]. This approach is known as Fourier fringe analysis [123]. Other spatial methods include the windowed Fourier transform [69], wavelet transform [124,125], Hilbert transform [126,127], and S-transform [128].
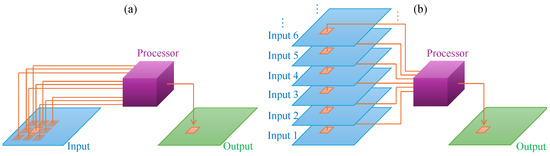
Figure 4.
(a) Spatial processing approach. (b) Temporal processing approach.
The primary advantage of Fourier fringe analysis is the requirement of a single fringe pattern, allowing straightforward implementation in real-time applications [129,130]. However, the fringe pattern must meet certain restrictive conditions for effective spectrum isolation, namely a high carrier frequency and continuity of the encoded phase [131]. Additionally, spatial methods can be computationally demanding [132], and the filtering might yield unsatisfactory results if the fringe pattern is affected by shadows from objects with intricate shapes.
3.2.2. Temporal Wrapped Phase Extraction (Phase-Shifting)
In contrast to using a single fringe pattern with a high carrier frequency, temporal wrapped phase extraction uses three or more fringe patterns with different phase shifts [133]. This approach, known as phase-shifting, computes the phase at each pixel by processing that pixel across all the available fringe patterns, as depicted in Figure 4b. Initially, this approach was difficult to implement due to the need for precise phase-shift control [134,135]. Digital projectors have mitigated the challenges of phase-shift control, leading to the widespread implementation of phase-shifting algorithms.
Several phase-shifting algorithms have been proposed, differing mainly in whether the phase shifts are known or unknown and how the phase shifts are distributed [136]. For instance, generalized phase-shifting algorithms are useful when the phase-shift values are unknown because they include a phase-shift estimation module [137,138,139]. If the phase shifts are known but their distribution is irregular, then the phase-shift least-squares algorithm can be applied [140,141]. Furthermore, if the phase shifts are distributed homogeneously, the so-called n-step method can be applied, which is computationally efficient [66].
3.3. Phase Unwrapping
The phase-unwrapping component receives one or more wrapped phase maps and returns the resulting unwrapped phase, as shown in Figure 3c. This component aims to remove the discontinuities caused by the periodicity of trigonometric functions and restore the continuity associated with the object shape [142,143]. Like the previous component, phase unwrapping can be performed using either the spatial or temporal approach.
3.3.1. Spatial Phase Unwrapping
In essence, spatial phase-unwrapping algorithms work by applying an identity operation. Specifically, the wrapped phase map is derived and then integrated, returning the initial phase without discontinuities [144,145,146]. Depending on how the integration is carried out, spatial phase-unwrapping algorithms are classified as either path-following or path-independent. Since wrapped phase maps are 2D functions, there are infinite paths that the integration process can follow. Accordingly, path-following algorithms are designed to identify the best integration path by detecting and avoiding noisy pixels [147,148,149]. Although path-following algorithms are simple to implement and computationally efficient, they can be quite sensitive to noise [150]. Alternatively, path-independent phase-unwrapping algorithms perform the integration by solving a global optimization problem [151,152,153], removing the need to specify a particular integration path. Although path-independent algorithms are robust to noise, they consume more computational resources. The requirement for a single wrapped phase map is convenient for real-time applications. However, the implementation of spatial algorithms in optical fringe projection is limited because they cannot preserve discontinuities in the object shape [154]. Nevertheless, spatial phase unwrapping is helpful for applications involving objects with continuous surfaces.
3.3.2. Temporal Phase Unwrapping and Multi-Frequency Approach
Instead of processing a single wrapped phase map, temporal phase unwrapping uses complementary images such as gray-coded binary sequences (intensity-based) [155,156,157,158] or additional wrapped phase maps (phase-based) [159,160,161]. Since typical noise sources have a greater impact on image intensity than on the phase of fringe patterns, phase-based temporal phase-unwrapping methods are generally preferred. In particular, the multi-frequency approach uses two or more wrapped phase maps obtained by projecting gratings with different frequencies. This approach relies on the fact that low-frequency wrapped phase maps have fewer synthetic discontinuities [162,163]. This observation forms the basis of the so-called heterodyne [164,165,166] and hierarchical [167,168,169] techniques. Heterodyne multi-frequency phase unwrapping exploits the beat phenomenon, which produces a low-frequency wave by superposing two high-frequency waves. Thus, heterodyne techniques can work exclusively with high-frequency wrapped phase maps. This feature is useful when the grating generator is an interferometer, as low-frequency gratings can be difficult to control. However, the unwrapped phase may contain distortion due to the phase synthesis process. On the other hand, hierarchical multi-frequency phase unwrapping uses both low- and high-frequency wrapped phase maps, overcoming the distortion issues encountered in the phase synthesis process [170].
3.4. Phase-to-Coordinate Conversion
Although the demodulated phase is closely related to the object topography, the phase (in radians) must be converted to spatial information (in length units) [171], as shown in Figure 3d. Earlier proposals were designed assuming particular configurations [172]; for instance, parallel optical axes [173] or orthographic illumination/capture using telecentric lenses [174]. In these systems, the phase encodes only the object’s height (z-coordinate), thus leading to the development of phase-to-height conversion methods [175,176,177,178]. However, in more versatile profilometers, the phase also contains information about the coordinates [179,180]; for instance, when the camera and projector are arranged arbitrarily [181,182], divergent illumination/capture is used [183], and the lenses introduce nonlinear distortion [184,185,186]. These flexible systems require the implementation of generalized phase-to-coordinate conversion methods [187,188].
Simple phase-to-coordinate algorithms can be developed by alleviating system parameter requirements through specific setup designs [57,189]. For instance, closed-form expressions can be derived assuming the optical elements are aligned on-axis [190], are parallel [191], or use a camera/projector with telecentric lenses [174,192,193]. Furthermore, knowing one or more points on the object can substitute for some of the system parameters [194]. However, the resulting phase-to-coordinate algorithms impose strict operating conditions, limiting their practical application. Alternatively, when the system parameters are available, generalized phase-to-coordinate algorithms can be designed using the triangulation principle [195]. Triangulation-based algorithms support multiple devices, even if they are misaligned or have lens distortion.
3.5. System Calibration
Since the calibrator component is inactive during a 3D reconstruction experiment [196], it is often underestimated and even excluded. Nonetheless, the contribution of this component is essential for producing metric object reconstructions [197,198,199], as shown in Figure 3e. The process by which a fringe projection system registers 3D shapes involves a complicated phase-encoding mechanism regulated by system parameters [200]. However, even with the complexity of the phase encoding, clever strategies can be employed to obtain the system parameters in a practical manner [201,202,203]. Assuming the fringe projection system consists of a camera–projector pair [204,205,206], the camera and projector can be calibrated independently [207]. Although this approach is simple, the experimental work is time-consuming and inaccurate. In contrast, with the advent of modern camera–projector calibration methods [208,209,210], experimental work has been substantially simplified, resulting in higher accuracy levels [211,212,213].
3.6. Miscellaneous
The performance of fringe projection techniques depends significantly on the assumption that gratings and fringe patterns have ideal cosine profiles [214,215,216]. However, consumer cameras and projectors often exhibit a nonlinear intensity response [217,218,219], resulting in gamma distortion [220,221,222,223], as illustrated in Figure 5. To address this issue, advanced methods have been proposed for processing distorted fringe patterns [224,225,226,227,228,229]. Moreover, a recommended approach involves preventing distortion by complementing the calibrator component with a gamma value estimator and pre-distorting the generated gratings accordingly [230,231].
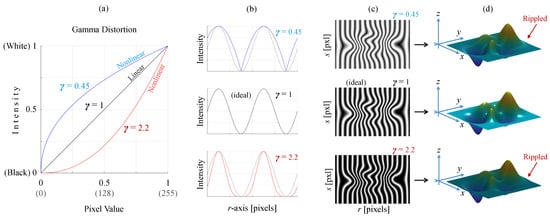
Figure 5.
(a) Intensity response of cameras or projectors for different gamma values. (b) Sine profiles generated using three gamma values. (c) Fringe patterns simulated using three values of gamma. (d) Effect of gamma distortion on the reconstructed object.
Color cameras and projectors also exhibit crosstalk and grayscale imbalance issues [232,233]. These imperfections reduce the accuracy of fringe projection systems that use color multiplexing [234]. Special attention is essential for high-quality reconstructions with color-based profilometer systems [235,236,237,238]. It is important to note that the projector’s brightness and the camera’s exposure time are also important parameters when working with shiny objects [239]. For these challenging applications, particular strategies must be implemented to avoid saturated or underexposed fringe patterns [240,241].
3.7. Hierarchical Multi-Frequency Phase-Shifting Fringe Projection
This section concludes by highlighting the abundant literature on fringe projection systems available nowadays [242,243,244,245]. This review aims to be more panoramic than exhaustive, serving as a starting point for readers interested in studying optical fringe projection systems [246,247,248]. To this end, we provide valuable insights and tools, offering the reader elemental knowledge to construct and operate an optical fringe projection profilometer. This learning-by-doing approach utilizes a simple yet powerful system in which a digital projector serves as the grating generator, phase-shifting and hierarchical multi-frequency methods are implemented for phase demodulation, a triangulation-based algorithm is employed for phase-to-coordinate conversion, and the system parameters are estimated using the camera–projector calibration method. The following sections provide a comprehensive analysis of the recommended hierarchical multi-frequency phase-shifting fringe projection system.
4. Theoretical Preliminaries
4.1. Camera Imaging
A digital camera is a sophisticated device consisting mainly of a compound lens and a photosensitive sensor [249]. Cameras are designed to collect light rays traveling from the 3D space and record their intensities. The resulting intensity map is the camera output, known as the image. Although the physical imaging process is a complicated phenomenon, it can be modeled with good approximation using the pinhole model [250,251]. Let be the vector of a point in the 3D space, and let be the pixel where was registered by the camera, as shown in Figure 6a. Considering the pinhole model, the vectors and are related as follows:
where is the homogeneous coordinate operator [252], denotes the inverse, and
is a matrix, known as the camera matrix. K is the intrinsic parameter matrix (non-singular upper triangular), R is a rotation matrix defining the camera orientation, denotes the transpose, and is a translation vector specifying the camera position.
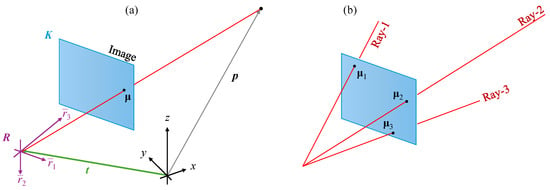
Figure 6.
(a) Camera pinhole model with the intrinsic parameters given by the upper-triangular matrix K and the extrinsic parameters (pose) consisting of the rotation matrix R and the translation vector . (b) Every image pixel is associated with a light ray from the 3D space with a unique direction.
4.2. Cameras as Direction Sensors
Although digital cameras are well-known for their ability to capture photographs, optical fringe projection systems employ cameras for an additional purpose. Note that a digital image is an array of pixels, and each pixel detects a light ray coming from the 3D space in a specific direction, as shown in Figure 6b. Thus, every pixel is associated with a particular light ray with a unique direction. In this context, a helpful insight is that cameras are direction sensors [187]. A more formal analysis is performed by reversing the imaging process to return a space point when the pixel is given. For this, Equations (1) and (2) can be rewritten as
where is an arbitrary real-valued variable. After a few algebraic manipulations of Equation (3), the following equation is reached:
which describes a line in the 3D space passing through the camera position , with the direction determined by the pixel as
4.3. Stereo Camera Systems and Triangulation
How can direction sensors be employed for 3D metrology? Consider two cameras forming a stereo system capturing an object from two different viewpoints, as shown in Figure 7a. Let us assume that the parameters of both cameras are known, say , , and for the first camera, and , , and for the second camera. Let be a point on the object surface captured by the two cameras at the pixels and , respectively. The lines representing the captured light rays can be reproduced using the available camera parameters and the given pixel points, as shown in Figure 7b, namely
This reasoning leads to computing the captured point as the intersection of Line-1 and Line-2. This computation is generically known as triangulation, although more general constructions for determining points are also possible, such as the intersection of multiple lines, planes, and other geometrical objects, even in combinations [195].
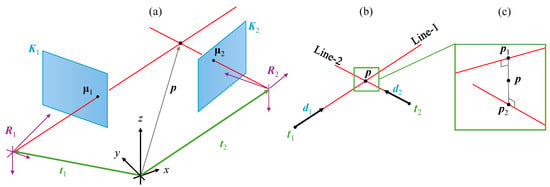
Figure 7.
(a) Two cameras capturing a point from different viewpoints. (b) The captured point is determined as the intersection of the lines defined by and . (c) Experimental noise may cause skewed lines; therefore, is determined as the mean point between the solution points and .
In particular, triangulation in a stereo system can be performed as follows. Since represents a common point of the intersecting lines, then Equations (6) and (7) can be equated as , which can be solved for the unknowns and using the least-squares method as
where is the regression matrix. The computed values of and allow determining the vector of the captured point using Equation (6) or using Equation (7). Ideally, and are equal due to the intersection assumption. Nevertheless, slight deviations caused by experimental errors may result in skewed lines, as shown in Figure 7c. For this reason, the vector is defined as the average , i.e.,
4.4. The Corresponding Point Problem
It is noteworthy that a 3D reconstruction requires the pair of pixels and where the captured point was imaged (see Figure 7). The pixels and , related by a common point , are known as a corresponding point pair, which is denoted by
Obtaining corresponding points is a challenging task because it depends on the object’s texture [253,254]. For example, no corresponding points can be established from a white object on a white background under homogeneous illumination because of the lack of feature points [255]. Even for objects with abundant texture, such as the human face in biometric applications, the resolution is low because more than one pixel is required to detect a feature, and not all image regions contain reliable features. As a result, stereo camera systems tend to produce low-resolution 3D reconstructions, and their accuracy depends on the texture of the object under study.
4.5. Equivalence Between Cameras and Projectors
Physically, the difference between a camera and a projector is that the light rays propagate in opposite directions, as shown in Figure 8. While a camera captures light rays traveling from space to its image pixels, a projector emits light rays from its slide pixels to space. However, if the sign of the direction vector of the light rays is omitted, cameras and projectors are identical. For this reason, cameras and projectors are mathematically equivalent, and both can be described by the pinhole model given in Equation (1). Therefore, in addition to cameras being direction sensors, another valuable insight is that projectors are direction-controlled ray generators.
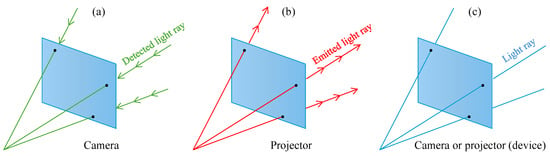
Figure 8.
Cameras and projectors differ only in that light rays travel in opposite directions. (a) Camera capturing light rays from space. (b) Projector emitting light rays towards space. (c) If the sign of the light direction vectors is omitted, cameras and projectors are mathematically equivalent (referred to generically as devices).
4.6. Camera–Projector Systems
The equivalence between cameras and projectors can be exploited to modify a stereo camera system by replacing one of the cameras with a projector. The resulting camera–projector system has the advantage of not having the corresponding point problem. This advantage is inferred from the following simplified description of the operation of a camera–projector system.
A computer-generated slide controls the brightness of every pixel of the projector. A black slide will turn off all the projector pixels. Suppose this slide is modified by setting the pixel to white; then, a light ray will be emitted to 3D space, illuminating the object at point , as shown in Figure 9. In the absence of additional light sources, the camera would capture a dark image, except for a bright point at the image pixel . In this way, the corresponding point is known by simply reading the coordinates of the bright image pixel and taking the coordinates of the white slide pixel . Therefore, sophisticated algorithms that search for corresponding points are unnecessary. For this reason, camera–projector systems can even reconstruct objects without texture, achieving high accuracy and resolution.
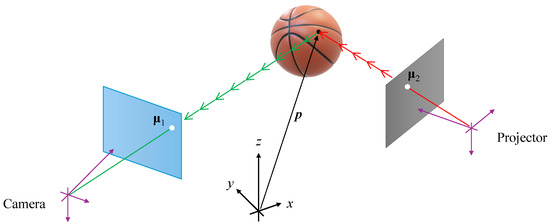
Figure 9.
Camera–projector systems lack the corresponding point problem because is directly identified as the image’s bright pixel, and is known from the slide design.
Although illustrative, the described working principle is impractical because one image is required to obtain only one corresponding point. Since modern digital projectors have millions of pixels, millions of images would be required for a single 3D reconstruction. Fortunately, efficient illumination techniques have been proposed to significantly reduce the number of required images.
4.7. Structured Illumination
The primary advantage of camera–projector systems is the absence of the corresponding point problem. Instead, slides are designed to “mark” the projector pixels such that they are recognized by the camera and paired with the image pixels, producing corresponding points. The different techniques for marking and recognizing projector pixels are known generically as structured illumination [78].
Typical structured illumination techniques include projecting dots, stripes, grids, codewords, rainbows, and fringes. These techniques can even be combined to produce hybrid structured illumination techniques. Each technique has different advantages and disadvantages in terms of accuracy, resolution, number of images, noise robustness, object color sensitivity, and other criteria. Depending on the application, one technique may be more appropriate. In particular, the fringe projection technique is recommended for applications requiring higher accuracy and resolution.
4.8. Fringe Projection
The “mark-based” approach helps to explain the different structured illumination techniques more intuitively. Alternatively, a powerful insight can be gained by considering a camera–projector setup as a telecommunication system. Remember that the projector-slide coordinates must be registered on the camera image plane to produce the corresponding points. In this context, the projector is considered a transmitter emitting the signals u and v, while the camera is a receiver detecting u and v to produce the corresponding points.
The projector-slide coordinates can be transmitted using phase modulation. For example, let us encode the values of u as the phase of a 2D cosine signal, known as a grating, of the form
where is the grating spatial frequency, is a reference phase known as a phase shift or grating displacement, and n is the number of images required to perform phase demodulation. Figure 10 shows two gratings, with low and high frequencies, respectively, and four phase shifts. When the grating is used as a slide, the object under study is illuminated with fringes, as shown in Figure 11. Consequently, this particular structured illumination technique is known as fringe projection. The image captured by the camera is known as a fringe pattern, which is modeled as
where is the background light, is the fringe amplitude, and is the phase containing the encoded signal u. Indeed, by comparing the arguments of the cosine functions in Equations (11) and (12), the slide projector coordinate u is read in the camera image plane from the demodulated phase as
The fringe projection process can be repeated for the projector axis v. Specifically, assuming that the gratings were created using the angular frequency w and that the recovered phase was , the projector-slide coordinate v is available in the camera image plane as
As a result, for every camera image pixel , the corresponding projector-slide coordinates are determined.
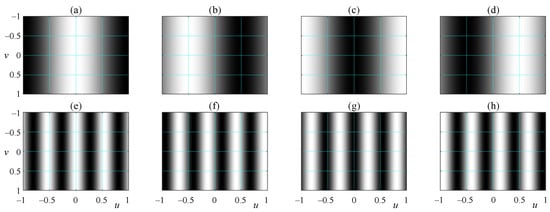
Figure 10.
(a–d) A grating with the frequency (one fringe) and four phase shifts. (e–h) A grating with a higher frequency, , and four phase shifts.
The phase retrieval algorithms used in fringe projection systems are inherited from optical metrology. Some adaptations are included considering the convenience of using digital camera–projector systems. For instance, the frequency of the gratings and the phase shifts are controlled precisely by the computer. Section 5 presents a phase retrieval algorithm suitable for fringe projection 3D metrology systems.
4.9. Phase and Object Profile Misconception
It is worth remarking on the frequent confusion occurring when the phase extracted from a fringe projection experiment is plotted, as shown in Figure 12. Since the phase looks like the object profile, inexperienced practitioners may conclude that elementary transformations on the phase, such as rotation and scaling, are sufficient to achieve metric 3D object reconstruction. Unfortunately, this misconception leads to the formulation of a transformation that, in addition to being excessively complicated, is unnecessary. It is important to remember that the phase simply provides the projector-slide coordinates required to establish corresponding points. Subsequently, the corresponding points are used to perform object reconstruction by triangulation.
Figure 12.
(a) Phase demodulated from the fringe patterns shown in Figure 11. (b) 3D plot of the phase shown in (a). It is worth emphasizing that the phase provides the projector-slide coordinates, and direct association with the object profile must be avoided.
5. Phase-Demodulation Fringe-Pattern Processing
The optical metrology community has developed a wide variety of fringe-pattern processing methods for different applications and requirements [52,256]. For instance, Fourier fringe analysis allows phase recovery from a single fringe pattern [58], but the intrinsic spectrum filtering limits the spatial resolution. On the other hand, the phase-shifting method achieves the highest (pixel-wise) spatial resolution [257], but multiple fringe patterns with prefixed phase shifts are required.
Nowadays, digital computer-controlled cameras and projectors allow the capture of multiple fringe patterns at high speed and precise control of the grating frequency and phase shift [84]. For this reason, phase demodulation through phase-shifting and multi-frequency phase unwrapping is the preferred choice for fringe projection profilometry [133].
5.1. Phase-Shifting Wrapped Phase Extraction
The design of phase-shifting algorithms depends mainly on the distribution of the phase shifts and whether they are known or unknown. Exploiting the fact that phase shifts can be controlled with high precision, they are required to be
For this particular case, the set of n fringe patterns given by Equation (12) can be processed to estimate the background light, the fringe amplitude, and the encoded phase using the Bruning method [66,257] as follows:
where represents the four-quadrant arctangent function, with the auxiliary functions defined as
As an illustration, the fringe patterns shown in Figure 11e–h were processed using Equations (16)–(18), obtaining the results presented in Figure 13. It is worth noting that the retrieved phase is , as shown in Figure 13c, and the required phase is , as shown in Figure 13d. These phases are displayed using 3D plots in Figure 13e,f for better visualization. The function is known as the wrapped phase due to its distinctive sawtooth-like shape. The phases and are equivalent since
Unfortunately, can take any real value, whereas is always constrained to the left-open interval known as principal values. Adding any multiple of to the wrapped phase still yields a value equivalent to , i.e.,
which leads to the general relationship between and as
where is an integer-valued function, known as a fringe order. Obtaining the actual phase from the available wrapped phase is a process known as phase unwrapping.
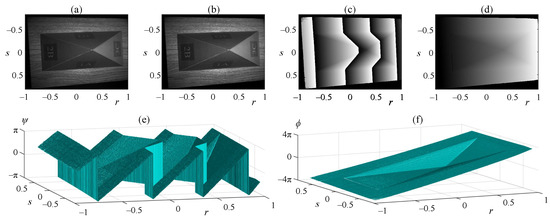
Figure 13.
Results of processing the fringe patterns shown in Figure 11e–h. (a) Background light. (b) Fringe amplitude. (c) Extracted wrapped phase, . (d) Required phase, . (e,f) 3D plots of the phases shown in (c) and (d), respectively.
5.2. Hierarchical Multi-Frequency Phase Unwrapping
Since the wrapping phenomenon appears when the encoded phase exceeds the principal values, the straightforward way to recover the required phase is by preventing it from exceeding the principal values. For this, the frequency of the grating should be chosen appropriately. For instance, assuming that the projector-slide axis u is normalized in the interval , the angular frequency
will limit the fringe-pattern phase within the principal values. Therefore, the required phase will coincide with that retrieved using Equation (18), i.e.,
Note that the frequency is so low that only one fringe is displayed, as shown in Figure 11a–d. However, low-frequency gratings cannot underline the fine details of the object. On the other hand, high-frequency gratings highlight shape details, as shown in Figure 11e–h, but the wrapping phenomenon appears.
Hierarchical multi-frequency phase unwrapping employs both low- and high-frequency gratings. The phase retrieved from low-frequency gratings assists in solving the wrapping problem, while the phase from high-frequency gratings permits achieving high fidelity. For example, let us consider a second grating with a frequency higher than :
Since the encoded phase exceeds the principal values, the required phase and the retrieved phase are related as in Equation (23), namely
The unknown function can be determined using the previous phase , as given by Equation (25). Specifically, substituting in Equation (27), we obtain
which leads to
where is the round operator ensuring that takes integer values. This process can be repeated for a third frequency , and so on, until the desired resolution is reached. In general, the k-th retrieved phase can be unwrapped using a previous phase as follows:
where is the amplification between the adjacent phases and , defined as
This phase-unwrapping method is a recursive process that works hierarchically. It starts with the lowest (single-fringe) grating frequency and ends with the highest grating frequency supported by the projector.
5.3. Choosing Grating Frequencies
The operation of the hierarchical phase-unwrapping method depends on how many frequencies can be used. Ideally, two frequencies, the lowest and highest, should be sufficient to attain a high-fidelity phase. However, in practice, using two frequencies often fails due to the excessive difference between the phases, as illustrated in Figure 14a. For this reason, intermediate frequencies are employed to produce phases with less drastic changes, as shown in Figure 14b–i.
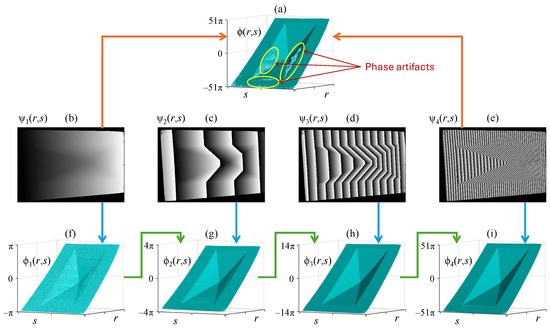
Figure 14.
(a) Phase obtained using only the lowest and highest wrapped phases (b,e). The phase artifacts are avoided by including the wrapped phases (c,d) with intermediate frequencies. (f–i) Unwrapped phases obtained recursively using the hierarchical multi-frequency method.
Although any set of increasing frequencies can be chosen, using the same amplification between adjacent phases is recommended [187], i.e.,
where m is the number of frequencies to be used. The grating frequencies fulfilling the constant amplification requirement are
The amplification coefficient is determined based on the projector resolution, which limits the supported maximum grating frequency. For instance, assuming that the projector has N pixels along the u-axis, the amplification coefficient is given as
where is the number of pixels per fringe at maximum frequency (usually between 10 and 20 pixels). The frequencies for the gratings that encode the v-axis of the projector are determined analogously.
6. System Calibration
In the theoretical preliminaries presented in Section 4, the camera and projector parameters were assumed to be known. In practice, these parameters need to be estimated through a process known as system calibration. Earlier methods used to calibrate a camera and a projector together employed cumbersome procedures. Nowadays, more practical alternatives are available to calibrate a camera–projector pair. In this section, a simple and flexible camera–projector calibration method is presented. First, the calibration of a single camera is explained to provide background. Then, the methodology is extended to projectors by exploiting the equivalence between cameras and projectors. Finally, the procedure for simultaneous camera and projector calibration is described.
6.1. Camera Calibration
Consider the pinhole model given by Equation (1), rewritten here as
where the rotation matrix was row-partitioned as . The camera can be seen as a black box that receives a point as input and returns an image pixel point as output. Therefore, a 3D target can be used to obtain a set of input–output pairs, as shown in Figure 15a, and estimate the camera matrix C by minimizing the output error [250], as shown in Figure 15c. The parameters K, R, and , can be extracted from C through triangular-orthogonal matrix decomposition. Nonetheless, despite the single-shot calibration feature, this approach is impractical because high-precision multi-point 3D targets are bulky and expensive.
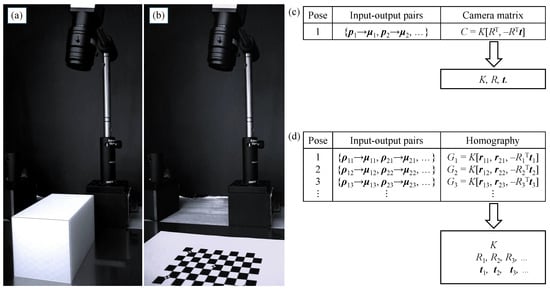
Figure 15.
(a) Camera calibration using a single image of a 3D target. (b) Camera calibration using multiple images of a 2D target captured from different viewpoints. (c) A set of 3D input–output pairs is processed to estimate C and extract the camera parameters through matrix decomposition. (d) Multiple sets of 2D input–output pairs are processed for homography estimation and further extraction of the camera parameters by exploiting the shape of K and the orthogonality of rotation matrices.
Alternatively, instead of capturing a single image of a 3D target, the camera can be calibrated using multiple images of a 2D target [258], as shown in Figure 15b. We refer to the plane where the calibration target is located as the reference plane. Without loss of generality, the reference plane is assumed to be the -plane. Therefore, since z is always zero, the third entry of and the vector in Equation (36) can be removed, simplifying the imaging process to
where represents the points on the calibration target and G is a non-singular matrix known as a homography, which is defined as
An image of the 2D calibration target establishes a set of input–output pairs, allowing a homography to be estimated by minimizing the output error, as shown in Figure 15d. Although a single homography is insufficient for camera calibration, multiple homographies provide enough information to recover the required intrinsic and extrinsic parameters. For this, the upper-triangular shape of K and the orthogonality property of rotation matrices are exploited.
6.2. Projector Calibration
The data required for homography-based calibration are input–output pairs consisting of points from the reference plane matched with points from the device plane. This requirement is independent of whether the device to be calibrated is a camera or a projector due to their mathematical equivalence. Accordingly, the method for calibrating a camera or a projector is the same [259]; they differ only in how the required input–output pairs are acquired.
For camera calibration, input–output pairs are acquired by placing the calibration target on the reference plane and capturing photographs, as shown in Figure 15b. The target provides known points on the reference plane, while the images provide the corresponding pixel points using automatic feature point detection [260]. Note that this input–output acquisition strategy is not suitable for projectors because they cannot take photographs of the reference plane.
For projector calibration, input–output pairs are acquired by placing the calibration target on the device plane as a slide and illuminating the reference plane, as shown in Figure 16a. The target provides known points on the projector plane, and the corresponding points are measured on the reference plane, for instance, using grid-ruled paper. Unlike camera calibration, where the input–output acquisition is automatic using dedicated image processing routines, projector calibration requires a manual measurement of feature point coordinates on the reference plane.

Figure 16.
(a) Projector calibration by displaying a 2D target on the reference plane covered with grid-ruled paper for manual feature point coordinate measurement. (b) Yellow target on the reference plane for camera calibration. (c) Camera–projector calibration by displaying a cyan 2D target on the reference-plane yellow target. (d) Color image captured by the camera. The captured image provides the displayed and reference calibration targets through its red (e) and blue (f) channels.
6.3. Camera–Projector Calibration
Calibrating a fringe projection system requires estimating the parameters of a camera and a projector that are working together. Although cameras and projectors can be calibrated independently, simultaneous calibration is advantageous because the camera assists the projector calibration process.
Remember that a physical target on the reference plane is required for camera calibration. In addition, a virtual target on the slide plane is necessary for projector calibration. Although both targets are superposed with each other on the reference plane, they can be distinguished using targets of different colors [208,261]; for instance, a yellow target on the reference plane (see Figure 16b), and a cyan target on the projector plane (see Figure 16c). In this manner, the two superposed targets are retrieved separately from the captured image through its red and blue channels, as shown in Figure 16d–f.
The image of the physical and virtual targets on the camera plane is opportune because manual measurements on the reference plane are avoided. First, the image of the physical target is used to estimate the camera homography from the relation
where is a feature point of the physical target (yellow) and is the corresponding point on the image (blue channel). In addition to using for camera calibration, this homography avoids manually measuring points on the reference plane for projector calibration. Specifically, let be an image point of the captured virtual target (red channel). The corresponding point on the reference plane (cyan) can be computed using the inverse of as follows:
As a result, since the feature points on the projector-slide plane are known because it contains the virtual calibration target, the projector homography can be estimated from the relation
This procedure is repeated for three or more poses, either by repositioning the devices or by moving the reference plane freely. Finally, the camera and projector parameters are estimated from the estimated homographies. This methodology, known as camera–projector calibration, remains valid even when more advanced imaging models are employed [185,251].
It is worth noting that the developed analysis was simplified using the pinhole model. However, the camera and projector may introduce significant lens distortion in practice. Even under these conditions, the fundamental principles remain valid using a lens distortion correction method [262,263].
For illustration purposes, the camera–projector calibration method was employed to calibrate the experimental system shown in Figure 17a using the software available in [259]. Then, the millimeter pyramid on the reference plane was reconstructed. Figure 11 and Figure 14i show some of the captured fringe patterns and the demodulated phase encoding the projector u-axis, respectively. Additional fringe patterns were captured to demodulate the phase encoding the v-axis. Equations (13) and (14) were used to obtain the projector-slide coordinates and from the demodulated phase. Finally, Equation (9) was used to compute an object point for each established corresponding point, resulting in the 3D reconstruction shown in Figure 17b.

Figure 17.
(a) Calibrated camera–projector system and an object on the reference plane. (b) Metric object reconstruction using fringe projection profilometry.
7. Optical 3D Metrology
Nowadays, fringe projection profilometry has been successfully implemented in several fields, ranging from science and engineering [200,264] to artwork inspection [265] and disease diagnosis [266]. Its valuable features, such as accuracy and high resolution, make it an outstanding 3D metrology tool. This section describes a few illustrative applications in which optical fringe projection has been employed.
Non-contact and high-accuracy features have motivated the implementation of fringe projection profilometry in medical applications [267]. Some representative applications include measurement of human respiration rates [268], diagnosis of tympanic membrane and middle-ear disease [269], skin assessment for research and evaluation of anti-aging products [270], tympanic membrane characterization [271], dynamic body measurement for guided radiotherapy [272], 3D imaging for assistance in laparoscopic surgery procedures [273], optical biomechanical studies for cardiovascular disease research [274], and intraoral measurement for orthodontic treatment [275]. As an example, Figure 18 shows a dental model reconstruction illustrating an intraoral measurement.
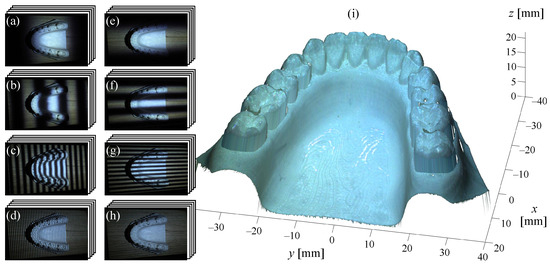
Figure 18.
Reconstruction of a dental model using the calibrated camera–projector system shown in Figure 17. (a–d) Fringe patterns of four gratings with eight phase shifts encoding the projector’s u-axis. (e–h) Fringe patterns encoding the projector’s v-axis. (i) 3D object reconstruction.
Automatic and uninterrupted inspection of items on production lines is essential to ensure high-quality products [276]. For this purpose, fringe projection profilometry is a valuable tool because of its capacity for visual inspection [277]. Other tasks for which fringe projection profilometry is useful include metal corrosion monitoring [278], crack recognition assistance [279], welding surface inspection [280], micro-scale component testing [276], turbine blade wear and damage characterization [281], aircraft surface defect detection [282], and electrical overload fault detection [19]. As an example, Figure 19 shows a visible–thermal profilometer for multimodal 3D reconstruction, detecting a heat source caused by a simulated fault.
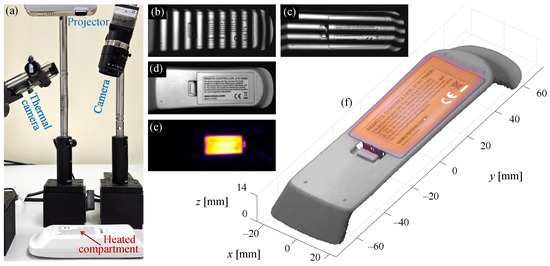
Figure 19.
(a) Visible–thermal fringe projection profilometry reconstructing a remote controller with a heated battery compartment simulating a failure [19]. (b,c) Two of the forty-eight fringe patterns used for 3D reconstruction. (d,e) Visible and thermal images providing multimodal texture on the object surface. (f) Multimodal (visible–thermal) 3D object reconstruction.
Conventional biometric-based security systems employ grayscale images to perform user authentication [283]. However, these systems lose valuable information by omitting important human biometric features such as the color and 3D shape of faces, palms, and fingers [284]. Fringe projection profilometry has been employed in security systems for face recognition [285], 3D palmprint and hand imaging [286,287], 3D fingerprint imaging [288], and ear recognition [289].
Other recent applications using fringe projection profilometry include robot vision for object detection and navigation [290], footwear and tire impression analysis in forensic science [13], shape and strain measurements for mechanical studies [291], plant phenotyping and leafy green evaluation in agriculture [292], high-precision panel telescope alignment [293], whole-body scanning for animation and entertainment [294], airbag inflation analysis for car safety studies [114,295], ancient coin and sculpture imaging for heritage preservation [296,297], fast prototyping and reverse engineering [298], three-dimensional color mural capture for cultural heritage documentation [299], animal body measurement for growth and health studies [300], 3D sensing for autonomous robot construction activities [301], local defect detection for quality inspection [302], wheel tread profile reconstruction for railway inspection [303], and many others.
This section is not intended to be exhaustive, but rather to describe motivating application examples. This paper aims to provide an elementary background for constructing and operating a fringe projection profilometer. Readers are encouraged to contribute innovative ideas, models, techniques, and applications to drive 3D metrology with even more efficient, accurate, practical, affordable, and valuable optical profilometers.
8. Conclusions
The theoretical and experimental fundamentals of fringe projection profilometry have been reviewed. Helpful insights explaining challenging and confusing concepts were provided, making this technology a straightforward tool. Simple yet powerful methods for fringe-pattern processing, triangulation, and calibration were presented. The studied methods provide the reader with an adequate background to understand and operate a fringe projection profilometer. Some applications were described to expand the reader’s scope and stimulate research on further developments, driving 3D metrology toward new frontiers.
Author Contributions
Conceptualization, R.J.-S.; methodology, R.J.-S.; software, R.J.-S.; visualization, R.J.-S.; validation, R.J.-S. and V.H.D.-R.; formal analysis, V.H.D.-R.; investigation, S.E.-H.; data curation, R.J.-S.; writing—original draft preparation, R.J.-S.; writing—review and editing, S.E.-H. and V.H.D.-R.; visualization, R.J.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Secretaría de Ciencia, Humanidades, Tecnología e Innovación (Cátedras CONACYT 880).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, M.; Chen, C.; Xie, L.; Zhang, C. Accurate measurement of high-reflective surface based on adaptive fringe projection technique. Opt. Lasers Eng. 2024, 172, 107820. [Google Scholar] [CrossRef]
- Grambow, N.; Hinz, L.; Bonk, C.; Krüger, J.; Reithmeier, E. Creepage Distance Estimation of Hairpin Stators Using 3D Feature Extraction. Metrology 2023, 3, 169–185. [Google Scholar] [CrossRef]
- Chen, F.; Brown, G.M.; Song, M. Overview of 3-D shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Zhang, S. (Ed.) Handbook of 3D Machine Vision: Optical Metrology and Imaging; Series in Optics and Optoelectronics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Leach, R. (Ed.) Advances in Optical Form and Coordinate Metrology; Emerging Technologies in Optics and Photonics; IOP Publishing Ltd.: Bristol, UK, 2020. [Google Scholar]
- Wang, Z. Review of real-time three-dimensional shape measurement techniques. Measurement 2020, 156, 107624. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, X. High-speed optical measurement for the drumhead vibration. Opt. Express 2005, 13, 3110–3116. [Google Scholar] [CrossRef]
- Su, X.; Zhang, Q. Dynamic 3-D shape measurement method: A review. Opt. Lasers Eng. 2010, 48, 191–204. [Google Scholar] [CrossRef]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Chen, L.C.; Huang, C.C. Miniaturized 3D surface profilometer using digital fringe projection. Meas. Sci. Technol. 2005, 16, 1061. [Google Scholar] [CrossRef]
- Munkelt, C.; Schmidt, I.; Brauer-Burchardt, C.; Kuhmstedt, P.; Notni, G. Cordless portable multi-view fringe projection system for 3D reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–2. [Google Scholar]
- Zaman, T.; Jonker, P.; Lenseigne, B.; Dik, J. Simultaneous capture of the color and topography of paintings using fringe encoded stereo vision. Herit. Sci. 2014, 2, 23. [Google Scholar] [CrossRef]
- Liao, Y.H.; Hyun, J.S.; Feller, M.; Bell, T.; Bortins, I.; Wolfe, J.; Baldwin, D.; Zhang, S. Portable high-resolution automated 3D imaging for footwear and tire impression capture. J. Forensic Sci. 2021, 66, 112–128. [Google Scholar] [CrossRef]
- Kulkarni, R.; Rastogi, P. Optical measurement techniques—A push for digitization. Opt. Lasers Eng. 2016, 87, 1–17. [Google Scholar] [CrossRef]
- Xing, H.; She, S.; Wang, J.; Guo, J.; Liu, Q.; Wei, C.; Yang, L.; Peng, R.; Yue, H.; Liu, Y. High-frame rate, large-depth-range structured light projector based on the step-designed LED chips array. Opt. Express 2024, 32, 24117–24127. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Lasers Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Peng, R.; Zhou, G.; Zhang, C.; Wei, C.; Wang, X.; Chen, X.; Yang, L.; Yue, H.; Liu, Y. Ultra-small, low-cost, and simple-to-control PSP projector based on SLCD technology. Opt. Express 2024, 32, 1878–1889. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, X.; Wang, H.; Chen, Z.; Zhang, Q.; Wu, Z. Multi-dimensional information sensing of complex surfaces based on fringe projection profilometry. Opt. Express 2023, 31, 41374–41390. [Google Scholar] [CrossRef] [PubMed]
- Juarez-Salazar, R.; Benjumea, E.; Marrugo, A.G.; Diaz-Ramirez, V.H. Three-dimensional object texturing for visible-thermal fringe projection profilometers. In Proceedings of the Optics and Photonics for Information Processing XVIII, San Diego, CA, USA, 18–23 August 2024; Volume 13136, p. 131360E. [Google Scholar]
- Benjumea, E.; Vargas, R.; Juarez-Salazar, R.; Marrugo, A.G. Toward a target-free calibration of a multimodal structured light and thermal imaging system. In Proceedings of the Dimensional Optical Metrology and Inspection for Practical Applications XIII, National Harbor, MD, USA, 21–26 April 2024; Volume 13038, p. 1303808. [Google Scholar]
- Feng, S.; Zuo, C.; Zhang, L.; Tao, T.; Hu, Y.; Yin, W.; Qian, J.; Chen, Q. Calibration of fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2021, 143, 106622. [Google Scholar] [CrossRef]
- Chen, R.; Xu, J.; Zhang, S.; Chen, H.; Guan, Y.; Chen, K. A self-recalibration method based on scale-invariant registration for structured light measurement systems. Opt. Lasers Eng. 2017, 88, 75–81. [Google Scholar] [CrossRef]
- Xiao, Y.L.; Xue, J.; Su, X. Robust self-calibration three-dimensional shape measurement in fringe-projection photogrammetry. Opt. Lett. 2013, 38, 694–696. [Google Scholar] [CrossRef]
- Wu, G.; Yang, T.; Liu, F.; Qian, K. Suppressing motion-induced phase error by using equal-step phase-shifting algorithms in fringe projection profilometry. Opt. Express 2022, 30, 17980–17998. [Google Scholar] [CrossRef]
- Jeon, S.; Geon Lee, H.; Sung Lee, J.; Min Kang, B.; Wook Jeon, B.; Young Yoon, J.; Hyun, J.S. Motion-Induced Error Reduction for Motorized Digital Fringe Projection System. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Guo, W.; Wu, Z.; Zhang, Q.; Hou, Y.; Wang, Y.; Liu, Y. Generalized Phase Shift Deviation Estimation Method for Accurate 3-D Shape Measurement in Phase-Shifting Profilometry. IEEE Trans. Instrum. Meas. 2025, 74, 1–11. [Google Scholar] [CrossRef]
- He, Q.; Ning, J.; Liu, X.; Li, Q. Phase-shifting profilometry for 3D shape measurement of moving objects on production lines. Precis. Eng. 2025, 92, 30–38. [Google Scholar] [CrossRef]
- Juarez-Salazar, R. Flat mirrors, virtual rear-view cameras, and camera-mirror calibration. Optik 2024, 317, 172067. [Google Scholar] [CrossRef]
- Almaraz-Cabral, C.C.; Gonzalez-Barbosa, J.J.; Villa, J.; Hurtado-Ramos, J.B.; Ornelas-Rodriguez, F.J.; Córdova-Esparza, D.M. Fringe projection profilometry for panoramic 3D reconstruction. Opt. Lasers Eng. 2016, 78, 106–112. [Google Scholar] [CrossRef]
- Flores, V.; Casaletto, L.; Genovese, K.; Martinez, A.; Montes, A.; Rayas, J. A Panoramic Fringe Projection system. Opt. Lasers Eng. 2014, 58, 80–84. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Hou, B.; Wang, B. Three-dimensional panoramic measurement based on fringe projection assisted by double-plane mirrors. Opt. Eng. 2024, 63, 114103. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; Shi, W.; Feng, L.; Jiao, L. 3D shape measurement method for high-reflection surface based on fringe projection. Appl. Opt. 2021, 60, 10555–10563. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, L.; Zuo, C.; Tao, T.; Chen, Q.; Gu, G. High dynamic range 3D measurements with fringe projection profilometry: A review. Meas. Sci. Technol. 2018, 29, 122001. [Google Scholar] [CrossRef]
- Zhang, S. Rapid and automatic optimal exposure control for digital fringe projection technique. Opt. Lasers Eng. 2020, 128, 106029. [Google Scholar] [CrossRef]
- Duan, M.; Jin, Y.; Chen, H.; Zheng, J.; Zhu, C.; Chen, E. Automatic 3-D Measurement Method for Nonuniform Moving Objects. IEEE Trans. Instrum. Meas. 2021, 70, 5015011. [Google Scholar] [CrossRef]
- Chen, R.; Xu, J.; Zhang, S. Digital fringe projection profilometry. In Advances in Optical Form and Coordinate Metrology; IOP Publishing: Bristol, UK, 2020; pp. 1–28. [Google Scholar]
- Zappa, E.; Busca, G. Static and dynamic features of Fourier transform profilometry: A review. Opt. Lasers Eng. 2012, 50, 1140–1151. [Google Scholar] [CrossRef]
- Keller, W.; Girard, J.; Goldberg, M.W.; Zhang, S. Precise calibration for error detection and correction in material extrusion additive manufacturing using digital fringe projection. Meas. Sci. Technol. 2025, 36, 025203. [Google Scholar] [CrossRef]
- Huang, H.; Niu, B.; Cheng, S.; Zhang, F. High-precision calibration and phase compensation method for structured light 3D imaging system. Opt. Lasers Eng. 2025, 186, 108788. [Google Scholar] [CrossRef]
- Yoshizawa, T. (Ed.) Handbook of Optical Metrology: Principles and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Rastogi, P.K. (Ed.) Digital Optical Measurement Techniques and Applications; Artech House Applied Photonics Series; Artech House: London, UK, 2015. [Google Scholar]
- Lv, S.; Tang, D.; Zhang, X.; Yang, D.; Deng, W.; Kemao, Q. Fringe projection profilometry method with high efficiency, precision, and convenience: Theoretical analysis and development. Opt. Express 2022, 30, 33515–33537. [Google Scholar] [CrossRef]
- Engel, T. 3D optical measurement techniques. Meas. Sci. Technol. 2023, 34, 032002. [Google Scholar] [CrossRef]
- Rowe, S.H.; Welford, W.T. Surface Topography of Non-optical Surfaces by Projected Interference Fringes. Nature 1967, 216, 786–787. [Google Scholar] [CrossRef]
- Wygant, R.W.; Almeida, S.P.; Soares, O.D.D. Surface inspection via projection interferometry. Appl. Opt. 1988, 27, 4626–4630. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ronchi, V. Forty Years of History of a Grating Interferometer. Appl. Opt. 1964, 3, 437–451. [Google Scholar] [CrossRef]
- Murty, M.V.R.K.; Shoemaker, A.H. Theory of Concentric Circular Grid. Appl. Opt. 1966, 5, 323–326. [Google Scholar] [CrossRef]
- Case, S.K.; Jalkio, J.A.; Kim, R.C. 3-D Vision System Analysis and Design. In Three-Dimensional Machine Vision; Kanade, T., Ed.; Springer: Boston, MA, USA, 1987; pp. 63–95. [Google Scholar]
- Malacara, D. (Ed.) Optical Shop Testing, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Juarez-Salazar, R.; Robledo-Sanchez, C.; Guerrero-Sanchez, F.; Barcelata-Pinzon, A.; Gonzalez-Garcia, J.; Santiago-Alvarado, A. Intensity normalization of additive and multiplicative spatially multiplexed patterns with n encoded phases. Opt. Lasers Eng. 2016, 77, 225–229. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Diaz-Ramirez, V.H. Estimation of amplitude and standard deviation of noisy sinusoidal signals. Opt. Eng. 2017, 56, 013109. [Google Scholar] [CrossRef]
- Servin, M.; Quiroga, J.A.; Padilla, M. Fringe Pattern Analysis for Optical Metrology: Theory, Algorithms, and Applications; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Takasaki, H. Moiré Topography. Appl. Opt. 1970, 9, 1467–1472. [Google Scholar] [CrossRef]
- Meadows, D.M.; Johnson, W.O.; Allen, J.B. Generation of Surface Contours by Moiré Patterns. Appl. Opt. 1970, 9, 942–947. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Cao, Y.; Chen, C.; Wan, Y.; Fu, G.; Wang, Y. Computer-generated moiré profilometry. Opt. Express 2017, 25, 26815–26824. [Google Scholar] [CrossRef] [PubMed]
- Takasaki, H. Moiré Topography. Appl. Opt. 1973, 12, 845–850. [Google Scholar] [CrossRef]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Toyooka, S.; Iwaasa, Y. Automatic profilometry of 3-D diffuse objects by spatial phase detection. Appl. Opt. 1986, 25, 1630–1633. [Google Scholar] [CrossRef]
- Rodriguez-Vera, R.; Servin, M. Phase locked loop profilometry. Opt. Laser Technol. 1994, 26, 393–398. [Google Scholar] [CrossRef]
- Villa, J.; Servin, M.; Castillo, L. Profilometry for the measurement of 3-D object shapes based on regularized filters. Opt. Commun. 1999, 161, 13–18. [Google Scholar] [CrossRef]
- Sajan, M.R.; Tay, C.J.; Shang, H.M.; Asundi, A. Improved spatial phase detection for profilometry using a TDI imager. Opt. Commun. 1998, 150, 66–70. [Google Scholar] [CrossRef]
- Berryman, F.; Pynsent, P.; Cubillo, J. A theoretical comparison of three fringe analysis methods for determining the three-dimensional shape of an object in the presence of noise. Opt. Lasers Eng. 2003, 39, 35–50. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef] [PubMed]
- Reich, C.; Ritter, R.; Thesing, J. 3-D shape measurement of complex objects by combining photogrammetry and fringe projection. Opt. Eng. 2000, 39, 224–231. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital Wavefront Measuring Interferometer for Testing Optical Surfaces and Lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Su, X.; Guo, L. Improved Fourier transform profilometry for the automatic measurement of three-dimensional object shapes. Opt. Eng. 1990, 29, 1439–1444. [Google Scholar]
- Juarez-Salazar, R.; Martinez-Laguna, J.; Diaz-Ramirez, V.H. Multi-demodulation phase-shifting and intensity pattern projection profilometry. Opt. Lasers Eng. 2020, 129, 106085. [Google Scholar] [CrossRef]
- Kemao, Q. Two-dimensional windowed Fourier transform for fringe pattern analysis: Principles, applications and implementations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- Casco-Vasquez, J.F.; Juarez-Salazar, R.; Robledo-Sanchez, C.; Rodriguez-Zurita, G.; Sanchez, F.G.; Arévalo Aguilar, L.M.; Meneses-Fabian, C. Fourier normalized-fringe analysis by zero-order spectrum suppression using a parameter estimation approach. Opt. Eng. 2013, 52, 074109. [Google Scholar] [CrossRef]
- Liu, Y.; Du, G.; Zhang, C.; Zhou, C.; Si, S.; Lei, Z. An improved two-step phase-shifting profilometry. Opt.—Int. J. Light Electron Opt. 2016, 127, 288–291. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Robledo-Sanchez, C.; Meneses-Fabian, C.; Guerrero-Sanchez, F.; Aguilar, L.A. Generalized phase-shifting interferometry by parameter estimation with the least squares method. Opt. Lasers Eng. 2013, 51, 626–632. [Google Scholar] [CrossRef]
- Wei, Z.; Cao, Y.; Wu, H.; Xu, C.; Ruan, G.; Wu, F.; Li, C. Dynamic phase-differencing profilometry with number-theoretical phase unwrapping and interleaved projection. Opt. Express 2024, 32, 19578–19593. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Guerrero-Sanchez, F.; Robledo-Sanchez, C. Theory and algorithms of an efficient fringe analysis technology for automatic measurement applications. Appl. Opt. 2015, 54, 5364–5374. [Google Scholar] [CrossRef]
- Su, X.; Su, L.; Li, W.; Xiang, L. New 3D profilometry based on modulation measurement. In Proceedings of the Automated Optical Inspection for Industry: Theory, Technology, and Applications II, Beijing, China, 16–19 September 1998; Ye, S., Ed.; SPIE: Bellingham, WA, USA, 1998; Volume 3558, pp. 1–7. [Google Scholar]
- Su, L.; Su, X.; Li, W.; Xiang, L. Application of modulation measurement profilometry to objects with surface holes. Appl. Opt. 1999, 38, 1153–1158. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Zheng, S. Linearly coded profilometry. Appl. Opt. 1997, 36, 2401–2407. [Google Scholar] [CrossRef] [PubMed]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photon. 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Deng, J.; Li, J.; Feng, H.; Ding, S.; Xiao, Y.; Han, W.; Zeng, Z. Efficient intensity-based fringe projection profilometry method resistant to global illumination. Opt. Express 2020, 28, 36346–36360. [Google Scholar] [CrossRef]
- An, H.; Cao, Y.; Wu, H.; Yang, N.; Xu, C.; Li, H. Spatial-temporal phase unwrapping algorithm for fringe projection profilometry. Opt. Express 2021, 29, 20657–20672. [Google Scholar] [CrossRef]
- Marrugo, A.G.; Gao, F.; Zhang, S. State-of-the-art active optical techniques for three-dimensional surface metrology: A review [Invited]. J. Opt. Soc. Am. A 2020, 37, B60–B77. [Google Scholar] [CrossRef]
- Gorthi, S.S.; Rastogi, P.K. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light. Sci. Appl. 2022, 11, 39. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S. High-Speed 3D Imaging with Digital Fringe Projection Techniques; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Harding, K. (Ed.) Handbook of Optical Dimensional Metrology; Series in Optics and Optoelectronics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Jiang, C.; Li, Y.; Feng, S.; Hu, Y.; Yin, W.; Qian, J.; Zuo, C.; Liang, J. Fringe Projection Profilometry. In Coded Optical Imaging; Springer International Publishing: Cham, Switzerland, 2024; Chapter 14; pp. 241–286. [Google Scholar]
- Yang, T.; Gu, F. Overview of modulation techniques for spatially structured-light 3D imaging. Opt. Laser Technol. 2024, 169, 110037. [Google Scholar] [CrossRef]
- Li, E.B.; Peng, X.; Xi, J.; Chicharo, J.F.; Yao, J.Q.; Zhang, D.W. Multi-frequency and multiple phase-shift sinusoidal fringe projection for 3D profilometry. Opt. Express 2005, 13, 1561–1569. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, S. Optimal fringe angle selection for digital fringe projection technique. Appl. Opt. 2013, 52, 7094–7098. [Google Scholar] [CrossRef] [PubMed]
- Geng, Z.J. Rainbow three-dimensional camera: New concept of high-speed three-dimensional vision systems. Opt. Eng. 1996, 35, 376–383. [Google Scholar] [CrossRef]
- Pan, J.; Huang, P.S.; Chiang, F.P. Color-coded binary fringe projection technique for 3-D shape measurement. Opt. Eng. 2005, 44, 023606. [Google Scholar] [CrossRef]
- Su, W.H. Color-encoded fringe projection for 3D shape measurements. Opt. Express 2007, 15, 13167–13181. [Google Scholar] [CrossRef]
- Waddington, C.; Kofman, J. Saturation avoidance by adaptive fringe projection in phase-shifting 3D surface-shape measurement. In Proceedings of the International Symposium on Optomechatronic Technologies, Toronto, ON, Canada, 25–27 October 2010; pp. 1–4. [Google Scholar]
- Salahieh, B.; Chen, Z.; Rodriguez, J.J.; Liang, R. Multi-polarization fringe projection imaging for high dynamic range objects. Opt. Express 2014, 22, 10064–10071. [Google Scholar] [CrossRef]
- Lagarde, J.M.; Rouvrais, C.; Black, D.; Diridollou, S.; Gall, Y. Skin topography measurement by interference fringe projection: A technical validation. Skin Res. Technol. 2001, 7, 112–121. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, H.; Lalor, M.J.; Burton, D.R. A novel design for fiber optic interferometric fringe projection phase-shifting 3-D profilometry. Opt. Commun. 2001, 187, 347–357. [Google Scholar] [CrossRef]
- Sánchez, J.R.; Martínez-García, A.; Rayas, J.A.; León-Rodríguez, M. LED source interferometer for microscopic fringe projection profilometry using a Gates’ interferometer configuration. Opt. Lasers Eng. 2022, 149, 106822. [Google Scholar] [CrossRef]
- Schaffer, M.; Große, M.; Harendt, B.; Kowarschik, R. Coherent two-beam interference fringe projection for highspeed three-dimensional shape measurements. Appl. Opt. 2013, 52, 2306–2311. [Google Scholar] [CrossRef] [PubMed]
- Sicardi-Segade, A.; Martinez-Garcia, A.; Toto-Arellano, N.I.; Rayas, J.A. Analysis of the fringes visibility generated by a lateral cyclic shear interferometer in the retrieval of the three-dimensional surface information of an object. Opt.—Int. J. Light Electron Opt. 2014, 125, 1320–1324. [Google Scholar] [CrossRef]
- Robledo-Sanchez, C.; Juarez-Salazar, R.; Meneses-Fabian, C.; Guerrero-Sánchez, F.; Aguilar, L.M.A.; Rodriguez-Zurita, G.; Ixba-Santos, V. Phase-shifting interferometry based on the lateral displacement of the light source. Opt. Express 2013, 21, 17228–17233. [Google Scholar] [CrossRef] [PubMed]
- Creath, K.; Schmit, J.; Wyant, J.C. Optical metrology of diffuse surfaces. In Optical Shop Testing, 3rd ed.; Malacara, D., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 756–807. [Google Scholar]
- Wang, L.; Cao, Y.; Li, C.; Wang, Y.; Wan, Y.; Fu, G.; Li, H.; Xu, C. Orthogonal modulated computer-generated moiré profilometry. Opt. Commun. 2020, 455, 124565. [Google Scholar] [CrossRef]
- Su, X.Y.; Zhou, W.S.; von Bally, G.; Vukicevic, D. Automated phase-measuring profilometry using defocused projection of a Ronchi grating. Opt. Commun. 1992, 94, 561–573. [Google Scholar] [CrossRef]
- Lei, S.; Zhang, S. Flexible 3-D shape measurement using projector defocusing. Opt. Lett. 2009, 34, 3080–3082. [Google Scholar] [CrossRef]
- Lei, S.; Zhang, S. Digital sinusoidal fringe pattern generation: Defocusing binary patterns VS focusing sinusoidal patterns. Opt. Lasers Eng. 2010, 48, 561–569. [Google Scholar] [CrossRef]
- Ayubi, G.A.; Ayubi, J.A.; Martino, J.M.D.; Ferrari, J.A. Pulse-width modulation in defocused three-dimensional fringe projection. Opt. Lett. 2010, 35, 3682–3684. [Google Scholar] [CrossRef]
- Silva, A.; Flores, J.L.; Muñoz, A.M.; Ayubi, G.A.; Ferrari, J.A. Three-dimensional shape profiling by out-of-focus projection of colored pulse width modulation fringe patterns. Appl. Opt. 2017, 56, 5198–5203. [Google Scholar] [CrossRef]
- Huang, P.S.; Hu, Q.; Jin, F.; Chiang, F.P. Color-encoded digital fringe projection technique for high-speed 3-D surface contouring. Opt. Eng. 1999, 38, 1065–1071. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Mu, G.; Fang, Z. Color-coded projection grating method for shape measurement with a single exposure. Appl. Opt. 2000, 39, 3504–3508. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, S. Three-dimensional shape measurement with binary dithered patterns. Appl. Opt. 2012, 51, 6631–6636. [Google Scholar] [CrossRef] [PubMed]
- Peng, R.; Tian, M.; Xu, L.; Yang, L.; Yue, H. A novel method of generating phase-shifting sinusoidal fringes for 3D shape measurement. Opt. Lasers Eng. 2021, 137, 106401. [Google Scholar] [CrossRef]
- Fujigaki, M.; Oura, Y.; Asai, D.; Murata, Y. High-speed height measurement by a light-source-stepping method using a linear LED array. Opt. Express 2013, 21, 23169–23180. [Google Scholar] [CrossRef]
- Wissmann, P.; Forster, F.; Schmitt, R. Fast and low-cost structured light pattern sequence projection. Opt. Express 2011, 19, 24657–24671. [Google Scholar] [CrossRef]
- Heist, S.; Lutzke, P.; Schmidt, I.; Dietrich, P.; Kühmstedt, P.; Tünnermann, A.; Notni, G. High-speed three-dimensional shape measurement using GOBO projection. Opt. Lasers Eng. 2016, 87, 90–96. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, Y.; Yu, X.; Hou, Y.; Chen, W. High-speed 3D shape measurement using a rotary mechanical projector. Opt. Express 2021, 29, 7885–7903. [Google Scholar] [CrossRef]
- Huang, P.S.; Zhang, C.; Chiang, F.P. High-speed 3-D shape measurement based on digital fringe projection. Opt. Eng. 2003, 42, 163–168. [Google Scholar] [CrossRef]
- Zhu, Z.; You, D.; Zhou, F.; Wang, S.; Xie, Y. Rapid 3D reconstruction method based on the polarization-enhanced fringe pattern of an HDR object. Opt. Express 2021, 29, 2162–2171. [Google Scholar] [CrossRef]
- Zhu, H.; Guo, H. Surface profile measurement of metal objects by use of a fringe projection system with polarized dual projectors. Appl. Opt. 2024, 63, 7883–7892. [Google Scholar] [CrossRef]
- Zhang, S.; Weide, D.V.D.; Oliver, J. Superfast phase-shifting method for 3-D shape measurement. Opt. Express 2010, 18, 9684–9689. [Google Scholar] [CrossRef] [PubMed]
- Zendejas-Hernández, E.; Trujillo-Schiaffino, G.; Anguiano-Morales, M.; Salas-Peimbert, D.P.; Corral-Martínez, L.F.; Tornero-Martínez, N. Spatial and temporal methods for fringe pattern analysis: A review. J. Opt. 2023, 52, 888–899. [Google Scholar] [CrossRef]
- Zhang, Z. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques. Opt. Lasers Eng. 2012, 50, 1097–1106. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Takeda, M. Fourier fringe analysis and its application to metrology of extreme physical phenomena: A review [Invited]. Appl. Opt. 2013, 52, 20–29. [Google Scholar] [CrossRef]
- Sandoz, P. Wavelet transform as a processing tool in white-light interferometry. Opt. Lett. 1997, 22, 1065–1067. [Google Scholar] [CrossRef]
- Zhong, J.; Weng, J. Spatial carrier-fringe pattern analysis by means of wavelet transform: Wavelet transform profilometry. Appl. Opt. 2004, 43, 4993–4998. [Google Scholar] [CrossRef]
- Xu, P.; Liu, J.; Zhang, W.; Shan, S.; Wang, J.; Shao, M.; Deng, Z. Few-fringe-based phase-shifting profilometry employing hilbert transform. Precis. Eng. 2023, 83, 1–11. [Google Scholar] [CrossRef]
- Ferrari, J.A.; Flores, J.L.; Fernandez Lakatos, M.; Ayubi, G.A.; Perciante, C.D.; Frins, E. Hilbert’s and Takeda’s single-shot interferometry with a linear-carrier: A comparison. Meas. Sci. Technol. 2024, 35, 055006. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, W.; Zheng, Z.; Zhong, M. Fringe pattern analysis by S-transform. Opt. Commun. 2012, 285, 209–217. [Google Scholar] [CrossRef]
- Massig, J.H.; Heppner, J. Fringe-Pattern Analysis with High Accuracy by Use of the Fourier-Transform Method: Theory and Experimental Tests. Appl. Opt. 2001, 40, 2081–2088. [Google Scholar] [CrossRef]
- Quan, C.; Chen, W.; Tay, C. Phase-retrieval techniques in fringe-projection profilometry. Opt. Lasers Eng. 2010, 48, 235–243. [Google Scholar] [CrossRef]
- Villa, J.; Luis Flores, J.; Garcia-Torales, G.; Montes-Flores, M. Fourier transform digital moiré interferometry. Meas. Sci. Technol. 2025, 36, 035208. [Google Scholar] [CrossRef]
- Zhang, Z.; Jing, Z.; Wang, Z.; Kuang, D. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase calculation at discontinuities in fringe projection profilometry. Opt. Lasers Eng. 2012, 50, 1152–1160. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Creath, K. V Phase-Measurement Interferometry Techniques. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 1988; Volume 26, pp. 349–393. [Google Scholar]
- Hariharan, P.; Oreb, B.F.; Eiju, T. Digital phase-shifting interferometry: A simple error-compensating phase calculation algorithm. Appl. Opt. 1987, 26, 2504–2506. [Google Scholar] [CrossRef] [PubMed]
- Malacara, D.; Servin, M.; Malacara, Z. Interferogram Analysis for Optical Testing, 2nd ed.; Taylor & Francis Group: Abingdon, UK, 2010. [Google Scholar]
- Carré, P. Installation et utilisation du comparateur photoélectrique et interférentiel du Bureau International des Poids et Mesures. Metrologia 1966, 2, 13. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Robledo-Sanchez, C.; Guerrero-Sanchez, F.; Rangel-Huerta, A. Generalized phase-shifting algorithm for inhomogeneous phase shift and spatio-temporal fringe visibility variation. Opt. Express 2014, 22, 4738–4750. [Google Scholar] [CrossRef]
- Meneses-Fabian, C.; Lara-Cortes, F.A. Phase retrieval by Euclidean distance in self-calibrating generalized phase-shifting interferometry of three steps. Opt. Express 2015, 23, 13589–13604. [Google Scholar] [CrossRef]
- Greivenkamp, J.E. Generalized data reduction for heterodyne interferometry. Opt. Eng. 1984, 23, 234350–234352. [Google Scholar] [CrossRef]
- Morgan, C.J. Least-squares estimation in phase-measurement interferometry. Opt. Lett. 1982, 7, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley & Sons, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Zappa, E.; Busca, G. Comparison of eight unwrapping algorithms applied to Fourier-transform profilometry. Opt. Lasers Eng. 2008, 46, 106–116. [Google Scholar] [CrossRef]
- Itoh, K. Analysis of the phase unwrapping algorithm. Appl. Opt. 1982, 21, 2470. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Romero, L.A. Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods. J. Opt. Soc. Am. A 1994, 11, 107–117. [Google Scholar] [CrossRef]
- Schofield, M.A.; Zhu, Y. Fast phase unwrapping algorithm for interferometric applications. Opt. Lett. 2003, 28, 1194–1196. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Flynn, T. Consistent 2-D phase unwrapping guided by a quality map. In Proceedings of the International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; Volume 4, pp. 2057–2059. [Google Scholar]
- Su, X.; Chen, W. Reliability-guided phase unwrapping algorithm: A review. Opt. Lasers Eng. 2004, 42, 245–261. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, L.; Zhang, Q.; Su, X.; Asundi, A.; Kemao, Q. Quality-guided phase unwrapping technique: Comparison of quality maps and guiding strategies. Appl. Opt. 2011, 50, 6214–6224. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Romero, L.A. Minimum Lp-norm two-dimensional phase unwrapping. J. Opt. Soc. Am. A 1996, 13, 1999–2013. [Google Scholar] [CrossRef]
- Flynn, T.J. Two-dimensional phase unwrapping with minimum weighted discontinuity. J. Opt. Soc. Am. A 1997, 14, 2692–2701. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. Geosci. Remote Sens. IEEE Trans. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Robledo-Sanchez, C.; Guerrero-Sanchez, F. Phase-unwrapping algorithm by a rounding-least-squares approach. Opt. Eng. 2014, 53, 024102. [Google Scholar] [CrossRef]
- Sansoni, G.; Corini, S.; Lazzari, S.; Rodella, R.; Docchio, F. Three-dimensional imaging based on Gray-code light projection: Characterization of the measuring algorithm and development of a measuring system for industrial applications. Appl. Opt. 1997, 36, 4463–4472. [Google Scholar] [CrossRef] [PubMed]
- Sansoni, G.; Carocci, M.; Rodella, R. Three-Dimensional Vision Based on a Combination of Gray-Code and Phase-Shift Light Projection: Analysis and Compensation of the Systematic Errors. Appl. Opt. 1999, 38, 6565–6573. [Google Scholar] [CrossRef]
- Wu, Z.; Zuo, C.; Guo, W.; Tao, T.; Zhang, Q. High-speed three-dimensional shape measurement based on cyclic complementary Gray-code light. Opt. Express 2019, 27, 1283–1297. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zheng, D.; Kemao, Q.; Christopoulos, G. Quaternary gray-code phase unwrapping for binary fringe projection profilometry. Opt. Lasers Eng. 2019, 121, 358–368. [Google Scholar] [CrossRef]
- Tian, J.; Peng, X.; Zhao, X. A generalized temporal phase unwrapping algorithm for three-dimensional profilometry. Opt. Lasers Eng. 2008, 46, 336–342. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Villa, J.; Rodríguez-Reveles, G.A.; Moreno, G.; de la Rosa, I. Temporal phase-unwrapping in fringe projection profilometry: Increasing the accuracy with equidistant long time-steps sampling. Opt. Lasers Eng. 2023, 167, 107591. [Google Scholar] [CrossRef]
- Zhang, S. Absolute phase retrieval methods for digital fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 107, 28–37. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, W.; Zhang, Q. Two-frequency phase-shifting method vs. Gray-coded-based method in dynamic fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2022, 153, 106995. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Wyant, J.C. Two-wavelength phase shifting interferometry. Appl. Opt. 1984, 23, 4539–4543. [Google Scholar] [CrossRef] [PubMed]
- Towers, C.E.; Towers, D.P.; Jones, J.D.C. Generalized frequency selection in multifrequency interferometry. Opt. Lett. 2004, 29, 1348–1350. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Towers, C.E.; Towers, D.P. Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency Selection. Opt. Express 2006, 14, 6444–6455. [Google Scholar] [CrossRef] [PubMed]
- Huntley, J.M.; Saldner, H. Temporal phase-unwrapping algorithm for automated interferogram analysis. Appl. Opt. 1993, 32, 3047–3052. [Google Scholar] [CrossRef]
- Saldner, H.O.; Huntley, J.M. Temporal phase unwrapping: Application to surface profiling of discontinuous objects. Appl. Opt. 1997, 36, 2770–2775. [Google Scholar] [CrossRef]
- He, X.; Kemao, Q. A comparative study on temporal phase unwrapping methods in high-speed fringe projection profilometry. Opt. Lasers Eng. 2021, 142, 106613. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Q.; Tao, T.; Feng, S.; Hu, Y.; Li, H.; Zuo, C. Robust and efficient multi-frequency temporal phase unwrapping: Optimal fringe frequency and pattern sequence selection. Opt. Express 2017, 25, 20381–20400. [Google Scholar] [CrossRef]
- Su, X.; Song, W.; Cao, Y.; Xiang, L. Phase-height mapping and coordinate calibration simultaneously in phase-measuring profilometry. Opt. Eng. 2004, 43, 708–712. [Google Scholar]
- Zhou, W.S.; Su, X.Y. A Direct Mapping Algorithm for Phase-measuring Profilometry. J. Mod. Opt. 1994, 41, 89–94. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, B.; Su, X.; Li, L.; Li, B.; Zhang, S.; Wang, Y. A convenient 3D reconstruction model based on parallel-axis structured light system. Opt. Lasers Eng. 2021, 138, 106366. [Google Scholar] [CrossRef]
- Liu, H.; Lin, H.; Yao, L. Calibration method for projector-camera-based telecentric fringe projection profilometry system. Opt. Express 2017, 25, 31492–31508. [Google Scholar] [CrossRef]
- Zhao, W.; Su, X.; Chen, W. Discussion on accurate phase-height mapping in fringe projection profilometry. Opt. Eng. 2017, 56, 104109. [Google Scholar] [CrossRef]
- Lu, J.; Mo, R.; Sun, H.; Chang, Z. Flexible calibration of phase-to-height conversion in fringe projection profilometry. Appl. Opt. 2016, 55, 6381–6388. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Cao, Y.; Wu, Y. Improved algorithm for phase-to-height mapping in phase measuring profilometry. Appl. Opt. 2012, 51, 1149–1155. [Google Scholar] [CrossRef]
- Wang, Z.; Du, H.; Bi, H. Out-of-plane shape determination in generalized fringe projection profilometry. Opt. Express 2006, 14, 12122–12133. [Google Scholar] [CrossRef]
- Villa, J.; Araiza, M.; Alaniz, D.; Ivanov, R.; Ortiz, M. Transformation of phase to (x,y,z)-coordinates for the calibration of a fringe projection profilometer. Opt. Lasers Eng. 2012, 50, 256–261. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Li, A.; Tang, Q.; Peng, X.; Gao, B.Z. Phase-3D mapping method developed from back-projection stereovision model for fringe projection profilometry. Opt. Express 2017, 25, 1262–1277. [Google Scholar] [CrossRef]
- Chen, L.; Quan, C. Fringe projection profilometry with nonparallel illumination: A least-squares approach. Opt. Lett. 2005, 30, 2101–2103. [Google Scholar] [CrossRef]
- Du, H.; Wang, Z. Three-dimensional shape measurement with an arbitrarily arranged fringe projection profilometry system. Opt. Lett. 2007, 32, 2438–2440. [Google Scholar] [CrossRef] [PubMed]
- Martinez, A.; Rayas, J.A.; Puga, H.J.; Genovese, K. Iterative estimation of the topography measurement by fringe-projection method with divergent illumination by considering the pitch variation along the x and z directions. Opt. Lasers Eng. 2010, 48, 877–881. [Google Scholar] [CrossRef]
- Huang, L.; Chua, P.S.K.; Asundi, A. Least-squares calibration method for fringe projection profilometry considering camera lens distortion. Appl. Opt. 2010, 49, 1539–1548. [Google Scholar] [CrossRef] [PubMed]
- Juarez-Salazar, R.; Diaz-Ramirez, V.H. Distorted pinhole camera model for tangential distortion. Proc. SPIE 2021, 11841, 118410D. [Google Scholar]
- Yang, S.; Liu, M.; Song, J.; Yin, S.; Ren, Y.; Zhu, J.; Chen, S. Projector distortion residual compensation in fringe projection system. Opt. Lasers Eng. 2019, 114, 104–110. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Giron, A.; Zheng, J.; Diaz-Ramirez, V.H. Key concepts for phase-to-coordinate conversion in fringe projection systems. Appl. Opt. 2019, 58, 4828–4834. [Google Scholar] [CrossRef]
- Pei, X.; Liu, J.; Yang, Y.; Ren, M.; Zhu, L. Phase-to-Coordinates Calibration for Fringe Projection Profilometry Using Gaussian Process Regression. IEEE Trans. Instrum. Meas. 2022, 71, 5008112. [Google Scholar] [CrossRef]
- Li, J.; Ding, S.; Zeng, Z.; Deng, J. Dual-biprism-based coaxial fringe projection system. Appl. Opt. 2022, 61, 3957–3964. [Google Scholar] [CrossRef]
- Sicardi-Segade, A.; Estrada, J.; Martínez-García, A.; Garnica, G. On axis fringe projection: A new method for shape measurement. Opt. Lasers Eng. 2015, 69, 29–34. [Google Scholar] [CrossRef]
- Weng, W.; Chang, M.; Zeng, L.; Zhou, J.; Zhang, L.; Yu, X.; Liu, H. A novel and calibration-simple structured light 3D reconstruction system based on parallel-axis-display system. Opt. Commun. 2025, 579, 131580. [Google Scholar] [CrossRef]
- Li, D.; Liu, C.; Tian, J. Telecentric 3D profilometry based on phase-shifting fringe projection. Opt. Express 2014, 22, 31826–31835. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Chen, Q.; Feng, S.; Tao, T.; Asundi, A.; Zuo, C. A new microscopic telecentric stereo vision system—Calibration, rectification, and three-dimensional reconstruction. Opt. Lasers Eng. 2019, 113, 14–22. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High-resolution, real-time 3D absolute coordinate measurement based on a phase-shifting method. Opt. Express 2006, 14, 2644–2649. [Google Scholar] [CrossRef] [PubMed]
- Juarez-Salazar, R.; Rodriguez-Reveles, G.A.; Esquivel-Hernandez, S.; Diaz-Ramirez, V.H. Three-dimensional spatial point computation in fringe projection profilometry. Opt. Lasers Eng. 2023, 164, 107482. [Google Scholar] [CrossRef]
- Wang, Z.; Nguyen, D.A.; Barnes, J.C. Some practical considerations in fringe projection profilometry. Opt. Lasers Eng. 2010, 48, 218–225. [Google Scholar] [CrossRef]
- Yin, Y.; Peng, X.; Li, A.; Liu, X.; Gao, B.Z. Calibration of fringe projection profilometry with bundle adjustment strategy. Opt. Lett. 2012, 37, 542–544. [Google Scholar] [CrossRef]
- Rao, L.; Da, F.; Kong, W.; Huang, H. Flexible calibration method for telecentric fringe projection profilometry systems. Opt. Express 2016, 24, 1222–1237. [Google Scholar] [CrossRef]
- Zhang, S. Flexible and accurate phase-to-coordinate calibration method. In Proceedings of the Dimensional Optical Metrology and Inspection for Practical Applications XI, Orlando, FL, USA, 3 April–13 June 2022; Harding, K.G., Zhang, S., Hyun, J.S., Li, B., Eds.; SPIE: Bellingham, WA, USA, 2022; Volume 12098, p. 1209802. [Google Scholar]
- Bai, Y.; Zhang, Z.; Fu, S.; Zhao, H.; Ni, Y.; Gao, N.; Meng, Z.; Yang, Z.; Zhang, G.; Yin, W. Recent Progress of Full-Field Three-Dimensional Shape Measurement Based on Phase Information. Nanomanuf. Metrol. 2024, 7, 9. [Google Scholar] [CrossRef]
- Vargas, R.; Romero, L.A.; Zhang, S.; Marrugo, A.G. Calibration method based on virtual phase-to-coordinate mapping with linear correction function for structured light system. Opt. Lasers Eng. 2024, 183, 108496. [Google Scholar] [CrossRef]
- Moreno, D.; Taubin, G. Simple, Accurate, and Robust Projector-Camera Calibration. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 464–471. [Google Scholar]
- Li, Z.; Shi, Y.; Wang, C.; Wang, Y. Accurate calibration method for a structured light system. Opt. Eng. 2008, 47, 053604. [Google Scholar] [CrossRef]
- Yu, J.; Gao, N.; Meng, Z.; Zhang, Z. High-accuracy projector calibration method for fringe projection profilometry considering perspective transformation. Opt. Express 2021, 29, 15053–15066. [Google Scholar] [CrossRef] [PubMed]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Legarda-Sáenz, R.; Bothe, T.; Jüptner, W.P. Accurate procedure for the calibration of a structured light system. Opt. Eng. 2004, 43, 464–471. [Google Scholar] [CrossRef]
- Kimura, M.; Mochimaru, M.; Kanade, T. Projector Calibration using Arbitrary Planes and Calibrated Camera. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–2. [Google Scholar]
- Juarez-Salazar, R.; Diaz-Ramirez, V.H. Flexible camera-projector calibration using superposed color checkerboards. Opt. Lasers Eng. 2019, 120, 59–65. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Lu, W.; Jiang, X.J. High-Accuracy Calibration of High-Speed Fringe Projection Profilometry Using a Checkerboard. IEEE/ASME Trans. Mechatronics 2022, 27, 4199–4204. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, P.S. Novel method for structured light system calibration. Opt. Eng. 2006, 45, 083601. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, D.; Shi, W.; Wang, L.; Li, J. Improved calibration and 3D reconstruction for micro fringe projection profilometry. Opt. Express 2025, 33, 13455–13471. [Google Scholar] [CrossRef]
- Huang, B.; Tang, Y.; Ozdemir, S.; Ling, H. A Fast and Flexible Projector-Camera Calibration System. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1049–1063. [Google Scholar] [CrossRef]
- Schreiber, W.; Notni, G. Theory and arrangements of self-calibrating whole-body 3-D-measurement systems using fringe projection technique. Opt. Eng. 2000, 39, 159–169. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Diaz-Ramirez, V.H.; Robledo-Sanchez, C.; Diaz-Gonzalez, G. On the use of video projectors for three-dimensional scanning. Proc. SPIE 2017, 10395, 103950C. [Google Scholar]
- Jiang, C.; Xing, S.; Guo, H. Fringe harmonics elimination in multi-frequency phase-shifting fringe projection profilometry. Opt. Express 2020, 28, 2838–2856. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Kong, L.; Peng, X.; Luo, Z.; Shi, J.; Tian, L. Multi-Color Channel Gamma Correction in Fringe Projection Profilometry. Photonics 2025, 12, 74. [Google Scholar] [CrossRef]
- Poynton, C.A. “Gamma” and its Disguises: The Nonlinear Mappings of Intensity in Perception, CRTs, Film, and Video. SMPTE J. 1993, 102, 1099–1108. [Google Scholar] [CrossRef]
- Ayubi, G.A.; Martino, J.M.D.; Alonso, J.R.; Fernández, A.; Perciante, C.D.; Ferrari, J.A. Three-dimensional profiling with binary fringes using phase-shifting interferometry algorithms. Appl. Opt. 2011, 50, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Son, S.J.; An, Y.; Hyun, J.S. Fringe projection profilometry using model-free distorted patterns. Opt. Express 2025, 33, 17527–17543. [Google Scholar] [CrossRef]
- Guo, H.; He, H.; Chen, M. Gamma correction for digital fringe projection profilometry. Appl. Opt. 2004, 43, 2906–2914. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Lau, D.L.; Hao, Q.; Hassebrook, L.G. Gamma model and its analysis for phase measuring profilometry. J. Opt. Soc. Am. A 2010, 27, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhu, L.; Li, Y.; Tu, D. Generic nonsinusoidal fringe model and gamma calibration in phase measuring profilometry. J. Opt. Soc. Am. A 2012, 29, 1047–1058. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, J.; Zhang, D.; Chen, X.; Wang, Y. Nonlinear Correction for Fringe Projection Profilometry with Shifted-Phase Histogram Equalization. IEEE Trans. Instrum. Meas. 2022, 71, 5005509. [Google Scholar] [CrossRef]
- Hoang, T.; Pan, B.; Nguyen, D.; Wang, Z. Generic gamma correction for accuracy enhancement in fringe-projection profilometry. Opt. Lett. 2010, 35, 1992–1994. [Google Scholar] [CrossRef]
- Yatabe, K.; Ishikawa, K.; Oikawa, Y. Compensation of fringe distortion for phase-shifting three-dimensional shape measurement by inverse map estimation. Appl. Opt. 2016, 55, 6017–6024. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Liu, Y.; Liu, N.; Fan, M.; Su, X. Flexible gamma calculation algorithm based on probability distribution function in digital fringe projection system. Opt. Express 2019, 27, 32047–32057. [Google Scholar] [CrossRef] [PubMed]
- García-Isáis, C.A.; Ochoa, N.A.; Cruz-Salgado, J. Simultaneous one-shot profilometry and gamma correction. Opt. Eng. 2019, 58, 034104. [Google Scholar] [CrossRef]
- Munoz, A.; Flores, J.L.; Parra-Escamilla, G.; Morales, L.A.; Ordones, S.; Servin, M. Least-squares gamma estimation in fringe projection profilometry. Appl. Opt. 2021, 60, 1137–1142. [Google Scholar] [CrossRef]
- Li, L.; Xu, X.; Pang, J.; Wu, J. Study on gamma correction for three-dimensional fringe projection measurement based on attention U-Net network. Opt. Eng. 2024, 63, 053103. [Google Scholar] [CrossRef]
- Zhang, S. Comparative study on passive and active projector nonlinear gamma calibration. Appl. Opt. 2015, 54, 3834–3841. [Google Scholar] [CrossRef]
- Gai, S.; Da, F. A novel fringe adaptation method for digital projector. Opt. Lasers Eng. 2011, 49, 547–552. [Google Scholar] [CrossRef]
- Yuan, L.; Kang, J.; Feng, L.; Chen, Y.; Wu, B. Accurate calibration for crosstalk coefficient based on orthogonal color phase-shifting pattern. Opt. Express 2023, 31, 23115–23126. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhao, H.; Zhao, Z. Research on iterative decoupling algorithm in color fringe projection profilometry. Opt. Laser Technol. 2023, 164, 109541. [Google Scholar] [CrossRef]
- Huang, P.S.; Hu, Q.; Jin, F.; Chiang, F.P. Color-encoded fringe projection and phase shifting for 3D surface contouring. Proc. SPIE 1998, 3407, 477–482. [Google Scholar]
- Hu, J.; Mai, S.; Jiang, Y.; Xu, Y. A high-precision crosstalk coefficient calibration method based on maximum distance rotating fringes and noise suppression by spatial matching filtering. Opt. Laser Technol. 2025, 183, 112301. [Google Scholar] [CrossRef]
- Liu, B.; Wang, C.; Wang, S.; Wu, G. Color crosstalk compensation method for color phase-shifting fringe projection profilometry based on the phase correction matrix. Opt. Express 2024, 32, 5793–5808. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Cao, Y.; He, D.; Chen, C. Grayscale imbalance correction in real-time phase measuring profilometry. Opt. Commun. 2016, 376, 72–80. [Google Scholar] [CrossRef]
- Pan, J.; Huang, P.S.; Chiang, F.P. Color-encoded digital fringe projection technique for high-speed 3-D shape measurement: Color coupling and imbalance compensation. In Proceedings of the Two- and Three-Dimensional Vision Systems for Inspection, Control, and Metrology, Philadelphia, PA, USA, 25–28 October 2004; Batchelor, B.G., Hugli, H., Eds.; Volume 5265, pp. 205–212. [Google Scholar]
- Zhao, X.; Yu, T.; Liang, D.; He, Z. A review on 3D measurement of highly reflective objects using structured light projection. Int. J. Adv. Manuf. Technol. 2024, 132, 4205–4222. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Vega, F.; Esquivel-Hernandez, S.; Diaz-Ramirez, V.H.; Marrugo, A.G. Phase feedback fringe projection profilometry for shiny objects. Opt. Lasers Eng. 2025, 191, 109013. [Google Scholar] [CrossRef]
- Feng, L.; Sun, Z.; Chen, Y.; Li, H.; Chen, Y.; Liu, H.; Liu, R.; Zhao, Z.; Liang, J.; Zhang, Z.; et al. Rapid in-situ accuracy evaluation and exposure optimization method for fringe projection profilometry. Opt. Laser Technol. 2025, 181, 111844. [Google Scholar] [CrossRef]
- Zhang, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Yin, W.; Chen, Q.; Feng, S.; Tao, T.; Huang, L.; Trusiak, M.; Asundi, A.; Zuo, C. Temporal phase unwrapping using deep learning. Sci. Rep. 2019, 9, 20175. [Google Scholar] [CrossRef]
- Wang, K.; Kemao, Q.; Di, J.; Zhao, J. Deep learning spatial phase unwrapping: A comparative review. Adv. Photonics Nexus 2022, 1, 014001. [Google Scholar] [CrossRef]
- Lv, S.; Kemao, Q. Modeling the measurement precision of Fringe Projection Profilometry. Light. Sci. Appl. 2023, 12, 257. [Google Scholar] [CrossRef]
- Shang, H.; Liu, C.; Wang, R. Measurement methods of 3D shape of large-scale complex surfaces based on computer vision: A review. Measurement 2022, 197, 111302. [Google Scholar] [CrossRef]
- An, H.; Cao, Y.; Li, H.; Zhang, H. Temporal Phase Unwrapping Based on Unequal Phase-Shifting Code. IEEE Trans. Image Process. 2023, 32, 1432–1441. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Cao, Y.; Dai, Y.; Qin, J. Spatial-Temporal 3-D Directional Binary Coding Method for Fringe Projection Profilometry. IEEE Trans. Instrum. Meas. 2025, 74, 1009211. [Google Scholar] [CrossRef]
- Ray, S. Applied Photographic Optics, 3rd ed.; Taylor & Francis: Abingdon, UK, 2002. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Juarez-Salazar, R.; Zheng, J.; Diaz-Ramirez, V.H. Distorted pinhole camera modeling and calibration. Appl. Opt. 2020, 59, 11310–11318. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Diaz-Ramirez, V.H. Operator-based homogeneous coordinates: Application in camera document scanning. Opt. Eng. 2017, 56, 070801. [Google Scholar] [CrossRef][Green Version]
- Maciel, J.; Costeira, J. A global solution to sparse correspondence problems. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 187–199. [Google Scholar] [CrossRef]
- Mouaddib, E.; Batlle, J.; Salvi, J. Recent progress in structured light in order to solve the correspondence problem in stereovision. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 1, pp. 130–136. [Google Scholar]
- Juarez-Salazar, R.; Rios-Orellana, O.I.; Diaz-Ramirez, V.H. Stereo-phase rectification for metric profilometry with two calibrated cameras and one uncalibrated projector. Appl. Opt. 2022, 61, 6097–6109. [Google Scholar] [CrossRef]
- Rastogi, P.; Hack, E. Phase Estimation in Optical Interferometry; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Juarez-Salazar, R.; Mendoza-Rodriguez, C.; Hernandez-Beltran, J.E.; Robledo-Sanchez, C. How do phase-shifting algorithms work? Eur. J. Phys. 2018, 39, 065302. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Juarez-Salazar, R.; Esquivel-Hernandez, S.; Diaz-Ramirez, V.H. Are camera, projector, and camera-projector calibrations different? Appl. Opt. 2023, 62, 5999–6006. [Google Scholar] [CrossRef]
- Geiger, A.; Moosmann, F.; Car, O.; Schuster, B. Automatic camera and range sensor calibration using a single shot. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 3936–3943. [Google Scholar]
- Juarez-Salazar, R.; Zheng, J.; Giron, A.; Diaz-Ramirez, V.H. Calibration of camera-projector fringe projection systems for three-dimensional scanning. Proc. SPIE 2019, 11136, 111360D. [Google Scholar]
- Xu, L.; Cao, Y.; Yu, Y.; Wang, J.; Zhou, L. Projector undistortion for high-accuracy fringe projection profilometry. Meas. Sci. Technol. 2021, 32, 105009. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, G.; Lau, D.L.; Zhang, B.; Xu, B.; Liu, K. Jointly correcting lens distortion of structured light systems. J. Opt. 2024, 27, 015702. [Google Scholar] [CrossRef]
- Rivera-Ortega, U.; Dirckx, J.; Meneses-Fabian, C. Fully automated low-cost setup for fringe projection profilometry. Appl. Opt. 2015, 54, 1350–1353. [Google Scholar] [CrossRef]
- Spagnolo, G.S.; Guattari, G.; Sapia, C.; Ambrosini, D.; Paoletti, D.; Accardo, G. Three-dimensional optical profilometry for artwork inspection. J. Opt. A Pure Appl. Opt. 2000, 2, 353. [Google Scholar] [CrossRef]
- Vairavan, R.; Retnasamy, V.; Shahimin, M.M.; Sauli, Z.; Leng, L.S.; Norhaimi, W.M.W.; Marimuthu, R.; Abdullah, O.; Kirtsaeng, S. 3D mapping of breast surface using digital fringe projection. Proc. SPIE 2017, 10043, 1004315. [Google Scholar]
- Norouzi, M.; Shirin, M.B. Investigating the precision of 3D scanner systems based on digital fringe projection method for biomedical engineering applications. In Proceedings of the 28th National and 6th International Iranian Conference on Biomedical Engineering, Tehran, Iran, 25–26 November 2021; pp. 58–64. [Google Scholar]
- Lorenz, A.L.; Zhang, S. Human Respiration Rate Measurement with High-Speed Digital Fringe Projection Technique. Sensors 2023, 23, 9000. [Google Scholar] [CrossRef]
- Muyshondt, P.G.; Van der Jeught, S.; Dirckx, J.J. A calibrated 3D dual-barrel otoendoscope based on fringe-projection profilometry. Opt. Lasers Eng. 2022, 149, 106795. [Google Scholar] [CrossRef]
- Bielfeldt, S.; Springmann, G.; Seise, M.; Wilhelm, K.P.; Callaghan, T. An updated review of clinical methods in the assessment of ageing skin—New perspectives and evaluation for claims support. Int. J. Cosmet. Sci. 2018, 40, 348–355. [Google Scholar] [CrossRef]
- Liang, J.; Luo, H.; Yokell, Z.; Nakmali, D.U.; Gan, R.Z.; Lu, H. Characterization of the nonlinear elastic behavior of chinchilla tympanic membrane using micro-fringe projection. Hear. Res. 2016, 339, 1–11. [Google Scholar] [CrossRef]
- Price, G.J.; Parkhurst, J.M.; Sharrock, P.J.; Moore, C.J. Real-time optical measurement of the dynamic body surface for use in guided radiotherapy. Phys. Med. Biol. 2011, 57, 415. [Google Scholar] [CrossRef]
- Le, H.N.D.; Nguyen, H.; Wang, Z.; Opfermann, J.; Leonard, S.; Krieger, A.; Kang, J.U. Demonstration of a laparoscopic structured-illumination three-dimensional imaging system for guiding reconstructive bowel anastomosis. J. Biomed. Opt. 2018, 23, 056009. [Google Scholar] [CrossRef]
- Genovese, K.; Humphrey, J.D. Multimodal optical measurement in vitro of surface deformations and wall thickness of the pressurized aortic arch. J. Biomed. Opt. 2015, 20, 046005. [Google Scholar] [CrossRef]
- Chen, S. Intraoral 3-D Measurement by Means of Group Coding Combined with Consistent Enhancement for Fringe Projection Pattern. IEEE Trans. Instrum. Meas. 2022, 71, 5018512. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Q.; Feng, S.; Zuo, C. Microscopic fringe projection profilometry: A review. Opt. Lasers Eng. 2020, 135, 106192. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Xu, M.; Tao, T.; Shang, Y.; Chen, Q.; Zuo, C. High-resolution real-time 360° 3D surface defect inspection with fringe projection profilometry. Opt. Lasers Eng. 2021, 137, 106382. [Google Scholar] [CrossRef]
- Casavola, C.; Pappalardi, P.; Pappalettera, G.; Renna, G. A Fringe Projection Based Approach for Corrosion Monitoring in Metals. Exp. Tech. 2018, 42, 291–297. [Google Scholar] [CrossRef]
- Ma, H.; Wang, J.; Shao, M. Crack recognition approach assisted by three-dimensional measurement technique. J. Opt. 2024, 53, 4981–4987. [Google Scholar] [CrossRef]
- Li, B.; Xu, Z.; Gao, F.; Cao, Y.; Dong, Q. 3D Reconstruction of High Reflective Welding Surface Based on Binocular Structured Light Stereo Vision. Machines 2022, 10, 159. [Google Scholar] [CrossRef]
- Schlobohm, J.; Bruchwald, O.; Frąckowiak, W.; Li, Y.; Kästner, M.; Pösch, A.; Reimche, W.; Maier, H.J.; Reithmeier, E. Advanced Characterization Techniques for Turbine Blade Wear and Damage. Procedia CIRP 2017, 59, 83–88. [Google Scholar] [CrossRef]
- Xia, R.; Zhao, J.; Zhang, T.; Su, R.; Chen, Y.; Fu, S. Detection method of manufacturing defects on aircraft surface based on fringe projection. Optik 2020, 208, 164332. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, G.; Li, W.; Zhang, L.; Luo, N. Palmprint Recognition Using 3-D Information. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2009, 39, 505–519. [Google Scholar] [CrossRef]
- Ou, P.; Li, B.; Wang, Y.; Zhang, S. Flexible real-time natural 2D color and 3D shape measurement. Opt. Express 2013, 21, 16736–16741. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Huang, P.S. Face recognition based on fringe pattern analysis. Opt. Eng. 2010, 49, 037201. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, S.; Xu, Y.; Chen, C.; Zhao, Y.; Gao, N.; Xiao, Y. 3D palmprint and hand imaging system based on full-field composite color sinusoidal fringe projection technique. Appl. Opt. 2013, 52, 6138–6145. [Google Scholar] [CrossRef]
- Bai, X.; Gao, N.; Zhang, Z.; Zhang, D. Person Recognition Using 3-D Palmprint Data Based on Full-Field Sinusoidal Fringe Projection. IEEE Trans. Instrum. Meas. 2019, 68, 3287–3298. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, Z.; Zhao, Y.; Dai, J.; Chen, C.; Xu, Y.; Zhang, E.; Xie, L. 3D fingerprint imaging system based on full-field fringe projection profilometry. Opt. Lasers Eng. 2014, 52, 123–130. [Google Scholar] [CrossRef]
- Chatterjee, A.; Singh, P.; Bhatia, V.; Prakash, S. Ear biometrics recognition using laser biospeckled fringe projection profilometry. Opt. Laser Technol. 2019, 112, 368–378. [Google Scholar] [CrossRef]
- Zhang, H.; Lee, S. Robot Bionic Vision Technologies: A Review. Appl. Sci. 2022, 12, 7970. [Google Scholar] [CrossRef]
- de Jesus Ortiz-Gonzalez, A.; Martinez-Garcia, A.; Pascual-Francisco, J.B.; Rayas-Alvarez, J.A.; de Jesus Flores-Garcia, A. 3D shape and strain measurement of a thin-walled elastic cylinder using fringe projection profilometry. Appl. Opt. 2021, 60, 1349–1356. [Google Scholar] [CrossRef]
- Balasubramaniam, B.; Li, J.; Liu, L.; Li, B. 3D Imaging with Fringe Projection for Food and Agricultural Applications—A Tutorial. Electronics 2023, 12, 859. [Google Scholar] [CrossRef]
- Berkson, J.; Hyatt, J.; Julicher, N.; Jeong, B.; Pimienta, I.; Ball, R.; Ellis, W.; Voris, J.; Torres-Barajas, D.; Kim, D. Systematic Radio Telescope Alignment Using Portable Fringe Projection Profilometry. Nanomanuf. Metrol. 2024, 7, 6. [Google Scholar] [CrossRef]
- Liberadzki, P.; Adamczyk, M.; Witkowski, M.; Sitnik, R. Structured-Light-Based System for Shape Measurement of the Human Body in Motion. Sensors 2018, 18, 2827. [Google Scholar] [CrossRef] [PubMed]
- Heist, S.; Dietrich, P.; Landmann, M.; Kühmstedt, P.; Notni, G.; Tünnermann, A. GOBO projection for 3D measurements at highest frame rates: A performance analysis. Light. Sci. Appl. 2018, 7, 71. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, G.; Ambrosini, D.; Paoletti, D. Low-cost optoelectronic system for three-dimensional artwork texture measurement. IEEE Trans. Image Process. 2004, 13, 390–396. [Google Scholar] [CrossRef]
- Sansoni, G.; Docchio, F. 3-D optical measurements in the field of cultural heritage: The case of the Vittoria Alata of Brescia. IEEE Trans. Instrum. Meas. 2005, 54, 359–368. [Google Scholar] [CrossRef]
- Burke, J.; Bothe, T.; Osten, W.; Hess, C.F. Reverse engineering by fringe projection. In Proceedings of the Interferometry XI: Applications, Seattle, WA, USA, 7–11 July 2002; Osten, W., Ed.; SPIE: Bellingham, WA, USA, 2002; Volume 4778, pp. 312–324. [Google Scholar]
- Hu, C.; Wang, Y.; Xia, G.; Han, Y.; Ma, X.; Jing, G. The generation method of orthophoto expansion map of arched dome mural based on three-dimensional fine color model. Herit. Sci. 2024, 12, 408. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, Y.; Zhang, Z.; Geng, N. A Non-Contact Measurement of Animal Body Size Based on Structured Light. Appl. Sci. 2024, 14, 903. [Google Scholar] [CrossRef]
- Hyun, J.S.; Carmichael, M.G.; Tran, A.; Zhang, S.; Liu, D. Evaluation of Fast, High-detail Projected Light 3D Sensing for Robots in Construction. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1262–1267. [Google Scholar]
- Nogales, S.O.; Servin, M.; Padilla, M.; Choque, I.; Nuñez, J.L.F.; Muñoz, A. Shape defect measurement by fringe projection profilometry and phase-shifting algorithms. Opt. Eng. 2020, 59, 014107. [Google Scholar] [CrossRef]
- Ma, R.; Li, J.; He, K.; Tang, T.; Zhang, Y.; Gao, X. Application of Moire Profilometry in Three-Dimensional Profile Reconstruction of Key Parts in Railway. Sensors 2022, 22, 2498. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).