Periodic Relief Fabrication and Reversible Phase Transitions in Amorphous Ge2Sb2Te5 Thin Films upon Multi-Pulse Femtosecond Irradiation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples and Experimental Techniques
2.2. Theoretical Simulation of Surface Photoexcitation and LIPSS Formation
3. Results and Discussion
3.1. Structural Properties
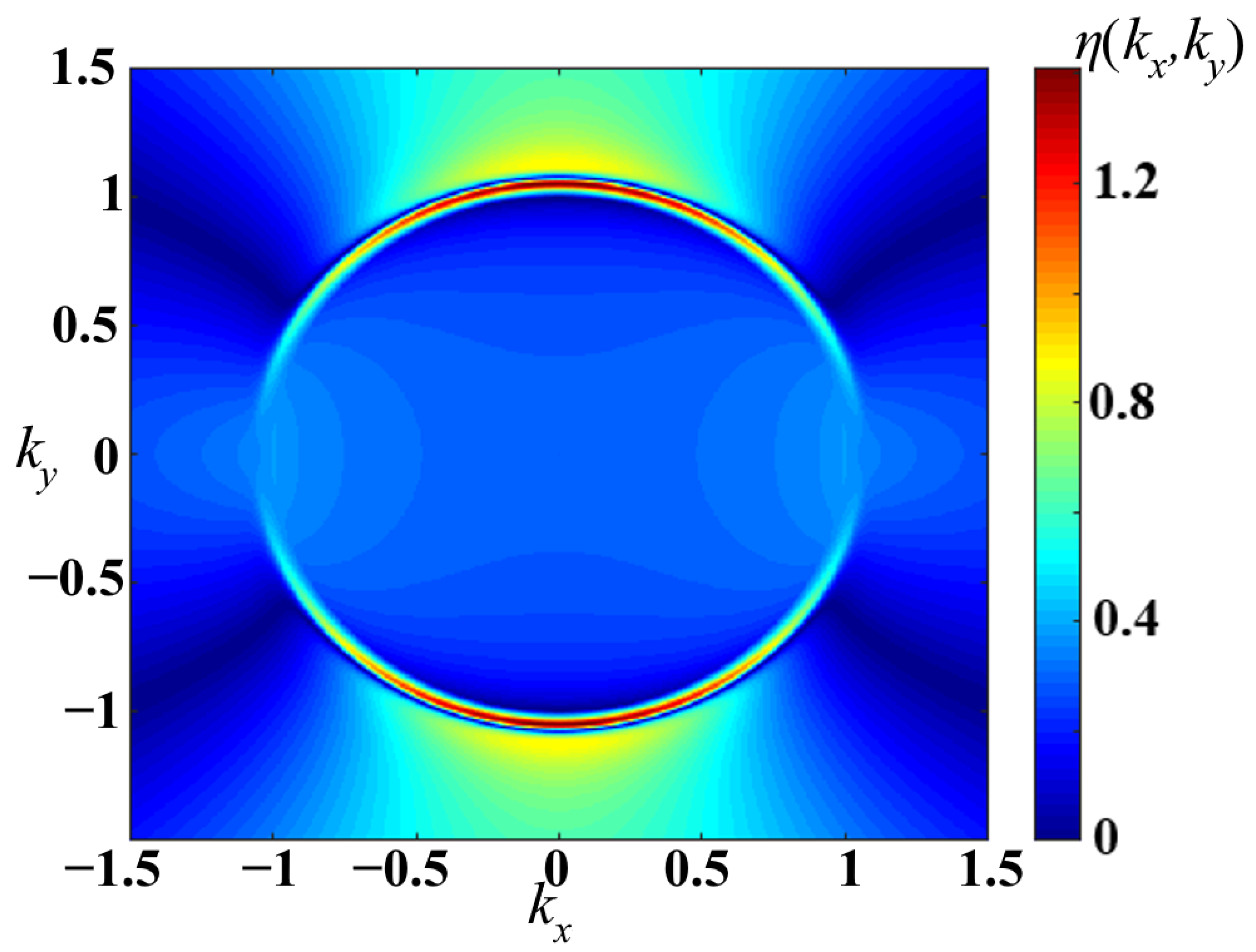
3.2. Modelling of LIPSS Formation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, P.; Sarangan, A.M.; Agha, I. A Review of Germanium-Antimony-Telluride Phase Change Materials for Non-Volatile Memories and Optical Modulators. Appl. Sci. 2019, 9, 530. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Chen, C.; Liu, S.; Li, G. Nonvolatile, Reconfigurable and Narrowband Mid-Infrared Filter Based on Surface Lattice Resonance in Phase-Change Ge2Sb2Te5. Nanomaterials 2020, 10, 2530. [Google Scholar] [CrossRef]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef]
- Sun, X.; Roß, U.; Gerlach, J.W.; Lotnyk, A.; Rauschenbach, B. Nanoscale Bipolar Electrical Switching of Ge2Sb2Te5 Phase-Change Material Thin Films. Adv. Electron. Mater. 2017, 3, 3. [Google Scholar] [CrossRef]
- Sun, X.; Ehrhardt, M.; Lotnyk, A.; Lorenz, P.; Thelander, E.; Gerlach, J.W.; Smausz, T.; Decker, U.; Rauschenbach, B. Crystallization of Ge2Sb2Te5 thin films by nano- and femtosecond single laser pulse irradiation. Sci. Rep. 2016, 6, 28246. [Google Scholar] [CrossRef]
- Liu, Y.; Aziz, M.M.; Shalini, A.; Wright, C.D.; Hicken, R.J. Crystallization of Ge2Sb2Te5 films by amplified femtosecond optical pulses. J. Appl. Phys. 2012, 112, 123526. [Google Scholar] [CrossRef] [Green Version]
- Kunkel, T.; Vorobyov, Y.; Smayev, M.; Lazarenko, P.; Veretennikov, V.; Sigaev, V.; Kozyukhin, S. Experimental observation of two-stage crystallization of Ge2Sb2Te5 amorphous thin films under the influence of a pulsed laser. J. Alloys Compd. 2021, 851, 156924. [Google Scholar] [CrossRef]
- Siegel, J.; Gawelda, W.; Puerto, D.; Dorronsoro, C.; Solis, J.; Afonso, C.N.; DE Sande, J.C.G.; Bez, R.; Pirovano, A.; Wiemer, C. Amorphization dynamics of Ge2Sb2Te5 films upon nano- and femtosecond laser pulse irradiation. J. Appl. Phys. 2008, 103, 023516. [Google Scholar] [CrossRef] [Green Version]
- Hada, M.; Oba, W.; Kuwahara, M.; Katayama, I.; Saiki, T.; Takeda, J.; Nakamura, K.G. Ultrafast time-resolved electron diffraction revealing the nonthermal dynamics of near-UV photoexcitation-induced amorphization in Ge2Sb2Te5. Sci. Rep. 2015, 5, 13530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.H.; Liu, F.R. Observation of the femtosecond laser-induced ultrafast amorphization in Ge2Sb2Te5 films by dynamics spectrum. J. Phys. Conf. Ser. 2020, 1676, 012161. [Google Scholar] [CrossRef]
- Ionin, A.A.; Kudryashov, S.I.; Samokhin, A. Material surface ablation produced by ultrashort laser pulses. Uspekhi Fizicheskih Nauk. 2017, 187, 159–172. [Google Scholar] [CrossRef]
- Inogamov, N.A.; Petrov, Y.V.; Khokhlov, V.A.; Zhakhovskii, V.V. Laser Ablation: Physical Concepts and Applications (Review). High Temp. 2020, 58, 632–646. [Google Scholar] [CrossRef]
- Bonse, J.; Kruger, J.; Höhm, S.; Rosenfeld, A. Femtosecond laser-induced periodic surface structures. J. Laser Appl. 2012, 24, 042006. [Google Scholar] [CrossRef]
- Kozyukhin, S.; Lazarenko, P.; Vorobyov, Y.; Baranchikov, A.; Glukhenkaya, V.; Smayev, M.; Sherchenkov, A.; Sybina, Y.; Polohin, A.; Sigaev, V. Laser-induced modification and formation of periodic surface structures (ripples) of amorphous GST225 phase change materials. Opt. Laser Technol. 2019, 113, 87–94. [Google Scholar] [CrossRef]
- Kozyukhin, S.; Smayev, M.; Sigaev, V.; Vorobyov, Y.; Zaytseva, Y.; Sherchenkov, A.; Lazarenko, P. Specific Features of Formation of Laser-Induced Periodic Surface Structures on Ge2Sb2Te5 Amorphous Thin Films under Illumination by Femtosecond Laser Pulses. Phys. Status Solidi 2020, 257, 257. [Google Scholar] [CrossRef]
- Kolchin, A.V.; Shuleiko, D.V.; Zabotnov, S.V.; Golovan, L.A.; Presnov, D.E.; Kaminskaya, T.P.; Lazarenko, P.I.; Kozyukhin, S.A.; Kashkarov, P.K. Formation of periodic surface structures in multilayer amorphous Ge2Sb2Te5 thin films irradiated by femtosecond laser pulses. J. Phys. Conf. Ser. 2020, 1686, 012006. [Google Scholar] [CrossRef]
- Bonse, J.; Gräf, S. Maxwell Meets Marangoni—A Review of Theories on Laser-Induced Periodic Surface Structures. Laser Photon. Rev. 2020, 14, 2000215. [Google Scholar] [CrossRef]
- Drevinskas, R.; Beresna, M.; Gecevičius, M.; Khenkin, M.; Kazanskii, A.G.; Matulaitienė, I.; Niaura, G.; Konkov, O.I.; Terukov, E.I.; Svirko, Y.P.; et al. Giant birefringence and dichroism induced by ultrafast laser pulses in hydrogenated amorphous silicon. Appl. Phys. Lett. 2015, 106, 171106. [Google Scholar] [CrossRef]
- Shuleiko, D.; Martyshov, M.; Amasev, D.; Presnov, D.; Zabotnov, S.; Golovan, L.; Kazanskii, A.; Kashkarov, P. Fabricating Femtosecond Laser-Induced Periodic Surface Structures with Electrophysical Anisotropy on Amorphous Silicon. Nanomaterials 2020, 11, 42. [Google Scholar] [CrossRef]
- Skoulas, E.; Tasolamprou, A.C.; Kenanakis, G.; Stratakis, E. Laser induced periodic surface structures as polarizing optical elements. Appl. Surf. Sci. 2021, 541, 148470. [Google Scholar] [CrossRef]
- Amasev, D.V.; Khenkin, M.V.; Drevinskas, R.; Kazansky, P.; Kazanskii, A.G. Anisotropy of optical, electrical, and photoelectrical properties of amorphous hydrogenated silicon films modified by femtosecond laser irradiation. Tech. Phys. 2017, 62, 925–929. [Google Scholar] [CrossRef]
- Lipatiev, A.S.; Fedotov, S.S.; Okhrimchuk, A.G.; Lotarev, S.V.; Vasetsky, A.M.; Stepko, A.A.; Shakhgildyan, G.Y.; Piyanzina, K.I.; Glebov, I.S.; Sigaev, V.N. Multilevel data writing in nanoporous glass by a few femtosecond laser pulses. Appl. Opt. 2018, 57, 978–982. [Google Scholar] [CrossRef] [PubMed]
- Fedotov, S.; Lipatiev, A.; Presniakov, M.; Shakhgildyan, G.; Okhrimchuk, A.; Lotarev, S.; Sigaev, V.N. Laser-induced cavities with controllable shape in nanoporous glass. Opt. Lett. 2020, 45, 5424–5427. [Google Scholar] [CrossRef] [PubMed]
- Lotarev, S.V.; Fedotov, S.S.; Kurina, A.I.; Lipatiev, A.S.; Sigaev, V.N. Ultrafast laser-induced nanogratings in sodium germanate glasses. Opt. Lett. 2019, 44, 1564–1567. [Google Scholar] [CrossRef] [PubMed]
- Dostovalov, A.; Bronnikov, K.; Korolkov, V.; Babin, S.; Mitsai, E.; Mironenko, A.; Tutov, M.; Zhang, D.; Sugioka, K.; Maksimovic, J.; et al. Hierarchical anti-reflective laser-induced periodic surface structures (LIPSSs) on amorphous Si films for sensing applications. Nanoscale 2020, 12, 13431–13441. [Google Scholar] [CrossRef]
- Varlamova, O.; Reif, J.; Stolz, M.; Borcia, R.; Borcia, I.D.; Bestehorn, M. Wetting properties of LIPSS structured silicon surfaces. Eur. Phys. J. B 2019, 92, 91. [Google Scholar] [CrossRef]
- Lazarenko, P.I.; Vorobyov, Y.V.; Fedyanina, M.E.; Sherchenkov, A.A.; Kozyukhin, S.; Yakubov, A.O.; Kukin, A.; Sybina, Y.S.; Sagunova, I.V. Peculiarities of Estimating the Optical Band Gap of Thin Films of Phase Change Memory Materials. Inorg. Mater. Appl. Res. 2020, 11, 330–337. [Google Scholar] [CrossRef]
- Gutwirth, J.; Wagner, T.; Bezdicka, P.; Hrdlička, M.; Vlček, M.; Frumar, M. On angle resolved RF magnetron sputtering of Ge–Sb–Te thin films. J. Non-Cryst. Solids 2009, 355, 1935–1938. [Google Scholar] [CrossRef]
- Agranat, M.B.; Ashitkov, S.I.; Ivanov, A.A.; Konyashchenko, A.V.; Ovchinnikov, A.V.; Podshivalov, A.A. Gigawatt Cr:forsterite regenerative amplifier of femtosecond pulses with a pulse repetition rate of 10 Hz. Quantum Electron. 2004, 34, 1018–1022. [Google Scholar] [CrossRef]
- Gordienko, V.M.; Ivanov, A.A.; Podshivalov, A.A.; Savel’Ev, A.B.; Rakov, E.V. Generation of superintense femtosecond pulses by the Cr:forsterite laser system. Laser Phys. 2006, 16, 427–435. [Google Scholar] [CrossRef]
- Andrikopoulos, K.S.; Yannopoulos, S.N.; Voyiatzis, G.A.; Kolobov, A.V.; Ribes, M.; Tominaga, J. Raman scattering study of the a-GeTe structure and possible mechanism for the amorphous to crystal transition. J. Phys. Condens. Matter 2006, 18, 965–979. [Google Scholar] [CrossRef] [Green Version]
- Emel’Yanov, V.I.; Zemskov, E.M.; Seminogov, V.N. Theory of formation of surface gratings under the action of laser radiation on surfaces of metals, semiconductors, and insulators. Sov. J. Quantum Electron. 1983, 13, 1556–1561. [Google Scholar] [CrossRef]
- Emel’Yanov, V.I.; Zemskov, E.M.; Seminogov, V.N. Theory of the formation of "normal" and "anomalous" gratings on the surfaces of absorbing condensed media exposed to laser radiation. Sov. J. Quantum Electron. 1984, 14, 1515–1521. [Google Scholar] [CrossRef]
- Shelimova, L.E.; Karpinskii, O.G.; Konstantinov, P.P.; Kretova, M.A.; Avilov, E.S.; Zemskov, V.S. Composition and Properties of Layered Compounds in the GeTe–Sb2Te3System. Inorg. Mater. 2001, 37, 342–348. [Google Scholar] [CrossRef]
- Dyukin, R.V.; Martsinovskiĭ, G.A.; Shandybina, G.D.; Yakovlev, E.B. Electrophysical phenomena accompanying femtosecond impacts of laser radiation on semiconductors. J. Opt. Technol. 2011, 78, 88–92. [Google Scholar] [CrossRef]
- Sipe, J.E.; Young, J.F.; Preston, J.; Van Driel, H.M. Laser-induced periodic surface structure. I. Theory. Phys. Rev. B 1983, 27, 1141–1154. [Google Scholar] [CrossRef]
- Bonse, J.; Rosenfeld, A.; Krüger, J. On the role of surface plasmon polaritons in the formation of laser-induced periodic surface structures upon irradiation of silicon by femtosecond-laser pulses. J. Appl. Phys. 2009, 106, 104910. [Google Scholar] [CrossRef]
- Bonse, J.; Rosenfeld, A.; Krüger, J. Implications of transient changes of optical and surface properties of solids during femtosecond laser pulse irradiation to the formation of laser-induced periodic surface structures. Appl. Surf. Sci. 2011, 257, 5420–5423. [Google Scholar] [CrossRef]
- Libenson, M.N. Laser-Induced Optical and Thermal Processes in Condensed Media and Their Mutual Influence; Nauka: Saint-Petersburg, Russia, 2007; p. 219. [Google Scholar]
- Němec, P.; Nazabal, V.; Moreac, A.; Gutwirth, J.; Beneš, L.; Frumar, M. Amorphous and crystallized Ge–Sb–Te thin films deposited by pulsed laser: Local structure using Raman scattering spectroscopy. Mater. Chem. Phys. 2012, 136, 935–941. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, C.; Wang, Z.; Wu, K.; Chong, H.; Ye, H. Optical constants acquisition and phase change properties of Ge2Sb2Te5 thin films based on spectroscopy. RSC Adv. 2018, 8, 21040–21046. [Google Scholar] [CrossRef] [Green Version]
- Yin, Q.; Chen, L. Microstructure and crystallization kinetics of Ge2Sb2Te5–Sn phase change materials. J. Mater. Sci. Mater. Electron. 2018, 29, 16523–16533. [Google Scholar] [CrossRef]
- Kozyukhin, S.; Veres, M.; Nguyen, H.; Ingram, A.; Kudoyarova, V. Structural Changes in Doped Ge2Sb2Te5 Thin Films Studied by Raman Spectroscopy. Phys. Procedia 2013, 44, 82–90. [Google Scholar] [CrossRef] [Green Version]
- Vorobyov, Y.; Lazarenko, P.; Sherchenkov, A.; Vishnyakov, N.; Ermachikhin, A.; Kozyukhin, S. Kinetics of volume and surface driven crystallization in thin films. J. Phys. Condens. Matter 2020, 32, 355401. [Google Scholar] [CrossRef] [PubMed]
- Yamada, N.; Ohno, E.; Nishiuchi, K.; Akahira, N.; Takao, M. Rapid-phase transitions of GeTe-Sb2Te3pseudobinary amorphous thin films for an optical disk memory. J. Appl. Phys. 1991, 69, 2849–2856. [Google Scholar] [CrossRef]
- Bogoslovskiy, N.A.; Tsendin, K.D. Physics of switching and memory effects in chalcogenide glassy semiconductors. Semiconductors 2012, 46, 559–590. [Google Scholar] [CrossRef]
- Huang, H.; Zuo, F.; Zhai, F.; Wang, Y.; Lai, T.; Wu, Y.; Gan, F. Fast phase transition process of Ge2Sb2Te5 film induced by picosecond laser pulses with identical fluences. J. Appl. Phys. 2009, 106, 63501. [Google Scholar] [CrossRef]
- Siegel, J.; Schropp, A.; Solis, J.; Afonso, C.N.; Wuttig, M. Rewritable phase-change optical recording in Ge2Sb2Te5 films induced by picosecond laser pulses. Appl. Phys. Lett. 2004, 84, 2250–2252. [Google Scholar] [CrossRef] [Green Version]
- Møller, S.H.; Eriksen, E.H.; Tønning, P.L.; Jensen, P.B.; Chevallier, J.; Balling, P. Femtosecond-laser-induced modifications of Ge2Sb2Te5 thin films: Permanent optical change without amorphization. Appl. Surf. Sci. 2019, 476, 221–231. [Google Scholar] [CrossRef]
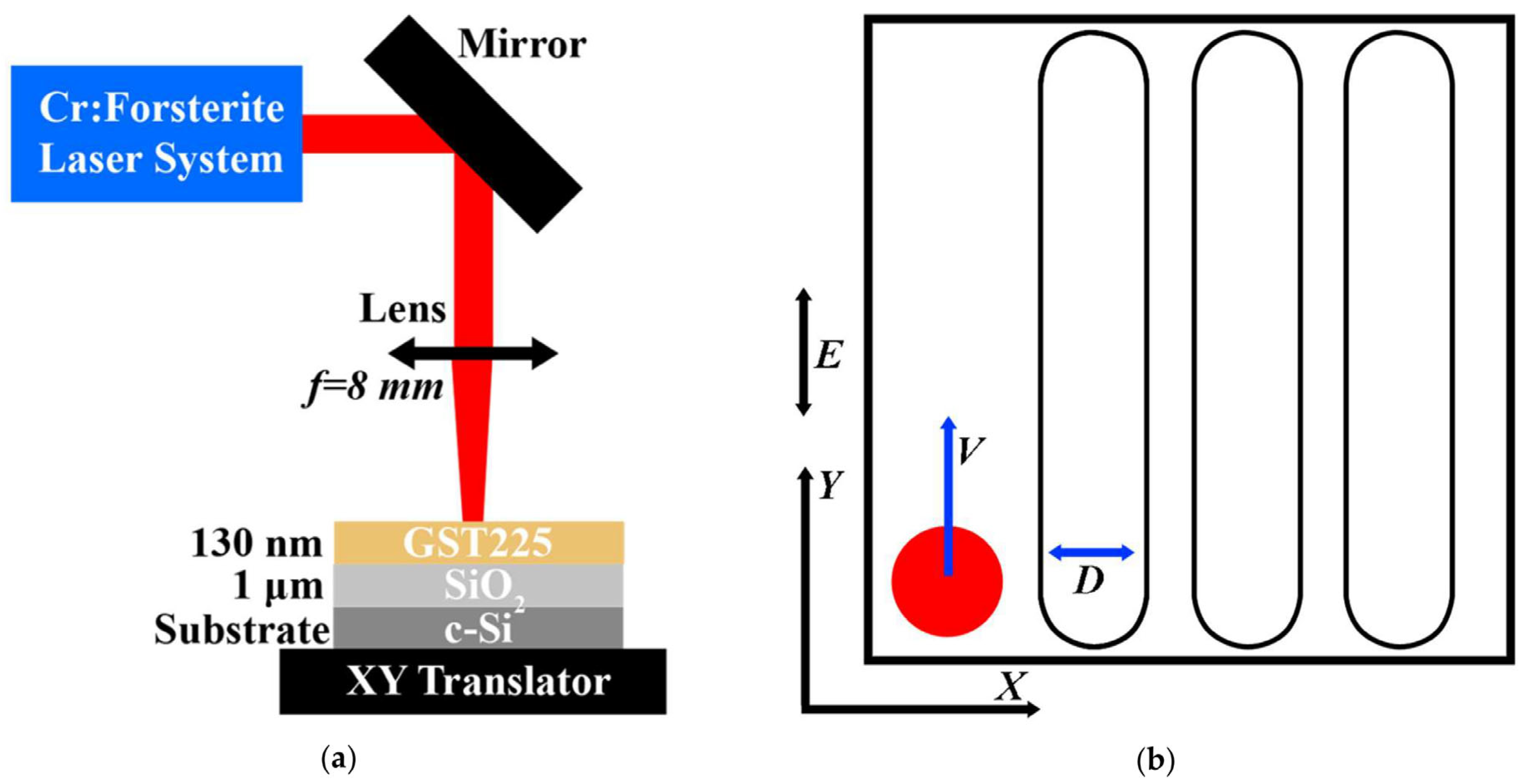



| Sample | Scan Speed, μm/s | Number of Overlapping Laser Spots |
|---|---|---|
| 1 | 500 | 3 |
| 2 | 250 | 6 |
| 3 | 100 | 15 |
| 4 | 50 | 30 |
| 5 | 25 | 60 |
| 6 | 10 | 150 |
| 7 | 5 | 300 |
| 8 | 2 | 750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabotnov, S.; Kolchin, A.; Shuleiko, D.; Presnov, D.; Kaminskaya, T.; Lazarenko, P.; Glukhenkaya, V.; Kunkel, T.; Kozyukhin, S.; Kashkarov, P. Periodic Relief Fabrication and Reversible Phase Transitions in Amorphous Ge2Sb2Te5 Thin Films upon Multi-Pulse Femtosecond Irradiation. Micro 2022, 2, 88-99. https://doi.org/10.3390/micro2010005
Zabotnov S, Kolchin A, Shuleiko D, Presnov D, Kaminskaya T, Lazarenko P, Glukhenkaya V, Kunkel T, Kozyukhin S, Kashkarov P. Periodic Relief Fabrication and Reversible Phase Transitions in Amorphous Ge2Sb2Te5 Thin Films upon Multi-Pulse Femtosecond Irradiation. Micro. 2022; 2(1):88-99. https://doi.org/10.3390/micro2010005
Chicago/Turabian StyleZabotnov, Stanislav, Aleksandr Kolchin, Dmitrii Shuleiko, Denis Presnov, Tatiana Kaminskaya, Petr Lazarenko, Victoriia Glukhenkaya, Tatiana Kunkel, Sergey Kozyukhin, and Pavel Kashkarov. 2022. "Periodic Relief Fabrication and Reversible Phase Transitions in Amorphous Ge2Sb2Te5 Thin Films upon Multi-Pulse Femtosecond Irradiation" Micro 2, no. 1: 88-99. https://doi.org/10.3390/micro2010005
APA StyleZabotnov, S., Kolchin, A., Shuleiko, D., Presnov, D., Kaminskaya, T., Lazarenko, P., Glukhenkaya, V., Kunkel, T., Kozyukhin, S., & Kashkarov, P. (2022). Periodic Relief Fabrication and Reversible Phase Transitions in Amorphous Ge2Sb2Te5 Thin Films upon Multi-Pulse Femtosecond Irradiation. Micro, 2(1), 88-99. https://doi.org/10.3390/micro2010005








