Buckling Electrothermal NEMS Actuators: Analytic Design for Very Slender Beams
Abstract
1. Introduction
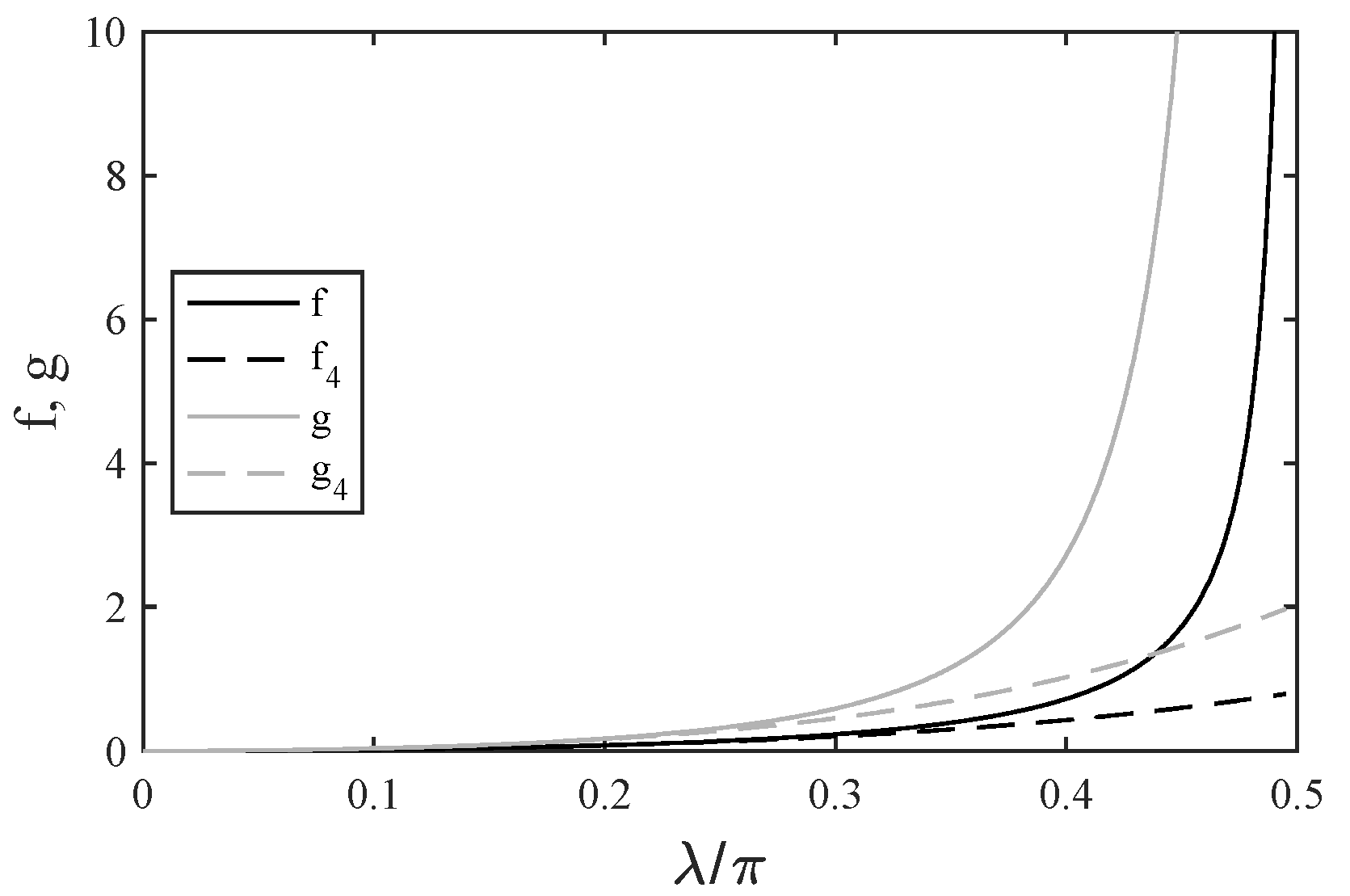
2. Methods
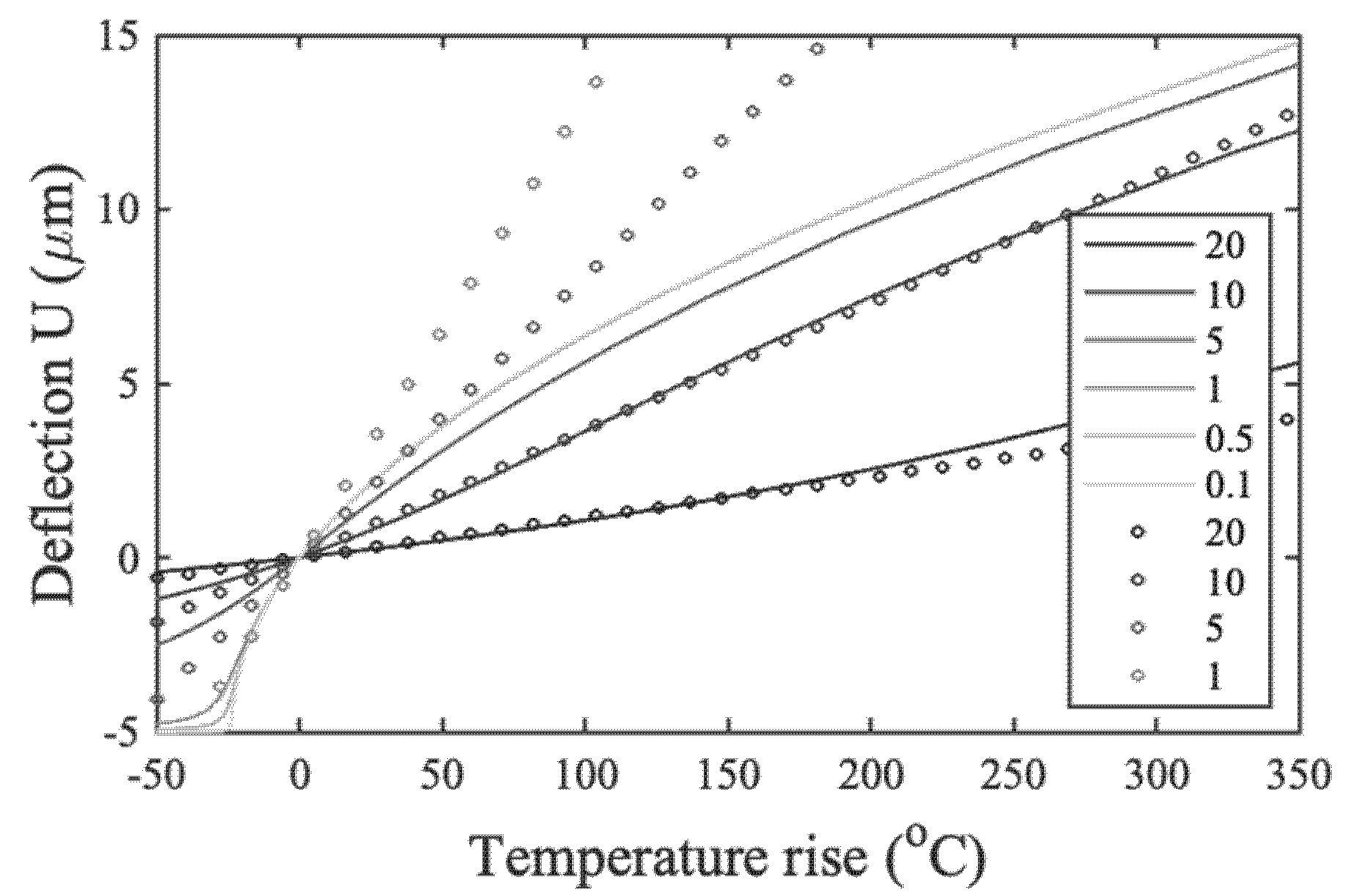
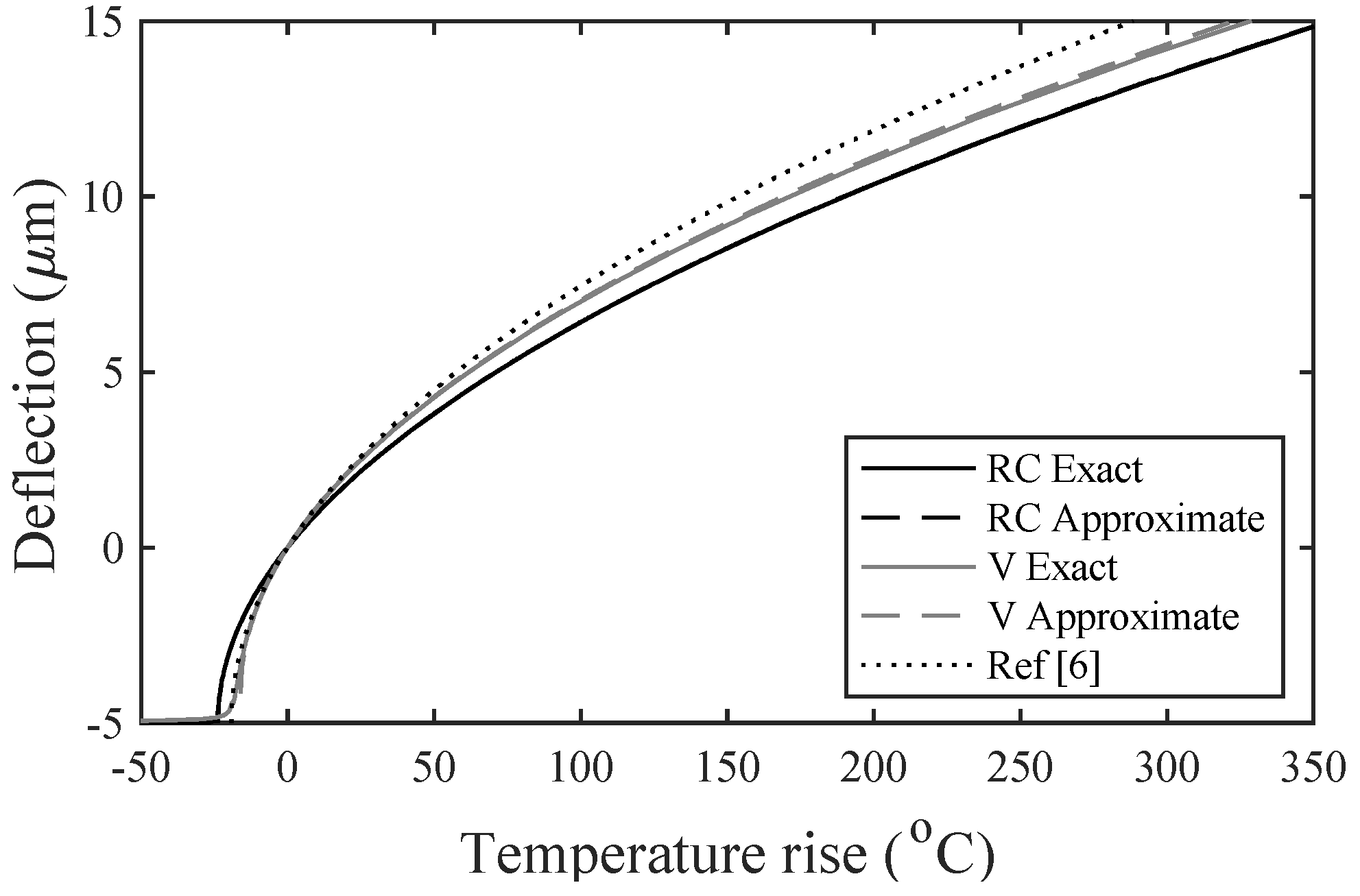
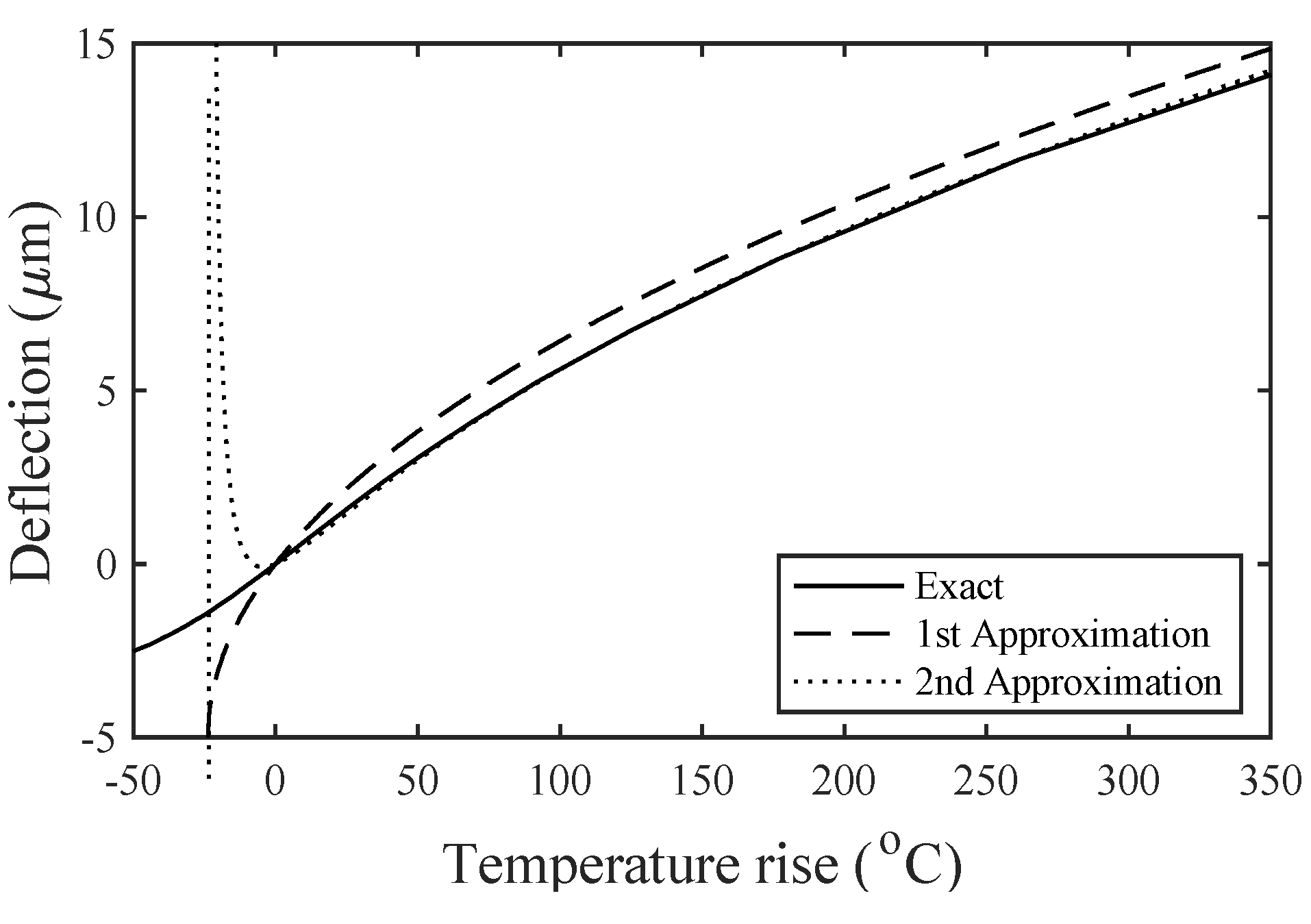
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Noworolski, J.M.; Klaassen, E.H.; Logan, J.R.; Petersen, K.E.; Maluf, N.I. Process for in-plane and out-of-plane single-crystal-silicon thermal microactuators. Sens. Actuators A 1996, 55, 65–69. [Google Scholar] [CrossRef]
- Pan, C.S.; Hsu, W. An electro-thermally and laterally driven polysilicon microactuator. J. Micromech. Microeng. 1997, 7, 7–13. [Google Scholar] [CrossRef]
- Comtois, J.H.; Michalecik, M.A.; Barron, C.C. Electrothermal actuators fabricated in four-level planarized surface micromachined polycrystalline silicon. Sens. Actuators A 1998, 70, 23–31. [Google Scholar] [CrossRef]
- Cragun, R.; Howell, L.L. Linear thermomechanical actuators. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 1999; Volume 16387, pp. 181–188. [Google Scholar] [CrossRef]
- Que, L.; Park, J.; Gianchandani, Y. Bent-beam electrothermal actuators for high force applications. In Proceedings of the Technical Digest. In Proceedings of the IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems, Orlando, FL, USA, 21 January 1999; pp. 31–36. [Google Scholar] [CrossRef]
- Sinclair, M.J. A high force low area MEMS thermal actuator. In Proceedings of the ITHERM 2000. The Seventh Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Las Vegas, NV, USA, 23–26 May 2000; pp. 127–132. [Google Scholar] [CrossRef]
- Que, L.; Park, J.-S.; Gianchandani, Y.B. Bent-beam electrothermal actuators—Part I: Single-beam and cascaded devices. J. Microelectromech. Syst. 2001, 10, 247–254. [Google Scholar] [CrossRef]
- Enikov, E.T.; Kedar, S.S.; Lazarov, K.V. Analytical model for analysis and design of V-shaped thermal microactuators. J. Microelectromech. Syst. 2005, 14, 788–798. [Google Scholar] [CrossRef]
- Hoang, K.T.; Nguyen, D.T.; Pham, P.H. Impact of design parameters on working stability of the electrothermal V-shaped actuator. Microsyst. Technol. 2020, 26, 1479–1487. [Google Scholar] [CrossRef]
- Hussein, H.; Fariborzi, H.; Younis, M.I. Modeling of beam electrothermal actuators. J. Microelectromech. Syst. 2020, 29, 1570–1581. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.-J.; Wang, J.; Xi, Z.-W. Analysis of the dynamic behaviour of a V-shaped electrothermal microactuator. J. Micromech. Microeng. 2020, 30, 085005. [Google Scholar] [CrossRef]
- Alcheikh, N.; Ouakad, H.M.; Younis, M.I. Dynamics of V-shaped electrothermal MEMS-based resonators. J. Microelectromech. Syst. 2020, 29, 1372–1381. [Google Scholar] [CrossRef]
- Baracu, A.; Voicu, R.; Müller, R.; Avram, A.; Pustan, M.; Chiorean, R.; Birleanu, C.; Dodescu, C. Design and fabrication of a MEMS Chevron-type thermal actuator. AIP Conf. Proc. 2015, 25, 25–30. [Google Scholar] [CrossRef]
- Shan, T.; Qi, X.; Cui, L.; Zhou, X. Thermal behaviour modelling and characteristics analysis of electrothermal microactuators. Microsyst. Technol. 2017, 23, 2629–2640. [Google Scholar] [CrossRef]
- Thangavel, A.; Rengaswamy, R.; Sukumar, P.K.; Sekar, R. Modelling chevron electrothermal actuator and its performance analysis. Microsyst. Technol. 2018, 24, 1767–1774. [Google Scholar] [CrossRef]
- Sciberras, T.; Demicoli, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. Coupled finite element-finite volume multi-physics analysis of MEMS electrothermal actuators. Micromachines 2022, 13, 8. [Google Scholar] [CrossRef]
- Vangbo, M. An analytical analysis of a compressed bistable buckled beam. Sens. Actuators A 1998, 69, 212–216. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, H.; Slocum, A.H. A curved-beam bistable mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- Park, S.; Hah, D. Pre-shaped buckled beam actuators: Theory and experiments. Sens. Actuators A 2008, 148, 186–192. [Google Scholar] [CrossRef]
- Lott, C.D.; McLain, T.W.; Harb, J.N.; Howell, L.L. Modeling the thermal behaviour of a surface micromachined linear-displacement thermomechanical microactuator. Sens. Actuators A 2002, 101, 239–250. [Google Scholar] [CrossRef]
- Hickey, R.; Sameoto, D.; Hubbard, T.; Kujath, M. Time and frequency response of two-arm micromachined thermal actuators. J. Micromech. Microeng. 2003, 13, 40. [Google Scholar] [CrossRef]
- Zhu, Y.; Reza Moheimani, S.O.; Yuce, M.R. Bidirectional electrothermal actuator with Z-shaped beams. IEEE Sens. J. 2012, 12, 2508–2509. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Wu, Q.; Yu, Y.; Liu, X.; Zhang, X. Closed-form modelling and design analysis of V- and Z-shaped electrothermal microactuators. J. Micromech. Microeng. 2017, 27, 015023. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, Y.; Liu, X.; Zhang, X. Dynamic modelling and analysis of V- and Z-shaped electrothermal microactuators. Microsyst. Technol. 2017, 23, 3775–3789. [Google Scholar] [CrossRef]
- Chu, L.L.; Hetrick, J.A.; Gianchandani, Y.B. High amplification compliant micro-transmissions for rectilinear electrothermal actuators. Sens. Actuators A 2002, 97–98, 776–783. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Q.-A.; Li, R.-G.; Li, W. Macro-modeling for polysilicon cascaded bent beam electrothermal microactuators. Sens. Actuators A 2006, 128, 165–175. [Google Scholar] [CrossRef]
- Hubbard, N.B.; Howell, L.L. Design and characterization of a dual-stage, thermally actuated nanopositioner. J. Micromech. Microeng. 2005, 15, 1482–1493. [Google Scholar] [CrossRef]
- Shen, X.; Chen, X. Mechanical performance of a cascaded V-shaped electrothermal actuator. J. Adv. Robot. Syst. 2013, 10, 379. [Google Scholar] [CrossRef]
- Alcheikh, N.; Hajjaj, A.Z.; Jaber, N.; Younis, M.I. Electrothermally actuated tunable clamped-guided resonant microbeams. Mech. Syst. Signal Process. 2018, 98, 1069–1076. [Google Scholar] [CrossRef]
- Varona, J.; Tecpoyotl-Torres, M. Design of MEMS vertical-horizontal chevron thermal actuators. Sens. Actuators A 2009, 153, 127–130. [Google Scholar] [CrossRef]
- Sassen, W.P.; Henneken, V.A.; Tichem, M.; Sarro, P.M. Contoured V-beam actuator with improved temperature uniformity. Sens. Actuators A 2008, 144, 341–347. [Google Scholar] [CrossRef]
- Kwan, A.M.H.; Song, S.; Lu, X.; Lu, L.; Teh, Y.K.; Teh, Y.F.; Chong, E.W.C.; Gao, Y.; Hau, W.; Zeng, F.; et al. Improved designs for an electrothermal in-plane microactuator. J. Microelectromech. Syst. 2012, 21, 587–595. [Google Scholar] [CrossRef]
- Wittwer, J.W.; Baker, M.S.; Howell, L.L. Simulation, measurement, and asymmetric buckling of thermal microactuators. Sens. Actuators A 2006, 128, 395–401. [Google Scholar] [CrossRef]
- Chu, L.L.; Gianchandani, Y.B. A micromachined 2D positioner with electrothermal actuation and sub-nanometer capacitive sensing. J. Micromech. Microeng. 2003, 13, 279–285. [Google Scholar] [CrossRef]
- Messenger, R.K.; Aten, Q.T.; McLain, T.W.; Howell, L.L. Piezoresistive feedback control of a MEMS thermal actuator. J. Microelectromech. Syst. 2009, 18, 1267–1278. [Google Scholar] [CrossRef]
- Park, J.; Chu, L.L.; Oliver, A.D.; Gianchandani, Y.B. Bent-beam electrothermal actuators—Part II: Linear and rotary microengines. J. Microelectromech. Syst. 2001, 10, 255–262. [Google Scholar] [CrossRef]
- Maloney, J.M.; Schreiber, D.S.; DeVoe, D.L. Large force electrothermal linear micromotors. J. Micromech. Microeng. 2004, 14, 226–234. [Google Scholar] [CrossRef]
- Brown, M.; Hubbard, T.; Kujath, M. Development of a long-range untethered frictional microcrawler. J. Micromech. Microeng. 2007, 17, 1025–1033. [Google Scholar] [CrossRef]
- Geisberger, A.; Kadylak, D.; Ellis, M. A silicon electrothermal rotational micro motor measuring one cubic millimeter. J. Micromech. Microeng. 2006, 16, 1943–1950. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; McCormick, D.T.; Tien, N.C. A micromachined RF microrelay with electrothermal actuation. Sens. Actuators A 2003, 103, 231–236. [Google Scholar] [CrossRef]
- Wang, Y.; McCormick, D.T.; Tien, N.C. A low-voltage lateral MEMS switch with high RF performance. J. Microelectromech. Syst. 2004, 13, 902–911. [Google Scholar] [CrossRef]
- Syms, R.R.A.; Zou, H.; Stagg, J. Robust latching MEMS translation stages for micro-optical systems. J. Micromech. Microeng. 2004, 14, 667–674. [Google Scholar] [CrossRef][Green Version]
- Unamuno, A.; Yao, J.; Uttamchandani, D. Alignment and fixing of fiber optics based on electrothermal MEMS actuators. IEEE Photon. Tech. Lett. 2005, 17, 816–818. [Google Scholar] [CrossRef]
- Syms, R.R.A.; Zou, H.; Stagg, J. MOEMS alignment stages with Vernier latch mechanisms. J. Opt. A: Pure Appl. Opt. 2006, 8, S305–S312. [Google Scholar] [CrossRef]
- Henneken, V.A.; Tichem, M.; Sarro, P.M. In-package MEMS-based thermal actuators for micro-assembly. J. Micromech. Microeng. 2006, 16, S107–S115. [Google Scholar] [CrossRef]
- Sinclair, M. 1D and 2D scanning mirrors using thermal buckle-beam actuation. Proc. SPIE 2001, 4592, 307–314. [Google Scholar] [CrossRef]
- Syms, R.R.A.; Zou, H.; Stagg, J.; Veladi, H. Sliding-blade MEMS iris and variable optical attenuator. J. Micromech. Microeng. 2004, 14, 1700–1710. [Google Scholar] [CrossRef]
- Unamuno, A.; Uttamchandani, D. MEMS variable optical attenuator with vernier latching mechanism. IEEE Photon. Tech. Lett. 2006, 18, 88–90. [Google Scholar] [CrossRef]
- Sameoto, D.; Hubbard, T.; Kujath, M. Operation of electrothermal and electrostatic MUMPS microactuators underwater. J. Micromech. Microeng. 2004, 14, 1359–1366. [Google Scholar] [CrossRef]
- Zhang, W.; Gnerlich, M.; Paly, J.J.; Sun, Y.; Jing, G.; Voloshin, A.; Tatic-Lucic, S. A polymer V-shaped electrothermal actuator array for biological applications. J. Micromech. Microeng. 2008, 18, 075020. [Google Scholar] [CrossRef]
- Holst, G.L.; Jensen, B.D. A silicon thermomechanical in-plane microactuation system for large displacements in aqueous environments. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2011; Volume 54976, pp. 491–502. [Google Scholar] [CrossRef]
- Muthuswamy, J.; Okandon, M.; Giletti, A.; Baker, M.S.; Jain, T. An array of microactuated electrodes for monitoring of single-neuronal activity in rodents. IEEE Trans. Biomed. Eng. 2005, 52, 1470–1477. [Google Scholar] [CrossRef]
- Jackson, N.; Sridharan, A.; Anand, S.; Baker, M.; Okandan, M.; Muthuswamy, J. Long-term neural recordings using MEMS-based movable microelectrodes in the brain. Front. Neuroeng. 2010, 3, 10. [Google Scholar] [CrossRef] [PubMed]
- Potekhina, A.; Wang, C. Review of electrothermal actuators and applications. Actuators 2019, 8, 69. [Google Scholar] [CrossRef]
- Liu, D.; Syms, R.R.A. NEMS by sidewall transfer lithography. IEEE J. Microelectromech. Syst. 2014, 23, 1366–1373. [Google Scholar] [CrossRef]
- Allen, H.G.; Bulson, P.S. Background to Buckling; McGraw-Hill Book Company (UK) Ltd.: Maidenhead, UK, 1980; Available online: http://worldcat.org/isbn/0070841004 (accessed on 9 January 2022).

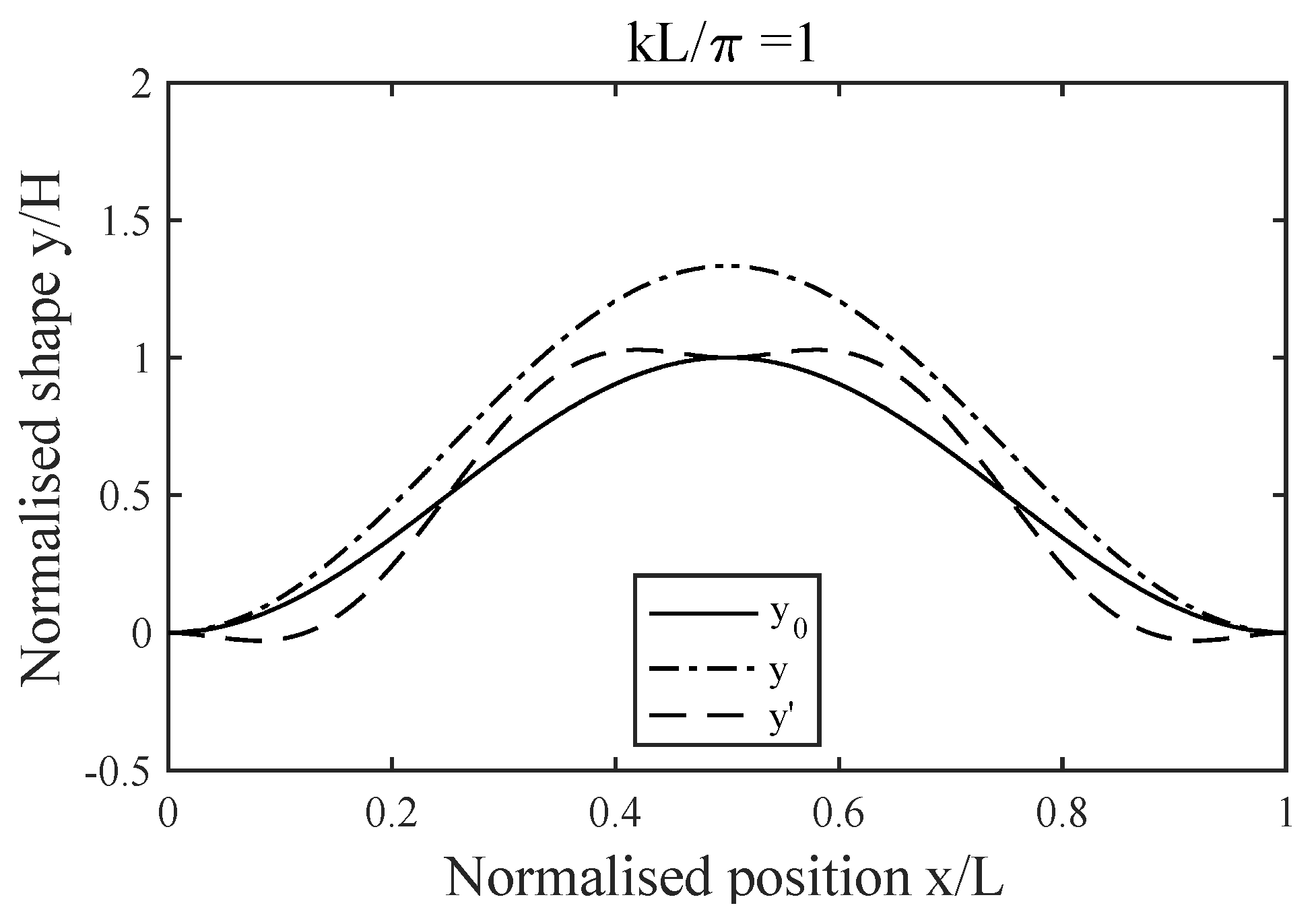
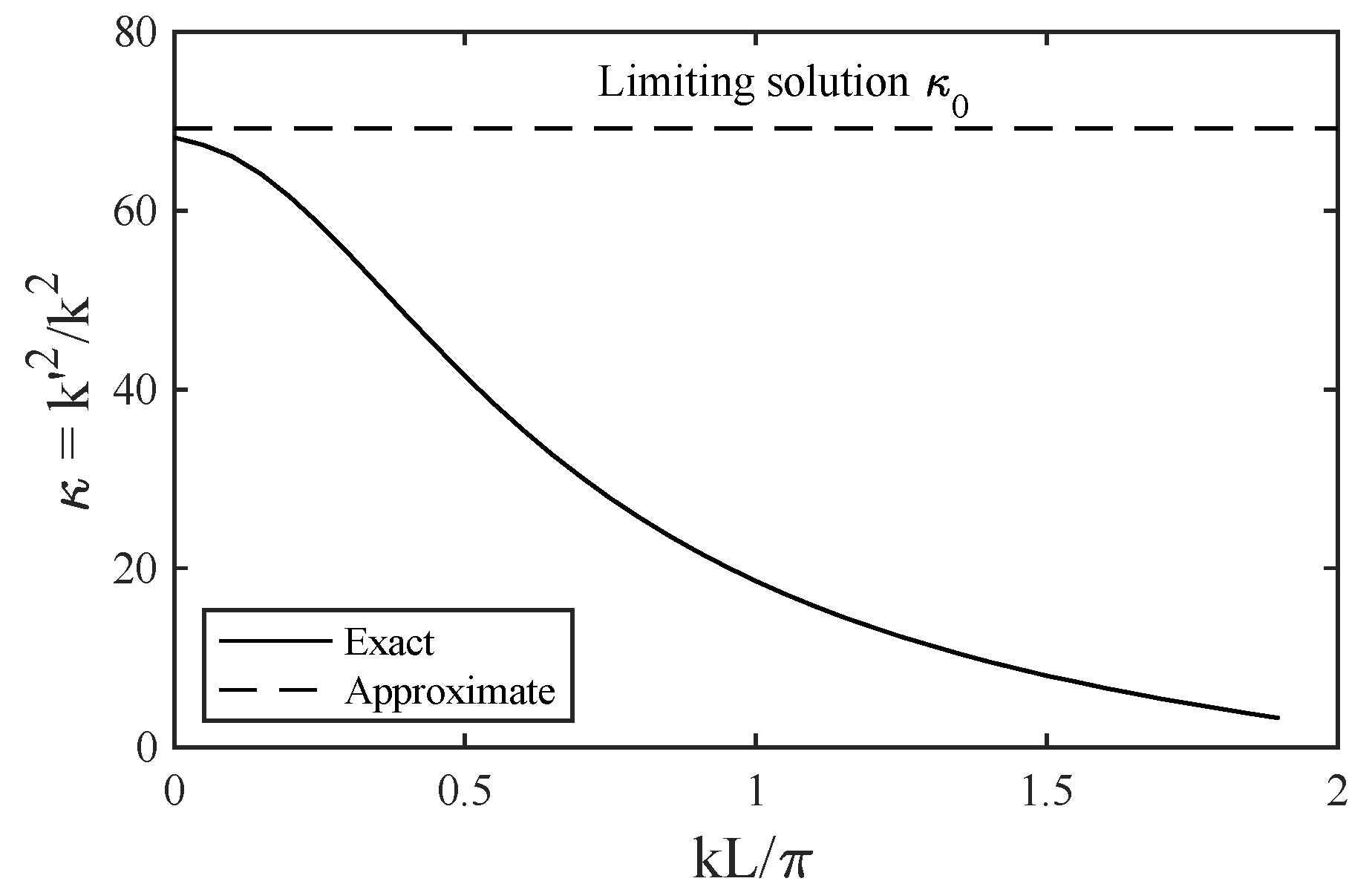
| Beam Width (μm) | Physical Memory (Gb) | Virtual Memory (Gb) | Run Time (s) |
|---|---|---|---|
| 20 | 1.23 | 1.32 | 155 |
| 10 | 1.37 | 1.49 | 342 |
| 5 | 1.72 | 1.86 | 816 |
| 1 | 4.37 | 4.69 | 5955 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syms, R.; Liu, D. Buckling Electrothermal NEMS Actuators: Analytic Design for Very Slender Beams. Micro 2022, 2, 54-67. https://doi.org/10.3390/micro2010003
Syms R, Liu D. Buckling Electrothermal NEMS Actuators: Analytic Design for Very Slender Beams. Micro. 2022; 2(1):54-67. https://doi.org/10.3390/micro2010003
Chicago/Turabian StyleSyms, Richard, and Dixi Liu. 2022. "Buckling Electrothermal NEMS Actuators: Analytic Design for Very Slender Beams" Micro 2, no. 1: 54-67. https://doi.org/10.3390/micro2010003
APA StyleSyms, R., & Liu, D. (2022). Buckling Electrothermal NEMS Actuators: Analytic Design for Very Slender Beams. Micro, 2(1), 54-67. https://doi.org/10.3390/micro2010003





