Electrical and Optical Doping of Silicon by Pulsed-Laser Melting
Abstract
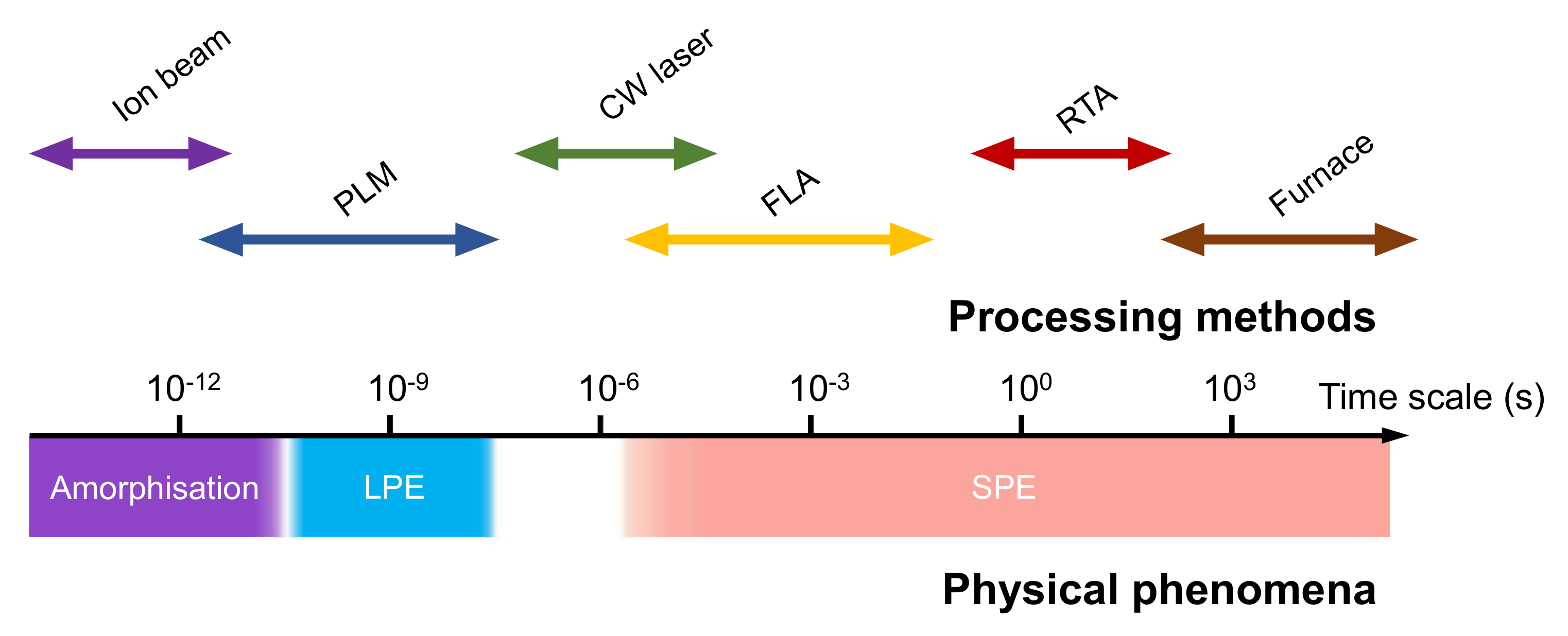
1. Introduction
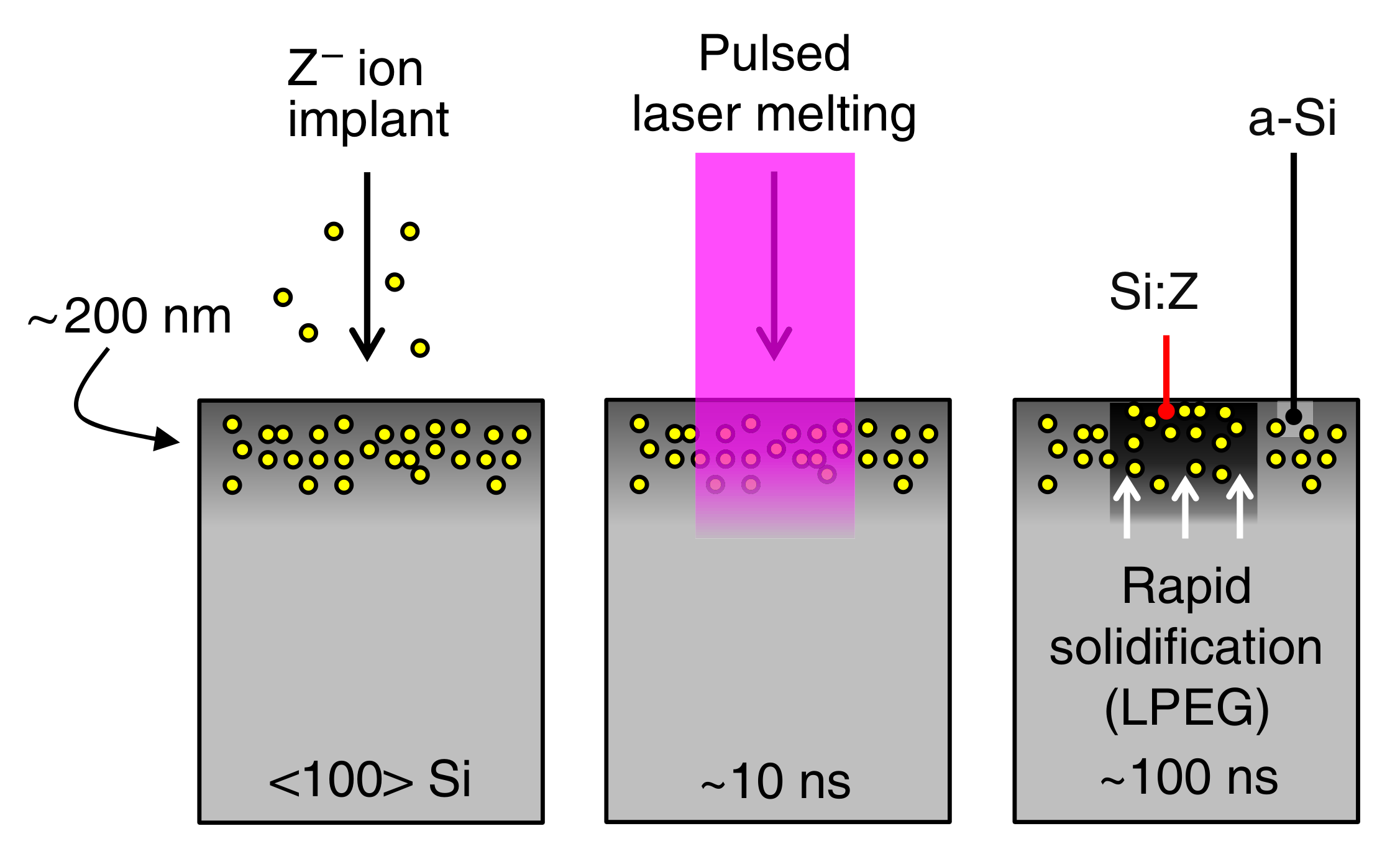
2. Electrical Doping of Silicon with Pulsed-Lasers
2.1. Historical Overview of Laser Processing (1970s to 1990s): Early Electrical Doping Studies
| P | B | As | Sb | In | Ga | Bi | |
|---|---|---|---|---|---|---|---|
| [15] | |||||||
| PLM | 5- | 5- | |||||
| (5-) | () | (5-) | () | [15] | [15] | [15] | |
| [12,17,37] | [11,17,37] | [15,17,37] | [15,38] | ||||
| Furnace | - | 1.3- | 5.0- | 4.0- | |||
| annealing | [31] | [33] | () | [33,34,39] | [39] | [35,39] | |
| and RTA | () | () | [33,34,39,40] | () | |||
| [41] | [31] | [28] | [39,42] |
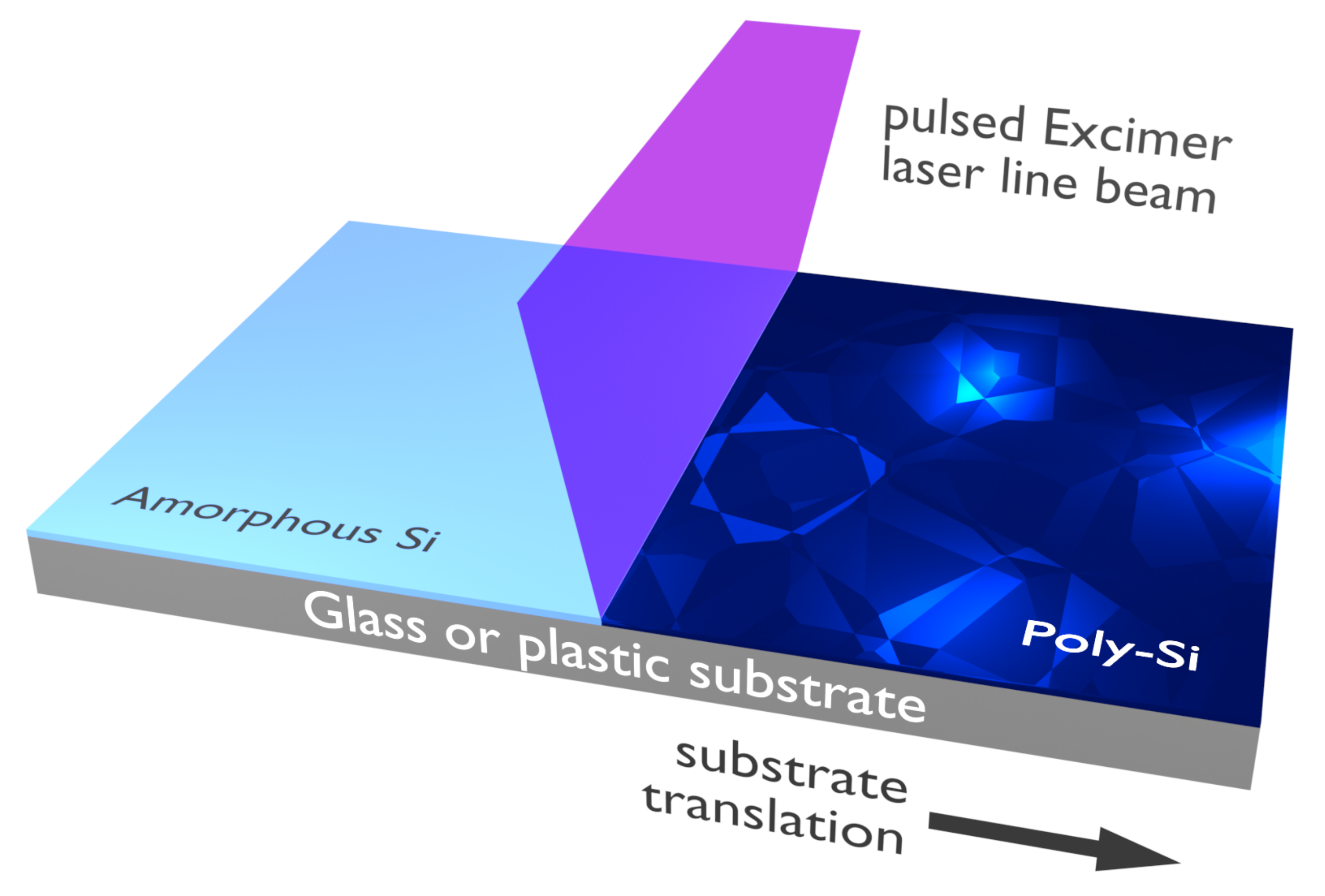
2.2. Electrical Doping by Plm beyond the 1990s: Flat Panel Displays
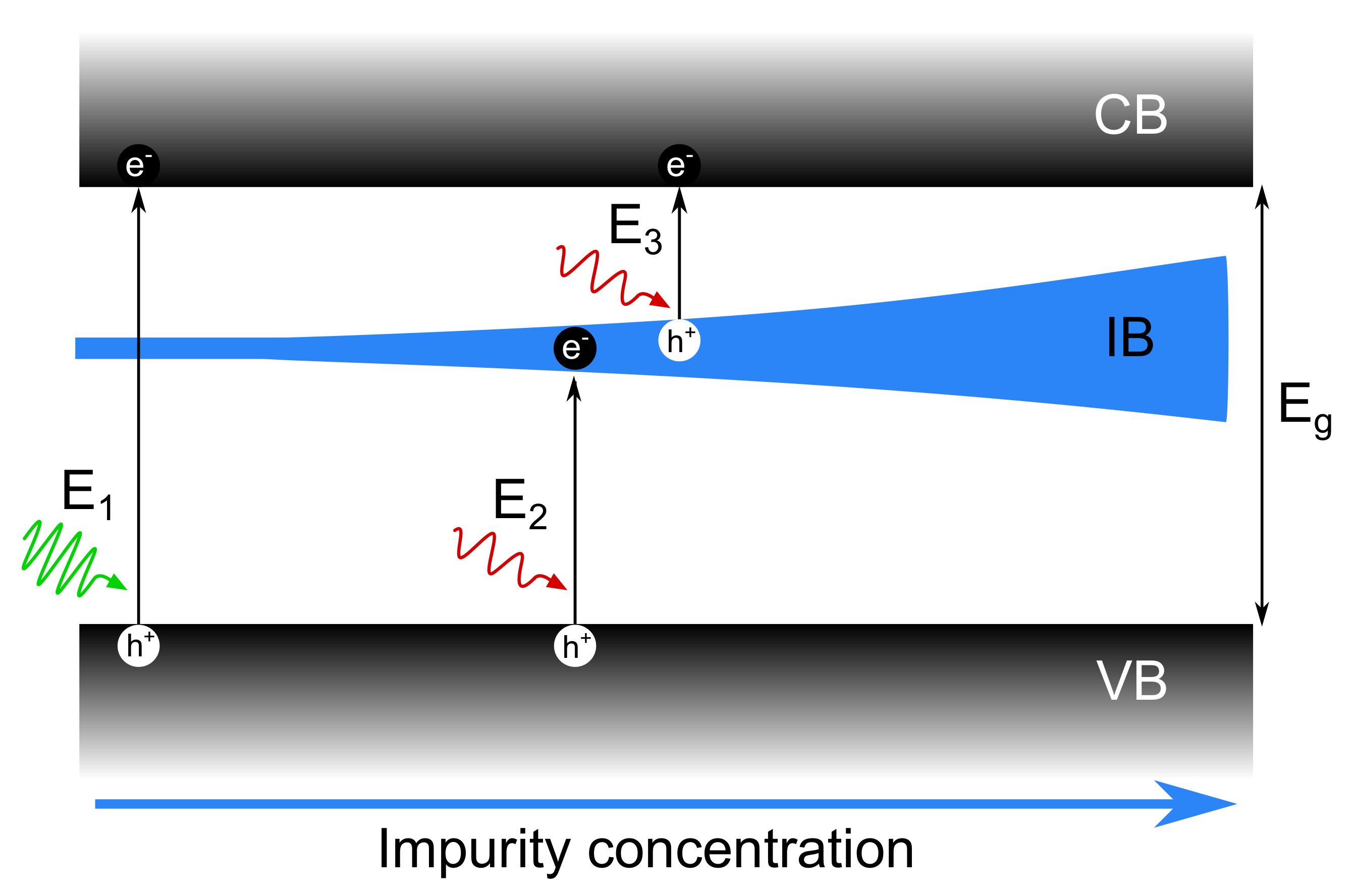
3. Optical Hyperdoping with Deep Level Impurities
3.1. Chalcogen-Hyperdoped Silicon
3.2. Transition-Metal-Hyperdoped Silicon
3.2.1. Physical and Structural Characterisation
3.2.2. Optical and Photodevice Characterisation
4. Summary and Future Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| PLM | Pulsed-laser melting |
| RTA | Rapid thermal annealing |
| FLA | Flash lamp annealing |
| S/LPE | Solid/liquid phase epitaxy |
| FPD | Flat panel display |
| TFT | Thin film transistor |
| RBS-C | Rutherford backscattering spectrometry with channelling analysis |
| T/SEM | Transmission/scanning electron microscopy |
| SIMS | Secondary ion mass spctrometry |
| APT | Atom probe tomography |
| PAS | Positron annihilation spectroscopy |
| DLTS | Deep level transient spectroscopy |
| DFT | Density functional theory |
| IMT | Insulator-to-metal transition |
| CB/VB/IB | Conduction/valence/intermediate band |
| EQE | External quantum efficiency |
References
- Yang, W.; Lim, S.Q.; Williams, J.S. Optical hyperdoping. In Laser Annealing Processes in Semiconductor Technology; Cristiano, F., Magna, A.L., Eds.; Woodhead Publishing: Cambridge, UK; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 8. [Google Scholar]
- Yang, W.; Mathews, J.; Williams, J. Hyperdoping of Si by ion implantation and pulsed laser melting. Mat. Sci. Semicon. Proc. 2017, 62, 103–114. [Google Scholar] [CrossRef]
- Capper, P.; Mauk, M. Liquid Phase Epitaxy of Electronic, Optical and Optoelectronic Materials; John Wiley & Sons: New York, NY, USA, 2007; Volume 21. [Google Scholar]
- Casalino, M.; Coppola, G.; Iodice, M.; Rendina, I.; Sirleto, L. Near-infrared sub-bandgap all-silicon photodetectors: State of the art and perspectives. Sensors 2010, 10, 10571–10600. [Google Scholar] [CrossRef] [PubMed]
- Bean, J.; Leamy, H.; Poate, J.; Rozgonyi, G.; Sheng, T.; Williams, J.; Celler, G. Epitaxial laser crystallization of thin-film amorphous silicon. Appl. Phys. Lett. 1978, 33, 227–230. [Google Scholar] [CrossRef]
- Bean, J.; Leamy, H.; Poate, J.; Rozgonyi, G.; Van der Ziel, J.; Williams, J.; Celler, G. Substrate and doping effects upon laser-induced epitaxy of amorphous silicon. J. Appl. Phys. 1979, 50, 881–885. [Google Scholar] [CrossRef]
- Shtyrkov, E.I.; Khaibullin, I.B.; Zaripov, M.M.; Galyatudinov, M.F.; Bayazitov, R.M. Local laser annealing of implantation doped semiconductor layers. Sov. Physics. Semicond. 1975, 9, 1309–1310. [Google Scholar]
- Wood, R.F.; White, C.W.; Young, R.T. Laser processing of semiconductors: An overview. Semicond. Semimetals 1984, 23, 1–41. [Google Scholar]
- Poate, J.M. Laser Annealing of Semiconductors; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Mailoa, J.P.; Akey, A.J.; Simmons, C.B.; Hutchinson, D.; Mathews, J.; Sullivan, J.T.; Recht, D.; Winkler, M.T.; Williams, J.S.; Warrender, J.M.; et al. Room-temperature sub-band gap optoelectronic response of hyperdoped silicon. Nat. Commun. 2014, 5, 3011. [Google Scholar] [CrossRef] [PubMed]
- Young, R.T.; White, C.W.; Clark, G.J.; Narayan, J.; Christie, W.H.; Murakami, M.; King, P.W.; Kramer, S.D. Laser annealing of boron-implanted silicon. Appl. Phys. Lett. 1978, 32, 139–141. [Google Scholar] [CrossRef]
- Finetti, M.; Negrini, P.; Solmi, S.; Nobili, D. Electrical properties and stability of supersaturated phosphorus-doped silicon layers. J. Electrochem. Soc. 1981, 128, 1313. [Google Scholar] [CrossRef]
- White, C.W.; Pronko, P.P.; Wilson, S.R.; Appleton, B.R.; Narayan, J.; Young, R.T. Effects of pulsed ruby-laser annealing on As and Sb implanted silicon. J. Appl. Phys. 1979, 50, 3261–3273. [Google Scholar] [CrossRef]
- Hoonhout, D.; Saris, F.W. Dopant segregation in silicon by pulsed-laser annealing: A test case for the concept of thermal melting. Phys. Lett. A 1979, 74, 253–255. [Google Scholar] [CrossRef]
- White, C.W.; Wilson, S.R.; Appleton, B.R.; Young Jr, F.W. Supersaturated substitutional alloys formed by ion implantation and pulsed laser annealing of group-III and group-V dopants in silicon. J. Appl. Phys. 1980, 51, 738–749. [Google Scholar] [CrossRef]
- Trumbore, F.A. Solid solubilities of impurity elements in germanium and silicon. Bell Syst. Tech. J. 1960, 39, 205–233. [Google Scholar] [CrossRef]
- Natsuaki, N.; Tamura, M.; Tokuyama, T. Nonequilibrium solid solutions obtained by heavy ion implantation and laser annealing. J. Appl. Phys. 1980, 51, 3373–3382. [Google Scholar] [CrossRef]
- Narayan, J.; White, C.W. Melting phenomenon and properties of defects associated with pulsed laser irradiation. Philos. Mag. A 1981, 43, 1515–1535. [Google Scholar] [CrossRef]
- Narayan, J. Development of morphological instability and formation of cells in silicon alloys during pulsed laser irradiation. J. Cryst. Growth 1982, 59, 583–598. [Google Scholar] [CrossRef]
- Jellison, G.E. Chapter 3 Optical and Electrical Properties of Pulsed Laser-Annealed Silicon. In Semiconductors and Semimetals; Wood, R.F., White, C.W., Young, R.T., Eds.; Elsevier: Amsterdam, The Netherlands, 1984; Volume 23, pp. 95–164. [Google Scholar]
- Gat, A.; Gibbons, J.F.; Magee, T.J.; Peng, J.; Williams, P.; Deline, V.; Evans, C., Jr. Use of a scanning cw Kr laser to obtain diffusion-free annealing of B-implanted silicon. Appl. Phys. Lett. 1978, 33, 389–391. [Google Scholar] [CrossRef]
- Gat, A.; Gibbons, J.F.; Magee, T.J.; Peng, J.; Deline, V.R.; Williams, P.; Evans, C., Jr. Physical and electrical properties of laser-annealed ion-implanted silicon. Appl. Phys. Lett. 1978, 32, 276–278. [Google Scholar] [CrossRef]
- Lietoila, A.; Gibbons, J.F.; Magee, T.J.; Peng, J.; Hong, J.D. Solid solubility of As in Si as determined by ion implantation and cw laser annealing. Appl. Phys. Lett. 1979, 35, 532–534. [Google Scholar] [CrossRef]
- Williams, J.S.; Brown, W.L.; Leamy, H.J.; Poate, J.M.; Rodgers, J.W.; Rousseau, D.; Rozgonyi, G.A.; Shelnutt, J.A.; Sheng, T.T. Solid-phase epitaxy of implanted silicon by cw Ar ion laser irradiation. Appl. Phys. Lett. 1978, 33, 542–544. [Google Scholar] [CrossRef]
- Poate, J.M.; Bean, J.C.; Brown, W.L.; Cohen, R.L.; Feldman, L.C.; Leamy, H.J.; Rodgers, J.W.; Rousseau, D.; Rozgonyi, G.A.; Shelnutt, J.A.; et al. Liquid and solid phase regrowth of Si by laser irradiation and thermally assisted flash annealing. Radiat. Eff. 1980, 48, 167–174. [Google Scholar] [CrossRef]
- Rebohle, L.; Prucnal, S.; Skorupa, W. A review of thermal processing in the subsecond range: Semiconductors and beyond. Semicond. Sci. Technol. 2016, 31, 103001. [Google Scholar] [CrossRef]
- Cohen, R.L.; Williams, J.S.; Feldman, L.C.; West, K.W. Thermally assisted flash annealing of silicon and germanium. Appl. Phys. Lett. 1978, 33, 751–753. [Google Scholar] [CrossRef]
- Duffy, R.; Dao, T.; Tamminga, Y.; Van Der Tak, K.; Roozeboom, F.; Augendre, E. Groups III and V impurity solubilities in silicon due to laser, flash, and solid-phase-epitaxial-regrowth anneals. Appl. Phys. Lett. 2006, 89, 071915. [Google Scholar] [CrossRef]
- Gat, A. Heat-pulse annealing of arsenic-implanted silicon with a CW arc lamp. IEEE Electron Device Lett. 1981, 2, 85–87. [Google Scholar] [CrossRef]
- Sadana, D.K.; Shatas, S.C.; Gat, A. Heatpulse Annealing of Ion-Implanted Silicon: Structural Characterization by Transmission Electron Microscopy; Inst. Phys., Conf. Ser.; (United Kingdom); CRC Press: Boca Raton, FL, USA, 1983. [Google Scholar]
- Narayan, J.; Holland, O.W.; Eby, R.E.; Wortman, J.J.; Ozguz, V.; Rozgonyi, G.A. Rapid thermal annealing of arsenic and boron-implanted silicon. Appl. Phys. Lett. 1983, 43, 957–959. [Google Scholar] [CrossRef]
- Nylandsted Larsen, A.; Pedersen, F.T.; Weyer, G.; Galloni, R.; Rizzoli, R.; Armigliato, A. The nature of electrically inactive antimony in silicon. J. Appl. Phys. 1986, 59, 1908–1917. [Google Scholar] [CrossRef]
- Williams, J.S.; Elliman, R.G. Limits to solid solubility in ion implanted silicon. Nucl. Instruments Methods 1981, 182, 389–395. [Google Scholar] [CrossRef]
- Williams, J.S.; Elliman, R.G. Substitutional solid solubility limits during solid phase epitaxy of ion implanted (100) silicon. Appl. Phys. Lett. 1982, 40, 266–268. [Google Scholar] [CrossRef]
- Campisano, S.U.; Rimini, E.; Baeri, P.; Foti, G. Supersaturated solid solutions after solid phase epitaxial growth in Bi-implanted silicon. Appl. Phys. Lett. 1980, 37, 170–172. [Google Scholar] [CrossRef]
- Götzlich, J.; Tsien, P.H.; Ryssel, H. Relaxation behavior of metastable As and P concentrations in Si after pulsed and CW laser annealing. MRS Online Proc. Libr. (OPL) 1983, 23, 235. [Google Scholar] [CrossRef]
- Chikawa, J.i.; Sato, F. Solid Solubilities of Group-III and Group-V Dopants in Pulsed Laser-Annealed Silicon. Jpn. J. Appl. Phys. 1980, 19, L577. [Google Scholar] [CrossRef]
- White, C.W.; Narayan, J.; Young, R.T. Laser annealing of ion-implanted semiconductors. Science 1979, 204, 461–468. [Google Scholar] [CrossRef]
- Narayan, J.; Holland, O.W. Formation of metastable supersaturated solid solutions in ion implanted silicon during solid phase crystallization. Appl. Phys. Lett. 1982, 41, 239–242. [Google Scholar] [CrossRef]
- Williams, J.S.; Short, K.T. Metastable doping behavior in antimony-implanted (100) silicon. J. Appl. Phys. 1982, 53, 8663–8667. [Google Scholar] [CrossRef]
- Landi, E.; Armigliato, A.; Solmi, S.; Kögler, R.; Wieser, E. Electrical activation of boron-implanted silicon during rapid thermal annealing. Appl. Phys. A 1988, 47, 359–366. [Google Scholar] [CrossRef]
- De Souza, J.P.; Fichtner, P.F.P. Electrical activation of bismuth implanted into silicon by rapid thermal annealing and kinetics of defects. J. Appl. Phys. 1993, 74, 119–122. [Google Scholar] [CrossRef][Green Version]
- Chu, W.K. Stability study of laser irradiation of silicon diffused with arsenic. Appl. Phys. Lett. 1980, 36, 273–275. [Google Scholar] [CrossRef]
- Graziani, T.; Short, K.T.; Williams, J.S. Comparison of solubility limits and electrical activities for antimony and arsenic ion implanted silicon. Phys. Lett. A 1982, 91, 231–233. [Google Scholar] [CrossRef]
- Williams, J.S. Solid phase epitaxial regrowth phenomena in silicon. Nucl. Instruments Methods Phys. Res. 1983, 209, 219–228. [Google Scholar] [CrossRef]
- Jain, S.H.; Griffin, P.B.; Plummer, J.D.; Mccoy, S.; Gelpey, J.; Selinger, T.; Downey, D.F. Metastable boron active concentrations in Si using flash assisted solid phase epitaxy. J. Appl. Phys. 2004, 96, 7357–7360. [Google Scholar] [CrossRef]
- Priolo, F.; Poate, J.M.; Jacobson, D.C.; Batstone, J.L.; Custer, J.S.; Thompson, M.O. Trapping of Au in Si during pulsed laser irradiation: A comparison with ion beam induced segregation. Appl. Phys. Lett. 1988, 53, 2486–2488. [Google Scholar] [CrossRef]
- Cullis, A.G.; Webber, H.C.; Poate, J.M.; Simons, A.L. Segregation and increased dopant solubility in Pt-implanted and laser-annealed Si layers. Appl. Phys. Lett. 1980, 36, 320–322. [Google Scholar] [CrossRef]
- Brotherton, S.D.; McCulloch, D.J.; Clegg, J.B.; Gowers, J.P. Excimer-laser-annealed poly-Si thin-film transistors. IEEE Trans. Electron Devices 1993, 40, 407–413. [Google Scholar] [CrossRef]
- Kohno, A.; Sameshima, T.; Sano, N.; Sekiya, M.; Hara, M. High performance poly-Si TFTs fabricated using pulsed laser annealing and remote plasma CVD with low temperature processing. IEEE Trans. Electron Devices 1995, 42, 251–257. [Google Scholar] [CrossRef]
- Smith, P.M.; Carey, P.G.; Sigmon, T.W. Excimer laser crystallization and doping of silicon films on plastic substrates. Appl. Phys. Lett. 1997, 70, 342–344. [Google Scholar] [CrossRef]
- Sigmon, T.W.; Toet, D.; Carey, P.G.; Smith, P.M.; Wickboldt, P. Applications of pulsed lasers in low-temperature thin film electronics fabrication. In Proceedings of the First International Symposium on Laser Precision Microfabrication. International Society for Optics and Photonics, Saitama, Japan, 6 November 2000; Volume 4088, pp. 73–79. [Google Scholar]
- Suzuki, T. Flat panel displays for ubiquitous product applications and related impurity doping technologies. J. Appl. Phys. 2006, 99, 3. [Google Scholar] [CrossRef]
- Warrender, J.M. Laser hyperdoping silicon for enhanced infrared optoelectronic properties. Appl. Phys. Rev. 2016, 3, 031104. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; Antolín, E.; Tablero, C. Intermediate bands versus levels in non-radiative recombination. Phys. B Condens. Matter 2006, 382, 320–327. [Google Scholar] [CrossRef]
- Ramiro, Í.; Martí, A.; Antolín, E.; Luque, A. Review of Experimental Results Related to the Operation of Intermediate Band Solar Cells. IEEE J. Photovoltaics 2014, 4, 736–748. [Google Scholar] [CrossRef]
- Okada, Y.; Ekins-Daukes, N.J.; Kita, T.; Tamaki, R.; Yoshida, M.; Pusch, A.; Hess, O.; Phillips, C.C.; Farrell, D.J.; Yoshida, K.; et al. Intermediate band solar cells: Recent progress and future directions. Appl. Phys. Rev. 2015, 2, 021302. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A. Increasing the Efficiency of Ideal Solar Cells by Photon Induced Transitions at Intermediate Levels. Phys. Rev. Lett. 1997, 78, 5014–5017. [Google Scholar] [CrossRef]
- Crouch, C.H.; Carey, J.E.; Shen, M.; Mazur, E.; Genin, F.Y. Infrared absorption by sulfur-doped silicon formed by femtosecond laser irradiation. Appl. Phys. A 2004, 79, 1635–1641. [Google Scholar] [CrossRef]
- Crouch, C.H.; Carey, J.E.; Warrender, J.M.; Aziz, M.J.; Mazur, E.; Génin, F.Y. Comparison of structure and properties of femtosecond and nanosecond laser-structured silicon. Appl. Phys. Lett. 2004, 84, 1850–1852. [Google Scholar] [CrossRef]
- Vorobyev, A.Y.; Guo, C. Direct femtosecond laser surface nano/microstructuring and its applications. Laser Photonics Rev. 2013, 7, 385–407. [Google Scholar] [CrossRef]
- Wu, C.; Crouch, C.H.; Zhao, L.; Carey, J.E.; Younkin, R.; Levinson, J.A.; Mazur, E.; Farrell, R.M.; Gothoskar, P.; Karger, A. Near-unity below-band-gap absorption by microstructured silicon. Appl. Phys. Lett. 2001, 78, 1850–1852. [Google Scholar] [CrossRef]
- Kim, T.G.; Warrender, J.M.; Aziz, M.J. Strong sub-band-gap infrared absorption in silicon supersaturated with sulfur. Appl. Phys. Lett. 2006, 88, 241902. [Google Scholar] [CrossRef]
- Tabbal, M.; Kim, T.; Warrender, J.M.; Aziz, M.J.; Cardozo, B.L.; Goldman, R.S. Formation of single crystal sulfur supersaturated silicon based junctions by pulsed laser melting. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2007, 25, 1847–1852. [Google Scholar] [CrossRef]
- Bob, B.P.; Kohno, A.; Charnvanichborikarn, S.; Warrender, J.M.; Umezu, I.; Tabbal, M.; Williams, J.S.; Aziz, M.J. Fabrication and subband gap optical properties of silicon supersaturated with chalcogens by ion implantation and pulsed laser melting. J. Appl. Phys. 2010, 107, 123506. [Google Scholar] [CrossRef]
- Said, A.J.; Recht, D.; Sullivan, J.T.; Warrender, J.M.; Buonassisi, T.; Persans, P.D.; Aziz, M.J. Extended infrared photoresponse and gain in chalcogen-supersaturated silicon photodiodes. Appl. Phys. Lett. 2011, 99, 073503. [Google Scholar] [CrossRef]
- Umezu, I.; Warrender, J.M.; Charnvanichborikarn, S.; Kohno, A.; Williams, J.S.; Tabbal, M.; Papazoglou, D.G.; Zhang, X.; Aziz, M.J. Emergence of very broad infrared absorption band by hyperdoping of silicon with chalcogens. J. Appl. Phys. 2013, 113, 213501. [Google Scholar] [CrossRef]
- Winkler, M.T.; Recht, D.; Sher, M.J.; Said, A.J.; Mazur, E.; Aziz, M.J. Insulator-to-metal transition in sulfur-doped silicon. Phys. Rev. Lett. 2011, 106, 178701. [Google Scholar] [CrossRef]
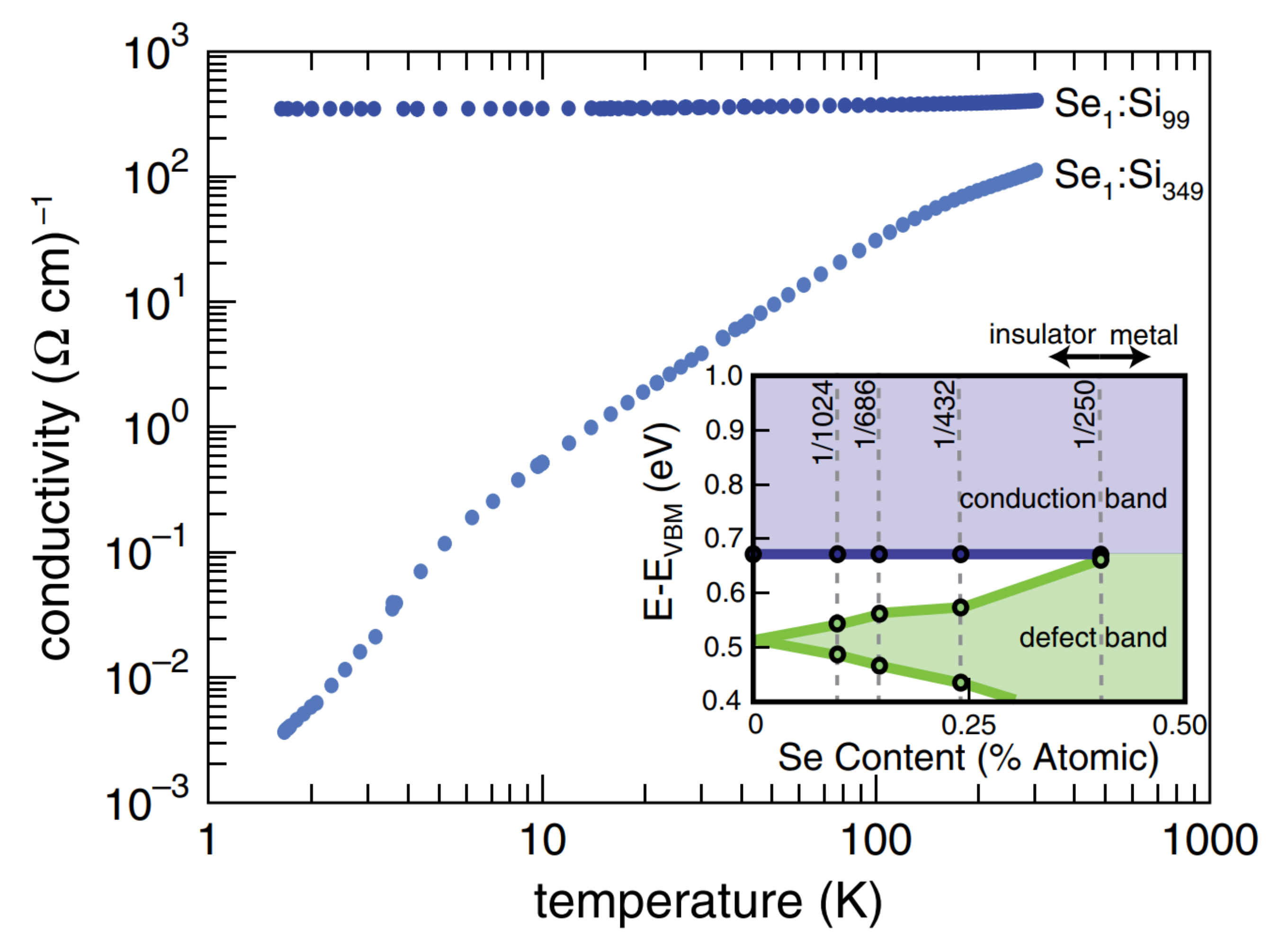
- Ertekin, E.; Winkler, M.T.; Recht, D.; Said, A.J.; Aziz, M.J.; Buonassisi, T.; Grossman, J.C. Insulator-to-metal transition in selenium-hyperdoped silicon: Observation and origin. Phys. Rev. Lett. 2012, 108, 026401. [Google Scholar] [CrossRef]
- Simmons, C.B.; Akey, A.J.; Mailoa, J.P.; Recht, D.; Aziz, M.J.; Buonassisi, T. Enhancing the infrared photoresponse of silicon by controlling the Fermi level location within an impurity band. Adv. Funct. Mater. 2014, 24, 2852–2858. [Google Scholar] [CrossRef]
- Recht, D.; Smith, M.J.; Charnvanichborikarn, S.; Sullivan, J.T.; Winkler, M.T.; Mathews, J.; Warrender, J.M.; Buonassisi, T.; Williams, J.S.; Gradečak, S.; et al. Supersaturating silicon with transition metals by ion implantation and pulsed laser melting. J. Appl. Phys. 2013, 114, 124903. [Google Scholar] [CrossRef]
- Akey, A.J.; Recht, D.; Williams, J.S.; Aziz, M.J.; Buonassisi, T. Single-phase filamentary cellular breakdown via laser-induced solute segregation. Adv. Funct. Mater. 2015, 25, 4642–4649. [Google Scholar] [CrossRef]
- Olea, J.; Toledano-Luque, M.; Pastor, D.; González-Díaz, G.; Mártil, I. Titanium doped silicon layers with very high concentration. J. Appl. Phys. 2008, 104, 016105. [Google Scholar] [CrossRef]
- Olea, J.; Toledano-Luque, M.; Pastor, D.; San-Andrés, E.; Mártil, I.; González-Díaz, G. High quality Ti-implanted Si layers above the Mott limit. J. Appl. Phys. 2010, 107, 103524. [Google Scholar] [CrossRef]
- Mathews, J.; Akey, A.J.; Recht, D.; Malladi, G.; Efstathiadis, H.; Aziz, M.J.; Warrender, J.M. On the limits to Ti incorporation into Si using pulsed laser melting. Appl. Phys. Lett. 2014, 104, 112102. [Google Scholar] [CrossRef]
- Liu, F.; Wang, M.; Berencén, Y.; Prucnal, S.; Engler, M.; Hübner, R.; Yuan, Y.; Heller, R.; Böttger, R.; Rebohle, L.; et al. On the insulator-to-metal transition in titanium-implanted silicon. Sci. Rep. 2018, 8, 4164. [Google Scholar] [CrossRef] [PubMed]
- Akey, A.J.; Mathews, J.; Warrender, J.M. Maximum Ti concentrations in Si quantified with atom probe tomography (APT). J. Appl. Phys. 2021, 129, 175701. [Google Scholar] [CrossRef]
- García-Hemme, E.; García-Hernansanz, R.; Olea, J.; Pastor, D.; del Prado, A.; Mártil, I.; González-Díaz, G. Far infrared photoconductivity in a silicon based material: Vanadium supersaturated silicon. Appl. Phys. Lett. 2013, 103, 032101. [Google Scholar] [CrossRef]
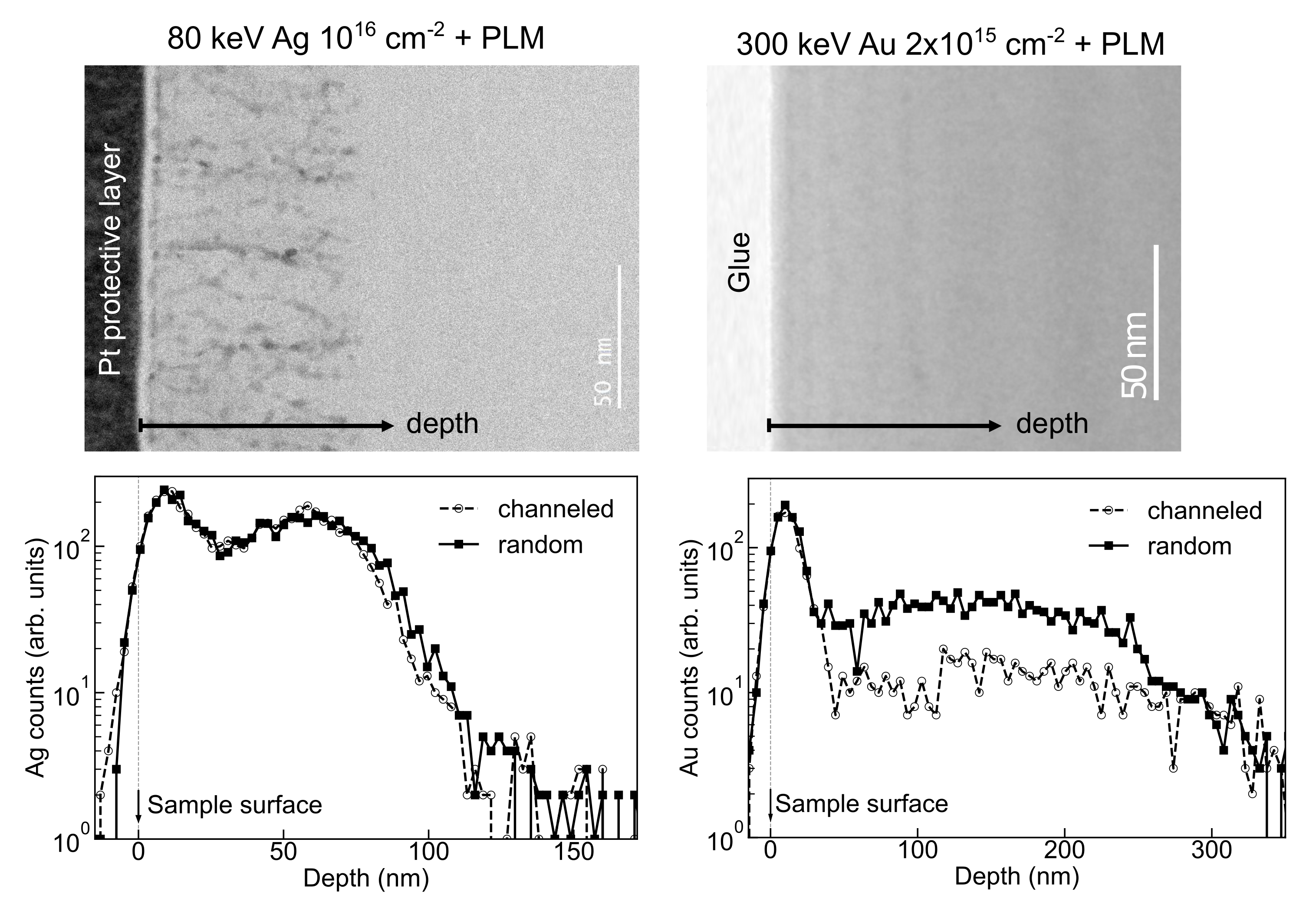
- Lim, S.Q.; Akey, A.J.; Napolitani, E.; Chow, P.K.; Warrender, J.M.; Williams, J.S. A critical evaluation of Ag- and Ti-hyperdoped Si for Si-based infrared light detection. J. Appl. Phys. 2021, 129, 065701. [Google Scholar] [CrossRef]
- Yang, W.; Akey, A.J.; Smillie, L.A.; Mailoa, J.P.; Johnson, B.C.; McCallum, J.C.; Macdonald, D.; Buonassisi, T.; Aziz, M.J.; Williams, J.S. Au-rich filamentary behavior and associated subband gap optical absorption in hyperdoped Si. Phys. Rev. Mater. 2017, 1, 074602. [Google Scholar] [CrossRef]
- Graff, K. Metal Impurities in Silicon-Device Fabrication; Springer Science & Business Media: New York, NY, USA, 2013; Volume 24. [Google Scholar]
- Ferdous, N.; Ertekin, E. Atomic scale origins of sub-band gap optical absorption in gold-hyperdoped silicon. AIP Adv. 2018, 8, 055014. [Google Scholar] [CrossRef]
- Markevich, V.P.; Leonard, S.; Peaker, A.R.; Hamilton, B.; Marinopoulos, A.G.; Coutinho, J. Titanium in silicon: Lattice positions and electronic properties. Appl. Phys. Lett. 2014, 104, 152105. [Google Scholar] [CrossRef]
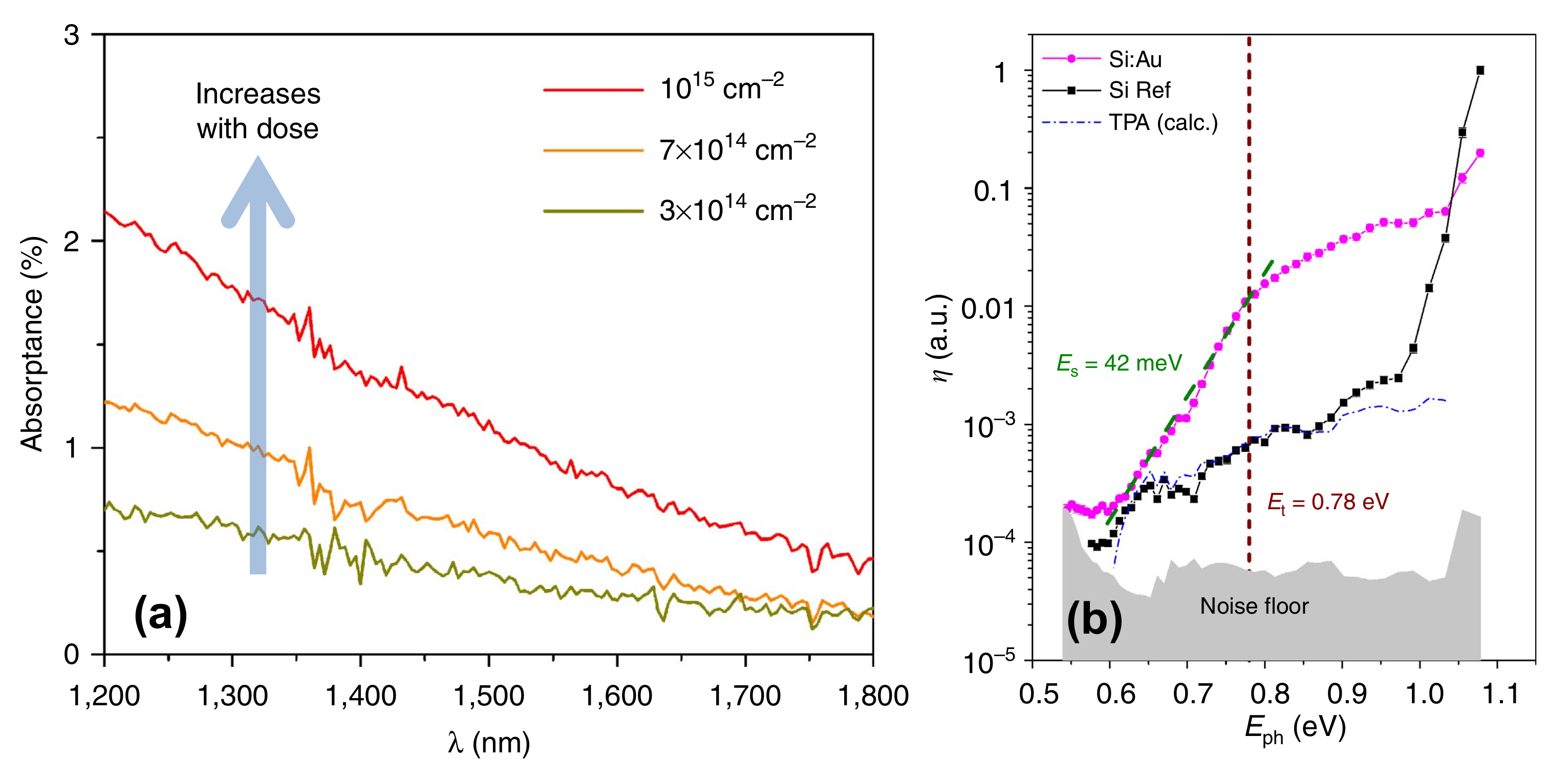
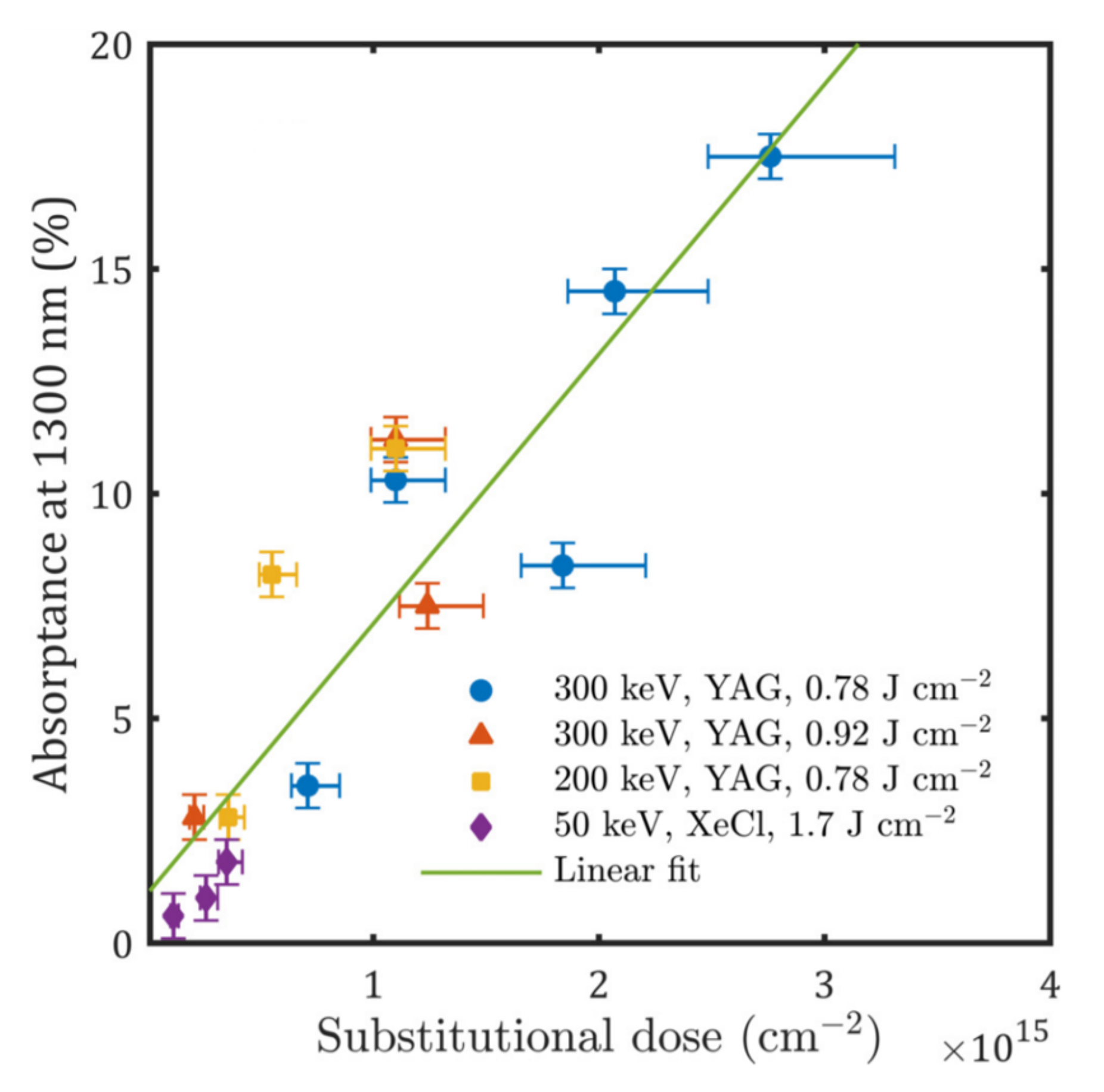
- Chow, P.K.; Yang, W.; Hudspeth, Q.; Lim, S.Q.; Williams, J.S.; Warrender, J.M. Observation of enhanced infrared absorption in silicon supersaturated with gold by pulsed laser melting of nanometer-thick gold films. J. Appl. Phys. 2018, 123, 133101. [Google Scholar] [CrossRef]
- Yang, W.; Hudspeth, Q.; Chow, P.K.; Warrender, J.M.; Ferdous, N.; Ertekin, E.; Malladi, G.; Akey, A.J.; Aziz, M.J.; Williams, J.S. Atomistic mechanisms for the thermal relaxation of Au-hyperdoped Si. Phys. Rev. Appl. 2019, 12, 024015. [Google Scholar] [CrossRef]
- Yang, W.; Ferdous, N.; Simpson, P.J.; Gaudet, J.M.; Hudspeth, Q.; Chow, P.K.; Warrender, J.M.; Akey, A.J.; Aziz, M.J.; Ertekin, E.; et al. Evidence for vacancy trapping in Au-hyperdoped Si following pulsed laser melting. APL Mater. 2019, 7, 101124. [Google Scholar] [CrossRef]
- Lim, S.Q.; Lew, C.T.K.; Chow, P.K.; Warrender, J.M.; Williams, J.S.; Johnson, B.C. Process-induced defects in Au-hyperdoped Si photodiodes. J. Appl. Phys. 2019, 126, 224502. [Google Scholar] [CrossRef]
- Lim, S.Q.; Lew, C.T.K.; Chow, P.K.; Warrender, J.M.; Williams, J.S.; Johnson, B.C. Toward understanding and optimizing Au-hyperdoped Si infrared photodetectors. APL Mater. 2020, 8, 061109. [Google Scholar] [CrossRef]
- Olea, J.; del Prado, A.; Pastor, D.; Mártil, I.; González-Díaz, G. Sub-bandgap absorption in Ti implanted Si over the Mott limit. J. Appl. Phys. 2011, 109, 113541. [Google Scholar] [CrossRef]
- Pastor, D.; Olea, J.; del Prado, A.; García-Hemme, E.; García-Hernansanz, R.; González-Díaz, G. Insulator to metallic transition due to intermediate band formation in Ti-implanted silicon. Sol. Energy Mater. Sol. Cells 2012, 104, 159–164. [Google Scholar] [CrossRef]
- Castán, H.; Pérez, E.; García, H.; Dueñas, S.; Bailón, L.; Olea, J.; Pastor, D.; García-Hemme, E.; Irigoyen, M.; González-Díaz, G. Experimental verification of intermediate band formation on titanium-implanted silicon. J. Appl. Phys. 2013, 113, 024104. [Google Scholar] [CrossRef]
- García-Hemme, E.; García-Hernansanz, R.; Olea, J.; Pastor, D.; del Prado, A.; Mártil, I.; Gónzalez-Díaz, G. Sub-bandgap spectral photo-response analysis of Ti supersaturated Si. Appl. Phys. Lett. 2012, 101, 192101. [Google Scholar] [CrossRef]
- García-Hemme, E.; García-Hernansanz, R.; Olea, J.; Pastor, D.; del Prado, A.; Mártil, I.; González-Díaz, G. Room-temperature operation of a titanium supersaturated silicon-based infrared photodetector. Appl. Phys. Lett. 2014, 104, 211105. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, S.Q.; Williams, J.S. Electrical and Optical Doping of Silicon by Pulsed-Laser Melting. Micro 2022, 2, 1-22. https://doi.org/10.3390/micro2010001
Lim SQ, Williams JS. Electrical and Optical Doping of Silicon by Pulsed-Laser Melting. Micro. 2022; 2(1):1-22. https://doi.org/10.3390/micro2010001
Chicago/Turabian StyleLim, Shao Qi, and James S. Williams. 2022. "Electrical and Optical Doping of Silicon by Pulsed-Laser Melting" Micro 2, no. 1: 1-22. https://doi.org/10.3390/micro2010001
APA StyleLim, S. Q., & Williams, J. S. (2022). Electrical and Optical Doping of Silicon by Pulsed-Laser Melting. Micro, 2(1), 1-22. https://doi.org/10.3390/micro2010001






