Silicon Nitride Interface Engineering for Fermi Level Depinning and Realization of Dopant-Free MOSFETs
Abstract
:1. Introduction
1.1. Metal-Semiconductor Contacts
1.1.1. Pinning Behavior without Interlayer ( → 0)
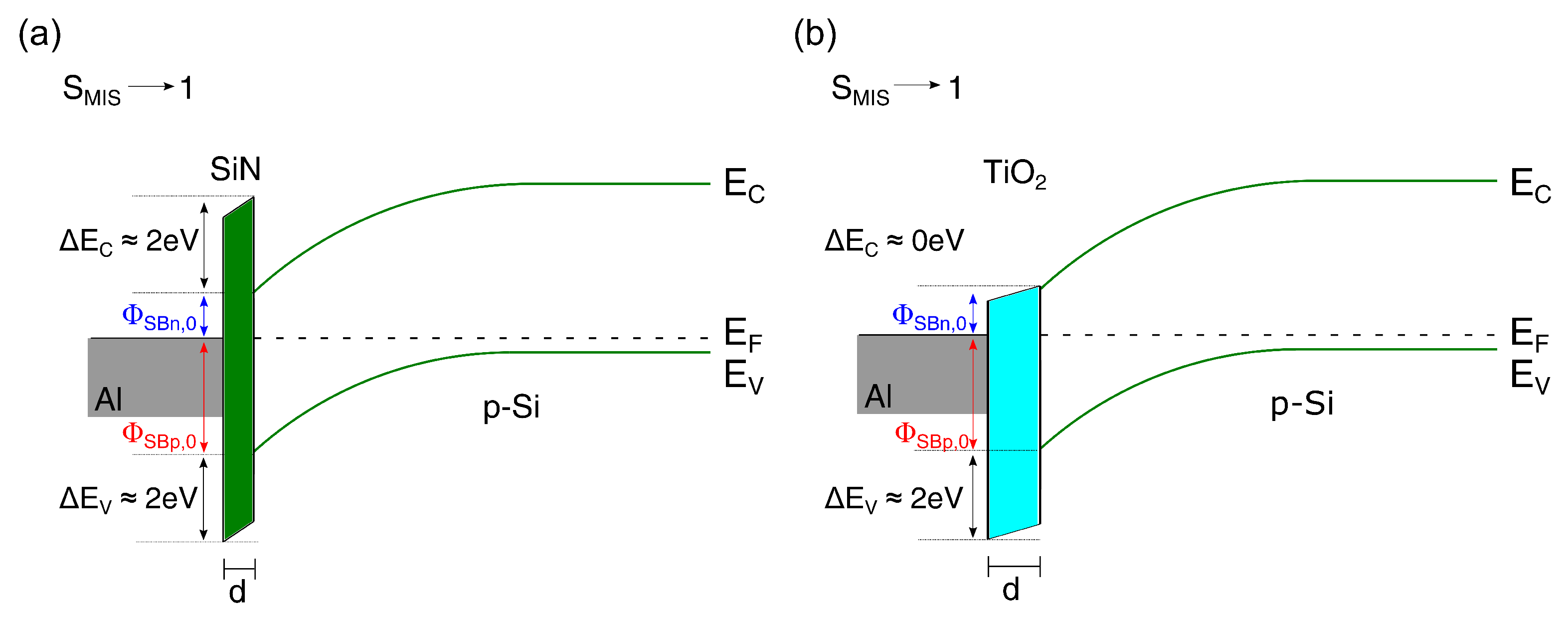
1.1.2. Pinning Behavior with Interlayer ( → 1) and Choice of Material
2. Materials and Methods
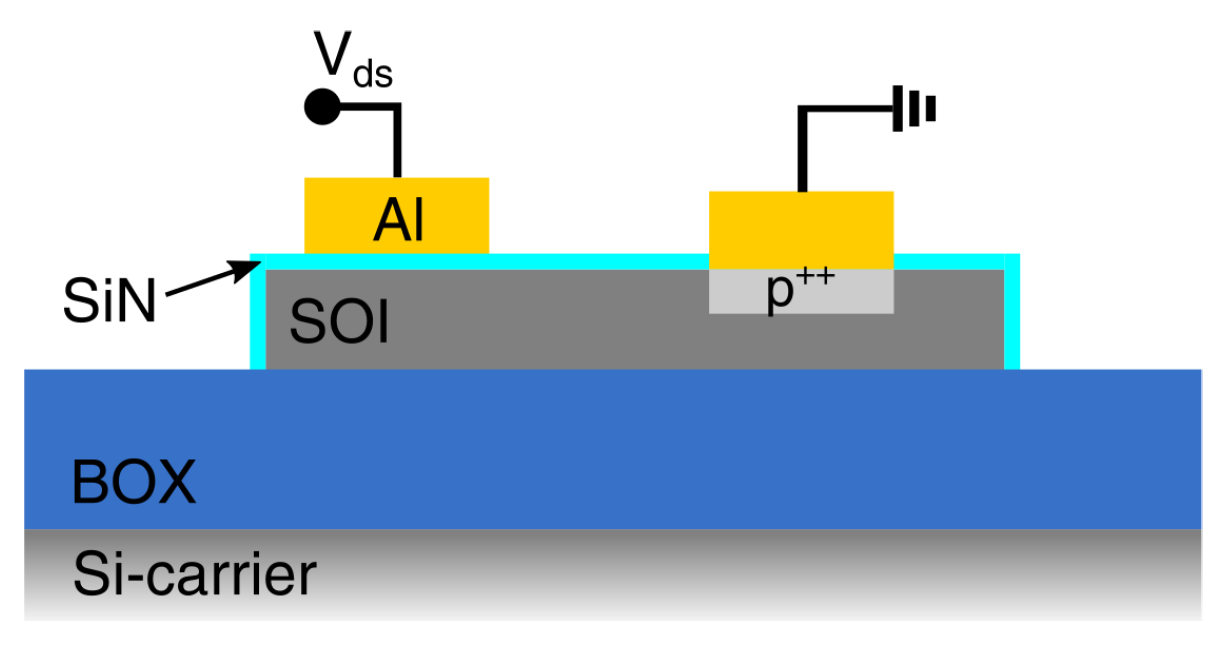
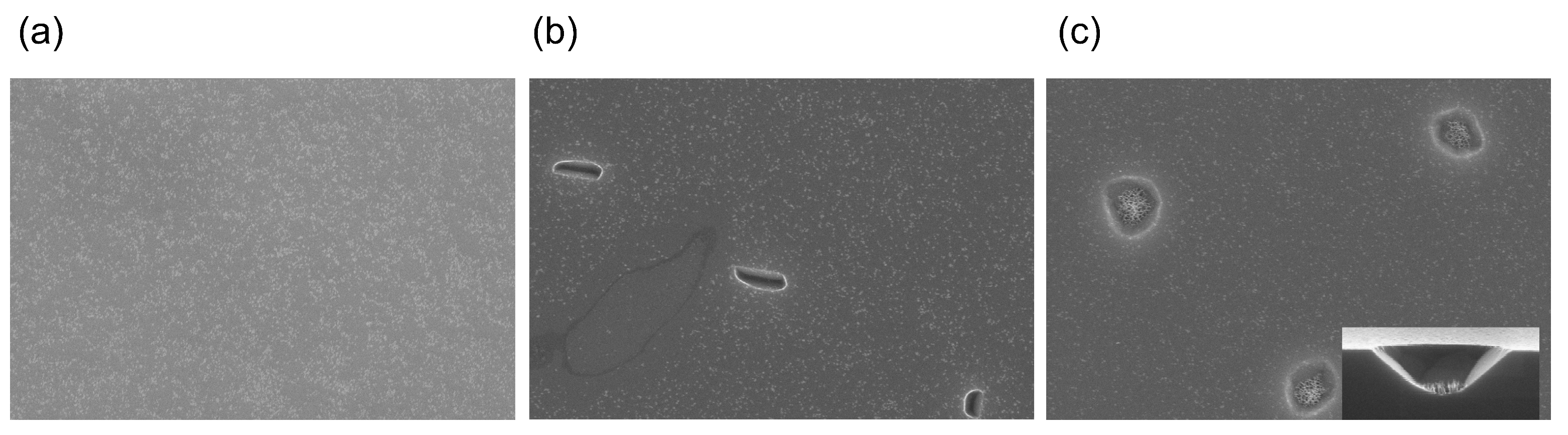
2.1. Fabrication of Schottky Diodes
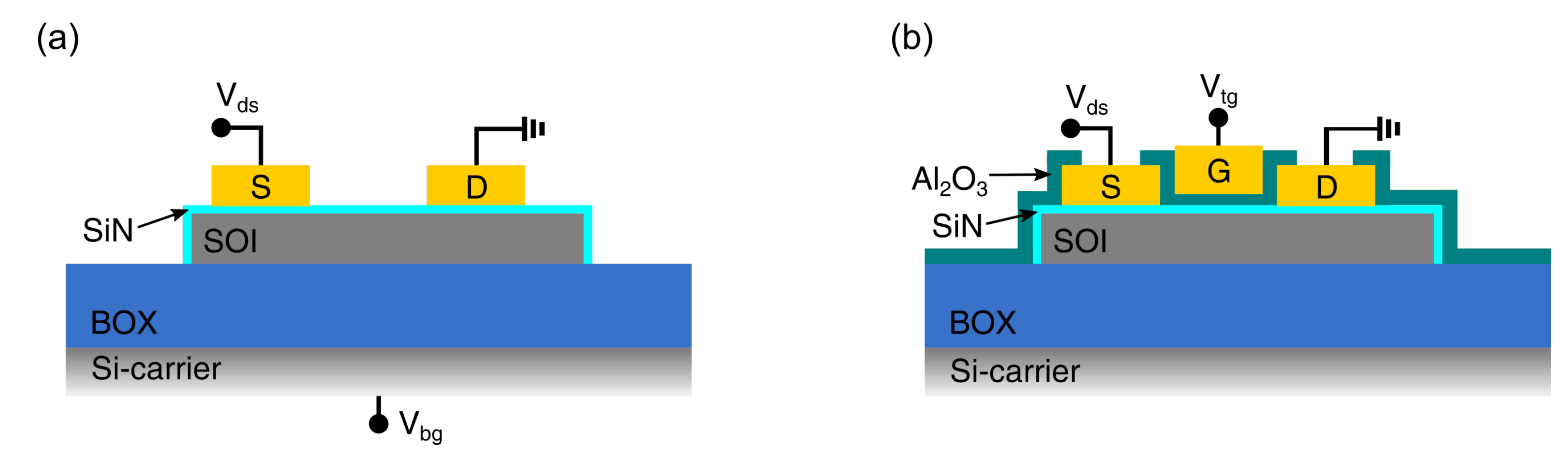
2.2. Fabrication of Schottky Barrier MOSFETs
2.3. Extraction of Schottky Barrier Heights
3. Results and Discussion
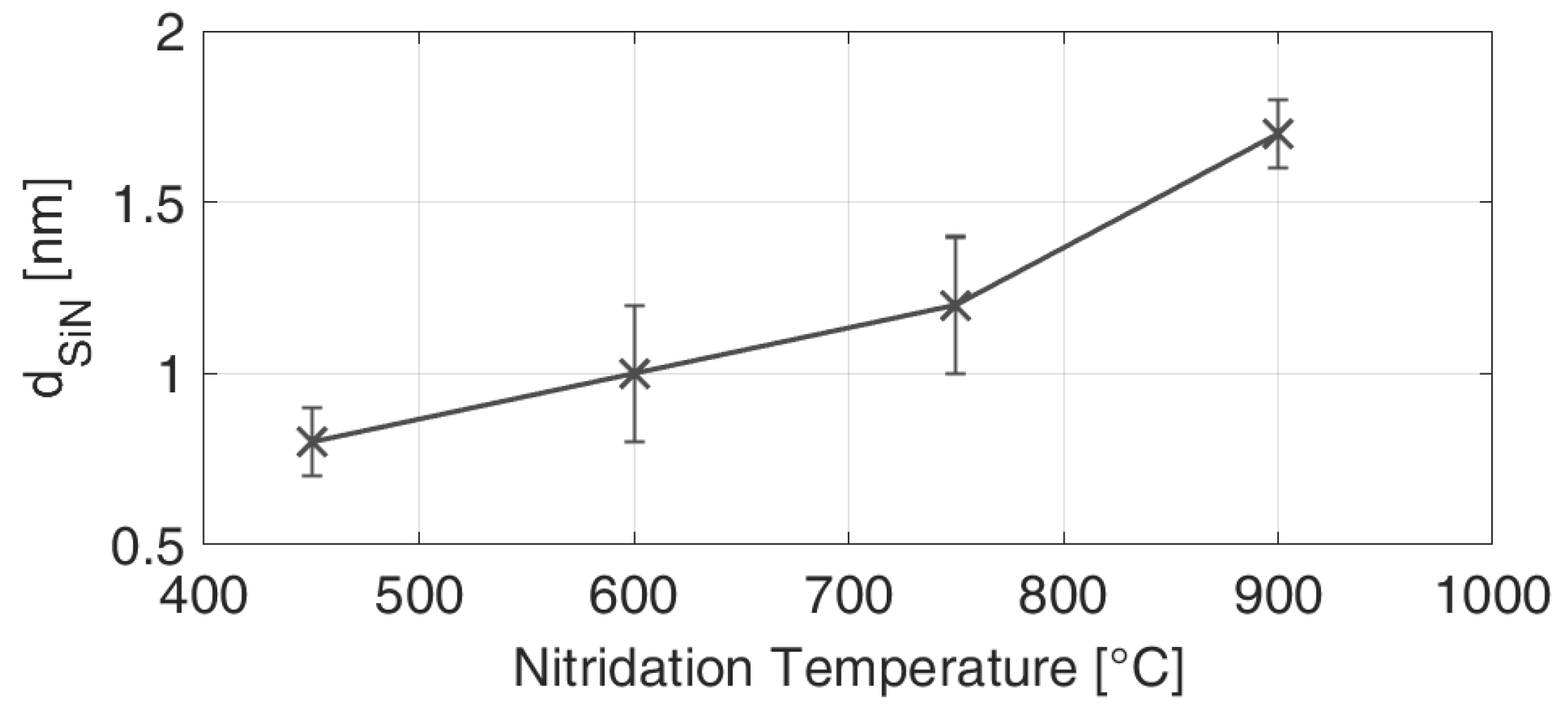
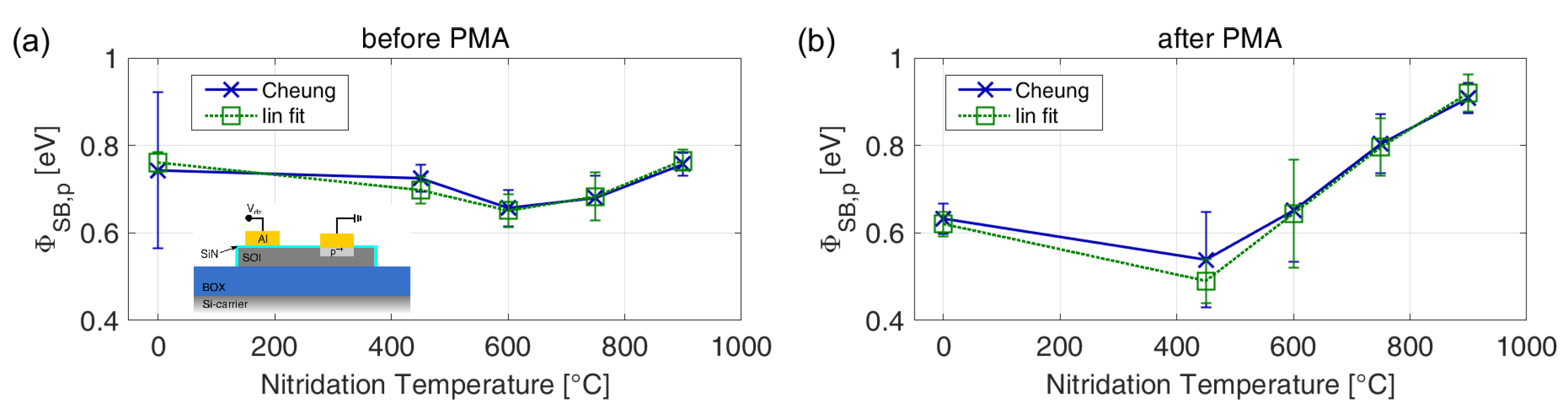
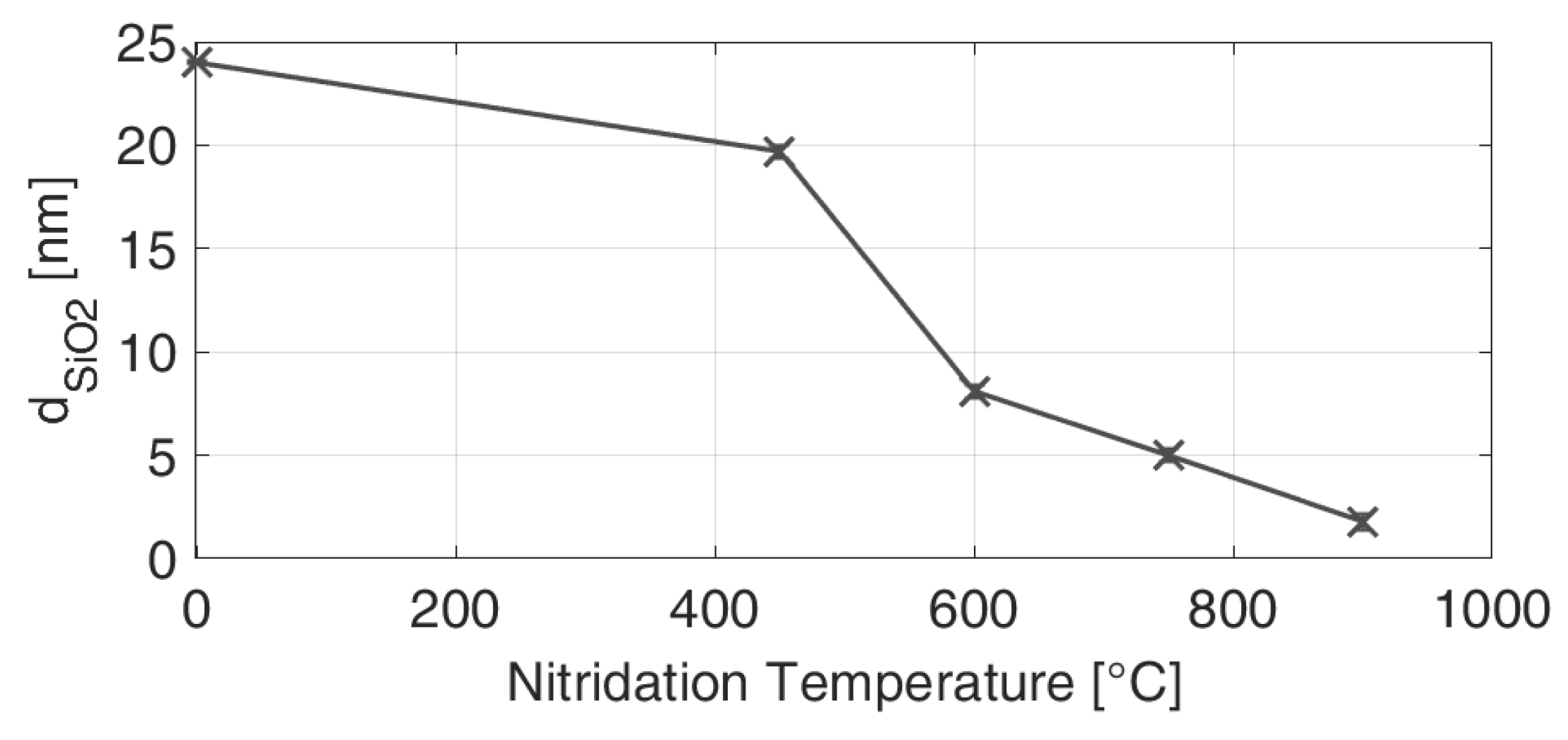
3.1. Schottky Barrier Height for Different SiN Interlayers
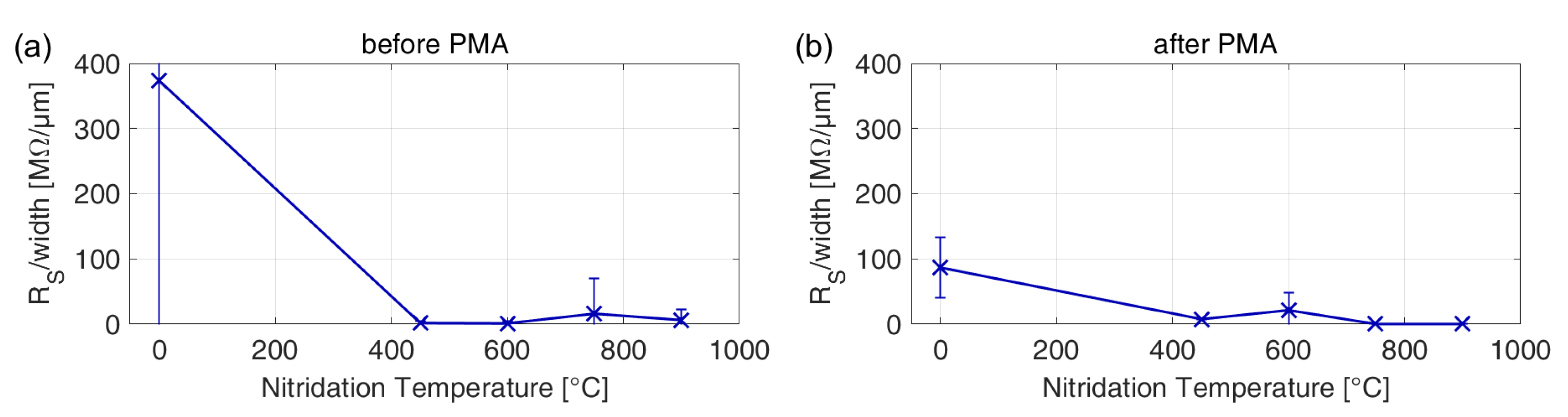
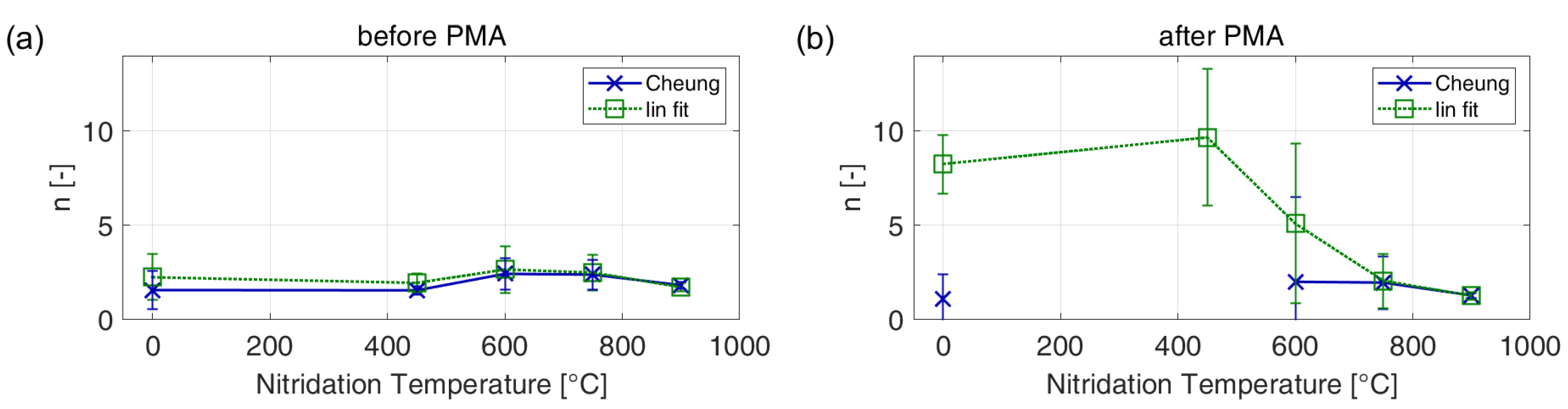
3.2. Ideality Factor and Series Resistance
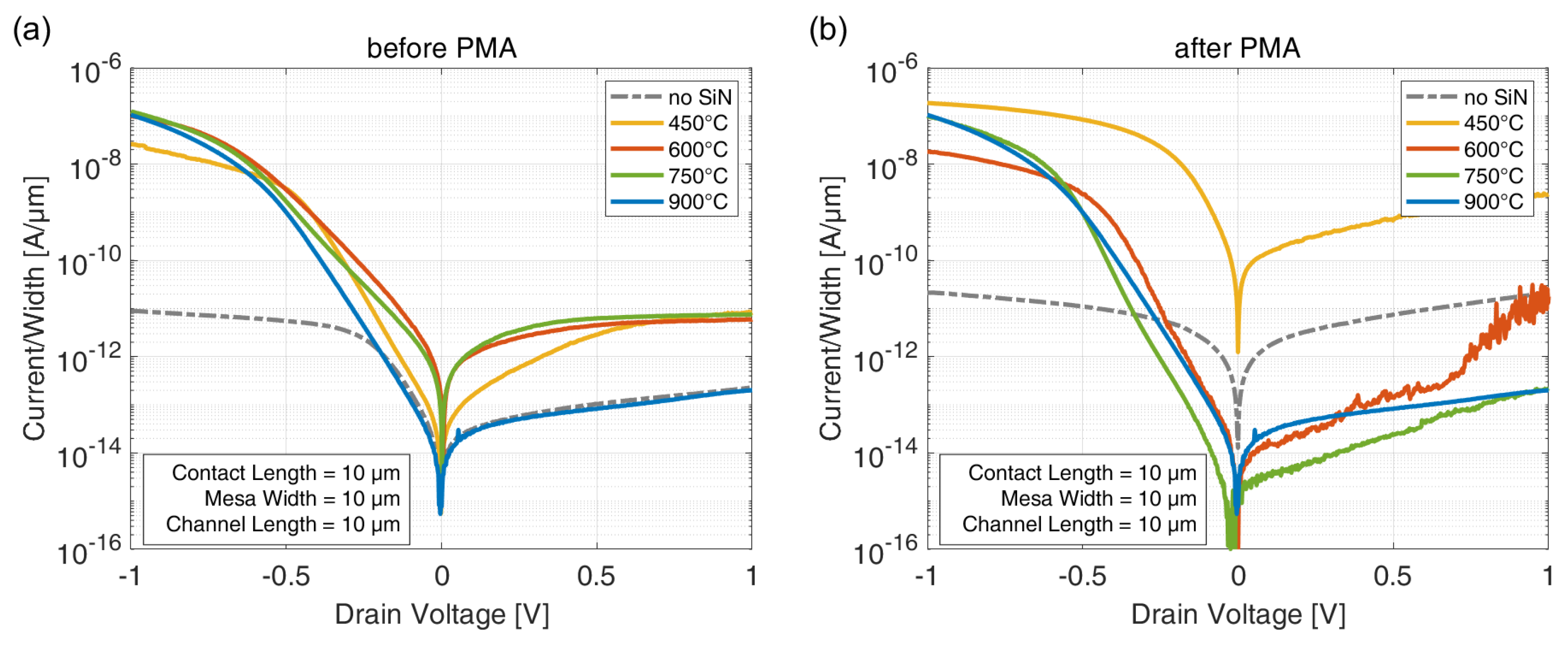
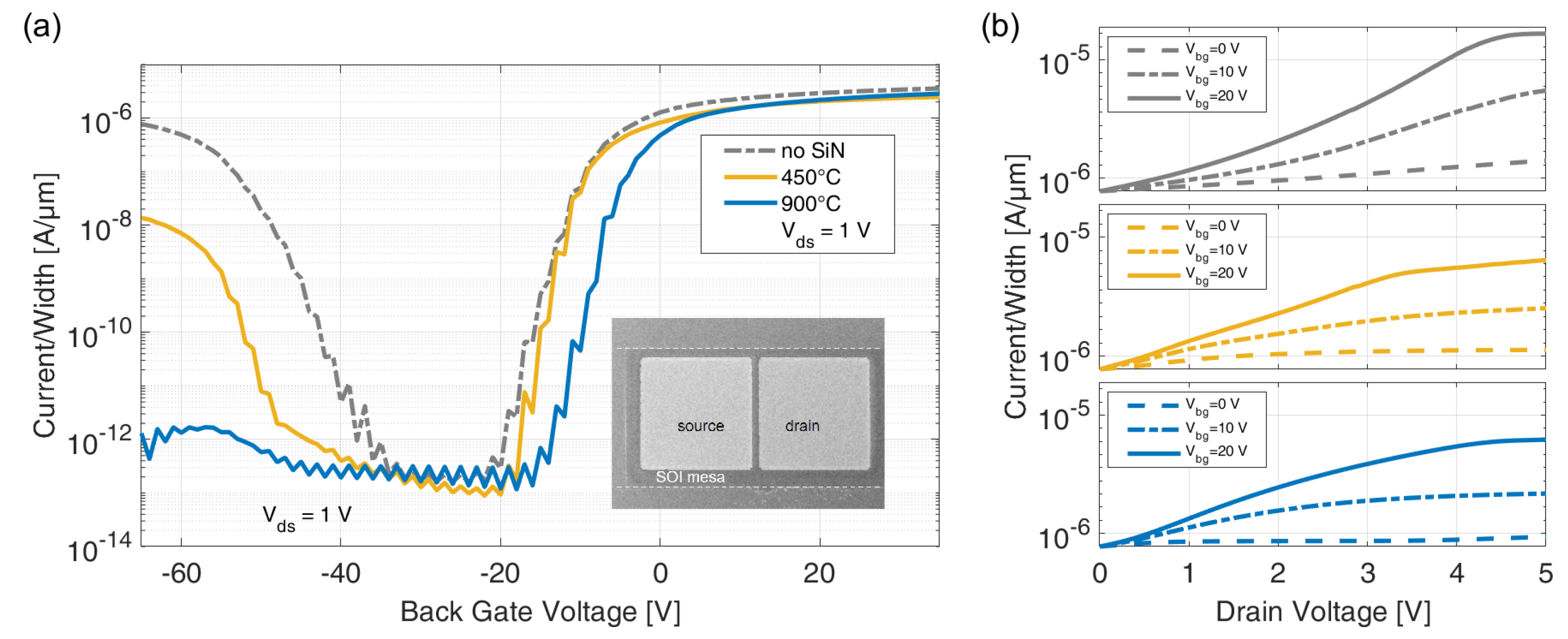
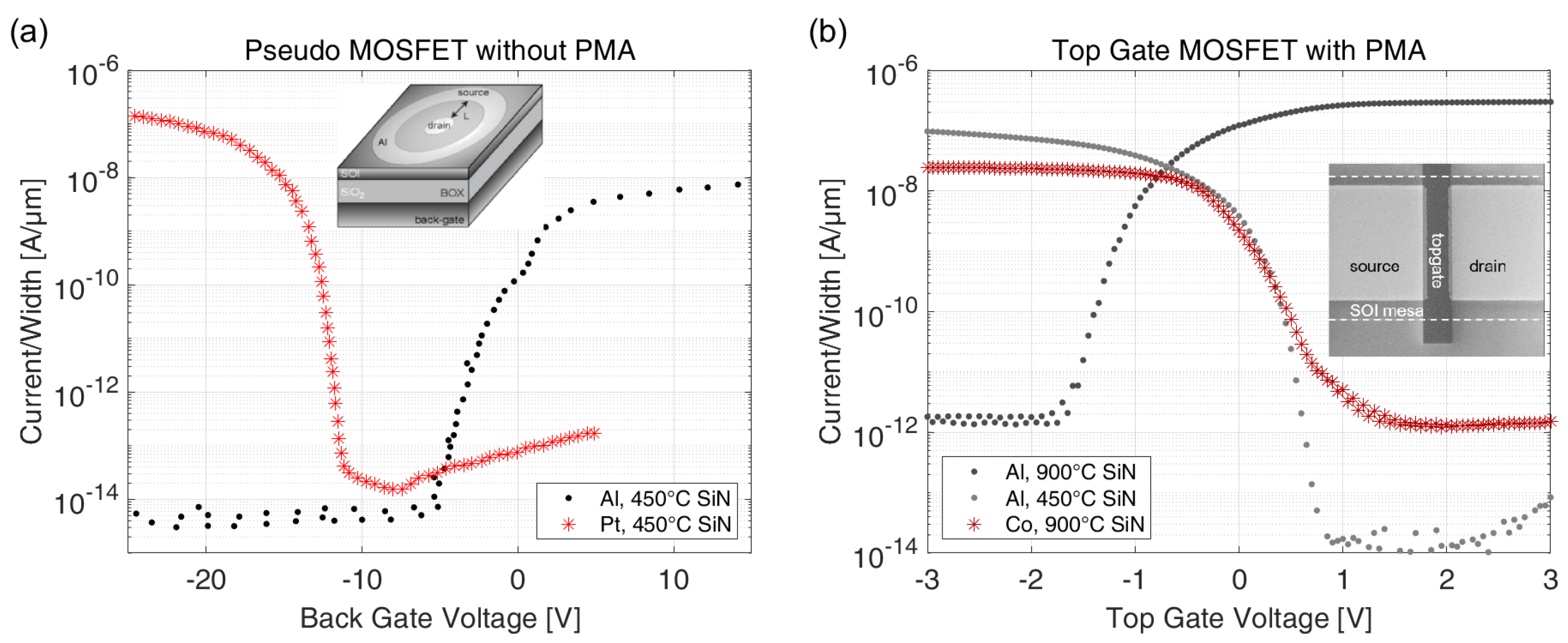
3.3. Electrical Characteristics of SB-MOSFETs with Varying Interlayers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shine, G.; Saraswat, K.C. Analysis of Atomistic Dopant Variation and Fermi Level Depinning in Nanoscale Contacts. IEEE Trans. Electron Devices 2017, 64, 3768–3774. [Google Scholar] [CrossRef]
- Björk, M.T.; Schmid, H.; Knoch, J.; Riel, H.; Riess, W. Donor deactivation in silicon nanostructures. Nat. Nanotech. 2009, 4, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Calderón, M.J.; Verduijn, J.; Lansbergen, G.P.; Tettamanzi, G.C.; Rogge, S.; Koiller, B. Heterointerface effects on the charging energy of the shallow D—Ground state in silicon: Role of dielectric mismatch. Phys. Rev. B 2010, 82, 075317. [Google Scholar] [CrossRef] [Green Version]
- Mol, J.A.; Salfi, J.; Miwa, J.A.; Simmons, M.Y.; Rogge, S. Interplay between quantum confinement and dielectric mismatch for ultrashallow dopants. Phys. Rev. B 2013, 87, 245417. [Google Scholar] [CrossRef] [Green Version]
- Khanal, D.R.; Yim, J.W.L.; Walukiewicz, W.; Wu, J. Effects of Quantum Confinement on the Doping Limit of Semiconductor Nanowires. Nano Lett. 2007, 7, 1186–1190. [Google Scholar] [CrossRef]
- Diarra, M.; Niquet, Y.M.; Delerue, C.; Allan, G. Ionization energy of donor and acceptor impurities in semiconductor nanowires: Importance of dielectric confinement. Phys. Rev. B 2007, 75, 045301. [Google Scholar] [CrossRef] [Green Version]
- Saraswat, K.C.; Shine, G. Low Resistance Contacts to Nanoscale Semiconductor Devices. ECS Trans. 2016, 75, 513–523. [Google Scholar] [CrossRef]
- Agrawal, A.; Lin, J.; Barth, M.; White, R.; Zheng, B.; Chopra, S.; Gupta, S.; Wang, K.; Gelatos, J.; Mohney, S.E.; et al. Fermi level depinning and contact resistivity reduction using a reduced titania interlayer in n-silicon metal-insulator-semiconductor ohmic contacts. Appl. Phys. Lett. 2014, 104, 112101. [Google Scholar] [CrossRef] [Green Version]
- Connelly, D.; Faulkner, C.; Clifton, P.A.; Grupp, D.E. Fermi-level depinning for low-barrier Schottky source/drain transistors. Appl. Phys. Lett. 2006, 88, 012105. [Google Scholar] [CrossRef]
- Islam, R.; Shine, G.; Saraswat, K.C. Schottky barrier height reduction for holes by Fermi level depinning using metal/nickel oxide/silicon contacts. Appl. Phys. Lett. 2014, 105, 182103. [Google Scholar] [CrossRef] [Green Version]
- Moench, W. On the physics of metal-semiconductor interfaces. Rep. Prog. Phys. 1990, 53, 221–278. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Knoch, J. Nanoelectronics; De Gruyter Oldenbourg: Berlin, Germany, 2020. [Google Scholar]
- Xiao, S.; Xu, S. High-Efficiency Silicon Solar Cells—Materials and Devices Physics. Crit. Solid State Mater. Sci. 2014, 39, 277–317. [Google Scholar] [CrossRef]
- Seiffe, J.; Gautero, L.; Hofmann, M.; Rentsch, J.; Preu, R.; Weber, S.; Eichel, R.A. Surface passivation of crystalline silicon by plasma-enhanced chemical vapor deposition double layers of silicon-rich silicon oxynitride and silicon nitride. J. Appl. Phys. 2011, 109, 034105. [Google Scholar] [CrossRef]
- Shen, F.; Ke, L.L. Numerical Study of Coupled Electrical-Thermal-Mechanical-Wear Behavior in Electrical Contacts. Metals 2021, 11, 955. [Google Scholar] [CrossRef]
- Fillon, A.; Abadias, G.; Michel, A.; Jaouen, C.; Villechaise, P. Influence of Phase Transformation on Stress Evolution during Growth of Metal Thin Films on Silicon. Phys. Rev. Lett. 2010, 104, 096101. [Google Scholar] [CrossRef] [PubMed]
- Card, H. Aluminum—Silicon Schottky barriers and ohmic contacts in integrated circuits. IEEE Trans. Electron Devices 1976, 23, 538–544. [Google Scholar] [CrossRef]
- Hlil, E.K.; Kubler, L.; Bischoff, J.L.; Bolmont, D. Photoemission study of ammonia dissociation on Si(100) below 700 K. Phys. Rev. B 1987, 35, 5913–5916. [Google Scholar] [CrossRef] [PubMed]
- Borrel, J.; Hutin, L.; Rozeau, O.; Jaud, M.A.; Martinie, S.; Gregoire, M.; Dubois, E.; Vinet, M. Modeling of Fermi-Level Pinning Alleviation With MIS Contacts: n and pMOSFETs Cointegration Considerations—Part I. IEEE Trans. Electron Devices 2016, 63, 6. [Google Scholar]
- Riederer, F.; Grap, T.; Fischer, S.; Mueller, M.R.; Yamaoka, D.; Sun, B.; Gupta, C.; Kallis, K.T.; Knoch, J. Alternatives for Doping in Nanoscale Field-Effect Transistors. Phys. Status Solidi A 2018, 215, 1700969. [Google Scholar] [CrossRef]
- Fischer, S.; Knoch, J.; Vescan, A. Ultra Thin Silicon Nitride Interface Engineering. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2017. [Google Scholar]
- Gupta, S.; Paramahans Manik, P.; Kesh Mishra, R.; Nainani, A.; Abraham, M.C.; Lodha, S. Contact resistivity reduction through interfacial layer doping in metal-interfacial layer-semiconductor contacts. J. Appl. Phys. 2013, 113, 234505. [Google Scholar] [CrossRef]
- Sankey, O.F.; Allen, R.E.; Dow, J.D. Si/transition-metal Schottky barriers: Fermi-level pinning by Si dangling bonds at interfacial vacancies. Solid State Commun. 1984, 49, 1–5. [Google Scholar] [CrossRef]
- Mönch, W. Barrier heights of real Schottky contacts explained by metal-induced gap states and lateral inhomogeneities. J. Vac. Sci. Technol. B 1999, 17, 1867. [Google Scholar] [CrossRef]
- Heine, V. Theory of Surface States. Phys. Rev. 1965, 138, A1689–A1696. [Google Scholar] [CrossRef]
- Lu, H.; Guo, Y.; Li, H.; Robertson, J. Modeling of surface gap state passivation and Fermi level de-pinning in solar cells. Appl. Phys. Lett. 2019, 114, 222106. [Google Scholar] [CrossRef]
- Islam, R.; Saraswat, K.C. Metal/insulator/semiconductor carrier selective contacts for photovoltaic cells. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; IEEE: New York, NY, USA; pp. 285–289. [Google Scholar] [CrossRef]
- Kern, W. The Evolution of Silicon Wafer Cleaning Technology. J. Electrochem. Soc. 1990, 137, 1887–1892. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization; John Wiley & Sons, Inc.: Hoboken, NJ, USA; pp. i–xv. [CrossRef]
- Cheung, S.K.; Cheung, N.W. Extraction of Schottky diode parameters from forward current-voltage characteristics. Appl. Phys. Lett. 1986, 49, 85–87. [Google Scholar] [CrossRef]
- Card, H. Thermally-induced changes in barrier heights of aluminium contacts to p- and n-type silicon. Solid State Commun. 1975, 16, 87–89. [Google Scholar] [CrossRef]
- McCaldin, J.O.; Sankur, H. Diffusivity and Solubility of Si in the Al Metallization of Integrated Circuits. Appl. Phys. Lett. 1971, 19, 524–527. [Google Scholar] [CrossRef] [Green Version]
- Basterfield, J.; Shannon, J.; Gill, A. The nature of barrier height variations in alloyed Al-Si Schottky barrier diodes. Solid-State Electron. 1975, 18, 290. [Google Scholar] [CrossRef]
- Fischer, S.; Kremer, H.I.; Berghoff, B.; Maß, T.; Taubner, T.; Knoch, J. Dopant-free complementary metal oxide silicon field effect transistors: Dopant-free MOSFETs. Phys. Status Solidi A 2016, 213, 1494–1499. [Google Scholar] [CrossRef]
- Sankur, H.; McCaldin, J.; Devaney, J. Solid-phase epitaxial growth of Si mesas from al metallization. Appl. Phys. Lett. 1973, 22, 64–66. [Google Scholar] [CrossRef] [Green Version]
- Ito, T.; Nozaki, T.; Arakawa, H.; Shinoda, M. Thermally grown silicon nitride films for high-performance MNS devices. Appl. Phys. Lett. 1978, 32, 330–331. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richstein, B.; Hellmich, L.; Knoch, J. Silicon Nitride Interface Engineering for Fermi Level Depinning and Realization of Dopant-Free MOSFETs. Micro 2021, 1, 228-241. https://doi.org/10.3390/micro1020017
Richstein B, Hellmich L, Knoch J. Silicon Nitride Interface Engineering for Fermi Level Depinning and Realization of Dopant-Free MOSFETs. Micro. 2021; 1(2):228-241. https://doi.org/10.3390/micro1020017
Chicago/Turabian StyleRichstein, Benjamin, Lena Hellmich, and Joachim Knoch. 2021. "Silicon Nitride Interface Engineering for Fermi Level Depinning and Realization of Dopant-Free MOSFETs" Micro 1, no. 2: 228-241. https://doi.org/10.3390/micro1020017
APA StyleRichstein, B., Hellmich, L., & Knoch, J. (2021). Silicon Nitride Interface Engineering for Fermi Level Depinning and Realization of Dopant-Free MOSFETs. Micro, 1(2), 228-241. https://doi.org/10.3390/micro1020017





