Reliability and Agreement of Free Web-Based 3D Software for Computing Facial Area and Volume Measurements

Abstract

Background: Facial surgeries require meticulous planning and outcome assessments, where facial analysis plays a critical role. This study introduces a new approach by utilizing three-dimensional (3D) imaging techniques, which are known for their ability to measure facial areas and volumes accurately. The purpose of this study is to introduce and evaluate a free web-based software application designed to take area and volume measurements on 3D models of patient faces. Methods: This study employed the online facial analysis software to conduct ten measurements on 3D models of subjects, including five measurements of area and five measurements of volume. These measurements were then compared with those obtained from the established 3D modeling software called Blender (version 3.2) using the Bland–Altman plot. To ensure accuracy, the intra-rater and inter-rater reliabilities of the web-based software were evaluated using the Intraclass Correlation Coefficient (ICC) method. Additionally, statistical assumptions such as normality and homoscedasticity were rigorously verified before analysis. Results: This study found that the web-based facial analysis software showed high agreement with the 3D software Blender within 95% confidence limits. Moreover, the online application demonstrated excellent intra-rater and inter-rater reliability in most analyses, as indicated by the ICC test. Conclusion: The findings suggest that the free online 3D software is reliable for facial analysis, particularly in measuring areas and volumes. This indicates its potential utility in enhancing surgical planning and evaluation in facial surgeries. This study underscores the software’s capability to improve surgical outcomes by integrating precise area and volume measurements into facial surgery planning and assessment processes.

1. Introduction

Reconstructive and aesthetic facial surgery involves preoperative planning and postoperative evaluation. This process requires a detailed examination of the face. Traditionally, a facial analysis is performed directly on a patient’s face using a ruler or miter. However, this method can cause discomfort to patients and limit the reproducibility of the results [1]. Computer-assisted 2D images (photographic capture) have been widely used for the analysis of the face, although this involves the inherent drawback of representing the 3D structure of the face in 2D [2]. Thanks to the latest advances in technology, surgeons are now able to perform facial analyses on 3D computer models of patients [3]. Increasing the adoption of 3D imaging and 3D facial analysis is predicted [2,4,5,6].

Besides various commercial applications [7,8,9], free web-based software tools that use 3D imaging to perform facial analysis have been introduced [10]. However, these facial analysis tools still only perform traditional 2D measurements, such as measurements of the distances and angles between facial landmarks. The benefit of utilizing more advanced measurements, such as area and volume, has been pointed out in the literature [5,11]. We have recently introduced area and volume measurement techniques for facial surgeries, aimed at augmenting surgeons’ abilities to precisely analyze facial structures and plan surgeries. This novel addition to facial analysis is intended to significantly improve surgical outcomes and enhance the overall success of facial surgical procedures [12,13]. We have developed open-source algorithms to measure area and volume on a 3D facial model [13] and then utilized these algorithms to enhance the free web-based software called Face Analyzer [14] to help surgeons perform a more in-depth analysis of a patient’s face [1]. The Face Analyzer software, hosted at digitized-rhinoplasty.com, is now capable of measuring the area and volume of certain regions, such as the dorsal hump, nasal dorsum, root of the nose (Radix), and tip of the nose, and it is based on several previous works [10,12,13].

When a new measurement device is developed in the medical field, it is crucial to compare it with a gold standard or established standard to ensure its validity, reliability, and effectiveness [15]. The gold standard is typically a measurement method or instrument that is widely accepted as the best available or the most accurate. It is used as a reference point to evaluate new tools or methods. The Bland–Altman plot has been upheld within the medical community as the quintessential statistical method to ascertain the degree of agreement, particularly when introducing new measurement methodologies.

This study introduces a new free web-based software application designed for comprehensive facial analysis, which is crucial for planning facial operations and evaluating their results. By leveraging three-dimensional (3D) imaging techniques, the software enables precise measurements of facial areas and volumes, enhancing the capabilities of facial surgery planning and evaluation. The Bland–Altman analytical framework is employed in this study to verify the fidelity of this web-based facial analysis software, comparing its measurements against those obtained from the well-established 3D modeling software called Blender. This comparison involves ten distinct measurements on 3D models of subjects, encompassing five area measurements and five volume measurements.

Moreover, the Intraclass Correlation Coefficient (ICC) analysis is utilized to assess the intra-rater and inter-rater reliabilities of the web software for these 3D area and volume measurements. The meticulous verification of statistical assumptions, such as normality and homoscedasticity, ensures the robustness of the analysis. The results affirm that the web-based facial analysis software not only demonstrates agreement within 95% confidence limits with the 3D software Blender, but also exhibits excellent performance in most intra-rater and inter-rater reliability analyses. This underscores the utility of the free online 3D software in providing accurate, repeatable area and volume measurements, thereby paving the way for substantial progress in facial surgery planning and assessment. The findings from this study, therefore, highlight the potential of the web-based software as an innovative and accessible tool, set to revolutionize the precision and effectiveness of surgical outcomes in facial analysis [16].

In this study, we explain the development and operational aspects of the software and showcase the results based on the observed and experimented data from our evaluations of its reliability and agreement. This thorough examination is carried out to confirm that the web-based 3D face analyzer [14] not only enhances the analytical capabilities of facial surgeons [1] but also aligns with strict methodological standards [17,18]. The subsequent sections of this article will present an in-depth analysis of our findings, which indicate a promising level of agreement and reliability of the web-based software when compared to the 3D software Blender. We will discuss how these results underscore the potential efficacy of the free online 3D software in enhancing facial analysis, thereby contributing to more effective surgical planning and evaluation. This study ultimately aims to illuminate the potential of integrating precise area and volume measurements into the field of facial surgery, potentially leading to improved surgical outcomes.

2. Related Concepts and Research

The following section describes the general definition of reliability and the Intraclass Correlation Coefficient (ICC) used to assess it. This includes an explanation of the ICC’s underlying assumptions and guidelines for ensuring these assumptions are met. Following this, we explore the concept of agreement and the use of the Bland–Altman plot to evaluate agreement between measurement devices. The process of constructing and interpreting a Bland–Altman plot is detailed. The section concludes by highlighting various studies that have employed ICC and Bland–Altman plots to assess both reliability and agreement.

2.1. Reliability

In the context of medical measurement devices, ‘reliability’ refers to the consistency and dependability of the device in providing accurate measurements across different instances of use [19,20]. It implies that the device consistently produces the same results under the same conditions. Two key aspects of reliability include repeatability and reproducibility [21]. Repeatability is the ability of the device to produce the same results when the same parameter is measured repeatedly under identical conditions. Reproducibility is the device’s capacity to provide consistent measurements under varying conditions, such as different times [22].

Measuring the reliability of a new medical measurement device is crucial because it ensures patient safety by providing accurate diagnoses and treatment decisions, thus reducing the risk of harm [23]. Reliability is important for cost-effectiveness as it minimizes the need for repeat testing and additional treatments. In the realm of clinical research, reliable devices are essential to ensure the integrity and validity of study results [16]. Additionally, the trust of healthcare professionals in their products also hinges on the reliability of these devices. Overall, the reliability of medical devices is a cornerstone of effective, safe, and efficient healthcare delivery.

2.2. Intraclass Correlation Coefficient (ICC)

The ICC is a statistical measure used to assess the reliability or consistency of measurements made by different raters (observers, instruments, or measurement techniques) on the same subject. In the context of medical devices, the ICC is a key tool used to evaluate both intra- and inter-reliability [24].

The ICC quantifies the degree of agreement or correlation between different sets of measurements. It ranges from 0 to 1, where 0 indicates no agreement and 1 represents perfect agreement [25].

The ICC is commonly used in the medical field to assess the reliability of various types of devices, especially those involved in diagnostic measurements, physical assessments, and laboratory tests [26,27].

Checking the Assumptions of ICC

Many statistical methods, including certain forms of ICC, assume that the data being analyzed are normally distributed. The Shapiro–Wilk test is used to check this assumption. The Shapiro–Wilk test provides a p-value for each test. A p-value less than the chosen alpha level (commonly 0.05) suggests that the data do not follow a normal distribution. A non-significant result (p-value greater than alpha level) indicates that the normality assumption has not been violated. If the data significantly deviate from a normal distribution, the results of the ICC may not be reliable [28,29].

If the Shapiro–Wilk test has significant results, skewness and kurtosis values can be used as additional measures to judge normality. Skewness and kurtosis provide insights into the shape of the data distribution, which can help in understanding how the data deviate from a normal distribution. Skewness measures the asymmetry of the data distribution. Kurtosis measures the ‘tailedness’ of the data distribution. If skewness is between −2 and +2 and kurtosis is between −7 and +7, the data are considered to be normal [30].

Another assumption for certain statistical analyses, including some types of ICCs, is that the variance within each group (e.g., measurements from each rater or instrument) is consistent across all groups. If variances are unequal (heteroscedasticity), they can affect the validity of the ICC. Checking for consistent variance is therefore crucial.

Levene’s test specifically checks whether the assumption of equal variances holds true for a set of data. Levene’s test allows one to choose the measure of central tendency (mean, median, and trimmed mean) to use for the test. The median is often a good choice as it is less sensitive to outliers. The output of Levene’s test will include a p-value. If this p-value is less than the alpha level (commonly 0.05), this suggests that there is a statistically significant difference in the variances between groups, indicating a violation of the homoscedasticity assumption. If the p-value is greater than the alpha level, the null hypothesis of equal variances is not rejected, suggesting that the assumption of homoscedasticity is reasonable. A significant result from Levene’s test indicates that the variances are not equal (heteroscedasticity), which is a violation of one of the key assumptions for certain statistical tests, including some types of ICCs [29,31].

2.3. Agreement

In the context of comparing two measurement instruments, ‘agreement’ refers to how closely the measurements obtained from these instruments match each other [32]. It is important to differentiate this from accuracy or reliability:

Accuracy: This refers to how close a measurement is to the true or actual value. When evaluating the agreement between two instruments, accuracy is not directly assessed, unless one of the instruments is considered a ‘gold standard’ or known to produce accurate results.

Reliability: This concerns the consistency of the measurements. A reliable instrument will produce the same results under consistent conditions [33].

When discussing agreement between two measurement instruments, we are concerned with questions like the following:

• Do the instruments produce similar results when measuring the same item? This involves looking at the differences in the measurements from the two instruments for the same subject or sample.
• Is there a consistent bias? If one instrument consistently measures higher or lower than the other, this is referred to as a bias. The Bland–Altman analysis, for example, helps identify and quantify this bias.
• How much do the measurements vary? This refers to the variability in the differences between the two instruments.
• Are discrepancies related to the magnitude of the measurement? Sometimes, the difference between instruments might change depending on the actual size or value of what is being measured. For instance, two scales might agree closely for lighter weights but diverge for heavier weights [32,33].

In summary, agreement in this context is about how well two measurement instruments concur in their readings, taking into account both the consistency of the measurements (lack of random error) and any systematic differences (bias) between them.

2.4. Bland–Altman Plot

The Bland–Altman plot is a widely used statistical method for assessing the agreement between two different measurement methods. It is particularly useful in the medical field to compare a new measurement technique against an established gold standard [34]. The way it works is as follows:

Interpretation: If the differences within the limits of agreement are clinically acceptable, the two methods may be used interchangeably. The presence of any trends or biases can also be assessed, such as a tendency for differences to increase as the magnitude of the measurement increases.

Difference Plotting: In this study, the difference between the measurements of the two methods for each subject is plotted against the mean of these measurements. This is carried out to explore the potential relationship between measurement error and true value.

Limits of Agreement: The mean difference (estimating systematic bias) and 95% limits of agreement (typically defined as 1.96 times the standard deviation of the mean difference plus and minus the differences) are graphically calculated. These limits are used to determine how different the new and gold standard methods are and to indicate whether the new method can be used interchangeably with the gold standard [34,35].

Interpretation: If the differences within the limits of agreement are clinically acceptable, the two methods can be used interchangeably. The presence of any trend or bias, such as a tendency for differences to increase with an increasing measurement size, can also be assessed.

Assumptions: The method assumes that the differences between the two methods are normally distributed. Before using the Bland–Altman plot, it is important to check for normality and that there is consistency in the measurement error across the range of measurements.

The Bland–Altman plot does not test whether the two methods are equivalent or whether either method is accurate. Instead, it assesses the consistency of the differences between the two methods, which is an important distinction. It is a valuable tool for method comparison studies because it highlights the magnitude of disagreement and helps to make a judgment about whether this is acceptable for clinical application [35,36,37].

The following steps are used to draw the Bland–Altman plot:

• Collect Data: Two sets of measurements, taken on the same subjects or samples using two different methods, are needed.
• Calculate the Mean and Difference: For each pair of measurements, calculate the mean (average) and the difference (typically, Method 1–Method 2). Plot the mean on the x-axis and the difference on the y-axis.
• Plot the Points: On a graph, plot each pair of means and differences as a single point. The x-coordinate of the point is the mean of the two measurements, and the y-coordinate is the difference between the two measurements.
• Calculate and Plot the Average Difference (Bias): Compute the average of all of the differences. This represents the systematic bias between the two methods. Draw a horizontal line at this value on the plot.
• Calculate and Plot the Limits of Agreement: The limits of agreement are calculated as the average difference ± 1.96 times the standard deviation of the differences. These limits estimate the range in which most differences between the two measurement methods will fall. Draw two more horizontal lines on the plot: one at the upper limit of agreement and another at the lower limit.
• Analyze the Plot: The plot can now be used to assess the agreement. Points that lie within the limits of agreement suggest that the differences between the methods are not clinically significant. The distribution of points can also indicate patterns, such as increasing differences at higher measurement values. A regression analysis may also need to be performed on the differences vs. means to check if there is a proportional bias.

A regression analysis can determine the proportional bias in a Bland–Altman plot by examining the relationship between differences in measurements (between two methods) and the means of those measurements. Typically, a simple linear regression is run with the differences between the two measurement techniques as the dependent parameter and the means of the two techniques as the independent variable. The primary focus of this regression analysis is the slope of the regression line: a considerable deviation of the gradient from zero (positive or negative) signals a directional bias. This means that the discrepancy between the two measurement techniques tends to increase or decrease as the mean value increases. A slope that approaches zero and does not deviate significantly from zero indicates that there is no proportional bias and a consistent agreement between the techniques across the measurement spectrum. The importance of the slope is often determined by examining the p-value in the regression results: A small p-value (typically below 0.05) indicates that the slope deviates significantly from zero and thus confirms the presence of proportional bias. Conversely, a large p-value indicates that there is no significant deviation of the slope from zero, implying the absence of proportional bias.

In the assessment of the agreement, the Bland–Altman plot is utilized as the statistical method of choice within medical research to ascertain the accuracy of a novel measurement technique against the established or gold standard [3,17,38].

For the evaluation of reliability, which pertains to the consistency and reproducibility of the test outcomes, the Intraclass Correlation Coefficient (ICC) score is employed [38,39,40,41]. Numerous studies have evaluated the reliability of three-dimensional solutions, including investigations on 3dMDFace [42,43,44,45,46,47,48,49], Canfield Vectra [8], and LifeViz (QuantifiCare) [9]. However, these studies have not encompassed the assessment of area and volume measurements, and they were executed using commercial tools that may not be economically accessible to many healthcare establishments.

Additional studies have contributed to the field. Marin Dit Bertoud et al. evaluated an algorithm for its effectiveness and reliability in determining the percentage coefficient of vitiligo depigmentation in facial areas, as reported in their publication [50]. Pieadra-Cascon and colleagues undertook research to assess the accuracy and precision of extraoral 3D facial reconstructions using a dual-structured illuminated face scanner, with a particular focus on the consistency of measurements across different examiners. Their results revealed significant variations between manual and digital methods in inter-regional landmark measurements for all subjects, registering a mean accuracy of 0.32 mm for both approaches and demonstrating a high intraclass correlation coefficient of 0.99 between operators [51]. Furthermore, Tomasik et al. conducted comprehensive research over five years into the application of AI in automated 2D and 3D cephalometric analysis, specifically within digital orthodontics. Their extensive investigations also encompassed facets such as facial analysis, decision making based on algorithms, and the monitoring of treatment outcomes and retention rates [52].

3. Methods and Materials

In the upcoming subsections, we will first present an overview of the web-based software in Section 3.1. This will be followed by an introduction to the area and volume measurements employed in this study, which are outlined in Section 3.2. We then explain the 3D testing dataset (facial scans) used for this study in Section 3.3. Subsequently, in Section 3.4, we delve into the specifics of the methodology adopted for assessing reliability, and in Section 3.5, we focus on the agreement analysis.

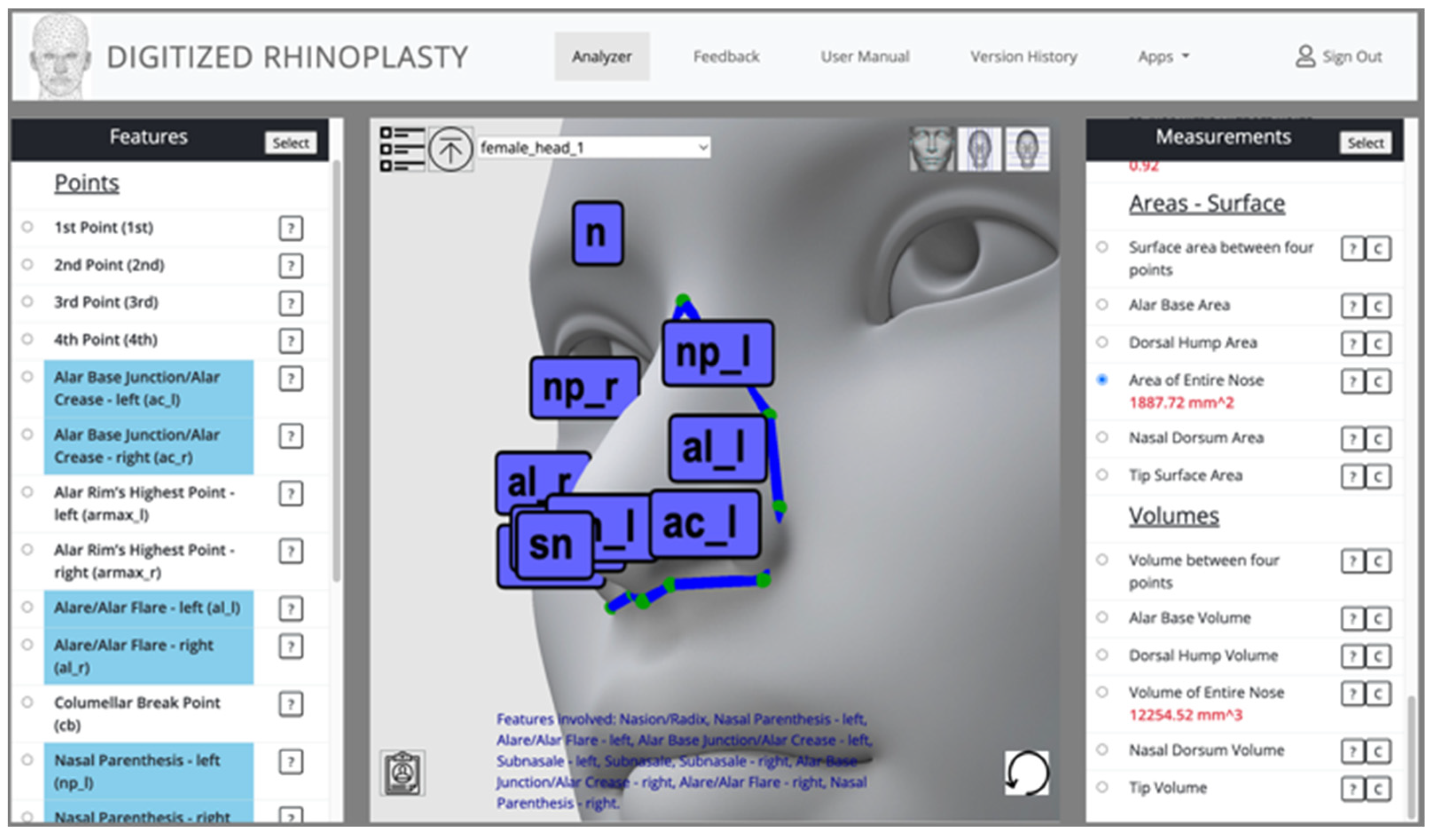
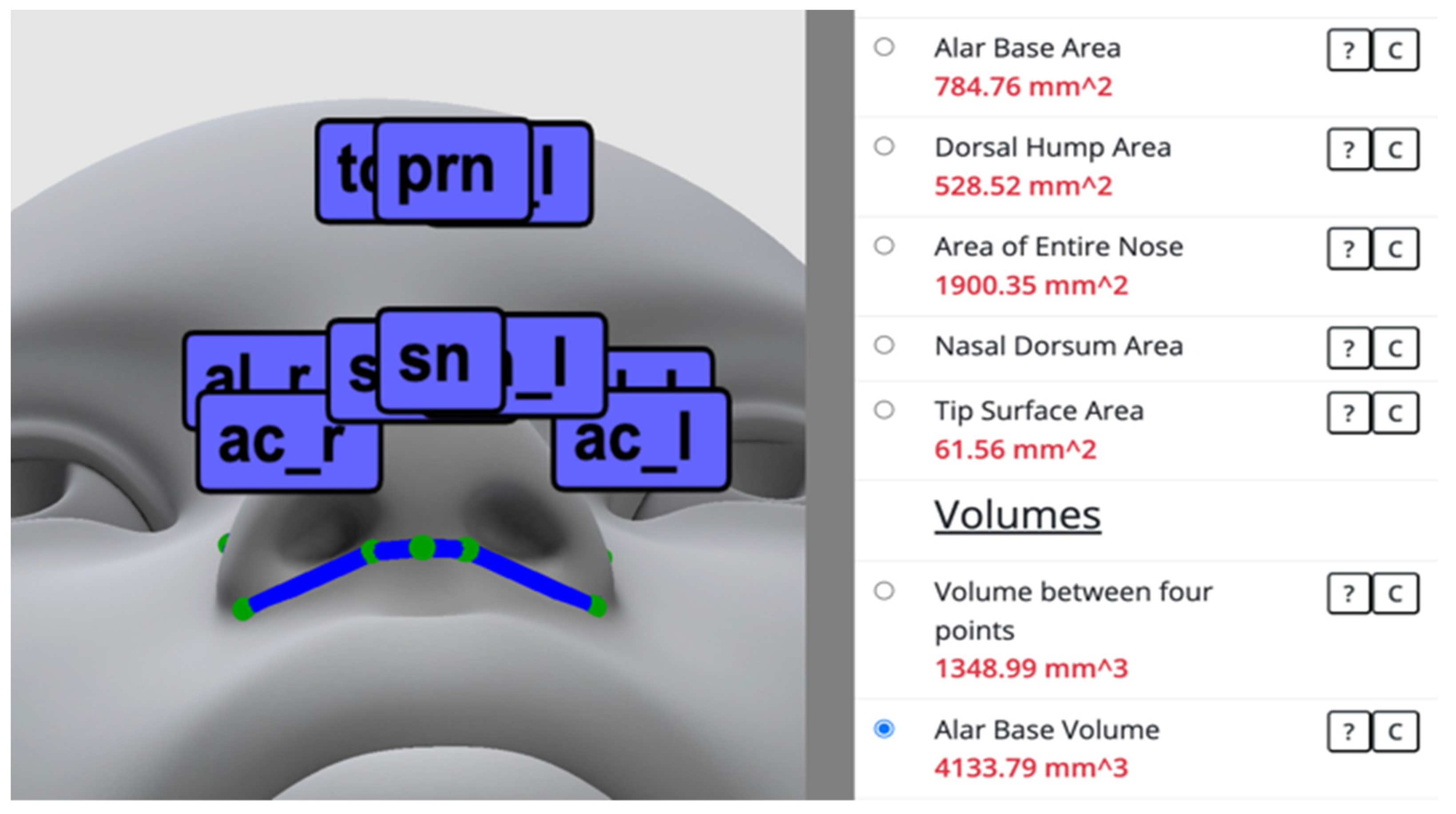
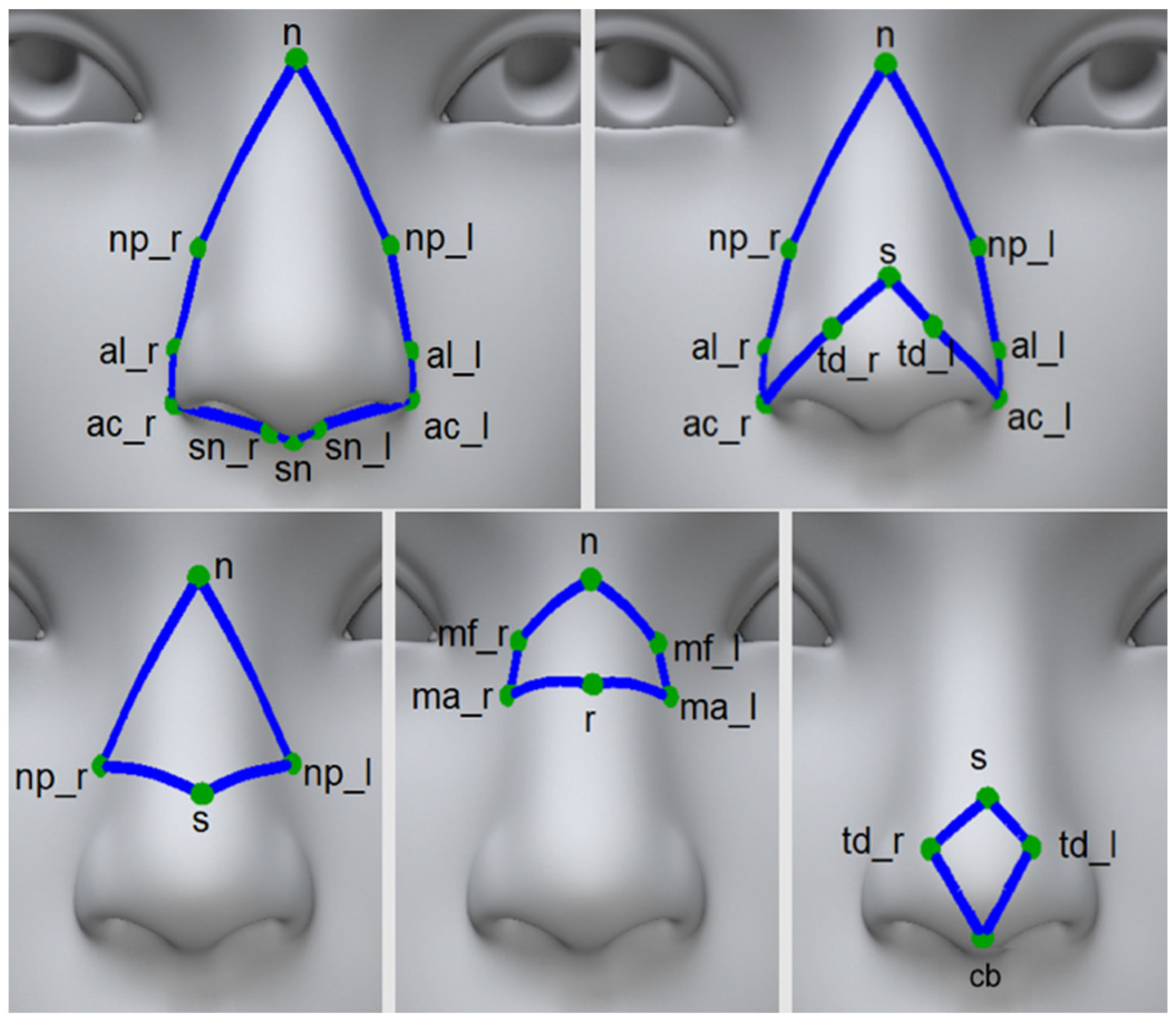
3.1. Web-Based Software to Measure Area and Volume on 3D Facial Models

A free web-based software, Face Analyzer, was developed to help facial surgeons perform facial analysis, a crucial part of pre-surgery planning and post-surgery evaluation [10].

Face Analyzer worked with 3D facial models to provide a more reliable and accurate facial analysis. However, it utilized traditional measurements such as distance and angle. We introduced novel area and volume measurements for certain regions of the face [12] and developed algorithms to compute these measurements [13].

In this study, we present the enhanced web-based tool Face Analyzer that incorporates algorithms using JavaScript language to enable facial surgeons to measure the area and volume of selected regions for the first time.

Figure 1 shows the enhanced Face Analyzer with the area and volume measurements listed on the right panel. When a measurement is selected, all of the facial feature points (landmarks) used in the computation of that measurement are listed on the left panel. After selecting a landmark from the list on the left, the user can double-click on a point on the face to mark and save its location. Once all of the landmarks for measurement are saved, the user can click on the ‘C’ button to calculate the measurement. Figure 2 shows the value and boundaries for the ‘Alar Base’ area measurement on a generic 3D female face model. A green dot indicates the landmark location, and its landmark abbreviation is displayed in a blue box at the upper left side of the green dot.

Figure 1. Snapshot of Face Analyzer, the web-based tool.

Figure 2. Snapshot of the web-based tool Face Analyzer showing the boundaries and the calculated value for the volume of the alar base.

The user can select an area or volume measurement with pre-defined boundaries, as shown in Figure 2 and Figure 3. Moreover, the user can identify any four points on the face’s surface as boundary points by double-clicking on the face. When ‘Surface area between four points’ or ‘Volume between four points’ measurements is selected, the measurements are calculated between these four points, as shown in Figure 4.

Figure 3. Snapshot of the web-based tool Face Analyzer showing the boundaries and the calculated value for the area of the tip.

Figure 4. Boundaries of a region can be identified by marking four points on the face, and Face Analyzer will compute the surface area and volume for the region.

3.2. Area and Volume Measurements

We defined area and volume measurements utilizing the facial landmarks described in the literature [43,44,45]. These area and volume measurements focus on the regions around the nose and can be utilized to quantify the alterations performed via rhinoplasty. However, new area and volume measurements can be defined for any region of the face, and web-based software can be utilized for the computation of the measurements.

The same boundary landmarks define area and volume measurements with the same name. For example, the supratip break point, tip defining points (left and right), and columellar break point are the boundary landmarks used to compute both the area and volume of the tip measurement. The boundaries of each measurement, as illustrated in Figure 5, are denoted using standard landmark abbreviations (np_r, al_l, ac_r, sn_r, etc.) [13].

Figure 5. Area and volume measurements from top left to bottom right: entire nose, nasal dorsum, dorsal hump, root of the nose (radix), tip.

When an area measurement is performed, the area of the surface polygons is computed and summed up within the boundary lines to find the total area. When a volume measurement is performed, the maximum depth point is used to identify the base area. The volume of the space between the base area and the surface area is computed. The details of the area and volume algorithms are described in Topsakal et al. [13].

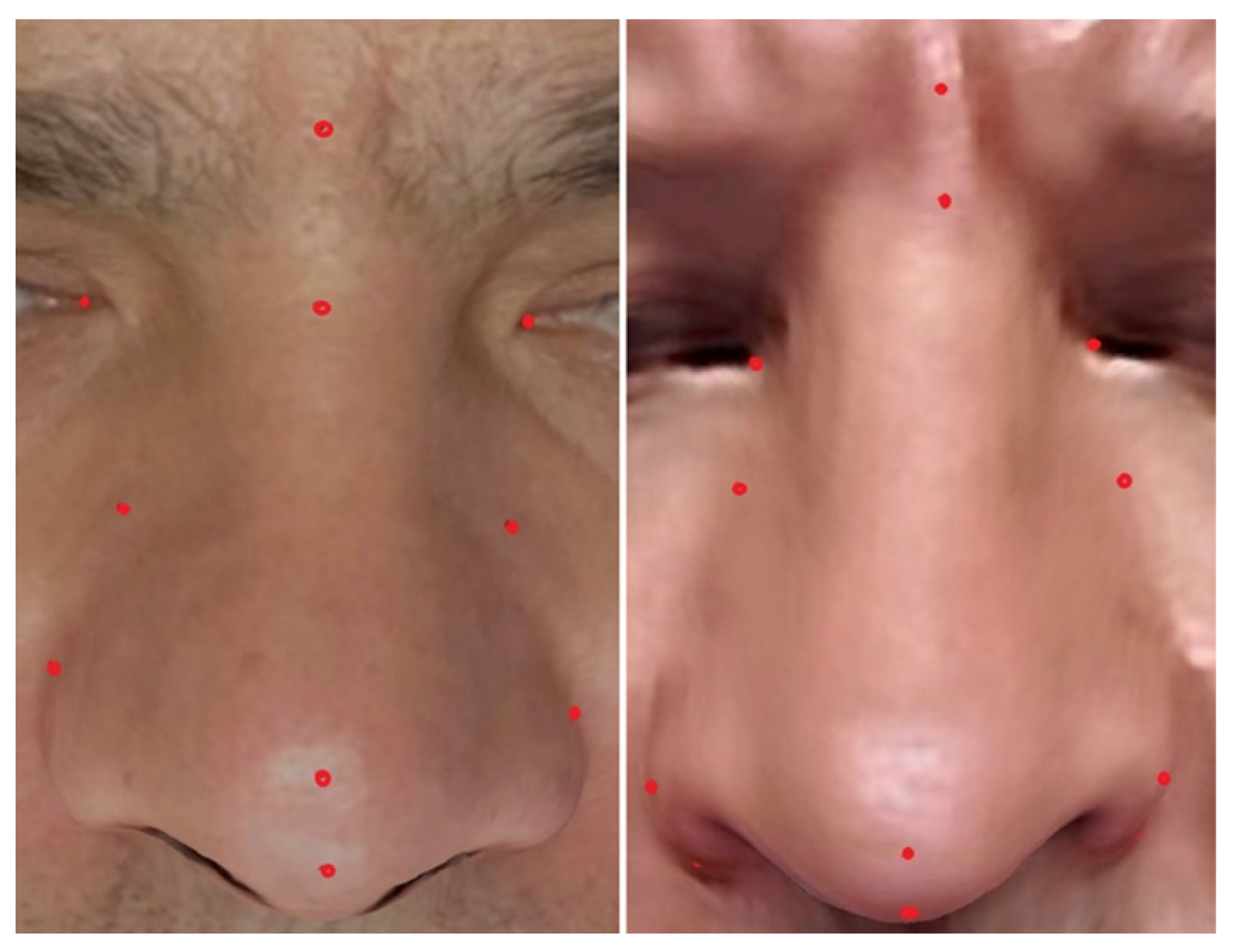
3.3. Test Dataset

The area and volume measurements were computed on 3D models from twenty Caucasian subjects (10 female and 10 male) who volunteered for the research study. We utilized a face scanning software library provided by the company Bellus3D, which utilized the true depth camera of iPhone X or later to scan 3D objects without the need for an external camera. These 3D models are part of a larger 3D facial scan dataset collected in a previous study [49]. The 3D models had around 200K polygons. The 3D models were imported into the 3D software Blender and the web-based software for taking the measurements.

Red dots were placed on the texture images of the 3D models to indicate each facial landmark used in the measurements. This approach maintained consistent landmark identification, minimizing variations in landmark positioning when comparing agreement between the web software and Blender software (version 3.2, Amsterdam, The Netherlands). Figure 6 illustrates these texture images with the red dots.

Figure 6. Facial landmarks are marked with red dots on the textured image of the 3D model to reduce marking discrepancies for the agreement measurements.

3.4. Intra- and Inter-Reliability Analysis

The evaluation of the intra-rater and inter-rater reliabilities of the facial analyzer software for computing area and volume measurements was conducted utilizing the Intraclass Correlation Coefficient (ICC) test. This analysis was carried out by two raters, who were computer science students with specific training in identifying cue locations, who performed the necessary measurements. Each rater independently undertook two distinct measurement sessions, separated by a minimum one-week interval, to mitigate the potential influence of recall bias. The intra-rater reliability was ascertained by comparing the two sets of measurements from a single rater, whereas the inter-rater reliability was derived from the second measurement set of both raters.

In the process of executing the ICC analysis, the Shapiro–Wilk statistical test was employed to verify the consistency of variance assumptions, as referenced in sources [40,53]. Additionally, Levene’s test was applied to ascertain the homogeneity of variances, or homoscedasticity.

Subsequent to the validation of these assumptions, an ICC analysis was carried out, with the results being articulated alongside 95% confidence intervals. The computation of both the intra-rater and inter-rater reliabilities was achieved through the utilization of the absolute agreement criterion and the implementation of a two-way mixed effects model, as delineated in sources [54,55]. We calculated the required sample size to achieve an expected reliability of 85%, with a 95% confidence level, for the assessments conducted by two raters. The analysis indicated that a minimum sample size of 15 is necessary to meet these statistical parameters [56,57].

3.5. Agreement Analysis

An agreement analysis was undertaken to assess the efficacy of a measurement instrument relative to an established gold standard. Blender is recognized as a robust 3D modeling platform, and it is employed extensively in the generation of three-dimensional visual artworks [55]. We utilize the 3D software Blender as the gold standard for measuring the areas and volumes in 3D models, leveraging its advanced capabilities to ensure precise and accurate assessments that are essential for high-quality modeling. There are other established proprietary software that can measure the areas and volumes of 3D models, such as 3ds Max and Maya. However, using open-source software like Blender can be advantageous for reasons like accessibility and transparency. Moreover, Blender is a widely used software for comparison studies in the medical field [58].

Area and volume quantifications were conducted on the subjects’ three-dimensional representations by employing Blender along with web-based facial analysis applications. In the agreement analysis, we meticulously marked the texture map of the 3D constructs with a red point at each critical landmark pertinent to the measurements. This procedure was instrumental in diminishing variability and precluding inaccuracies attributable to the annotation process.

The Bland–Altman plot, which represents a scatter diagram of discrepancies against the mean of two separate measurements, was used [16]. As explained in the Related Concepts Section, this plot shows three different lines: the central line represents the mean discrepancy, while the upper and lower lines represent the 95% confidence limits (upper bound = mean + 1.96 × SD, lower bound = mean − 1.96 × SD), as shown in Figure 7. The mean, standard deviation, lower bound, and upper bound values used to draw the Bland–Altman plot in Figure 7 are presented in Table 1. One of the critical assumptions of the Bland–Altman fit analysis is that these variances are normally distributed. Normality was verified using the Shapiro–Wilk statistical test. Once the Bland–Altman plot is defined, it becomes important to understand whether there is a pattern between points that deviate above or below the mean discrepancy, as such a pattern would indicate a proportional bias. To measure proportional bias, a linear regression analysis was conducted with the difference as the dependent variable and the mean as the independent variable. The Shapiro–Wilk statistical test and significance values for linear regression are listed in Table 1. The steps for developing a Bland–Altman plot and checking its assumptions are explained in the Related Concepts Section.

Figure 7. Bland–Altman plots for each measurement. The (left column) represents the area, and the (right column) represents the volume measurements.

Table 1. The mean, std, lower, and upper limit values used to draw the Bland–Altman plot and the significance values of the Shapiro–Wilk test and linear regression.

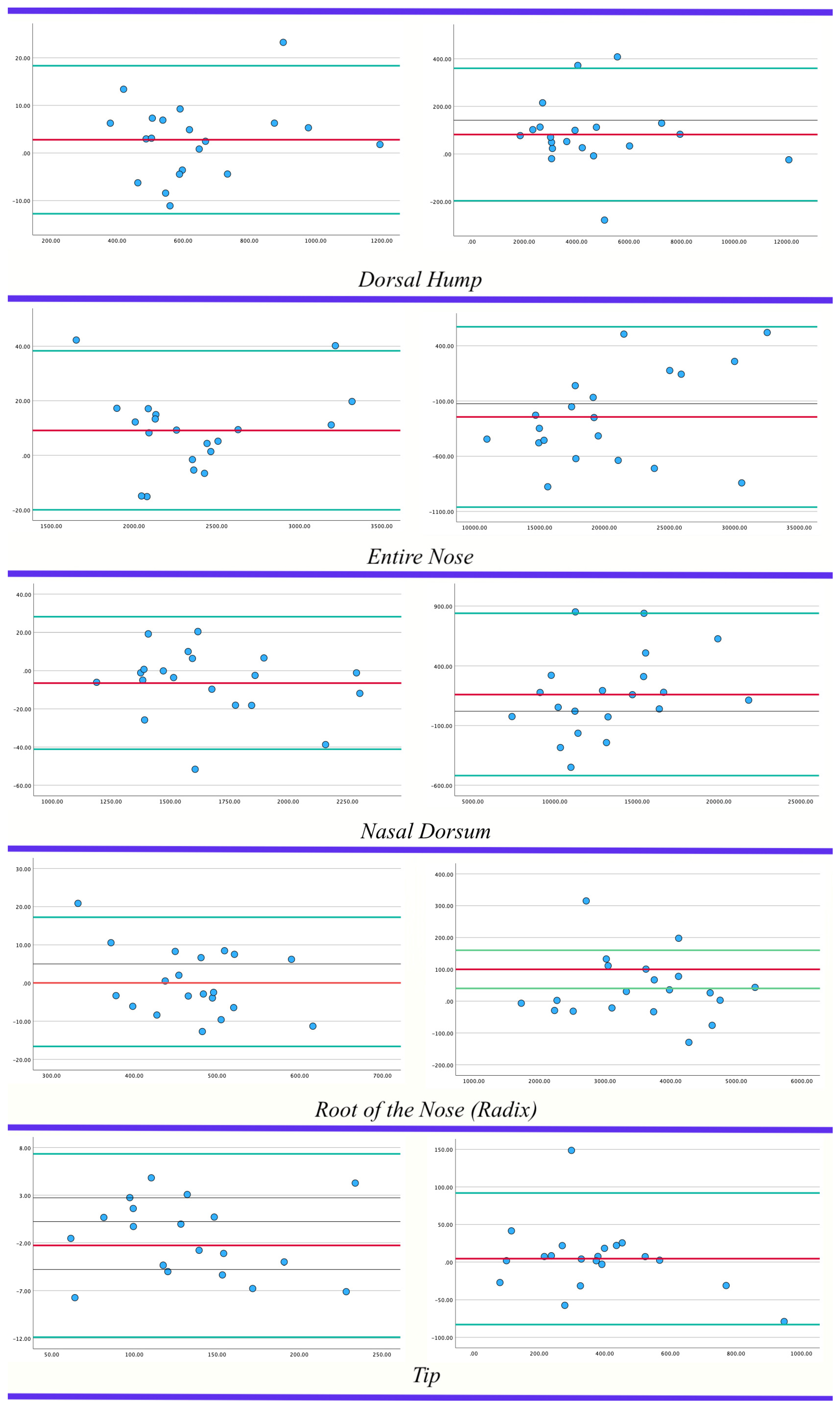
	Mean	Std	Lower	Upper	Shapiro–Wilk Significance	Linear Regression Significance
Area—Tip	−2.28	4.91	−11.89	7.34	0.05	0.68
Area—Nasal Dorsum	−6.50	17.68	−41.15	28.15	0.12	0.34
Area—Entire Nose	9.11	14.90	−20.09	38.31	0.07	0.56
Area—Dorsal Hump	2.79	7.93	−12.76	18.33	0.13	0.45
Area—Root of Nose	0.34	8.62	−16.57	17.24	0.99	0.11
Volume—Tip	4.48	44.61	−82.96	91.92	0.66	0.11
Volume—Nasal Dorsum	160.00	346.60	−519.34	839.34	0.05	0.15
Volume—Entire Nose	−244.36	416.56	−1060.82	572.10	0.17	0.81
Volume—Dorsal Hump	81.75	142.00	−196.57	360.07	0.02	0.15
Volume—Root of Nose	40.74	99.10	−153.50	234.98	0.82	0.67

The area measurements are in mm² and the volume measurements are in mm³.

4. Results

The presented statistical analysis of reliability and internal/external evaluability was conducted using IBM SPSS Statistics, Version 29 (IBM Corp., Armonk, NY, USA) software.

4.1. Statistical Analysis of Intra- and Inter-Reliability

An ICC analysis was employed to ascertain the dependability of the measurements. To determine adherence to the presuppositions of normality and constant variance, the Shapiro–Wilk statistical method was applied for the normality assessment, and Levene’s test was utilized to evaluate homoscedasticity. Table 2 presents the results of the Levene test, Shapiro–Wilk test, Skewness, and Kurtosis. An introduction to these concepts was given in the Related Concepts Section.

Table 2. Checking the assumptions of the ICC.

Measurement Type	Levene—Signif.	No.	Shapiro–Wilk—Signif.	Skewness	Kurtosis
Area—tip	0.997	1	0.34	0.67	0.01
		2	0.26	0.68	−0.06
		3	0.28	0.70	−0.02
Area—nasal dorsum	0.999	1	0.14	0.75	−0.12
		2	0.10	0.80	−0.04
		3	0.14	0.75	−0.12
Area—entire nose	1	1	0.04	0.94	0.51
		2	0.04	0.92	0.51
		3	0.04	0.93	0.50
Area—dorsal hump	0.998	1	0.02	1.30	1.54
		2	0.02	1.33	1.66
		3	0.02	1.29	1.37
Area—root of nose	0.947	1	0.85	0.00	0.15
		2	0.86	−0.04	0.52
		3	0.42	0.09	1.44
Volume—tip	0.987	1	0.15	1.02	1.43
		2	0.31	1.28	2.25
		3	0.12	1.03	1.37
Volume—nasal dorsum	0.994	1	0.51	0.64	0.14
		2	0.53	0.68	0.33
		3	0.45	0.66	0.21
Volume—entire nose	0.995	1	0.17	0.69	−0.34
		2	0.18	0.68	−0.31
		3	0.17	0.73	−0.17
Volume—dorsal hump	0.995	1	0.03	1.86	4.31
		2	0.03	1.86	4.34
		3	0.03	1.77	3.82
Volume—root of nose	0.959	1	0.96	−0.09	−0.63
		2	0.92	−0.08	−0.81
		3	0.85	0.29	−0.22

The Shapiro–Wilk test’s p-values for four measurements were significant: ‘area—entire nose’ (p-value = 0.04 for all raters), ‘area—dorsal hump’ (p-value = 0.02 for all raters), and ‘volume—dorsal hump’ (p-value = 0.03 for all raters). The rest of the measurements were not significant and hence conformed to normality.

For the measurements, we assessed the skewness and kurtosis values of the data for which a significant p-value was obtained in the Shapiro–Wilk test. The data are considered normal if the skewness is between −2 and +2 and the kurtosis is between −7 and +7 [30]. The skewness and kurtosis values for ‘area of the entire nose’, ‘area of the dorsal ridge’, and ‘volume of the dorsal ridge’ were less than 1, 2, and 4, respectively. Therefore, we concluded that the skewness and kurtosis values were within acceptable ranges for a normal distribution. We elaborated on how skewness and kurtosis can be utilized to check normality in the Related Concepts Section when the Shapiro–Wilk test yielded significant values.

Levene’s test was performed to check the homoscedasticity assumption for the ICC. The results of Levene’s test showed that the significance for all measures was above 0.9, indicating that the variances for the measures were equal.

Table 3 presents the ICC analysis outcomes pertaining to the intra-program reliability and inter-program reliability.

Table 3. The results of the ICC statistical analysis (N = 20). The lower and upper bounds of the 95% confidence interval is given in parenthesis.

Measurement	Intra-Reliability	Inter-Reliability
Area—Dorsal Hump	1.0 (0.999–1.0)	1.0 (0.999–1.0)
Area—Entire Nose	1.0 (0.999–1.0)	1.0 (1.0–1.0)
Area—Nasal Dorsum	0.999 (0.999–1.0)	0.999 (0.999–1.0)
Area—Root of Nose	0.996 (0.991–0.999)	0.820 (0.553–0.928)
Area—Tip	0.998 (0.995–0.999)	0.999 (0.997–1.0)
Volume—Dorsal Hump	1.0 (0.999–1.0)	0.999 (0.999–1.0)
Volume—Entire Nose	0.999 (0.998–1.0)	0.999 (0.997–1.0)
Volume—Root of Nose	0.998 (0.984–0.999)	0.899 (0.741–0.960)
Volume—Nasal Dorsum	0.999 (0.998–1.0)	0.998 (0.996–0.999)
Volume—Tip	0.994 (0.984–0.997)	0.995 (0.987–0.998)

An ICC of less than 0.5 is considered poor, 0.50 to 0.75 is considered moderate, 0.75 to 0.90 is considered good, and 0.90 to 1.00 is considered excellent [59,60,61]. The intra-reliability of the web-based software for all measurements is excellent, the inter-reliability of the ‘area—the root of nose’ measurement is good, and the rest of the inter-reliability is excellent.

4.2. Statistical Analysis of Agreement

Ten measurements were performed on the 3D models of twenty of the subjects utilizing either the Face Analyzer tool or the Blender application. Figure 7 describes the Bland–Altman charts that were methodically used to assess the agreement of the measurements obtained from both Blender and the web application. In these plots, the central tendency of measurement discrepancies is represented by a blue line, while the red contours define the 95% limits of certainty for these observations. The fact that the observations fall predominantly within these confidence intervals indicates statistical agreement between the two measurement methods.

The assumption of data normality was rigorously examined via the Shapiro–Wilk test. During this test, four measurements surfaced with statistically noteworthy p-values, prompting further investigation into their skewness and kurtosis metrics, which ultimately were ascertained to be within the conventional thresholds for a normal distribution. Consequently, there was no significant evidence to suggest a deviation from normality across the dataset [28,29,60,61].

To ensure that there was no proportional bias in the measurements, a linear regression test was performed using the SPSS package program, with the ‘difference’ between the two sets of measurements as the dependent variable and their ‘mean’ value as the independent variable. The ensuing p-values exceeded the 0.05 threshold, thereby substantiating the absence of proportional bias within the comparative dataset.

5. Discussion

Facial analysis is a vital component of many plastic and reconstructive surgical procedures. In recent years, 3D models have become increasingly popular for facial analysis due to their ability to capture a more detailed and accurate representation of the face. Several studies have highlighted the advantages of using 3D models for facial analysis, including improved accuracy, reproducibility, and visualization [5,6,11,61,62,63].

The Face Analyzer web app is a software tool that utilizes 3D models for facial analysis and incorporates these advantages. In this study, the Face Analyzer software has been further enhanced with area and volume measurements, providing a more in-depth analysis of the face. This allows facial surgeons to consider these parameters during pre-operative and post-operative evaluations, which are critical in achieving optimal surgical outcomes [64]. The web-based software is free and publicly available at digitized-rhinoplasty.com, making it accessible to a broad range of users.

With the increasing availability of smart mobile devices capable of capturing 3D images, we expect the utilization of 3D measurements, such as area and volume, to become more widespread for facial analysis and, in turn, for facial surgeries [65]. The Face Analyzer web-based software is well suited for this purpose as it provides a reliable and accurate means of measuring the facial area and volume, which are essential parameters for many facial surgical procedures [66].

To assess the accuracy and reliability of the Face Analyzer software, we examined the agreement between the area and volume calculations obtained through the web application and Blender, an online 3D modeling program.

It is important to recognize that discrepancies between the two software systems’ markings can arise from two main factors: errors in the marking process and differences in the software algorithms. To minimize marking errors, red dot markers were placed on landmarks in the texture images of the 3D models, as demonstrated in Figure 6. This strategy aimed to ensure that the majority of the measurement differences could be attributed to the software algorithms.

Our observations showed that the time required to take the area and volume measurements using the Face Analyzer web app was significantly less than that of the Bellus3D software [57,58]. This is because preparation for taking measurements in Blender requires carefully cutting the region using boundary landmarks, while the web app enables users to simply double-click to identify the boundary landmarks and automatically creates the boundary lines between them. Once the boundary landmarks are identified, the computation of the area and volume is instantaneous for both software.

The intra-reliability and inter-reliability scores of the web-based software Face Analyzer were also evaluated using the intraclass correlation coefficient (ICC) test. The results showed that the software’s reliability for all but one measurement was considered excellent, with one measurement rated as good, as listed in Table 3 [59].

While the findings of this study are promising, indicating substantial agreement and reliability between the newly introduced web-based software and the established 3D software Blender, it is important to note the limitation imposed by the small sample size. The scope of data, restricted to ten measurements on 3D models, may not fully represent the diverse range of facial structures encountered in clinical practice. Consequently, further research involving a larger and more varied sample is essential to validate these initial findings and ensure the robustness and generalizability of the software’s performance in real-world surgical planning and outcome assessment.

The free web software designed for volume and area measurements holds significant potential in facial analysis. Additionally, it could prove useful in assessing facial changes, particularly when comparing superimposed serial 3D patient images. Häner et al. points out the limitations of 2D imaging and suggests using 3D photography for greater accuracy, identifying specific forehead and nose areas for effective superimposition in growing individuals [67]. Wampfler and Gkantidis stressed the importance of systematically evaluating superimposition methods, suggesting that surface-based registration may be more effective than landmark-based approaches, although further research is needed due to the variability and biases in current studies [68].

The utilization of 3D facial model analyses emerges as a pivotal tool in dental pathology, offering a vast scope for exploration due to the diverse diagnostic and therapeutic phases encountered in patient care. Particularly in orthodontics, these models are instrumental for the extraction of facial landmarks, which are crucial for categorizing dental occlusion types and quantifying the asymmetry resulting from such conditions [69].

Moreover, the study by Cai et al. underscores the extensive application of 3D facial models in the domains of oculoplastic, eyelid, orbital, and lacrimal diseases, providing a holistic approach to patient assessment. The methodology is recognized for its role in the early detection and diagnosis of conditions like blepharoptosis and in monitoring the progression of thyroid eye disease. Notably, these models are integral in enhancing the precision of therapeutic strategies, particularly in formulating meticulous surgical plans for the treatment of blepharoptosis [70].

6. Conclusions

Recent technological advancements have enabled the integration of 3D technologies into surgeons’ pre-operative analyses and post-operative assessments. However, existing software tools for facial analysis lacked the inclusion of area and volume measurements. This study introduces a web-based software, Facial Analyzer, which integrates area and volume measurements to enhance pre-operative and post-operative facial analysis in surgery. The software’s agreement and reliability, validated using 3D facial scans and metrics like the Bland–Altman plot and ICC, demonstrate its effectiveness and accuracy in measuring the area and volume of certain regions of the face. The web-based user-friendly interface underscores its potential to significantly improve surgical planning and outcome assessment, marking a substantial advancement in 3D facial analysis technology.