Detecting Patient Health Trajectories Using a Full-Body Burn Physiology Model
Abstract
:1. Introduction
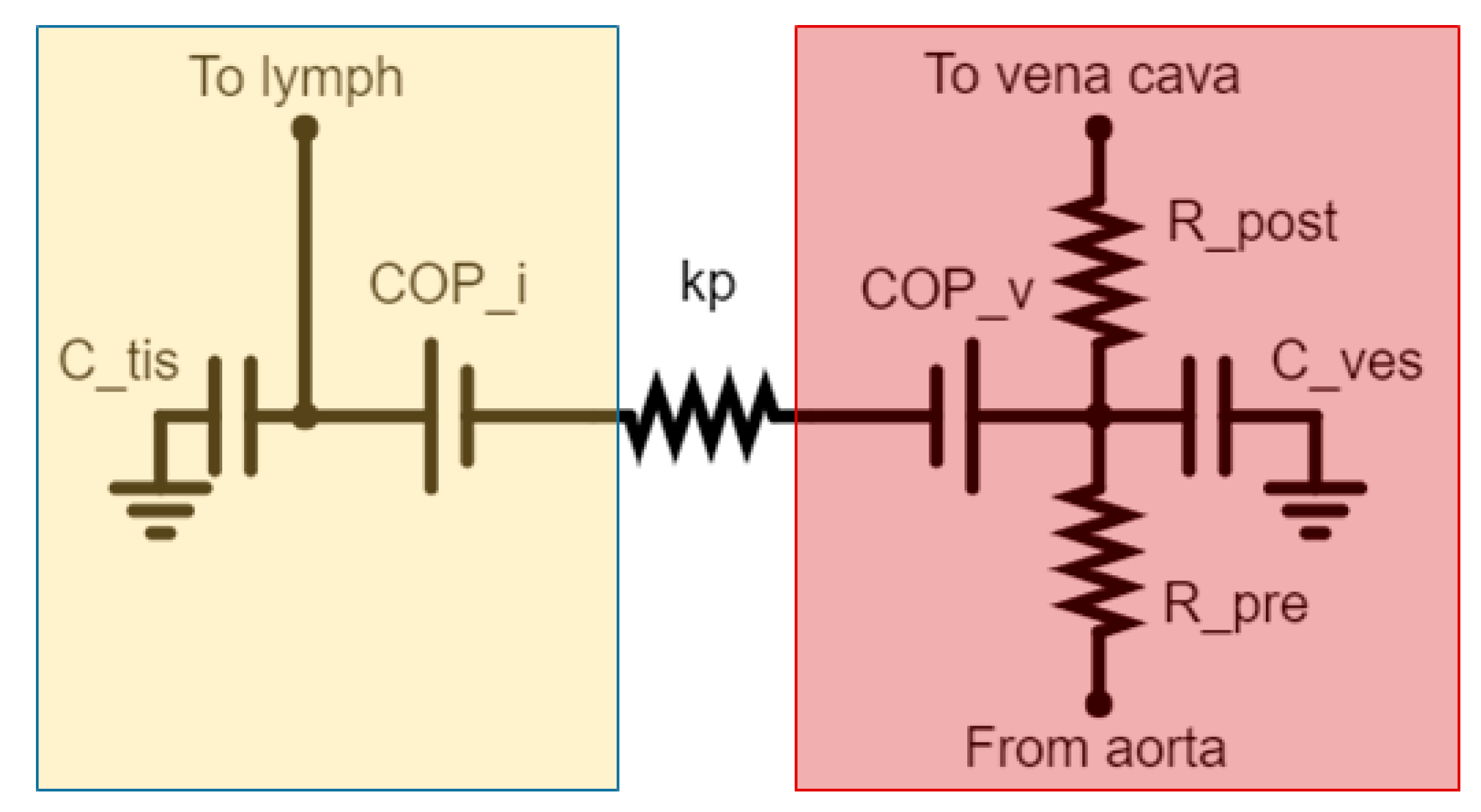
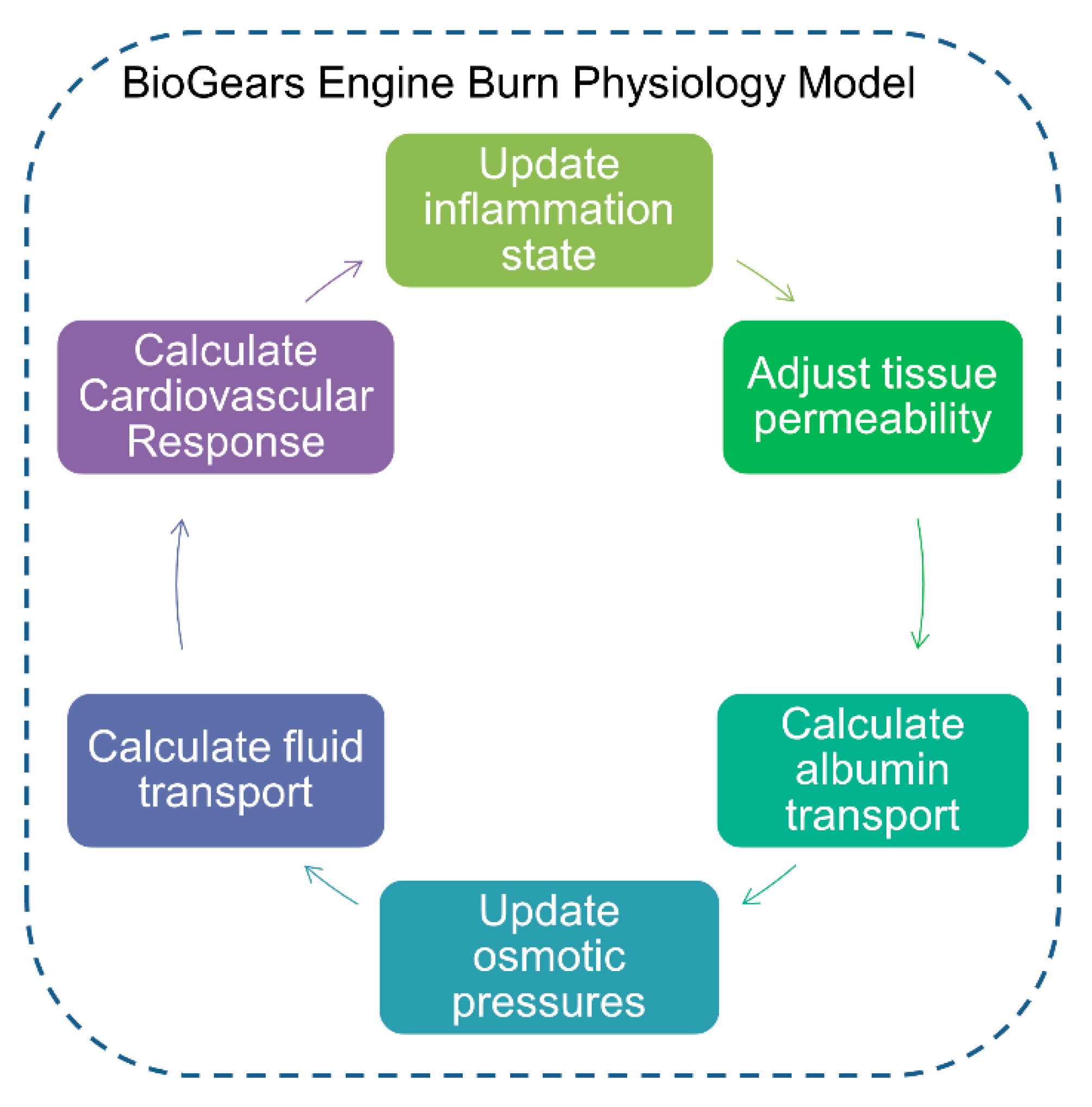
2. Materials and Methods
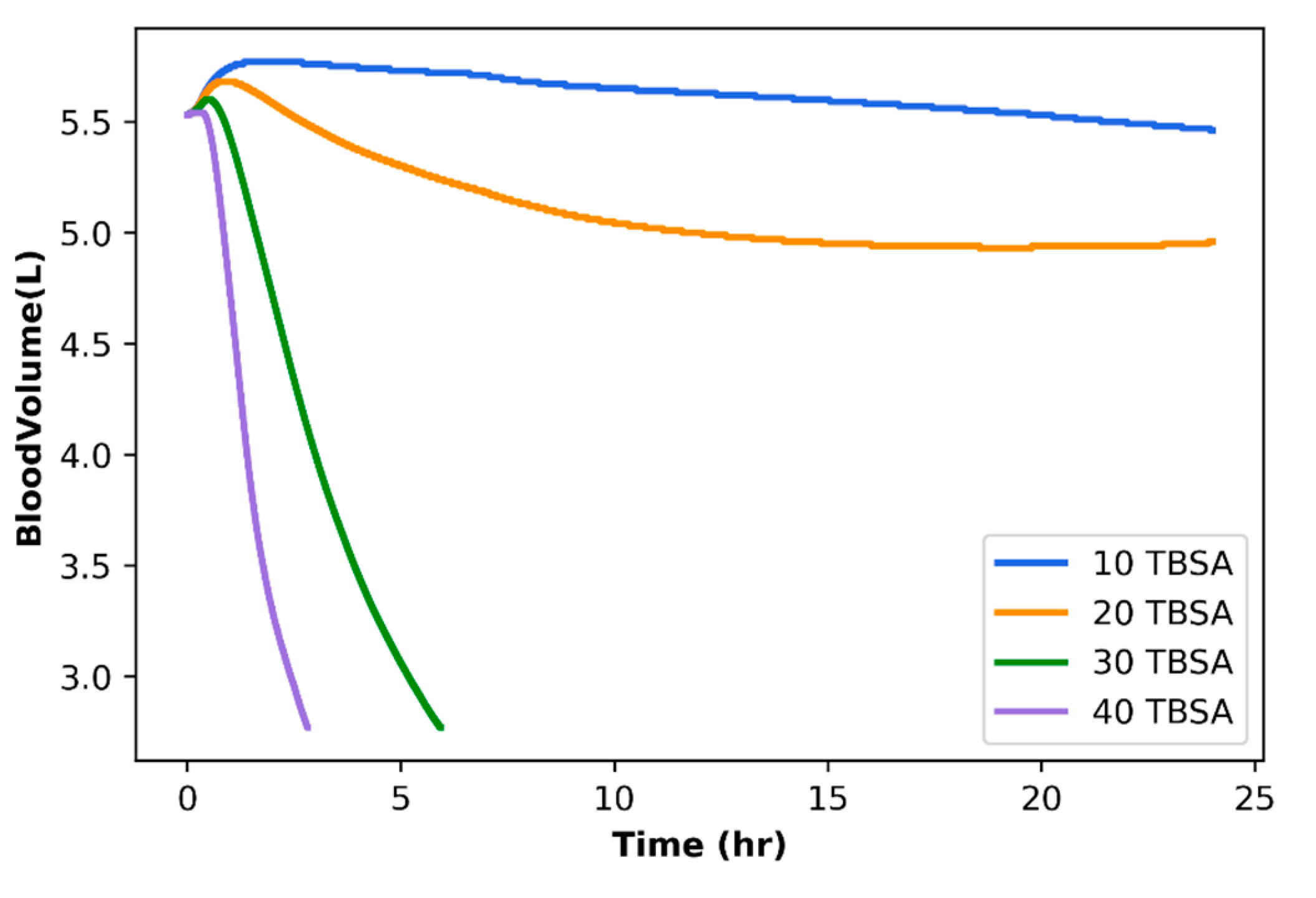
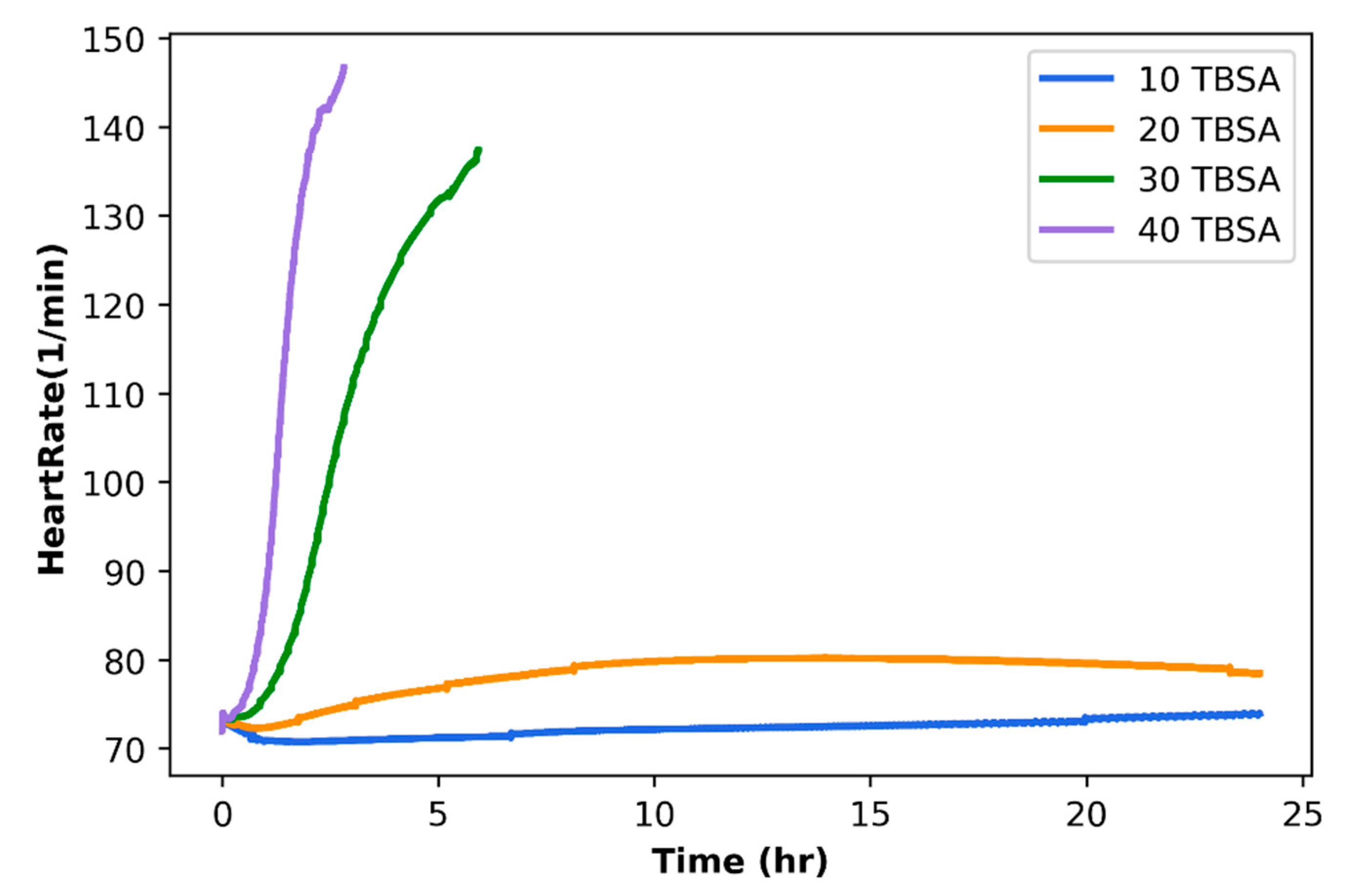
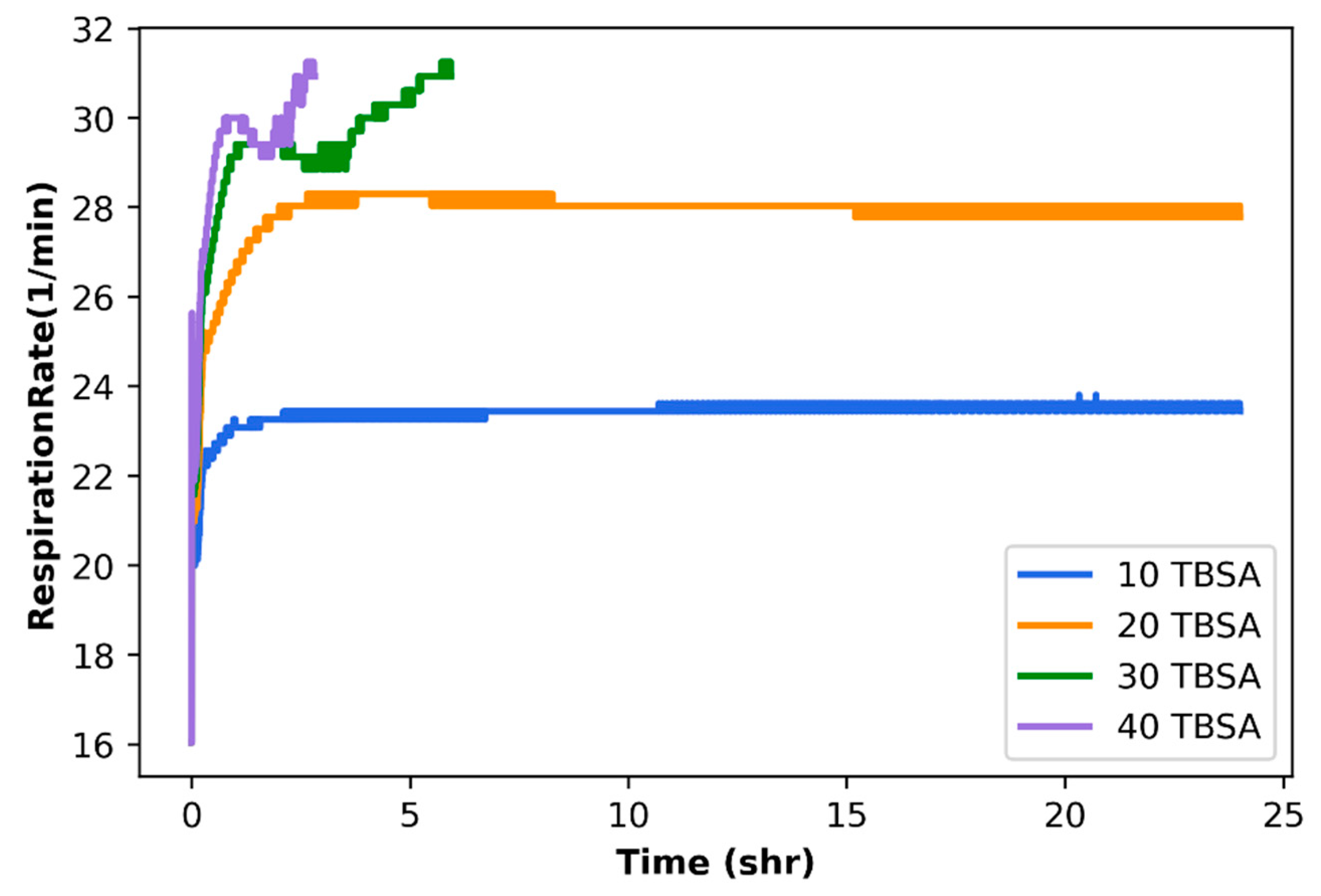
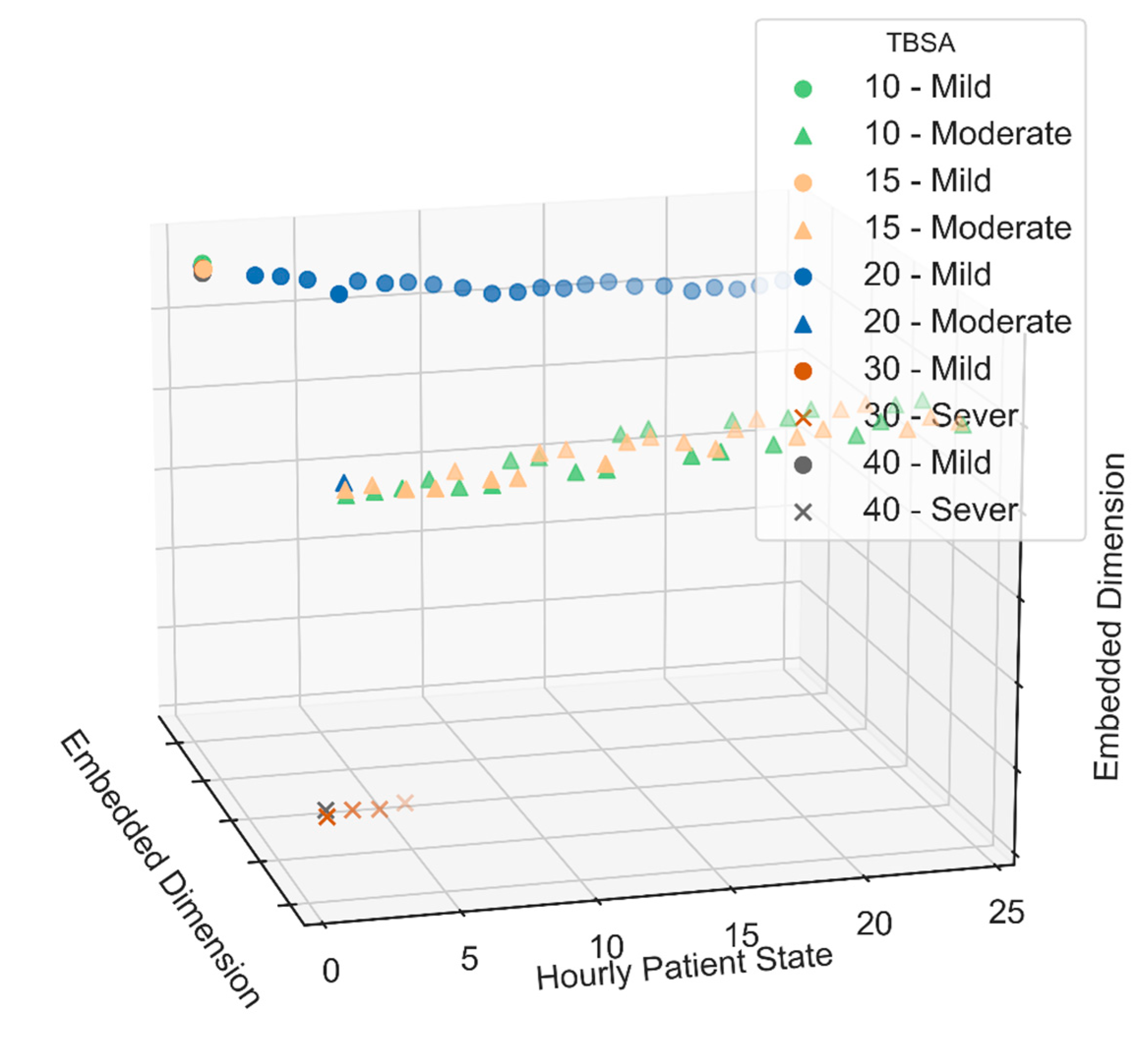
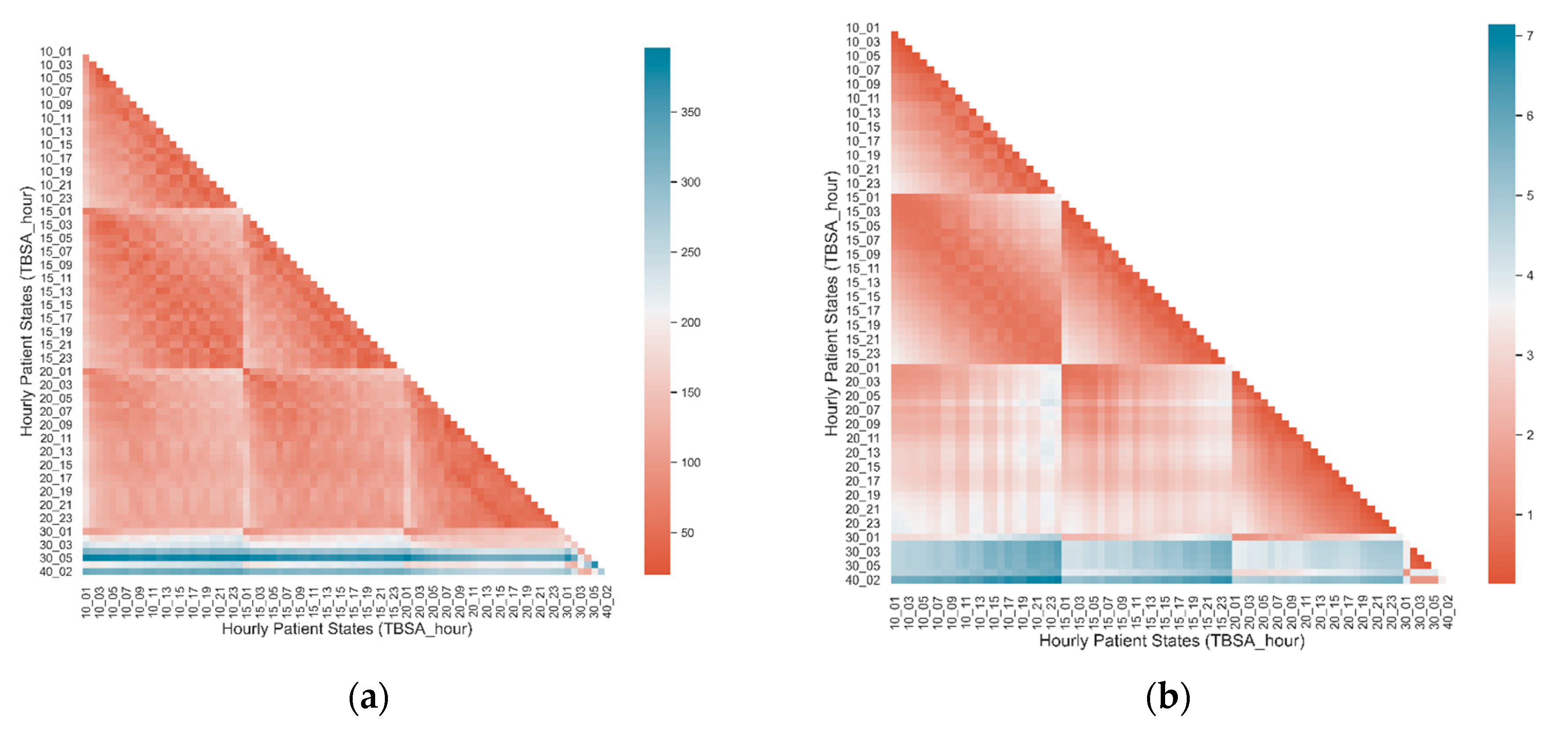
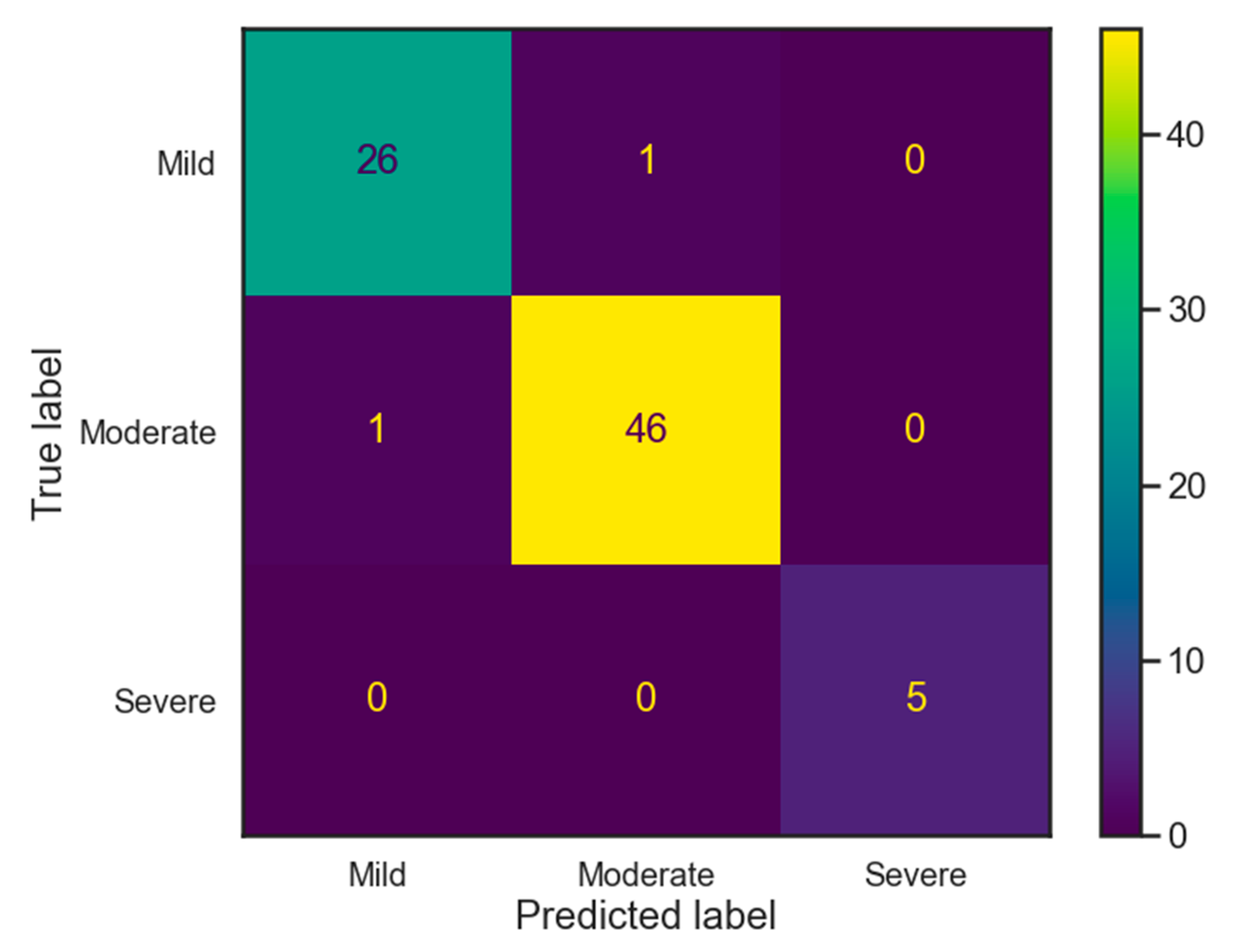
3. Results
4. Discussion
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nielson, C.B.; Duethman, N.C.; Howard, J.M.; Moncure, M.; Wood, J.G. Burns: Pathophysiology of systemic complications and current management. J. Burn Care Res. 2017, 38, e469–e481. [Google Scholar] [CrossRef] [PubMed]
- American Burn Association. Burn Incidence and Treatment in the United States: 2016; National Burn Repository: Chicago, IL, USA, 2016. [Google Scholar]
- Reeves, P.T.; Borgman, M.A.; Caldwell, N.W.; Patel, L.; Aden, J.; Duggan, J.P.; Serio-Melvin, M.L.; Mann-Salinas, E.A. Bridging burn care education with modern technology, an integration with high fidelity human patient simulation. Burns 2018, 44, 1106–1129. [Google Scholar] [CrossRef]
- Rowan, M.P.; Cancio, L.C.; Elster, E.A.; Burmeister, D.M.; Rose, L.F.; Natesan, S.; Chan, R.K.; Christy, R.J.; Chung, K.K. Burn wound healing and treatment: Review and advancements. Crit. Care 2015, 19, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Kaddoura, I.; Abu-Sittah, G.; Ibrahim, A.; Karamanoukian, R.; Papazian, N. Burn injury: Review of pathophysiology and therapeutic modalities in major burns. Ann. Burn. Fire Disasters 2017, 30, 95–102. [Google Scholar]
- Ng, C.-J.; You, S.-H.; Wu, I.-L.; Weng, Y.-M.; Chaou, C.-H.; Chien, C.-Y.; Seak, C.-J. Introduction of a mass burn casualty triage system in a hospital during a powder explosion disaster: A retrospective cohort study. World J. Emerg. Surg. 2018, 13, 38. [Google Scholar] [CrossRef] [PubMed]
- Madni, T.D.; Imran, J.B.; Clark, A.T.; Arnoldo, B.A.; Phelan, H.A.; Wolf, S.E. Analysis of Operating Room Efficiency in a Burn Center. J. Burn. Care Res. 2017, 39, 89–93. [Google Scholar] [CrossRef] [PubMed]
- ISBI Practice Guidelines Committee; Ahuja, R.B.; Gibran, N.; Greenhalgh, D.; Jeng, J.; Mackie, D.; Moghazy, A.; Moiemen, N.; Palmieri, T.; Peck, M.; et al. ISBI Practice Guidelines for Burn Care. Burns 2016, 42, 953–1021. [Google Scholar] [CrossRef]
- Ker, J.; Wang, L.; Rao, J.; Lim, C.T. Deep Learning Applications in Medical Image Analysis. IEEE Access 2017, 6, 9375–9389. [Google Scholar] [CrossRef]
- Mani, S.; Ozdas, A.; Aliferis, C.; Varol, H.A.; Chen, Q.; Carnevale, R.; Chen, Y.; Romano-Keeler, J.; Nian, H.; Weitkamp, J.-H. Medical decision support using machine learning for early detection of late-onset neonatal sepsis. J. Am. Med. Inform. Assoc. 2014, 21, 326–336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Desautels, T.; Calvert, J.; Hoffman, J.; Jay, M.; Kerem, Y.; Shieh, L.; Shimabukuro, D.; Chettipally, U.; Feldman, M.D.; Barton, C.; et al. Prediction of Sepsis in the Intensive Care Unit with Minimal Electronic Health Record Data: A Machine Learning Approach. JMIR Med. Inform. 2016, 4, e28. [Google Scholar] [CrossRef]
- Shimabukuro, D.W.; Barton, C.W.; Feldman, M.D.; Mataraso, S.; Das, R. Effect of a machine learning-based severe sepsis prediction algorithm on patient survival and hospital length of stay: A randomised clinical trial. BMJ Open Respir. Res. 2017, 4, e000234. [Google Scholar] [CrossRef]
- Rashidi, H.H.; Sen, S.; Palmieri, T.L.; Blackmon, T.; Wajda, J.; Tran, N.K. Early Recognition of Burn- and Trauma-Related Acute Kidney Injury: A Pilot Comparison of Machine Learning Techniques. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Rowland, R.A.; Ponticorvo, A.; Baldado, M.L.; Kennedy, G.T.; Burmeister, D.M.; Christy, R.J.J.; Bernal, N.P.; Durkin, A.J. Burn wound classification model using spatial frequency-domain imaging and machine learning. J. Biomed. Opt. 2019, 24, 056007. [Google Scholar] [CrossRef]
- Klein, M.B.; Goverman, J.; Hayden, D.L.; Fagan, S.P.; McDonald-Smith, G.P.; Alexander, A.K.; Gamelli, R.L.; Gibran, N.S.; Finnerty, C.C.; Jeschke, M.G.; et al. Benchmarking Outcomes in the Critically Injured Burn Patient. Ann. Surg. 2014, 259, 833–841. [Google Scholar] [CrossRef]
- Jeschke, M.G.; Mlcak, R.P.; Finnerty, C.C.; Norbury, W.B.; Gauglitz, G.G.; Kulp, G.A.; Herndon, D.N. Burn size determines the inflammatory and hypermetabolic response. Crit. Care 2007, 11, R90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chow, C.C.; Clermont, G.; Kumar, R.; Lagoa, C.; Tawadrous, Z.; Gallo, D.; Betten, B.; Bartels, J.; Constantine, G.; Fink, M.P.; et al. The acute inflammatory response in diverse shock states. Shock 2005, 24, 74–84. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Berthiaume, F.; Androulakis, I.P. A quantitative model of thermal injury-induced acute inflammation. Math. Biosci. 2011, 229, 135–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McDaniel, M.; Baird, A. A full-body model of burn pathophysiology and treatment using the BioGears engine. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 261–264. [Google Scholar]
- Baird, A.; McDaniel, M.; White, S.A.; Tatum, N.; Marin, L. BioGears: A C++ library for whole body physiology simulations. J. Open Source Softw. 2020, 5, 2645. [Google Scholar] [CrossRef]
- Reynolds, A.M. Mathematical Models of Acute Inflammation and a Full Lung Model of Gas Exchange under Inflammatory Stress. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2008. [Google Scholar]
- Mazzoni, M.C.; Borgström, P.; Arfors, K.E.; Intaglietta, M. Dynamic fluid redistribution in hyperosmotic resuscitation of hypovolemic hemorrhage. Am. J. Physiol. Content 1988, 255, H629–H637. [Google Scholar] [CrossRef] [PubMed]
- Rippe, B.; Haraldsson, B. Transport of macromolecules across microvascular walls: The two-pore theory. Physiol. Rev. 1994, 74, 163–219. [Google Scholar] [CrossRef]
- McDaniel, M.; Keller, J.M.; White, S.; Baird, A. A Whole-Body Mathematical Model of Sepsis Progression and Treatment Designed in the BioGears Physiology Engine. Front. Physiol. 2019, 10, 1321. [Google Scholar] [CrossRef] [PubMed]
- Ashburn, M.A. Burn Pain: The Management of Procedure-Related Pain. J. Burn. Care Rehabil. 1995, 16, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Perry, S.W.; Heidrich, G. Management of pain during debridement: A survey of U.S. burn units. Pain 1982, 13, 267–280. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv Preprint arXiv:1802.03426.
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.-A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2018, 37, 38–44. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means clustering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef] [Green Version]
- Ennis, J.L.; Chung, K.K.; Renz, E.M.; Barillo, D.J.; Albrecht, M.C.; Jones, J.A.; Blackbourne, L.H.; Cancio, L.C.; Eastridge, B.J.; Flaherty, S.F.; et al. Joint Theater Trauma System Implementation of Burn Resuscitation Guidelines Improves Outcomes in Severely Burned Military Casualties. J. Trauma Inj. Infect. Crit. Care 2008, 64, S146–S152. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baird, A.; Amos-Binks, A.; Tatum, N.; White, S.; Hackett, M.; Serio-Melvin, M. Detecting Patient Health Trajectories Using a Full-Body Burn Physiology Model. BioMedInformatics 2021, 1, 127-137. https://doi.org/10.3390/biomedinformatics1030009
Baird A, Amos-Binks A, Tatum N, White S, Hackett M, Serio-Melvin M. Detecting Patient Health Trajectories Using a Full-Body Burn Physiology Model. BioMedInformatics. 2021; 1(3):127-137. https://doi.org/10.3390/biomedinformatics1030009
Chicago/Turabian StyleBaird, Austin, Adam Amos-Binks, Nathan Tatum, Steven White, Matthew Hackett, and Maria Serio-Melvin. 2021. "Detecting Patient Health Trajectories Using a Full-Body Burn Physiology Model" BioMedInformatics 1, no. 3: 127-137. https://doi.org/10.3390/biomedinformatics1030009
APA StyleBaird, A., Amos-Binks, A., Tatum, N., White, S., Hackett, M., & Serio-Melvin, M. (2021). Detecting Patient Health Trajectories Using a Full-Body Burn Physiology Model. BioMedInformatics, 1(3), 127-137. https://doi.org/10.3390/biomedinformatics1030009




