Gibbs Free Energy, a Thermodynamic Measure of Protein–Protein Interactions, Correlates with Neurologic Disability

Abstract

Modern network science has been used to reveal new and often fundamental aspects of brain network organization in physiological as well as pathological conditions. As a consequence, these discoveries, which relate to network hierarchy, hubs and network interactions, have begun to change the paradigms of neurodegenerative disorders. In this paper, we explore the use of thermodynamics for protein–protein network interactions in Alzheimer’s disease (AD), Parkinson’s disease (PD), multiple sclerosis (MS), traumatic brain injury and epilepsy. To assess the validity of using network interactions in neurological diseases, we investigated the relationship between network thermodynamics and molecular systems biology for these neurological disorders. In order to uncover whether there was a correlation between network organization and biological outcomes, we used publicly available RNA transcription data from individual patients with these neurological conditions, and correlated these molecular profiles with their respective individual disability scores. We found a linear correlation (Pearson correlation of −0.828) between disease disability (a clinically validated measurement of a person’s functional status) and Gibbs free energy (a thermodynamic measure of protein–protein interactions). In other words, we found an inverse relationship between disease disability and thermodynamic energy. Because a larger degree of disability correlated with a larger negative drop in Gibbs free energy in a linear disability-dependent fashion, it could be presumed that the progression of neuropathology such as is seen in Alzheimer’s disease could potentially be prevented by therapeutically correcting the changes in Gibbs free energy.

1. Introduction

The treatment and management of neurological dysfunction/neurodegeneration is an area of great medical need. The World Health Organization (WHO) estimates that neurological disorders contribute 10.9% and 8.7% of the global disease burden in high- and medium-income countries, respectively [1]. Moreover, as the average age of the populations in developed countries will increase in the coming decades, it is expected that the disease burden will continue to increase. However, the present treatment of neurological diseases constitutes, by and large, the management of disease symptoms, because the etiology remains unclear. In Alzheimer’s disease, for example, the earlier etiological hypothesis that amyloid deposits are caused by environmental stimuli is being supplanted by a growing body of evidence that it is the genomic dysregulation of cellular and molecular pathways that cause accumulation of beta amyloid and MAP tau proteins [2]. This may not only explain why targeting amyloid and/or tau proteins has been unsuccessful so far, but it also unlocks the possibility of using targeted therapies. However, to realize the full potential of targeting these newly identified genomic patterns in Alzheimer’s disease [3,4] and in order to pursue these novel, molecularly guided therapies, an improved understanding of the complexity of the system biology of neurological diseases is needed.

Many pathologic conditions, such as, for example, neurodegenerative diseases, chronic inflammatory disorders or cancer, are associated not only with mutational activation of genes, but also with re-activation of developmentally silenced pathways. Because the processes of tissue invasion, proliferation, inflammation and angiogenesis are common not only to oncogenic induction, but also to embryonal development and normal host response to tissue injury, a simple DNA mutation analysis would not provide sufficient information. Therefore, the activation of pathways associated with inflammation and tissue injury is best studied using mRNA expression as a quantitative measure. However, until very recently, it has been very difficult to directly correlate the levels of gene expression with the cellular effect of specific proteins. In fact, high gene expression did not always imply increased protein function or activation of a biological process. The intensity of a biological effect is dependent on the interactions of the affected (overexpressed) gene with its neighbors, and the quorum effect of the innumerable feedback loops on the global protein–protein interaction network (PPIN).

The realization that the perturbations of individual genes can be measured by their effect on the global response of a network has led many scientists to find alternative approaches for genomic interpretations. The one proposed and presented in this manuscript is based on using not only the level of expression of a gene, but also its topology as a measure of its connectivity within a network. This novel approach has been enabled by the vast amounts of well-curated information accumulated in publicly available PPINs over the last 4 decades, and has emerged quite recently [5,6,7,8].

The underlying premise of our analysis is that biological systems are in essence complex chemical networks. A cell, for example, consists mainly of a large molecular network made of DNA, RNA, proteins, peptides, small molecules and lipids. Each of these molecules is associated with potential energy contributing to an even larger energetic network. The energetic state exists in or close to thermodynamic equilibrium, and any perturbation sets off a cascade of events striving to bring the overall network back to the same entropy level, which is a hallmark of homeostasis. The prime force pushing the reaction back toward equilibrium is the Gibbs free energy, an expression of the thermodynamic energy reflecting the chemical potential between interacting proteins. This Gibbs free energy is used as a measure of the changes occurring within a disease-related PPIN.

In an earlier work, Rietman et al. [9] described an inverse correlation between the Gibbs free energy and 5-year survival probability for ten different types of cancers. The study showed that poor prognosis cancers such as glioblastoma multiforme have low thermodynamic entropy, less negative Gibbs free energy and very low 5-year survival. This was consistent with the clinical status of the disease, which has an average survival post diagnosis of 6 months, and a 5-year survival of 2%. Similarly, it was found that in breast carcinoma, which had a higher thermodynamic entropy, a more negative Gibbs free energy and a much higher 5-year survival were also congruent with the clinical observation, as the average 5-year survival for breast cancers of all stages is ~88%.

In this manuscript, we describe a linear relationship between Gibbs free energy (a measure of thermodynamic energy for a specific disease), and disability weight (a clinically validated measurement of a person’s functional status) for several neurological diseases for which consistent data were available. The choice of thermodynamics for the analysis was not fortuitous. Thermodynamic energy represents an important driving factor of chemical and biological interactions for all living organisms, and its correlation with biological events is not unexpected. Gibbs free energy, which incorporates information on both the mRNA expression and the complexity of the protein–protein interactions, would be expected to have the ability to discriminate between “passenger genomic events” and “driving genomic events”. This remains the main quandary—finding ways to differentiate between causative, as opposed to ancillary molecular changes. The use of Gibbs free energy in this context represents a novel approach, and may be of particular usefulness in understanding neurological disorders/neurodegenerative diseases where complex and by and large unclear etiology, pathogenesis and clinical response prevent identification of effective therapeutic strategies.

Gibbs free energy (G) is the energy associated with a chemical reaction that can be used to do work. The free energy of a system is the sum of its enthalpy (H) plus the product of the absolute temperature (in Kelvin) and the entropy (S) of the system.

We propose that the use of this well-established thermodynamic measure is useful for analyzing the interplay between patient’s genomic information and the existing knowledge about PPINs [7]. Its use is based on a number of important observations. First, a system comprising proteins interacting with a large number of other proteins (even if not simultaneously) has a higher entropy. Because each protein–protein interaction has a different molecular configuration, given by Boltzmann’s classic equation (S = k ln(W) where k is the Boltzmann constant), the entropy, S, increases as the natural logarithm of the number of available configurations (microstates), W. As such, proteins with many interaction partners exhibit many possible configurations, and each protein–partner interaction leads to a different configuration. Highly interconnected proteins such as, for example, ubiquitin (UBC) or p53 (encoded by the TP53 gene) can undergo a simultaneous physical interaction with hundreds of their respective interaction partners, because at any given time one UBC molecule interacts with a protein and a different UBC molecule interacts with another protein within the same cell. An RNA transcriptome from a tissue biopsy thus represents an ideal mixture of UBC and its interacting partners for a given condition.

Second, transcription (RNA expression levels) data are good surrogates for protein concentration values. Unlike the DNA-level gene alterations, which are transcribed with variable frequencies to RNA, the number of mRNA copies is translated into individual proteins with great fidelity. Several research groups have confirmed this fidelity: Greenbaum et al. [10] and Maier et al. [11] report a Pearson correlation in the range of 0.4–0.9 for a large set of experiments across five different species. Similarly, Kim et al. [12] and Wilhlem et al. [13] found an 83% correlation between human transcription data and mass spectrometry proteomic data for multiple tissue types, supporting the use of human transcriptome as a surrogate for protein concentration data.

Third, the use of a real-world dataset contains an inherent level of noise, but as new mRNA data sets emerge from ongoing clinical trials, the accuracy of the information in protein–protein interaction databases as well as in the gene expression datasets will improve as well. For the time being, the preliminary findings represent a convenient way to discover new avenues for future analysis, but as data integrity and quality of our conclusions improve, we should be able to use these data for increasingly more reliable therapeutic decisions. In addition, the ability to combine different data sources (mRNA expression data from individual patients and existing PPINs) as introduced in this manuscript is likely to deliver new insight into biologically complex diseases than traditional approaches.

2. Materials and Methods

Because the study of chemical thermodynamics embodies chemical potential, for two molecules A and B interacting to form a new molecule, or an A-B molecular complex, the amount of A-B formed would be dictated by the amount of A and B. In cases where A is present in a higher concentration than B, a chemical potential develops. As such, a protein, D, interacting with proteins, C, E and F, has a chemical potential represented by:

$${\mu }_D=ln\left[\frac{c_D}{c_C+c_D+c_E+c_F}\right]$$

(1)

where the chemical potential is the natural logarithm of the concentration of protein D divided by the sum of the concentrations of protein D and the combined concentrations of all its neighbors. Because the argument of the natural logarithm is a ratio, we can use scaled “concentrations”, or in this case, scaled expression values. The log-2 normalized expression data typically fall in the range (–10,10). Rescaling sets the range to be [0,1], and we can compute the minimum, e_min, and the maximum, e_max, for a given expression data set. The normalized expression values for each gene are then computed as follows:

$$c_i=\frac{\left(e_i-e_{min}\right)}{\left(e_{max}-e_{min}\right)}$$

(2)

The rescaling is justified from a mathematical perspective by the fact that the argument of the natural logarithm must be positive. Furthermore, if a gene mutation leads to loss of its RNA transcription (RNA transcription is said to be downregulated), the concentration for the respective protein would essentially be zero. Likewise, when a gene alteration leads to constitutive activation of its transcription, multiple copies of its mRNA will be made (the RNA transcription is said to be highly upregulated), and very large quantities of protein will be produced. In this case, the protein concentration would be effectively set to the maximum value of 1.

Thus, the computation of Gibbs free energy for a single protein in the PPI would be

$$G_i=ln\frac{c_i}{{{\displaystyle \sum }}_{j=i}{c}_j}$$

(3)

which suggests that we should first compute the chemical potential for protein i with neighbors j, and multiply it by the [0,1] scaled concentration to obtain the Gibbs free energy for protein i. For the overall Gibbs free energy for the network, the individual G’s for each of the protein within the network are summed up. In the final calculation, the normalized expression data are overlaid on the BioGRID PPI and G_i followed by use of the above equation. Note, the SI units in Equation (3) are J/mole; we use a modification of Equation (3) by multiplying moles, c_i, on the right-hand side. Therefore, we have the mapping—a quasi-Gibbs energy:

$$q{G}_i\left[\frac{J}{mole}\right]\leftarrow c_{i}ln\frac{c_i}{{{\displaystyle \sum }}_{j=i}{c}_j}\left[J\right]$$

(4)

The mapping is simply a scaling factor, but the actual units on the graphs and in the table would, at best, be difficult to interpret because we do not have molar concentration of the proteins, only their relative expression levels.

We used three main data sources for our analysis: (1) World Health Organization data on disability associated with neurological diseases, (2) protein–protein interaction data from Biological General Repository for Interaction Datasets (BioGRID, Human ver. 3.4.139, September 2016, https://thebiogrid.org/ accessed on 7 April 2020) and (3) RNA transcription data sets from Gene Expression Omnibus (GEO).

2.1. WHO Tools and Statistics for Neurodegenerative Diseases

Unlike terminal conditions such as cancer, there is no direct correlation between death rate and disability in neurodegenerative diseases, and death rate is not a meaningful measure of morbidity. For example, although epilepsy may cause more deaths, multiple sclerosis (MS) far outweighs its impact in the sense of morbidity and disability during a person’s lifetime. For this reason, the World Health Organization has selected Disability-Adjusted Life Years (DALYs) as a measure to use for evaluation of disability associated with neurodegenerative diseases. DALYs combine two components: years of life lost due to premature mortality, and years lived with disability. DALYs are an expression of the number of healthy years a person loses in life. It is a more accurate representation of the damage a disease exerts on a healthy human population, and its measure—Disability Weight—is a number between 0 (perfect health) and 1 (death). Although DALYs are population-dependent, and the same disease may lead to a larger apparent loss in a region where the disease is widespread, Disability Weight avoids the potential for biasing the numbers towards more prevalent diseases and away from uncommon diseases, because it rates the severity of a disease in an individual. The most recent public list of WHO for neurological diseases and their corresponding disability weights was published in 2006, and the “Neurological Disorders, public health challenges” [1] describes the demographics, geographic distributions, graphs and projections for many neurological diseases. It standardizes the comparison of neurological diseases, and was, therefore, used for our analysis.

2.2. Sources of Transcription Data

The source of the transcription data was Gene Expression Omnibus (GEO) repository of -omics and high-throughput data https://www.ncbi.nlm.nih.gov/geo (accessed on 7 April 2020). The data sets for each of the selected neurological diseases were collapsed from probe IDs to gene IDs using GenePattern software (Broad Institute, Cambridge, MA, USA; https://software.broadinstitute.org/cancer/software/genepattern, accessed on 25 November 2020), and the corresponding chip platform documented for the respective data set. The following datasets for specific diseases were examined: Alzheimer’s disease (GDS4136), Parkinson’s disease (GSE6613), Multiple Sclerosis (GSE19285), Epilepsy (GSE32534), Cerebrovascular disease (GSE36791) and Meningitis (GSE40586). Most data sets were already log-2 normalized, and we transformed those that were not.

Table 1. Disability score and Gibbs free energy for the neurological disorders studied.

Disease	Tissue Analyzed	GEO Number	PMID	Disability Weight	Gibbs Free Energy	Number of Patients
Alzheimer Disease	hippocampus	GSE28146	21756998	0.666	−14735	22
Cerebrovascular Disease	blood in ruptured intracranial aneurysms	GSE36791	23512133	0.266	−11761	43
Epilepsy	neocortex tissue	GSE32534	23418513	0.113	−11467	5
Meningitis	peripheral blood cells	GSE40586	23515576	0.615	−16918	21
Multiple Sclerosis	peripheral blood cells	GSE19285	22727118	0.411	−12109	30
Parkinson Disease	whole blood cells	GSE6613	17215369	0.351	−10043	50

lists the GEO dataset number and PubMed ID (PMID) for each of the diseases.

3. Results and Discussion

Neurological disorders are common and represent a major public health problem. Even though neurological impairment and its sequelae constitute over 6% of the global burden of disease [1], the management of neurological disorders has not significantly changed in the past few decades, and the mainstay of therapy remains focused on symptomatic management. As such, the already very high disease burden is likely to continue to increase as life spans across the world’s population increase. According to the recently published Global Burden of Disease 2010 Study (GBD 2010) [14], stroke is the second leading cause of death globally and the third leading cause of premature death and disability as measured in disability-adjusted life years (DALYs).

There are many reasons for the lack of effective therapies, but the principal challenge is the complexity of data and the inconsistency in assigning causality to genomic alterations. It is a great challenge to discriminate between incidental molecular findings, and those that may be driving disease pathogenesis. This not only hinders the search for effective therapies, but the absence of tissue targets also prevents effective clinical initiatives. Until recently, much effort was dedicated to statistical interpretation of RNA expression levels. However, the level of mRNA expression is not always reflective of the gene importance in a biological event or in a particular disease. An overexpressed gene that is peripheral to a major proliferative pathway will have a minimal effect on proliferation, whereas a mild elevation in the expression levels of a well-connected gene will have a crucial effect on the process. Minute changes in the levels of genes coding for very important growth factors such as VEGF, or inflammation regulators interleukins lead to biological events that are normally carefully managed through feedback loops.

Any measurement of disease activity must, therefore, incorporate the intracellular protein–protein interactions. We introduce a method for interrogating individual tissue expression of mRNA against existing, well-curated PPINs. We focus on proving that thermodynamics, i.e., the molecular changes defined by Gibbs free energy, can be correlated with disease state and progression. Figure 1 shows the correlation of Disability Weight with average Gibbs free energy values for six neurological conditions. The relationship between disease-related disability and Gibbs free energy is linear, with progressively worsening disability correlating with increasingly more negative Gibbs free energy. The respective values used for the figure are shown in Table 1. We confirm that low entropy (less negative Gibbs free energy) for epilepsy correlated with the lowest disability, whereas the higher entropy (more negative Gibbs free energy) in Alzheimer’s disease correlated with the highest disability. These findings correlate well with clinical observations that the severity of neurological dysfunction in multiple sclerosis, bacterial meningitis and Alzheimer’s disease is certainly higher than in epilepsy.

The mRNA expression values available from publicly available GEO data sets (Alzheimer’s disease GDS4136, Parkinson’s disease GSE6613, Multiple Sclerosis GSE19285, Epilepsy GSE32534, Cerebrovascular disease GSE36791 and Meningitis GSE40586) were used to calculate Gibbs free energy, a thermodynamic measure of protein–protein interactions. As would be expected based on the level of clinical disability, epilepsy has low Gibbs free energy (low entropy) and correlates with the lowest neurological disability. This is in stark contrast with the high Gibbs free energy (high entropy) and high neurologic disability in Alzheimer’s disease, as would be consistent with clinical observations in this disease. The respective values, and the size of the cohort are summarized in Table 1, and the error bars have been set to 5% of the average Gibbs Free energy value, given that the actual errors of the reported mRNA gene expression values were not reported.

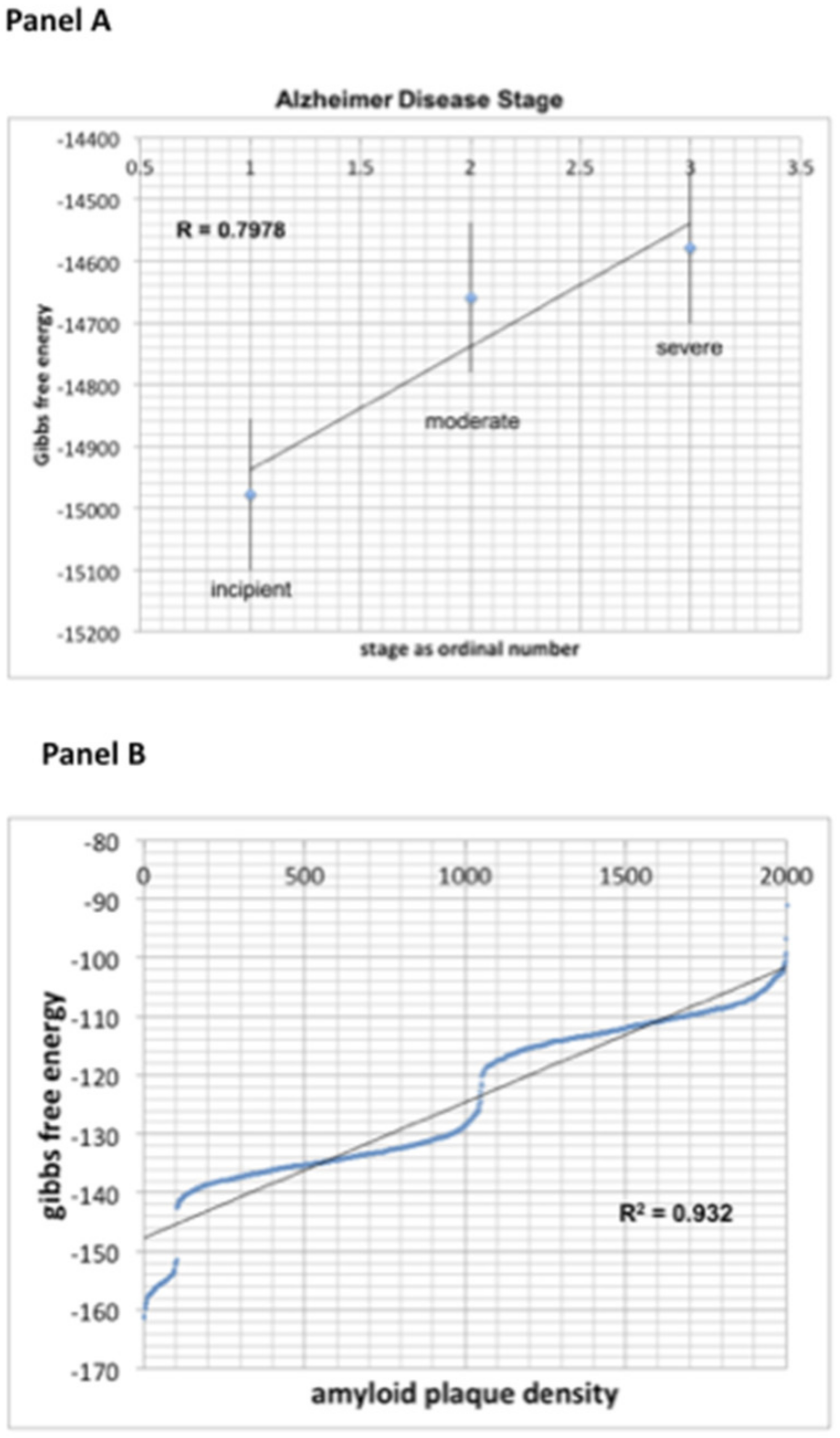
We further explored whether Gibbs free energy correlated not only with severity of the disease, but also with disease progression. Seven stages have been described in Alzheimer’s disease (AD) progression, from no impairment (Stage 1) to loss of ability to respond to their environment or communicate, needing assistance with all activities of daily living and loss of ability to swallow (Stage 7). The GEO data sets tend to simplify these stages into only four stages (Figure 2a), and we show a clear linear relationship (R = 0.7978) between thermodynamic energy (Gibbs free energy) and the four stages of the disease. The positivity of the slope is most likely reflective of neuronal loss, with less and less metabolically active tissue. This is in direct contrast with epilepsy, typified by an abnormality of conduction of an action potential across neuronal tissues rather than by a neuronal loss, where Gibbs free energy is less negative (i.e., more positive).

Similarly strong correlation (R = 0.932) was observed between Gibbs free energy and the degree of amyloid deposition in Alzheimer’s disease (see Figure 2b). In this case, progressive histological changes in the form of extracellular deposits of amyloid β peptides, senile plaques and intracellular neurofibrillary tangles of hyperphosphorylated tau in the brain relate to neuronal death and correlate with severe disability. The amyloid metabolic cascade and the post-translational modification of tau protein, often considered causal in AD, are sufficient to explain the diversity of biochemical and pathological abnormalities in AD. There is a multitude of cellular and biochemical changes leading to the accumulation of extracellular senile plaques made of deposits of Aβ peptide, and all have the outcome of neural degeneration and loss. The correlation of Gibbs free energy with histological changes and disease progression implies a global value of our measurement and the need for future evaluation of the hidden metabolic information.

The analysis of 2000+ Alzheimer’s Disease patients from GSE84422 data set revealed a correlation coefficient R = 0.7978 between Gibbs free energy and disease progression using disease stage (Figure 2A), and an even stronger correlation (R = 0.932) using tissue pathological analysis such as amyloid plaque density (Figure 2B).

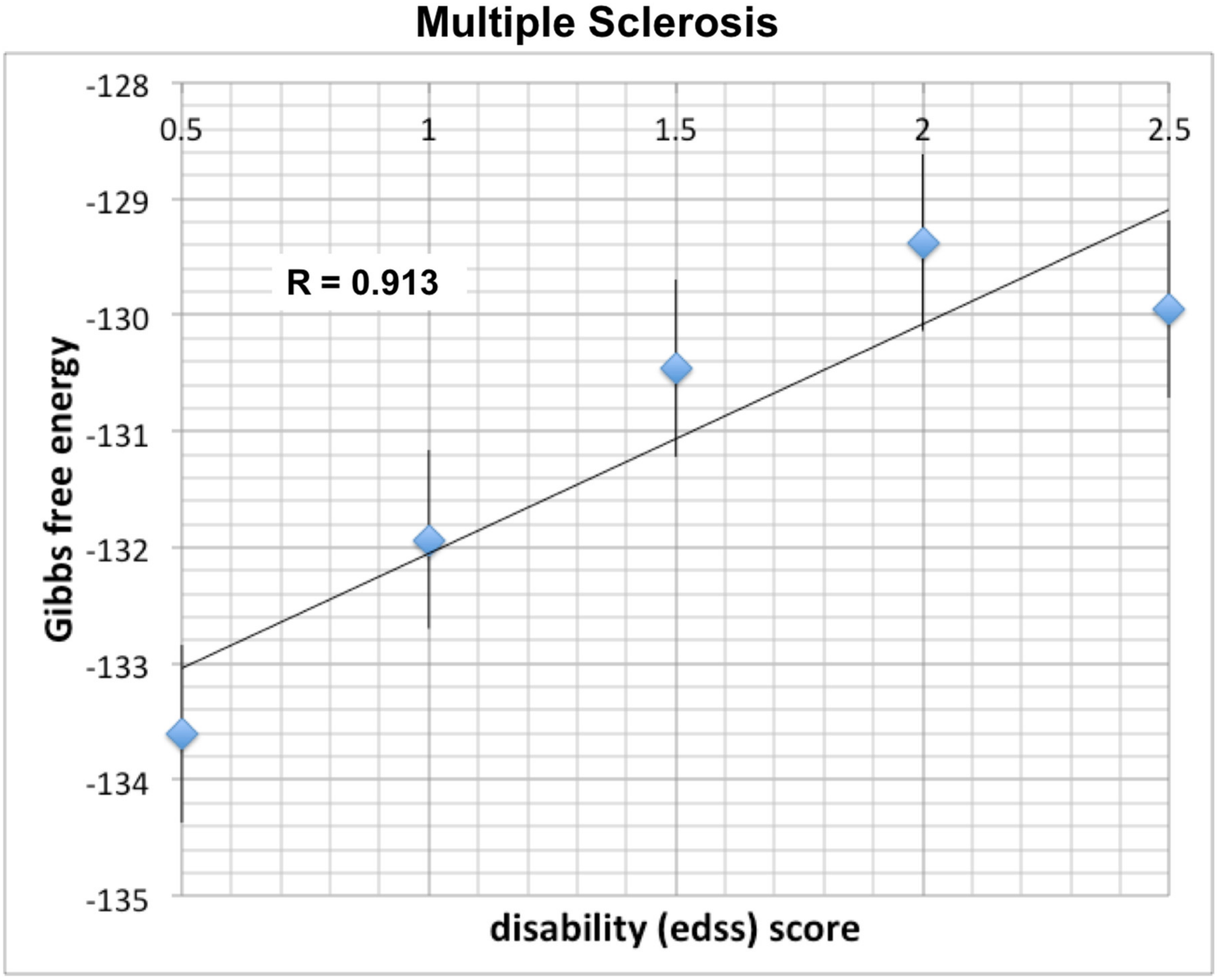
Yet, another scale is used by clinicians for evaluation of disability in multiple sclerosis (MS). The Expanded Disability Status Scale (EDSS) was developed by a neurologist (John Kurtzke) in 1983, and ranges between 0–10. It is based on neurological evaluation of pyramidal (limb movement), cerebellar (ataxia, coordination, tremor), brainstem (speech, swallowing and nystagmus), sensory, bowel and bladder, vision and cerebral (mental) functions. Its 0.5-unit increments represent progressively higher levels of disability. EDSS 1.0–4.5 refers to people with MS who are able to walk without any aid, whereas 5–6 refers to progressive motor and cognitive disability. Similarly to AD, we find a positive linear slope between Gibbs free energy and disability in MS (see Figure 3), as consistent with neuronal loss due to demyelination. The respective correlation coefficient between EDSS and Gibbs free energy in MS was found to be very strong at R = 0.913.

As shown in Figure 3, thirty patients with multiple sclerosis from the GEO data set GSE19285 revealed a correlation coefficient R = 0.913 between Gibbs free energy and disease progression as reflected by The Expanded Disability Status Scale (EDSS).

4. Conclusions

In this paper, we have provided early evidence for using not only expression data, but also connectivity/topology data obtained from the associated PPINs for analysis of genomic information in neurodegenerative diseases. One of the approaches is based on using a thermodynamic measure such as Gibbs free energy to identify the disease-related global changes in the associated PPIN resulting from changes in genomic profiles of individual patients. The ability to correlate these molecular profiles with disease severity and disease progression suggests that we can use Gibbs free energy in the future to evaluate causative versus ancillary molecular changes through mathematical simulations of the protein inhibition/stimulation. This is the first installment in developing mathematical algorithms that would facilitate identification of relevant, therapeutically targetable pathways in neurodegenerative diseases. The use of Gibbs free energy in genomic analysis would be beneficial not only from a therapeutic point of view, but also from a cost and sustainability perspective, because it would minimize futile clinical trials.