Adjusted Sample Size Calculation for RNA-seq Data in the Presence of Confounding Covariates
Abstract
:1. Introduction
2. Materials and Methods
2.1. A Generalized Linear Model with a NB Distribution
2.2. Simulation-Based Studies
2.2.1. Sample Size Estimation for a Single Gene
- Obtain the pre-specified parameters, such as fold change (ρ), the ratio of size factors w and the ratio of sample sizes k between two-sample groups.
- Specify a desired statistical power (i.e., 0.80) and significance level 0.05.
- Simulate control and treatment groups RNA-seq data given the mean counts in the control group () and common dispersion (ϕ) for a fixed n using an NB distribution with the aid of the rnbinom function in R.
- Simulate a confounding covariate under different scenarios given a fixed n and distribution with the aid of the rnorm function for a normal distribution, the rpois function for a Poisson distribution and rnbinom for a binomial distribution for a categorical confounder.
- Fit the GLM with a NB distribution using the R glm.nb function.
- Obtain the coefficient along with the standard error, z-score and p-value for statistical test on from the simulated data set. For a two-sided test, record whether a p-value in testing a single gene or p-value in testing multiple genes.
- Repeat steps 3–6 for 1000 times and impute the statistical power for the fixed sample size.
- Repeat steps 3–7 by increment of sample size by one () if the power is smaller than 0.7999 . Stop when a desired statistical power is obtained and then record the sample size n and the actual power.
2.2.2. Sample Size Estimation for Controlling FDR in Testing Multiple Genes
3. Results
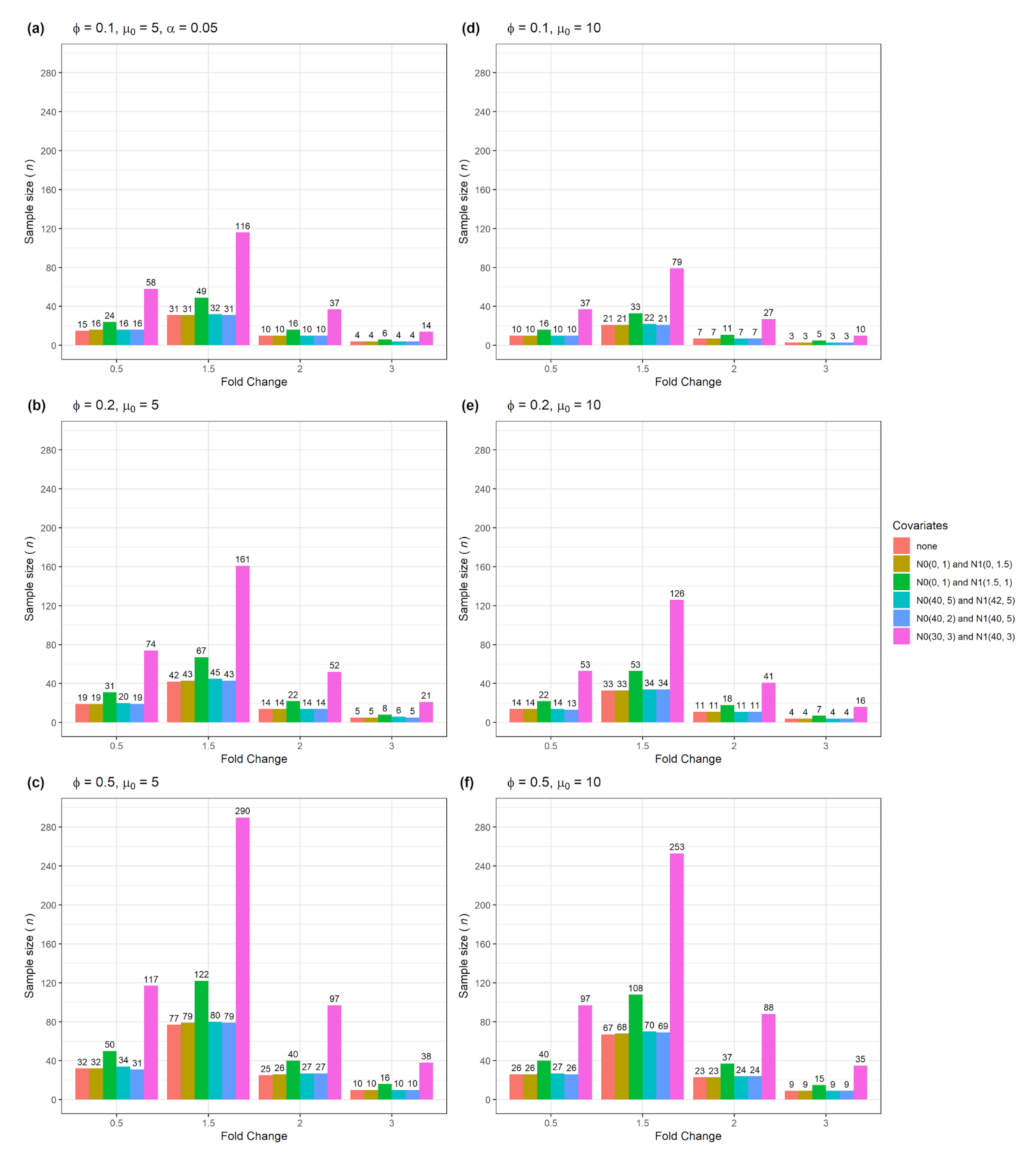
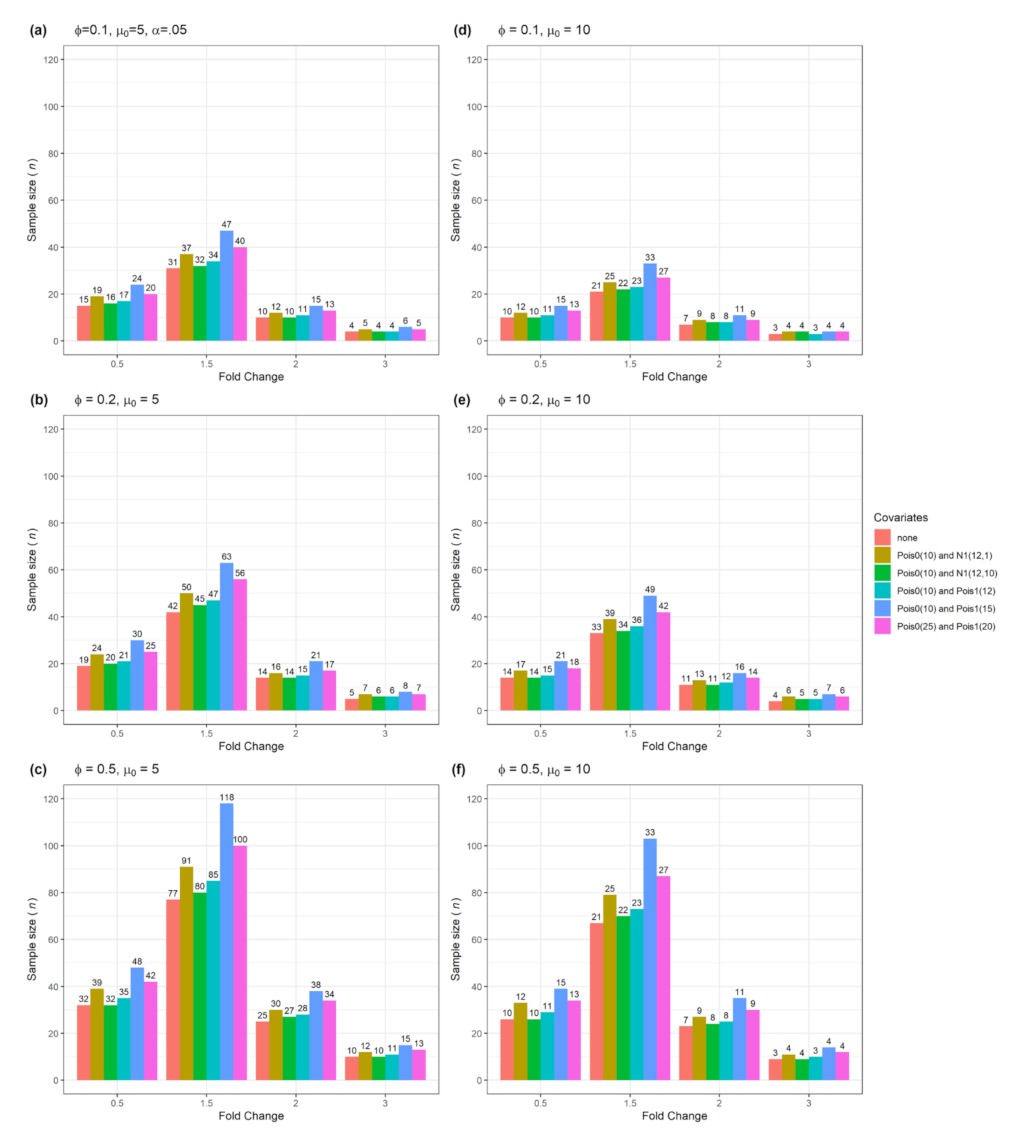
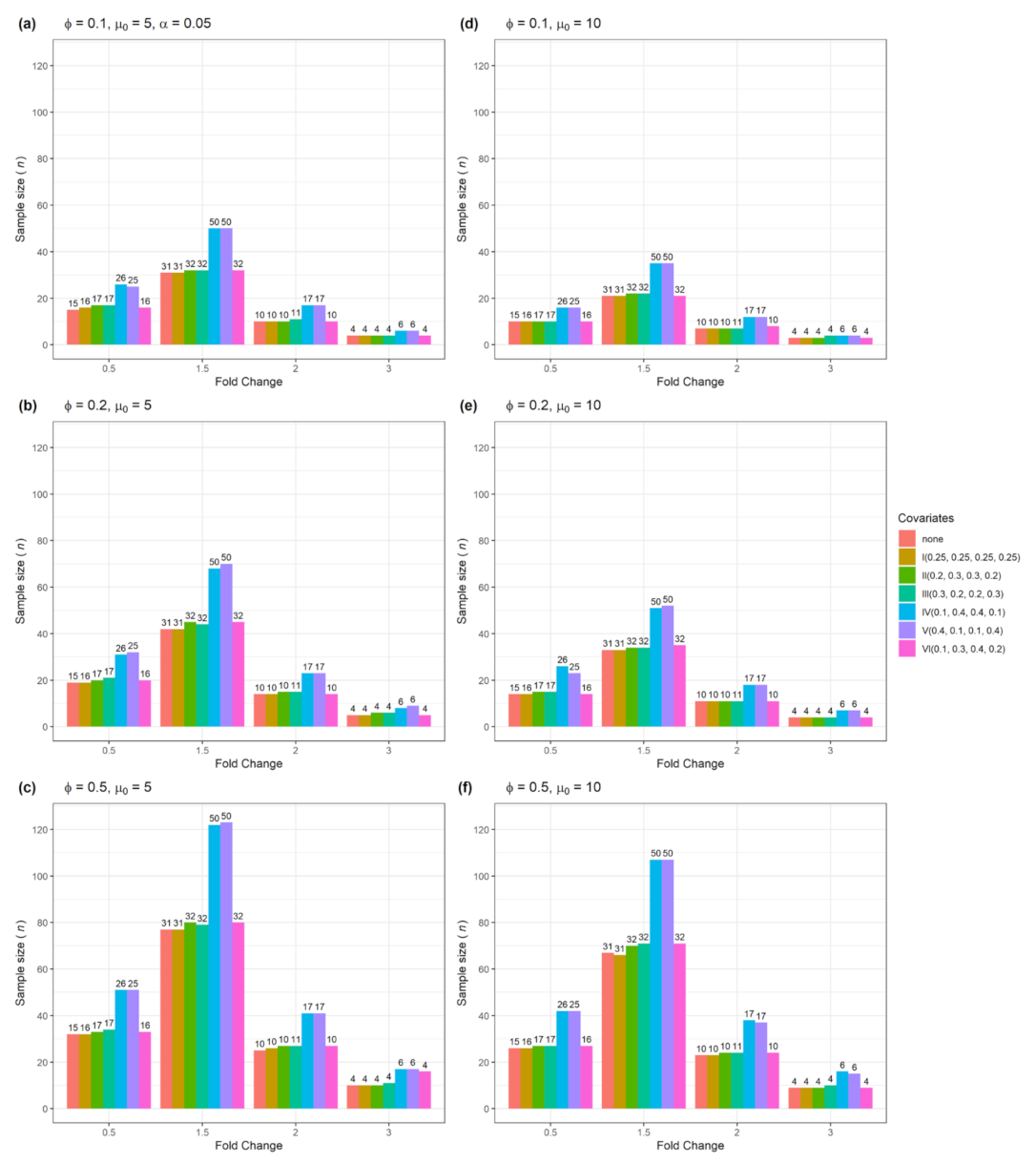
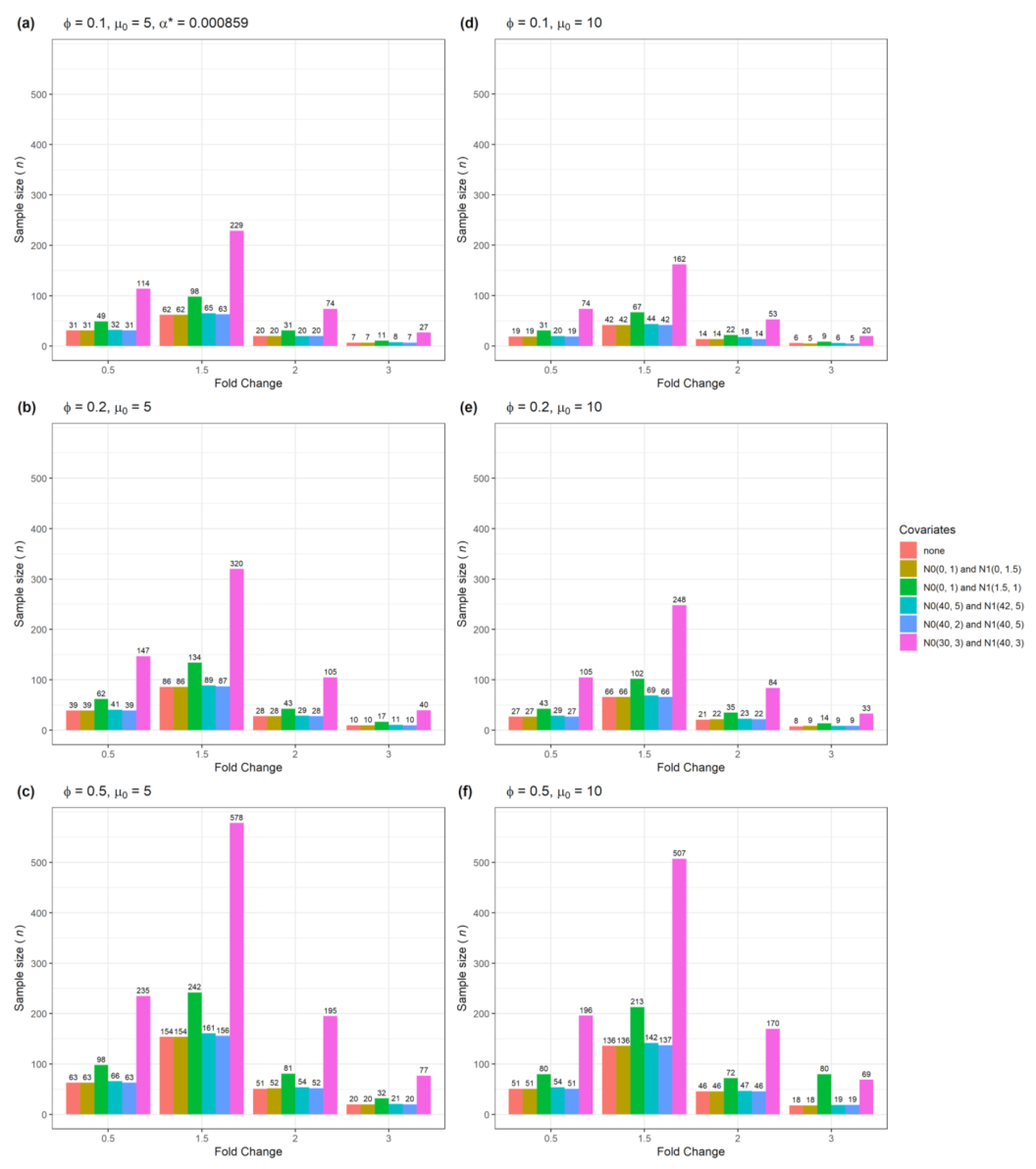
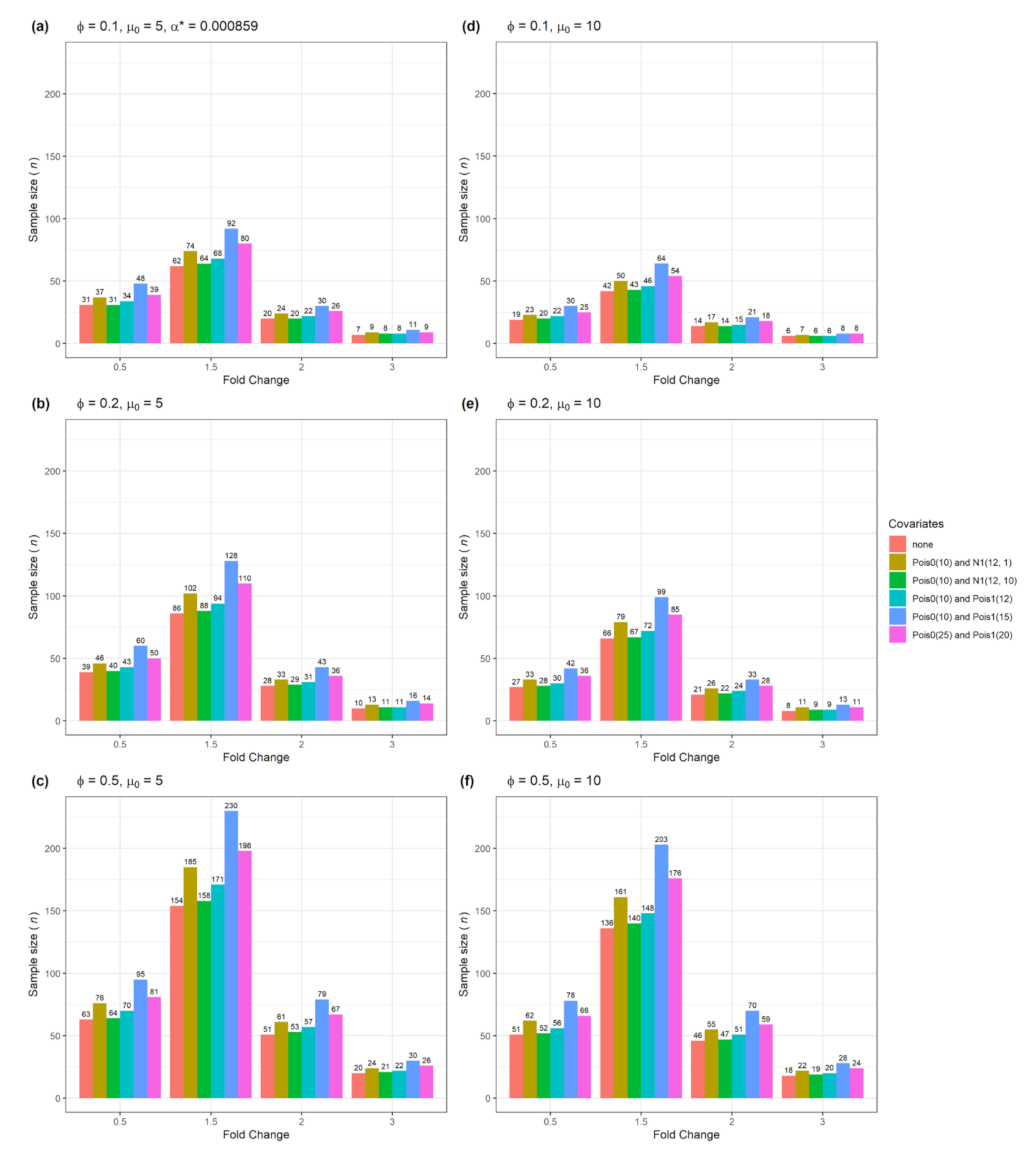
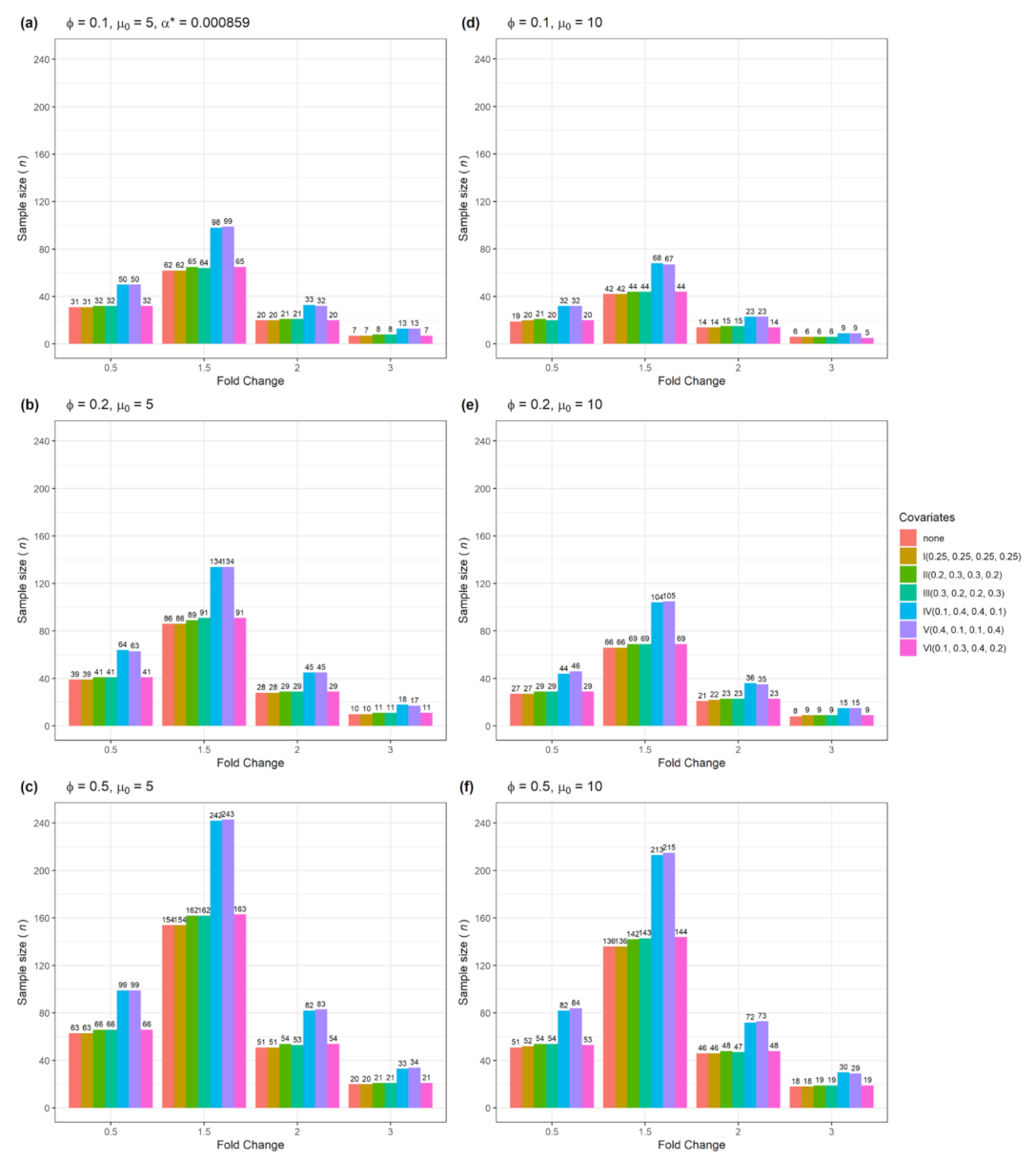
3.1. Sample size n and actual power from a single confounder variable for testing single gene
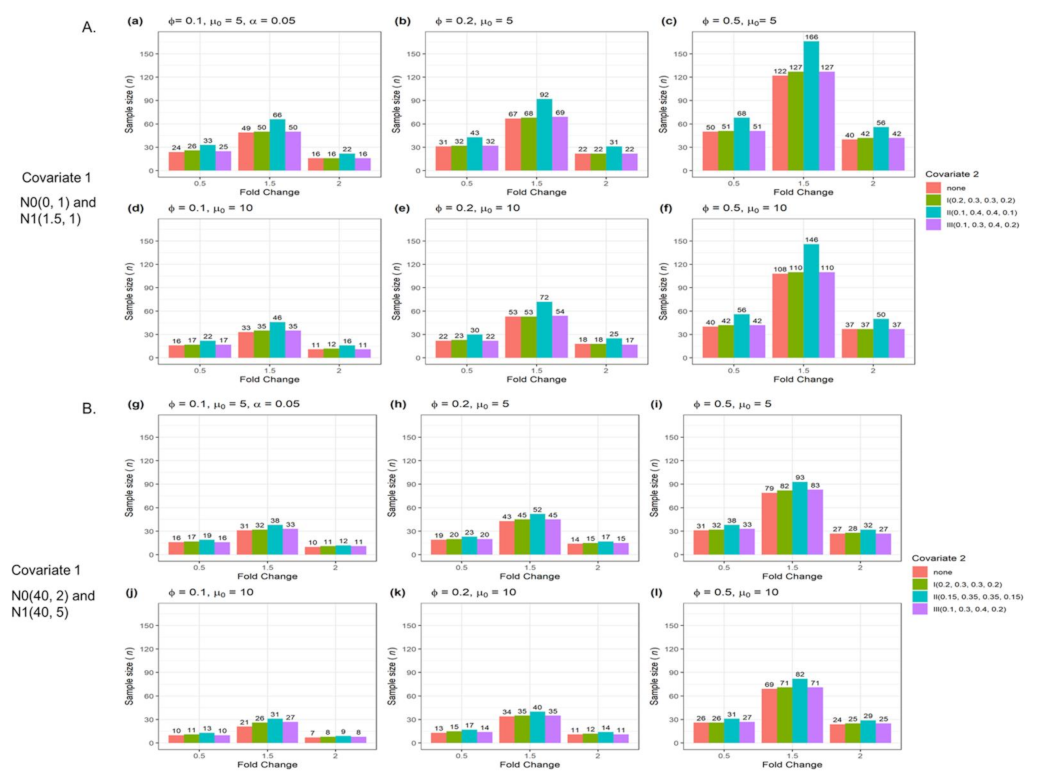
3.2. The n and Actual Power from Two Confounders for Testing a Single Gene
3.3. The n and Actual Power for Testing Multiple Genes
3.4. An Example Using COAD RNA-seq Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, Z.; Cui, X. Design and validation issues in RNA-seq experiments. Brief. Bioinform. 2011, 12, 280–287. [Google Scholar] [CrossRef] [Green Version]
- Li, C.I.; Su, P.F.; Guo, Y.; Shyr, Y. Sample size calculation for differential expression analysis of RNA-seq data under Poisson distribution. Int. J. Comput. Biol. Drug Des. 2013, 6, 358–375. [Google Scholar] [CrossRef] [PubMed]
- Li, C.I.; Su, P.F.; Shyr, Y. Sample size calculation based on exact test for assessing differential expression analysis in RNA-seq data. BMC Bioinform. 2013, 14, 357. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cooper, G.F.; Shyr, Y.; Wu, D.; Rouchka, E.C.; Gill, R.S.; O’Toole, T.E.; Brock, G.N.; Rai, S.N. Inference and Sample Size Calculations Based on Statistical Tests in a Negativ ebnomial Distribution for Differential Gene Expression in RNA-seq Data. J Biom. Biostat. 2017, 8. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wu, D.; Cooper, N.G.F.; Rai, S.N. Sample size calculations for the differential expression analysis of RNA-seq data using a negative binomial regression model. Stat. Appl. Genet. Mol. Biol. 2019, 18. [Google Scholar] [CrossRef] [PubMed]
- Ching, T.; Huang, S.; Garmire, L.X. Power analysis and sample size estimation for RNA-Seq differential expression. RNA 2014, 20, 1684–1696. [Google Scholar] [CrossRef] [Green Version]
- Hart, S.N.; Therneau, T.M.; Zhang, Y.; Poland, G.A.; Kocher, J.P. Calculating sample size estimates for RNA sequencing data. J. Comput. Biol. 2013, 20, 970–978. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhou, J.; White, K.P. RNA-seq differential expression studies: More sequence or more replication? Bioinformatics 2014, 30, 301–304. [Google Scholar] [CrossRef]
- Yu, L.; Fernandez, S.; Brock, G. Power analysis for RNA-Seq differential expression studies. BMC Bioinform. 2017, 18, 234. [Google Scholar] [CrossRef]
- Anders, S.; Huber, W. Differential expression analysis for sequence count data. Genome Biol. 2010, 11, R106. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.D.; Smyth, G.K. Small-sample estimation of negative binomial dispersion, with applications to SAGE data. Biostatistics 2008, 9, 321–332. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.D.; McCarthy, D.J.; Smyth, G.K. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 2010, 26, 139–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, S.; Li, C.I.; Guo, Y.; Sheng, Q.; Shyr, Y. RnaSeqSampleSize: Real data based sample size estimation for RNA sequencing. BMC Bioinform. 2018, 19, 191. [Google Scholar] [CrossRef]
- Wu, H.; Wang, C.; Wu, Z. PROPER: Comprehensive power evaluation for differential expression using RNA-seq. Bioinformatics 2015, 31, 233–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dillies, M.A.; Rau, A.; Aubert, J.; Hennequet-Antier, C.; Jeanmougin, M.; Servant, N.; Keime, C.; Marot, G.; Castel, D.; Estelle, J.; et al. A comprehensive evaluation of normalization methods for Illumina high-throughput RNA sequencing data analysis. Brief. Bioinform. 2013, 14, 671–683. [Google Scholar] [CrossRef] [Green Version]
- Kvam, V.M.; Liu, P.; Si, Y. A comparison of statistical methods for detecting differentially expressed genes from RNA-seq data. Am. J. Bot. 2012, 99, 248–256. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Brock, G.N.; Rouchka, E.C.; Cooper, N.G.F.; Wu, D.; O’Toole, T.E.; Gill, R.S.; Eteleeb, A.M.; O’Brien, L.; Rai, S.N. A comparison of per sample global scaling and per gene normalization methods for differential expression analysis of RNA-seq data. PLoS ONE 2017, 12, e0176185. [Google Scholar] [CrossRef]
- Li, X.; Cooper, N.G.F.; O’Toole, T.E.; Rouchka, E.C. Choice of library size normalization and statistical methods for differential gene expression analysis in balanced two-group comparisons for RNA-seq studies. BMC Genom. 2020, 21, 75. [Google Scholar] [CrossRef] [PubMed]
- Lund, S.P.; Nettleton, D.; McCarthy, D.J.; Smyth, G.K. Detecting differential expression in RNA-sequence data using quasi-likelihood with shrunken dispersion estimates. Stat. Appl. Genet. Mol. Biol. 2012, 11. [Google Scholar] [CrossRef]
- Seyednasrollah, F.; Laiho, A.; Elo, L.L. Comparison of software packages for detecting differential expression in RNA-seq studies. Brief. Bioinform. 2015, 16, 59–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized linear model. J. R. Stat. Soc. 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Self, S.G.; Mauritsen, R.H. Power Sample-Size Calculations for Generalized Linear-Models. Biometrics 1988, 44, 79–86. [Google Scholar] [CrossRef]
- Zhu, H.; Lakkis, H. Sample size calculation for comparing two negative binomial rates. Stat. Med. 2014, 33, 376–387. [Google Scholar] [CrossRef] [PubMed]
- Shieh, G. On power and sample size calculations for likelihood ratio tests in generalized linear models. Biometrics 2000, 56, 1192–1196. [Google Scholar] [CrossRef]
- Lamarre, S.; Frasse, P.; Zouine, M.; Labourdette, D.; Sainderichin, E.; Hu, G.; Le Berre-Anton, V.; Bouzayen, M.; Maza, E. Optimization of an RNA-Seq Differential Gene Expression Analysis Depending on Biological Replicate Number and Library Size. Front. Plant Sci. 2018, 9, 108. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Figure | Single Gene | Multiple Genes | Number of Confounders | Data Type |
|---|---|---|---|---|
| Figure 1 | Yes | No | 1 | Numerical with normal distribution |
| Figure 2 | Yes | No | 1 | Numerical with normal or Poisson distribution |
| Figure 3 | Yes | No | 1 | Categorical |
| Figure 4 | Yes | No | 2 | Numerical and categorical data |
| Figure 5 | No | Yes | 1 | Numerical with normal distribution |
| Figure 6 | No | Yes | 1 | Numerical with normal or Poisson distribution |
| Figure 7 | No | Yes | 1 | Categorical |
| Figure 8 | No | Yes | 2 | Numerical and categorical |
| ρ | No confounders | Age | Sex VII(0.24, 0.26, 0.26, 0.24) | Age and Sex | |||||
|---|---|---|---|---|---|---|---|---|---|
| n | Power (%) | n | Power (%) | n | Power (%) | n | Power (%) | ||
| 0.5 | 2 | 107 | 80.2 | 108 | 80.1 | 107 | 80.2 | 109 | 80.26 |
| 5 | 71 | 80.2 | 73 | 80.6 | 72 | 80.5 | 73 | 80.52 | |
| 10 | 59 | 80.8 | 59 | 80.1 | 59 | 80.6 | 60 | 80.90 | |
| 1.5 | 2 | 165 | 80.3 | 168 | 80.5 | 166 | 80.4 | 168 | 80.34 |
| 5 | 124 | 80.62 | 125 | 80.08 | 124 | 80.64 | 125 | 80.5 | |
| 10 | 107 | 80.4 | 109 | 80.16 | 108 | 80.28 | 109 | 80.26 | |
| 2 | 2 | 60 | 80.9 | 60 | 80.0 | 60 | 80.8 | 61 | 80.58 |
| 5 | 44 | 80.2 | 45 | 80.6 | 45 | 81.3 | 45 | 80.6 | |
| 10 | 40 | 80.7 | 41 | 80.8 | 40 | 80.6 | 41 | 80.46 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Rai, S.N.; Rouchka, E.C.; O’Toole, T.E.; Cooper, N.G.F. Adjusted Sample Size Calculation for RNA-seq Data in the Presence of Confounding Covariates. BioMedInformatics 2021, 1, 47-63. https://doi.org/10.3390/biomedinformatics1020004
Li X, Rai SN, Rouchka EC, O’Toole TE, Cooper NGF. Adjusted Sample Size Calculation for RNA-seq Data in the Presence of Confounding Covariates. BioMedInformatics. 2021; 1(2):47-63. https://doi.org/10.3390/biomedinformatics1020004
Chicago/Turabian StyleLi, Xiaohong, Shesh N. Rai, Eric C. Rouchka, Timothy E. O’Toole, and Nigel G. F. Cooper. 2021. "Adjusted Sample Size Calculation for RNA-seq Data in the Presence of Confounding Covariates" BioMedInformatics 1, no. 2: 47-63. https://doi.org/10.3390/biomedinformatics1020004
APA StyleLi, X., Rai, S. N., Rouchka, E. C., O’Toole, T. E., & Cooper, N. G. F. (2021). Adjusted Sample Size Calculation for RNA-seq Data in the Presence of Confounding Covariates. BioMedInformatics, 1(2), 47-63. https://doi.org/10.3390/biomedinformatics1020004







