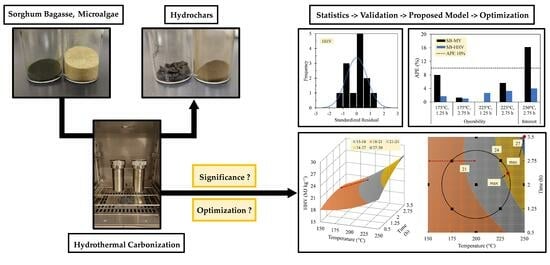
Significance and Optimization of Operating Parameters in Hydrothermal Carbonization Using RSM–CCD
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Hydrothermal Carbonization Experiment
2.3. Data Analysis
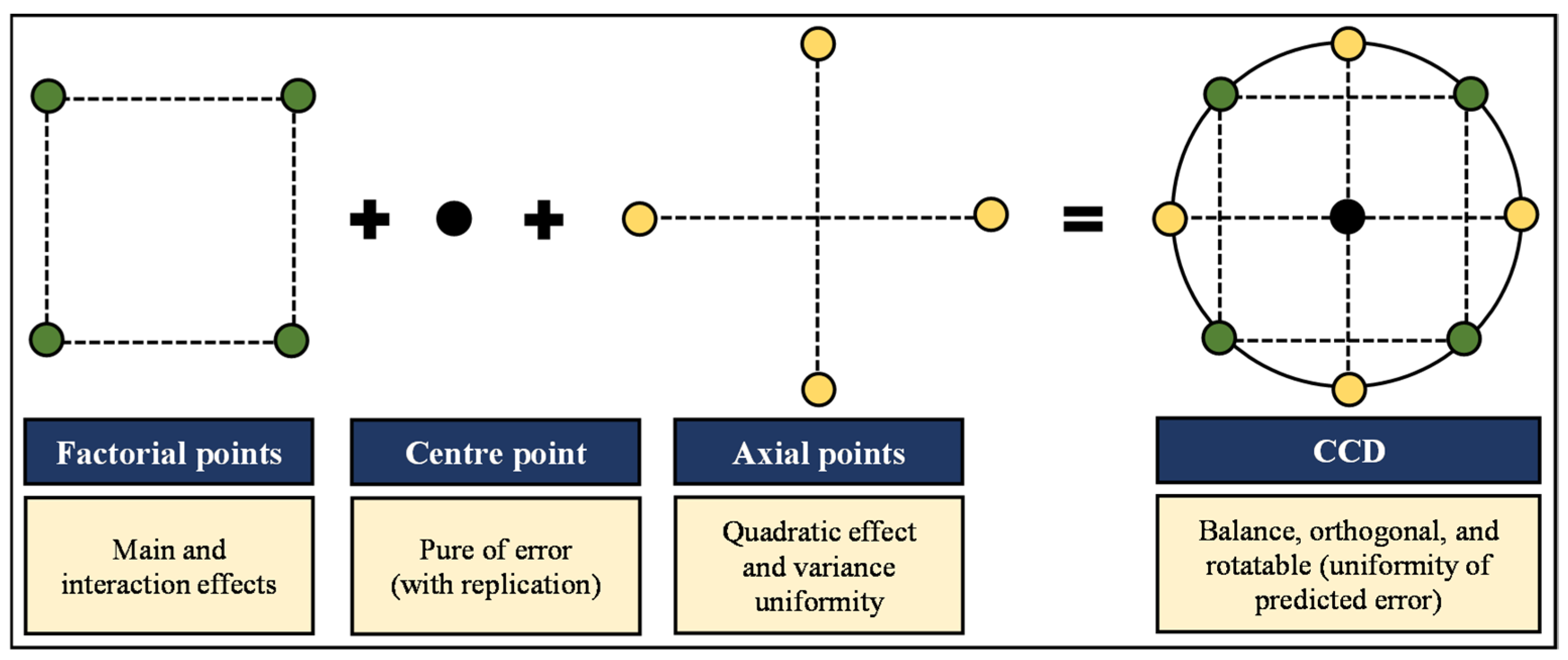
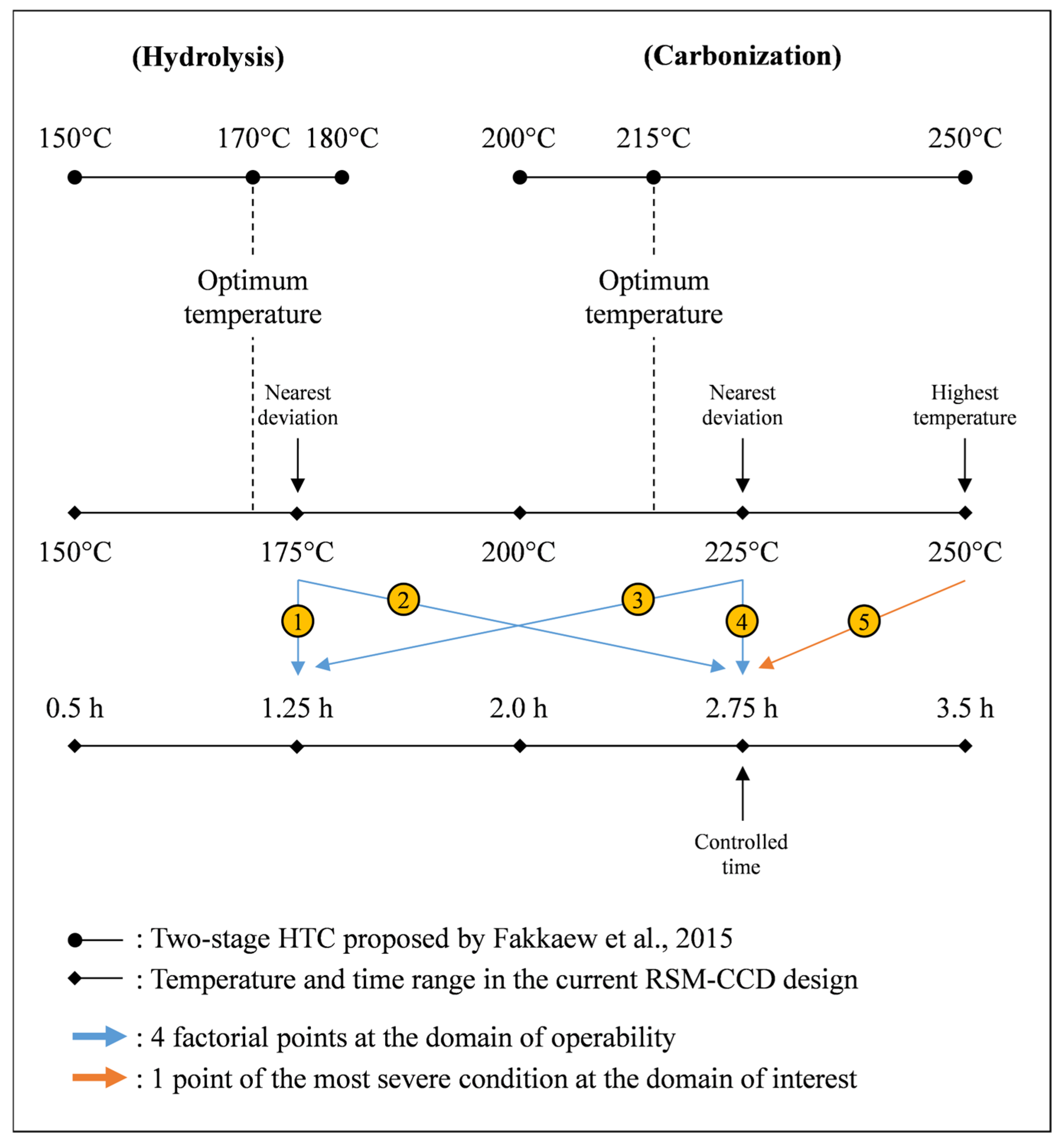
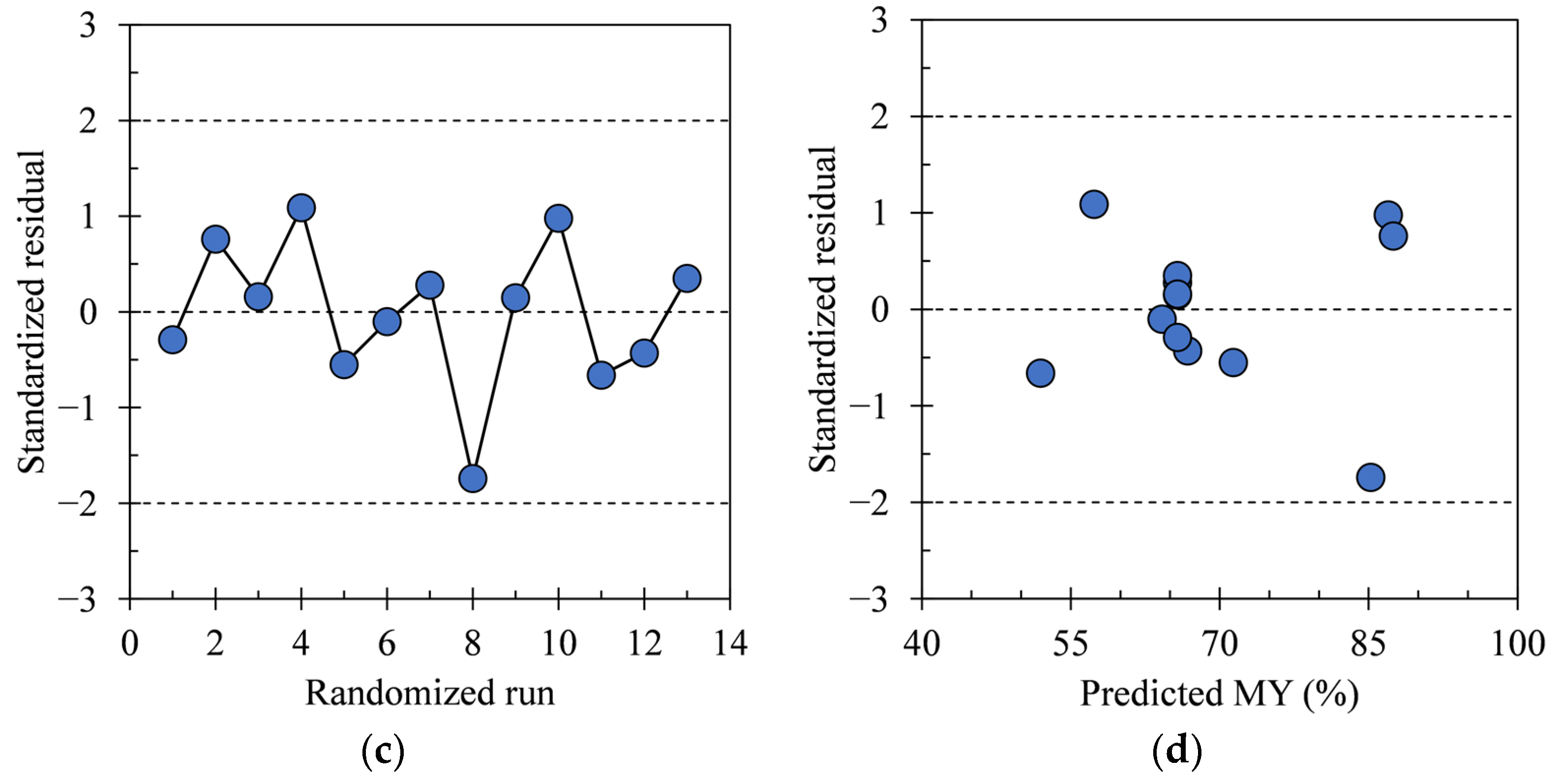
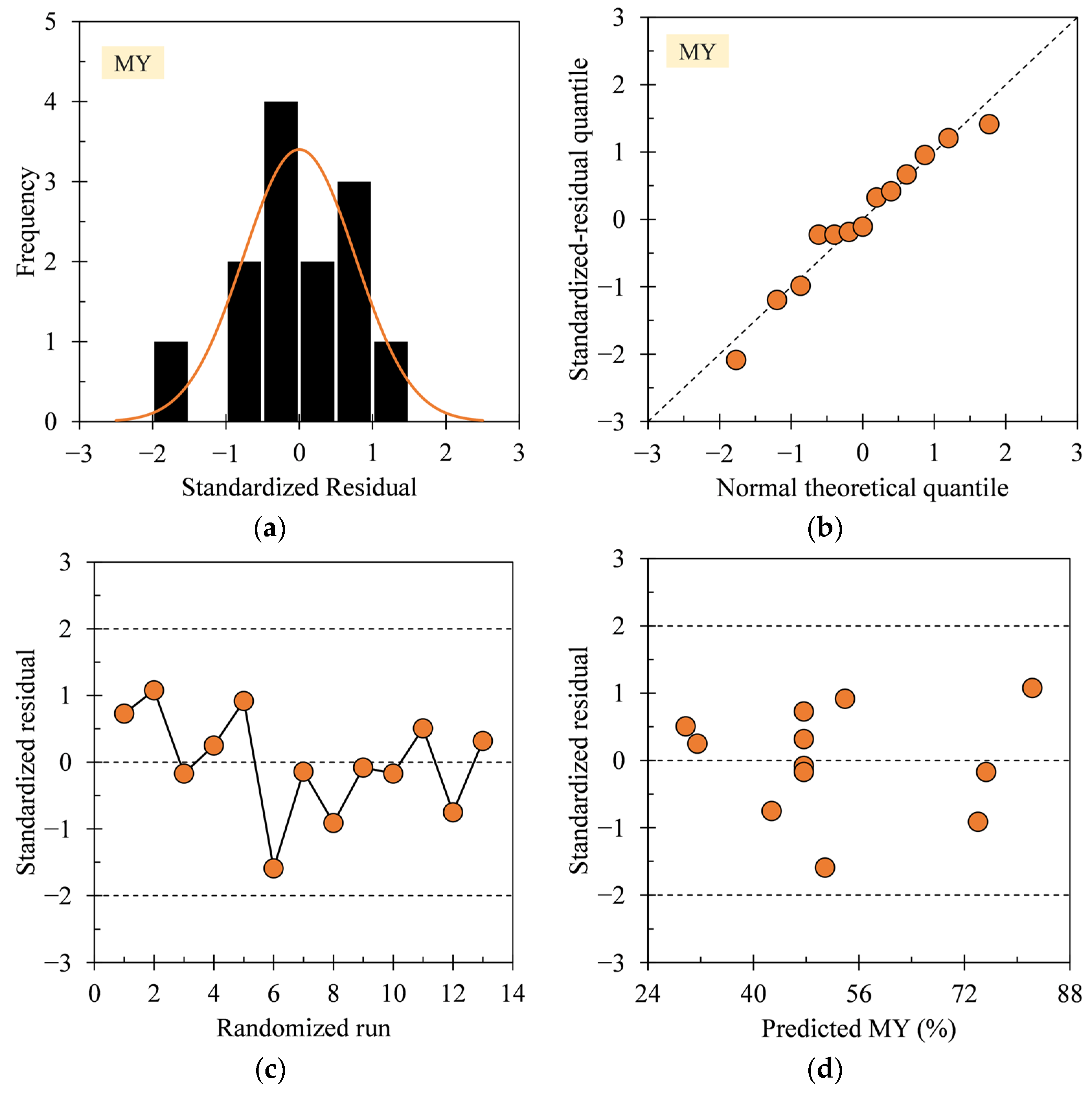
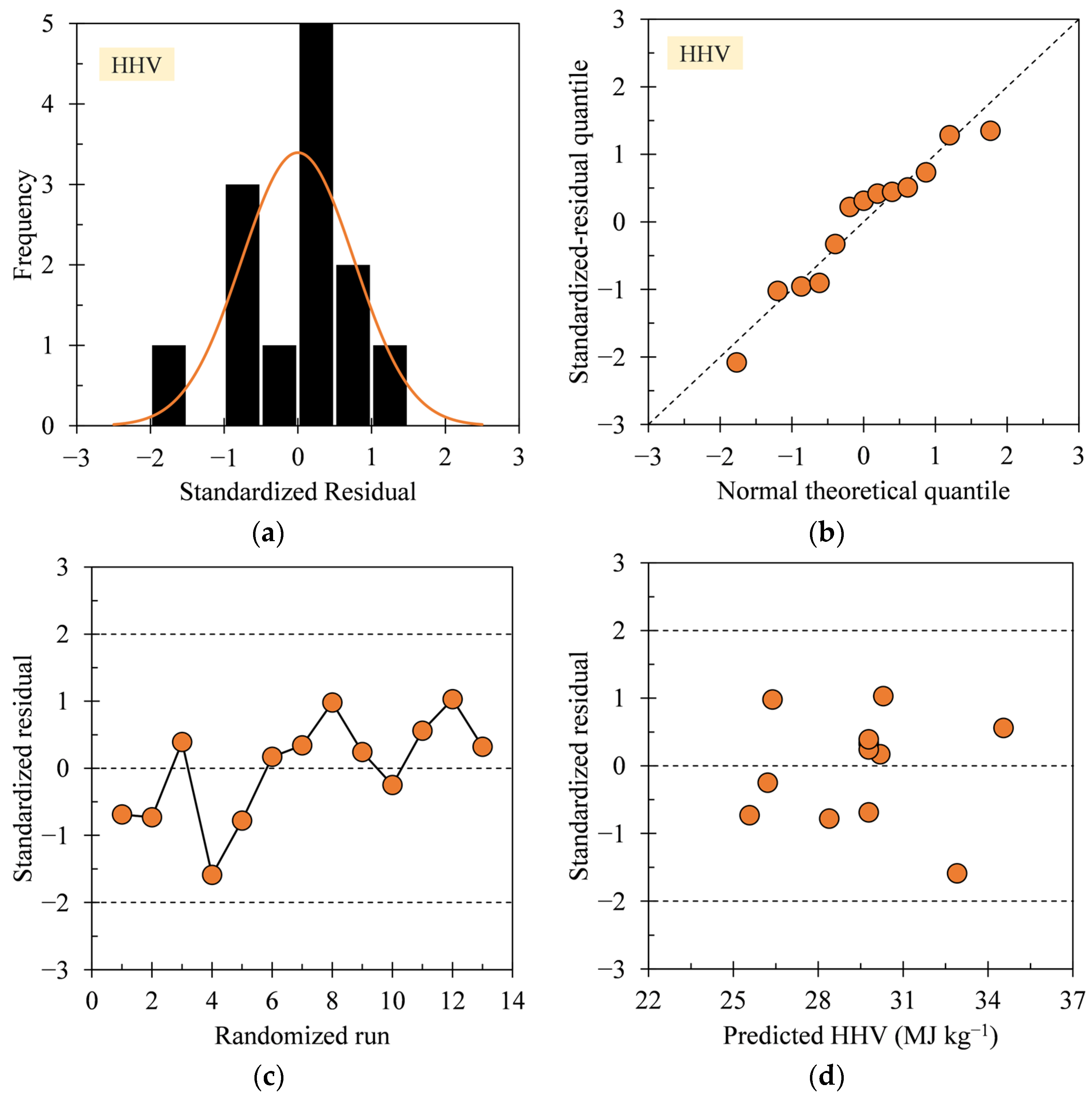
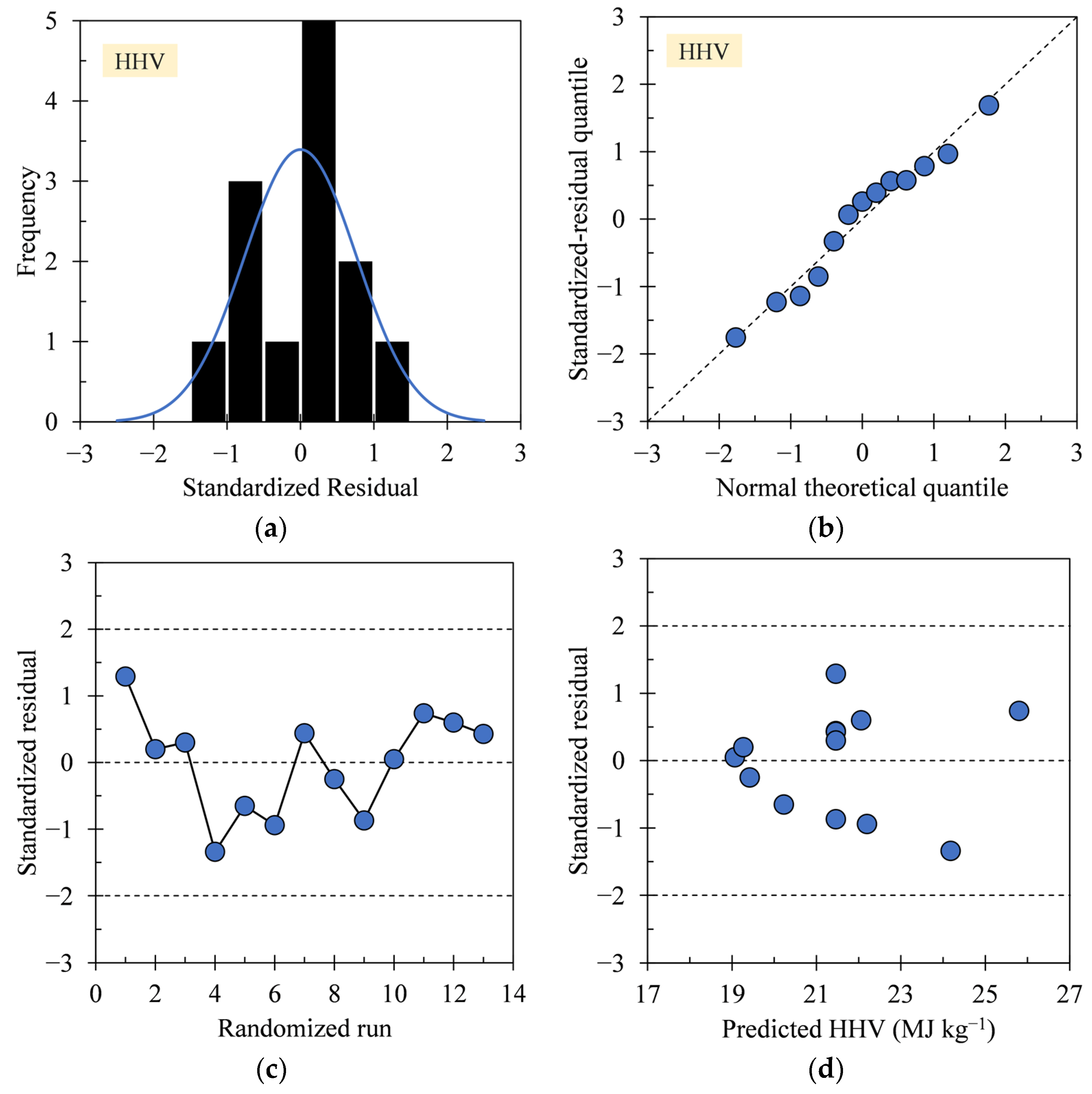
2.4. Experimental Design and Diagnostic Test
2.5. Data Validation
2.6. Optimum Conditions
3. Results and Discussion
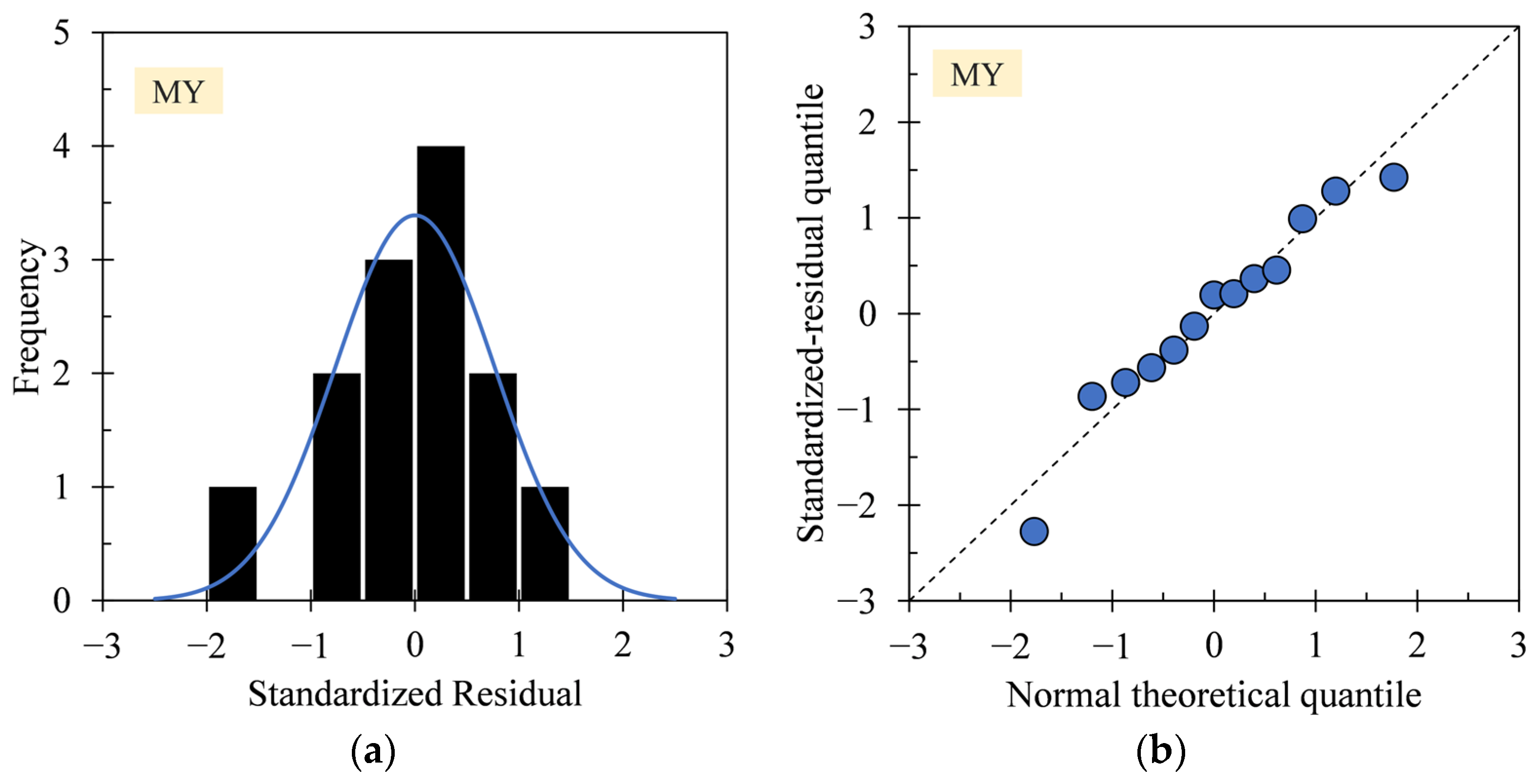
3.1. Regression Model Diagnosis
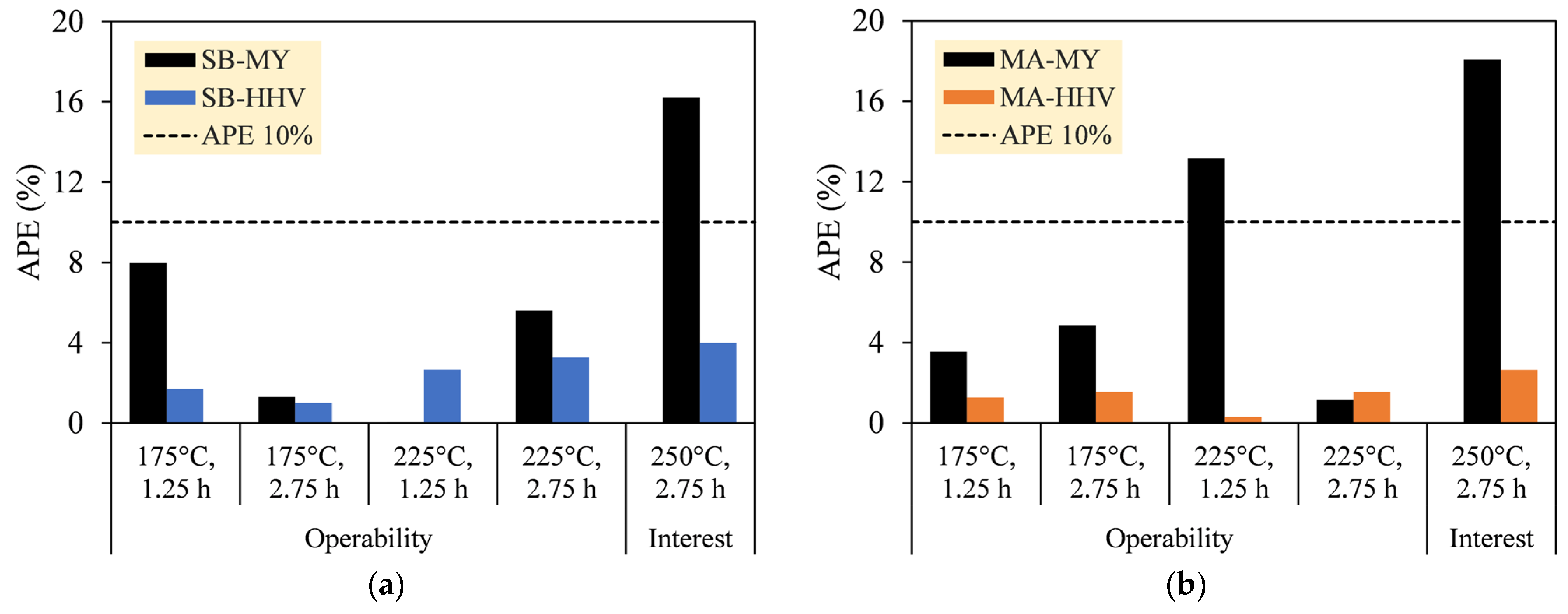
3.2. Data Validation
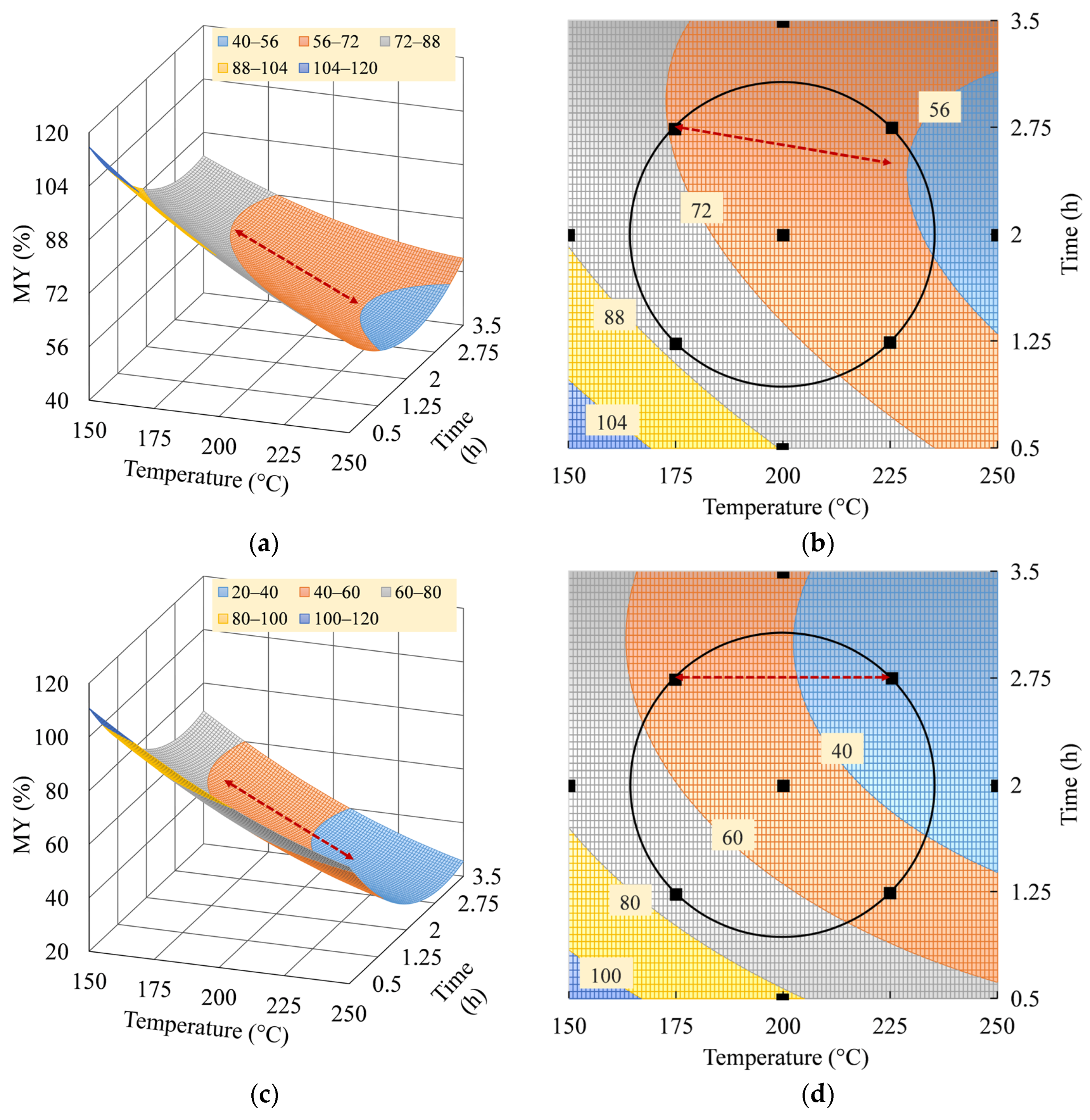
3.3. Interpretation of MY Model
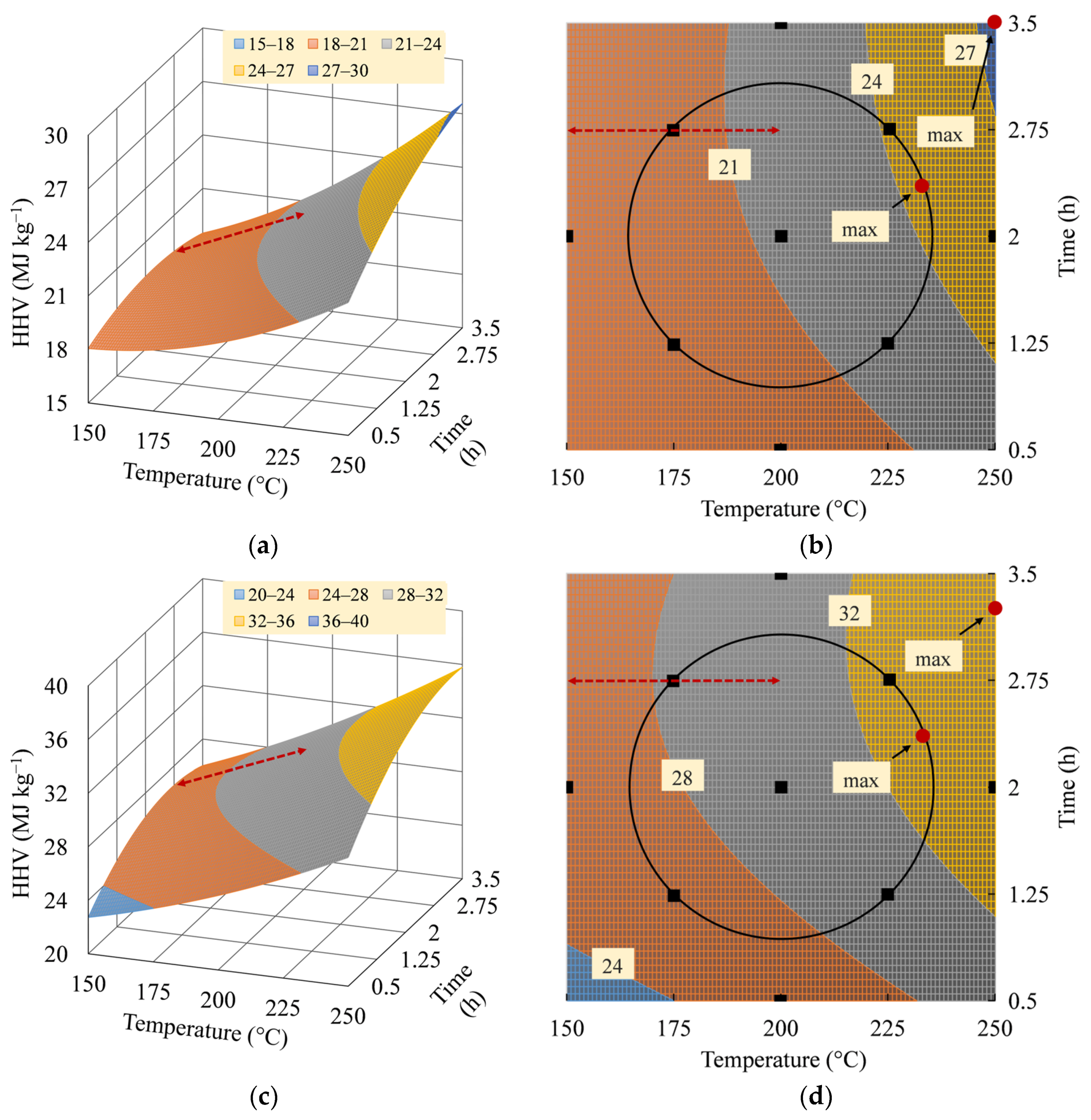
3.4. Interpretation of HHV Model
3.5. Optimum Operating Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wang, T.; Zhai, Y.; Zhu, Y.; Li, C.; Zeng, G. A review of hydrothermal carbonization of biomass waste for hydrochar formation: Process conditions, fundamentals, and physicochemical properties. Renew. Sustain. Energy Rev. 2018, 90, 223–247. [Google Scholar] [CrossRef]
- Kannan, S.; Gariepy, Y.; Raghavan, G.S.V. Optimization and characterization of hydrochar produced from microwave hydrothermal carbonization of fish waste. Waste Manag. 2017, 65, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Boutaieb, M.; Guiza, M.; Roman, S.; Cano, B.L.; Nogales, S.; Ouderni, A. Hydrothermal carbonization as a preliminary step to pine cone pyrolysis for bioenergy production. C. R. Chim. 2020, 23, 607–621. [Google Scholar] [CrossRef]
- Shen, Y. A review on hydrothermal carbonization of biomass and plastic waste to energy products. Biomass Bioenergy 2020, 134, 105479. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, S.; Wang, B.; Wang, Q.; Yang, G.; Chen, J. Effect of residence time on hydrothermal carbonization of corn cob residual. BioResources 2015, 10, 3979–3986. [Google Scholar] [CrossRef]
- Savage, P.E. Organic chemical reactions in supercritical water. Chem. Rev. 1999, 99, 603–622. [Google Scholar] [CrossRef]
- Perez, D.L.; Mayanga, P.C.T.; Abaide, E.R.; Zabot, G.L.; Castilhos, F.D. Hydrothermal carbonization and liquefaction: Differences, progress, challenges, and opportunities. Bioresour. Technol. 2022, 343, 126084. [Google Scholar]
- Cao, Z.; Hulsemann, B.; Wust, D.; Oechsner, H.; Lautenbach, A.; Kruse, A. Effect of residence time during hydrothermal carbonization of biogas digestate on the combustion characteristics of hydrochar and the biogas production of process water. Bioresour. Technol. 2021, 333, 125110. [Google Scholar] [CrossRef]
- Mariyam, S.; Alherbawi, M.; Pradhan, S.; Al-Ansari, T.; McKay, G. Biochar yield prediction using response surface methodology: Effect of fixed carbon and pyrolysis operating conditions. Biomass Convers. Biorefin. 2023, 2023, 1–14. [Google Scholar] [CrossRef]
- Xing, J.; Luo, K.; Wang, H.; Gao, Z.; Fan, J. A comprehensive study on estimating higher heating value of biomass from proximate and ultimate analysis with machine learning approaches. Energy 2019, 188, 116077. [Google Scholar] [CrossRef]
- McKendry, P. Energy production from biomass (part 1): Overview of biomass. Bioresour. Technol. 2002, 83, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Prins, M.J.; Ptasinski, K.J.; Janssen, F.J.J.G. From coal to biomass gasification: Comparison of thermodynamic efficiency. Energy 2007, 32, 1248–1259. [Google Scholar] [CrossRef]
- Tahir, M.H.; Zhao, Z.; Ren, J.; Naqvi, M.; Ahmed, M.S.; Shah, T.U.H.; Shen, B.; Elkamel, A.; Irfan, R.M.; Rahman, A.U. Fundamental investigation of the effect of functional groups on the variations of higher heating value. Fuel 2019, 253, 881–886. [Google Scholar] [CrossRef]
- Khunphakdee, P.; Korkerd, K.; Soanuch, C.; Chalermsinsuwan, B. Data-driven correlations of higher heating value for biomass, waste and their combination based on their elemental compositions. Energy Rep. 2022, 8, 36–42. [Google Scholar] [CrossRef]
- Trutna, L.; Spagon, P.; Castillo, E.D.; Moore, T.; Hartley, S.; Hurwitz, A. Chapter 5: Process improvement. In NIST/SEMATECH Engineering Statistics Handbook; Tobias, P., Trutna, L., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2003. [Google Scholar]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Sahoo, P.; Barman, T.K. 5—ANN modelling of fractal dimension in machining. In Mechatronics and Manufacturing Engineering; Davim, J.P., Ed.; Woodhead Publishing: Cambridge, UK, 2012; pp. 159–226. [Google Scholar]
- Arif, A.B.; Budiyanto, A.; Diyono, W.; Hayuningtyas, M.; Marwati, T.; Sasmitaloka, K.S.; Richana, N. Bioethanol production from sweet sorghum bagasse through enzymatic process. IOP Conf. Ser. Earth Environ. Sci. 2019, 309, 012033. [Google Scholar] [CrossRef]
- Wahyono, T.; Firsoni, F. The changes of nutrient composition and in vitro evaluation on gamma irradiated sweet sorghum bagasse. Sci. J. Appl. Isot. Radiat. 2016, 12, 69–77. [Google Scholar] [CrossRef][Green Version]
- Cabrita, A.R.J.; Fernandes, J.G.; Valente, I.M.; Almeida, A.; Lima, S.A.C.; Fonseca, A.J.M.; Maia, M.R.G. Nutritional composition and untargeted metabolomics reveal the potential of Tetradesmus obliquus, Chlorella vulgaris and Nannochloropsis oceanica as valuable nutrient sources for dogs. Animals 2022, 12, 2643. [Google Scholar] [CrossRef]
- Coelho, D.; Pestana, J.; Almeida, J.M.; Alfaia, C.M.; Fontes, C.M.G.A.; Moreira, O.; Prates, J.A.M. A high dietary incorporation level of Chlorella vulgaris improves the nutritional value of pork fat without impairing the performance of finishing pigs. Animals 2020, 10, 2384. [Google Scholar] [CrossRef]
- Queiroz, V.A.V.; Silva, C.S.D.; Menezes, C.B.D.; Schaffert, R.E.; Guimaraes, F.F.M.; Guimaraes, L.J.M.; Guimaraes, P.E.D.P.; Tardin, F.D. Nutritional composition of sorghum [Sorghum biocolor (L.) Moench] genotypes cultivated without and with water stress. J. Cereal Sci. 2015, 65, 103–111. [Google Scholar] [CrossRef]
- Gaxiola, J.E.B.; Ross, A.B.; Dupont, V. Multi-variate and multi-response analysis of hydrothermal carbonization of food waste: Hydrochar composition and solid fuel characteristics. Energies 2022, 15, 5342. [Google Scholar] [CrossRef]
- Sarstedt, M.; Mooi, E. Regression analysis. In A Concise Guide to Market Research; Springer: Berlin, Germany, 2014; pp. 193–233. [Google Scholar]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peer J. Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- University of Texas. Available online: https://web.ma.utexas.edu/users/m408m/Display14-8.shtml (accessed on 25 December 2022).
- Vadlamani, S.K.; Xiao, T.P.; Yablonovitch, E. Physics successfully implements Lagrange multiplier optimization. Proc. Natl. Acad. Sci. USA 2020, 117, 26639–26650. [Google Scholar] [CrossRef] [PubMed]
- Forthofer, R.N.; Lee, E.S.; Hernandez, M. 13–Linear regression. In Biostatistics, 2nd ed.; Forthofer, R.N., Lee, E.S., Hernandez, M., Eds.; Academic Press: Burlington, NJ, USA, 2007; pp. 349–386. [Google Scholar]
- Yang, H. Visual assessment of residual plots in multiple linear regression: A model-based simulation perspective. Mult. Linear Regres. Viewp. 2012, 38, 24–37. [Google Scholar]
- Eric, S. An introduction to graphical analysis of residual scores and outlier detection in bivariate least squares regression analysis. In Proceedings of the Annual Meeting of the Southwest Educational Research Association, New Orleans, LA, USA, 25 January 1996. [Google Scholar]
- Lewis, C.D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting; Butterworth Scientific: London, UK, 1982. [Google Scholar]
- Moller, M.; Nilges, P.; Harnisch, F.; Schroder, U. Subcritical water as reaction environment: Fundamentals of hydrothermal biomass transformation. ChemSusChem 2011, 4, 566–579. [Google Scholar] [CrossRef]
- Funke, A.; Ziegler, F. Hydrothermal carbonization of biomass: A summary and discussion of chemical mechanism for process engineering. Biofuels Bioprod. Biorefin. 2010, 4, 160–177. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Xiao, K.; Liu, X.; Hu, H.; Li, X.; Yao, H. Correlations between the physicochemical properties of hydrochar and specific components of waste lettuce: Influence of moisture, carbohydrates, proteins, and lipids. Bioresour. Technol. 2019, 272, 482–488. [Google Scholar] [CrossRef]
- Xiao, K.; Liu, H.; Li, Y.; Yi, L.; Zhang, X.; Hu, H.; Yao, H. Correlations between hydrochar properties and chemical constitution of orange peel waste during hydrothermal carbonization. Bioresour. Technol. 2018, 265, 432–436. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhan, H.; Song, Y.; He, C.; Huang, Y.; Yin, X.; Wu, C. Insights into the evolution of chemical structures in lignocellulose and non-lignocellulose biowastes during hydrothermal carbonization (HTC). Fuel 2019, 236, 960–974. [Google Scholar] [CrossRef]
- Saha, S.; Islam, M.T.; Calhoun, J.; Reza, T. Effect of hydrothermal carbonization on fuel and combustion properties of shrimp shell waste. Energies 2023, 16, 5534. [Google Scholar] [CrossRef]
- Smith, A.M.; Singh, S.; Ross, A.B. Fate of inorganic material during hydrothermal carbonisation of biomass: Influence of feedstock on combustion behaviour of hydrochar. Fuel 2016, 169, 135–145. [Google Scholar] [CrossRef]
- Demirbas, A.; Al-Ghamdi, K. Relationships between specific gravities and higher heating values of petroleum components. Pet. Sci. Technol. 2015, 33, 732–740. [Google Scholar] [CrossRef]
- Sarikoc, S. Fuels of the diesel-gasoline engines and their properties. In Diesel and Gasoline Engines; Viskup, R., Ed.; IntechOpen: London, UK, 2020. [Google Scholar]
- Gong, C.; Huang, J.; Feng, C.; Wang, G.; Tabil, L.; Wang, D. Effects and mechanism of ball milling on torrefaction of pine sawdust. Bioresour. Technol. 2016, 214, 242–247. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Balasubramanian, R.; Srinivasan, M.P. Hydrothermal conversion of biomass waste to activated carbon with high porosity: A review. Chem. Eng. J. 2016, 283, 789–805. [Google Scholar] [CrossRef]
- Fakkaew, K.; Koottatep, T.; Polprasert, C. Effects of hydrolysis and carbonization reactions on hydrochar production. Bioresour. Technol. 2015, 192, 328–334. [Google Scholar] [CrossRef]



| Biomass | Carbohydrate (%) 1 | Protein (%) | Lipid (%) | Fiber (%) 2 | Ash (%) | Reference |
|---|---|---|---|---|---|---|
| SB | 23.09 | 2.05 | 0.90 | 63.93 | 0.11 | [18] |
| 5.20 | 5.40 | 1.85 | 79.10 | 8.45 | [19] | |
| MA | 20.02 | 43.90 | 9.79 | 16.40 | 9.89 | [20] |
| 35.62 | 42.80 | 8.73 | 1.05 | 11.80 | [21] |
| Factor | Symbol | Coded and Un-Coded Factor Level | ||||
|---|---|---|---|---|---|---|
| −2 (−α) | −1 | 0 | 1 | 2 (α) | ||
| Temperature (°C) | x1 | 150 | 175 | 200 | 225 | 250 |
| Residence time (h) | x2 | 0.50 | 1.25 | 2.00 | 2.75 | 3.50 |
| Factor (x) | Response (y) | Remark | ||||
|---|---|---|---|---|---|---|
| MY (%) | HHV (MJ kg−1) | |||||
| x1 | x2 | SB | MA | SB | MA | |
| −1 | −1 | 79.49 | 71.13 | 19.33 | 26.62 | Factorial point |
| 1 | −1 | 63.88 | 45.78 | 21.87 | 30.23 | Factorial point |
| −1 | 1 | 69.55 | 56.82 | 20.00 | 28.20 | Factorial point |
| 1 | 1 | 60.94 | 32.27 | 23.71 | 32.53 | Factorial point |
| −2 | 0 | 90.23 | 74.71 | 19.09 | 26.15 | Axial point |
| 2 | 0 | 49.80 | 31.32 | 26.06 | 34.68 | Axial point |
| 0 | −2 | 89.98 | 85.75 | 19.34 | 25.39 | Axial point |
| 0 | 2 | 65.37 | 40.34 | 22.27 | 30.55 | Axial point |
| 0 | 0 | 66.69 | 47.18 | 21.61 | 29.86 | Center point |
| 0 | 0 | 66.91 | 48.66 | 21.61 | 29.86 | Center point |
| 0 | 0 | 66.27 | 47.37 | 21.15 | 29.84 | Center point |
| 0 | 0 | 66.30 | 47.09 | 21.57 | 29.87 | Center point |
| 0 | 0 | 64.80 | 49.97 | 21.91 | 29.61 | Center point |
| Source | Response (y) | F-Ratio | p-Value | R2 | |||
|---|---|---|---|---|---|---|---|
| SB | MA | SB | MA | SB | MA | ||
| Model | MY | 26.49 | 59.78 | 0.00 * | 0.00 * | 0.950 | 0.977 |
| HHV | 70.22 | 261.73 | 0.00 * | 0.00 * | 0.980 | 0.995 | |
| Response (y) | Factor System | Coefficient (β) | p-Value | Collinearity (VIF) | |||
|---|---|---|---|---|---|---|---|
| SB | MA | SB | MA | SB | MA | ||
| MY | Intercept | β0: 65.76 | 47.63 | 0.00 * | 0.00 * | ||
| x1: Temperature | β1: −8.76 | −11.39 | 0.00 * | 0.00 * | 1.00 | 1.00 | |
| x2: Time | β2: −5.18 | −9.89 | 0.00 * | 0.00 * | 1.00 | 1.00 | |
| x12 | β11: 0.93 | 1.21 | 0.22 | 0.11 | 1.09 | 1.09 | |
| x22 | β22: 2.84 | 3.72 | 0.00 * | 0.00 * | 1.09 | 1.09 | |
| x1x2 | β12: 1.75 | 0.20 | 0.32 | 0.90 | 1.00 | 1.00 | |
| HHV | Intercept | 21.46 | 29.78 | 0.00 * | 0.00 * | ||
| x1: Temperature | 1.68 | 2.08 | 0.00 * | 0.00 * | 1.00 | 1.00 | |
| x2: Time | 0.70 | 1.18 | 0.00 * | 0.00 * | 1.00 | 1.00 | |
| x12 | 0.24 | 0.15 | 0.01 * | 0.02 * | 1.09 | 1.09 | |
| x22 | −0.20 | −0.46 | 0.03 * | 0.00 * | 1.09 | 1.09 | |
| x1x2 | 0.29 | 0.18 | 0.14 | 0.18 | 1.00 | 1.00 | |
| Sample | Factor (x) | MY (%) | HHV (MJ kg−1) | Remark | |||
|---|---|---|---|---|---|---|---|
| x1 | x2 | Observation | Prediction | Observation | Prediction | ||
| SB | −1 | −1 | 78.93 | 85.22 | 19.75 | 19.41 | Operability |
| −1 | 1 | 70.44 | 71.36 | 20.44 | 20.23 | ||
| 1 | −1 | 64.17 | 64.20 | 21.62 | 22.19 | ||
| 1 | 1 | 60.75 | 57.34 | 23.40 | 24.17 | ||
| 2 | 1 | 45.71 | 53.12 | 27.98 | 26.86 | Interest | |
| MA | −1 | −1 | 71.51 | 74.04 | 26.73 | 26.39 | Operability |
| −1 | 1 | 56.60 | 53.86 | 27.96 | 28.39 | ||
| 1 | −1 | 44.94 | 50.86 | 30.28 | 30.19 | ||
| 1 | 1 | 31.12 | 31.48 | 32.41 | 32.91 | ||
| 2 | 1 | 29.20 | 23.92 | 36.59 | 35.62 | Interest | |
| Factor and Response | Domain of Operability | Domain of Interest | ||
|---|---|---|---|---|
| SB | MA | SB | MA | |
| Temperature (°C) | 233.24 (1.33) 1 | 233.10 (1.32) | 250.00 (2.00) | 250.00 (2.00) |
| Residence time (h) | 2.36 (0.48) | 2.37 (0.50) | 3.50 (2.00) | 3.25 (1.67) |
| HHV (MJ kg−1) | 24.61 | 33.39 | 27.54 | 35.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luthfi, N.; Fukushima, T.; Wang, X.; Takisawa, K. Significance and Optimization of Operating Parameters in Hydrothermal Carbonization Using RSM–CCD. Thermo 2024, 4, 82-99. https://doi.org/10.3390/thermo4010007
Luthfi N, Fukushima T, Wang X, Takisawa K. Significance and Optimization of Operating Parameters in Hydrothermal Carbonization Using RSM–CCD. Thermo. 2024; 4(1):82-99. https://doi.org/10.3390/thermo4010007
Chicago/Turabian StyleLuthfi, Numan, Takashi Fukushima, Xiulun Wang, and Kenji Takisawa. 2024. "Significance and Optimization of Operating Parameters in Hydrothermal Carbonization Using RSM–CCD" Thermo 4, no. 1: 82-99. https://doi.org/10.3390/thermo4010007
APA StyleLuthfi, N., Fukushima, T., Wang, X., & Takisawa, K. (2024). Significance and Optimization of Operating Parameters in Hydrothermal Carbonization Using RSM–CCD. Thermo, 4(1), 82-99. https://doi.org/10.3390/thermo4010007