Numerical Evaluation of the Benefits Provided by the Ground Thermal Inertia to Urban Greenhouses
Abstract
:1. Introduction
2. Methodology
2.1. Greenhouse Characteristics
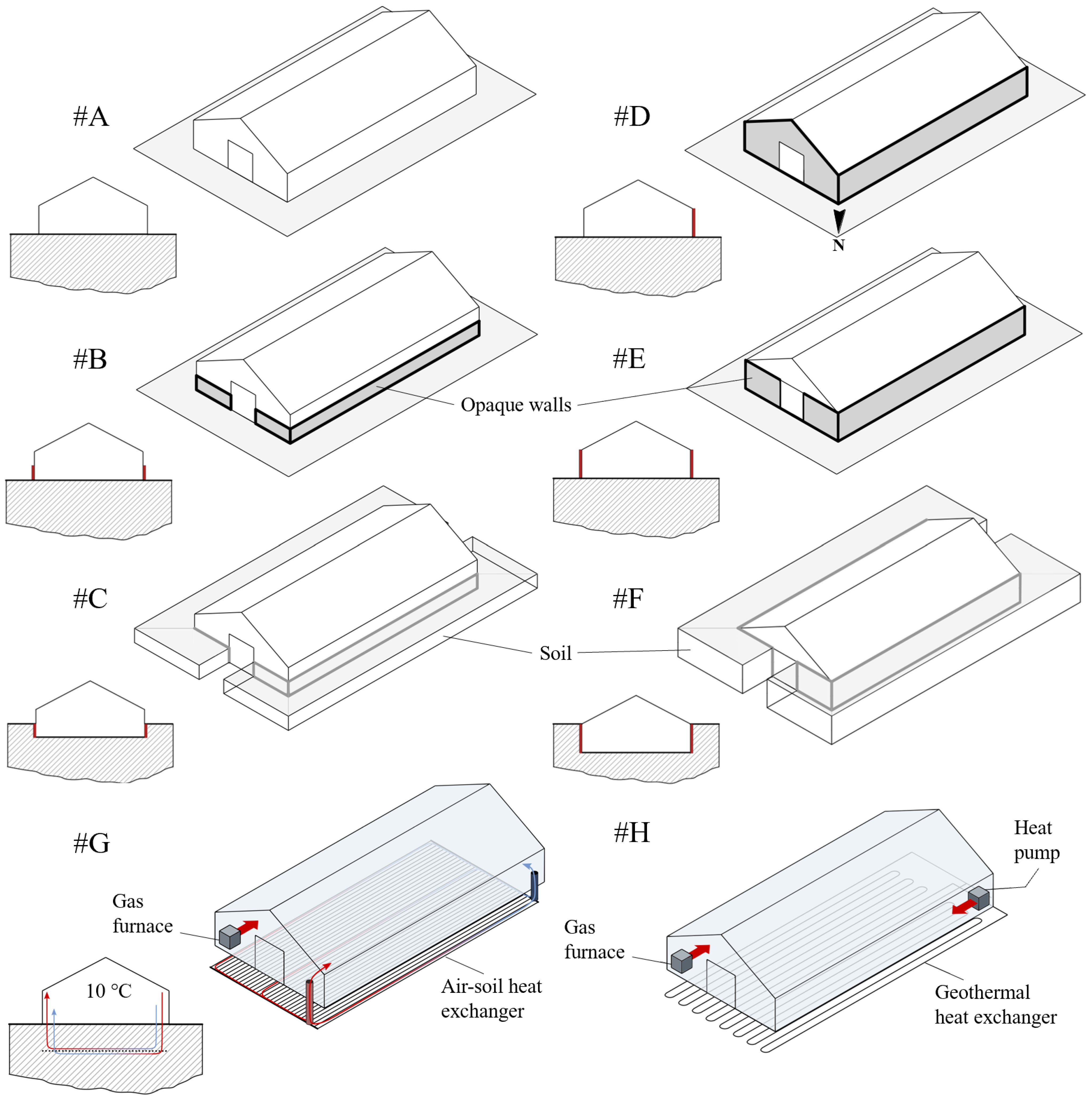
2.2. Scenarios Description
2.3. Greenhouse Model Description
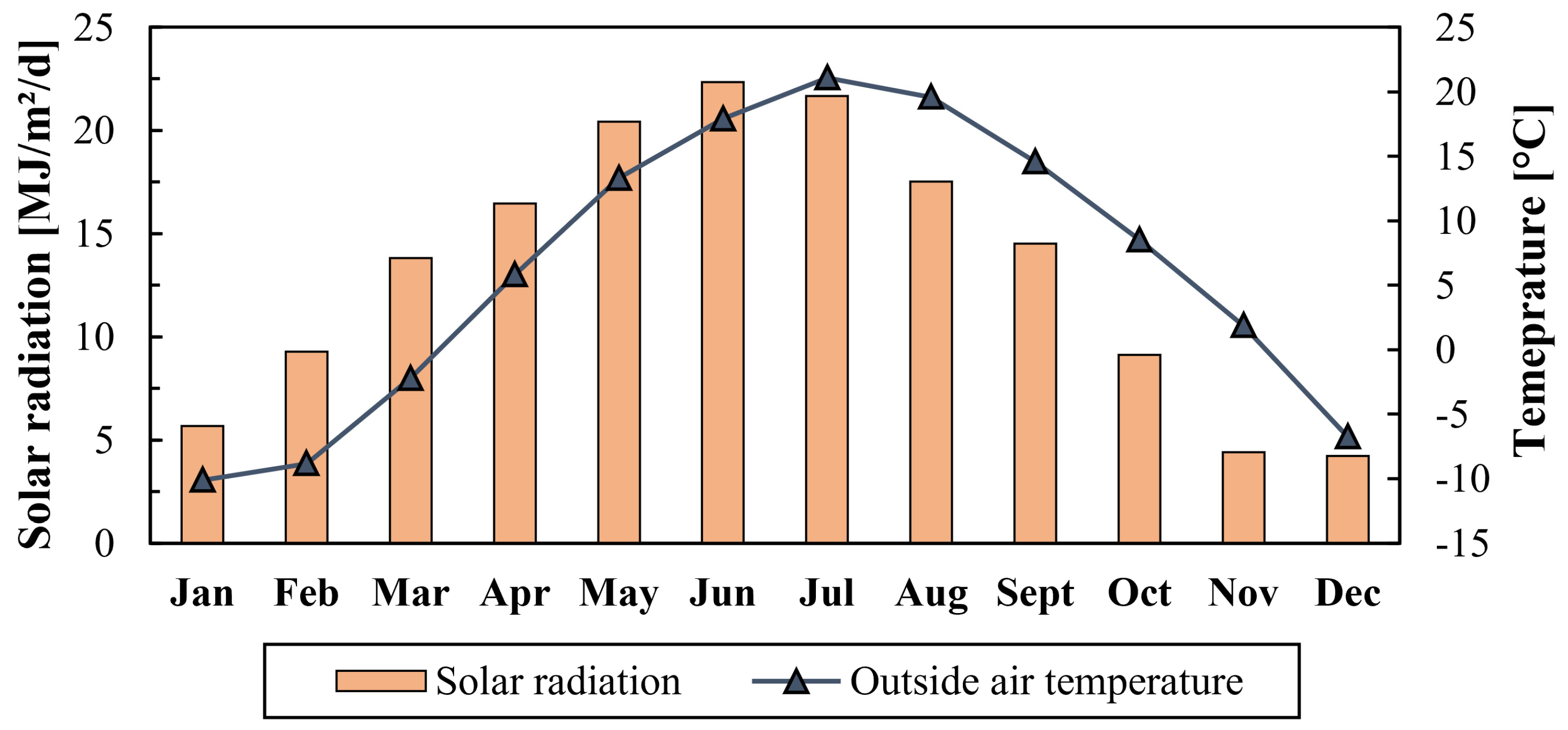
2.3.1. Weather Data
2.3.2. Envelope and Structure
2.3.3. Internal Loads
2.3.4. Control of Indoor Temperature Conditions and Natural Ventilation
2.3.5. Indoor Humidity Conditions
2.3.6. Lighting Control and Artificial Lighting
2.3.7. Modeling of the Evapotranspiration and Water Condensation
2.3.8. Soil Thermal Properties in All Scenarios
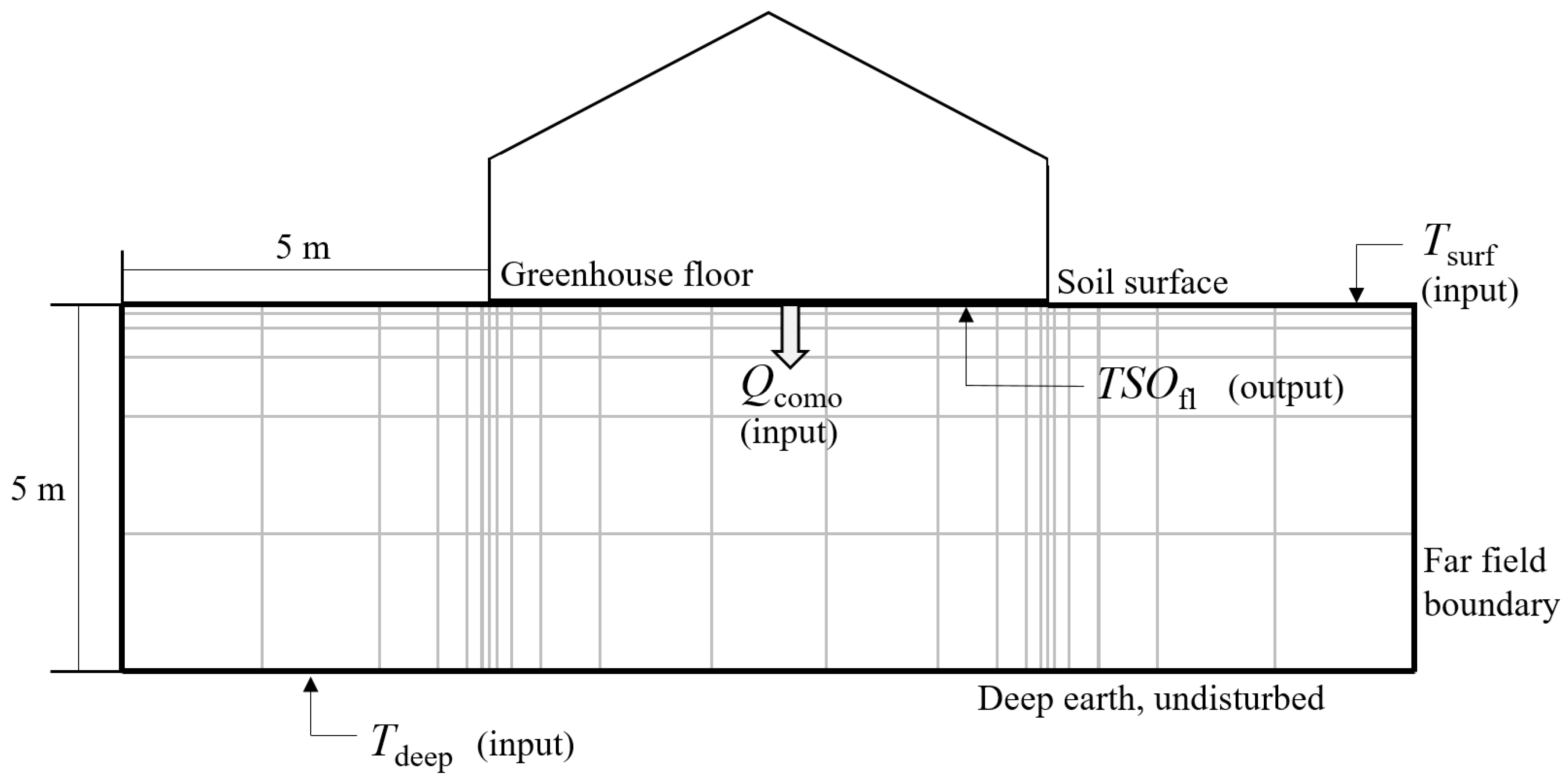
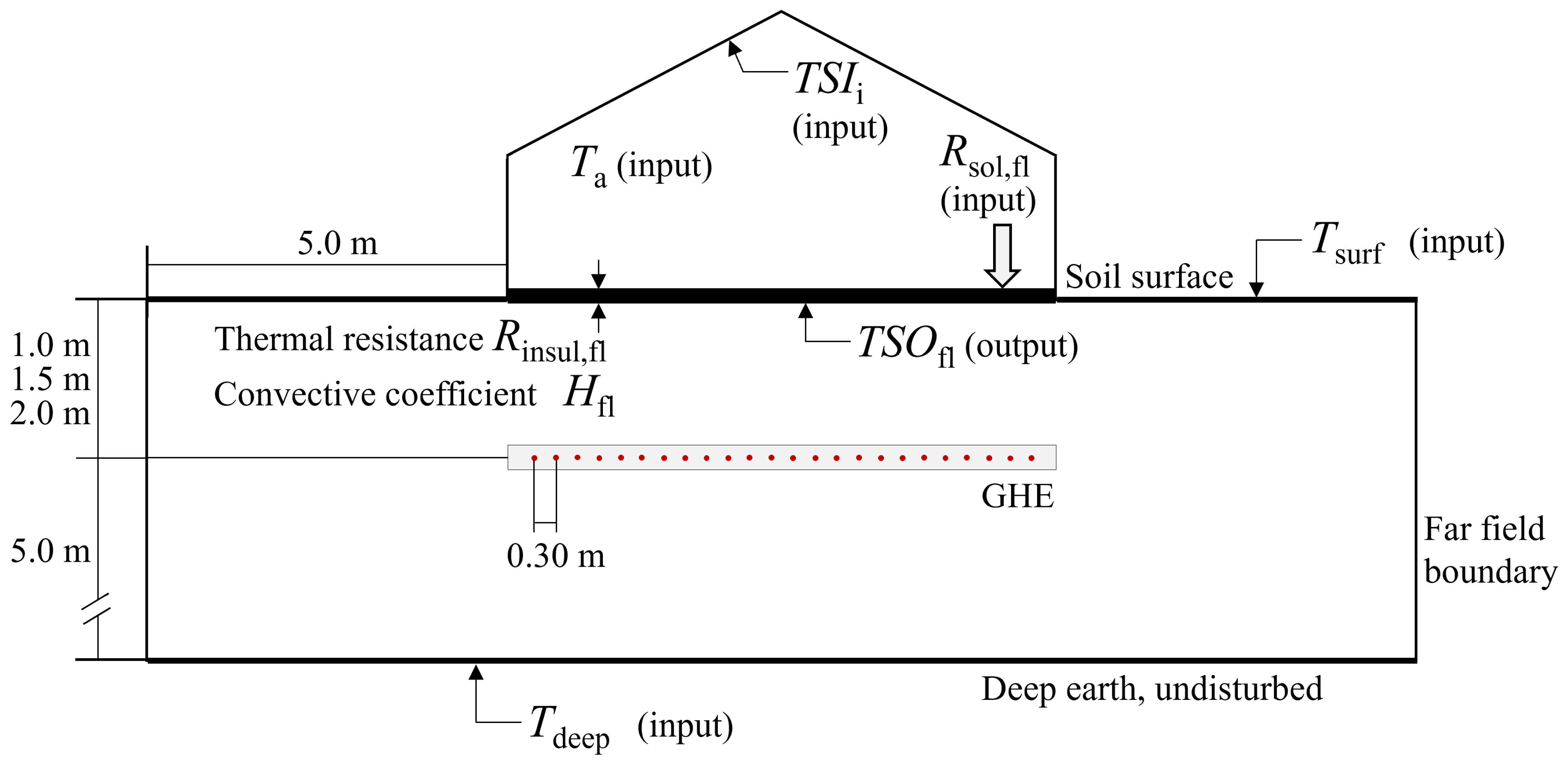
2.3.9. Modeling of the Ground and of the Interaction with the Greenhouse in Scenarios #A–F and #10 °C
2.3.10. Modeling of the ASHE and Its Interaction with the Greenhouse in Scenario #G
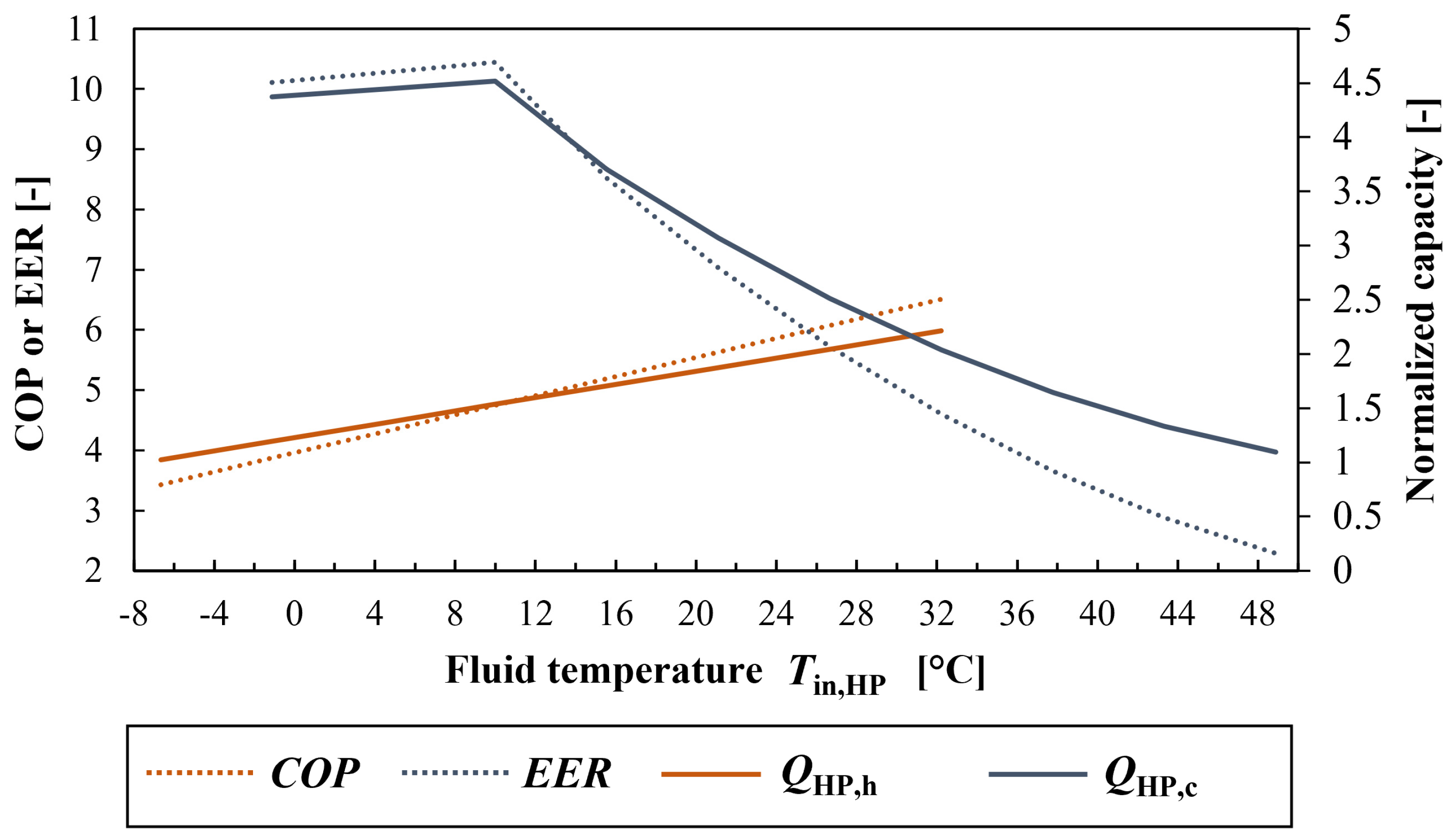
2.3.11. Modeling of the GHE, the HP, and Its Interaction with the Greenhouse in Scenario #H
2.4. Parametric Studies
3. Results
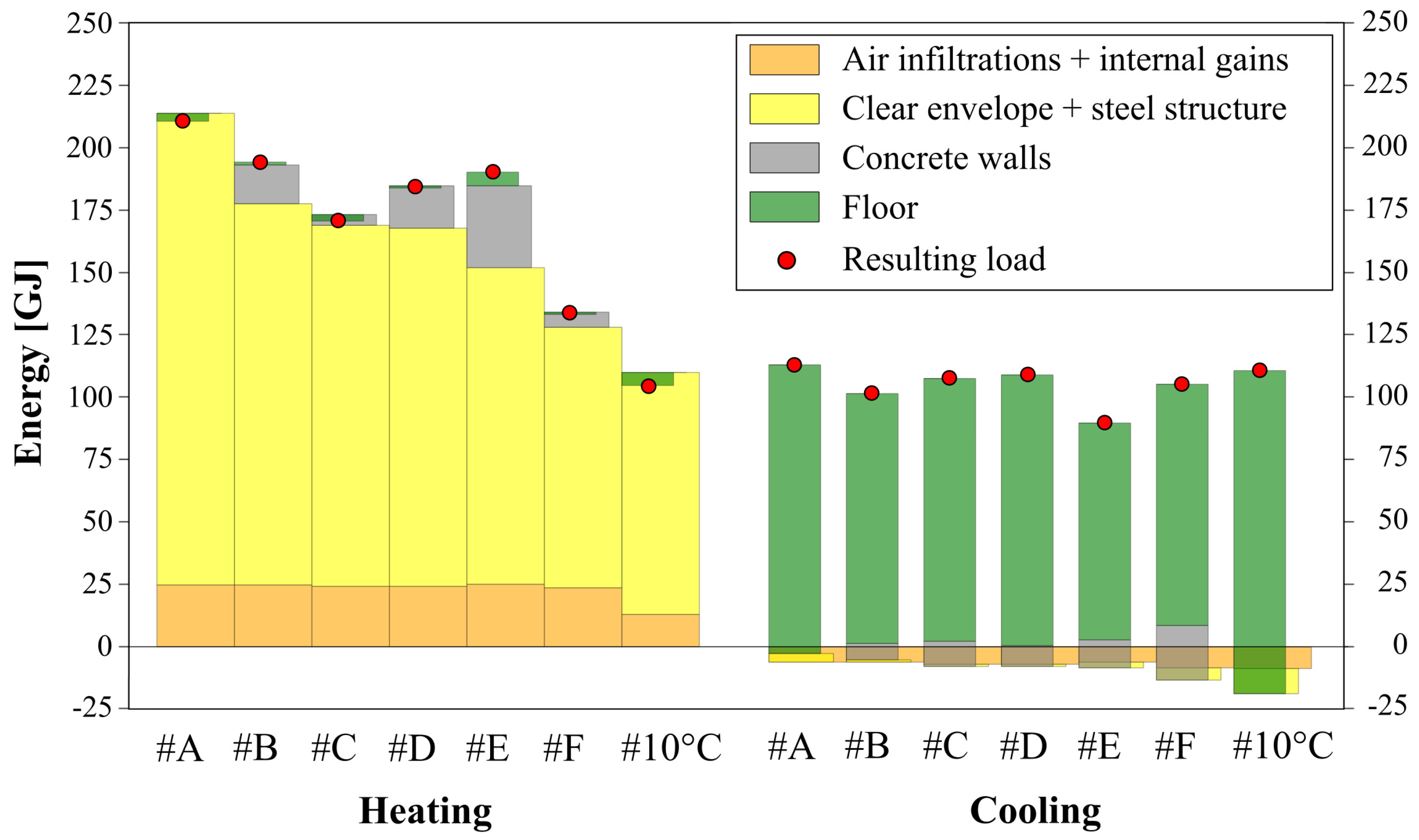
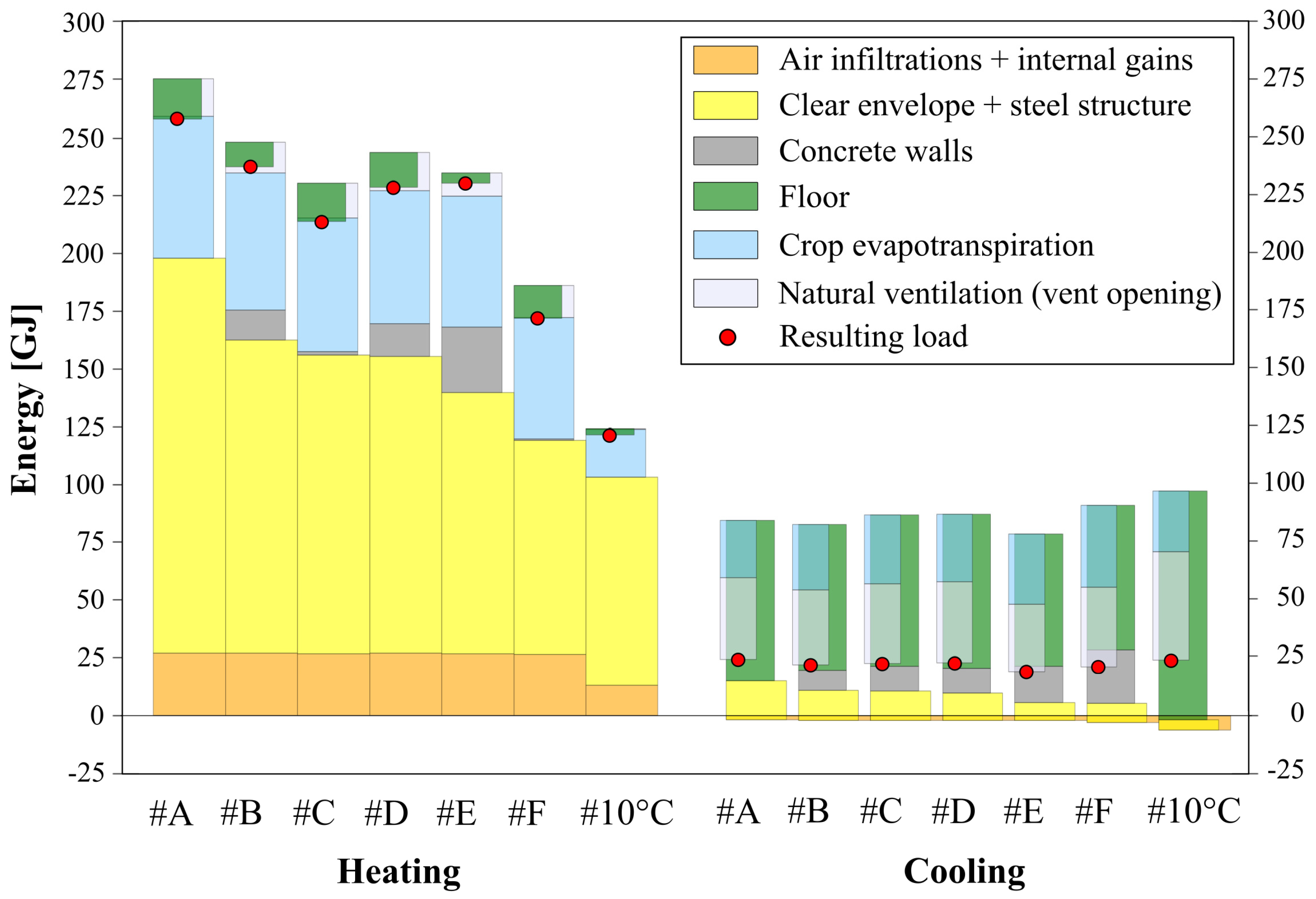
3.1. Energy Savings in Scenarios #A–F and #10 °C
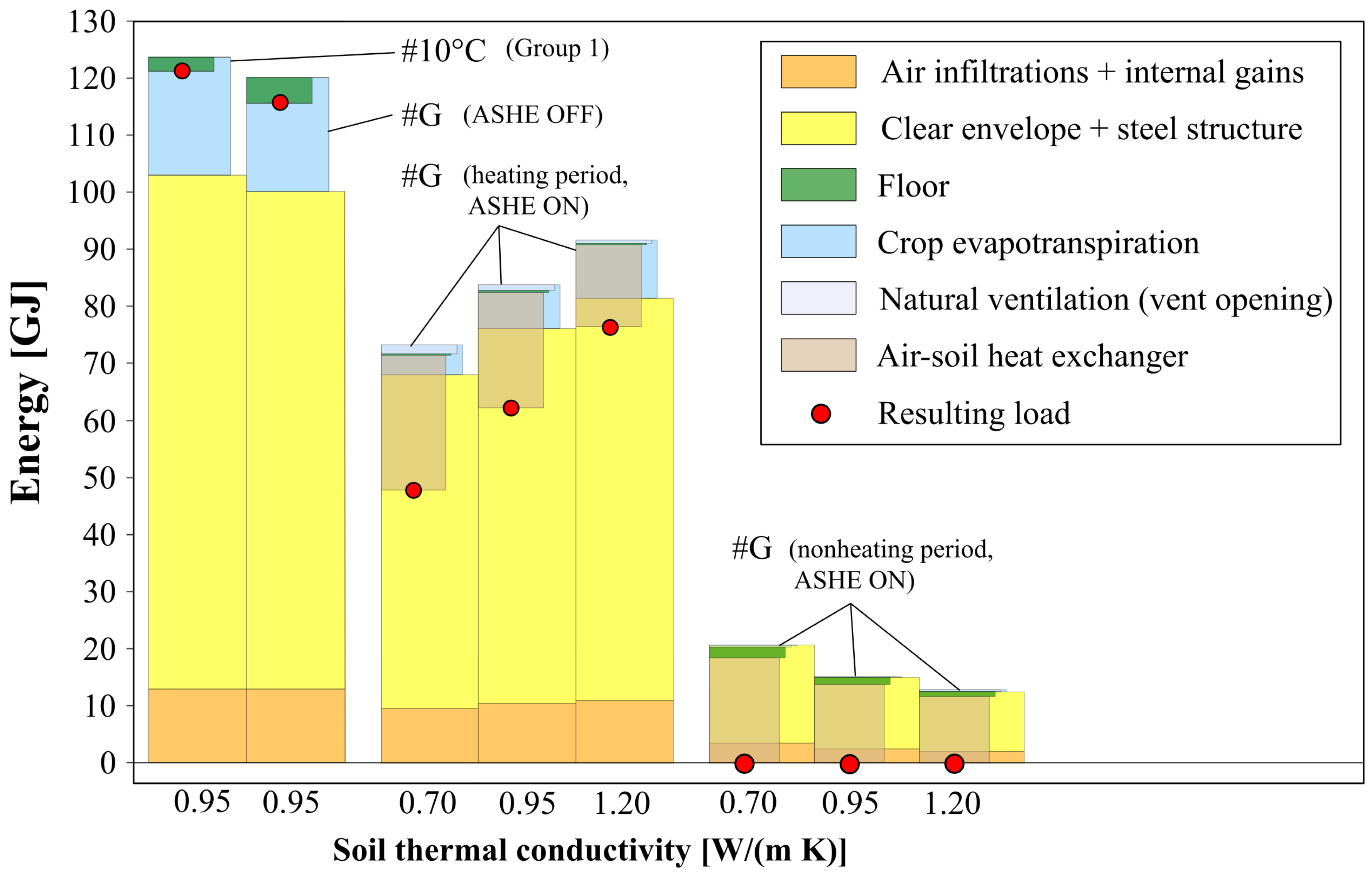
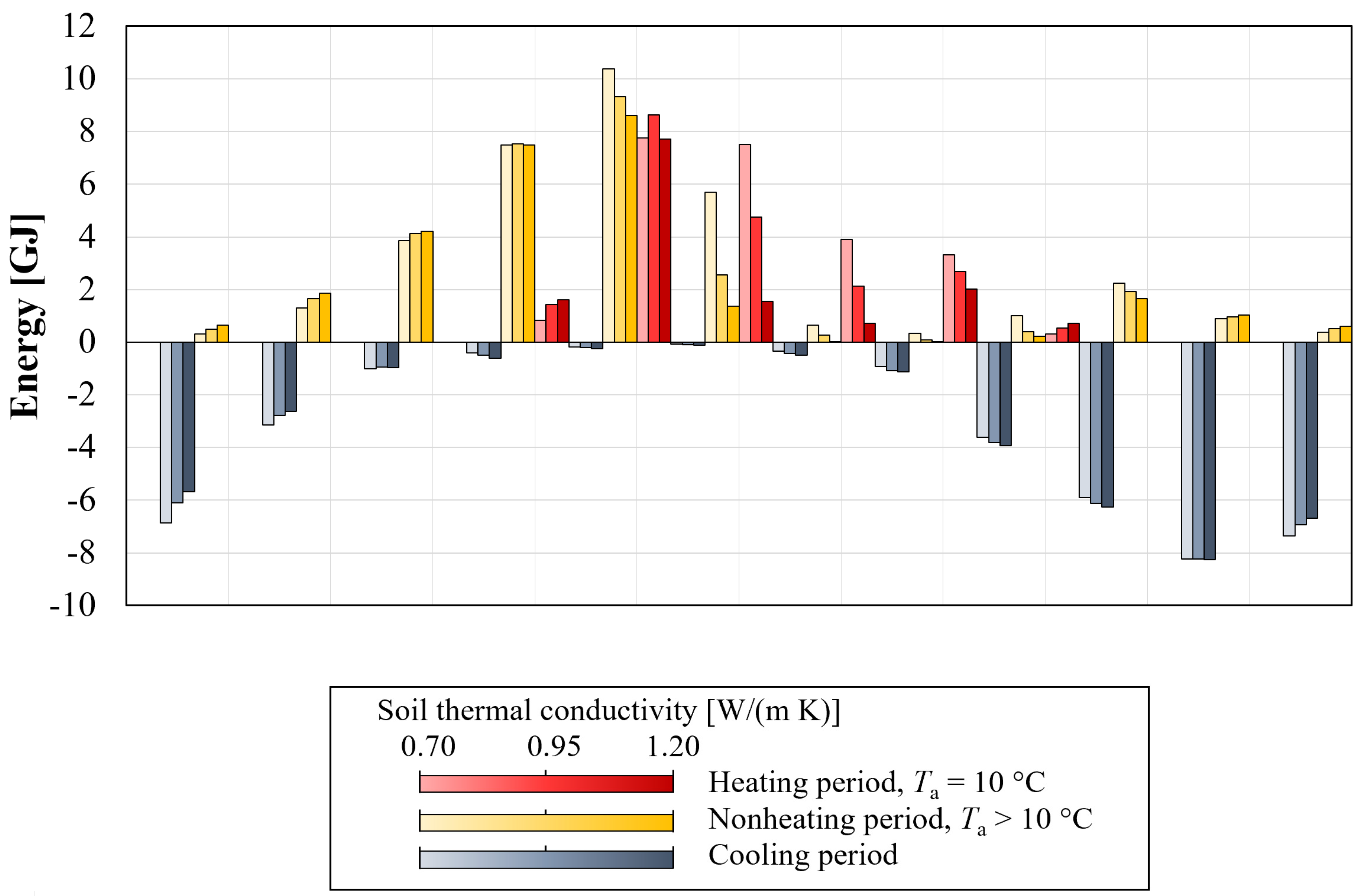
3.2. Energy Savings in Scenario #G
- It can provide heat during the heating period while the heating needs still exceed the ASHE output. Then, the zone is minimally heated at 10 °C, and the gas furnace operation is still required.
- The ASHE can provide an amount of heat that exceeds the initial greenhouse heating load (#10 °C scenario). In this case, the zone temperature initially reaches 10 °C in scenario #10 °C, while in scenario #G, the new zone temperature exceeds 10 °C, and the gas furnace is not required anymore. The ASHE then operates during the nonheating period.
- The ASHE changes the zone humidity conditions and, thus, changes the sensible and latent gains from evapotranspiration and condensation.
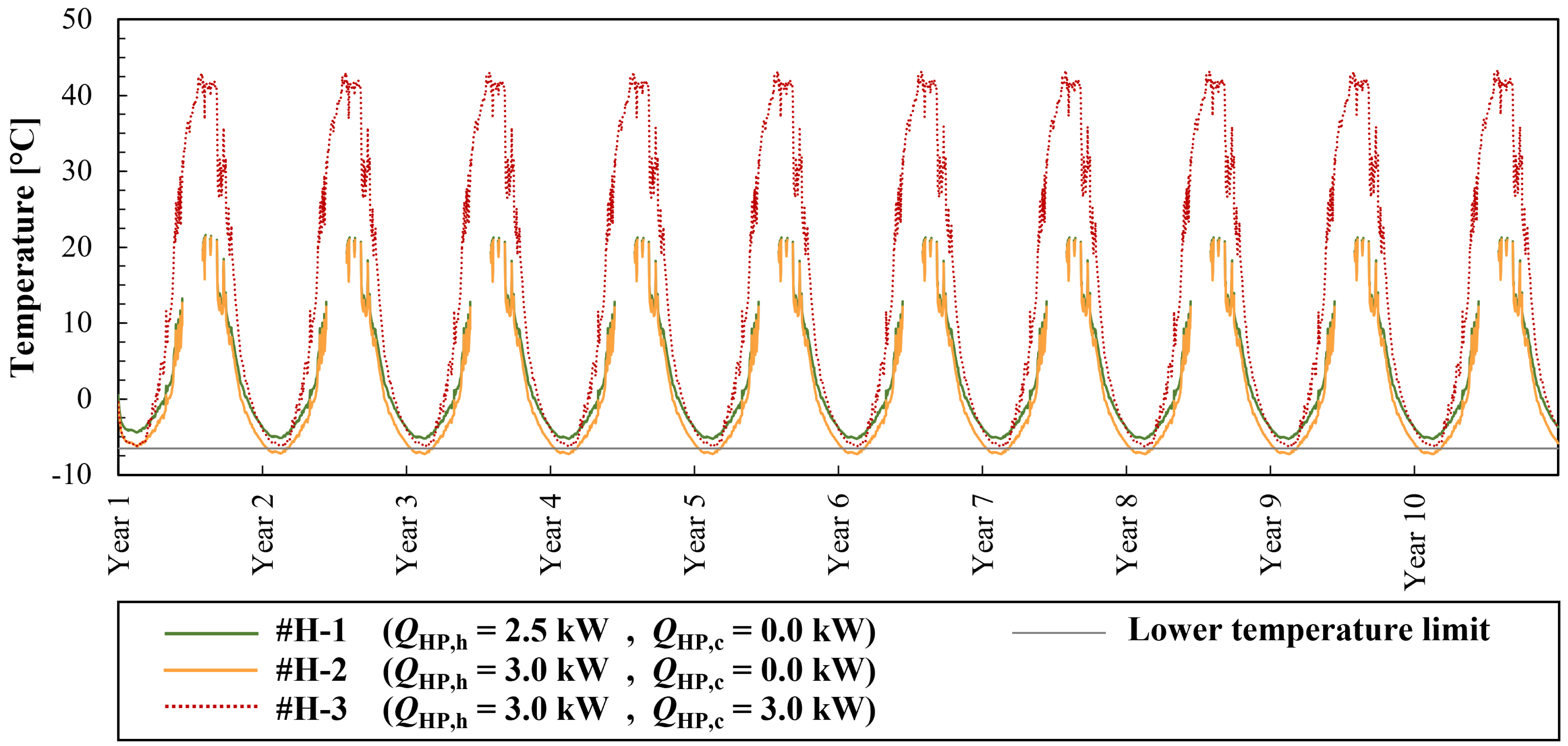
3.3. Required Size of GHE and Energy Savings in Scenario #H
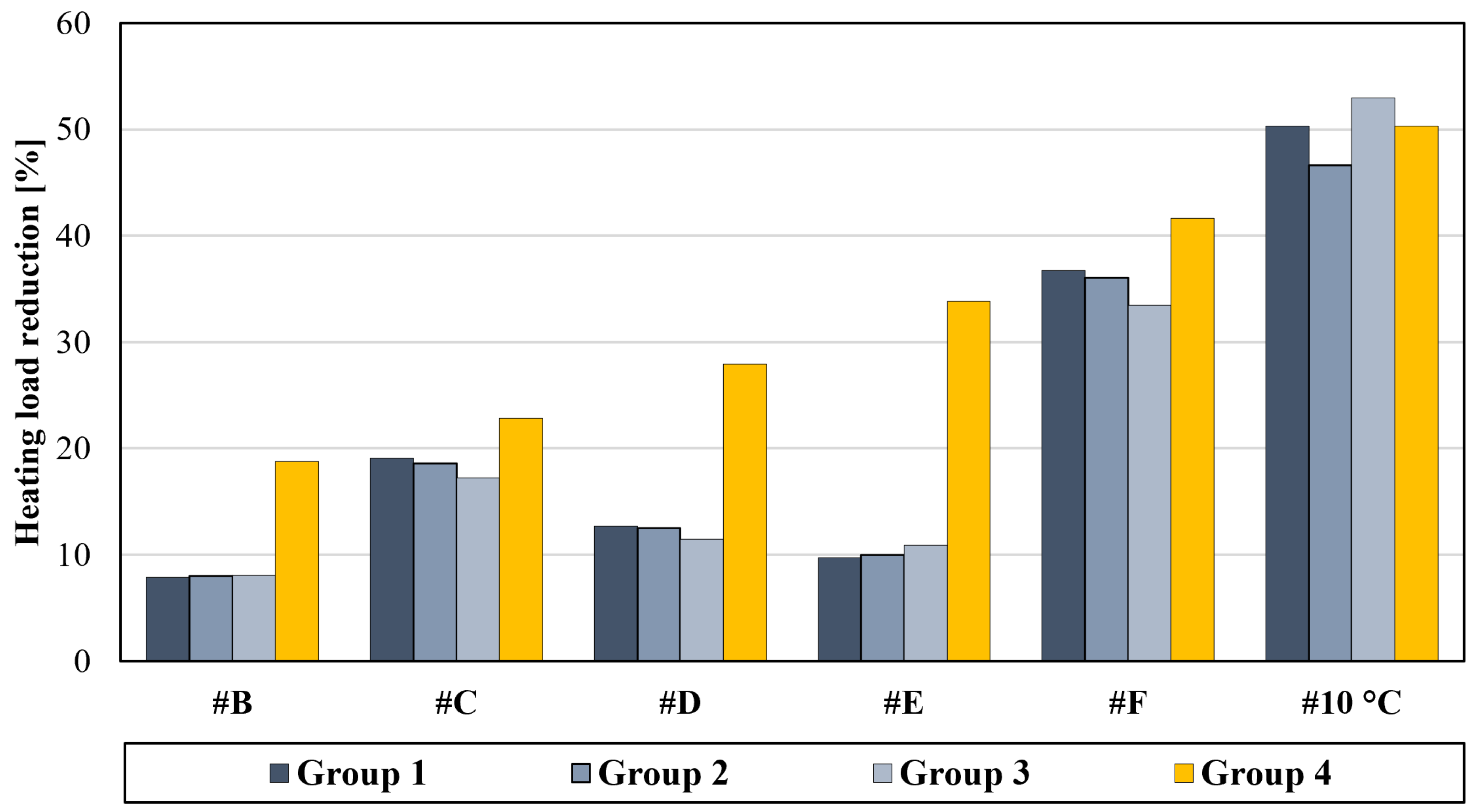
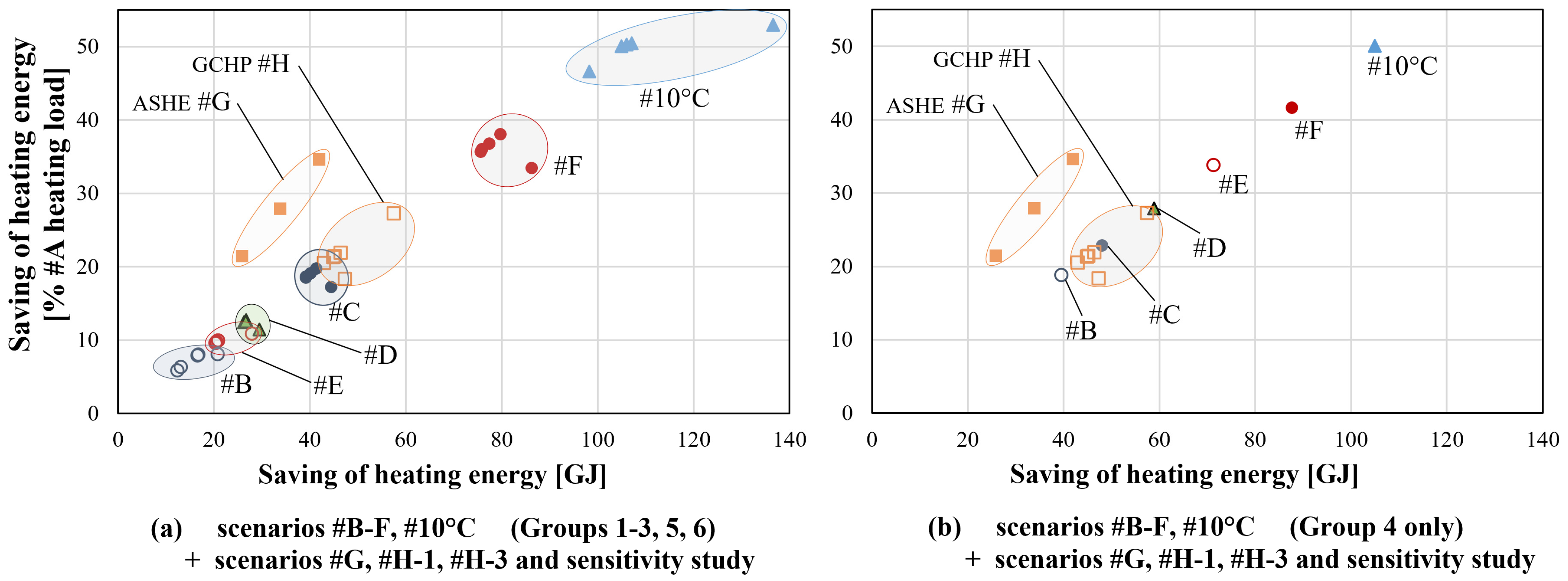
4. Comparison of All Scenarios and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin letters | |
| Afl | Area of the greenhouse floor [m2] |
| Ai | Area of a given wall of the greenhouse [m2] |
| Cp | Specific heat of air [J/(kg K)] |
| Ea | Inside air vapor pressure [kPa] |
| Eelec,HP | Electrical energy consumed by the heat pump compressor [GJ] |
| EHP→zone | Heat transferred from the heat pump condenser to the greenhouse [GJ] |
| Eo | Saturated vapor pressure [kPa] |
| fcult | Fraction of greenhouse footprint dedicated to crops [−] |
| g | Clear wall solar heat gain [−] |
| He | Convective heat transfer coefficient of the outer side of walls [W/(m2 K)] |
| He,c | Convective heat transfer coefficient of the outer side of opaque walls [W/(m2 K)] |
| Hfl | Convective heat transfer coefficient of greenhouse floor [W/(m2 K)] |
| Hfl,#A | Convective heat transfer coefficient of greenhouse floor in scenario #A [W/(m2 K)] |
| Hin,#A | Convective heat transfer coefficient of the inner side of clear walls in scenario #A [W/(m2 K)] |
| Hin,c | Convective heat transfer coefficient of the inner side of opaque walls [W/(m2 K)] |
| Hin,i | Convective heat transfer coefficient of the inner side of a given wall [W/(m2 K)] |
| ks | Short-wave radiation extinction coefficient of canopy [−] |
| LAI | Leaf area index coefficient [−] |
| mλE | Water evapotranspiration mass flow rate [kg/h] |
| mλEc | Water condensation mass flow rate [kg/h] |
| PPFD | Photosynthetic photon flux density [μmol/(m2 s)]. |
| Qcomo | Heat transfer rate from the greenhouse floor toward the soil [W/m2] |
| QHP,c | Rated cooling capacity of the heat pump [kW] |
| QHP,h | Rated heating capacity of the heat pump [kW] |
| Qsens | Sensible heat exchange [W/m2] |
| ra | Aerodynamic boundary layer resistance [s/m] |
| Rabs,t | Solar radiation absorbed by the vegetation and the greenhouse floor [W/m2] |
| Rinsul,fl | Thermal resistance of the floor separating the greenhouse zone from the soil [m2 K/W] |
| Rnet | Short-wave solar radiation absorbed by the vegetation [W/m2] |
| rs | Surface (stomatal) resistance [s/m] |
| Rsol | Solar radiation transmitted in the greenhouse [W] |
| Rsol,crop | Solar radiation intercepted by the vegetation [W/m2] |
| Rsol,fl | Solar radiation intercepted by the floor calculated in Type 56 [W/m2] |
| Ta | Inside air temperature [°C] |
| Tdeep | Deep earth undisturbed temperature [°C] |
| Te | Outside atmosphere temperature [°C] |
| Te,m | Monthly average of the atmosphere temperature [°C] |
| Tin,HP | Temperature of the fluid entering the heat pump evaporator [°C] |
| Tmin,in,HP | Minimum temperature of the fluid entering the heat pump evaporator during a given period [°C] |
| Ts | Crop canopy (vegetation) temperature [°C] |
| TSIfl | Temperature of the inner side of the greenhouse floor [°C] |
| TSIi | Temperature of the inner side of a given wall of the greenhouse [°C] |
| TSOfl | Temperature at the interface between the greenhouse floor and the soil (outer side) [°C] |
| Tsurf | Temperature at the interface between the soil surface and the outside atmosphere [°C] |
| Tsurf,Mirabel,m | Monthly average of the temperature at the interface between the soil surface and the outside atmosphere, recorded in Mirabel [°C] |
| U | Overall heat transfer coefficient of a given envelope element [W/(m2 K)] |
| We | Wind speed [m/s] |
| Greek symbols | |
| αfl | Solar absorptance of greenhouse floor [−] |
| αm | Solar absorptance of Type 56 model floor [−] |
| γ | Psychometric constant [Pa/K] |
| Δ | Slope of vapor pressure curve [kPa/K] |
| ΔT | Temperature difference [°C] |
| λ | Latent heat of vaporization of water [kJ/kg] |
| λE | Latent exchange flux with the inside air from the vegetation due to crop evapotranspiration [W/m2] |
| λEc | Latent flux to the walls due to water condensation [W/m2] |
| ρa | Inside air density [kg/m3] |
| ρsol | Solar reflectivity [−] |
| τsol | Solar transmissivity [−] |
| Φa | Inside air relative humidity [%] |
| χa | Vapor concentration in the inside air [g/m3] |
| χs | Vapor concentration at the canopy (vegetation) level [g/m3] |
| Acronyms | |
| ACH | Air change per hour |
| ASHE | Air–soil heat exchanger |
| ASHRAE | American Society of Heating, Refrigerating and Air-Conditioning Engineers |
| COP | Coefficient of performance |
| EER | Energy efficiency ratio |
| GCHP | Ground-coupled heat pump |
| GHE | Ground heat exchanger |
| HP | Heat pump |
| LAI | Leaf area index coefficient |
| PC | Polycarbonate |
| PE | Polyethylene |
| PPFD | Photosynthetic photon flux density |
| TMY | Typical meteorological year |
| TRNSYS | Transient Systems Simulation Program |
References
- McCartney, L.; Lefsrud, M.G. Protected Agriculture in Extreme Environments: A Review of Controlled Environment Agriculture in Tropical, Arid, Polar, and Urban Locations. Appl. Eng. Agric. 2018, 34, 455–473. [Google Scholar] [CrossRef]
- Kulak, M. Reducing greenhouse gas emissions with urban agriculture: A Life Cycle Assessment perspective. Landsc. Urban Plan. 2013, 111, 68–78. [Google Scholar] [CrossRef]
- Eigenbrod, C.; Gruda, N. Urban vegetable for food security in cities. A review. Agron. Sustain. Dev. 2015, 35, 438–498. [Google Scholar] [CrossRef]
- Deelstra, T.; Girardet, H. Urban Agriculture and Sustainable Cities. In Growing Cities, Growing Food: Urban Agriculture on the Policy Agenda; Zentralstelle für Ernährung und Landwirtschaft (ZEL): Feldafing, Germany, 2000; pp. 43–65. [Google Scholar]
- Syndicat des Producteurs en Serre du Québec. Rapport Final: Projet D’initiatives Structurantes en Technologies Efficaces; Syndicat des Producteurs en Serre du Québec: Longueil, QC, Canada, 2008; Available online: https://www.serres.quebec/energie-3/ (accessed on 11 February 2023).
- Lalonde, T.; Monfet, D.; Haillot, D. Proposition of a humidity control strategy for a calibrated greenhouse model with realistic controls in TRNSYS. In eSim, Proceedings of the eSim 2020: 11th Conference of IBPSA-Canada, Vancouver, BC, Canada, 29 January 2020; IBPSA-Canada: Oakville, ON, Canada, 2020; Volume 11, Available online: https://publications.ibpsa.org/conference/paper/?id=esim2020_1244 (accessed on 12 February 2023).
- Tong, G.; Chen, Q.; Xu, H. Passive solar energy utilization: A review of envelope material selection for Chinese solar greenhouses. Sustain. Energy Technol. Assess. 2022, 50, 101833. [Google Scholar] [CrossRef]
- Revéret, J.-P.; Brodeur, C.; Michaud, C.; Charron, I. Documentation des Innovations Technologiques Visant L’efficacité Énergétique et L’utilisation de Sources D’énergie Alternatives Durables en Agriculture; Groupe AGÉCO: Quebec, QC, Canada, 2006; Available online: https://www.agrireseau.net/documents/73781/ (accessed on 2 December 2022).
- De Halleux, D. Chauffer à moindres coûts. In Proceedings of the Colloque Sur La Serriculture, Montréal-Longueil, QC, Canada, 29 September 2005; Available online: https://www.agrireseau.net/legumesdeserre (accessed on 2 December 2022).
- Minea, V. Géothermie—Source Alternative de Chauffage pour les Serres. In Proceedings of the Journée D’information—Horticulture Ornementale, Sainte-Julie, QC, Canada, 24 January 2006; Available online: https://www.serres.quebec/energie-3/ (accessed on 12 February 2023).
- Cadotte, G.; Girouard, M. Bilan Technico-Economique de L’utilisation de Tuyaux de Chauffe (Growing Pipe) à L’intérieur de la Canopée des Plants de Tomate de Serre; Syndicat des Producteurs en Serres du Québec: Longueil, QC, Canada, 2015; Available online: https://www.serres.quebec/energie-3/ (accessed on 12 February 2023).
- Gilli, C.; Kempkes, F.; Munoz, P.; Montero, J.I.; Giuffrida, F.; Baptista, F.J.; Stepowska, A.; Stanghellini, C. Potential of different energy saving strategies in heated greenhouse. Acta Hortic. 2017, 1164, 467–474. [Google Scholar] [CrossRef]
- Kempkes, F.; de Zwart, H.F.; Munoz, P.; Montero, J.I.; Baptista, F.J.; Giuffrida, F.; Gilli, C.; Stepowska, A.; Stanghellini, C. Heating and dehumidification in production greenhouses at northern latitudes: Energy use. Acta Hortic. 2017, 1164, 445–452. [Google Scholar] [CrossRef]
- Léveillé-Guillemette, F.; Monfet, D. Calibration d’un modèle énergétique et analyse économique de mesures de conservation d’énergie d’une serre communautaire à Montréal. In eSim, Proceedings of the eSim 2018: 10th Conference of IBPSA-Canada, Montréal, QC, Canada, 9–10 May 2018; IBPSA-Canada: Oakville, ON, Canada, 2018; pp. 512–521. Available online: http://ibpsa.org/esim-2018-conference-proceedings (accessed on 12 February 2023).
- Notre Quartier Nourricier Pôle Production. Available online: https://www.quartiernourricier.com/produits-serre/ (accessed on 11 February 2023).
- Ahamed, S. Energy saving techniques for reducing the heating cost of conventional greenhouses. Biosyst. Eng. 2019, 178, 9–33. [Google Scholar] [CrossRef]
- Piché, P. Design, construction and analysis of a thermal energy storage system adapted to greenhouse cultivation in isolated northern communities. Sol. Energy 2020, 204, 90–105. [Google Scholar] [CrossRef]
- Sethi, V.P.; Sharma, S.K. Survey and evaluation of heating technologies for worldwide agricultural greenhouse applications. Sol. Energy 2008, 82, 832–859. [Google Scholar] [CrossRef]
- Bernier, H.; Raghavan, G.S.V.; Paris, J. Evaluation of a soil heat exchanger-storage system for a greenhouse. Part I: System performance. Can. Agric. Eng. 1991, 33, 93–98. [Google Scholar]
- D’Arpa, S.; Colangelo, G.; Starace, G.; Petrosillo, I.; Bruno, D.E.; Uricchio, V.; Zurlini, G. Heating requirements in greenhouse farming in southern Italy: Evaluation of ground-source heat pump utilization compared to traditional heating systems. Energy Effic. 2016, 9, 1065–1085. [Google Scholar] [CrossRef]
- Nawalany, G.; Radon, J.; Bieda, W.; Sokolowski, P. Influence of Selected Factors on Heat Exchange with the Ground in a Greenhouse. Trans. ASABE 2017, 60, 479–487. [Google Scholar] [CrossRef]
- Environnement Canada Données des Stations Pour le Calcul des Normales Climatiques au Canada de 1971 à 2000—MONTREAL/MIRABEL INT’L A. Available online: https://climat.meteo.gc.ca/climate_normals/results_f.html?searchType=stnName&txtStationName=montr%C3%A9al&searchMethod=contains&txtCentralLatMin=0&txtCentralLatSec=0&txtCentralLongMin=0&txtCentralLongSec=0&stnID=5616&dispBack=0 (accessed on 15 February 2023).
- Lalonde, T. Développement D’un Modèle Calibré Pour la Simulation Énergétique de Serres et Analyse des Résultats à L’aide D’indicateurs de Performance. Mémoire de Maîtrise Électronique; École de Technologie Supérieure: Montréal, QC, Canada, 2022; Available online: https://espace.etsmtl.ca/id/eprint/2963 (accessed on 12 February 2023).
- Rasheed, A.; Lee, J.W.; Lee, H.W. Development of a model to calculate the overall heat transfer. Span. J. Agric. Res. 2017, 15, e0208. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. ASHRAE Handbook: Heating, Ventilating, and Air-conditioning Applications, SI ed.; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. (ASHRAE): Atlanta, GA, USA, 2015. [Google Scholar]
- Papadakis, G.; Frangoudakis, A.; Kyritsis, S. Mixed, forced and free convection heat transfer at the greenhouse cover. J. Agric. Eng. Res. 1992, 51, 191–205. [Google Scholar] [CrossRef]
- Transolar Software Engineering. TYPE 460: Hypocaust (Air-To-Soil Exchanger). Available online: https://trnsys.de/en/addons-en (accessed on 12 February 2023).
- Talbot, M.-H.; Monfet, D. Estimating the impact of crops on peak loads of a Building-Integrated Agriculture space. Sci. Technol. Built Environ. 2020, 26, 1448–1460. [Google Scholar] [CrossRef]
- Graamans, L. Plant factories; crop transpiration and energy balance. Agric. Syst. 2017, 153, 138–147. [Google Scholar] [CrossRef]
- Allan, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration—Guidelines for computing crop water requirements—FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Katsoulas, N.; Stanghellini, C. Modelling Crop Transpiration in Greenhouses: Different Models for Different Applications. Agronomy 2019, 9, 392. [Google Scholar] [CrossRef]
- Tei, F. Growth of Lettuce, Onion, and Red Beet. 1. Growth Analysis, Light Interception, and Radiation Use Efficiency. Ann. Bot. 1996, 78, 633–643. [Google Scholar] [CrossRef]
- Léveillée-Dallaire, X.; Raymond, J.; Fujii, H.; Tsuya, S. Sizing Horizontal Geothermal Heat Exchangers for Community Greenhouses in Montreal. In Proceedings of the Geothermal Resources Council Transactions, Reno, NV, USA, 28–31 August 2022; Geothermal Rising: Davis, CA, USA, 2022; Volume 46, pp. 793–803. Available online: https://www.geothermal-library.org/index.php?mode=pubs&action=view&record=1034635 (accessed on 21 March 2023).
- Hollmuller, P.; Lachal, B. Air–soil heat exchangers for heating and cooling of buildings: Design guidelines, potentials and constraints, system integration and global energy balance. Appl. Energy 2014, 119, 476–487. [Google Scholar] [CrossRef]
- Geostar. Sycamore Series Specification Catalog. 2017. Available online: https://www.geostar-geo.com/downloads/literature/SC2700AG.pdf (accessed on 1 October 2020).
- Bierhuizen, J.F.; Ebbens, J.L.; Koomen, N.C.A. Effects of temperature and radiation on lettuce growing. Neth. J. Agric. Sci. 1973, 21, 110–116. [Google Scholar] [CrossRef]
- Robert, F.; Gosselin, L. New methodology to design ground coupled heat pump systems based on total cost minimization. Appl. Therm. Eng. 2014, 62, 481–491. [Google Scholar] [CrossRef]



| Layer | Total Thickness [m] | Thermal Resistance [m2 K/W] | Internal Convective Coefficient [W/(m2 K)] | External Convective Coefficient [W/(m2 K)] | Solar Absorptance in [−] | Solar Absorptance out [−] | Long-Wave Emission Coefficient in [−] | Long-Wave Emission Coefficient out [−] |
|---|---|---|---|---|---|---|---|---|
| Steel structure | 0.05 | 0.003 | 3.06 | He | 0.8 | 0.8 | 0.28 | 0.28 |
| Floor | − | 0.10 | Parametric study | − | 0.9 | 0.9 | 0.8 | 0.8 |
| Concrete wall (not insulated) | 0.20 | 0.21 | 3.06 | 17.8 | 0.6 | 0.6 | 0.9 | 0.9 |
| Concrete wall (with insulation) | 0.30 | 2.71 | 3.06 | 17.8 | 0.6 | 0.6 | 0.9 | 0.9 |
| Plywood door | 0.05 | 0.33 | 3.06 | 17.8 | 0.6 | 0.6 | 0.9 | 0.9 |
| Glazing | Frame | Convective Heat Transfer Coefficient | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Windows | Slope [deg] | U-Value (Convection not Included) [W/(m2 K)] | g [−] | τsol [−] | ρsol [−] | U-Value [W/(m2 K)] | Solar Absorptance [−] | Emissivity [−] | Internal [W/(m2 K)] | External [W/(m2 K)] |
| PE 90° (side walls) | 90 | 4.38 | 0.773 | 0.747 | 0.175 | 8.17 | 0.6 | 0.9 | Parametric study | He |
| PE 28° (roof) | 28 | 4.28 | 0.775 | 0.747 | 0.175 | 8.17 | 0.6 | 0.9 | Parametric study | He |
| PC (front–back walls) | 90 | 3.64 | 0.671 | 0.62 | 0.227 | 8.17 | 0.6 | 0.9 | Parametric study | He |
| Parameter | Value | Unit | Additional Information |
|---|---|---|---|
| Cp | 1006 | J/(kg K) | − |
| fcult | 0.6 | − | The crops cover 60% of the floor surface area. |
| ks | 0.66 | − | Coefficient of extinction reported by Tei et al. (1996) for lettuce. Crops, with cultivated density of 27.5 plants/m2 [32]. |
| LAI | 3.0 | − | Presumed by Graamans et al. (2017) for lettuce crops, based on literature [23,29]. |
| λ | 2489 | kJ/kg | − |
| γ | 66.5 | Pa/K | − |
| ρa | 1.2 | kg/m3 | The density of humid air lies between 1.18 and 1.23 kg/m3 according to the simulated temperature and relative humidity. |
| Component | Parameter | Unit | Value |
|---|---|---|---|
| ASHE: Type 460 Scenario #G | Total air flow rate | m3/s | 0.83 |
| Number of pipes (all in parallel connection) | − | 40 | |
| Pipe inner diameter | m | 0.08 | |
| Pipe outer diameter | m | 0.09 | |
| Single pipe length | m | 15.0 | |
| Pipe spacing | m | 0.3 | |
| Burial depth of pipes | m | 0.9 and 1.9 | |
| Pipe thermal conductivity | W/(m K) | 2.0 | |
| Pipe heat capacity | MJ/(m3 K) | 1.0 | |
| Soil thermal conductivity | W/(m K) | Parametric study | |
| Soil heat capacity | MJ/(m3 K) | 2.25 | |
| GHE: Type 997 Scenario #H | Number of pipes (all in serial connection) | − | 24 |
| Pipe inner diameter | m | 0.019 | |
| Pipe outer diameter | m | 0.024 | |
| Single pipe length | m | 15.0 | |
| Pipe spacing | m | 0.30 | |
| Burial depth of pipes | m | Parametric study | |
| Pipe thermal conductivity | W/(m K) | 0.4 | |
| Pipe heat capacity | W/(m K) | 0.95 | |
| Soil thermal conductivity | W/(m K) | Parametric study | |
| Soil heat capacity | MJ/(m3 K) | 2.25 | |
| HP: Equations Scenario #H | Rated heating capacity | kW | Parametric study |
| Rated cooling capacity | kW | Parametric study | |
| Heat carrier fluid (volume mixture of 65% water + 35% propylene glycol) Scenario #H | Specific heat capacity | kJ/(kg K) | 3.726 |
| Density | kg/m3 | 1037 | |
| Thermal conductivity | W/(m K) | 0.4 | |
| Volume flow rate | L/s | 0.28 | |
| Dynamic viscosity | kg/(m h) | 33 |
| Group 1 #A–F, H, 10 °C | Group 2 #A–F, 10 °C | Group 3 #A–F, H, 10 °C | Group 4 #A–F, 10 °C | Group 5 #A–F, H, 10 °C | Group 6 #A–F, H, 10 °C | |
|---|---|---|---|---|---|---|
| Calculation of internal convective coefficient | Equations (2) and (3) | Hin,i of scenario #A, calculated with Equations (2) and (3) | Equations (2) and (3) | Equations (2) and (3) | Equations (2) and (3) | Equations (2) and (3) |
| Evapotranspiration | no | no | yes | no | no | no |
| Condensation | no | no | yes | no | no | no |
| Natural ventilation | no | no | yes | no | no | no |
| Concrete wall thermal resistance [m2 K/W] | 0.21 (no insulation) | 0.21 (no insulation) | 0.21 (no insulation) | 2.71 (with insulation) | 0.21 (no insulation) | 0.21 (no insulation) |
| Soil thermal conductivity [W/(m K)] | 0.95 | 0.95 | 0.95 | 0.95 | 0.7 | 1.2 |
| Soil Thermal Conductivity [W/(m K)] | Heat from ASHE to Zone during Heating Period [GJ] | Heat from ASHE to Zone during Nonheating Period [GJ] | Heat from ASHE to Zone during Cooling Period [GJ] | ||
|---|---|---|---|---|---|
| Total | Part Contributing to Saving | Total | Part Contributing to Saving | Total (Soil Heat Injection) | |
| 0.70 | 23.6 | 23.6 | 34.6 | 18.4 | −38.2 |
| 0.95 | 20.2 | 20.2 | 29.9 | 13.7 | −37.4 |
| 1.20 | 14.3 | 14.3 | 27.8 | 11.6 | −37.2 |
| QHP,h – QHP,c [kW] | Maximum Yearly Ground Load (Heating) [W] | Maximum Monthly Ground Load (Heating) [W] | Maximum Hourly Ground Load (Heating) [W] | Minimum Fluid Temperature Tmin,in,HP [°C] |
|---|---|---|---|---|
| 2.5–0.0 (#H-1) | 1187.4 | 2302.1 | 3474.9 | −5.3 |
| 3.0–0.0 (#H-2) | 1326.1 | 2689.4 | 3948.5 | −7.3 |
| 3.0–3.0 (#H-3) | 16.8 | 2919.1 | 5300.0 | −6.2 |
| QHP,h − QHP,c [kW] | Yearly Heating Load [GJ] | Yearly Cooling Load [GJ] | EHP→zone Heating [GJ] | EHP→zone Cooling [GJ] | Eelec,HP Heating [GJ] | Eelec,HP Cooling [GJ] |
|---|---|---|---|---|---|---|
| 2.5–0.0 (#H-1) | 215.5 | 115.6 | 49.7 | 0.0 | 12.7 | 0.0 |
| 3.0–0.0 (#H-2) | 216.3 | 115.3 | 56.0 | 0.0 | 14.9 | 0.0 |
| 3.0–3.0 (#H-3) | 212.6 | 121.9 | 59.3 | −32.6 | 14.5 | 11.6 |
| QHP,h – QHP,c [kW] | Fraction of the Heating Load Provided by the HP [%] | Fraction of the Cooling Load Provided by the HP [%] | Savings in Heating Energy [% of #A Heating Load, Group 1] | Savings in Cooling Energy [% of #A Cooling Load, Group 1] | Minimum Fluid Temperature Tmin,in,HP [°C] |
|---|---|---|---|---|---|
| 2.5–0.0 (#H-1) | 23.1 | 0.0 | 21.3 | 2.7 | −5.3 |
| 3.0–0.0 (#H-2) | 25.9 | 0.0 | 23.8 | 2.9 | −7.3 |
| 3.0–3.0 (#H-3) | 27.9 | 26.7 | 27.3 | 24.8 | −6.2 |
| Soil Thermal Conductivity [W/(m K)] | GHE Depth [m] | Yearly Heating Load [GJ] | EHP→zone [GJ] | Eelec,HP [GJ] | Fraction of the Heating Load Provided by the HP [%] | Savings in Heating Energy [% of #A Heating Load, Groups 1, 3, 5, or 6] | Minimum Fluid Temperature Tmin,in,HP [°C] |
|---|---|---|---|---|---|---|---|
| 0.95 * (Group 1) | 1.5 * | 215.5 | 49.7 | 12.7 | 23.1 | 21.3 | −5.3 |
| 0.70 (Group 5) | 1.5 | 213.4 | 46.7 | 12.5 | 21.9 | 20.5 | −7.8 |
| 1.20 (Group 6) | 1.5 | 217.6 | 51.8 | 12.8 | 23.8 | 21.9 | −3.5 |
| 0.95 (Group 1) | 1.0 | 218.1 | 52.2 | 12.8 | 23.9 | 21.3 | −3.9 |
| 0.95 (Group 1) | 2.0 | 213.7 | 48.1 | 12.6 | 22.5 | 21.4 | −6.5 |
| 0.95 ** (Group 3) | 1.5 ** | 263.9 | 53.3 | 13.8 | 20.2 | 18.3 | −5.6 |
| Reference and Equivalent Studied Scenario | Solution | Base Case Heating Load [GJ/y] | Allowed Savings [GJ] | Allowed Savings [% of Base Case Load] | Place | Remarks |
|---|---|---|---|---|---|---|
| Léveillé-Guillemette et al. (2018) [14] | Insulation of northwest wall with 10 cm expanded polystyrene layer | 209.3 | 14.7–16.7 | 7–8 | Emily- De-Witt greenhouse, Montreal | TRNSYS 18 software No condensation and no evapotranspiration One wall insulated |
| Scenario #D (Group 1) | Insulation of northwest and northeast walls with 20 cm concrete wall | 210.8 | 26.6 | 12.6 | − | TRNSYS 18 software Two walls insulated |
| Scenario #D (Group 3) | Insulation of northwest and northeast walls with 20 cm concrete wall | 257.9 | 29.5 | 11.4 | ||
| Scenario #D (Group 4) | Insulation of northwest and northeast walls with 20 cm concrete wall and 10 cm expanded polystyrene layer | 210.8 | 58.9 | 27.9 | ||
| Nawalany et al. (2017) [21] | Earth-sheltered greenhouse 1 m below ground surface, 30 cm concrete walls | 842.4 | 93.6 | 11 | South Poland (50.1° N, 19.5° E) | WUFI Plus software Greenhouse footprint 10.6 m × 43 m, height 4.3 m No condensation and no evapotranspiration Temperature range 17 °C–27 °C |
| Nawalany et al. (2017) [21] | Earth-sheltered greenhouse 1 m below ground surface, 30 cm concrete walls | 237.6 | 32.4 | 13.6 | (50.1° N, 19.5° E) | Temperature range 8 °C–24 °C |
| Scenario #C (Group 1) | 1 m below ground surface, 20 cm concrete walls | 210.8 | 40.2 | 19.1 | − | TRNSYS 18 software |
| Scenario #C (Group 3) | 1 m below ground surface, 20 cm concrete walls | 257.9 | 44.5 | 17.2 | ||
| Nawalany et al. (2017) [21] | Earth-sheltered greenhouse 1 m below ground surface, 30 cm concrete walls, insulation of 10 cm extruded polystyrene layer | 842.4 | 172.8 | 20.5 | South Poland (50.1° N, 19.5° E) | WUFI Plus software Greenhouse footprint 10.6 m × 43 m, height 4.3 m No condensation and no evapotranspiration Temperature range 17 °C–27 °C |
| Nawalany et al. (2017) [21] | Earth-sheltered greenhouse 1 m below ground surface, 30 cm concrete walls, insulation of 10 cm extruded polystyrene layer | 237.6 | 54 | 22.7 | (50.1° N, 19.5° E) | Temperature range 8 °C–24 °C |
| Scenario #C (Group 4) | 1 m below ground surface, 20 cm concrete walls, insulation of 10 cm expanded polystyrene | 210.8 | 48.1 | 22.8 | − | TRNSYS software |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maranghi, F.; Raymond, J. Numerical Evaluation of the Benefits Provided by the Ground Thermal Inertia to Urban Greenhouses. Thermo 2023, 3, 452-482. https://doi.org/10.3390/thermo3030028
Maranghi F, Raymond J. Numerical Evaluation of the Benefits Provided by the Ground Thermal Inertia to Urban Greenhouses. Thermo. 2023; 3(3):452-482. https://doi.org/10.3390/thermo3030028
Chicago/Turabian StyleMaranghi, Florian, and Jasmin Raymond. 2023. "Numerical Evaluation of the Benefits Provided by the Ground Thermal Inertia to Urban Greenhouses" Thermo 3, no. 3: 452-482. https://doi.org/10.3390/thermo3030028
APA StyleMaranghi, F., & Raymond, J. (2023). Numerical Evaluation of the Benefits Provided by the Ground Thermal Inertia to Urban Greenhouses. Thermo, 3(3), 452-482. https://doi.org/10.3390/thermo3030028







