Assessment of Semi-Empirical Soot Modelling in Turbulent Buoyant Pool Fires from Various Fuels
Abstract
:1. Introduction
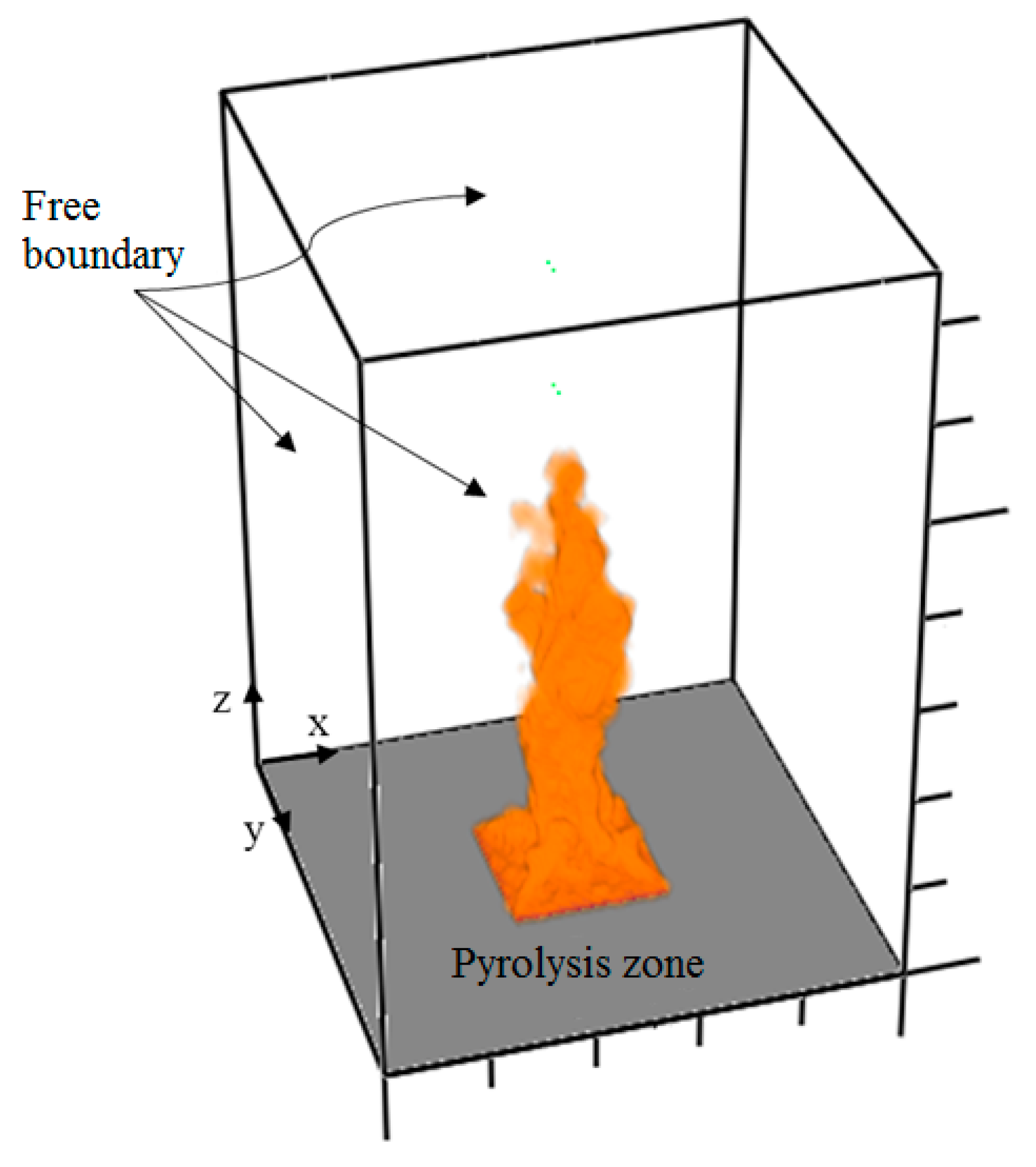
2. Numerical Modelling
2.1. Combustion Model
2.2. Soot Formation Model
2.3. Boundary Condition at Interface
3. Results and Discussion
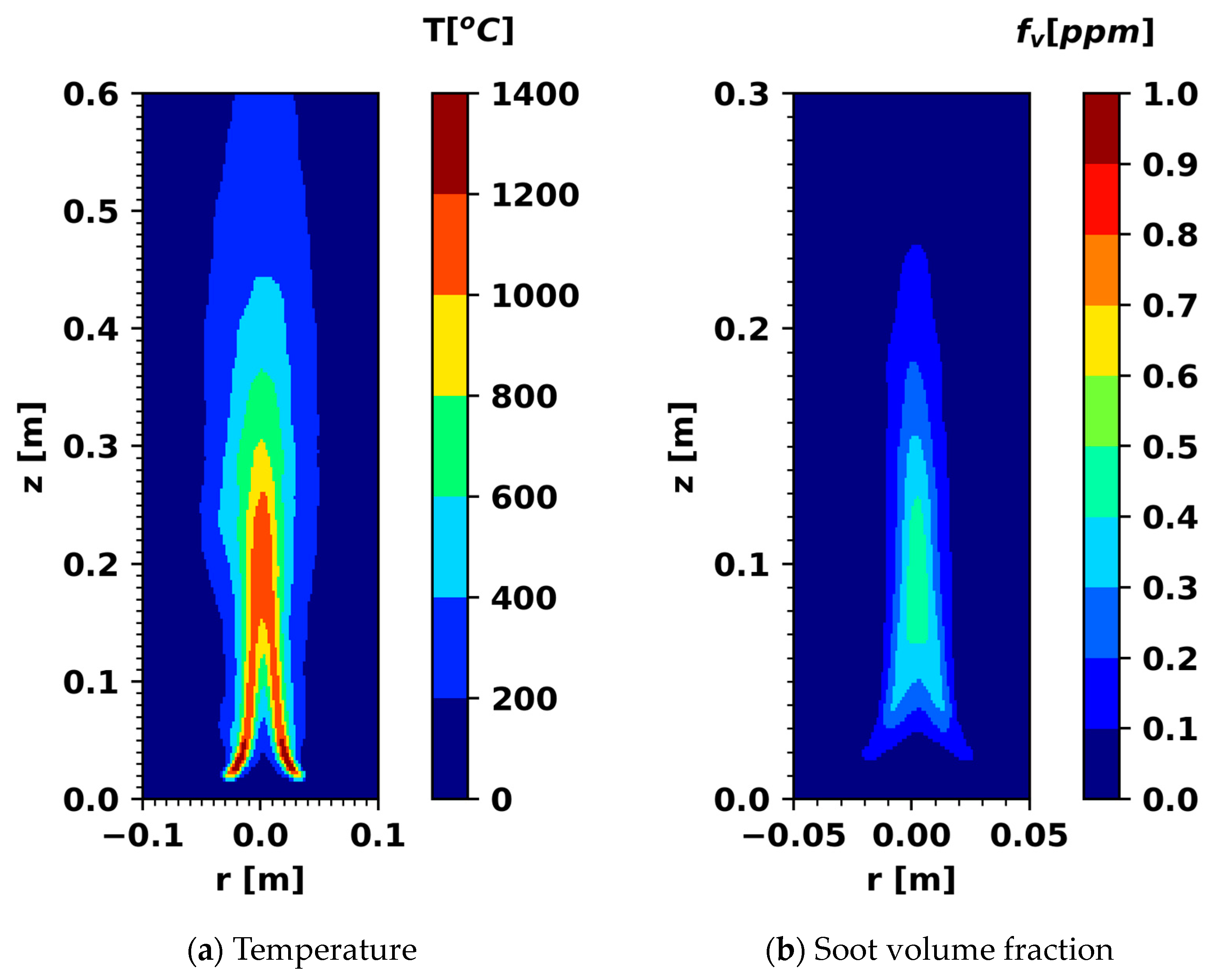
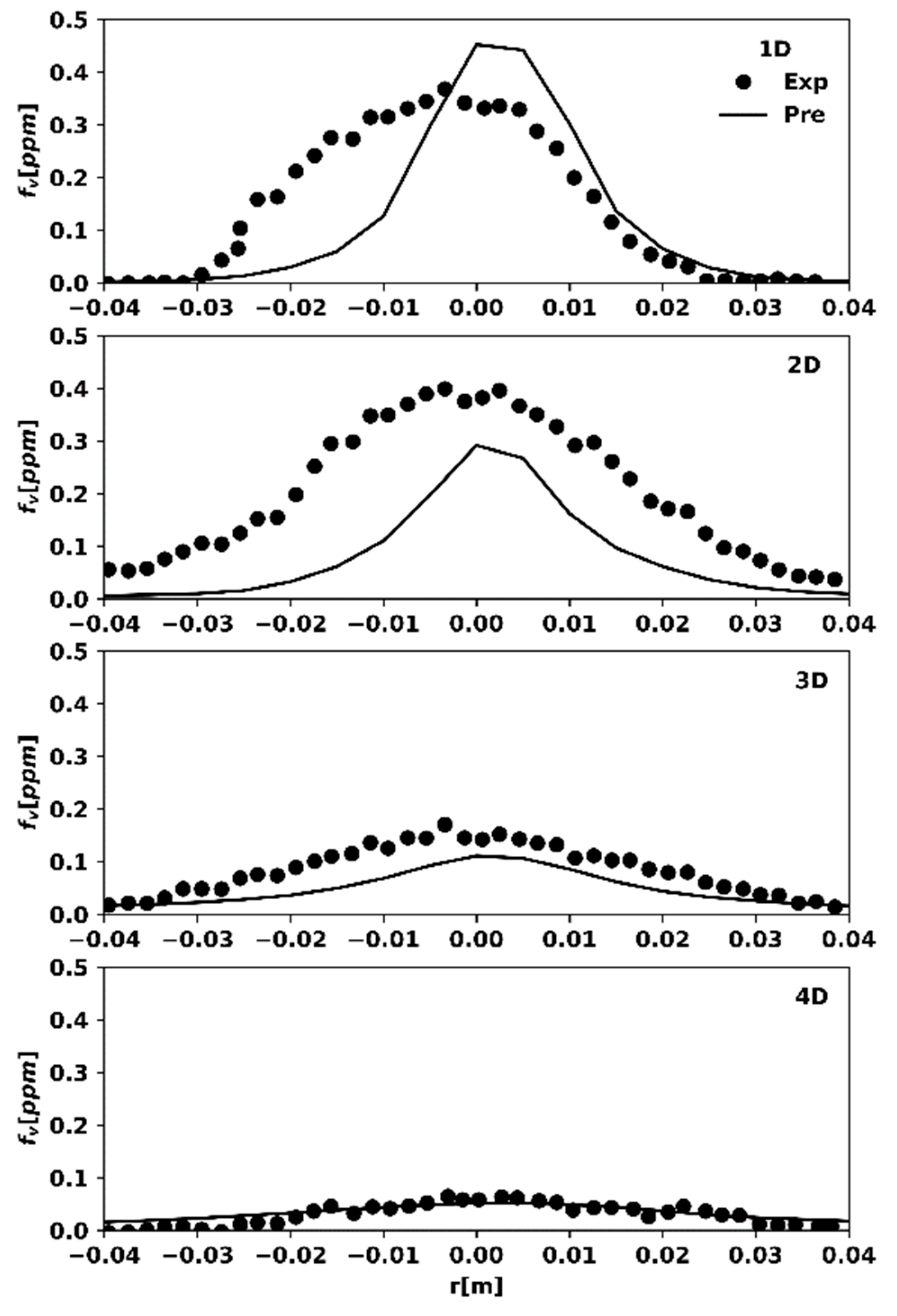
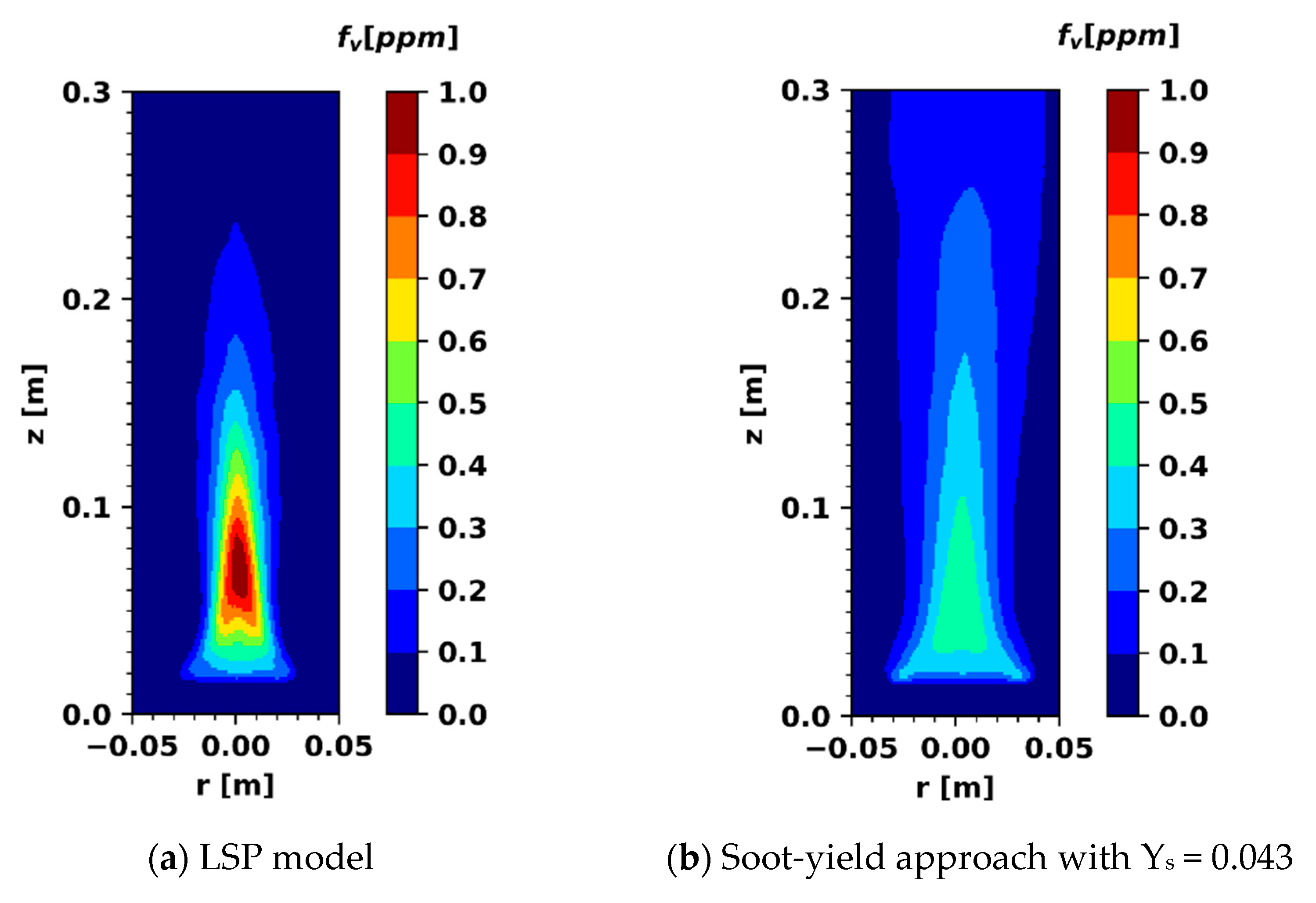
3.1. Methane and Ethylene Pool Fires
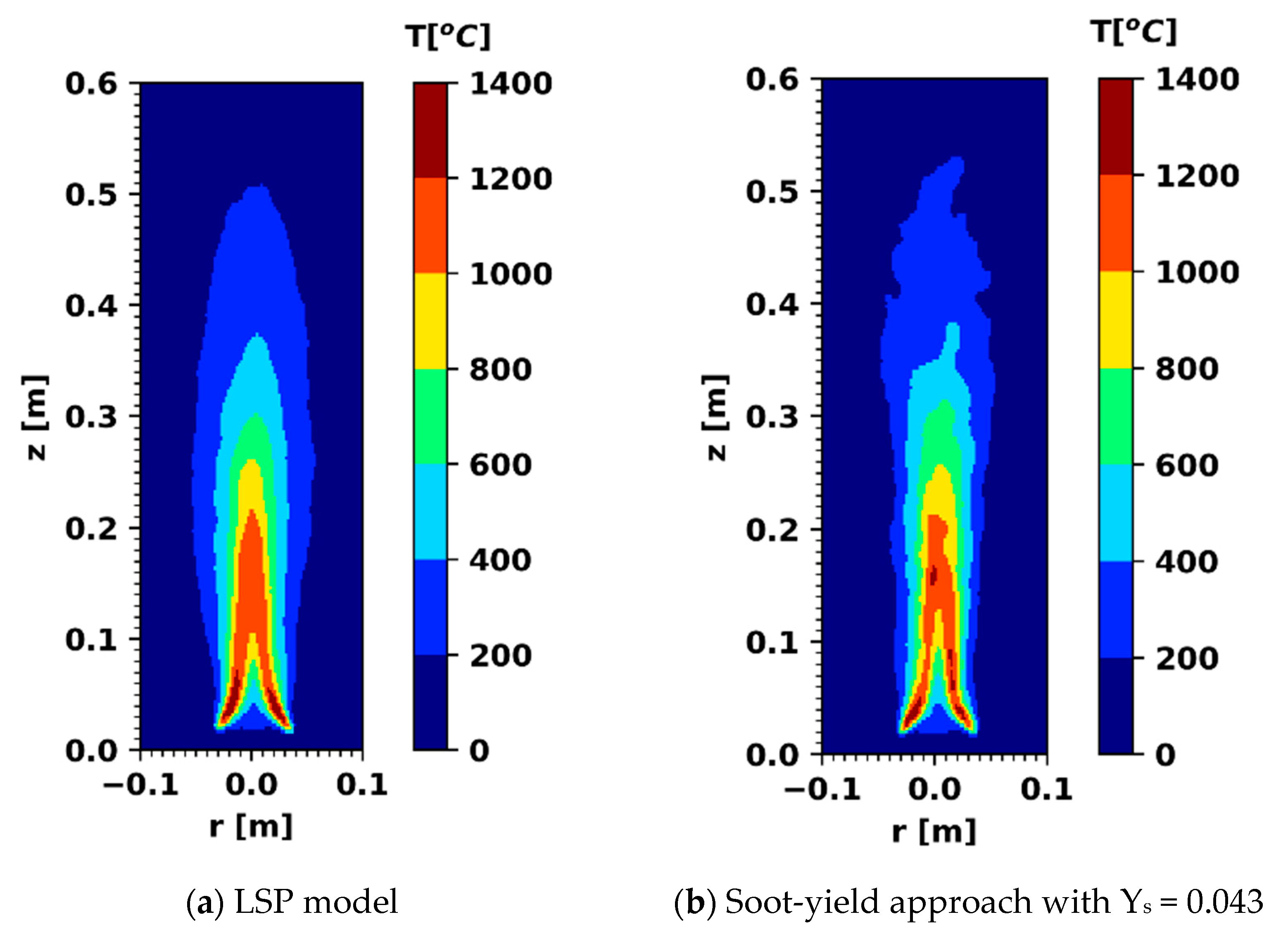
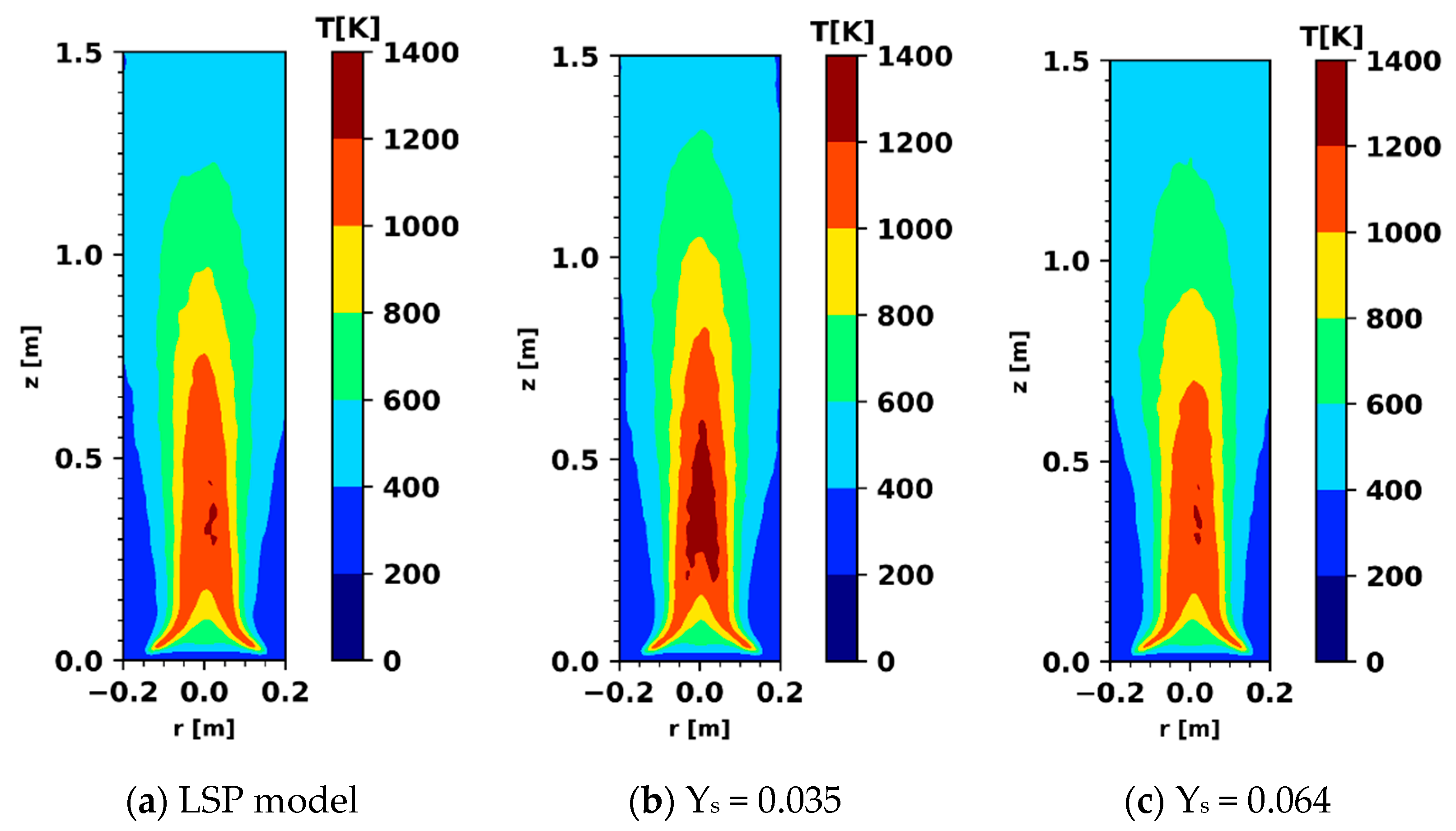
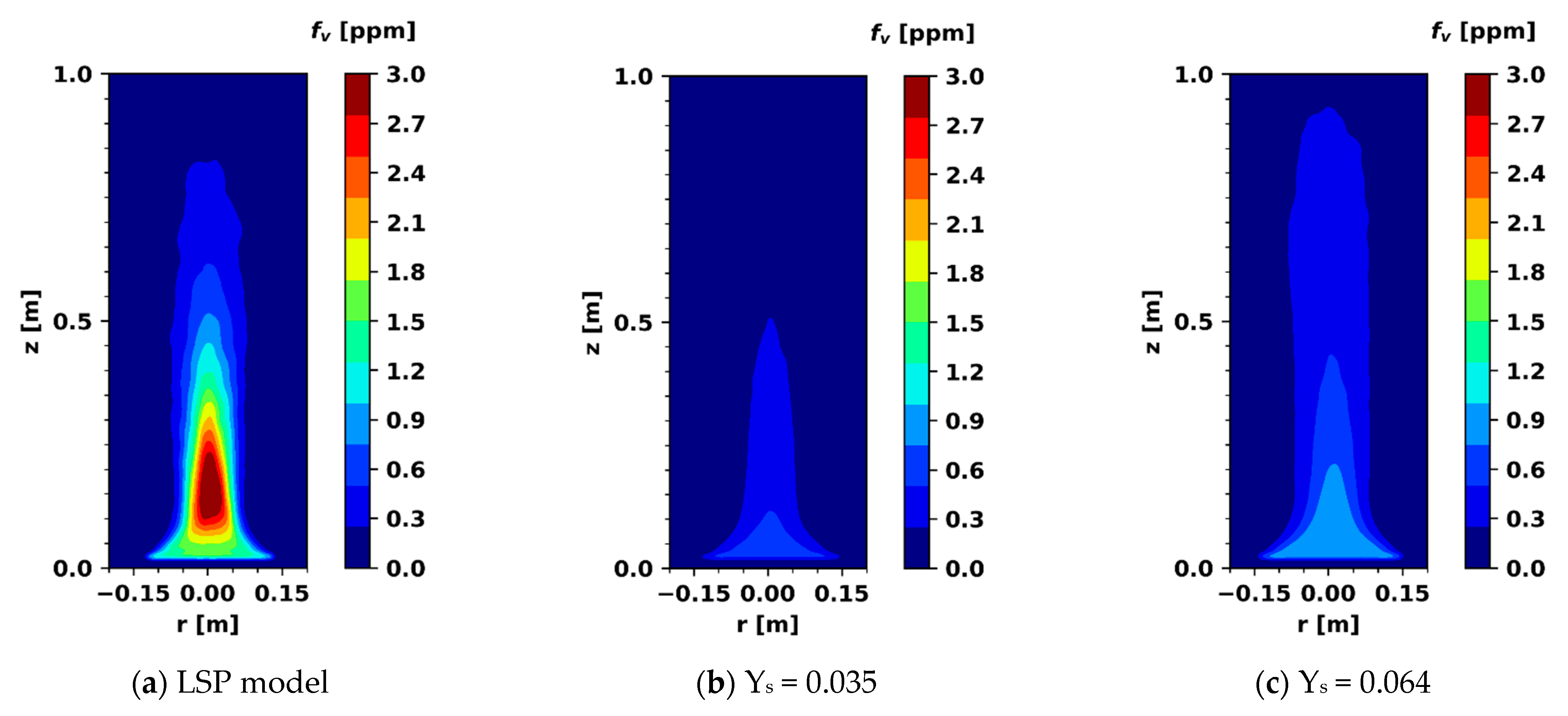
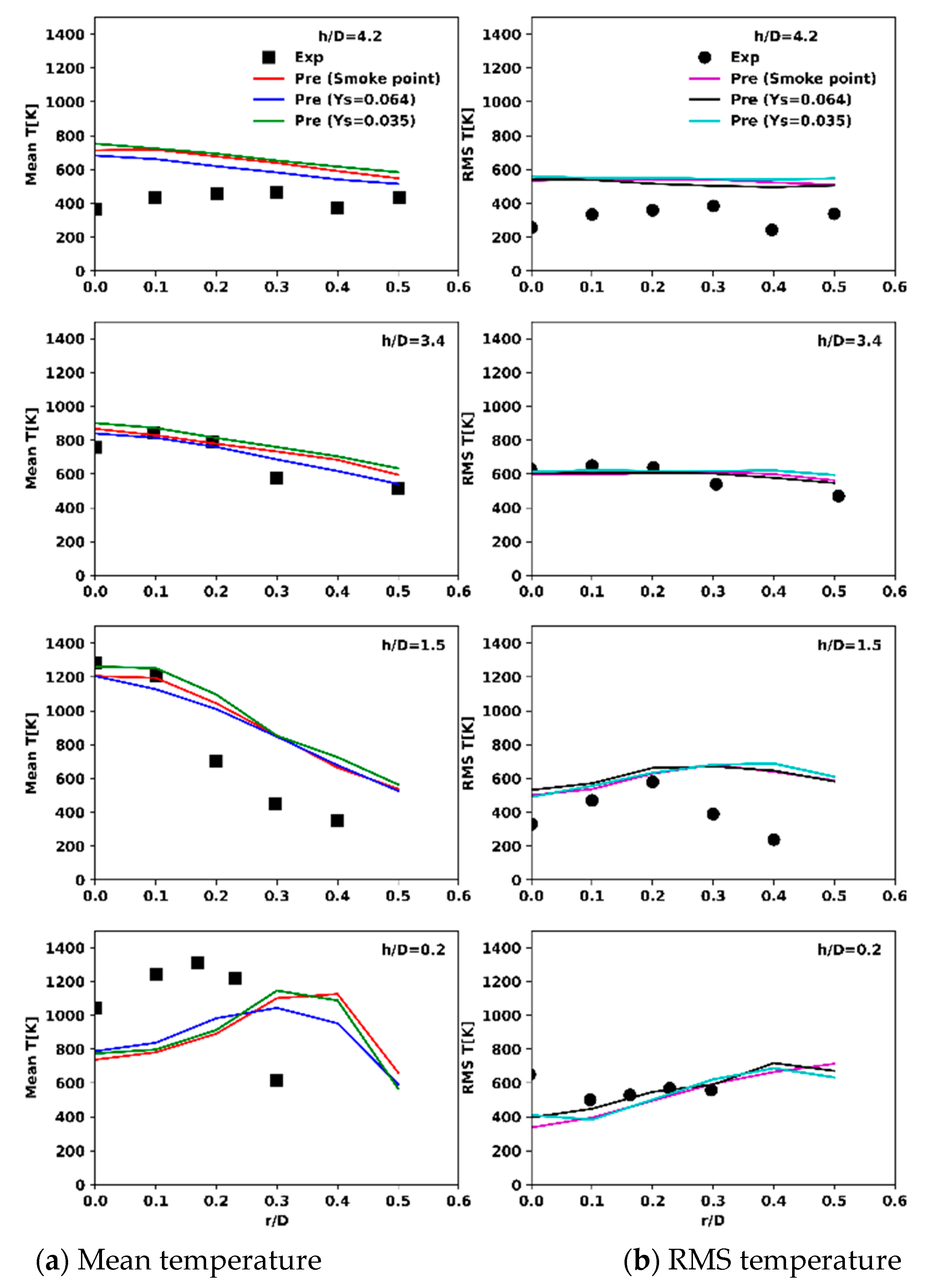
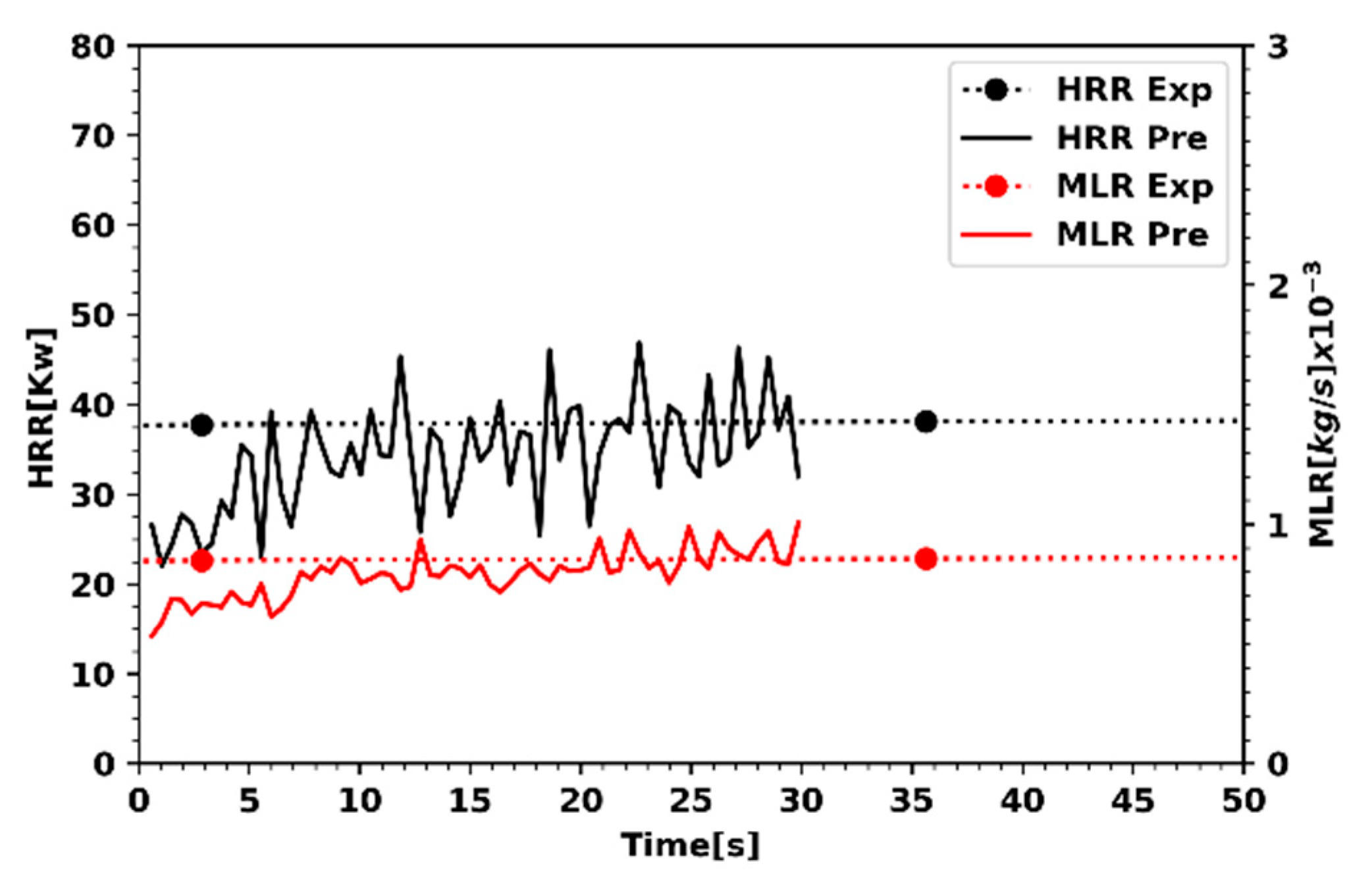
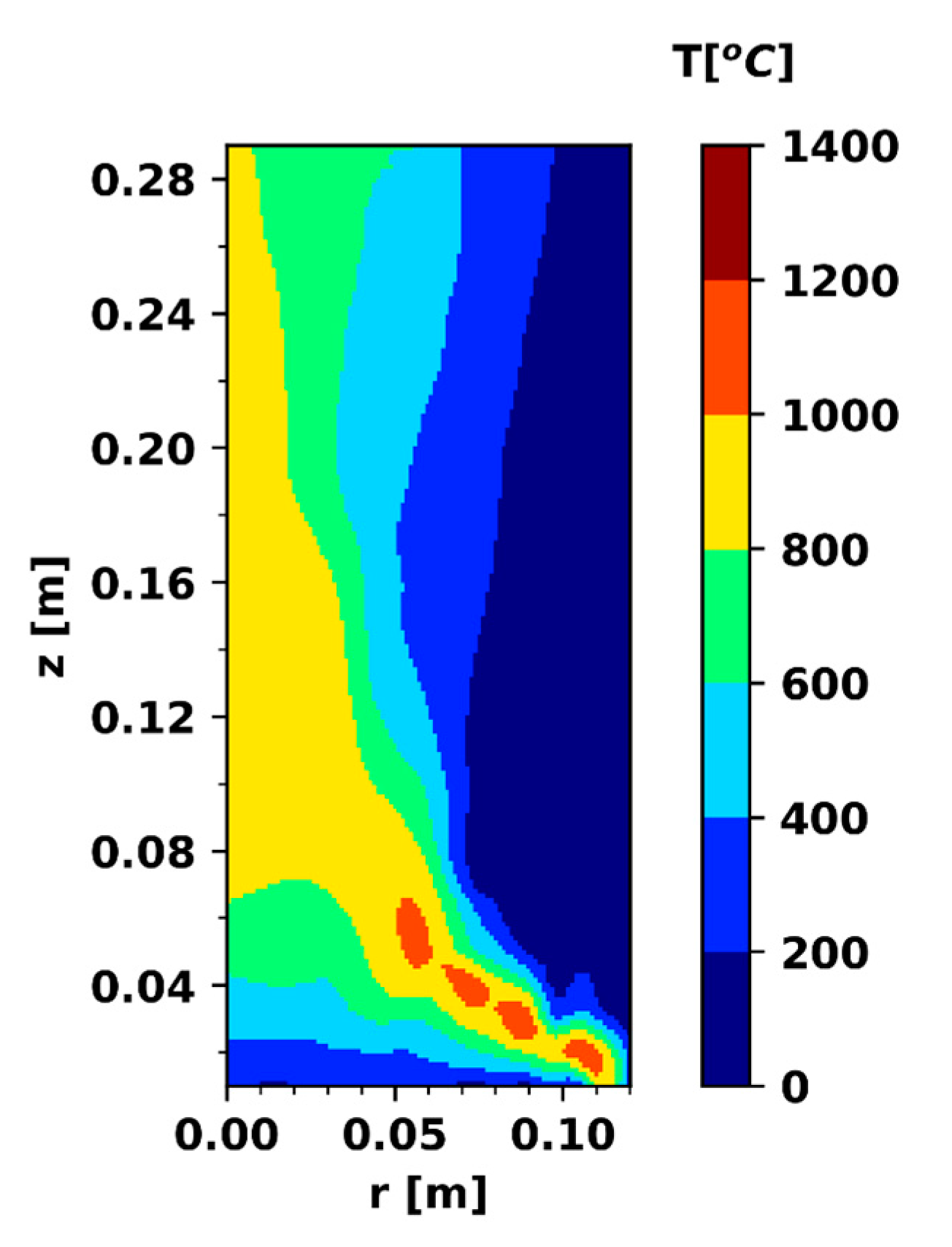
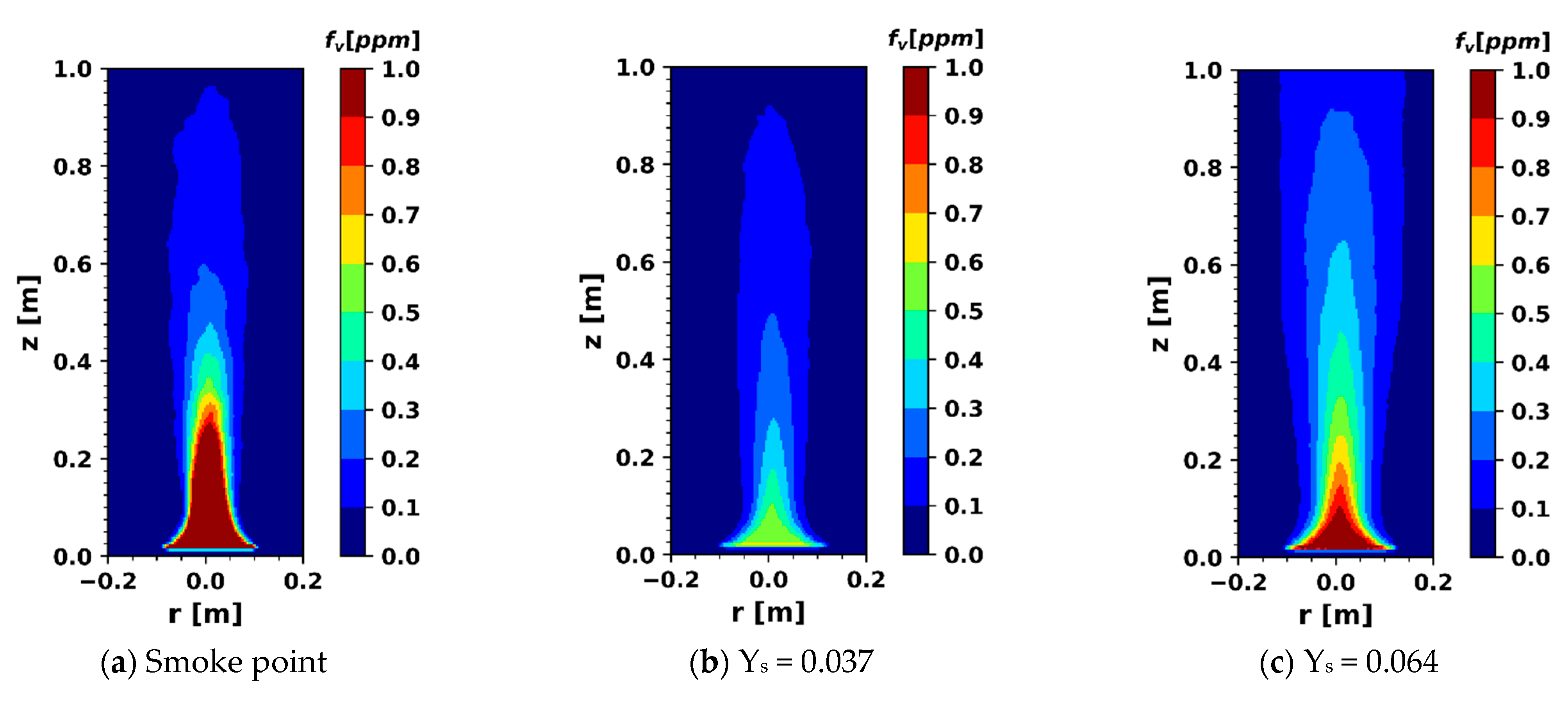
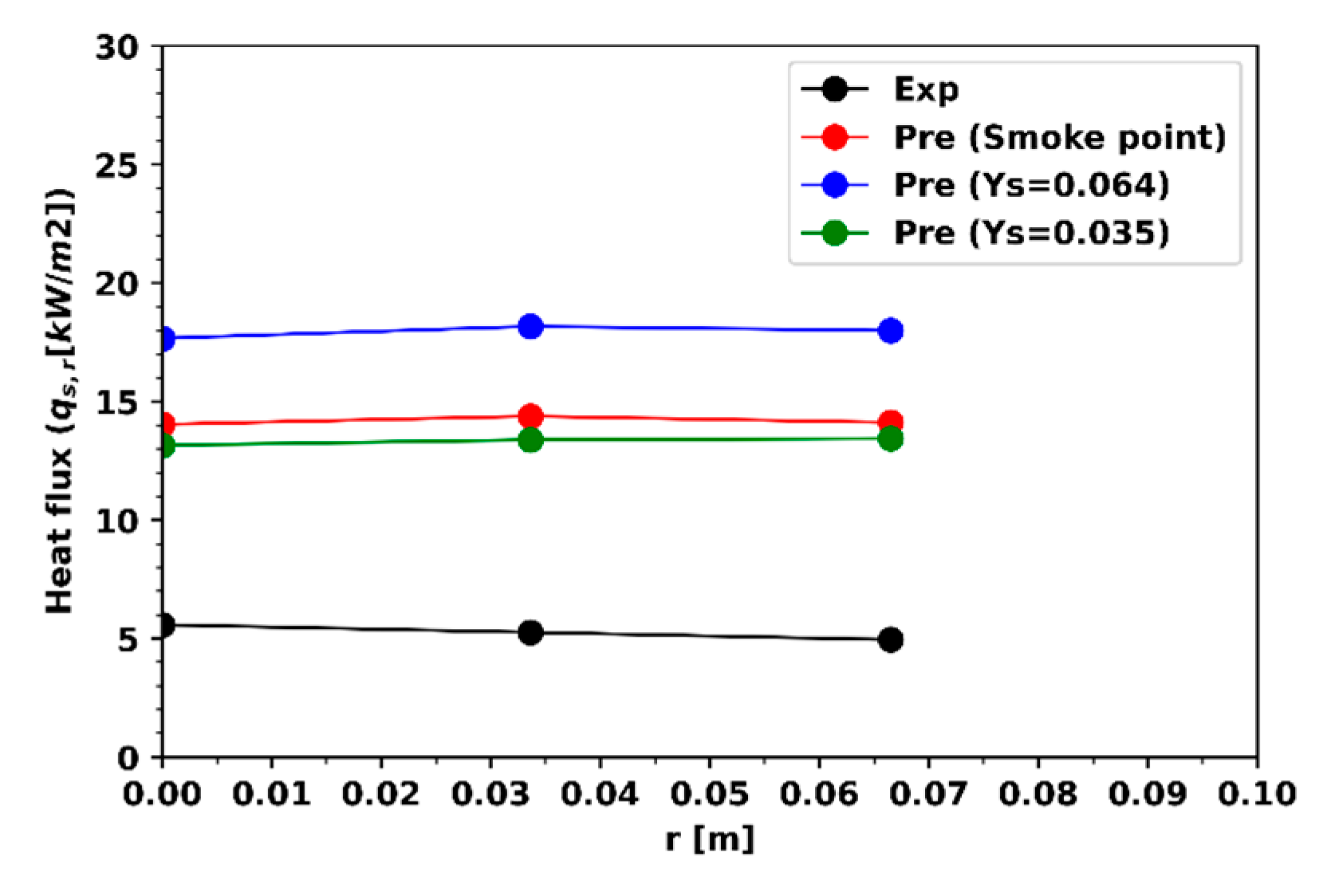
3.2. Heptane Pool Fire of 30 cm
3.3. Heptane Fire of 23 cm
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guibaud, A.; Consalvi, J.L.; Orlac’h, J.M.; Citerne, O.J.M.; Legros, G. Soot production and radiative heat transfer in opposed flame spread over a polyethylene insulated wire in microgravity. Fire Technol. 2020, 56, 287–314. [Google Scholar] [CrossRef]
- Lui, F.; Guo, H.S.; Gregory, J.; Smallwood, J.; Ömer, L. Effects of gas and soot radiation on soot formation in a coflow laminar ethylene diffusion flame. J. Quant. Spectrosc. Radiat. Transf. 2002, 73, 409–421. [Google Scholar]
- Anderson, H.; McEnally, C.S.; Pfefferle, L.D. Experimental study of naphthalene formation pathways in non-premixed methane flames poped with alkylbenzenes. Proc. Combust. Inst. 2000, 28, 2577–2585. [Google Scholar] [CrossRef]
- Leung, K.M.; Lindstedt, R.P.; Jones, W.P. A simplified reaction mechanism for soot formation in nonpremixed flames. Combust. Flame 1991, 87, 289–305. [Google Scholar] [CrossRef]
- Nmira, F.; Consalvi, J.L.; Demarco, R.; Gay, L. Assessment of semi-empirical soot production models in C1-C3 axisymmetric laminar diffusion flames. Fire Saf. J. 2015, 73, 79–92. [Google Scholar] [CrossRef]
- Wen, Z.; Yun, S.; Thomson, M.J.; Lightstone, M.F. Modeling soot formation in turbulent kerosene/air jet diffusion flames. Combust. Flame 2003, 135, 323–340. [Google Scholar] [CrossRef]
- Yao, W.; Zhang, J.; Nadjai, A.; Beji, T.; Delichatsios, M.A. A global soot model developed for fires: Validation in laminar flames and application in turbulent pool fires. Fire Saf. J. 2011, 7, 371–387. [Google Scholar] [CrossRef]
- Chatterjee, P.; Wang, Y.; Meredith, K.V.; Porofeev, S.B. Application of a subgrid soot-radiation model in the numerical simulation of a heptane pool fire. Proc. Combust. Inst. 2015, 35, 2573–2580. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire Dynamics Simulator, Technical Reference Guide, 6th ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Xin, Y.; Gore, J.P. GORE, Two-dimensional soot distributions in buoyant turbulent fires. Proc. Combust. Inst. 2005, 30, 719–726. [Google Scholar] [CrossRef]
- Klassen, M.; Gore, J.P. Structure and Radiation Properties of Pool Fires; Technical Report NIST-GCR-94-651; US Department of Commerce: Washington, DC, USA, 1994. [Google Scholar]
- Garo, J.P.; Vantelon, J.P.; Lemonnier, D. Effect on radiant heat transfer at the surface of a pool fire interacting with a water mist. J. Heat Transf. 2010, 132, 023503. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Andersen, J.; Rasmussen, C.L.; Giselsson, T.; Glarborg, P. Global combustion mechanisms for use in CFD modelling under oxy-fuel conditions. Energy Fuels 2009, 23, 1379–1389. [Google Scholar] [CrossRef]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Torero, J.L.; Watts, J.M., Jr.; Wieczorek, C.J. SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Hunt, R.A. Relation of smoke point to molecular structure. Ind. Eng. Chem. 1953, 45, 602–606. [Google Scholar] [CrossRef]
- Frenklach, M.; Wang, H. Detailed modelling of soot particle nucleation and growth. Proc. Combust. Inst. 1990, 23, 1559–1566. [Google Scholar] [CrossRef]
- Moss, J.B.; Stewart, C.D.; Young, K.J. Modelling soot formation and burnout in a high temperature laminar diffusion flame burning under oxygen-enriched conditions. Combust. Flame 1995, 101, 491–500. [Google Scholar] [CrossRef]
- Delichatsios, M.A. A phenomenological model for smoke point and soot formation in laminar flames. Combust. Sci. Technol. 1994, 100, 283–298. [Google Scholar] [CrossRef]
- Lee, K.B.; Thring, M.W.; Beer, J.M. On the rate of combustion of soot in a laminar soot flame. Combust. Flame 1962, 6, 137–145. [Google Scholar] [CrossRef]
- Murty Kanury, A. Introduction to Combustion Phenomena; Gordon: New York, NY, USA, 1984; ISBN 0-677-02690-0. [Google Scholar]
- Stroup, D.; Lindeman, A. Verification and Validation of Selected Fire Models for Nuclear Power Plant Applications; NUREG-1824, Supplement 1; United States Nuclear Regulatory Commission: Washington, DC, USA, 2013; pp. 37–48. [Google Scholar]
- Acherar, L.; Wang, H.Y.; Garo, J.P.; Coudour, B. Impact of air intake position on fire dynamics in mechanically ventilated compartment. Fire Saf. J. 2020, 118, 103210. [Google Scholar] [CrossRef]





| Property | Heptane |
|---|---|
| Conductivity, k (W/m.K) | 0.17 |
| Density, (kg/m3) | 684 |
| Heat capacity, Cp (kJ/kg.K) | 2.24 |
| Pyrolysis heat, Lv (kJ/kg) | 321 |
| (kJ/kg) | 44,500 |
| Boiling temperature, Tb (°C) | 98 |
| Absorption coefficient (m−1) | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acherar, L.; Wang, H.-Y.; Coudour, B.; Garo, J.P. Assessment of Semi-Empirical Soot Modelling in Turbulent Buoyant Pool Fires from Various Fuels. Thermo 2023, 3, 424-442. https://doi.org/10.3390/thermo3030026
Acherar L, Wang H-Y, Coudour B, Garo JP. Assessment of Semi-Empirical Soot Modelling in Turbulent Buoyant Pool Fires from Various Fuels. Thermo. 2023; 3(3):424-442. https://doi.org/10.3390/thermo3030026
Chicago/Turabian StyleAcherar, Lahna, Hui-Ying Wang, Bruno Coudour, and Jean Pierre Garo. 2023. "Assessment of Semi-Empirical Soot Modelling in Turbulent Buoyant Pool Fires from Various Fuels" Thermo 3, no. 3: 424-442. https://doi.org/10.3390/thermo3030026
APA StyleAcherar, L., Wang, H.-Y., Coudour, B., & Garo, J. P. (2023). Assessment of Semi-Empirical Soot Modelling in Turbulent Buoyant Pool Fires from Various Fuels. Thermo, 3(3), 424-442. https://doi.org/10.3390/thermo3030026





