Abstract
This paper outlines the key developments in the second generation of the Eurocodes, with a focus on the integration of rock engineering into the updated Eurocode 7—Geotechnical Design (EN 1997). It introduces the various methodologies used for safety verification of geotechnical structures and provides a brief overview of limit state design, including the semi-probabilistic approach and other reliability-based methods. The paper details the introduction of specific partial factors for intact rock, rock mass, and discontinuities and discusses specific aspects of the design of spread foundations on rock using calculations. This includes the shift from traditional global safety factor methods to the partial factor format prescribed by Eurocode 7, as well as the use of fully probabilistic analyses. To assess the practical implications of these updates, a case study on the design of a spread foundation is presented. The study compares three design approaches: the global safety factor method (based on mean values of actions and strength properties), the Eurocode 7 partial factor method (using characteristic values), and a probabilistic method (based on statistical distributions). Additionally, the paper examines the application of two failure criteria—Mohr–Coulomb and Hoek–Brown—in the calculation process.
1. Introduction
1.1. The Structural Eurocode System and Its Evolution to the Second Generation
The structural Eurocodes are a suite of European standards (EN 199x) for the design of buildings and civil engineering works. EN 1990 [1] sets the basis of structural and geotechnical design, while the other Eurocodes address different materials and specific design aspects. Geotechnical design is covered by EN 1997 [2,3,4], also known as Eurocode 7.
Their implementation started in 2010, when contradictory national standards were withdrawn. The revision of the Eurocode system was initiated in 2012 by the European Committee for Standardization (CEN). The primary goals were to incorporate improvements reflecting the state of the art in engineering design and the needs of the civil engineering market, to improve the ease of use, and to harmonize practice between countries. While the original version of Eurocode 7 [5,6] was developed largely based on soil mechanics, the revised version aims to give equal consideration to both soil and rock in geotechnical design.
For Eurocode 7, plans were laid to make the following changes:
- Restructuring the document to make it more consistent with other Eurocodes, easier to understand and navigate, more comprehensive in its technical coverage, and easier to add new topics.
- Improving guidance on selecting characteristic ground parameters and designing water pressures, application of numerical methods, rock engineering, and dynamic design.
- Improving ease of use by clarifying existing clauses, removing repetitions, and removing unnecessary information.
The second generation of the Eurocodes is now nearly completed, with the revised EN 1997 formally approved and published. All updated Eurocodes share a common latest date of publication set for September 2027. This will be followed by the latest date of withdrawal in March 2028, by which time existing standards must be withdrawn. From that point forward, all rock engineering design will be required to comply with the new Eurocode provisions.
Eurocode 7 has undergone significant restructuring and is now divided into three parts:
- Part 1—General rules (EN 1997-1 [2]). This part supplements EN 1990 [1] by setting out additional principles and requirements for the safety, serviceability, robustness, and durability of geotechnical structures. Design and verification are based on the partial factor method or other reliability-based methods, prescriptive rules, testing, or the observational method.
- Part 2—Ground properties (EN 1997-2 [3]). This part establishes rules for obtaining information about the ground at a site, necessary for the design and execution of geotechnical structures, including temporary geotechnical structures.
- Part 3—Geotechnical structures (EN 1997-3 [4]). This part establishes principles and requirements for the design and verification of: (i) permanent or temporary geotechnical structures (slopes, cuttings, embankments, shallow foundations, piled foundations, retaining structures, reinforced fill structures, soil nailed structures, and ground improvement); (ii) supporting elements (anchors, reinforcing elements in reinforced fill structures, soil nails, rock bolts and rock surface support, and ground improvement); (iii) groundwater control measures (reduction of hydraulic conductivity, dewatering and infiltration, and the use of impermeable barriers).
Significant changes and additions have been made to EN 1997 concerning rock engineering [7,8,9,10]. These include:
- Clear definitions of rock, rock masses, and discontinuities, with explicit consideration of the discontinuous nature of rock masses.
- Recognition that rock mass geometrical properties—such as discontinuity spacing and orientation—can be treated probabilistically.
- Recognition that ground properties must consider the geometrical properties of the discontinuities when they affect the mechanical behavior of the ground.
- Recognition that reliability-based methods may be used.
- Understanding that risk-informed approaches may apply in design situations where uncertainties or consequences are outside common ranges.
- Inclusion of rock mass classification systems.
- Inclusion of the physical and chemical properties relevant to rock.
- Acknowledgement of the potential need to determine in situ stress states, along with methods for their assessment.
- Introduction of specific failure envelopes for rock, rock masses, and discontinuities, along with specific aspects of rock and rock mass deformability.
- Identification of failure mechanisms specific to rock masses.
- Specification of partial factor values on ground properties for rock, rock masses, and discontinuities.
- Increased attention given to the use of the observational method and prescriptive rules in rock engineering design.
- Design considerations for rock anchors, rock bolts, and surface support systems.
- Guidance on groundwater control measures in rock engineering applications.
1.2. Application of the Second Generation of the Eurocodes to the Design of Spread Foundations
Limit state design, as defined in EN 1990 [1], is applied consistently across all Eurocodes, including those for geotechnical structures. Verification of limit states, such as bearing failure, may be carried out through calculation (using the partial factor method or other reliability-based approaches), prescriptive rules, testing, or the observational method.
The design of spread foundations follows the principles given in EN 1997-1 [2] and is addressed in detail in Clause 5 of EN 1997-3 [4]. While this clause primarily focuses on foundations on soil and fill, it also includes provisions for spread foundations on rock. Regarding the design situations, reference is made to the particular features of rock, such as discontinuities, weathering, and susceptibility to scouring.
For the bearing resistance of spread foundations on a rock mass, Eurocode 7 distinguishes between two cases: the rock mass may be treated either as a discontinuous medium or as an equivalent continuous medium. In the discontinuous case, the bearing resistance is verified using the shear strength along discontinuities, determined in accordance with EN 1997-2 [3], where the Barton–Bandis and Mohr–Coulomb failure envelopes are referenced. Potential failure mechanisms such as planar sliding, wedge sliding, and toppling must be considered in the analysis. In the continuous case, the bearing resistance is verified using the shear strength of the intact rock or rock mass. Both the Hoek–Brown and the Mohr–Coulomb failure envelopes may be applied. A calculation model based on rock wedge equilibrium is provided in Annex B of EN 1997-3 [4] to support this analysis.
The aim of this paper is to present the key aspects involved in the design of spread foundations on rock masses in accordance with the second generation of the Eurocodes. A very simple geotechnical structure has been selected to clearly illustrate the complete design process, as outlined in the relevant Eurocode provisions. The study also explores various approaches for verifying the bearing failure limit state, thereby providing a comprehensive understanding of the procedures and options available within the updated regulatory framework.
Section 2 provides a detailed overview of the relevant sections of Eurocode 7 pertaining to the design of spread foundations on rock masses. These provisions form the basis for the calculations and verifications developed in the subsequent sections. Section 3 introduces the case study—a strip spread foundation on a rock mass—describing its geometry, the applied actions, and the ground properties. This section also outlines the methodologies used for safety verification by means of deterministic, semi-probabilistic, and probabilistic approaches, using the Hoek–Brown and the Mohr–Coulomb failure envelopes. Section 4 explains how the fundamental input parameters required for each verification approach are obtained, including data related to actions, geometry, and ground conditions. Section 5 presents the verification of the bearing failure limit state using the three approaches, along with a comparative analysis of the results. Section 6 discusses the rationale behind the choices made, the procedures adopted, and the results obtained. Finally, Section 7 summarizes the main conclusions of the study.
2. Design of Spread Foundations on Rock Mass in Eurocode 7
2.1. Basis of Limit State Design in Eurocode 7 in EN 1990 and EN 1997-1
2.1.1. General
The limit state design framework of the Eurocodes requires the consideration of all the relevant failure modes associated with a given geotechnical structure. For spread foundations, the bearing and sliding failures due to possible load combinations are considered as primary ultimate limit states (ULSs) in most practical design applications.
For spread foundations, to prove that a given ULS is not exceeded at the design stage, verification by calculation is the preferred method, where a specific reliability level needs to be achieved. This reliability level is achieved by appropriate adoption of representative values of loads and ground properties, selection of an appropriate calculation model, and providing a sufficient margin of safety to ensure the probability of failure is sufficiently low [11,12,13,14]. Such an approach is intended to address the design uncertainties closer to their source. This contrasts with the traditional practice of using global safety factors (SF), often on the order of SF = 2 to 3 [15], which were intended to provide sufficiently large margins of safety without the need for detailed consideration of uncertainties [12].
The calculation methods for verification of adequate performance presented in the Eurocodes are based on the partial factor method (semi-probabilistic approach) or other reliability-based methods, including fully probabilistic approaches. The former combines the selection of representative values and the use of prescribed partial factors to address the design uncertainties and the reliability level (or safety margin), while the latter makes use of probabilistic concepts and explicit consideration of design uncertainties. The partial factor method is the default method of limit state verification in the Eurocodes, used in common design situations, while fully probabilistic approaches are intended primarily for unusual design situations, including limit states sensitive to geometrical uncertainties, and code calibration.
As an alternative to calculations, prescriptive measures may be applied for limit state verification, although no default prescriptive approach is specified. The chart-based approach to estimate the presumed bearing capacity, presented in the first-generation Eurocode 7, following an older British standard [16], was removed in the new version of the standard. However, it could still be used if allowed in the national annex of a specific country.
2.1.2. Reliability-Based Design
In reliability-based design, probabilistic models consisting of random variables, stochastic processes, and random fields are applied to represent design uncertainties [14,17,18]. All sources of uncertainties relevant to the verification of performance should be considered. The exception is the uncertainty associated with the possibility of gross human error, which is difficult to address explicitly, and it is supposedly minimized by appropriate quality control procedures and measures [1,2,19].
Three consequence classes (CC1, CC2, and CC3) are considered for geotechnical structures and the target reliability levels have different values for each of them, as presented in Table 1 [1]. The target reliability indexes (β) and probabilities of failure (Pf) associated with them are generally based on the risk tolerance of the society rather than the number of observed failures.

Table 1.
Target values of reliability index in relation to consequence classes [1].
2.1.3. Partial Factors in the Semi-Probabilistic Framework
In the semi-probabilistic framework, utilizing partial factors for ensuring a sufficient reliability level, partial factors are applied to representative values of actions, material properties, and resistances to obtain their design values. For spread foundations, the verification of the ULS of bearing failure using partial factors is based on the material factor approach (MFA) or the resistance factor approach (RFA). It is worth noting that, conceptually, the RFA is very similar to the load and resistance factor design (LRFD) used in many guidelines [20,21]. The sets of partial factors relevant for spread foundations on rock mass, as considered in this paper, are presented in Table 2. The factoring approach is based on the use of combinations of sets of factors for actions or effects of actions represented by verification cases (VC), and for material properties (M).

Table 2.
Partial factors for verification of bearing resistance of spread foundations for fundamental design situations [4].
The default values of the partial factors in the Eurocodes were selected based on theory combined with calibration to existing practice [22]. Furthermore, the use of MFA and RFA resulted from the different national approaches adopted in European countries. Those default values can be further modified in national annexes to better match overall safety levels achieved in past practices [23]. This gives each country more flexibility in the selection of their targeted level of reliability.
When the MFA is used, either both (a) and (b) or single (c) combination is used. For RFA, the distinction is made between factoring actions (VC1) and effects of actions (VC4). Design values of actions or effects of actions (Ed) are obtained based on the following general equations, respectively:
where Fd, Fk, and Frep denote the design, characteristic, and representative values of actions, respectively, ad denotes the design value of geometrical properties, XRd and Xrep denote the design and representative values of material properties, γF, γE are partial factors on actions and effects of actions, respectively, and ψ denotes the set of combination factors.
The partial factors for actions and effects of actions for persistent and transient design situations for different types of structures are presented in EN 1990 [1], which ensures consistency of factoring of loads between structural and geotechnical design. Selected values for verification cases for structural resistance and geotechnical design of building structures are presented in Table 3. Those partial factors are applied to load values together with combination factors, which are relevant when more than one source of variable actions is considered in the analysis. To allow for differentiation of reliability levels in the semi-probabilistic framework, consequence factors (kF = 0.9 to 1.1) are used to modify the basic values of the factors.

Table 3.
Partial factors on actions and their effects for verification cases VC1 to VC4 [1].
The design value of resistance (Rd) considering a specific design situation and load combination should be calculated based on the following general equation:
where γRd is the partial factor associated with the uncertainty of the resistance model and geometric deviations not modeled explicitly, η is a conversion factor accounting for scale effects and other relevant parameters, γm is the partial factor on material property, accounting for unfavorable deviation of material property from its characteristic value, Xk represents the characteristic values of material properties, and FEd is for design values of actions.
This equation takes the following forms depending on whether the MFA or RFA factoring approach is considered, respectively:
where Xd is the design value of a material property.
The design values of material properties in the MFA are obtained by applying the specified partial factors to relevant ground properties using the equation below. Selected values of partial factors for material properties relevant for design of spread foundations on rock are summarized in Table 4. Similarly to factors on actions, in this case consequence factors (kM = 0.9 to 1.1) are also implemented for reliability differentiation.

Table 4.
Partial factors on material properties [2].
It should be noted that partial factors to be used for rock material or for rock mass should be applied to the shear strength and not to parameters specific to a failure envelope. They can be used for linear and non-linear envelopes, such as Mohr–Coulomb and Hoek–Brown. With regard to the value of γqu, its inclusion in this table may cause some confusion, because its application to the unconfined compressive strength in the context of a shear failure envelope, such as Hoek–Brown, basically reverts the verification to the equivalent of the RFA.
As can be seen in Table 3 and Table 4, the values of partial factors for consideration in the respective sets of factors should be modified by consequence factors, increasing or decreasing the expected reliability level depending on the importance of the structure and potential consequences of failure. Default values of consequence factors are summarized in Table 5. It should be noted that the consequence factor should be applied to either actions, material properties, or resistances, not to all of them. In the context of spread foundation analysis, the consequence factors for resistances are not used in either the MFA or RFA since only a single consequence factor should be applied. Furthermore, when the single MFA combination (c) is considered, the consequence factor on material properties is omitted and only the consequence factor on actions is applied.

Table 5.
Consequence factors [2].
2.1.4. Consideration of Geometrical Uncertainties
In addition to the application of partial safety factors, geometrical uncertainties should be considered when the design is sensitive to deviations of geometrical properties. The design value of geometrical properties (ad) can be obtained from the following equation [1]:
When the design is not significantly sensitive to those deviations (Δa), the design value can be assumed as equal to the nominal value (anom).
In the case of spread foundations [4], the design width of a rectangular foundation (Bd) should be calculated as the nominal width (Bnom) reduced by the assumed deviation (ΔB), following Equation (8), unless said otherwise in the national annex or unless measures are specified and taken to control the dimensions of a cast-in-place concrete foundation. The default value of the considered deviation is ΔB = 0.1 m.
2.2. Rock Mass Behavior and Ground Properties in EN 1997-1 and EN 1997-2
EN 1997-1 [2] clearly distinguishes continuous and discontinuous behavior of rock mass and its implications for the design process. In EN 1997-2 [3], for rock masses considered as a continuum medium the Hoek–Brown failure envelope [24] may be used, with Mohr–Coulomb as an acceptable alternative approach. This assumption applies when the limit state considered in the analysis is not controlled by discontinuities or other discreate geological features.
Strength of discontinuities with rock-to-rock surface contact may be described using linear (Mohr–Coulomb) or non-linear (Barton–Bandis) failure envelopes. For infilled rock discontinuities without rock-to-rock surface contact, only the Mohr–Coulomb failure envelope is recommended by the standard. Other alternative approaches are permitted provided they are sufficiently validated.
Characteristic values of ground properties are defined as statistically determined values of ground properties that affect the occurrence of a limit state. Conversely, nominal values are cautious estimates established on a non-statistical basis, usually based on expert judgement. The values considered as representative in the verification of a considered limit state are selected based on these nominal or characteristic values. Although the standard allows for the use of either of those approaches, in reality, a combination of statistical methods and expert judgement is often used in practical design when selecting the ground properties.
The described selection process is intended to address the underlying uncertainties involved in characterization of the ground. The underlying assumption behind the selection of representative ground properties in the Eurocodes on a statistical basis is to achieve a sufficient probability that the actual value is not lower than the characteristic value (Xk). When statistical analysis is used to estimate the relevant ground property, the following equation can be used when normal or log-normal (after proper data transformation) distributions can be assumed:
where Xmean is the mean value of the material property, kn is the coefficient that depends on the number of sample-derived values used to evaluate the mean, and Vx is the coefficient of variation of the material property, considering inherent ground variability and measurements and transformation errors.
As the coefficient of variation can be known from prior knowledge only based on evaluation of previous tests conducted in comparable situations, in many design situations, this approach will not be applicable due to a lack of reference data. Furthermore, the alternative approach, based on the lack of initial assumptions about the ground property variability, will often lead to very conservative estimates. Therefore, indicative values of Vx were proposed in EN 1997-1 [2], as presented in Table 6, which are expected to be used most often. However, it should be noted that, even in this case, as the range of values is provided, some level of expert judgement must be utilized.

Table 6.
Indicative values of coefficient of variation for different rock properties [2].
These ranges of coefficients of variation, as presented in an informative annex of EN 1997-1 [2], were based on literature review; however, most of those values were derived from data obtained for soils. No indicative values are given for the parameters of non-linear failure envelopes, such as Hoek–Brown. This difficulty will be treated in the case study presented in this paper.
2.3. Bearing Failure Limit State for Spread Foundations in EN 1997-3
Specific design requirements for spread foundations are presented in clause 5 of EN 1997-3 [4]. This includes the specific requirements of verification of the bearing failure limit state. The main text of the standard outlines the procedure of verification, only generally addressing the choice of calculation model used for prediction of bearing capacity. Eurocode 7 states that the calculation model should account, among other things, for failure mechanisms and the associated strength of the ground, including its discontinuities. Although not explicitly stated, it is the designer’s responsibility to use a calculation model which is sufficiently representative for the design situation and the limit state considered.
As jointing characteristics usually govern the possible failure modes of the rock, the main design decision is related to the assumed behavior of the rock mass. Depending on the level of jointing, rock may be considered as a discontinuum or equivalent continuum medium. However, it has to be recognized that, in both cases, the simple analytical or empirical methods can provide only an approximate estimate of the bearing capacity [25].
Eurocode 7 requires that the design bearing resistance normal to base (RNd) shall be sufficient to resist the normal component of the resulting force acting on the foundation base (Nd), based on the following equation:
Depending on the possible load combinations, more than one design situation might have to be considered, e.g., when normal force acts as a favorable or unfavorable action, as this affects the design eccentricity of the applied load. When the foundation is subjected to such eccentric loading, the eccentricity should be determined using design values of actions, considering the partial factors.
Limits on maximum design eccentricity may be imposed at the national level. However, to limit the physical gap beneath the strip foundation, Eurocode 7 requires that the ratio of eccentricity (eB) to the foundation width (B), under permanent and variable action effects at serviceability limit states, should not exceed:
2.4. Calculation Model for Spread Foundations on Continuous Rock
The normative text of Eurocode 7 does not prescribe a specific calculation model for prediction of bearing resistance, but it suggests using the calculation model presented in the informative Annex B of EN1997-3 [4], in section B.16. This is an analytical limit equilibrium model, retrieved from Wyllie [15], based on rock mass strength properties and wedge equilibrium, as presented in Figure 1.
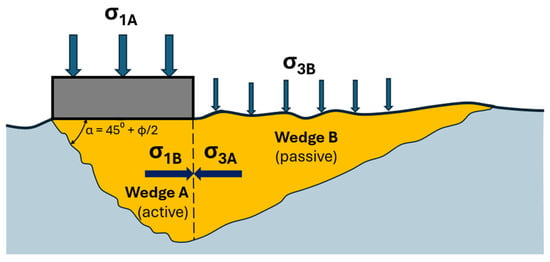
Figure 1.
Bearing capacity model for spread foundations based on wedge failure [4,15].
Although not explicitly stated in Eurocode 7, according to the original reference [15], different equations should be used for foundations, which are embedded deeper in the rock mass, or for weak rocks with little fracturing, considering different confining stresses. Moreover, when joint sets are aligned with the surfaces of the passive wedge, the joint strength will dictate the capacity rather than equivalent continuum behavior. For more complex cases, numerical models, accounting for particular design situations, should be used.
The bearing resistance RN normal to the base of the spread foundation is given by
where A′ is the effective area of the footing; Cf1 is a shape correction factor (1.0 for strip footing); and σ1A is the major principal stress. Assuming the rock mass as a continuous medium and the wedge failure mechanism, the Hoek–Brown and the Mohr–Coulomb failure envelopes, expressed in terms of principal stresses are, respectively, given by:
where σci is the unconfined compressive strength, mb, s, and a are the parameters of the Hoek–Brown failure criterion, and c′ and φ′ are the parameters of the Mohr–Coulomb failure criterion, effective cohesion and effective friction angle, respectively.
The effective area of the foundation (A′) is estimated based on effective width (B′) and length (L′ = 1 m for strip foundation) of the foundation (EN 1997-3 [4], 5.5.2.1 (2), Formula (5.2)) as:
where the design eccentricity (eb) for a strip foundation is determined using design actions in terms of overturning moment (Md) and the force normal to the base (Nd):
3. Case Study
3.1. Basic Assumptions
The calculation example of a strip spread foundation on rock mass is considered. Its assumptions are based on the example to be published in the Report of the Joint Research Centre of the European Union (JRC), containing design examples using the second-generation Eurocode 7 [26], intended to provide additional guidance for the implementation of the second-generation Eurocode.
The purpose of this example is to calculate the bearing resistance of a strip footing, with an assumed thickness of 1.0 m, founded on a rock mass considered as a continuous medium, to support the actions shown in Figure 2, applied at the top of the foundation. No ground inclination is present near the foundation and the nominal width of the foundation is assumed to be Bnom = 4.0 m. The footing is composed of reinforced concrete with unit weight of 25 kN/m3. The permanent action is a vertical force, and the variable action is a combination of a vertical force and an overturning moment (i.e., resulting in eccentric vertical load), considered as coming from the same source; therefore, no combination factors are considered in the analysis. Characteristic values are used to quantify the actions, namely 1000 kN/m for the permanent vertical force and 500 kN/m and 200 kNm/m for the variable vertical force and the moment, respectively.
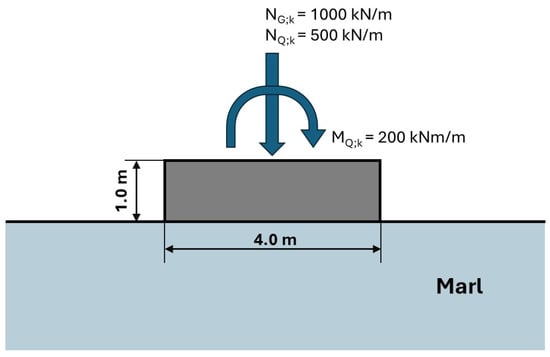
Figure 2.
Spread foundations geometry and applied actions [26].
No measures are specified for controlling the dimensions of the foundation during execution (assuming possible deviation of ∆B = 0.1 m). Therefore, the design width is determined based on EN 1997-3 [4], Equation (5.10), as:
The considered structure is assigned to consequence class CC3, with corresponding consequence factors of 1.10 on either the actions or properties (Table 5), depending on the considered verification case.
The design should be based on Eurocode 7, following the methodology detailed in Section 2. No requirements for settlement limitation were defined; therefore, verification of SLS is not considered in this example.
3.2. Ground Conditions
The ground at the site is composed primarily of a relatively homogeneous, fractured marl rock mass to a significant depth, reaching beyond the expected zone of influence of the foundation, with no water table identified. No relevant set of rock discontinuities, coinciding with the potential bearing failure path, occurs in the zone of influence of the foundation, which could form a failure mechanism driven only by joint strength; therefore, the rock mass is considered as an equivalent continuous medium. Therefore, the model presented in Eurocode 7 is applicable in its default form.
The Hoek–Brown strength envelope is considered to characterize the rock mass. Selection of representative values of the rock mass properties was originally beyond the scope of the example. The characteristic values of parameters for the rock material within the zone of influence of the foundation were assumed as representative in the design:
- Geological Strength Index: GSI = 40
- Uniaxial compressive strength of intact rock: σci = 5.0 MPa
- Non-dimensional material parameter: mi = 7
- Disturbance factor: D = 0
Based on those values, the following parameters of the Hoek–Brown failure criterion for the rock mass were calculated based on EN 1997-2 [3] Annex E.6, Equations (11)–(13):
3.3. Methodologies Used for Safety Verification
In the paper, safety verification methodologies using deterministic, semi-probabilistic, and probabilistic approaches are explained and applied and the results are compared. On one hand, since the application of Eurocodes is a paradigm shift from traditional design practice, it is interesting to compare the solutions obtained following the semi-probabilistic approach of the Eurocodes, based on the partial factor method, and the traditional deterministic approach of global safety factors. On the other hand, the harmonized Eurocode methodology for safety verification is a coarse approximation of a more complex probabilistic framework aimed at complying, in a simpler way, with the underlying reliability requirements. Therefore, it is also worthwhile comparing results with a fully probabilistic approach where the relevant sources of uncertainties are explicitly considered.
However, the different input data used, and the safety verification rationale followed, must be consistent across all alternatives. The basic data used in the case study are assumed to be in the format suitable for application of the Eurocode procedure—specifically as characteristic, representative, and nominal values of actions, ground properties, and geometrical properties, respectively. For the deterministic approach, mean values of actions, ground properties, and geometrical properties are needed, which were not presented in the original benchmark example, while, for the probabilistic approach, a complete set of probabilistic models are required.
Additionally, in the absence of objective data, realistic coefficients of variation and probabilistic distributions must be assumed. As noted in Table 6, there are no indicative values for the coefficients of variation of Hoek–Brown parameters. Although some studies have addressed this issue [27,28], these parameters are inherently dependent on the Geological Strength Index (GSI), which is a property often determined subjectively in practice. This makes it challenging to establish a common dataset suitable for all approaches. As an alternative, expressing the bearing resistance (Equation (12)) in terms of Mohr–Coulomb parameters offers a solution. In this case, one can adopt indicative values of coefficient of variation presented in Table 6 and the probability distributions suggested in the Eurocodes to derive probabilistic models consistent with the given information.
For this reason, the next section focuses on deriving the input data required for all approaches, not only in terms of ground properties but also regarding actions and other sources of uncertainty expected to be relevant to the analysis.
4. Derivation of Basic Input Data
4.1. Representative Values of the “Equivalent” Mohr–Coulomb Parameters
As mentioned, the case study data given presuppose the utilization of the Hoek–Brown model to estimate the bearing resistance. The given values of GSI, σci, mi, and D, and the corresponding values of mb, s, and a, are considered as representative values. To proceed with the analysis, the statistical background of these values must be recognized, making them also the characteristic values. This assumption is relevant since the equivalent values for cohesion and friction angle would then also be considered as characteristic.
Equivalent values for the friction angle and cohesion can be obtained by linearizing the Hoek–Brown envelope within a predefined range of minor principal stresses. According to the wedge equilibrium (see Figure 1), the minor principal stresses range from σ3B to σ3A, whose values in this case, according to the Hoek–Brown parameters, are, respectively,
Linearization is an optimization procedure where the squared differences between the two models are minimized by changing the unknown c and φ parameters, i.e.,
where σ1A,HB and σ1A,MC are the major principal stress below the foundation computed in terms of the Hoek–Brown parameters (Equation (13)) and Mohr–Coulomb parameters (Equation (14)), respectively. Considering the representative values of σci, mb, s, and a, equivalent values of c′ and φ′ of 60.7 kPa and 39.9° were obtained; it is worth noting that, in the semi-probabilistic approach of Eurocode 7 [2], the partial factor is not applied to the friction angle but to the coefficient of friction tanφ′ = 0.84. Figure 3 shows the adjustment of the Mohr–Coulomb envelope to the Hoek–Brown envelope, within the range of minor principal stresses between 0 and 165.25 kPa (shadowed in grey). The fitted linear approximation beyond this range would not comply with the assumed loading conditions. If significant differences between minor principal stresses would exist for different design situations, a similar fitting procedure would have to be employed to each of them.
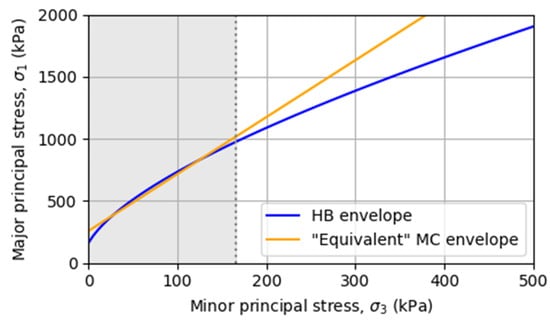
Figure 3.
Adjustment of the Mohr–Coulomb envelope to the Hoek–Brown envelope within the range of minor principal stresses from 0 to 165.25 kPa.
4.2. Mean Values of the “Equivalent” Mohr–Coulomb Parameters
In the absence of objective data, the estimation of mean values from characteristic values requires information regarding the associated percentile, the coefficient of variation, and the probability distribution adopted.
Table 6 summarizes the coefficient of variations for different ground properties, including cohesion (30 to 50%) and coefficient of friction (5 to 15%), indicated in EN 1997-1 [2], Table A.1. Although not mandatory, EN 1990 [1] and EN 1997-1 [2] state that “adopting a log-normal distribution for certain variables has the advantage that no negative values can occur” as, for instance, for geometrical, material, and resistance properties. Having that in mind and considering the large values of the coefficient of variation indicated, specifically for the cohesion, a log-normal distribution is chosen for both cohesion and coefficient of friction.
The characteristic value of a variable property Y following a log-normal distribution can be calculated based on EN 1990 [1] Annex C “Reliability analysis and code calibration”, Equation (C.15):
where Yk and Ym are the characteristic (5th percentile, p = 0.05) and mean values, respectively, VY is the coefficient of variation, and Φ−1 is the inverse normal cumulative distribution function. In this case, the distribution models illustrated in Figure 4 are obtained for the coefficient of friction and cohesion, respectively. Considering an intermediate value for the coefficient of variation (40% for the cohesion and 10% for the coefficient of friction), mean values for the cohesion and coefficient of friction of 123.3 kPa and 0.99 (φ′ = 44.7°), respectively, were obtained.
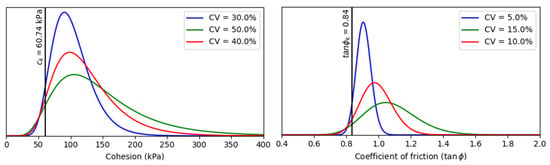
Figure 4.
Probability distributions of coefficient of friction tan φ′ (left) and cohesion c′ (right).
However, it should be recognized that, for marl rock mass, such high mean angles of friction, as presented in this example, are the result of fitting the Mohr–Coulomb envelope to the Hoek–Brown envelope at relatively low confining stresses, as well as back-calculating the mean value from the characteristic one; the latter is performed for the benefit of the calculation example and comparison with the use of the deterministic approach utilizing global safety factors. Marls are generally considered as low-friction rocks [29]. In practical design, care should be taken when selecting values of angle of friction above 40°, as, due to the nature and composition of such sedimentary material, high values of friction angles would be in the upper ranges of values reported in the literature [30,31].
4.3. Mean Values of Actions
According to the EN 1990 [1], the permanent action should be represented by a single characteristic value, taken as a mean value, provided that its coefficient of variation is small (<10%). Since it is reasonable to consider the permanent action as a dead load due to the weight of the superstructure, the JCSS Probabilistic Model Code [32] suggests, in such a case, a coefficient of variation of 4% for ordinary concrete. Furthermore, a normal distribution is assumed, also according to EN 1990 [1].
For variable actions, the procedure to determine representative values is more complex. To address the time-dependent nature of actions, such as imposed (live), wind, or snow loads, EN 1990 [1] introduces several representative values—characteristic, combination, frequent, and quasi-permanent values—each associated with a specific level of severity. This framework establishes a harmonized procedure for accounting for expected combinations of actions and for verifying both ultimate and serviceability limit states.
A representative value of a time-variable action also reflects its duration and frequency of occurrence, typically expressed in terms of a return period. Since the target values specified in EN 1990 [1] are based on a reference period of 50 years, it is generally assumed, unless stated otherwise, that the return period of the associated variable actions is also 50 years. Consequently, the probabilistic analysis to be conducted will yield a probability of failure over this time frame. Moreover, extreme-value probability distributions, such as the Gumbel distribution, are to be adopted [33] to model the uncertainty of time-variable actions. This is assumed in the case study presented.
The variable loads acting on the spread foundation, namely vertical load and moment, are assumed as imposed loads, which is typically the case for residential buildings. Modeling this type of load can be challenging, since it typically encompasses both sustained and intermittent load components with complex stochastic characteristics. For simplicity, in this case study, the variable actions are assumed to account only for the sustained component of an imposed load, for which the JCSS Probabilistic Model Code [32] indicates values for the coefficient of variation of about 50%. According to EN 1990 [1], characteristic values of variable actions correspond to the 98th percentile of their underlying probabilistic model (assuming a Gumbel distribution). In that case, the mean value can also be computed from the characteristic value, based on EN 1990 [1] Annex C, Equation (C.19):
where Yk and Ym are the characteristic (98th percentile, p = 0.98) and mean values, respectively, and VY is the coefficient of variation. Therefore, mean values of 217.8 kN/m and 87.1 kNm/m for the vertical load and moment, respectively, were obtained. In addition, given that both loads come from a single source, they should plausibly be correlated. Therefore, in the probabilistic analysis, a correlation coefficient of 0.7, reflecting a strong correlation between variable vertical load and moment, is conservatively assumed.
4.4. Other Sources of Uncertainty
4.4.1. Geometrical Properties
As mentioned, the Eurocodes recommend geometrical properties to be defined in a conservative way, especially in case the design is sensitive to deviations in their value. In the case study analyzed in this paper, a possible deviation of 0.10 m in the width of the spread foundation is assumed, due to the expected lack of execution control measures employed. This source of uncertainty can be relevant since the eccentricity of the load directly depends on the considered width of the foundation. For that reason, the nominal value adopted in the semi-probabilistic approach accounts for such deviation, and, in the probabilistic analysis, the width of the spread foundation is also considered as a random variable. The nominal value (Bnom = 4.00 m) is considered as a mean value, and the given geometrical deviation is assigned with a probability of non-exceedance of 5%, corresponding to the 5th percentile (p = 5). A normal distribution is assumed. The corresponding coefficient of variation can be estimated from EN 1990 [1] Annex C, Equation (C.13).
where again Yk and Ym are the characteristic (here assuming the design Bnom − ∆B) and mean values and VY is the coefficient of variation. A coefficient of variation of 1.5% was obtained (corresponding to a standard deviation of 0.06 m).
On the other hand, the geometric uncertainties on the superstructure are assumed irrelevant and covered by the probability distribution of the permanent action exerted on the foundation.
4.4.2. Bearing Resistance Model
Model uncertainties come across different calculation situations where simplifications or idealizations of structural or material behavior are assumed. They are expected to be covered in the Eurocodes through the partial factors and model coefficients recommended. However, in probabilistic calculations, model uncertainties should be explicitly accounted for by incorporating model error terms, treated as random variables, as outlined in EN 1990 [1] Annex C.
The calculation model for bearing resistance (Equation (12)) is affected by several sources of uncertainty due to simplifications made and idealizations of a more complex problem:
- When expressing the bearing resistance in terms of Mohr–Coulomb parameters, which are obtained by linearizing the Hoek–Brown failure envelope [24] within a specific range of minor principal stresses, there is an error due to a second-order behavior that is being ignored. A small coefficient of variation of 1% was obtained when analysing the ratio between equivalent Mohr–Coulomb and Hoek–Brown models within the fitting range (Figure 3).
- The Hoek–Brown envelope itself is an empirical model obtained after curve fitting to testing data [34]. The standard deviations obtained could be considered a measurement of the Hoek-Brown model’s uncertainty, but such values are not given. A roughly estimate of 10% for the coefficient of variation can be assumed, given the coefficients of determination between 0.68 and 0.99 obtained for different rock materials [34].
- The wedge failure mechanism is an idealization of the true mechanism of bearing failure of spread foundations on rock mass. Other failure mechanisms have been proposed by other authors [35]. Because of that, there is a model uncertainty, which is difficult to quantify.
Forrest and Orr [36] examined the effect of different coefficients of variation on the resistance model of spread foundations on soil and found that values up to 15% do not considerably affect the reliability of the structure. The JRC report on the reliability background of the Eurocodes [37] suggests a coefficient of variation of the model uncertainty of the bearing resistance of spread foundations of 15%.
The model uncertainty is considered in probabilistic calculations by a random variable multiplying the bearing resistance computed using Equation (12), leading to
where θM is then a random variable representing the calculation model uncertainty, supposedly following a normal distribution, with unit mean and a coefficient of variation that accounts for the abovementioned sources of uncertainty. For the reasons presented, a value of 10% to 15% is considered realistic. A coefficient of variation of 15% is then considered, as suggested in the JRC report [37], Table A.29.
5. Safety Verification Against Bearing Failure
5.1. Deterministic Approach—Allowable Stress Design
The traditional deterministic approach follows a classical design methodology for safety verification based on the computation of global safety factors. This is a straightforward design approach for spread foundations, consisting of computing a global safety factor SF, given by the ratio between the calculated bearing resistance (RN) and the normal action (N):
Uncertainties on the estimation of actions, material properties, geometrical properties, and other factors (e.g., model uncertainties) are accounted for by requiring a sufficiently large safety factor, while their mean values are used in the calculations. This way, the safety margin is concentrated into a single factor, to which rock engineers have developed a particular sensitivity. As a rule of thumb, values between 2 and 3 are commonly suggested [15] for the safety verification against bearing failure of spread foundations. This approach essentially means that the designer only accounts for one third to one half of the expected resistance to face external actions, which roughly corresponds to the allowable stress design principles.
For the calculation of bearing resistance with the deterministic approach, the Mohr–Coulomb envelope was considered, and the mean values of its parameters were calculated in Section 4.2. The mean values of the permanent and the variable actions were calculated in Section 4.3, and for the geometrical parameter, the nominal value was used, as explained in Section 4.4.1. They were used in the calculations as listed in Table 7.

Table 7.
Mean values of actions, geometrical properties, and ground properties.
Table 8 presents the values of some quantities computed during the intermediate steps of the safety verification procedure and the obtained safety factor.

Table 8.
Relevant output data obtained during the deterministic safety verification.
The obtained safety factor of 4.52 is clearly above the range of traditionally used values (2 to 3) for the design of spread foundations, indicating a comfortable global safety margin.
5.2. Semi-Probabilistic Eurocode 7 Solution—Limit State Design
5.2.1. General
The semi-probabilistic approach presented in Eurocode 7 addresses several uncertainties involved in the structural problems by setting, as detailed earlier, representative values of actions, ground properties, and geometrical properties, whose selection can have a statistical background (characteristic values) or solely subjective judgement (nominal values). In addition, the semi-probabilistic approach applies partial factors, according to the methodology presented in Section 2, to obtain the design values actually used in the calculations. The integration of rock engineering problems in the scope of the second generation of Eurocode 7 introduced partial factors specifically defined for ground properties related to the rock material, rock mass, and rock discontinuities. Although also recommending partial factors for the unconfined compressive strength (see Table 4), these mostly apply to those situations where the resistance models are strongly (or solely) dependent on this ground property. For the general cases, it is the shear strength that should be factored, ensuring the generalization that is needed in rock engineering, since different failure criteria, linear and non-linear, are used in specific problems. Otherwise, factoring the uniaxial compressive strength is equivalent to the resistance factor approach.
For the case study presented, the Hoek–Brown parameters are given as input. Expressing the major principal stress below the spread foundation in terms of Mohr–Coulomb parameters (c′ and φ′) offers a low-cost workaround, since Mohr–Coulomb is a linear failure criterion—as presented in Section 4.1—and factoring the shear strength is equivalent to equally factoring each of its components (cohesion and coefficient of friction). Although for the deterministic and the fully probabilistic approaches it is not possible to proceed with the safety verification, directly considering the Hoek–Brown envelope, the semi-probabilistic verification presented in Eurocode 7 can be carried out. Therefore, in this following section, the safety verification is conducted using the “equivalent” Mohr–Coulomb failure envelope but also the Hoek–Brown failure envelope.
Actions are similarly computed for both variations. According to Table 3, the partial factors for verification of bearing resistance of spread foundations for fundamental design situations are applied to actions or effects of actions, depending on the verification case. Table 9 presents quantities computed during the procedure to obtain the design value of the actions and effect of actions for different verification cases. As detailed before, for VC1, both permanent (1.35 kf) and variable actions (1.5 kf) are factored. For VC3, only variable actions are factored (1.3). And for VC4, not only are variable actions factored (1.5/1.35) but also the resulting effect of actions (1.35 kf).

Table 9.
Design values of actions, effects of actions, and geometry for different verification cases.
5.2.2. Using the “Equivalent” Mohr–Coulomb Failure Envelope
As mentioned, Mohr–Coulomb is a linear shear failure criterion, given in terms of cohesion and friction angle. Factoring the shear strength is equivalent, in this case, to factoring the ground properties c′ and tanφ′ by the corresponding partial factor (γτr). As derived already, representative values of c′ and φ′ are 60.7 kPa and 39.9°, respectively.
According to Table 2, combinations (a) to (c) correspond to the MFA, where ground properties are factored but not the computed resistance, whereas combinations (d) and (e) correspond to the RFA, where ground properties are not factored but the resistance is. Table 10 shows the values computed during the safety verification procedure, namely the major principal stresses (according to Equation (14)), the design bearing resistance, and the design vertical load. The utilization ratio, quantifying the portion of the design resistance mobilized, and the overdesign factor, representing a safety margin, are also presented.

Table 10.
Relevant output data obtained in the semi-probabilistic safety verification procedure using the Mohr–Coulomb model.
In combination (a) the set M1 of partial factors is used, in which, according to Table 4, ground properties remain unfactored in practice (γτr = 1.0). In this combination VC1 is used to factor actions. In combinations (b) and (c) the set M2 of partial factors should be used but the consequence factor is omitted in combination (c), resulting in γτr = 1.25 kM and γτr = 1.25, respectively. In these combinations, verification cases VC3 and VC1 are used, respectively.
In combinations (d) and (e), the ground properties are not factored, but the design bearing resistance is computed after factoring the obtained resistance (γRN = 1.4). These combinations differ based on the verification case used to compute the design value of actions, namely VC1 in combination (d) and VC4 in combination (e), affecting the design value of the bearing resistance. This is due to its dependency on the effective width, which is calculated based on the eccentricity calculated either using design or representative actions, respectively, in the case of RFA (d) and RFA (e).
5.2.3. Using the Hoek–Brown Failure Envelope
The challenge arising from using the Hoek–Brown model to estimate the bearing resistance of a spread foundation is due to the difficulty in expressing the major principal stress below the foundation in terms of the shear strength. If that was possible, factoring the shear strength would allow direct calculation of the design (factored) value of the major principal stress. However, the Hoek–Brown model is given in terms of principal stresses, and both shear and normal stresses are computed from them, respectively, by [38]
There is no closed-form solution for the reverse problem, i.e., to retrieve the principal stresses from these quantities. A workaround of this limitation can be found in Hammah et al. [38], who present a methodology employed in numerical analysis software to perform the shear reduction method using the Hoek–Brown failure criterion. The rationale is to find another set of Hoek–Brown parameters (GSI, σci, and mi) whose shear envelope better adjusts the original model after factorization. This new set of parameters can then define a “design” Hoek–Brown model and be used directly to compute the design bearing resistance. This optimization problem is expressed as
where σn,min and σn,max are the minimum and maximum normal stresses, computed using Equation (30), considering the range of values of the minor principal stresses (σ3B to σ3A). To reduce the number of parameters to be determined, the design value of the unconfined compressive strength is suggested to be obtained by factoring the given representative values exactly by the reduction factor [38], in this case the partial factor, i.e., σci,d = σci,rep/γτ. This assumption is justified since (σ1 − σ3) in Equation (29) is, according to Equation (13), linearly proportional to σci. Furthermore, assuming GSI and mi as the unknown parameters (keeping D = 0, which is logical), instead of mb, s, and a, simplifies the calculations at a minimal penalty to accuracy [38]. Since mb is linearly proportional to mi, and s and a are both dependent on GSI, this assumption also avoids numerical inconsistencies, while preserving the physical meaning of these parameters.
This procedure is needed for the MFA combinations. For combinations (b) and (c), the shear strength must be factored by γτr = 1.25 kM and by γτr = 1.25, respectively. For combination (a), the shear strength remains unfactored in practice (γτr = 1.00), so the original values of the Hoek–Brown parameters can be used to compute the design bearing resistance. For combinations (d) and (e), corresponding to the RFA, it is the resulting bearing resistance that shall be factored, and, therefore, the original set of representative Hoek–Brown parameters can still be used.
Table 11 shows the Hoek–Brown parameters computed considering the original parameters (GSI = 40, mi = 7, σci =5 MPa) and partial factors γτr of 1.00 (for combination (a)), 1.25 kM (for combination (b)), and 1.25 (for combination (c)). Although in practice the use of fractional GSI values is not used [39], these back-calculated values do not carry the physical meaning of the original parameters. Instead, they should be interpreted as design values obtained from the representative ones, accounting not only for the inherent variability but also for the reliability requirements of the Eurocodes.

Table 11.
Design values of the Hoek–Brown parameters considering different partial factors applied to the shear strength.
Figure 5 and Figure 6 show the outcome of this procedure in principal stresses and normal shear stresses plots, respectively. A very good match between approximate factored (AF-HB) and original factored (F-HB) shear envelopes, within the range expected normal stress shadowed in grey, is observed.
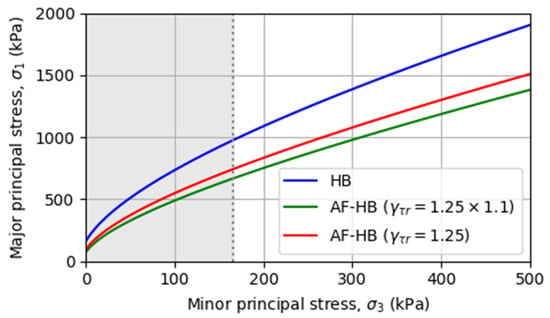
Figure 5.
Original (HB) and approximate factored Hoek–Brown (AF-HB) envelopes in a principal stresses plot.
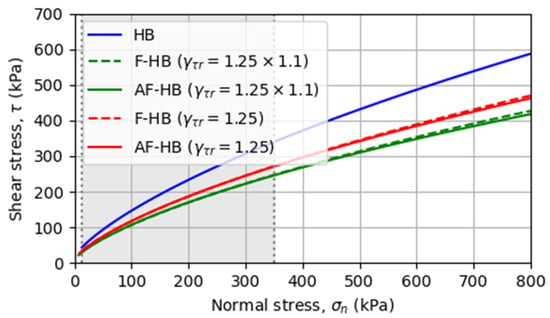
Figure 6.
Original (HB), original factored (F-HB), and approximate factored Hoek–Brown (AF-HB) envelopes in a normal shear stress plot.
Finally, Table 12 shows the values computed during the safety verification procedure, namely the major principal stresses (according to Equation (13)), the design bearing resistance, the design vertical load, as well as the utilization ratio and overdesign factor.

Table 12.
Values computed during the safety verification procedure using the Hoek–Brown model.
When compared to the values of the bearing resistance computed using the Mohr–Coulomb model, a decrease in resistance is observed. This is a consequence of the linearization process, with the “equivalent” Mohr–Coulomb model slightly overestimating the major principal stress below the foundation σ1A for a value of the principal minor stress of σ3A (see Figure 3).
5.3. Probabilistic Analysis—Limit State Design
The probabilistic approach consists of estimating the probability of bearing failure of the spread foundation and comparing it against threshold values. To achieve this, the relevant sources of uncertainty must be considered through probabilistic models, and reliability analysis techniques are employed to estimate the probability of failure.
Probabilistic methods are also recognized in EN 1997-1 [2] as an alternative to the partial factor method for the safety verification by calculation, with particular utility when the limit state is sensitive to variations on geometrical properties, such as often happens in rock mechanics, namely when discontinuities are involved. These methods offer well-established advantages, including the explicit treatment of various uncertainties and the generation of tailored results since the harmonization constraints inherent in standard-based design, due to wide coverage, are avoided. Nonetheless, probabilistic methods for safety verification have their own complexities and challenges. These include reliance on the engineering judgement in identifying and appropriately modeling the relevant sources of uncertainty, and, for most practical problems, the need to perform multiple structural analyses. This requirement can become a time-consuming task, especially for complex structural models.
Probabilistic methods are also grounded in the limit state design principles. In fact, the limit state function is defined to represent the boundary conditions between the occurrence of failure and its avoidance. It is given in terms of random variables, and the probability of failure is computed, according to the probability theory, using the following integral:
where fX(x) denotes the joint probability density function of the random variables X. Analytical and direct numerical evaluation of this integral is often infeasible due to the high dimensionality that such problems can easily attain and the difficulty in constructing an accurate joint probability density function from marginal distributions.
To address these challenges, several approximation techniques can be employed. These include reliability approximation methods such as the first-order and second-order reliability methods (FORM and SORM), as well as simulation-based approaches like the Monte Carlo method, which can provide cost-effective estimates of the probability of failure. The applicability, and thus the selection, of a specific method is largely determined by the computational effort required to evaluate the limit state function [18]. In the problem analyzed in this paper, the number of random variables is moderate, and the limit state function is explicitly defined, through a closed-form expression, making any method suitable. FORM was selected, which is an iterative method that not only provides an estimate of the reliability index, related to the probability of failure through pf = Φ(-β), but also outputs influence factors α, expressing the sensitivity of the standardized limit state to changes of each random variable.
The limit state function for the safety verification against bearing failure of a spread foundation, given the description of the bearing resistance in terms of cohesion and friction angle (Equation (13)), can be given by
Table 13 summarizes the marginal (individual) probabilistic models adopted for each random variable. In addition, a coefficient of correlation of 0.7 between the variable moment and vertical load was considered, as when the semi-probabilistic approach was used.

Table 13.
Marginal probabilistic models of each random variable adopted in the analysis.
A reliability index of β = 4.87, corresponding to a probability of failure of 5.63 × 10−6, was computed after 29 iterations and 248 realizations of the limit state function. This value exceeds the reference threshold value for consequence class CC3, namely βref = 4.3 (see Table 1), for a 50-year reference period. This means that safety is verified according to the reliability requirements specified in the code. The influence factors α obtained are listed in Table 14.

Table 14.
Influence factors α obtained after FORM analysis.
These values provide valuable insights. Small absolute values of the influence factors indicate that changes in the corresponding variables have little impact on the probability of failure. Consequently, the base width, the permanent vertical load, and the variable moment could, in principle, be considered as deterministic in the analysis and represented only by their mean or design values. For the base width and the permanent vertical action, this is justified by their low coefficients of variation. In the case of the variable moment, its limited influence is due to its minimal effect on the calculation of the effective base width, through the eccentricity, in this particular case.
6. Discussion
Uncertainty in the design of geotechnical structures in general, and spread foundations in particular, cannot be neglected or eliminated but has to be recognized and managed in practice. The paper addresses this problem by applying three different design approaches to a simple geotechnical structure—a spread foundation on rock. They include: a deterministic approach based on traditional design using a global safety factor; a semi-probabilistic approach aligned with the second-generation Eurocode principles using partial factors; and a fully probabilistic approach, also consistent with the Eurocode principles. For ease of comparison, the final results for each approach, specifically regarding the verification of the bearing failure limit state, are summarized in Table 15.

Table 15.
Summary of the final results obtained following all approaches.
In the traditional deterministic approach, uncertainty is implicitly accounted for by setting large safety factors. These are necessary because structural models are idealizations of complex behavior, where the intensity of actions often cannot be precisely predicted, and material and geometrical properties cannot be perfectly known. However, the global safety factor method cannot address specifically the uncertainties inherent in the design. As a result, the traditional approach may significantly underestimate or overestimate the actual safety level, potentially leading to overconservative and uneconomical designs or a false sense of security, respectively. In the case study presented, a global safety factor of 4.52 was computed, substantially higher than the typical range of 2 to 3 used in current practice. Although the global safety factor a designer may adopt should reflect not only the uncertainties but also the consequences of a structural failure, the obtained final result illustrates how uncalibrated deterministic approaches may distort the perceived safety margin.
The Eurocodes address uncertainty in a codified and harmonized manner to ensure consistency across different countries and structural types. In this framework, random variables, such as actions, material properties, and geometrical properties are represented by representative values, whose quantification should be based on statistical analysis of data (characteristic values) or may be obtained from informed engineering judgement (nominal values). These values serve as cautious estimates, intended to reflect the uncertain nature of the underlying phenomena. Additionally, partial factors are applied to these variables, distributing the overall safety margin according to their relative influence on the design outcome.
The Eurocodes present alternative safety verification approaches and provide recommended values for partial factors. Nonetheless, permission is granted for the national standardization bodies to adopt the approach that best aligns with national practice and to modify the partial factors accordingly. In the case study that was analyzed, a considerable difference was observed between the outcomes produced by the MFA and the RFA. As shown in Table 15, large overdesign factors were computed for combinations (a) and (b), respectively, 1.50 and 1.44 using the Mohr–Coulomb failure criterion and 1.40 and 1.37 using the Hoek–Brown failure criterion. These values align with the final results of the deterministic approach, given the ratio between the computed global safety factor and the upper bound of its typical range (4.52/3 = 1.51). Although smaller overdesign factors were computed for combinations (c), (d), and (e), respectively, 1.12, 1.07, and 1.09, using the Mohr–Coulomb failure criterion and 1.10, 1.03, and 1.05, using the Hoek–Brown failure criterion, safety is still verified. For the MFA, this is mostly due to either actions or material properties being significantly factored in combinations (a) and (b), respectively, while for combination (c) both are factored, simplifying the verification at the expense of a higher safety margin being required. In the RFA, both actions and resistances are factored, yielding close results to combination (c). This divergence in results suggests that these combinations are suited to different contexts, each reflecting distinct treatment of uncertainties. For spread foundations, if the overdesign factor is considered as a proper indicator of the suitability of the approach, the combinations (c), (d), and (e) would offer a more tailored and realistic representation of resistance-related uncertainties.
Eurocode 7 specifies that, for the rock material, rock mass, and rock discontinuities, the shear strength is the ground property to be factored. However, challenges arise when attempting to apply partial factors to a non-linear failure criterion, such as Hoek–Brown, which is expressed in terms of principal stresses. In such cases, no straightforward solution currently exists, and practical workarounds must be employed to approximate the factorization process. A procedure often considered for the strength reduction method using the Hoek–Brown failure criterion within numerical analysis software was successfully used to obtain design values of the Hoek–Brown parameters GSI, σci, and mi. The final results of the limit state verification closely match those obtained using “equivalent” Mohr–Coulomb failure criterion.
However, the trade-off between harmonization and ease of use in the Eurocodes may result in solutions less tailored to specific design situations. Moreover, the semi-probabilistic approach cannot adequately account for geometrical uncertainties when these significantly affect the structural behavior, i.e., when the limit states become sensitive to deviations in geometric parameters. In such cases, or in design situations beyond the scope of the semi-probabilistic framework, the Eurocodes recognize that more advanced reliability-based methods, including fully probabilistic approaches, may be appropriate.
In probabilistic approaches, uncertainty is addressed explicitly by modeling input parameters as random variables with defined probability distributions. While this provides a more transparent and quantifiable treatment of risk, it also introduces subjectivity. Designers must make decisions about the sources of uncertainty, the choice of probability distributions, and the estimation of their parameters, whether based on data, possibly limited, skewed, or non-representative, or on expert judgment. Therefore, while probabilistic methods offer a more rigorous understanding of reliability and promise more tailored solutions, they require careful implementation and professional expertise to be applied effectively.
In the case study presented, a reliability index of 4.89 was computed, exceeding the target value of 4.3, attesting to the structural safety of the spread foundation. This outcome suggests that, given the assumed actions, material properties, and geometrical properties, the foundation may in fact be overdesigned. This is in line with the larger overdesign factors computed with the semi-probabilistic approach. Furthermore, the obtained influence factors α (Table 14) suggest a strong sensitivity of the estimated reliability index to the variable vertical load and ground properties, but even more to the model uncertainty.
Indeed, the calculation model used, based on wedge equilibrium and the Hoek–Brown failure criterion, is a simplified representation of the actual, more complex behavior of the geotechnical structure. The associated model uncertainty was shown to have a significant impact on the computed reliability index, suggesting that it is a critical variable deserving special attention in uncertainty modeling. In fact, reducing the model uncertainty may yield substantial improvements in reliability assessment. To that end, it may be worthwhile, in certain cases, to invest in the choice and development of more realistic models that better capture the structural response. As long as such models offer the potential for a more accurate representation of structural behavior, they ultimately lead to more informed and efficient design decisions. The model considered in this paper is suggested in an informative annex to Eurocode 7, but its use is not mandatory. The standard leaves it to the designer to select an appropriate model and to quantify the associated uncertainty.
The partial factor method itself is not intended to cover incorrect idealizations of the failure mechanism or improper selection of the calculation model. To that end, model factors were incorporated in Eurocode 7 to compensate for any significant bias or additional uncertainty in a calculation model compared with a reference model. Physical, analytical, or numerical models may serve as reference models, provided that they accurately reproduce the limit states being considered. In the absence of such information, comparable experience based on case studies shall be used to set model factors.
7. Conclusions
Eurocode 7 establishes a comprehensive framework for the design of spread foundations on rock masses, accommodating both semi-probabilistic and fully probabilistic approaches. This framework addresses all relevant sources of uncertainty in the design process, promoting a more robust and transparent assessment of structural safety. To assess the suitability of Eurocodes for the design of spread foundations, three methods of limit state verification by calculations were compared: the global safety factor method (based on mean values of actions and strength properties), the Eurocode 7 partial factor method (using characteristic values), and a probabilistic method (based on statistical distributions).
The results obtained using the deterministic, semi-probabilistic, and fully probabilistic approaches demonstrated a consistent safety margin across all methodologies, reinforcing the reliability of the semi-probabilistic Eurocode design framework. In the considered case study, the results of the traditional deterministic approach are aligned with the results of the Eurocode 7 semi-probabilistic framework, specifically, the combinations (a) and (b) that either factor actions or material properties. Combinations (c), (d), and (e), where both actions and material properties or resistances are being factored, show consistency with the underlying reliability requirements, given the small overdesign factor computed. The probabilistic analysis, which explicitly modeled the uncertainty in input parameters, resulted in a reliability index slightly higher than the target value, further validating the adequacy of the Eurocode methodology in achieving the intended safety performance for spread foundations on rock. This convergence of results confirms that the semi-probabilistic method, as implemented in Eurocode 7, provides a balanced and dependable means of satisfying underlying reliability requirements.
Eurocode 7 permits multiple safety verification approaches, including the material factor approach and resistance factor approach, offering flexibility in the implementation at a national level. The existence of alternative design combinations reflects the recognition that no single method is universally optimal. As such, national standardization bodies were encouraged to evaluate the suitability of each approach in the context of their local design traditions, construction practices, and typical ground conditions. Adopting the format that best aligns with national practices while still maintaining conformity with the Eurocode framework will ensure both harmonization and practical applicability across diverse geotechnical design contexts.
Author Contributions
Conceptualization, R.P., W.B., and L.L.; methodology, R.P., W.B., and L.L.; software, R.P. and W.B.; validation, R.P., W.B., and L.L.; formal analysis, R.P.; investigation, R.P. and W.B.; resources, W.B. and L.L.; data curation, R.P. and W.B.; writing—original draft preparation, R.P., W.B., and L.L.; writing—review and editing, L.L.; visualization, R.P. and W.B.; supervision, L.L.; project administration, R.P.; funding acquisition, R.P. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by LNEC’s Research and Innovation Plan 2023-27, through research project “MetProbRoc—Testing and observation methodologies, probabilistic studies and reliability analysis of structures in rock masses” (Proc. 0402/1102/24147).
Data Availability Statement
The data presented in this study are openly available in the article.
Conflicts of Interest
Witold Bogusz was employed by the company Jacobs. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Conflicts of Interest Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| CEN | European Committee for Standardization |
| ULS | Ultimate Limit State |
| CC | Consequence Class |
| SF | Global Safety Factor |
| MFA | Material Factor Approach |
| RFA | Resistance Factor Approach |
| VC | Verification Case |
| JRC | Joint Research Centre |
| GSI | Geological Strength Index |
| JCSS | Joint Committee on Structural Safety |
| FORM | First-Order Reliability Method |
| SORM | Second-Order Reliability Method |
References
- EN 1990; Eurocode—Basis of Structural and Geotechnical Design. European Committee for Standardization: Bruxelles, Belgium, 2023.
- EN 1997-1; Geotechnical Design—Part 1: General Rules. European Committee for Standardization: Bruxelles, Belgium, 2024.
- EN 1997-2; Geotechnical Design—Part 2: Ground Properties. European Committee for Standardization: Bruxelles, Belgium, 2024.
- EN 1997-3; Geotechnical Design—Part 3: Geotechnical Structures. European Committee for Standardization: Bruxelles, Belgium, 2025.
- EN 1997-1; Geotechnical Design—Part 1: General Rules. European Committee for Standardization: Bruxelles, Belgium, 2004.
- EN 1997-2; Geotechnical Design—Part 2: Ground Investigation and Testing. European Committee for Standardization: Bruxelles, Belgium, 2007.
- Lamas, L.; Burbaum, U.; Estaire, J.; Harrison, J.; Nuijten, G.; Pereira, R. Rock engineering design in tomorrow’s geotechnical toolbox: Eurocode and the basis of structural and geotechnical design (the second generation of EN 1990 and EN 1997). Geomech. Tunn. 2023, 16, 469–490. [Google Scholar] [CrossRef]
- Estaire, J.; Muralha, J.; Segalini, A.; Johansson, E.; Nuijten, G.; Heintz, R. Rock engineering design in tomorrow’s geotechnical toolbox: Eurocode 7—Ground properties (EN 1997-2:2024). Geomech. Tunn. 2023, 16, 510–523. [Google Scholar] [CrossRef]
- Stille, H.; Ashcroft, B.; Boley, C.; Labiouse, V.; Pinto, P. Rock engineering design in tomorrow’s geotechnical toolbox: Eurocode 7—Geotechnical structures: Slopes, spread foundations and retaining structures (EN 1997-3:2024). Geomech. Tunn. 2023, 16, 524–535. [Google Scholar] [CrossRef]
- Maca, N.; Dietz, K.; Stille, H.; Virely, D. Rock engineering design in tomorrow’s geotechnical toolbox: Eurocode 7—Geotechnical structures: Anchors, rock bolts soil nails, and groundwater control (EN 1997-3:2024). Geomech. Tunn. 2023, 16, 536–558. [Google Scholar] [CrossRef]
- Low, B.K. Rock Engineering Insights from Reliability Analysis to Improve Eurocode 7 Design Approach. In Proceedings of the 7th International Symposium on Geotechnical Safety and Risk (ISGSR), Taipei, Taiwan, 11–13 December 2019; Research Publishing: Singapore, 2019; pp. 489–494. [Google Scholar]
- Bogusz, W.; Godlewski, T. Philosophy of geotechnical design in civil engineering—Possibilities and risks. In Bulletin of Polish Academy of Sciences Technical Sciences; American Society of Civil Engineers: Reston, VA, USA, 2019; Volume 67, pp. 289–306. [Google Scholar]
- Lesny, K.; Akbas, S.; Bogusz, W.; Burlon, S.; Vessia, G.; Zhang, L. Evaluation of the uncertainties related to the geotechnical design method and its consideration in reliability-based design. In Proceedings of the Geo-Risk Conference, Denver, CO, USA, 4–7 June 2017; pp. 435–444. [Google Scholar]
- ISSMGE TC205/304; Report on the Joint TC205/TC304 Working Group on Discussion on Statistical/Reliability Methods for Eurocodes. International Society of Soil Mechanics and Geotechnical Engineering: London, UK, 2017.
- Wyllie, D.C. Rock Slope Engineering, Civil Applications, 5th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- BS 8004; Code of Practice for Foundations. BSI: Sydney, Australia, 1986.
- ISSMGE TC304; State-of-the-Art Review of Inherent Variability and Uncertainty in Geotechnical Properties and Models. International Society of Soil Mechanics and Geotechnical Engineering: London, UK, 2021.
- van Den Eijnden, B.; Knuuti, M.; Lesny, K.; Löfman, M.; Mavritsakis, A.; Roubos, A.; Schweckendiek, T.; Sciarretta, F.; Ebener, A.; Escher, K.; et al. Reliability-Based Verification of Limit States for Geotechnical Structures—Guidelines for the Application of the 2nd Generation of Eurocode 7; Joint Research Centre Technical Report; Publication Office of European Commission: Luxembourg, 2024. [Google Scholar]
- Bogusz, W.; Caplane, C.; Hard, D.; Idda, K.; Ingram, P.; Kanty, P.; Kushwaha, A.; Nayrand, N.; Sand, O.; Sciarretta, F.; et al. Implementation of Design During Execution & Service Life—Guidelines for the Application of the 2nd Generation of Eurocode 7; Joint Research Centre Technical Report; Publication Office of European Commission: Luxembourg, 2024. [Google Scholar]
- AASHTO. LFRD Bridge Design Specifications; American Association of State 845 Highway and Transportation Officials: Washington, DC, USA, 2020. [Google Scholar]
- AREMA. Manual for Railway Engineering; American Railway Engineering and Maintanance-of-Way Association: Lanham, MD, USA, 2020. [Google Scholar]
- Vrouwenvelder, T. Treatment of risk and reliability in the Eurocodes. Struct. Build. 2008, 161, 209–214. [Google Scholar] [CrossRef]
- Orr, T.L.L. How Eurocode 7 has affected geotechnical design: A review. Geotech. Eng. 2012, 165, 337–350. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek-Brown failure criterion and GSI—2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Miranda, T.; Martins, F.; Araújo, N. Design of spread foundations on rock masses according to Eurocode 7. In Harmonising Rock Engineering and the Environment, Proceedings of the 12th ISRM International Congress on Rock Mechanics, Beijing, China, 16–21 October 2011; Zhou, Q., Ed.; Taylor & Francis: London, UK, 2011; pp. 1959–1962. [Google Scholar]
- CEN TC250/SC7/TG-B2; Design Examples Using 2nd Generation Eurocode 7, Joint Research Centre Technical Report. Publication Office of European Commission: Luxembourg, 2024.
- Muralha, J.; Lamas, L. Assessment of characteristic failure envelopes for intact rock using results from triaxial tests. In Rock Engineering and Rock Mechanics: Structures in and on Rock Masses, Proceedings of the ISRM Regional Symposium—EUROCK 2014, Vigo, Spain, 27–29 May 2014; Perucho, A., Alejano, R., Olalla, C., Jiménez, R., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 1525–2530. [Google Scholar]
- Russo, G.; Kalamaras, G.S.; Origlia, L.; Grasso, P. A probabilistic approach for characterizing the complex geologic environment for design of the new Metro do Porto. In Progress in Tunneling After 2000, Proceedings of the AITES-ITA World Tunnel Congress, Milan, Italy, 10–13 June 2001; Teuscher, A., Colombo, P., Eds.; CRC Press: Boca Raton, FL, USA, 2001; Volume 3, pp. 463–470. [Google Scholar]
- Wyllie, D.C.; Norrish, N.I. Chapter 14: Rock strength properties and their measurement. In Landslides: Investigation and Mitigation—Special Report 247; US Transportation Research Board: Washington, DC, USA, 1996. [Google Scholar]
- Alonso, E.E.; Pineda, J.A.; Cardoso, R. Degradation of Marls; Two Case Studies from the Iberian Peninsula; Geological Society, London, Engineering Geology Special Publications: London, UK, 2010; Volume 23, pp. 47–75. [Google Scholar]
- Singh, R.N.; Eksi, M. Rock characterization of gypsum and marl. Min. Sci. Technol. 1987, 6, 105–112. [Google Scholar] [CrossRef]
- JCSS. Probabilistic Model Code. Joint Committee on Structural Safety. 2001. Available online: https://www.jcss-lc.org/jcss-probabilistic-model-code/ (accessed on 27 September 2016).
- ISO 2394:2015; General Principles on Reliability for Structures. 4th ed. International Organization for Standardization: Geneva, Switzerland, 2015.
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Geotech. Engrg. Div. 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Serrano, A.; Olalla, C. Allowable bearing capacity of rock foundations using a non-linear failure criterium. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 327–345. [Google Scholar] [CrossRef]
- Forrest, W.S.; Orr, T.L.L. The effect of model uncertainty on the reliability of spread foundations. In Proceedings of the 3rd International Symposium on Geotechnical Safety and Risk (ISGSR), Munich, Germany, 1–4 June 2011. [Google Scholar]
- Vrouwenvelder, T.; Dimova, S.; Sousa, M.L.; Marková, J.; Mancini, G.; Kuhlmann, U.; Taras, A.; Jockwer, R.; Jäger, W.; Schweckendiek, T.; et al. Reliability Background of the Eurocodes; Joint Research Centre Technical Report; Publication Office of European Commission: Luxembourg, 2024. [Google Scholar]
- Hammah, R.E.; Yacoub, T.E.; Corkum, B.C.; Curran, J.H. The Shear Strength Reduction Method for the Generalized Hoek-Brown Criterion. In Rock Mechanics for Energy, Mineral and Infrastructure Development in the Northern Regions, Proceedings of the Alaska Rocks 2005: The 40th U.S. Symposium on Rock Mechanics (ARMA 05), Anchorage, AK, USA, 25–29 June 2005; American Rock Mechanics Association (ARMA): Alexandria, VA, USA, 2005. [Google Scholar]
- Narimani, S.; Davarpanah, S.M.; Bar, N.; Török, Á.; Vásárhelyi, B. Geological Strength Index Relationships with the Q-System and Q-Slope. Sustainability 2023, 15, 11233. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).