Correlations for Estimating Coefficients for the Prediction of Maximum and Minimum Index Void Ratios for Mixtures of Sand and Non-Plastic Silt
Abstract
:1. Introduction
2. Terminology
- (1)
- “Silt” is used to describe a fine-grained, non-plastic material.
- (2)
- “Sand–silt combinations” refers to the pairing of one specific sand with one specific silt and is independent of the amount of each soil present.
- (3)
- “Sand–silt mixture” refers to the pairing of one specific sand with one specific silt at some specific ratio of the two materials (e.g., a silt content of 17%).
- (4)
- “Main data set” refers to the data set consisting of maximum and minimum index void ratio values at various silt contents for the 60 silt-sand combinations. These data were used for developing the correlations.
- (5)
- “Independent sand–silt combinations” refers to the three sand–silt combinations that were not included in the main data set. These data were used for validating the correlations.
3. Background
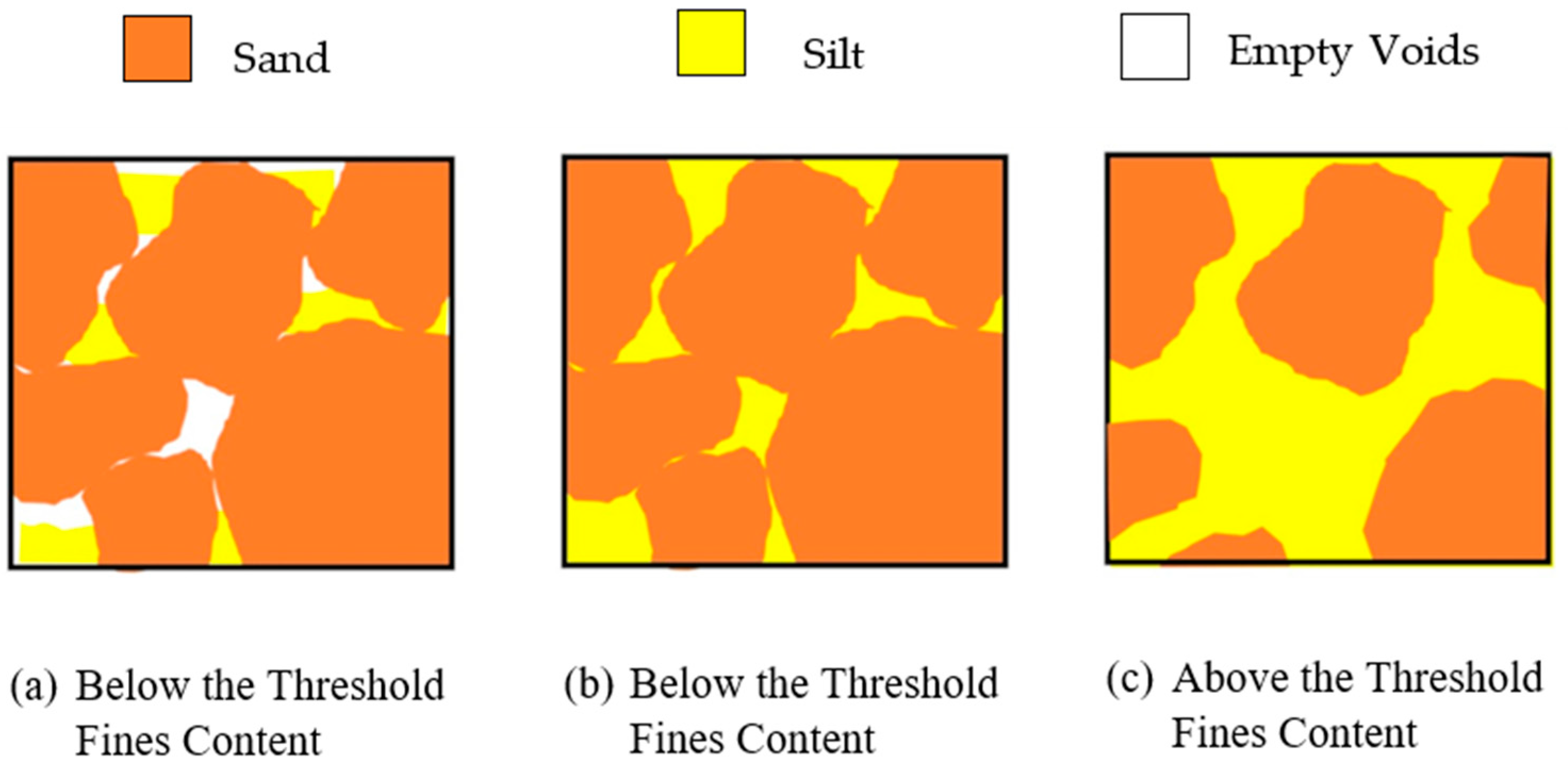
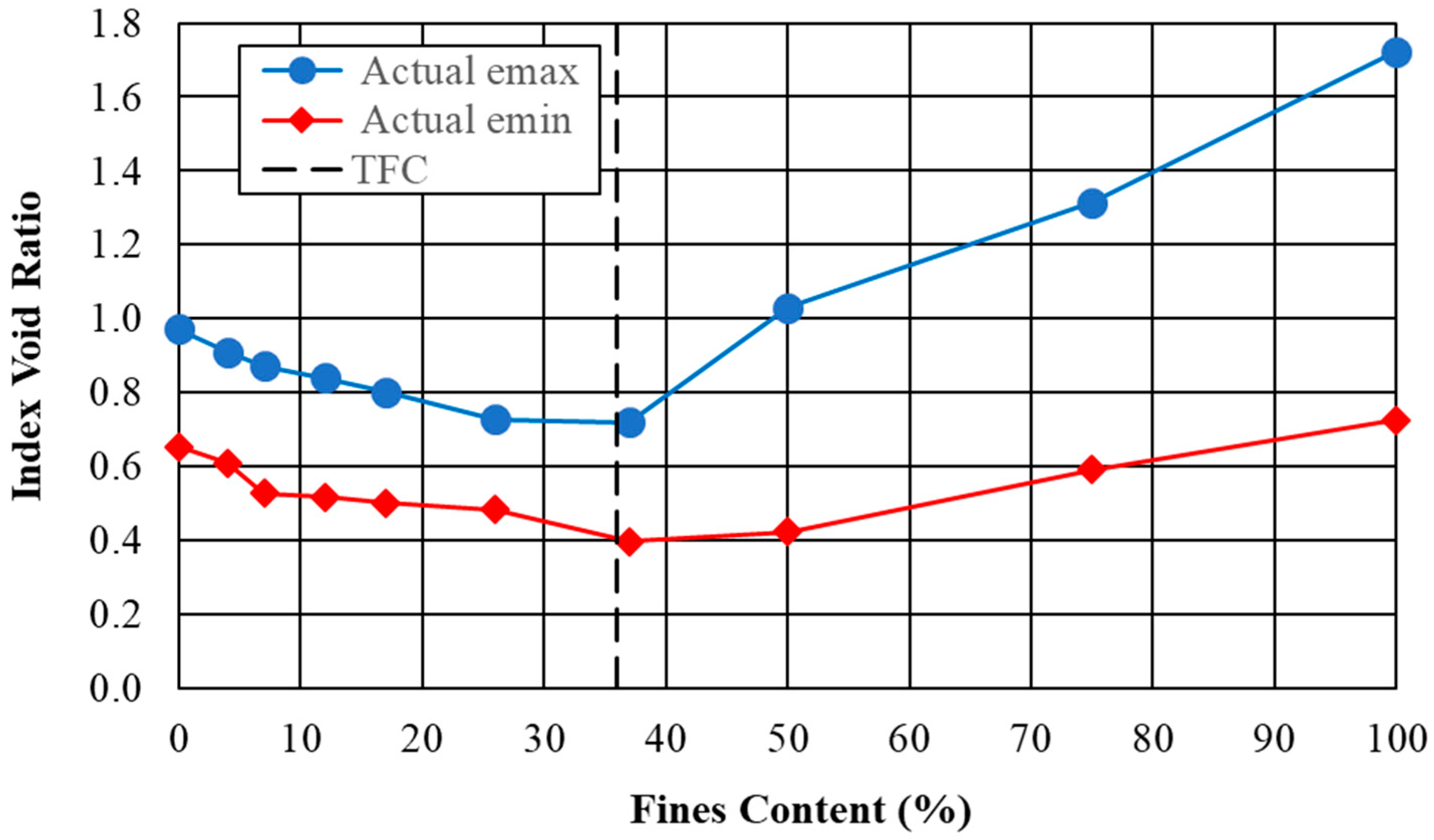
3.1. Threshold Fines Content
3.2. Equations for Estimating Index Void Ratios
4. Methodology for Developing the Correlations for Estimating a and b
4.1. Data Sets Used
4.2. Development of the Correlations
4.3. Equation Validation
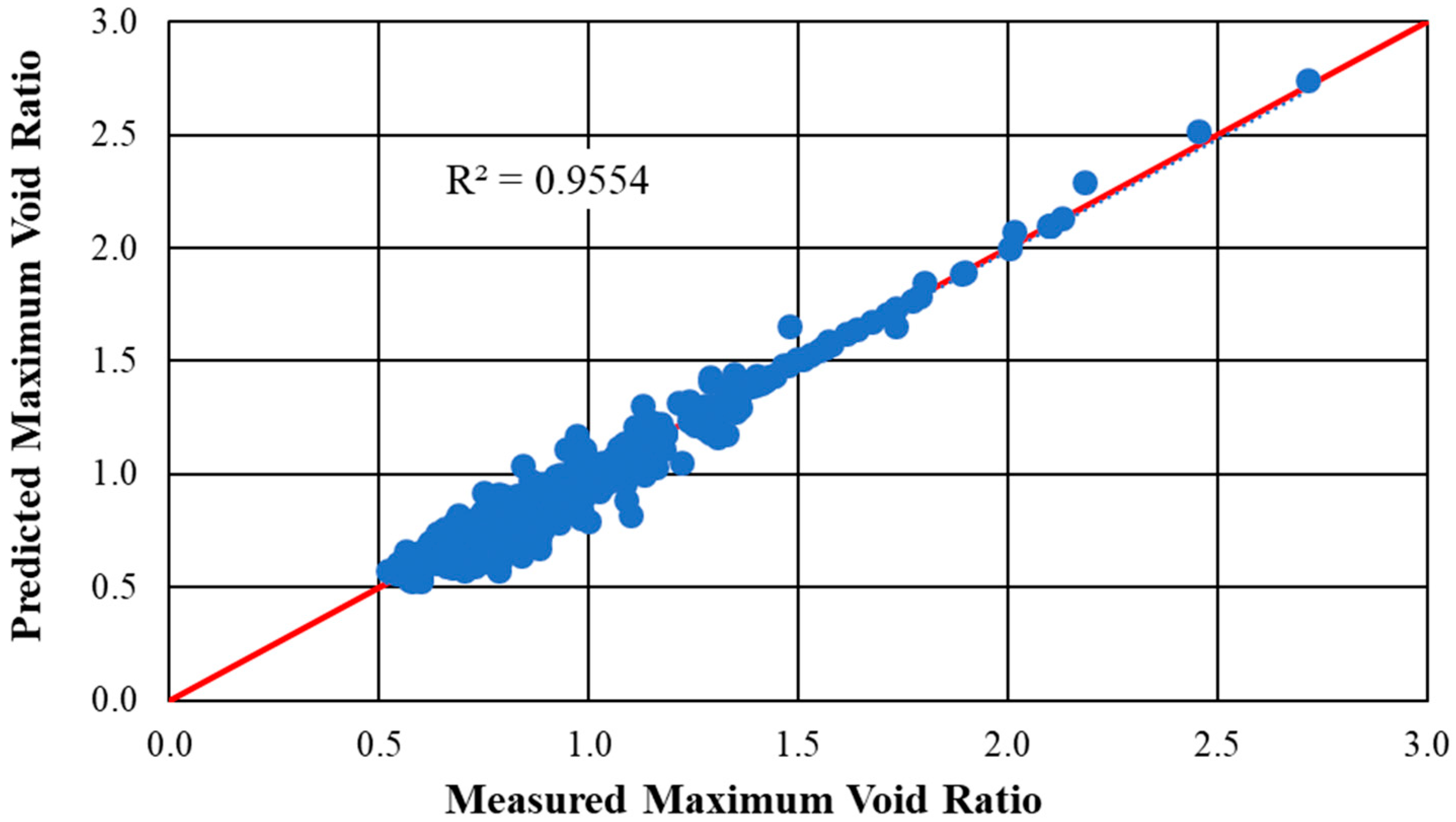
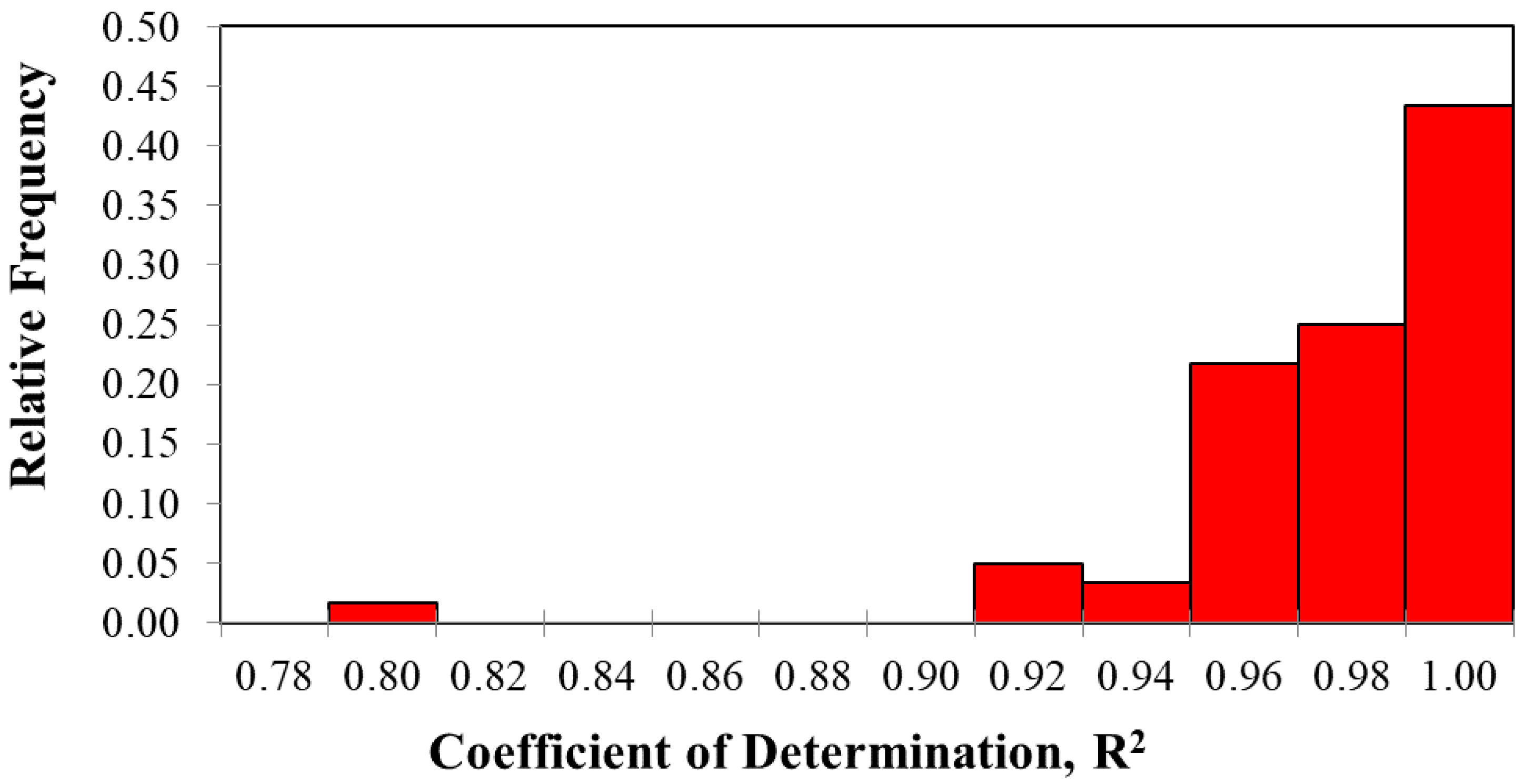
5. Results
6. Limitations
7. Conclusions
- Four correlations were developed for estimating the filling coefficients, a, and embedment coefficients, b. These correlations were developed using a data set collected from the literature and are presented as Equations (6)–(9).
- These correlations use only the median grain size of the sand, D50, the median grain size of the silt, d50, and their ratio, d50:D50. Both D50 and d50 can be obtained from a standard grain-size analysis consisting of a sieve analysis and a hydrometer.
- When values of a and b determined based on the correlations were used in Chang et al.’s equations [7], accurate values of maximum and minimum index void ratios for sand–silt mixtures were produced.
- The values maximum and minimum index void ratios predicted generally had R2 values greater than 0.94 when compared to the laboratory-measured values.
- The true strength of these correlations lies in their simplicity and ability to accurately estimate values of the filling and embedment coefficients while requiring only data from simple, common laboratory tests.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature/Abbreviations
| a | Generalized filling coefficient |
| amax | Filling coefficient for estimating the maximum index void ratio |
| amin | Filling coefficient for estimating the minimum index void ratio |
| b | Generalized embedment coefficient |
| bmax | Filling coefficient for estimating the maximum index void ratio |
| bmin | Embedment coefficient for estimating the minimum index void ratio |
| d50 | Median grain size in mm for silt |
| emax | Maximum index void ratio |
| Maximum index void ratio of the sand fraction of a sand–silt combination | |
| Maximum index void ratio of the sand fraction of a sand–silt combination | |
| Maximum index void ratio of soil below the threshold fines content | |
| Maximum index void ratio of soil above the threshold fines content | |
| emin | Minimum index void ratio |
| Minimum index void ratio of the sand fraction of a sand–silt combination | |
| Minimum index void ratio of the silt fraction of a sand–silt combination | |
| Minimum index void ratio of soil below the threshold fines content | |
| Maximum index void ratio of soil above the threshold fines content | |
| y1 | Fraction of the sand–silt mixture that is sand |
| y2 | Fraction of the sand–silt mixture that is silt |
| D50 | Median grain size in mm for sand |
| M1 | Silt content of soil below the threshold fines content |
| M2 | Silt content of soil above the threshold fines content |
References
- ASTM D 4254-00; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2014. Available online: http://www.astm.org (accessed on 19 July 2023).
- ASTM D 4253-00; Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2014. Available online: http://www.astm.org (accessed on 19 July 2023).
- Cubrinovski, M.; Ishihara, K. Maximum and minimum void ratio characteristics of sands. Soils Found. 2002, 42, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.S.; Deng, Y.; Yang, Z. Modeling of minimum void ratio for granular soil with effect of particle size distribution. J. Eng. Mech. 2017, 143, 04017060. [Google Scholar] [CrossRef]
- Shen, C.; Liu, S.; Xu, S.; Wang, L. Rapid estimation of maximum and minimum void ratios of granular soils. Acta Geotech. 2019, 14, 991–1001. [Google Scholar] [CrossRef]
- Qian, X.; Liu, X.; Shao, Z.; Shi, Y.; Zhang, S.; Hong, B. Modeling of Minimum and Maximum Void Ratios of Granular Soils. Math. Probl. Eng. 2021, 2021, 5092612. [Google Scholar] [CrossRef]
- Chang, C.; Wang, L.; Ge, L. Maximum and minimum void ratios for sand-silt mixtures. Eng. Geol. 2016, 211, 7–18. [Google Scholar] [CrossRef]
- Polito, C. Regression models for estimating parameters a and b for Chang, Wang and Ge’s maximum and minimum void ratio models. In Proceedings of the GeoNiagra 2021 Conference, Niagara Falls, ON, Canada, 26–29 September 2021. [Google Scholar]
- Thevanayagam, S.; Shenthan, T.; Mohan, S.; Liang, J. Undrained fragility of clean sands, silty sands, and sandy silts. J. Geotech. Geoenviron. Eng. 2002, 128, 849–859. [Google Scholar] [CrossRef]
- Polito, C. The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 10 December 1999. [Google Scholar]
- Selig, E.; Ladd, R. Evaluation of Relative Density Measurements and Applications, Evaluation of Relative Density and Its Role in Geotechnical Projects Involving Cohesionless Soils; ASTM International: West Conshohocken, PA, USA, 1973; pp. 487–509. [Google Scholar]
- Youd, T.L. Factors Controlling Maximum and Minimum Densities of Sands. In Evaluation of Relative Density and Its Role in Geotechnical Projects Involving Cohesionless Soils; ASTM International: West Conshohocken, PA, USA, 1973; pp. 98–112. [Google Scholar]
- Santamarina, J.; Cho, G. Soil Behaviour: The Role of Particle Shape. Advanced Geotechnical. Engineering Proceedings Skempton Conference, London, 2004. pp. 1–14. Available online: http://pmrl.ce.gatech.edu/tools/santamarina_cho_2004.pdf (accessed on 21 August 2023).
- Cho, A.G.; Dodds, J.; Santamarina, J.C. Particle Shape Effects on Packing Density, Stiffness and Strength—Natural and Crushed Sands. J. Geotech. Geoenviron. Eng. 2006, 132, 591–602. [Google Scholar] [CrossRef]
- Hazirbaba, K. Pore Pressure Generation Characteristics of Sands and Silty Sands: A Strain Approach. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2005. [Google Scholar]
- Yang, S.; Lacasse, S.; Sandven, R. Determination of the transitional fines content of mixtures of sand and non-plastic fines. Geotech. Test. J. 2006, 29, 102–107. [Google Scholar]
- Kokusho, T. Liquefaction Strengths of Poorly-Graded and Well-Graded Granular Soils Investigated By Lab Tests. In Proceedings of the 4th International Conference on Earthquake Geotechnical Engineering-Invited Lectures, Thessaloniki, Greece, 25–28 June 2007; Springer: Dordrecht, The Netherlands, 2007; Volume 6, pp. 159–184. [Google Scholar]
- Belkhatir, M.; Schanz, T.; Arab, A. Effect of fines content and void ratio on the saturated hydraulic conductivity and undrained shear strength of sand–silt mixtures. Environ. Earth Sci. 2013, 70, 2469–2479. [Google Scholar] [CrossRef]
- Bensoula, M.; Missoum, H.; Bendani, K. Critical undrained shear strength of sand-silt mixtures under monotonic loading. Int. J. Civ. Eng. Technol. 2018, 9, 447–455. [Google Scholar] [CrossRef]
- Fourie, A.; Blight, G.E.; Papageorgiou, G. Static liquefaction as a possible explanation for the Merriespruit tailings dam failure. Can. Geotech. J. 2001, 38, 707–719. [Google Scholar] [CrossRef]
- Hazirbaba, K.; Rathje, E.M. Pore pressure generation of silty sands due to induced cyclic shear strains. J. Geotech. Geoenviron. Eng. 2009, 135, 1892–1905. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, M.Z.; Khan, M.B. Experimental approach for assessment of liquefaction in fine sand and silty sand. Int. J. Eng. Sci. Invent. 2016, 5, 68–72. [Google Scholar]
- Lade, P.V.; Liggio, C.D., Jr.; Yamamuro, J.A. Effects of non-plastic fines on minimum and maximum void ratios of sand. Geotech. Test. J. 1998, 21, 336–347. [Google Scholar]
- Teng, J.; Araki, K.; Yasufuku, N.; Ikeda, H. Experimental study on void ratio characteristics of sand-fines mixture. In Proceedings of the 66th Annual Scientific Lecture Meeting of the Japan Society of Civil Engineers (JSCE), Matsuyama, Japan, 7–9 September 2011; pp. 785–786. [Google Scholar]
- Yilmaz, Y.; Mollamahmutoglu, M. Characterization of liquefaction susceptibility of sands by means of extreme void ratios and/or void ratio range. J. Geotech. Geoenviron. Eng. 2009, 135, 1986–1990. [Google Scholar] [CrossRef]
- Thevanayagam, S. Intergrain Contact Density Indices for Granular Mixes-II: Liquefaction Resistance. J. Earthq. Eng. Eng. Vib. 2007, 6, 135–146. [Google Scholar] [CrossRef]
- Lade, P.V.; Yamamuro, J.A. Effects of Non-Plastic Fines on Static Liquefaction of Sands. Can. Geotech. J. 1997, 34, 918–928. [Google Scholar] [CrossRef]
- Yamamuro, J.; Covert, K. Monotonic and Cyclic Liquefaction of Very Loose Sands with High Silt Content. J. Geotech. Geoenviron. Eng. 2001, 127, 314–324. [Google Scholar] [CrossRef]
- Pitman, T.; Robertson, P.; Sego, D. Influence of fines on the collapse of loose sands. Can. Geotech. J. 1994, 31, 728–739. [Google Scholar] [CrossRef]
- Zlatovic, S.; Ishihara, K. Normalized behavior of very loose non-plastic soils: Effects of fabric. Soils Found. 1997, 37, 47–56. [Google Scholar] [CrossRef]
- Yang, S.L. Characterization of the Properties of Sand-Silt Mixtures. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2004. [Google Scholar]
- Cho, Y.T. The Study of GCTS Triaxial Apparatus Function and Mixing Sand Void Ratio. Master’s Thesis, National Taiwan University, Taipei City, Taiwan, 2014. [Google Scholar]
- Mahmoudi, Y.; Taiba, A.; Hazout, L.; Baille, W.; Belkhatir, M. Influence of Soil Fabrics and Stress State on the Undrained Instability of Overconsolidated Binary Granular Assemblies. Stud. Geotech. Mech. 2018, 40, 96–116. [Google Scholar] [CrossRef]
- Askari, F.; Dabiri, R.; Shafiee, A.; Jafari, M. Liquefaction resistance of sand-silt mixtures using laboratory-based shear wave velocity. Int. J. Civ. Eng. 2011, 9, 135–144. [Google Scholar]
- Phan, V.; Hsiao, D.; Nguyen, P. Effects of fine contents on engineering properties of sand-fines mixtures. Procedia Eng.-Sustain. Dev. Civ. Urban Transp. Eng. Conf. 2016, 142, 213–220. [Google Scholar] [CrossRef]
- Karim, M.; Alam, M. Effect of nonplastic silt content on undrained shear strength of sand–silt mixtures. Int. J. Geo-Eng. 2017, 8, 14. [Google Scholar] [CrossRef]
- El Takch, A.; Sadrekarimi, A.; El Naggar, H. Cyclic resistance and liquefaction behavior of silt and sandy silt soils. Soil Dyn. Earthq. Eng. 2016, 83, 98–109. [Google Scholar] [CrossRef]
- Enomoto, T. Liquefaction and post-liquefaction properties of sand-silt mixtures and undisturbed silty sands. Soils Found. 2019, 59, 2311–2323. [Google Scholar] [CrossRef]
- Gobbi, S.; Reiffsteck, P.; Lenti, L.; d’Avila, M.P.S.; Semblat, J.F. Liquefaction triggering in silty sands: Effects of non-plastic fines and mixture-packing conditions. Acta Geotech. 2022, 17, 391–410. [Google Scholar] [CrossRef]
- Ingabire, E.-P. Influence of Fines Content on Cyclic Resistance and Residual Strength of Base Metal Tailings. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2019. [Google Scholar]
- Jhuo, Y.S.; Yeh, Y.H.; Ge, L. Shear Strength and Volume Change Behavior of Binary Granular Mixtures. J. GeoEngineering 2020, 15, 103–108. [Google Scholar]
- Karakan, E.; Altun, S. Liquefaction Behavior and Post-Liquefaction Volumetric Strain Properties of Low Plasticity Silt Sand Mixtures. Tek. Dergi 2016, 27, 7593–7617. [Google Scholar]
- Kolay, P.K.; Puri, V.K.; Lama Tamang, R.; Regmi, G.; Kumar, S. Effects of fly ash on liquefaction characteristics of Ottawa sand. Int. J. Geosynth. Ground Eng. 2019, 5, 1–14. [Google Scholar] [CrossRef]
- Missoum, H.; Belkhatir, M.; Bendani, K.; Maliki, M. Laboratory investigation into the effects of silty fines on liquefaction susceptibility of Chlef (Algeria) sandy soils. Geotech. Geol. Eng. 2013, 31, 279–296. [Google Scholar] [CrossRef]
- Naghavi, N. Liquefaction Assessment of Carbonate-Silica Silty Sands Using Energy, State Parameter and Shear Wave Velocity. Ph.D. Thesis, The University of Western Ontario (Canada), London, ON, Canada, 2017. [Google Scholar]
- Rahemi, N. Evaluation of Liquefaction Behavior of Sandy Soils Using Critical State Soil Mechanics and Instability Concept. Ph.D. Thesis, Ruhr-Universitat Bochum, Bochum, Germany, 2018. [Google Scholar]
- Sitharam, T.G.; Dash, H.K. Effect of non-plastic fines on cyclic behaviour of sandy soils. In GeoCongress 2008: Geosustainability and Geohazard Mitigation; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 319–326. [Google Scholar]
- Chakrabortty, P.; Nilay, N.; Das, A. Effect of silt content on liquefaction susceptibility of fine saturated river bed sands. Int. J. Civ. Eng. 2021, 19, 549–561. [Google Scholar] [CrossRef]
- Janalizadeh Choobbasti, A.; Selatahneh, H.; Karimi Petanlar, M. Effect of fines on liquefaction resistance of sand. Innov. Infrastruct. Solut. 2020, 5, 1–16. [Google Scholar] [CrossRef]
- Polito, C.; Sibley, E. Threshold fines content and the behavior of sands with non-plastic silts. Can. Geotech. J. 2020, 57, 462–465. [Google Scholar] [CrossRef]



| Soil Number | Silt Contents | D50 (mm) | d50 (mm) | d50:D50 | Sand emin | Silt emin | Sand emax | Silt emax | Source |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 0.39 | 0.15 | 0.385 | 0.601 | 0.622 | 0.79 | 2.098 | [7] |
| 2 | 9 | 0.15 | 0.02 | 0.133 | 0.54 | 0.58 | 0.77 | 0.85 | [7] |
| 3 | 5 | 0.21 | 0.01 | 0.048 | 0.579 | 0.461 | 0.872 | 1.897 | [7] |
| 4 | 7 | 0.596 | 0.023 | 0.039 | 0.632 | 0.991 | 0.795 | 1.563 | [7] |
| 5 | 6 | 0.3 | 0.045 | 0.150 | 0.59 | 0.75 | 0.98 | 1.39 | [7] |
| 6 | 14 | 0.5 | 0.01 | 0.020 | 0.58 | 0.85 | 0.85 | 2 | [7] |
| 7 | 14 | 0.5 | 0.01 | 0.020 | 0.57 | 0.86 | 0.78 | 1.48 | [11] |
| 8 | 7 | 0.77 | 0.04 | 0.052 | 0.54 | 0.72 | 0.85 | 1.42 | [15] |
| 9 | 9 | 0.21 | 0.017 | 0.081 | 0.57 | 0.87 | 0.83 | 1.77 | [15] |
| 10 | 6 | 0.68 | 0.01 | 0.015 | 0.52 | 0.71 | 0.84 | 1.43 | [16] |
| 11 | 14 | 1.08 | 0.14 | 0.130 | 0.579 | 0.748 | 0.851 | 1.176 | [16] |
| 12 | 17 | 0.12 | 0.01 | 0.078 | 0.755 | 1.000 | 1.247 | 2.740 | [17] |
| 13 | 8 | 0.61 | 0.05 | 0.082 | 0.52 | 0.71 | 0.86 | 1.05 | [19] |
| 14 | 14 | 0.21 | 0.05 | 0.237 | 0.581 | 0.754 | 0.855 | 1.183 | [20] |
| 15 | 6 | 0.12 | 0.05 | 0.417 | 0.617 | 0.754 | 0.938 | 1.169 | [20] |
| 16 | 13 | 0.17 | 0.05 | 0.302 | 0.581 | 0.754 | 0.876 | 1.180 | [20] |
| 17 | 12 | 1.50 | 0.05 | 0.033 | 0.538 | 0.754 | 0.765 | 1.176 | [20] |
| 18 | 5 | 0.22 | 0.017 | 0.077 | 0.59 | 0.46 | 0.88 | 1.89 | [20] |
| 19 | 8 | 0.23 | 0.02 | 0.087 | 0.84 | 0.62 | 1.44 | 1.41 | [20] |
| 20 | 6 | 0.25 | 0.01 | 0.040 | 0.608 | 0.627 | 0.800 | 2.100 | [20] |
| 21 | 8 | 0.23 | 0.03 | 0.130 | 0.84 | 0.67 | 1.44 | 1.15 | [21] |
| 22 | 8 | 2 | 0.03 | 0.015 | 0.83 | 0.67 | 1.12 | 1.15 | [21] |
| 23 | 8 | 2 | 0.02 | 0.010 | 0.83 | 0.62 | 1.12 | 1.41 | [21] |
| 24 | 8 | 0.9 | 0.03 | 0.033 | 0.5 | 0.67 | 0.97 | 1.15 | [21] |
| 25 | 8 | 0.9 | 0.02 | 0.022 | 0.5 | 0.62 | 0.97 | 1.41 | [21] |
| 26 | 11 | 1.08 | 0.40 | 0.370 | 0.633 | 0.644 | 0.970 | 1.048 | [22] |
| 27 | 11 | 1.08 | 0.42 | 0.389 | 0.633 | 0.590 | 0.970 | 0.996 | [22] |
| 28 | 11 | 1.08 | 0.26 | 0.244 | 0.633 | 0.696 | 0.970 | 1.114 | [22] |
| 29 | 11 | 1.08 | 0.17 | 0.155 | 0.633 | 0.682 | 0.970 | 1.121 | [22] |
| 30 | 11 | 1.08 | 0.14 | 0.130 | 0.63 | 0.7 | 0.97 | 1.12 | [22] |
| 31 | 11 | 1.08 | 0.10 | 0.095 | 0.633 | 0.651 | 0.970 | 1.084 | [22] |
| 32 | 11 | 1.08 | 0.10 | 0.095 | 0.633 | 0.668 | 0.970 | 1.084 | [22] |
| 33 | 11 | 1.08 | 0.10 | 0.090 | 0.633 | 0.682 | 0.970 | 1.115 | [22] |
| 34 | 11 | 1.08 | 0.06 | 0.053 | 0.633 | 0.700 | 0.970 | 1.091 | [22] |
| 35 | 8 | 0.25 | 0.01 | 0.040 | 0.615 | 0.634 | 0.829 | 2.100 | [23] |
| 36 | 14 | 0.20 | 0.05 | 0.248 | 0.548 | 0.754 | 0.806 | 1.181 | [24] |
| 37 | 12 | 0.16 | 0.05 | 0.307 | 0.580 | 0.754 | 0.868 | 1.179 | [24] |
| 38 | 12 | 0.14 | 0.04 | 0.314 | 0.570 | 0.754 | 0.878 | 1.181 | [24] |
| 39 | 9 | 0.45 | 0.04 | 0.078 | 0.570 | 0.760 | 0.949 | 1.413 | [28] |
| 40 | 12 | 0.15 | 0.01 | 0.067 | 0.542 | 0.622 | 0.765 | 0.934 | [28] |
| 41 | 5 | 0.37 | 0.16 | 0.432 | 0.552 | 0.583 | 0.703 | 0.755 | [29] |
| 42 | 7 | 0.6 | 0.02 | 0.033 | 0.63 | 0.99 | 0.79 | 1.56 | [30] |
| 43 | 8 | 0.11 | 0.02 | 0.182 | 0.67 | 0.68 | 1.03 | 1.71 | [31] |
| 44 | 11 | 0.39 | 0.04 | 0.103 | 0.49 | 0.776 | 0.77 | 1.317 | [32] |
| 45 | 7 | 0.365 | 0.026 | 0.071 | 0.671 | 0.479 | 1.023 | 1.676 | [33] |
| 46 | 5 | 0.1 | 0.03 | 0.300 | 0.62 | 0.87 | 1.17 | 1.53 | [34] |
| 47 | 8 | 0.2 | 0.05 | 0.250 | 0.65 | 0.74 | 0.95 | 1.24 | [35] |
| 48 | 8 | 0.3 | 0.08 | 0.267 | 0.6 | 0.71 | 0.95 | 1.36 | [36] |
| 49 | 8 | 0.25 | 0.014 | 0.056 | 0.664 | 0.987 | 0.941 | 1.511 | [37] |
| 50 | 15 | 0.37 | 0.038 | 0.103 | 0.41 | 0.65 | 0.66 | 1.64 | [38] |
| 51 | 9 | 0.2 | 0.016 | 0.080 | 0.57 | 0.9 | 0.86 | 1.79 | [39] |
| 52 | 7 | 0.68 | 0.057 | 0.084 | 0.535 | 0.72 | 0.854 | 1.42 | [40] |
| 53 | 11 | 0.72 | 0.017 | 0.024 | 0.6 | 0.81 | 0.78 | 1.4 | [41] |
| 54 | 11 | 0.6 | 0.027 | 0.045 | 0.61 | 0.99 | 0.79 | 1.56 | [42] |
| 55 | 11 | 0.2 | 0.027 | 0.135 | 0.62 | 0.97 | 0.99 | 1.55 | [43] |
| 56 | 11 | 0.33 | 0.027 | 0.082 | 0.63 | 0.98 | 0.79 | 1.54 | [44] |
| 57 | 12 | 0.13 | 0.043 | 0.331 | 0.65 | 0.8 | 0.87 | 1.31 | [45] |
| 58 | 4 | 0.45 | 0.012 | 0.027 | 0.43 | 0.72 | 0.72 | 2.13 | [46] |
| 59 | 5 | 0.21 | 0.01 | 0.048 | 0.579 | 0.461 | 0.872 | 1.897 | [47] |
| 60 | 9 | 0.45 | 0.04 | 0.089 | 0.57 | 0.76 | 0.95 | 1.41 | [48] |
| 61 | 11 | 0.18 | 0.03 | 0.167 | 0.653 | 0.727 | 0.972 | 1.723 | [10] |
| 62 | 11 | 0.43 | 0.03 | 0.070 | 0.631 | 0.727 | 0.821 | 1.723 | [10] |
| 63 | 9 | 0.35 | 0.023 | 0.066 | 0.47 | 0.67 | 0.75 | 1.49 | [46] |
| Sand Type | Silt Type | emax | emin | Average |
|---|---|---|---|---|
| Monterey | Yatesville | 0.963 | 0.936 | 0.949 |
| Ottawa C-109 | #6 Sil-CO-Sil | 0.994 | 0.991 | 0.993 |
| Yatesville | Yatesville | 0.979 | 0.906 | 0.943 |
| 60 sand–silt combination data set | 0.956 | 0.884 | 0.920 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polito, C.P. Correlations for Estimating Coefficients for the Prediction of Maximum and Minimum Index Void Ratios for Mixtures of Sand and Non-Plastic Silt. Geotechnics 2023, 3, 1033-1046. https://doi.org/10.3390/geotechnics3040056
Polito CP. Correlations for Estimating Coefficients for the Prediction of Maximum and Minimum Index Void Ratios for Mixtures of Sand and Non-Plastic Silt. Geotechnics. 2023; 3(4):1033-1046. https://doi.org/10.3390/geotechnics3040056
Chicago/Turabian StylePolito, Carmine P. 2023. "Correlations for Estimating Coefficients for the Prediction of Maximum and Minimum Index Void Ratios for Mixtures of Sand and Non-Plastic Silt" Geotechnics 3, no. 4: 1033-1046. https://doi.org/10.3390/geotechnics3040056
APA StylePolito, C. P. (2023). Correlations for Estimating Coefficients for the Prediction of Maximum and Minimum Index Void Ratios for Mixtures of Sand and Non-Plastic Silt. Geotechnics, 3(4), 1033-1046. https://doi.org/10.3390/geotechnics3040056








