Borehole Analysis with the Modification of RQD Value
Abstract
:1. Introduction
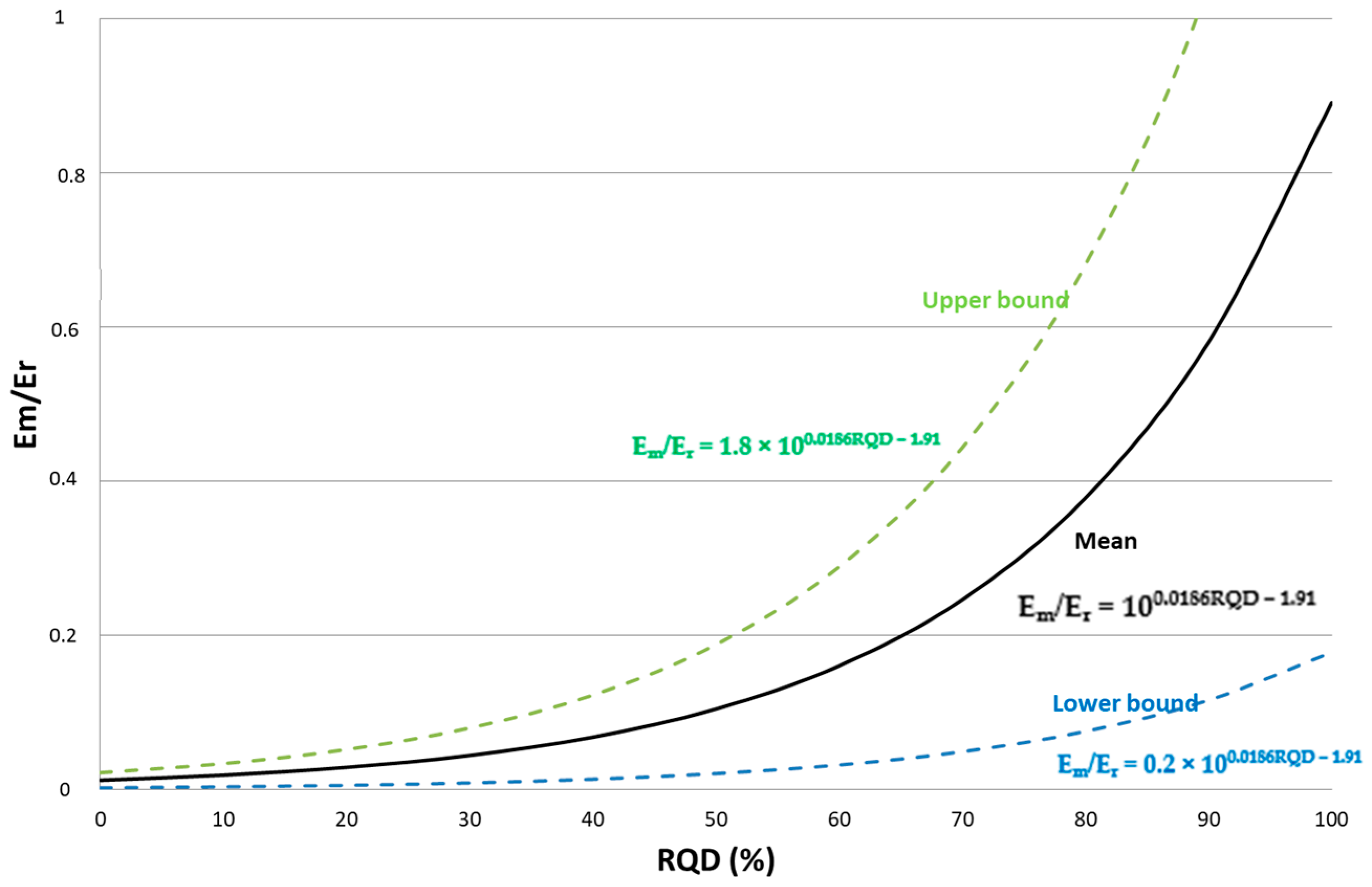
- Lower bound:
- Upper bound:
- Mean:
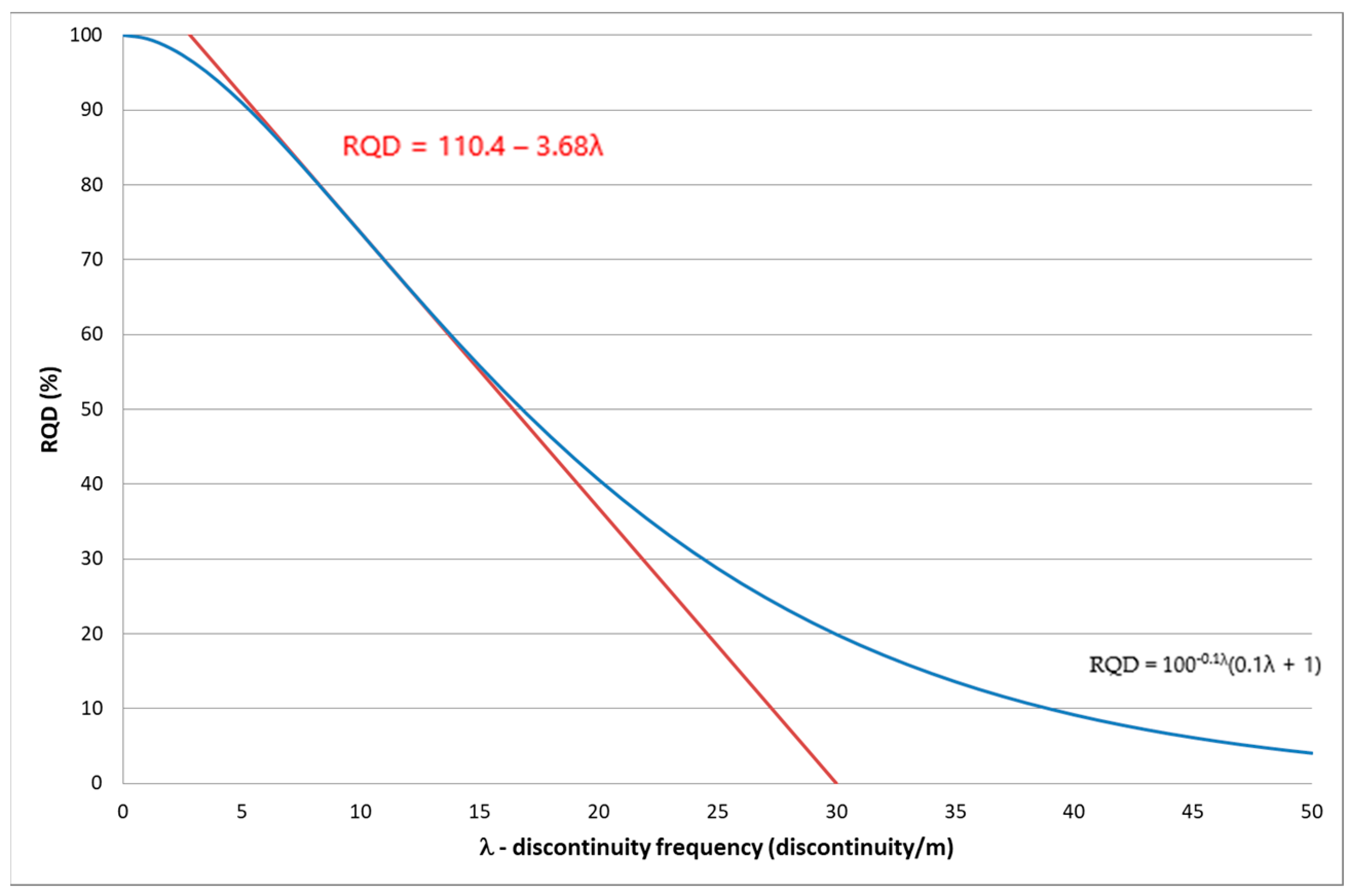
2. Disadvantages of the RQD Method
3. Investigated Rock and Data
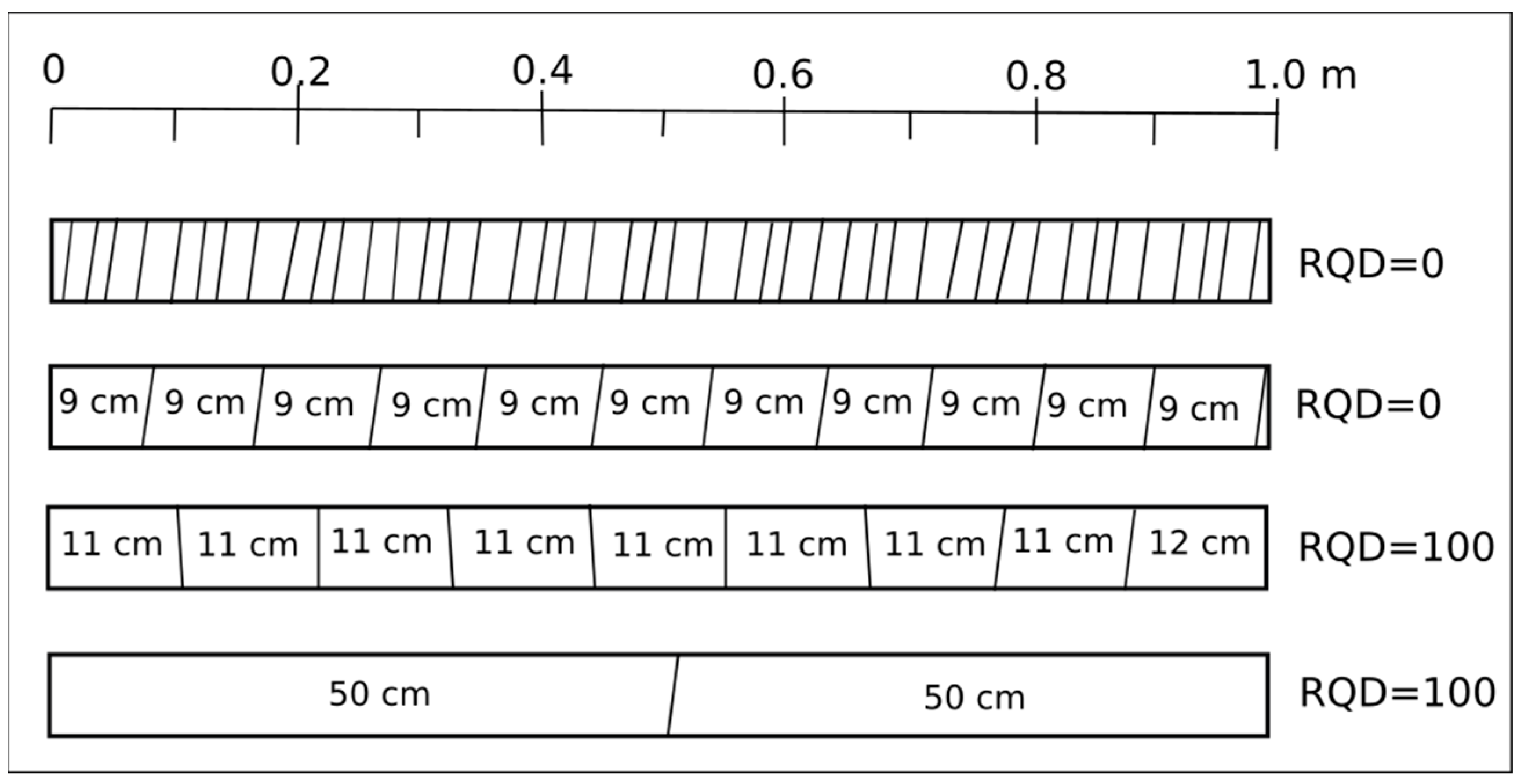
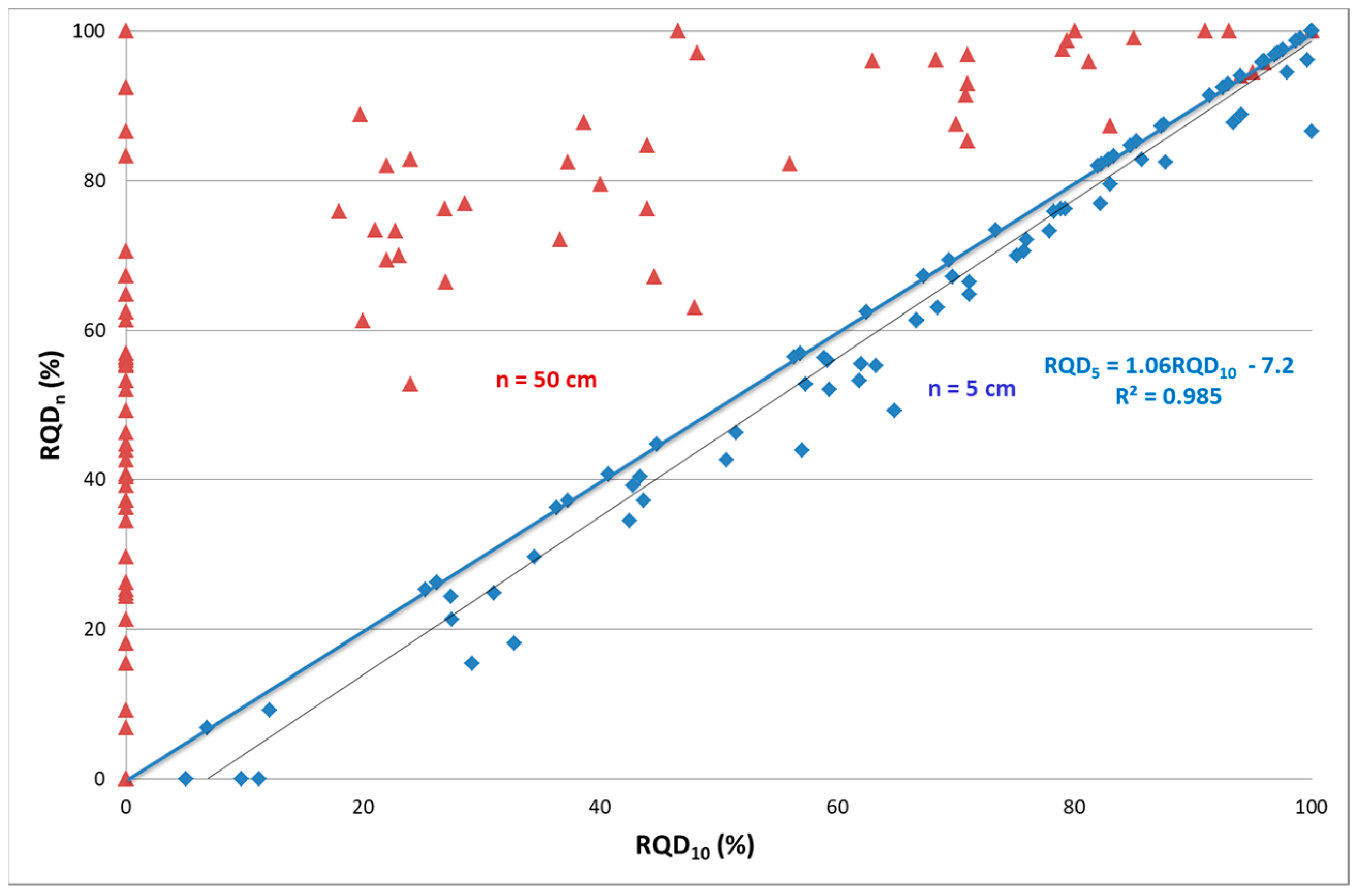
4. RQD and the Length of Core Pieces
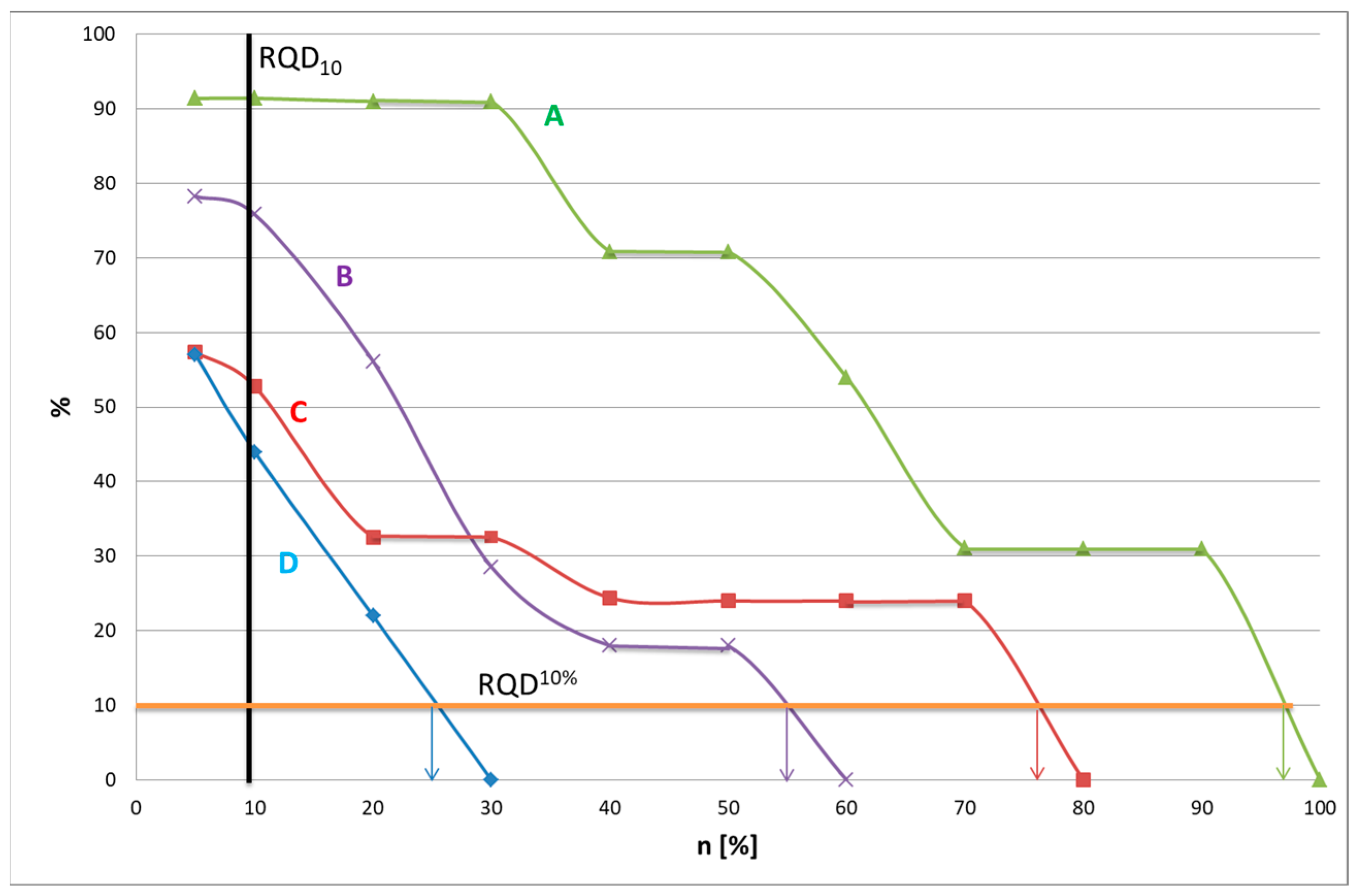
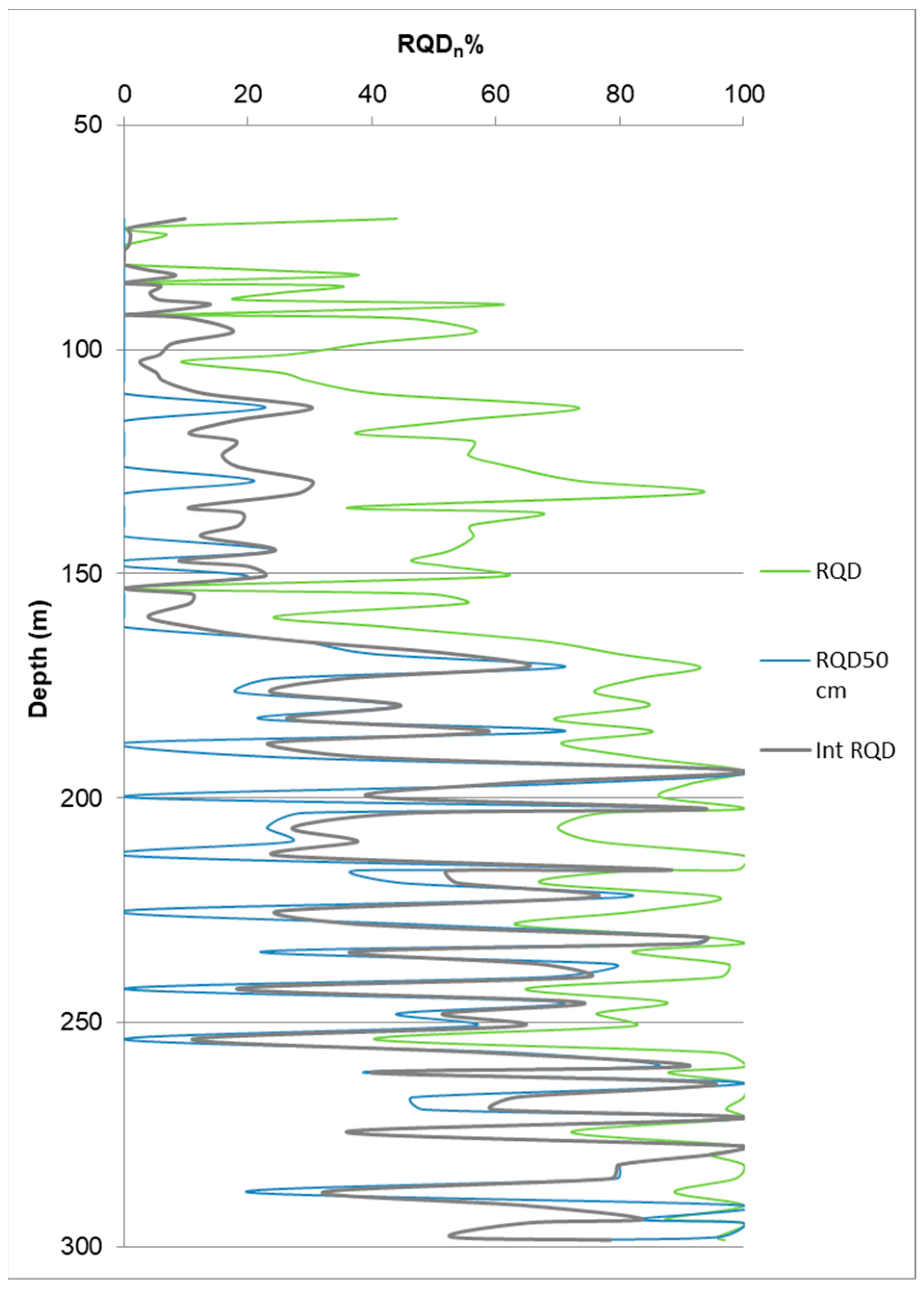
5. Implementation of Integrated RQD
6. Discussions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deere, D.U. Technical description of rock cores for engineering purposes. Rock Mech. Eng. Geol. 1964, 1, 17–22. [Google Scholar]
- Bieniawski, Z.T. Engineering classification of jointed rock masses. Trans. S. Afr. Inst. Civ. Eng. 1973, 15, 335–344. [Google Scholar]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; Wiley-Interscience: Hoboken, NJ, USA, 1989. [Google Scholar]
- Barton, N.R.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–239. [Google Scholar] [CrossRef]
- Rehman, H.; Ali, W.; Naji, A.M.; Kim, J.-J.; Abdullah, R.A.; Yoo, H.-K. Review of Rock-Mass Rating and Tunneling Quality Index Systems for Tunnel Design: Development, Refinement, Application and Limitation. Appl. Sci. 2018, 8, 1250. [Google Scholar] [CrossRef]
- Rehman, H.; Naji, A.M.; Kim, J.-J.; Yoo, H.-K. Empirical Evaluation of Rock Mass Rating and Tunneling Quality Index System for Tunnel Support Design. Appl. Sci. 2018, 8, 782. [Google Scholar] [CrossRef]
- Hoek, E.; Carter, T.G.; Diederichs, M.S. Quantification of the Geological Strength Index Chart. In Proceedings of the 47th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013. [Google Scholar]
- Xia, K.; Chen, C.; Wang, T.; Pang, H.; Liu, X. Quantification of the GSI and D values in the Hoek–Brown criterion using the rock quality designation (RQD) and discontinuity surface condition rating (SCR). Bull. Eng. Geol. Environ. 2022, 81, 4. [Google Scholar] [CrossRef]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations Is Hard Rock; Balkema: Rotterdam, The Netherlands, 1995. [Google Scholar]
- Hoek, E.; Brown, E.T. The Hoek-Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Deere, D.U. Rock Quality Designation (RQD) after 20 Years; US Army Corps. Engrs Rep.: Gainesville, FL, USA, 1989; p. GL-89-1. [Google Scholar]
- Deere, D.U.; Deere, D.W. The RQD Index in Practice, Rock Classification Systems for Engineering Purposes; ASTM Special Technical Publications 984: West Conshohocken, PA, USA, 1988; pp. 91–101. [Google Scholar]
- Eurocode 1997-1: Geotechnical design, Part 1: General rules.
- Priest, S.D.; Hudson, J. Discontinuity spacing in rock. Int. J. Rock Mech. Mining Sci. Geomech. 1976, 13, 135–148. [Google Scholar] [CrossRef]
- Vučemilović, H.; Mulabdić, M.; Miščević, P. Corrected Rock Fracture Parameters and Other Empirical Considerations for the Rock Mechanics of Rock Masses of Doha, Qatar. Geotech. Geol. Eng. 2021, 39, 2823–2847. [Google Scholar] [CrossRef]
- Hasan, M.; Shang, Y.; Shao, P.; Yi, X.; Meng, H. Geophysical research on rock mass quality evaluation for infrastructure design. Earth Space Sci. 2022, 9, e2021EA002017. [Google Scholar] [CrossRef]
- Zilahi-Sebess, L. A repedezettség hatása a mélyfúrásgeofizikai mérésekre. Magy. Geofiz. Hung. Geophys. 2010, 51, 124–142. [Google Scholar]
- Egerer, F.; Kertész, P. Bevezetés a Kőzetfizikába (Introduction to Rock Physics); Akadémiai Kiadó: Budapest, Hungary, 1993. [Google Scholar]
- Kirkby, A.; Heinson, G.; Krieger, L. Relating permeability and electrical resistivity in fractures using random resistor network models. J. Geophys. Res. Solid Earth 2016, 121, 1546–1564. [Google Scholar] [CrossRef]
- Alemdag, S.; Sari, M.; Seren, A. Determination of rock quality designation (RQD) in metamorphic rocks: A case study (Bayburt-Kirklartepe Dam). Bull. Eng. Geol. Environ. 2022, 81, 214. [Google Scholar] [CrossRef]
- Palmström, A. The Volumetric Joint Count—A Useful and Simple Measure of the Degree of Rock Mass Jointing; IAEG Congress: New Delhi, India, 1982; pp. V.221–V.228. [Google Scholar]
- Ding, Q.; Wang, F.; Chen, J.; Wang, M.; Zhang, X. Research on Generalized RQD of Rock Mass Based on 3D Slope Model Established by Digital Close-Range Photogrammetry. Remote Sens. 2022, 14, 2275. [Google Scholar] [CrossRef]
- Deere, D.U.; Hendron, A.J.; Patton, F.D.; Cording, E.J. Design of surface and near surface constructions in rock. In Proceedings of the 8th U.S. Symposium on Rock Mechanics, Minneapolis, MN, USA, 15 September 1966; AIME: New York, NY, USA, 1967; pp. 237–302. [Google Scholar]
- Deere, D.U.; Merritt, A.H.; Coon, R.F. Engineering Classification of In-Situ Rocks; Report by University of Illinois to Air Force Weapons Lab; Kirtland Air Force Base: Albuquerque, NM, USA, 1968; p. 272, Publication No. AFWL-TW-67-144, National Technical Information Service (NTIS) Publication No. AD 848798. [Google Scholar]
- Coon, R.F.; Marritt, A.H. Predicting in Situ Modulus of Deformation Using Rock Quality Index. In Determination of the In Situ Modulus of Deformation of Rock; ASTM International: West Conshohocken, PA, USA, 1970; pp. 154–173. [Google Scholar]
- Zhang, L.; Einstein, H.H. Using RQD to estimate the deformation modulus of rock masses. Int. J. Rock Mech. Mining Sci. 2004, 41, 337–341. [Google Scholar] [CrossRef]
- Zhang, L. Estimating the Strength of Jointed Rock Masses. Rock Mech. Rock Eng. 2010, 43, 391–402. [Google Scholar] [CrossRef]
- Zhang, L. Determination and applications of rock quality designation (RQD). J. Rock Mech. Geotech. Eng. 2016, 8, 389–397. [Google Scholar] [CrossRef]
- Vásárhelyi, B.; Kovács, D. Empirical methods of calculating the mechanical parameters of the rock mass. Period. Polytech. Civ. Eng. 2017, 61, 39–50. [Google Scholar] [CrossRef]
- Ván, P.; Vásárhelyi, B. Relation of rock mass characterization and damage. In Rock Engineering in Difficult Ground Conditions–Soft Rocks and Karst; Vrkljan, I., Ed.; CRC Press: Omis, Croatia, 2010; pp. 399–404. [Google Scholar]
- Pells, P.J.; Bieniawski, Z.T.; Hencher, S.R.; Pells, S.E. Rock quality designation (RQD): Time to rest in peace. Can. Geotech. J. 2017, 54, 825–834. [Google Scholar] [CrossRef]
- Su, R.; Zhao, Q.; Zheng, T.; Han, G.; Jlang, J.; Hu, J. A Framework for RQD Calculation Based on Deep Learning. Min. Metall. Explor. 2023. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Wang, Q.; Ma, D.; Niu, C.; Zhang, W. Investigation of RQD variation with scanline length and optimal threshold based on three-dimensional fracture network modeling. Sci. China Technol. Sci. 2013, 56, 739–748. [Google Scholar] [CrossRef]
- Li, L.; Ouellet, S.; Aubertin, M. An improved definition of rock quality designation, RQDc. In Proceedings of the ROCKENG09: Proceedings of the 3rd CANUS Rock Mechanics Symposium, Toronto, ON, Canada, 9–15 May 2009. [Google Scholar]
- Palmström, A. Measurement and characterization of rock mass jointing. In In Situ Characterization of Rocks; Sharma, V.M., Saxena, K.R., Eds.; Taylor & Francis: Abingdon, UK, 2001; pp. 49–97. [Google Scholar]
- Palmström, A. Measurements of and correlations between block size and rock quality designation (RQD). Tunn. Undergr. Space Technol. 2005, 20, 362–377. [Google Scholar] [CrossRef]
- Azimian, A. A New Method for Improving the RQD Determination of Rock Core in Borehole. Rock Mech. Rock Eng. 2016, 49, 1559–1566. [Google Scholar] [CrossRef]
- Lowson, A.; Bieniawski, Z. Critical Assessment of RMR-Based Tunnel Design Practices: A Practical Engineer’s Approach. In Proceedings of the SME, Rapid Excavation and Tunnelling Conference, Washington, DC, USA, 23–26 June 2013; pp. 180–198. [Google Scholar]
- Celada, B.; Tardáguila, I.; Varona, P.; Rodríguez, A.; Bieniawski, Z. Innovating Tunnel Design by an Improved Experience-Based RMR System. In Proceedings of the World Tunnel Congress, Foz do Iguaçu, Brazil, 9–15 May 2014; p. 9. [Google Scholar]
- Rehman, H.; Naji, A.M.; Kim, J.-J.; Yoo, H. Extension of tunneling quality index and rock mass rating systems for tunnel support design through back calculations in highly stressed jointed rock mass: An empirical approach based on tunneling data from Himalaya. Tunn. Undergr. Space Technol. 2019, 85, 29–42. [Google Scholar] [CrossRef]
- Balla, Z.; Albert, G.; Chikán, G.; Dudko, A.; Fodor, L.; Forián-Szabó, M.; Földvári, M.; Gyalog, L.; Havas, G.; Horváth, I.; et al. A Felszíni Földtani Kutatási Zárójelentése, Bátaapáti (Üveghuta), 2002–2003. (Final Report of the Surface Geological Survey, Bátaapáti (Üveghuta), 2002–2003)); MÁFI, Bátatom Kft.: Budapest, Hungary, 2003; p. BA–03–156. (In Hungarian) [Google Scholar]
- MBFSZ Mining and Geological Survey of Hungary. Geological Base Sections of Hungary on the 1:100.000 Scale Surface Geology Base Map of Hungary. Mining and Geological Survey of Hungary: Budapest, Hungary, 2021. Available online: https://map.mbfsz.gov.hu/fdt_alapszelvenyek/ (accessed on 18 August 2023).
- Kovács, L.; Kádár, B.; Krupa, Á.; Mészáros, E.; Pöszmet, T.; Rátkai, O.; Somodi, G.; Amigyáné Reisz, K.; Vásárhelyi, B. The Revision and Upgrade of Geotechnical Interpretative Report. Manuscript. Puram (RHK Kft.), RHKK-028/16. (In Hungarian). 2016. Available online: https://www.mta-kozettan.hu/sites/default/files/pdf/IV_KGV_kiadv%C3%A1nya.pdf (accessed on 27 September 2023).
- Deák, F.; Kovács, L.; Vásárhelyi, B. Geotechnical rock mass documentation in the Bátaapáti radioactive waste repository. Centr. Eur. Geol. 2014, 57, 197–211. [Google Scholar] [CrossRef]
- Somodi, G.; Krupa, Á.; Kovács, L.; Vásárhelyi, B. Comparison of different calculation methods of Geological Strength Index (GSI) is a specific underground site. Eng. Geol. 2018, 243, 50–58. [Google Scholar] [CrossRef]
- Vásárhelyi, B.; Somodi, G.; Krupa, Á.; Kovács, L. Determining the Geological Strength Index (GSI) using different methods. In Proceedings of the 2016 ISRM International Symposium, EUROCK 2016, Cappadocia, Turkey, 29–31 August 2016; pp. 1049–1054. [Google Scholar]
- Davarpanah, M.; Somodi, G.; Kovács, L.; Vásárhelyi, B. Complex analysis of uniaxial compressive tests of the Mórágy granitic rock formation (Hungary). Stud. Geotech. Mech. 2019, 41, 21–32. [Google Scholar] [CrossRef]
- Davarpanah, M.; Somodi, G.; Kovács, L.; Vásárhelyi, B. Experimental Determination of the Mechanical Properties and Deformation Constants of Mórágy Granitic Rock Formation (Hungary). Geotech. Geol. Eng. 2020, 38, 3215–3229. [Google Scholar] [CrossRef]
- Narimani, S.; Davarpanah, S.M.; Kovács, L.; Vásárhelyi, B. Variation of Elastic Stiffness Parameters of Granitic Rock during Loading in Uniaxial Compressive Test. Appl. Mech. 2023, 4, 445–459. [Google Scholar] [CrossRef]
- Somodi, G.; Kovács, L.; Máté, K.; Geiger, J. A Geotechnikai Értelmező Jelentés (GÉJ) Felülvizsgálatát és Kiterjesztését Megalapozó Geostatisztikai Vizsgálatok. RHK Kft. Irattár. Paks. RHK-K031/122013. Available online: https://wslpwstoreprd.blob.core.windows.net/kentico-media-libraries-prod/watercarepublicweb/media/watercare-media-library-2/ci-consents/appendix_e_geotechnical_interpretive_report_volume_1.pdf (accessed on 27 September 2023).
- Somodi, G.; Krupa, Á.; Kovács, L.; Szujó, G. Reviewing length, density and orientation data of fractures in a granitic rock mass. In Geomechanics and Geodynamics of Rock Masses; Vladimir, L., Ed.; Taylor and Francis Group: Abingdon, UK, 2018; pp. 439–443. [Google Scholar]
- Deere, D.U.; Peck, R.B.; Monsees, J.E.; Schmidt, B. Design of Tunnel Liners and Support Systems; Report of University of Illinois to Office of High-Speed Ground Transportation; U.S. Department of Transportation (DOT): Washington, DC, USA, 1969; p. 420, NTIS Publication No. PB-183799.







| RQD % | Rock Mass Classification (EUROCODE 7) | Description |
|---|---|---|
| >25 | very poor | Disintegrated/Soil |
| 25–50 | poor | Shattered, very blocky |
| 50–75 | fair | Blocky and seamy |
| 75–90 | good | Massive, slightly blocky |
| 90–100 | excellent | Intact |
| Property | Value |
|---|---|
| Uniaxial compressive strength | 102 MPa |
| Tensile strength | 6.4 MPa |
| Young’s modulus | 45.9 GPa |
| Poisson’s ratio | 0.17 |
| Bulk density | 27.10 kN/m3 |
| RQD5 | RQD10 | RQD50 | RQD10% | |
|---|---|---|---|---|
| A | 91 | 91 | 71 | 98 |
| B | 78 | 76 | 18 | 54 |
| C | 57 | 53 | 24 | 77 |
| D | 57 | 44 | 0 | 25 |
| Infilling Rating (Rf) | Value |
|---|---|
| None | 6 |
| Hard (<5 mm) | 4 |
| Hard (>5 mm) | 2 |
| Soft (<5 mm) | 2 |
| Soft (>5 mm) | 0 |
| Weathering Rating (Rw) | Value |
| Unweathered | 6 |
| Slightly weathered | 5 |
| Moderately weathered | 3 |
| Highly weathered | 1 |
| Decomposed | 0 |
| Roughness Rating (Rw) | Value |
| Very rough | 6 |
| Rough | 5 |
| Slightly rough | 3 |
| Smooth | 1 |
| Slickensided | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somodi, G.; Vásárhelyi, B. Borehole Analysis with the Modification of RQD Value. Geotechnics 2023, 3, 1017-1032. https://doi.org/10.3390/geotechnics3040055
Somodi G, Vásárhelyi B. Borehole Analysis with the Modification of RQD Value. Geotechnics. 2023; 3(4):1017-1032. https://doi.org/10.3390/geotechnics3040055
Chicago/Turabian StyleSomodi, Gábor, and Balázs Vásárhelyi. 2023. "Borehole Analysis with the Modification of RQD Value" Geotechnics 3, no. 4: 1017-1032. https://doi.org/10.3390/geotechnics3040055
APA StyleSomodi, G., & Vásárhelyi, B. (2023). Borehole Analysis with the Modification of RQD Value. Geotechnics, 3(4), 1017-1032. https://doi.org/10.3390/geotechnics3040055







