Biomechanical Modeling and Simulation of the Knee Joint: Integration of AnyBody and Abaqus
Abstract
1. Introduction
2. Methods
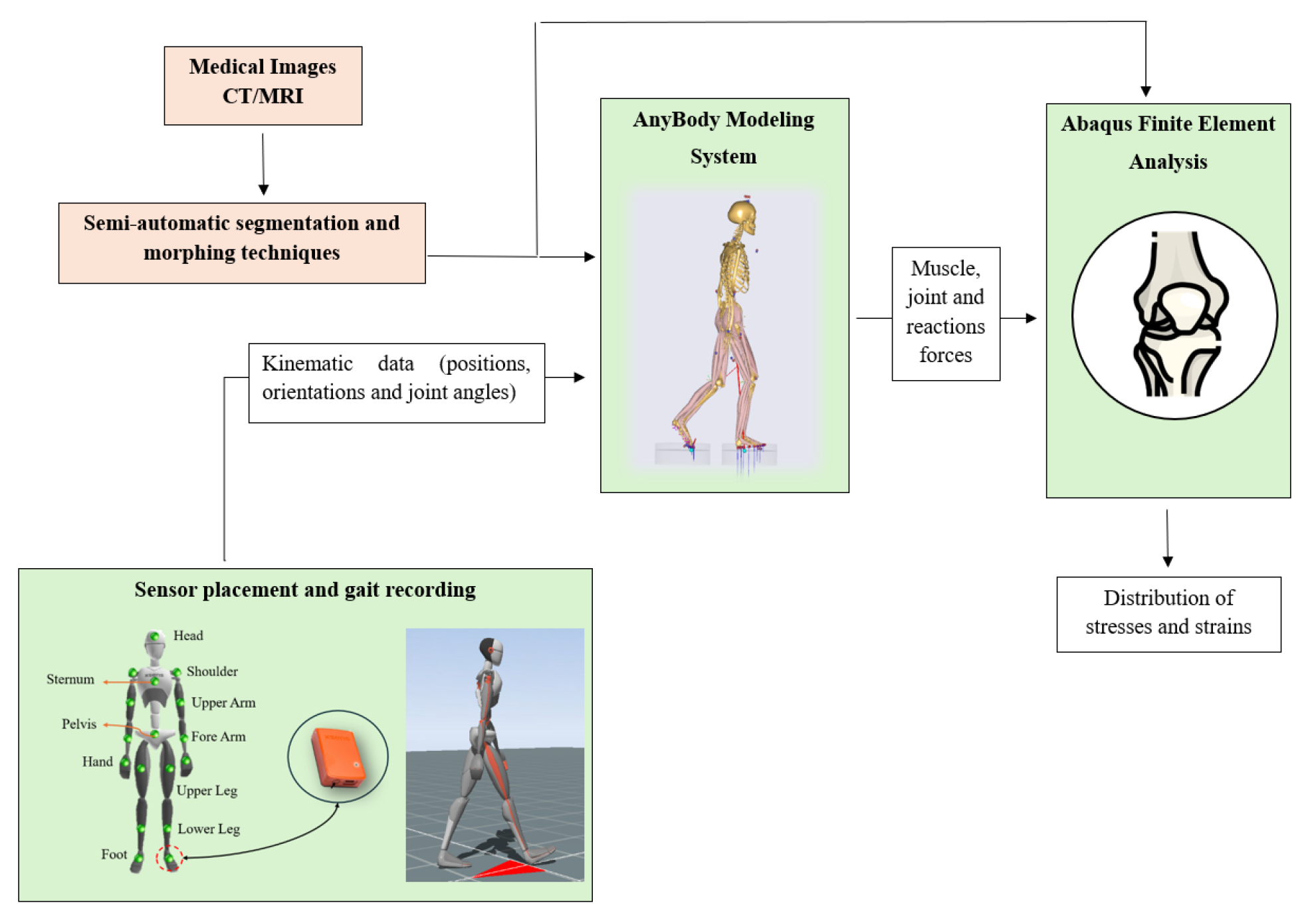
2.1. Workflow and Subject Information
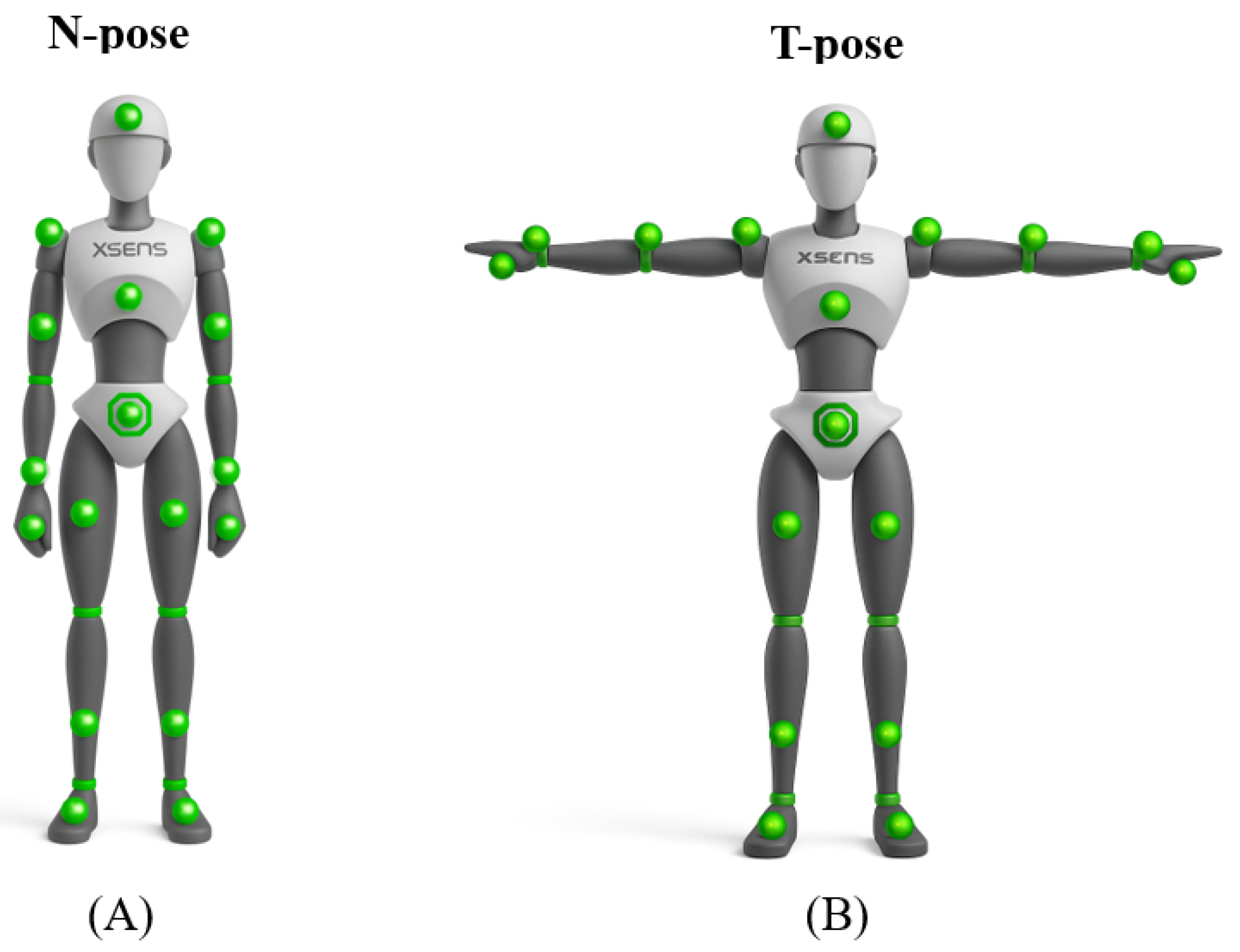
2.2. Data Collection
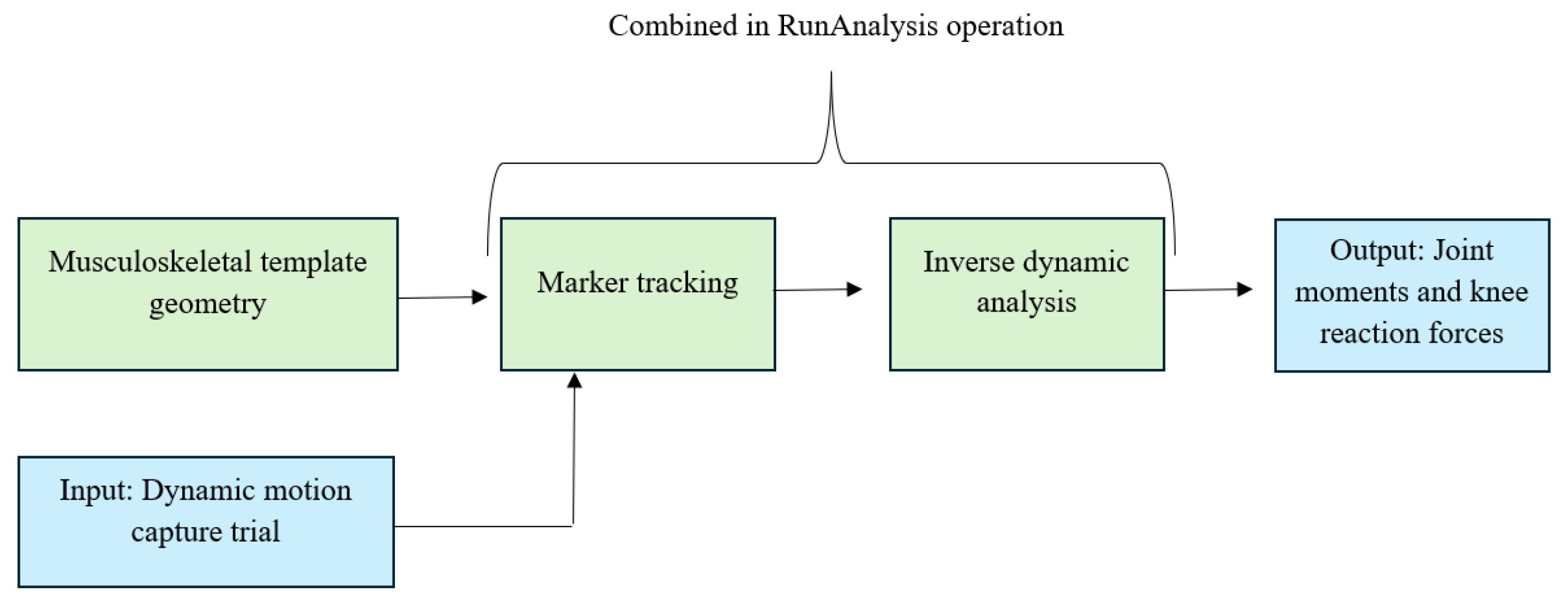
2.3. Musculoskeletal Model
- LabSpecificData: this part ensures that ground contact is correctly detected (indicated by red spheres). In this case, the ground contact threshold was adjusted to 0.045 for both legs, as this parameter significantly affects knee joint forces;
- SubjectSpecificData: the subject’s weight and height are set according to their specific characteristics.
- TrialSpecificData: the start and end frames of the analyzed trial were set to 10 and 300, respectively. Only the frames corresponding to forward walking, i.e., when the subject moved in the positive direction of the gait cycle, were considered for analysis. This ensured that the musculoskeletal modeling focused exclusively on the phases of consistent and natural forward locomotion, minimizing variability due to turns or changes in walking direction.
- AnyMocap Model: used to drive the musculoskeletal simulation using the processed motion capture data.
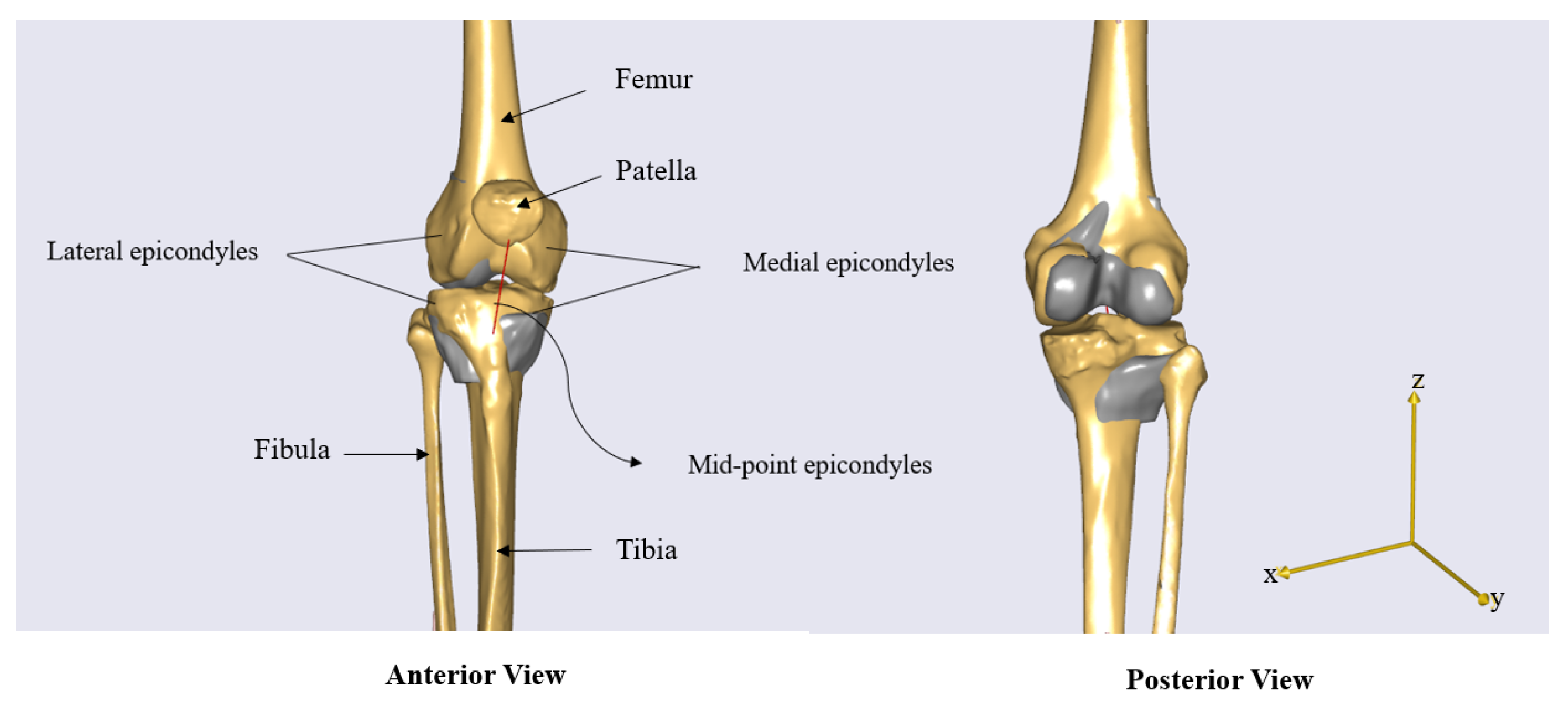
- Points 0: Source landmarks extracted from the STL files, including the medial and lateral femoral epicondyles, their midpoint, the KneeJointAnatomicalFrame for the femur, and the TibialTuberosity for the tibia.
- Points 1: Target landmarks defined within the AnyBody model’s anatomical hierarchy.
2.4. Abaqus
- Ligament-to-bone connections:
- –
- Medial collateral ligament (MCL), ACL, and posterior cruciate ligament (PCL) to femur and tibia;
- –
- Lateral collateral ligament (LCL) to femur (note: anatomically, the LCL inserts on the fibula, which is not yet included in the current model but is intended to be added in future developments);
- Cartilage-to-bone connections:
- –
- Left and right tibial cartilage to tibia;
- –
- Femoral cartilage to femur;
- Between the surfaces of the left tibial cartilage and the femoral cartilage;
- Between the surfaces of the right tibial cartilage and the femoral cartilage;
- Between the surfaces of the ACL and the PCL.
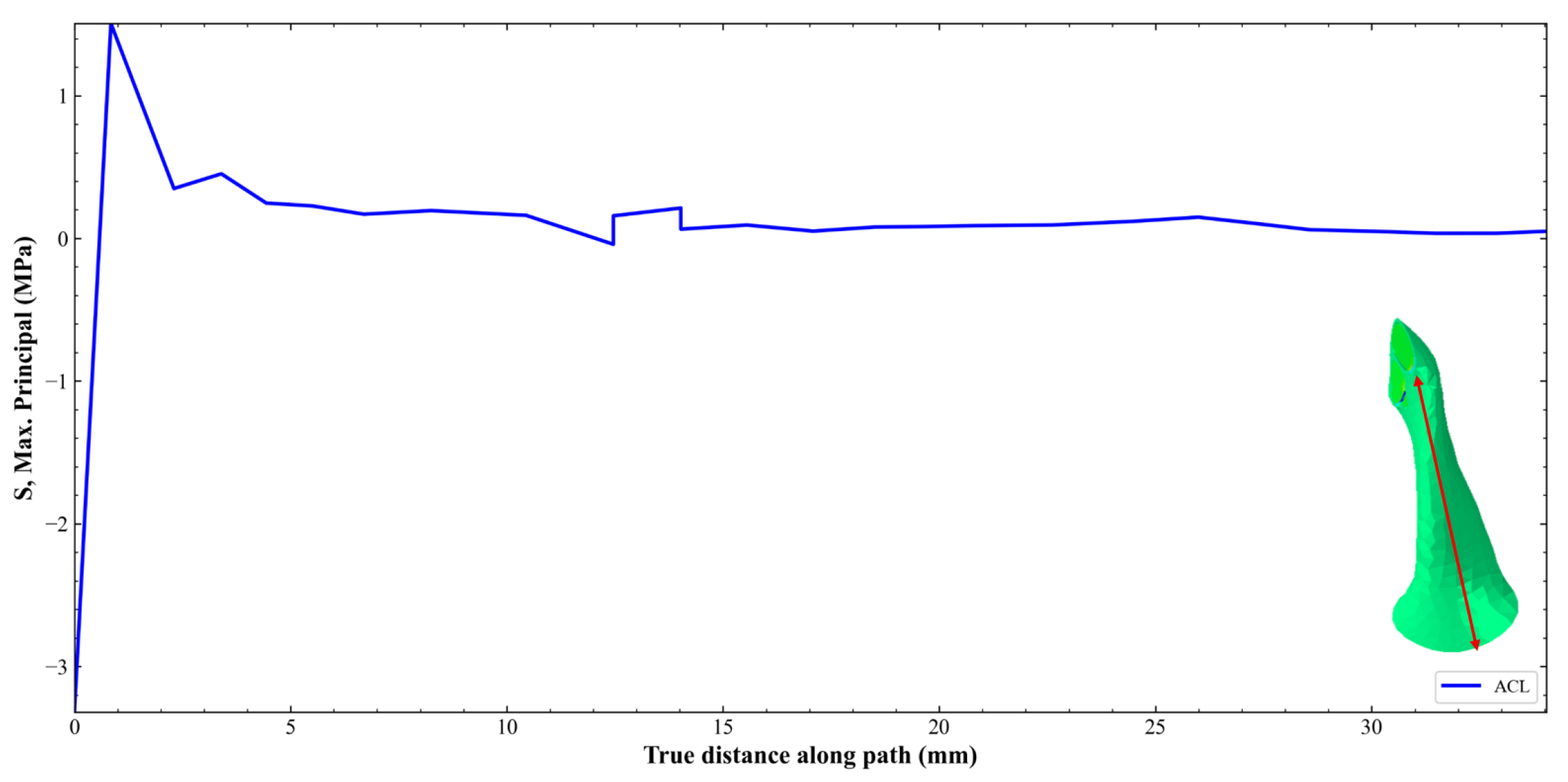
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Yan, Y.; Ma, J.; Wei, P. Knee Joint Biomechanics in Physiological Conditions and How Pathologies Can Affect It: A Systematic Review. Appl. Bionics Biomech. 2020, 2020, 7451683. [Google Scholar] [CrossRef] [PubMed]
- Halloran, J.P.; Ackermann, M.; Erdemir, A.; van den Bogert, A.J. Concurrent Musculoskeletal Dynamics and Finite Element Analysis Predicts Altered Gait Patterns to Reduce Foot Tissue Loading. J. Biomech. 2010, 43, 2810–2815. [Google Scholar] [CrossRef] [PubMed]
- Peitola, J.P.J.; Esrafilian, A.; Eskelinen, A.S.A.; Andersen, M.S.; Korhonen, R.K. Sensitivity of knee cartilage biomechanics in finite element analysis to selected Musculoskeletal models. Comput. Methods Biomech. Biomed. Eng. 2024, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Shu, L.; Yamamoto, K.; Yoshizaki, R.; Yao, J.; Sato, T.; Sugita, N. Multiscale finite element musculoskeletal model for intact knee dynamics. Comput. Biol. Med. 2022, 141, 105023. [Google Scholar] [CrossRef] [PubMed]
- Karimi Dastgerdi, A.; Esrafilian, A.; Carty, C.P.; Lloyd, D.G.; Saxby, D.J. Validation and evaluation of subject-specific finite element models of the pediatric knee. Sci. Rep. 2023, 13, 18328. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.; Gatti, A.A.; Fan, B.; Shea, K.G.; Sherman, S.L.; Uhlrich, S.D.; Hicks, J.L.; Delp, S.L.; Shull, P.B.; Chaudhari, A.S. A scoping review of portable sensing for out-of-lab anterior cruciate ligament injury prevention and rehabilitation. NPJ Digit. Med. 2023, 6, 46. [Google Scholar] [CrossRef] [PubMed]
- Cox, K.; Hamrock, D.; Lawrence, S.; Lynch, S.; Romness, J.; Saksvig, J.; Warner, A.; Gutierrez, R.; Hart, J.; Boukhechba, M. How wearable sensing can be used to monitor patient recovery following ACL reconstruction. In Proceedings of the 2022 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 28–29 April 2022; pp. 234–239. [Google Scholar] [CrossRef]
- Halonen, K.S.; Dzialo, C.M.; Mannisi, M.; Venäläinen, M.S.; de Zee, M.; Andersen, M.S. Workflow assessing the effect of gait alterations on stresses in the medial tibial cartilage—Combined musculoskeletal modelling and finite element analysis. Sci. Rep. 2017, 7, 17396. [Google Scholar] [CrossRef] [PubMed]
- Andres, A.; Roland, M.; Wickert, K.; Ganse, B.; Pohlemann, T.; Orth, M.; Diebels, S. Individual postoperative and preoperative workflow for patients with fractures of the lower extremities. Clin. Biomech. 2025, in press. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, M.; Hulleck, A.A.; Katmah, R.; Trebes, N.; Damm, P.; Duda, G.N.; List, R.; Trepczynski, A. Multibody dynamics-based musculoskeletal modeling for gait analysis: A systematic review. J. Neuroeng. Rehabil. 2024, 21, 178. [Google Scholar] [CrossRef] [PubMed]
- Ebenbichler, M.; Heinrich, D.; Mohr, M.; Ueno, R.; Eberle, R. Coupling a finite element knee model with musculoskeletal multibody simulations. A case study of ACL force during a change-of-direction movement before and after injury prevention training. Curr. Issues Sport Sci. (CISS) 2024, 9, 004. [Google Scholar] [CrossRef]
- Movella. Five Steps to Quickly Set Up Your Xsens In-home Mocap Studio. 2020. Available online: https://www.movella.com/resources/blog/five-steps-to-set-up-your-xsens-in-home-studio (accessed on 28 April 2025).
- AnyBody Technology. The AnyBody Modeling System. 2024. Available online: https://www.anybodytech.com/ (accessed on 28 April 2025).
- Dassault Systèmes. Abaqus Unified FEA. 2024. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 28 April 2025).
- Lund, M.E.; Chander, D.S.; Galibarov, P.; Tørholm, S.; Engelund, B.K.; Shayestehpour, H.; Damsgaard, M. The AnyBody ManagedModel Repository (AMMR). 2025. Version 3.1.0. Available online: https://www.anybodytech.com/software/ammr/ (accessed on 28 April 2025).
- Andersen, M.S. 4—Introduction to musculoskeletal modelling. In Computational Modelling of Biomechanics and Biotribology in the Musculoskeletal System, 2nd ed.; Jin, Z., Li, J., Chen, Z., Eds.; Woodhead Publishing Series in Biomaterials; Woodhead Publishing: Sawston, UK, 2021; pp. 41–80. [Google Scholar] [CrossRef]
- Santos, C.F.; Bastos, R.; Andrade, R.; Pereira, R.; Parente, M.P.L.; Jorge, R.N.; Espregueira-Mendes, J. Revisiting the Role of Knee External Rotation in Non-Contact ACL Mechanism of Injury. Appl. Sci. 2023, 13, 3802. [Google Scholar] [CrossRef]
- AnyBody Technology. Scaling and Personalizing Your Model—Lesson 1. 2024. Available online: https://anyscript.org/tutorials/Scaling/lesson1.html (accessed on 29 April 2025).
- Erdemir, A. Open Knee: Open Source Modeling and Simulation in Knee Biomechanics. J. Knee Surg. 2016, 29, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Kubicek, M.; Florian, Z. Stress Strain Analysis of Knee Joint. Eng. Mech. 2009, 16, 315–322. [Google Scholar]
- Completo, A.; Fonseca, F. Fundamentos de Biomecânica Músculo-Esquelética e Ortopédica, 2nd ed.; Medicabook: Lisbon, Portugal, 2019; p. 444. [Google Scholar]
- Shi, H.; Yu, Y.; Huang, H.; Li, H.; Ren, S.; Ao, Y. Biomechanical Determinants of Anterior Cruciate Ligament Stress in Individuals Post—ACL Reconstruction During Side-Cutting Movements. Bioengineering 2025, 12, 222. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.C.; Ye, L.M.; Li, X.F.; Shi, L.J. Sequential damage assessment of the posterolateral complex of the knee joint: A finite element study. J. Orthop. Surg. Res. 2022, 17, 185. [Google Scholar] [CrossRef] [PubMed]
- Mao, Z.M.; Wang, Z.W.; Xu, C.; Liu, C.H.; Zhang, Z.Y.; Ren, X.L.; Xue, A.Q.; Li, Z.N.; Zhao, F.; Yao, Q.; et al. Intra-Articular Biomechanical Changes of the Meniscus and Ligaments During Stance Phase of Gait Circle after Different Anterior Cruciate Ligament Reconstruction Surgical Procedures: A Finite Element Analysis. Orthop. Surg. 2022, 14, 3367–3377. [Google Scholar] [CrossRef] [PubMed]
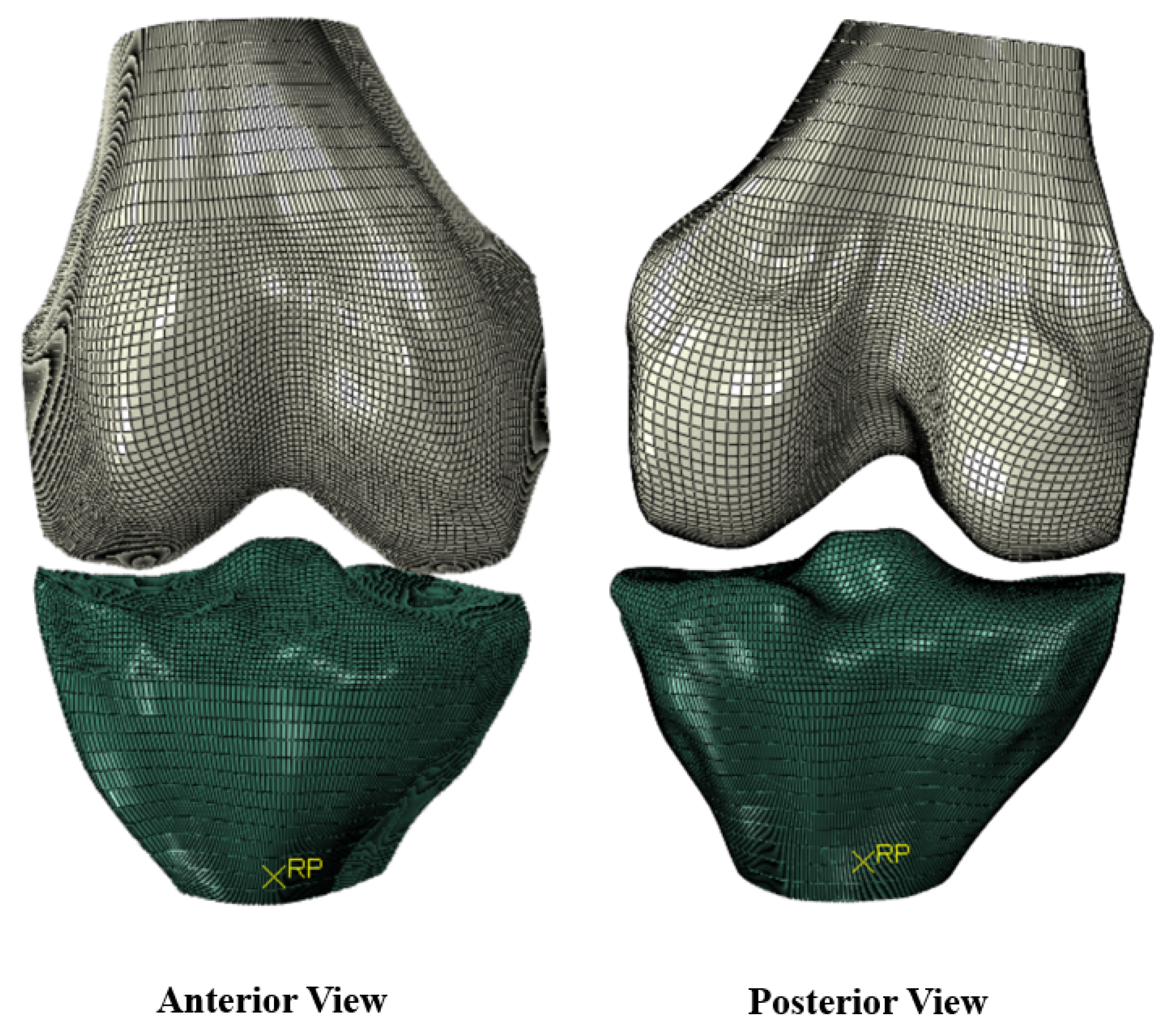
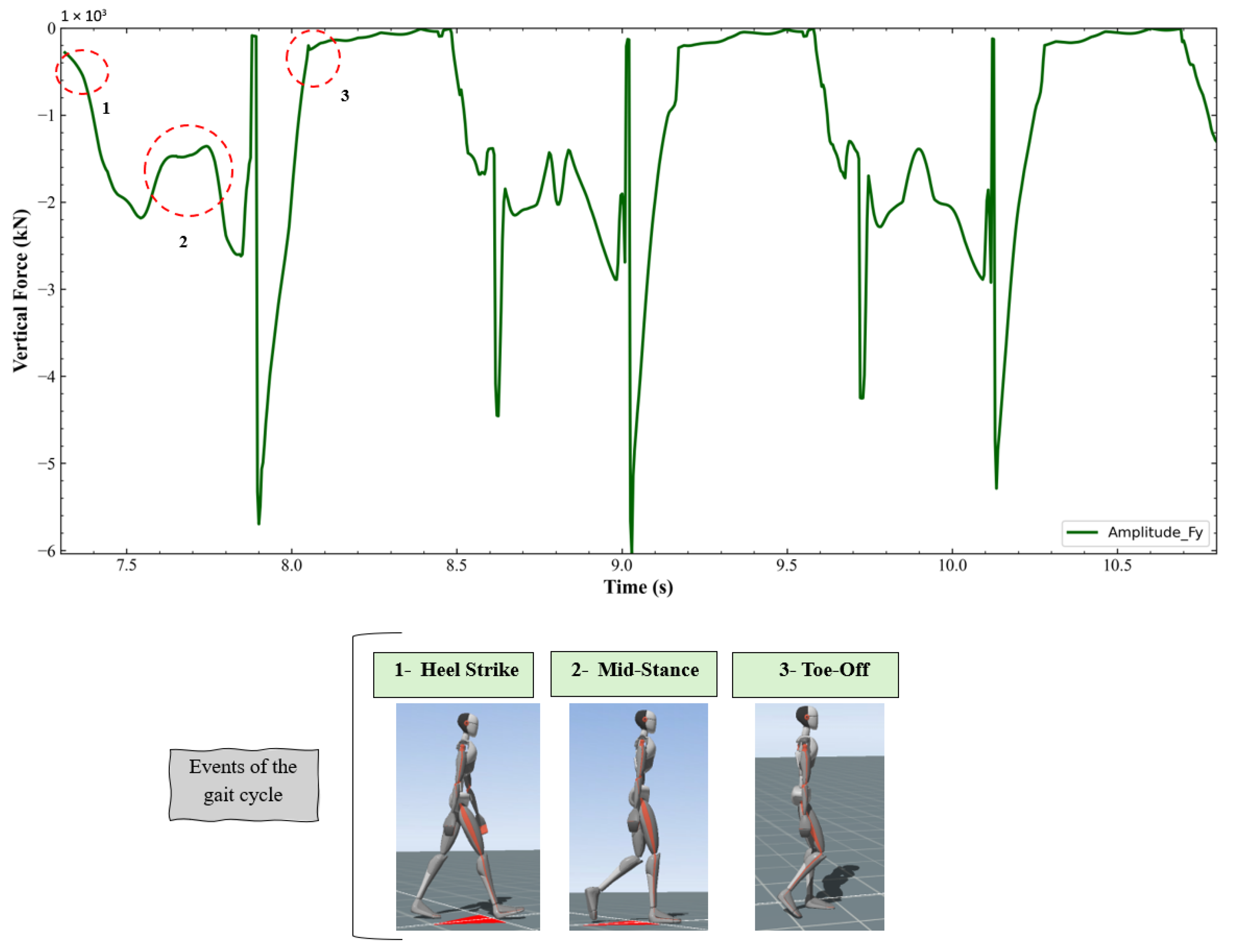
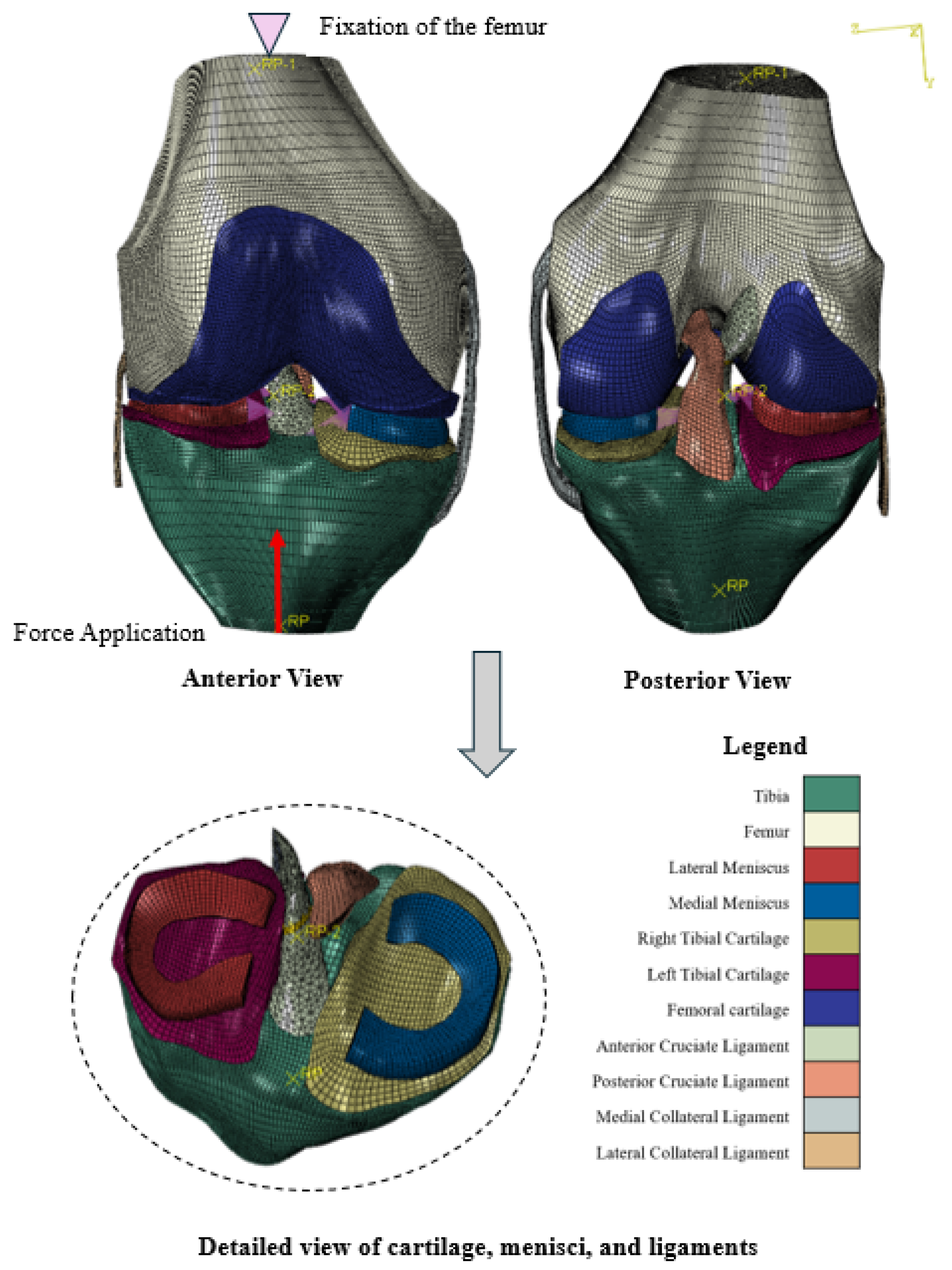
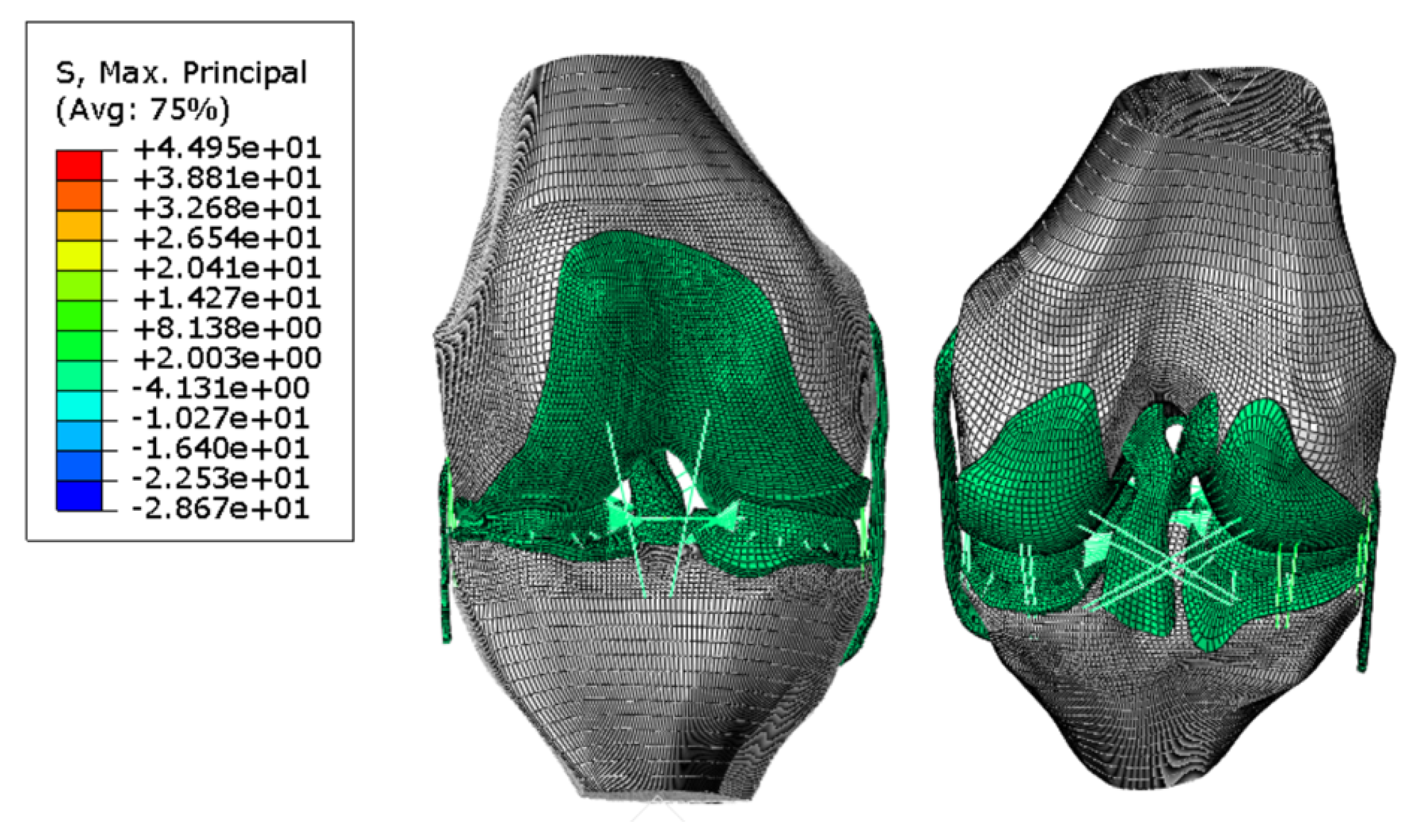



| Measurement | Value (cm) |
|---|---|
| Body Height | 169.00 |
| Foot or Shoe Length | 25.00 |
| Shoulder Height | 147.86 |
| Shoulder Width | 37.98 |
| Elbow Span | 94.20 |
| Wrist Span | 143.39 |
| Arm Span | 180.14 |
| Hip Height | 88.00 |
| Hip Width | 28.00 |
| Ankle Height | 8.00 |
| Extra Shoe Sole Thickness | 0.00 |
| Structure | Material Type | Constitutive Parameters |
|---|---|---|
| Femur/Tibia | Elastic | MPa, |
| Articular Cartilage | Elastic | MPa, |
| Menisci | Elastic | MPa, |
| ACL Connective Tissue | Hyperelastic (Neo–Hookean) | MPa, |
| Anterior Cruciate Ligament | Anisotropic Hyperelastic (HGO) | MPa, , |
| Posterior Cruciate Ligament | Anisotropic Hyperelastic (HGO) | MPa, , |
| Lateral Collateral Ligament | Anisotropic Hyperelastic (HGO) | MPa, , |
| Medial Collateral Ligament | Anisotropic Hyperelastic (HGO) | MPa, , |
| Structure | Elements | Nodes |
|---|---|---|
| Femur | 13,860 | 13862 |
| Tibia | 11,360 | 11,362 |
| Articular Cartilage | 25,721 | 35,712 |
| Menisci | 9100 | 11,616 |
| ACL Connective Tissue | 3875 | 1288 |
| ACL | 3000 | 3796 |
| PCL | 5248 | 5922 |
| LCL | 6656 | 7425 |
| MCL | 5120 | 5781 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha, C.; Lobo, J.; Parente, M.; Oliveira, D. Biomechanical Modeling and Simulation of the Knee Joint: Integration of AnyBody and Abaqus. Biomechanics 2025, 5, 57. https://doi.org/10.3390/biomechanics5030057
Rocha C, Lobo J, Parente M, Oliveira D. Biomechanical Modeling and Simulation of the Knee Joint: Integration of AnyBody and Abaqus. Biomechanics. 2025; 5(3):57. https://doi.org/10.3390/biomechanics5030057
Chicago/Turabian StyleRocha, Catarina, João Lobo, Marco Parente, and Dulce Oliveira. 2025. "Biomechanical Modeling and Simulation of the Knee Joint: Integration of AnyBody and Abaqus" Biomechanics 5, no. 3: 57. https://doi.org/10.3390/biomechanics5030057
APA StyleRocha, C., Lobo, J., Parente, M., & Oliveira, D. (2025). Biomechanical Modeling and Simulation of the Knee Joint: Integration of AnyBody and Abaqus. Biomechanics, 5(3), 57. https://doi.org/10.3390/biomechanics5030057







