Assessing the Contribution of Arm Swing to Countermovement Jump Height Using Three Different Measurement Methods in Physically Active Men

Abstract

Background/Objectives: This study evaluated the reliability and validity of three methods to measure jump height during countermovement jumps performed with (CMJ_AS) and without (CMJ_NAS) arm swing: (1) an impulse–momentum method with force platforms (FP_imp), (2) a flight time method with force platforms (FP_time), and (3) an inertial measurement unit (PUSH Band 2.0; PUSH2). Methods: Eighteen physically active men performed CMJ_AS and CMJ_NAS on force platforms while wearing PUSH2 over two days. Besides jump height, we computed intraclass correlation coefficients (ICC) and the absolute and relative increases in jump height due to arm swing, compared to CMJ_NAS. Results: The reliability of intra-session, inter-session, and concurrent measures were good to excellent (intra-session ICC_2,1 = 0.957–0.979, inter-session ICC_2,1 = 0.806–0.990, concurrent ICC_3,1 = 0.940–0.973) for CMJ_AS and CMJ_NAS heights, in all three methods. The three methods showed high to very high reliability for both the absolute and relative indices of arm swing contribution (ICC_2,1 = 0.649–0.812). FP_time significantly overestimated CMJ_NAS height relative to FP_imp (p < 0.01). The absolute index of arm swing contribution was similar in FP_imp and FP_time (p = 0.38) but higher in PUSH2 (p < 0.01), indicating that arm swing amplified overestimation. Conclusions: All three methods demonstrated high reliability for jump height measurements, but FP_time and PUSH2 misestimated jump height depending on jump modalities. Caution is advised when assessing the absolute and relative contribution of arm swing, because errors in CMJ_NAS and CMJ_AS height measurements can affect these values and their interpretation.

1. Introduction

Jump performance evaluation is an important training tool in many sports, e.g., American football [1] and basketball [2]. For example, routine countermovement jump (CMJ) testing helps practitioners prescribe exercises and manage fatigue in athletes [3,4,5]. While various technologies and methods have emerged to measure CMJ performance, the validity and reliability of these measurement methods must be rigorously established to ensure diagnostic accuracy. Yet, this information is often lacking.

CMJ height is commonly measured with or without arm swing [6,7,8,9], with arm swing possibly enhancing CMJ height [6,10]. For example, previous research suggests that athletes can improve jump height by over 20% with arm swing compared to without arm swing [6,7,11], whereas non-athletes show more modest improvements [12]. Therefore, not only are reliable and valid measures of CMJ height crucial for practitioners and researchers, but understanding whether arm swing alters the reliability and validity of measurements is also important in evaluating athletes.

Different methods have different merits and demerits. The gold standard for measuring jump height involves recording ground reaction forces using force platforms (FPs) to derive the impulse (FP_imp), utilizing the impulse–momentum relationship [13,14]. However, while extensively validated, implementing FP_imp can be challenging due to the hardware costs, limited portability, and complex calculation processes. Alternatively, jump height can be derived from the flight time (FP_time) using not only a FP but also simpler, more affordable technology like a contact mat, photoelectric cell, or smartphone application [15]. Although the flight time method may overestimate jump height compared with FP_imp, it remains widely used because the overestimation is considered reasonable [14,16]. Another method involves the use of commercially available inertial measurement units (IMUs) consisting of wireless accelerometers and gyroscopes. While all IMUs rely on similar technology, manufacturers often use proprietary computing algorithms generally treated as a “black box” [17,18]. One such IMU popular among strength and conditioning coaches is PUSH Band 2.0 (PUSH2; Push Inc., Toronto, Canada). To the authors’ knowledge, few studies have examined the validity and reliability of PUSH2, showing reliable measures but overestimating CMJ without arm swing (CMJ_NAS) height compared to FP_imp [19] or the flight time method using FPs [20] and optical sensors [21]. However, although the PUSH2 approach is an attractive approach due to its lower cost, whether its measures are robust across CMJ modalities, i.e., CMJ with arm swing (CMJ_AS) or CMJ_NAS, has yet to be established.

In particular, it remains unclear whether the arm swing amplifies these overestimations. For example, CMJ height overestimation may affect the calculation of arm contribution—the difference in CMJ height between CMJ_NAS and CMJ_AS or the ratio of CMJ_AS and CMJ_NAS [6,7,11]—thus yielding an erroneous diagnostic. Indeed, if both CMJ_AS and CMJ_NAS heights are overestimated by the same amount (e.g., 4 cm), the relative arm contribution would appear smaller with PUSH2 or FP_time than with FP_imp because the denominator (CMJ_NAS height) increases. Consequently, investigating how arm swing impacts IMU system reliability and validity compared to FP_time and FP_imp would be valuable for practitioners to select the appropriate measuring tool.

Therefore, the purpose of this study was (1) to investigate the impact of the FP_imp, FP_time, and PUSH2 methods on the reliability and validity of CMJ_NAS and CMJ_AS height measurements, and (2) to determine how the observed misestimation influences the computation of arm contribution indices. We hypothesized that the degree of overestimation in jump height calculated using the IMU compared to the FP_imp method would be greater than using the FP_time method, whereas the degree of overestimation would be comparable between CMJ_NAS and CMJ_AS, regardless of the method used. Such outcomes would suggest that the evaluation of arm contributions can vary depending on the method employed.

2. Materials and Methods

2.1. Participants

Eighteen physically active men (age: 34.4 ± 5.4 years; height: 171.8 ± 6.1 cm; body mass: 74.1 ± 8.6 kg), free from any injury affecting CMJ performance, provided written informed consent to participate in this study. This study was approved by the Institutional Ethics Committee of the Japanese Institute of Sports Sciences (No. 2019-062, approved on 10 February 2020) in accordance with the Declaration of Helsinki. Power analysis using G*Power software (version 3.1.9.2, Heinrich-Heine-Universität Düsseldorf, Düsseldorf, Germany) showed that to achieve a power of 80% at an alpha level of 5%, at least eighteen participants were needed to achieve a medium effect size of partial η_p² = 0.06 (f = 0.253) [22] in a within-subject repeated-measures 3 × 2 analysis of variance (ANOVA) (1 group, 6 measurements, correlation among measures = 0.5, non-sphericity correction = 1).

2.2. Procedures

To evaluate inter-day reliability, all participants completed two testing sessions 3–7 days apart, as used in previous research [23,24,25], to allow for neuromuscular recovery, limit possible fatigue, and minimize any potential learning effect. Testing was conducted around the same time of the day (within a 2 h window) to minimize circadian influences [26]. The participants were also asked to maintain their normal routines and avoid strenuous exercise 48 h before each test and during the interval between sessions.

The participants first completed a standardized warm-up consisting of jogging, dynamic stretching, and jumping. PUSH2 was then attached to the participant’s waist using the manufacturer-provided waist belt. Finally, the participants performed three CMJ_NAS and three CMJ_AS with each foot on a different FP (1200 Hz, 0.6 m × 0.4 m, type 9281E; Kistler, Winterthur, Switzerland). For CMJ_NAS, the participants were instructed to jump as high as possible using a rapid countermovement while keeping their hands on their hips. For CMJ_AS, they were instructed to jump as high as possible using a rapid countermovement while swinging their arms. For both jump types, the participants were instructed to initiate landing with their legs straight to limit the influence of posture on flight time. In addition, for CMJ_AS, they were asked to land with their arms raised to approximately the same height as at take-off to minimize potential overestimation of CMJ_AS height (Figure 1) [14]. A minimum of 30 s of rest was given between each jump trial and 180 s of rest between each jump modality. One experimenter watched each trial and, if instructions were not respected (e.g., leg tucking upon landing), the trial was repeated 30 s later.

Unfiltered left- and right-side vertical ground reaction forces (GRF_v) were then summed for analysis, because low-pass filtering can cause substantial underestimation of jump height [27]. Jump height obtained from PUSH2 (sampled at 1000 Hz) was sent via Bluetooth to an iPad Pro (Apple Inc., Cupertino, CA, USA) using the manufacturer’s software (PUSH Pro, v7.7.0). Body weight was calculated from the 0.5 s (600 data points) moving average of GRFv, shifted by one frame, displaying the smallest standard deviation (SD) during quiet standing. The start of the motion was identified as the moment when GRF_v deviated from body weight by 1% [14], and take-off was defined as the first point when GRFv fell below 10 N (Figure 2) [28]. To estimate the vertical velocity at take-off (V_to), GRF_v was integrated from the start of the motion until take-off by trapezoid rule integration [14]. Jump height from FP_imp was then calculated as

$$\mathit{Jump} \mathit{height} \mathit{from} {\mathit{FP}}_{\mathit{imp}}={\displaystyle \frac{1}{2g}}{V}_{to}^2,$$

(1)

where g represents the gravitational acceleration (9.81 m/s²). Jump height from FP_time was calculated as [20]

$$\mathit{Jump} \mathit{height} \mathit{from} {\mathit{FP}}_{\mathit{time}}={\displaystyle \frac{1}{8}}{gT}_{\mathit{flight}}^2,$$

(2)

where T_flight represents the flight time from take-off to landing, defined as the first and second time that GRF_v crosses the 10 N threshold [28]. The results from FP_imp were the reference measurements [19].

The arm contribution indices (AI) were defined as previously reported [7,8]. The absolute AI (AI_abs) was thus the difference in CMJ height with and without arm swing:

$${AI}_{abs}\left(cm\right)={CMJ}_{AS}-{CMJ}_{NAS}.$$

(3)

The relative AI (AI_rel) was AI_abs relative to CMJ_NAS:

$${AI}_{rel}\left(\%\right)={\displaystyle \frac{{AI}_{abs}}{{CMJ}_{NAS}}}\times 100.$$

(4)

2.3. Statistical Analysis

The height of each participant’s three CMJ_NAS or CMJ_AS trials was used to compute intra-session and concurrent reliability, along with Bland–Altman analyses. The average of the three trials was used for the other analyses, including ANOVAs, assessments of inter-day test–retest reliability, and concurrent validity. Means and SDs were calculated after confirming the data’s normal distribution using Kolmogorov–Smirnov statistics (p ≥ 0.05).

The intra-session reliability for CMJ_NAS and CMJ_AS height from the FP_imp, FP_time, and PUSH2 methods was determined by calculating the coefficient of variation (CV) and the intraclass correlation coefficient (ICC_2,1; two-way mixed-effects model with absolute agreement) with a 95% confidence interval (CI) [29,30,31]. In addition, the test–retest inter-day reliability of all variables between Day 1 and 2 was assessed using ICC_2,1 (i.e., two-way random-effects model with absolute agreement) with a 95% CI [31].

A two-way repeated-measures ANOVA with Bonferroni post hoc paired t-tests was used to evaluate the effect of the two jump modalities (CMJ_AS and CMJ_NAS) and the three methods on CMJ height. One-way repeated-measures ANOVAs with Bonferroni post hoc paired t-tests were used to test the differences in AI_abs and AI_rel across the three methods. The Greenhouse–Geisser correction was applied if the Mauchly sphericity test revealed that the assumption of sphericity was violated. Partial eta-squared values (${\eta }_p^2$) were reported as a measure of effect size: small (0.01–0.06), medium (0.06–0.14), and large (>0.14) [22].

The concurrent validity among the three methods was assessed using Pearson’s correlation coefficients (r). To further evaluate agreement, Bland–Altman plots were analyzed to quantify the systematic bias and 95% limits of agreement (LoA) among the three methods [30,32]. The 95% LoA was corrected for repeated measures [33]. Proportional bias was identified when the coefficient of determination (R²) was greater than 0.1 [34]. In addition, concurrent reliability among the three methods was assessed using ICC_3,1 (i.e., two-way mixed-effects model for consistency) with a 95% CI [31].

For ICC and r interpretations, we used the following criteria: poor (<0.50), moderate (0.50–0.75), good (0.75–0.90), and excellent (>0.90) [31]. For CV, we used the following criteria: poor (>10%), moderate (5–10%), and good (<5%) [35,36]. Statistical significance was set at p < 0.05. Analyses were performed using SPSS 19.0 (IBM Corp., Chicago, IL, USA) and Microsoft Excel (Microsoft Corporation, Redmond, WA, USA).

3. Results

Intra-session reliability analysis showed good reliability based on CV (1.56–2.48%) and excellent reliability based on ICC_2,1 (0.96–0.98) for all variables (

Table 1. Intra-session reliability of the CMJ height from FP_imp, FP_time, and PUSH2.

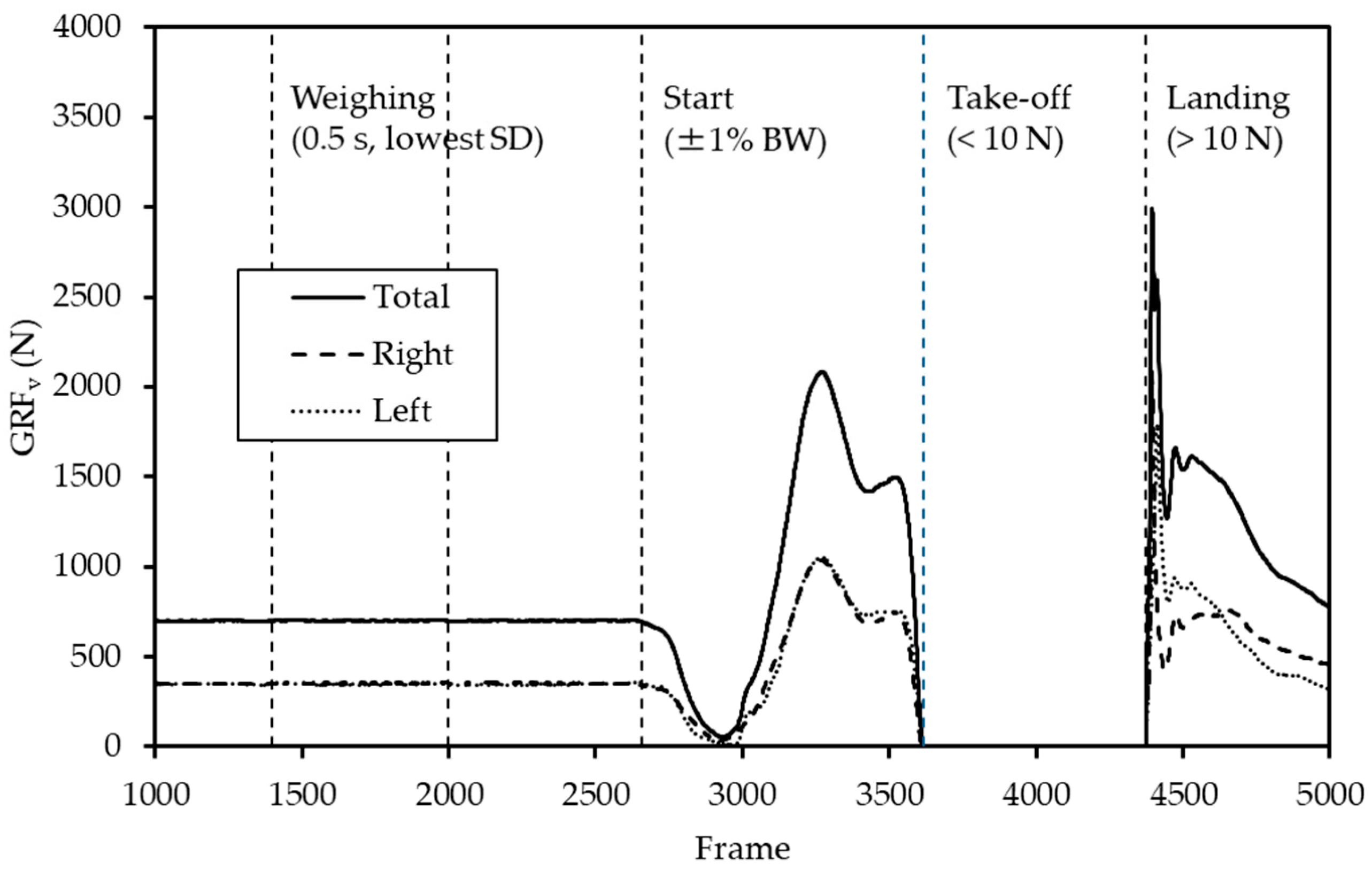
		Day 1		Day 2
		Mean CV (95% CI)	ICC2,1 (95% CI)	Mean CV (95% CI)	ICC2,1 (95% CI)
CMJNAS	FPimp	1.89 (1.26, 2.52)	0.98 (0.96, 0.99)	2.21 (1.45, 2.98)	0.97 (0.93, 0.99)
	FPtime	1.91 (1.31, 2.52)	0.97 (0.94, 0.99)	2.48 (1.63, 3.33)	0.95 (0.89, 0.98)
	PUSH2	1.98 (1.40, 2.57)	0.98 (0.95, 0.99)	2.37 (1.38, 3.35)	0.93 (0.86, 0.97)
CMJAS	FPimp	1.68 (1.15, 2.21)	0.97 (0.94, 0.99)	1.56 (0.97, 2.15)	0.98 (0.95, 0.99)
	FPtime	1.99 (1.33, 2.65)	0.96 (0.92, 0.99)	2.06 (1.29, 2.83)	0.96 (0.90, 0.98)
	PUSH2	1.60 (1.21, 2.84)	0.96 (0.91, 0.98)	1.69 (1.22, 2.17)	0.96 (0.91, 0.98)

FP_imp = impulse–momentum method using force platforms; FP_time = flight time method using force platforms; PUSH2 = PUSH Band 2.0; CMJ_NAS = countermovement jump without arm swing; CMJ_AS = countermovement jump with arm swing; CV = coefficient of variation; CI = confidence interval; ICC = intraclass correlation coefficient.

). The inter-day test–retest reliability analysis showed excellent reliability for CMJ_NAS and CMJ_AS height in each method (ICC_2,1 = 0.940–0.973), but moderate to excellent reliability for AI_abs and AI_rel in all three methods (ICC_2,1 = 0.62–0.78) (

Table 2. Comparison of CMJ heights measured using three methods across two jump modalities, with corresponding inter-day reliability.

	Mean ± SD (Day 1)	Mean ± SD (Day 2)	ICC2,1 (95% CI)
CMJNAS (cm)
FPimp	40.04 ± 6.36	39.86 ± 6.19	0.97 (0.93, 0.99)
FPtime	42.27 ± 6.26 †	41.86 ± 5.87 †	0.96 (0.90, 0.99)
PUSH2	44.03 ± 6.46 † ‡	43.24 ± 5.41 † ‡	0.96 (0.89, 0.98)
CMJAS (cm)
FPimp	44.90 ± 6.07 *	44.41 ±6.18 *	0.96 (0.91, 0.99)
FPtime	46.67 ± 5.55 † *	45.92 ± 6.17 † *	0.95 (0.86, 0.98)
PUSH2	50.68 ± 7.72 † ‡ *	49.42 ± 6.87 † ‡ *	0.94 (0.81, 0.98)
AIabs (cm)
FPimp	4.86 ± 2.18	4.54 ± 2.16	0.77 (0.48, 0.91)
FPtime	4.40 ± 2.68	4.05 ± 2.13	0.65 (0.28, 0.85)
PUSH2	6.65 ± 3.50 † ‡	6.18 ± 2.86 † ‡	0.81 (0.57, 0.93)
AIrel (%)
FPimp	12.72 ± 6.26 ‡	11.77 ± 5.81	0.74 (0.44, 0.89)
FPtime	10.75 ± 6.37	9.91 ± 5.50	0.62 (0.23, 0.84)
PUSH2	15.39 ± 8.29 ‡	14.37 ± 6.54 ‡	0.78 (0.50, 0.91)

FP_imp = impulse–momentum method using force platforms; FP_time = flight time method using force platforms; PUSH2 = PUSH Band 2.0; CMJ_NAS = countermovement jump without arm swing; CMJ_AS = countermovement jump with arm swing; AI_abs = absolute arm contribution index; AI_rel = relative arm contribution index; CV = coefficient of variation; CI = confidence interval; ICC = intraclass correlation coefficient. * Significantly higher than CMJ_NAS (p < 0.05). ^† Significantly higher than FP_imp (p < 0.05). ^‡ Significantly higher than FP_time (p < 0.05).

).

The two-way repeated-measures ANOVA revealed a significant interaction between jump modalities and methods in CMJ height (F [1.50, 25.47] = 14.22, p < 0.001, η_p² = 0.455, large effect size) (Table 2). Regarding jump modalities, post hoc paired t-tests with Bonferroni corrections revealed that CMJ_AS height was significantly greater than CMJ_NAS height across all three measurement methods (p < 0.01). Furthermore, regarding measurement methods, both the CMJ_NAS height and the CMJ_AS height were greater for PUSH2 than FP_time and greater for FP_time than FP_imp (p < 0.01).

One-way repeated-measures ANOVA revealed a significant main effect of measurement methods on AI_abs (Day 1: F [2, 34] = 14.21, p < 0.001, η_p² = 0.455; Day 2: F [2, 34] = 14.03, p < 0.001, η_p² = 0.452) and AI_rel (Day 1: F [1.50, 25.55] = 9.11, p < 0.01, η_p² = 0.349; Day 2: F [2, 34] = 10.71, p < 0.01, η_p² = 0.386), indicating large effect sizes across both days (

Table 3. Systematic bias, proportional bias, and concurrent reliability of CMJ height measurements.

	Day 1			Day 2
	Systematic Bias (cm) (95% LoA)	R2	ICC3,1 (95% CI)	Systematic Bias (cm) (95% LoA)	R2	ICC3,1 (95% CI)
CMJNAS
FPtime vs. FPimp	2.23 (−1.83, 6.29)	<0.01	0.95 (0.87, 0.98)	2.00 (−2.24, 6.24)	0.02	0.95 (0.86, 0.98)
PUSH2 vs. FPimp	3.99 (−0.73, 8.72)	<0.01	0.94 (0.84, 0.98)	3.38 (−0.97, 7.73)	0.17	0.94 (0.84, 0.98)
PUSH2 vs. FPtime	1.76 (−1.89, 5.42)	<0.01	0.96 (0.90, 0.99)	1.38 (−3.69, 6.46)	0.12	0.96 (0.89, 0.98)
CMJAS
FPtime vs. FPimp	1.77 (−3.16, 6.70)	0.04	0.93 (0.83, 0.98)	1.51 (−3.31, 6.33)	<0.01	0.93 (0.84, 0.98)
PUSH2 vs. FPimp	5.78 (−0.16, 11.82)	0.15	0.91 (0.77, 0.97)	5.01 (−1.47, 11.50)	<0.01	0.88 (0.70, 0.95)
PUSH2 vs. FPtime	4.01 (−1.27, 9.29)	0.06	0.93 (0.83, 0.97)	3.50 (−1.03, 8.04)	<0.01	0.94 (0.86, 0.98)

FP_imp = impulse–momentum method using force platforms; FP_time = flight time method using force platforms; PUSH2 = PUSH Band 2.0; CMJ_NAS = countermovement jump without arm swing; CMJ_AS = countermovement jump with arm swing; LoA = limit of agreement; CI = confidence interval. R² = coefficient of determination. The 95% LoA was corrected for repeated measures [33].

). On both days, AI_abs was significantly higher when using PUSH2 compared to FP_imp (p < 0.01) and FP_time (p < 0.01). However, there was no significant difference in AI_abs between FP_time and FP_imp (Day 1: p = 0.384; Day 2; p = 0.60) (Table 3). This greater difference in AI_abs from PUSH2 explains the significant interaction between jump modality and measurement method. For AI_rel, values were significantly lower when using FP_time compared to PUSH2 (p < 0.01) and FP_imp (p = 0.04) on Day 1. On Day 2, AI_rel from FP_time remained significantly lower than PUSH2 (p < 0.01), while the difference in AI_rel between FP_time and FP_imp was not statistically significant (p = 0.23).

For concurrent validity, Pearson’s correlation coefficients revealed excellent agreement between the methods (r = 0.92–0.96) (Figure 3). Concurrent reliability, accounting for within-subject variation across repeated trials, was also excellent between methods (ICC (3,1) = 0.88–0.96) (Table 3).

The systematic and proportional biases between measurement devices, assessed using Bland–Altman plots, are summarized in Table 3. For CMJ_AS height on Day 1, a proportional bias was observed between FP_imp and PUSH2 (R² = 0.15). On Day 2, proportional bias was found for CMJ_NAS height between FP_imp and PUSH2 (R² = 0.17) and FP_time and PUSH2 (R² = 0.12).

4. Discussion

This study evaluated the reliability and validity of force platform-derived impulse (FP_imp), force platform-derived flight time (FP_time), and an inertial measurement unit (PUSH2) in assessing CMJ height, both with and without arm swing, and subsequently examined the implications of these methods on arm contribution indices. The main findings were that FP_time and PUSH2 can be considered reliable methods for assessing CMJ_NAS and CMJ_AS heights, but both overestimated CMJ_AS and CMJ_NAS heights. Among the three methods, PUSH2 overestimated AI_abs and AI_rel the most and was less reliable between sessions.

The intra-session and inter-day reliability of the CMJ_NAS height for all three methods was good to excellent (ICC > 0.75) [31]. This result aligns with previous studies using FP_imp, FP_time, and PUSH2 [19,20,21]. In addition, for all three methods, the intra-session and inter-day reliability of CMJ_AS height in the present study was acceptable. Consequently, all these methods offered reliable and valid evaluations of jump height.

Regarding CMJ height, there was an interaction between jump modalities and measurement methods. CMJ heights were consistently ranked, from the highest to the lowest, PUSH2-FP_time-FP_imp for both CMJ_AS and CMJ_NAS. Critically, AI_abs using PUSH2 was significantly greater than FP_imp and FP_time. Hence, the arm swing amplified the intrinsic overestimation of jump height from PUSH2, but not FP_time. Although the coefficients of determination were not large and the specific jump modality showing a bias varied by day, given the proportional bias observed between FP_imp and PUSH2, PUSH2 may differentially affect CMJ height measurements based on jump performance level. However, PUSH Inc. has not disclosed their algorithms, making it uncertain whether the algorithms for the two CMJ modalities are identical. This is problematic because the computation algorithm, which includes data filtering, can have a sizeable effect on the measurement [37]. Still, we can speculate that the kinematics of the IMU device fixed on the waist level would vary between CMJ_AS and CMJ_NAS among participants (i.e., owing to trunk length, angle, and angular velocity). For example, the trunk segment at take-off may be more forward-tilted in untrained participants [38] but more upright in volleyball players [39] during CMJ_AS than during CMJ_NAS. Consequently, kinematic differences in the trunk might lead to a more pronounced overestimation of jump height from PUSH2 attached to the participants’ waist when arm swing is involved.

In this study, arm swing improved jump height by 4.86 cm (12.72%) for FP_imp, 4.40 cm (10.75%) for FP_time, and 6.65 cm (15.39%) for PUSH2. Previous studies have suggested that arm swing enhances the effect of proximal-to-distal sequencing during jumping [10], and the contribution of CMJ height influences proper jump techniques in sports such as volleyball [11]. However, our results revealed that the metrics used to evaluate arm contribution (i.e., AI_abs and AI_rel) differed across methods. PUSH2 overestimated AI_rel because its overestimation of CMJ_AS height was greater than that of CMJ_NAS height, but FP_time underestimated AI_rel by similarly overestimating CMJ_NAS and CMJ_AS, which appear in the numerator and denominator of Equation (4). A previous study speculated that the overestimation by FP_time in CMJ_AS would be greater than that in CMJ_NAS because the height of the arm at take-off tends to be higher than that at landing [14]. In contrast, participants in this study were instructed to ensure that their arm height at landing matched that at take-off. This suggests that specific instructions regarding arm swing at landing could effectively mitigate the potential systematic bias of the CMJ_AS height from FP_time.

Regarding inter-session reliability, AI_abs and AI_rel displayed lower ICCs than CMJ_AS and CMJ_NAS, although CMJ_AS and CMJ_NAS heights from the three methods demonstrated acceptable inter-day reliability. Specifically, while the reliability for FP_time was below the acceptable threshold, the reliability of the other methods slightly exceeded this threshold. It is crucial to consider that indices derived from two numbers typically exhibit lower reliability, owing to the inherent variability of both numbers [40]. Thus, caution is advised when using such indices. Additionally, it is worth highlighting that the participants in this study were neither competitive athletes nor engaged in sports involving arm-swing techniques. AI_rel from FP_imp (12–13%) was considerably lower than the 24% in collegiate male and female basketball players reported in Heishman et al. [6] or the 38% in elite male volleyball players reported in Vaverka et al. [11]. Consequently, our findings may not apply to populations with pronounced arm contribution, such as basketball and volleyball athletes used to jumping with an arm swing.

Jump height in CMJ_AS and CMJ_NAS from all three methods showed good to excellent intra-session, inter-session, and concurrent reliability. Each method therefore appears reproducible and robust in evaluating CMJ height, with no proportional bias between methods. While proportional bias was generally not observed between FP_imp and FP_time, it tended to be present or higher in comparisons involving PUSH2 against the other two methods, which aligns with findings from other studies using PUSH2 [20]. Previous studies reported that PUSH2 overestimated CMJ_NAS height by 3.8 cm [20] and 7.9 cm [41] compared to the FP_time, and 6.0 cm compared to the FP_imp [19], which was higher than presently (1.4–1.8 cm from FP_time and 3.4–4.0 cm from FP_imp). This greater overestimation could be attributed to differences in software versions used across studies. In our study, we used PUSH2 software version 7.7.0. In contrast, Watkins et al. [20] used version 4.5.0, Comyns et al. [41] used version 4.6.2, and McMaster et al. [19] used version 2.0.5. Software updates are typically designed to enhance measurement accuracy; hence, practitioners should be mindful of variations induced by the computation algorithm.

Among limitations to this study, whether the low inter-day reliability of AI_abs and AI_rel extends to athletes with greater arm contribution must be carefully considered. All participants were men, so whether the present results are applicable to female individuals may need confirmation. Strict control of participants’ behavior between sessions was practically not possible, but the high reliability and validity reported suggest that any confounding influence would have been minimal. Lastly, the current findings of PUSH2 might not be applicable to other IMUs likely using a different algorithm, although the hardware technology is essentially the same. Future research may need to clarify how the arm swing impacts the reliability of jump performance measurement across populations of athletes, notably higher-level athletes implementing jumping as a tool to monitor training implementations over longer time periods.

5. Conclusions

All three methods showed high intra-session and inter-session reliability for jump height, supporting their use in athlete monitoring when applied consistently. However, compared to the gold-standard FP_imp method, both FP_time and PUSH2 overestimated jump height. Because it overestimated jump heights similarly in both CMJ modalities, FP_time misestimated the relative effect of arm swing. PUSH2 potentially misestimated both the absolute and relative effects of arm swing, owing to different degrees of overestimation between CMJ_NAS and CMJ_AS. Also, since arm contribution indices showed lower inter-day reliability, their use in monitoring should be approached with caution.