Abstract
Following the trend of finding better thermoelectric materials among synthetic analogs of copper–chalcogenide minerals, we have synthesized iron-bearing colusites of a general formula Cu26−xFexV2Sn6S32. They crystallize in the cubic space group P-43n with the unit cell parameter increasing linearly with the iron content. At a low iron concentration, the crystal structure features disorder manifested by an anti-site effect and a shift of a part of the tin atoms from their ideal positions, which is absent for higher iron contents. The magnetization and 57Fe/119Sn Mössbauer studies showed that, for x = 1, iron is present as Fe3+, whereas for x > 1, Fe2+ and Fe3+ coexist. Additionally, weak antiferromagnetic interactions between iron atoms and fast on the 57Fe Mössbauer time scale (107–109 s−1) electron transfer between adjacent Fe2+ and Fe3+ centers were revealed. Thermoelectric studies showed that iron-bearing colusites are p-type semiconductors with low thermal conductivity stemming from their complex crystal structure and structural disorder. The highest ZT of 0.78 at 700 K was found for the x = 1 iron content, where iron is present as Fe3+ only.
1. Introduction
State-of-the-art thermoelectric materials can be subdivided into two principal groups. Those operating near room temperature are always based on bismuth telluride, which outplays all other thermoelectric materials at these temperatures. However, at elevated temperatures, from ca. 450 K and up to above 1000 K, other materials have found applications as they exhibit a reasonably high thermoelectric figure-of-merit, ZT ≈ 1, and considerable chemical and thermal stability [1,2,3]. Their main drawback is that most of them consist of toxic or expensive chemical elements. In this respect, efforts have been made to create materials for thermoelectric power generation that contain low-cost and environmentally friendly constituents.
Recent reports have proven that copper-based materials mimicking natural chalcogenide minerals can be viewed as promising candidates for developing thermoelectric materials for mid-temperature power generation [4,5,6,7,8,9,10,11,12,13,14,15].
Among copper sulfides, binary Cu2−xS demonstrates superior thermoelectric properties, reaching ZT = 1.9 at 973 K, mainly due to its cubic structure that combines a rigid sulfur framework with fluid-arranged copper atoms; however, mechanical instability caused by electron migration prevents the use of this compound [16,17,18,19]. With regard to complex sulfides, widely investigated Cu12−xTMxSb4S13 (TM = Mn, Fe, Co, Ni, Zn) tetrahedrites possess the highest ZT, varying from 0.5 to 1.2 in the 550−700 K temperature range depending on the composition. Their high thermoelectric efficiency is explained by a unique combination of the crystal and electronic structure and involve variable-range hopping of charge carriers, facilitated by the thermally activated electron exchange, and low thermal conductivity of the complex yet slightly disordered cubic crystal structure [20,21,22,23,24,25,26,27].
Less studied colusites are another family of naturally occurring copper sulfides that show promises as thermoelectric materials for mid-temperature power generation. Although natural colusites are toxic as a rule as they contain arsenic, synthetic colusites can be prepared from cheap and environmentally friendly elements. Among them are synthetic colusites of a general formula Cu26−xTMxT2M6S32, where TM = Co, Ni, or Zn, T = Ti, V, Nb, Ta, Cr, Mo, W, and M = Ge, Sn, Sb. [28,29,30,31,32]. Similar to tetrahedrites, colusites crystallize in the cubic crystal structure with a unit cell volume of about 103 Å3. Both tetrahedrite and colusite are degenerate semiconductors with metallic-like behavior. This is explained by the concept of Cu+-Cu2+ copper mixed valency, resembling that of “Cu2+-Cu3+” in superconducting cuprates [33]. It is worth noting that static Cu2+ does not occur in sulfides with the exception of CuS. The existence of the Cu+-Cu2+ mixed valency, however, is undeniable and controls the hole doping in TE sulfides, with a high proportion of “mobile” divalent copper being achievable. In both phases, the partial substitution of copper by transition metals is possible, which leads to a change in the formal charge distribution over the metal sites of the crystal structures. However, the crystal structures exhibit a very important difference. In tetrahedrites, copper atoms occupy two sites with a distinctly different coordination, in which only those having a tetrahedral coordination can be partially replaced by another transition metal. In contrast, colusites feature three independent copper atom positions possessing similar tetrahedral coordination, and some difference can be found only in their second coordination spheres. As a consequence, the exact mechanism of charge transfer that may involve each of the three metal sites is not known, which hampers the optimization of the thermoelectric efficiency of synthetic colusites by the partial substitution of d-metals for copper [34,35,36,37].
In this work, we present a series of iron-substituted colusites. We report on the range of iron solubility in Cu26−xFexV2Sn6S32, analysis of the crystal structure, charge distribution within the transition metal substructure, and thermoelectric properties. The choice of iron as a substituent is explained by the fact that previous studies have shown that iron is present in congenial tetrahedrites in +2 and +3 oxidation states [38] and that the Fe2+/Fe3+ balance may be a key to finding the optimal composition and achieving the highest thermoelectric performance. Therefore, we pay utmost attention to the interplay of the Fe2+/Fe3+ distribution and thermoelectric properties within the studied series of synthetic colusites.
2. Materials and Methods
2.1. Starting Materials and Synthesis
Elemental Fe (powder, 99%), V (powder, 99.5%), Sn (powder, 99%), S (powder, 99.9%), and polycrystalline CuO (99.9%) were used as received (all from Reachim, Moscow, Russia). Copper was obtained by heating CuO under hydrogen flow.
Cu26−xFexV2Sn6S32 (x = 1.0, 2.0, 3.0, 4.0, 4.2, 4.5, and 5.0) samples were prepared by a standard ampoule technique. The mixtures of the starting materials were sealed in evacuated quartz ampules under vacuum, 1 × 10−2 Torr. The ampules were heated to 523 K for 3 h, annealed at this temperature for 8 h, then heated up to 1373 K in 8 h, annealed for 50 h, and finally cooled down to room temperature in a switched-off furnace. The reaction products were finely ground and pressed into pellets at a pressure of 80−100 bar at room temperature. The pellets were sealed in evacuated quartz ampules and heated up to 1073 K in 8 h, annealed at this temperature for 50 h followed by switching off the furnace and cooling down to room temperature. After that, the pellets were ground and used for phase and composition analyses.
Samples for 57Fe Mössbauer spectroscopy measurements enriched in 57Fe for increasing the rate of signal accumulation were obtained by the same method using elemental iron 10% enriched by the respective isotope.
Samples for the thermoelectric property measurements were compacted by spark plasma sintering (SPS). Densification was performed using a Labox-625 machine (Sinter Land Inc., Nagaoka, Japan) in 10 mm graphite dies by heating the samples to 723 K at 60 K min−1 under a pressure of 60 MPa in vacuum, keeping it at this temperature for 10 min, and then cooling down to room temperature. The purity of the product, which had a relative density of 91−92%, was verified by X-ray diffraction (XRD) and energy-dispersive X-ray spectroscopy (EDXS) analyses, which confirmed that neither chemical nor phase composition changed during the densification.
2.2. Phase Composition, Characterization, and Crystal Structure Investigation
Phase composition of all obtained samples was initially investigated on an Imaging Plate Guinier Camera (Huber G670, Cu-Kα1 radiation, λ = 1.540598 Å, Rimsting, Germany) with the 2θ ranging from 3 to 100 deg. The data were collected by scanning the image plate 4 times after an exposure time of 1200 s at room temperature. The program package STOE WinXPOW (v. 1.06) was used for data processing.
Energy-dispersive X-ray spectroscopy (EDXS) was employed to study the elemental composition of the samples using a scanning electron microscope (SEM, JEOL Ltd., Tokyo, Japan) JSM JEOL 6490-LV operated at 30 kV and equipped with an EDX detection system INCA x-Sight. The data were collected from 10 points for each sample and then averaged. In all cases, pure elemental Co was used as a standard.
Thermal analysis was performed in an argon atmosphere using a STA 409 PC Luxx thermal analyzer (Netzsch, Selb, Germany) in the temperature range of 300−1223 K with a ramp rate of 10 K min−1. For each sample, three cycles of heating and cooling were performed to check for the data reproducibility.
High-resolution (HR) powder X-ray diffraction (XRD) data for the precise phase composition analysis and structure refinement were collected at the ID22 beamline of the European Synchrotron Radiation Facility (ESRF, France) (λ = 0.35422 Å, 2θmax = 35 deg.). Measurements were performed at room temperature on powder samples enclosed in glass capillaries with an outer diameter of 0.5 mm. The capillaries were spun during the measurement. The Crystallographica Search-Match program was used for phase analysis of the obtained data, while JANA2006 software was used for the structure refinement [39].
2.3. Mössbauer Spectroscopy
Mössbauer spectra were recorded using a conventional constant-acceleration spectrometer MS-1104Em in the transmission geometry (Condor, Rostov-on-Don, Russia). 57Fe spectra were recorded at 15 and 298 K using a 57Co(Rh) radiation source kept at room temperature, whereas 119Sn spectra were recorded at 298 K with a Ca119mSnO3 radiation source. The sources were kept at room temperature. All isomer shifts are referred to α-Fe and CaSnO3 at 298 K in the cases of 57Fe and 119Sn spectra, respectively. Experimental spectra were processed and analyzed using methods of spectral simulations implemented in the SpectrRelax program [40].
2.4. Magnetization Measurements
Magnetic susceptibility of Cu26−xFexV2Sn6S32 for x = 1, 2, 3, and 4 was measured on cylindrical pellets with a diameter and height of 3 mm and 1 mm, respectively, pressed from the powder samples at room temperature at the external pressure of 1.5 kbar. Measurements were conducted using the Vibrating Sample Magnetometry Setup of a Physical Property Measurement System (Quantum Design) in the temperature range of 1.8−380 K in 0.1 T, 0.5 T, 2 T, and 5 T magnetic fields. Magnetization was measured by raising the magnetic field from 0 T to 14 T at the base temperature of 2 K or 5 K.
A modified Curie–Weiss formula χ = χ0 + C(T − Θ)−1 was used for fitting the paramagnetic parameters, where χ is the observed magnetic susceptibility in 5 T magnetic field, χ0 is the temperature-independent Pauli paramagnetic term, C is the Curie constant, T is measured temperature, and Θ is the Weiss constant. Effective magnetic moment (μeff) was extracted from the Curie constant according to the formula C = NAμ0μeff2(3kB)−1, where NA is the Avogadro number, μ0 is magnetic permeability of free space, and kB is the Boltzmann constant.
2.5. Thermoelectric Properties Measurements
High temperature electrical resistivity (ρ) and Seebeck coefficient (S) were simultaneously measured with an ULVAC ZEM-3 system by using the four-probe method and differential method, respectively. The measurements were conducted in the temperature range from 300 K to 700 K under partial pressure of helium on approximately 10 × 2 × 2 mm3 samples cut from the SPS-compacted pellets. The thermal diffusivity (α) was measured by the laser flash method using an LFA-457 apparatus on square samples (6 × 6 × 1 mm3) from 300 K to 700 K. The specific heat (Cp) was calculated with the Dulong–Petit approximation. Finally, the thermal conductivity (κ) was calculated as a product of measured thermal diffusivity, specific heat, and sample density, which was measured geometrically.
3. Results and Discussion
3.1. Phase Composition and Homogeneity Range
All synthesized samples of the Cu26−xFexV2Sn6S32 series appeared as black polycrystalline powders. They were stable in moist air for months. The thermal analysis showed that all samples melted incongruently, releasing sulfur in the range of 825−975 K depending on the iron content.
XRD analysis indicated that all the samples with 1 ≤ x ≤ 4.2 were phase pure, whereas the samples with higher iron contents contained several admixtures, of which CuS, FeS, and VS2 were unambiguously identified. The cubic unit cell parameter linearly increased within the homogeneity range as shown in Figure 1. EDXS analysis confirmed the purity of all but x = 4.5 and 5 samples. For the latter two, admixtures containing iron and sulfur and/or vanadium and sulfur were detected (Figure 1). Based on those data, the limit of the homogeneity range was found to lie between x = 4.2 and 4.5. We note that the formal charge distribution in iron-free colusite can be written as (Cu+)22(Cu2+)4(V5+)2(Sn4+)6(S2−)32, suggesting that exactly four copper atoms are expected to be replaced by a divalent metal. The actual homogeneity range being wider, and the presence of Fe3+ (see Section 3.3) in Fe-rich samples suggest that a partial reduction of vanadium down to the oxidation state of +4 may take place; however, this issue requires further investigation.
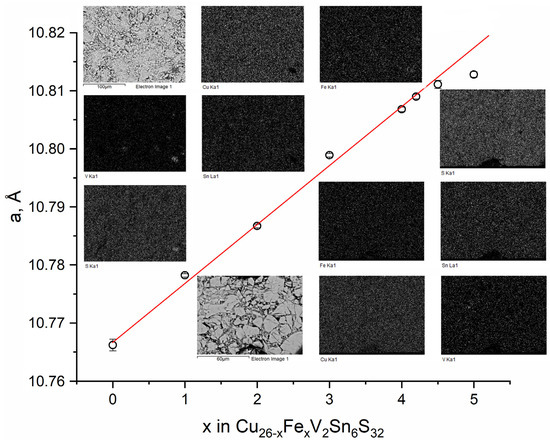
Figure 1.
Dependence of the unit cell on the iron content in the Cu26−xFexV2Sn6S32 series. Data for x = 0 are taken from the literature [35]. Insets show EDXS analysis data for x = 4.5 (top left) and x = 3 (bottom right).
3.2. Crystal Structure
The crystal structure was refined for the samples with the composition x = 1, 2, 3, and 4 against the synchrotron radiation diffraction data (Figure S1). The crystal data and refinement parameters are summarized in Table 1, whereas atomic parameters and interatomic distances are listed in Tables S1 and S2.

Table 1.
Data collection and refinement parameters for the crystal structures of Cu26−xFexV2Sn6S32.
We start the discussion of the crystal structure with the sample having the highest iron content, x = 4. Given the small concentration of iron, the initial refinement was performed assuming the idealized iron-free composition Cu26V2Sn6S32. The compound crystallizes in the cubic space group P-43n, and the crystal structure features three independent copper positions with tetrahedral coordination by sulfur atoms (Figure 2). Although very similar, the coordination spheres around the three copper atoms display small differences. The Cu1 atom is surrounded by a proper tetrahedron of sulfur atoms with the Cu−S distance of 2.31 Å, whereas a tetrahedron around the Cu2 atom shows a certain distortion of the tetrahedral environment with the Cu−S distances of 2.28−2.42 Å. The Cu3 atom is even more different; besides four sulfur atoms at 2.34−2.35 Å, it has a vanadium atom in the second coordination sphere separated by 2.72 Å, which is too distant to be a covalent bond but is close enough to have an impact on the electronic structure in total [41].
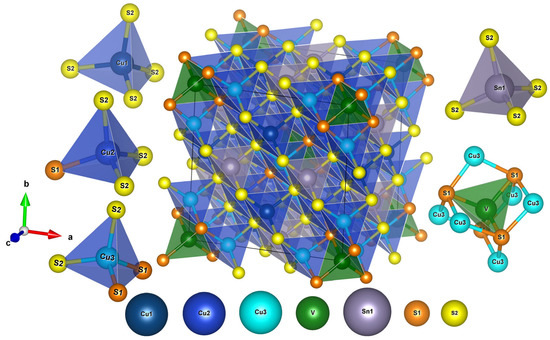
Figure 2.
View of the crystal structure of Cu26−xFexV2Sn6S32 colusites and coordination of Cu, Sn, and V atoms.
The other metal atom sites in the crystal structure of Cu22Fe4V2Sn6S32 are vanadium and tin. The V atom has four sulfur atoms in the first coordination sphere, d(V−S) = 2.32 Å, supplemented by six Cu3 atoms in the second coordination sphere, d(V−Cu) = 2.72 Å. The Sn atom possesses a regular tetrahedral coordination by sulfur atoms with the Sn-S bond length of 2.39 Å. The latter distance is typical for this kind of Sn4+ cations, whereas the V−S bond is only slightly longer than expected for V5+ in a sulfur environment.
The occupancies of all metal sites were refined independently to check for possible anti-site effects. It was found that, within the experimental error, the tin atom fully occupied its position and no sign of tin entering positions of other metal atoms was found. On the next step, the occupancies of all sulfur atoms were verified and found to be equal to 100% within the uncertainties of the refinement. Therefore, the results of the X-ray diffraction powder study showed, within the accuracy of the method, the absence of anti-site defects or sulfur non-stoichiometry in Cu22Fe4V2Sn6S32.
The remaining question was which metal position(s) in the crystal structures was(were) occupied by iron? Unconstrained refinements of three copper and one vanadium sites have led to surprising results. It was found that a heavier atom—iron or copper—entered the 2a position of vanadium. Furthermore, the Cu1 and Cu3 positions contained lighter elements—vanadium or iron—admixed to copper. Assuming that, according to the results of 57Fe Mössbauer spectroscopy (below), iron occupies only one position with a symmetrical environment, several models were refined and the best fit yielded copper and iron mixing on 6d and copper and vanadium mixing both on 2a and 12f sites, which led to the total composition Cu21.97(6)Fe3.96(8)V2.07(11)Sn6S32, the latter being close both to the nominal composition and to that obtained by the EDX spectroscopy (Table S3).
The refinement of the site occupancies for the samples with x = 3 and 2 exhibited the same atomic distribution as for the structure of Cu22Fe4V2Sn6S32, although less accuracy of the refinement was achieved. Given that the total number of iron atoms was 3 or 2 per 34 metal atoms, it was difficult to reliably refine the occupancies of the metal sites against the powder diffraction data. However, it became clear that iron mixed with copper on the 6d site (for x = 2, the Cu/Fe ratio was fixed), whereas the population of the 2a position by copper and the 12f position by vanadium were close to zero; specifically, the vanadium content in the 12f position was so close to zero that it could not be reliably calculated.
Contrastingly, for the sample with x = 1, a different distribution of atoms was observed. First of all, the check for a possible anti-site effect revealed a clear admixture of tin to the position of vanadium; the occupancy refinement revealed that the corresponding 2a site contained 80% V and 20% Sn. As a consequence, the distance from this position to the S(1) atom increased from 2.25 Å in Cu24Fe2V2Sn6S32 to 2.34 Å in Cu25Fe1V2Sn6S32. Secondly, the tin atom (the 6c site) was split into two. Part of the tin atoms remained in the original 6c position, whereas the rest of tin shifted to a nearby 24-fold position with partial occupancy such that the originally regular Sn−S tetrahedron became distorted (Figure S2). Unfortunately, due to the partial occupancy of these positions, it was not possible to determine whether Sn mixed with lighter metals (Cu, Fe, or V) on this site or not. We also note that, in contrast with the literature data for Cu26T2Sn6S32 (T = V, Nb, Ta) [37,42], neither interstitial atom at the 6b (0, ½, ½) position nor sulfur deficiency were observed in the crystal structure of Cu25Fe1V2Sn6S32. The refined composition was Cu25Fe1V1.6(1)Sn6.4(7)S32, compared to Cu24.1(3)Fe1.18(7)V2.11(7)Sn6.51(7)S32.1(3) obtained by the EDX spectroscopy; however, it was difficult to decide whether the structure was vanadium-depleted or the complexity of the crystal structure, that included mixed occupancy of several positions and a split of the tin position, hampered determination of the exact composition by the Rietveld refinement.
We note that, for all samples, the EDXS results show a slight systematic overestimation of tin content. However, the apparent Sn-rich composition of all samples observed by EDX spectroscopy may be a systematic deviation, which is close to the limiting precision of this method.
3.3. Mössbauer Spectroscopy
The 57Fe Mössbauer spectrum for the Cu25Fe1V2Sn6S32 sample (Figure 3) recorded at 298 K has a rather different shape compared to those for the samples having higher iron contents. This spectrum can be presented as the superposition of two quadrupole doublets, major Fe(1A) and minor Fe(1B), which differ from each other by the values of the isomer shift, δFe, and quadrupole splitting, ΔFe (Table 2). The δFe values for both components are typical for high-spin Fe3+ cations in the sulfur tetrahedral environment. The quadrupole splitting of the Fe(1A) component is frequently observed in various compounds having Fe3+ in a regular tetrahedral coordination of sulfur atoms [38,43,44]. The high quadrupole splitting, ΔFe = 0.63 mm s−1, found for the Fe(1B) doublet can indicate either a distortion of the sulfur regular tetrahedral symmetry, or the existence of disordered region embedded into a matrix of the regular structure, as was previously observed for iron-free colusites [35], or the major influence of the second coordination sphere consisting of the asymmetric distribution of copper and iron ions. Given that iron atoms are located in the 6d positions, the latter scenario seems to be more probable. The same kind of the second sphere influence was previously examined in detail for Fe-substituted tetrahedrites [45].
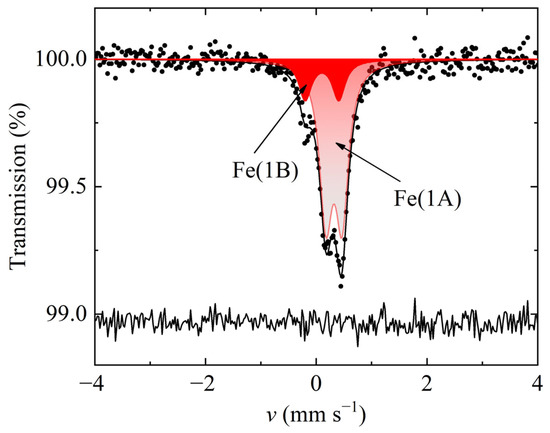
Figure 3.
57Fe Mössbauer spectrum of Cu25Fe1V2Sn6S32 sample recorded at 298 K.

Table 2.
Hyperfine parameters of the 57Fe Mössbauer spectra for Cu26−xFexV2Sn6S32 (x = 1, 2, 3, and 4) at 298 K.
Upon increasing the iron content to x = 2, 3, and 4, the shape of the 57Fe Mössbauer spectra at 298 K changed drastically (Figure 4a). The spectra could be fitted as a superposition of three components with the parameters presented in Table 2. The Fe(1) doublet corresponds to Fe3+ in the symmetric tetrahedral coordination, similar to the Fe(1A) component in Cu25FeV2Sn6S32. The Fe(2) component clearly represents high-spin Fe2+ ions in a tetrahedral sulfur environment [46]. The third component labeled “relax” has a very broad and diffuse shape, which cannot be represented as a discrete partial spectrum with Lorentzian components. Moreover, at low temperatures (Figure 4b), this component is completely split into Fe(1) and Fe(2) subspectra. Previously, similar partial components were observed for the Cu12−xFexSb4S13 tetrahedrite-like family [45] and were assigned to iron ions involved in the fast electron hopping Fe2++ Fe3+ ↔ Fe2+ + Fe3+ [38,45]. However, taking into account the localization of iron only in the “isolated” 6d sites, such behavior (i.e., the appearance of averaged values of hyperfine parameters and their temperature evolution) may be associated with electron hopping Cu+ + Fe3+ ↔ Cu2+ + Fe2+. Since the Fe3+/2+ redox level is known to be at a higher energy than the Cu2+/+ redox couple in sulfides, such electron-transfer reaction brings no particular surprise. However, the electron exchange between cations of different elements in this case is not as pronounced as in tetrahedrites, which corresponds to a higher activation energy of the transfer process. Our assumption is also supported by experiments conducted with several sulfides [47]. The observed indistinguishable iron sites (i.e., “average valence”) on the 57Fe Mössbauer time scales means that the electron transfer rate is greater than ~107 s−1. In this case, both isomer shift and quadrupole splitting “fluctuate” simultaneously between the characteristic values for Fe2+ and Fe3+ ions. Clearly, for the x = 2 sample, the “relax” component constituted the majority of the spectrum, amounting to ~75%, and pointed to the fact that the overwhelming majority of iron atoms were involved in the electron hopping process. The same scenario was previously exhibited by the Cu12−xFexSb4S13 tetrahedrite-like family with a ratio of Fe3+/Fe2+ of approximately 1:1, thus underlying that the electron hopping energy barrier EA [45] has a minimum value for the composition with the same amounts of iron cations having different oxidation states. Upon increasing the iron content to x = 3 and further to x = 4, the contribution of the “relax” component decreased to 65% and then to about 29%, whereas the Fe(2) component became dominant. This showed that the Fe2+ state was becoming prevailing for the greater iron contents, but the Fe3+ and the relaxation components were still present in the compound.

Figure 4.
57Fe Mössbauer spectra of Cu26−xFexV2Sn6S32 (x = 2, 3, and 4) colusites recorded at 298 K (a) and 15 K (b).
Taking into account the above relaxation processes, we analyzed the spectra using a stochastic Tjon–Blume model [48]. A satisfactory description of the spectra at 298 K was achieved under the assumption that there is a distribution of averaged relaxation frequency (Ω) value. The resulting distribution p(Ω) function (Figure S4) demonstrates a bimodal profile with two maxima which can be attributed to different crystallographic iron sites. Such analysis enables us to determine the mean electron hopping frequencies <Ω> (Table 2), which reflect the average rate of the electron transfer between the adjacent Fe2+/Fe3+ centers. The calculated values of (1.7–2.0)·107 s−1 are greater than the respective values for Fe-substituted tetrahedrites (~0.9·107 s−1 at RT) [45], pointing to the faster electron hopping in Fe-bearing colusites. Seemingly, the observed electron hopping is a thermally activated process, as deduced from the disappearance of the continuous absorption upon decreasing the temperature. The spectra at T = 15 K can be described as a superposition of two narrow distributions of quadrupole patterns (Figure 4b) corresponding to the Fe3+ (Fe(1)) and Fe2+ (Fe(2)) ions in the nonequivalent local environments.
The 119Sn spectra shown in Figure 5 reveal that, for the x = 1 sample, the spectrum could not be fitted as a single quadrupole doublet with narrow resonant lines; therefore, we performed the reconstruction of the quadrupole splitting distribution (Figure 5b). The average value of the isomer shift <δSn> was close to 1.5 mm s−1, which is typical for tin(IV) in a tetrahedral environment [49]. The resulting almost symmetric quadrupole splitting distribution p(ΔSn) was presented as a superposition of two Gaussians components. The first Gaussian had a lower value of average quadrupole splitting, with <ΔSn1> ≈ 0.61 mm s−1 and an area ASn1 ≈ 68%, while the second one had a higher value of <ΔSn2> ≈ 0.89 mm s−1 and an area ASn2 ≈ 32%. This result is in good agreement with the crystal structure data for the Cu25FeV2Sn6S32 sample, where the share of the more symmetric tin environment (positions 2a and 6c) is about 73%. Thus, the lowest values of the quadrupole splitting could be assigned to the almost regular tetrahedral environment, whereas the right part of the distribution pointed at the asymmetrical coordination of tin. Therefore, the 119Sn spectroscopy data indicated that tin atoms were present at least at several different sites in the crystal structure of Cu25FeV2Sn6S32. The average values of the quadrupole splitting and deviation of this hyperfine parameter (Table 3) were in good agreement with the theoretical calculations of the electric field gradient (EFG). These quantitative calculations were performed using the crystal data in terms of monopole and dipole contributions to the main component VZZ; they are described in detail.
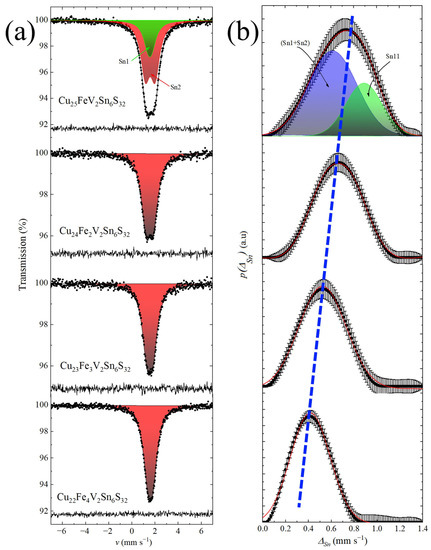
Figure 5.
119Sn Mössbauer spectra of Cu26−xFexV2Sn6S32 (x = 1, 2, 3, and 4) samples recorded at 298 K (a); and corresponding distributions p(ΔSn) of the quadrupole splittings (b). Colored areas represent contributions of SnS4 tetrahedra of high (blue) and low (green) local symmetries (see text). The dashed blue line is shown to demonstrate a monotonic decrease in ΔSn with increase in the iron content.

Table 3.
Hyperfine parameters of the 119Sn Mössbauer spectra for Cu26−xFexV2Sn6S32 (x = 1, 2, 3, and 4) at 298 K.
As the iron content increases, the shape of the spectra changes. For the samples with x = 2, 3, and 4, each spectrum, fitted as the distributions of quadrupole splittings (Figure 5b), exhibited a more narrow and symmetric shape of the quadrupole splitting distributions. It could be represented as a single quadrupole doublet with the close to unchanged isomer shift and the quadrupole splitting ΔSn decreasing from 0.66 down to 0.43 mm s−1 (Table 3). These spectra indicate that tin(IV) occupies a single position in the crystal structure with a tetrahedral coordination or the resonant linewidth exceeds the distortion effects in more iron-enriched compositions. Finally, all 119Sn spectra exhibit no sign of tin being reduced to a lower oxidation state.
It should be emphasized that, in this work, we used one of the possible relaxation models, which describes well the entire series of experimental spectra. Taking into account the inhomogeneity of the crystalline environment of iron cations, we used the distribution of the values of some relaxation parameters. We do not exclude the possibility of using other relaxation models, which are also capable of achieving good description of the spectra. However, our main task was to demonstrate that iron cations in the reported colusites take part in the electronic exchange with their environment, which should undoubtedly be considered when interpreting the properties of these systems.
3.4. Magnetic Properties
Temperature and field dependencies of magnetic susceptibility were measured for the samples with x = 1, 2, 3, and 4. All the samples exhibited Curie–Weiss paramagnetism in the entire range of measurements, from 2 to 380 K. No sign of phase transition known for pristine tetrahedrite and associated with the charge ordering [50,51] was observed. Except for the very low-T region, the magnetization curves recorded for each sample at different fields coincided, showing the absence of the field dependence. The linear increase in the reciprocal magnetic susceptibility with temperature was found for all magnetic fields (Figure S3). Application of the modified Curie–Weiss law revealed low negative Weiss constants for each sample, from −14.5 to −40.9, pointing at weak antiferromagnetic interactions of spins, which was additionally supported by almost linear M(H) dependencies at 2 K.
The dependence of the effective magnetic moments per formula unit on the iron content, extracted from the Curie–Weiss fits (Figure 6), provided further information on the behavior of the spin system. The moment increases with the increase in the iron content. For the sample with x = 1, the magnetic moment is 5.64 μB per formula unit. Given that all iron in the Cu25FeV2Sn6S32 sample is present, according to the 57Fe Mössbauer spectra, in the high-spin state, e2t23, the magnetic moment for this sample is reduced compared with the expected moment for Fe3+ in a high-spin configuration (5.92 μB). The reduction in the moment as compared to the free-ion value can be related to partial spin transfer to the ligands. The TC/C = λ relation provides further insights into the spin system behavior [24]; for the sample with x = 1, λ is equal to 3.65, pointing at a rather weak exchange energy; hence, the degree of d-electron localization on iron atoms is reduced. We also note that, for the x = 1 composition, the charge-balanced formula includes two divalent copper centers: (Cu+)23(Cu2+)2(Fe3+)1(V5+)2(Sn4+)6(S2−)32, which implies that the observed moment per formula is expected to be even greater than predicted for solely one Fe3+.
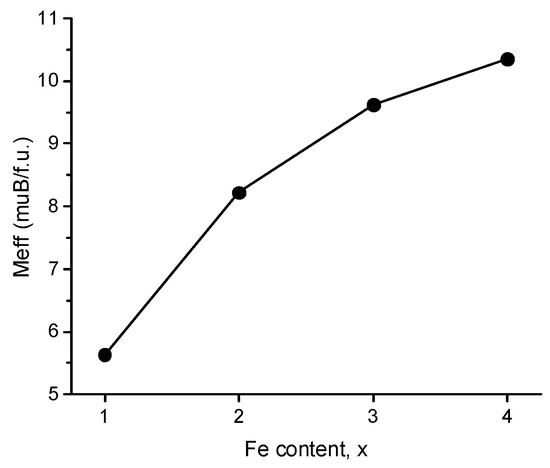
Figure 6.
Effective magnetic moment per formula versus iron contents, x, for Cu26−xFexV2Sn6S32 samples; see text for details.
Upon increasing the iron content, the magnetic moment increases, remaining at lower levels than expected for localized iron moments. We note that, in Cu25FeV2Sn6S32, electron transfer can occur between the Cu1+/2+ and Fe2+/3+ centers, which should lead to the change in the electron field gradient around an iron center and manifest itself as increased quadruple splitting in the 57Fe Mössbauer spectrum, which was indeed observed for this composition (Figure 3). It is worth noting that the significant difference between the copper and iron energy levels, εCu(I/II) << εFe(II/III), precludes fast electron transfer with a relaxation component in the spectrum. In all samples with higher iron contents, the Fe2+/Fe3+ exchange is fast and does manifest in the relaxation component.
3.5. Thermoelectric Properties
The thermoelectric properties of Cu26−xFexV2Sn6S32 (x = 1, 2, 3, and 4) colusites were measured in the temperature range of 300–700 K. The temperature dependencies of the electrical resistivity, Seebeck coefficient, and thermal conductivity are shown in Figure 7. Additionally, shown are the temperature dependencies of the thermoelectric figure-of-merit calculated as ZT = S2T(ρκ)−1.
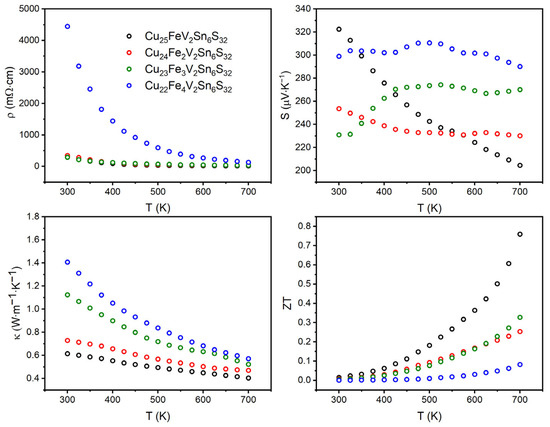
Figure 7.
Electrical resistivity (top left), Seebeck coefficient (top right), thermal conductivity (bottom left), and thermoelectric figure-of-merit (bottom right) as functions of temperature for Cu26−xFexV2Sn6S32 (x = 1, 2, 3, 4) colusites.
Electrical resistivity decreases with temperature for all compositions. The ρ vs. T function is linear on the logarithmic scale pointing at the semiconducting behavior; however, all dependencies except for x = 4 exhibit a change in the slope between 450 and 500 K (Figure 7).
For all samples, the Seebeck coefficient is positive over the entire temperature range, meaning that holes are dominant charge carriers. It is worth noting that the values of the Seebeck coefficient for all samples are high; they exceed 200 µV∙K−1 in the entire temperature range. However, the behavior of the temperature dependencies of the Seebeck coefficient is different for different samples. For the Cu25Fe1V2Sn6S32 sample, a gradual decrease in the Seebeck coefficient from 320 to 200 µV∙K−1 with increasing temperature was observed. For three other samples, the Seebeck coefficient varies only in a narrow range, the difference between the highest and lowest values does not exceed 15%.
Clearly, the S(T) dependencies discriminate the samples into two groups. The first group is presented by the sample with x = 1 exhibiting decreasing S(T), whereas the second group combines the samples with x ≥ 2 that exhibit very slight dependencies of the Seebeck coefficient on temperature. Such a discrimination seems to be in line with the 57Fe Mössbauer spectra and magnetic behavior. In particular, the properties of the colusites’ spin system should have an impact on the Seebeck coefficient, similar to that observed for diluted magnetic semiconductors [52,53]. However, other factors such as effects of stoichiometry cannot be ruled out.
Thermal conductivity (κ) was calculated from measured thermal diffusivity (α) according to κ = αdCp, where d is the density of the substance (g∙m−3), Cp is the heat capacity (J∙g−1∙K−1). The heat capacity was calculated according to the Dulong-Petit approximation Cp = 3R∙M−1, where R is the universal gas constant and M is the reduced molar mass of colusites. The thermal conductivity for all samples is low in the entire temperature range and decreases with the temperature as typical for semiconductors.
The total thermal conductivity increases with the degree of substitution of iron for copper; at 700 K, the total thermal conductivity increases from 0.40 to 0.57 W∙m−1∙K−1. The electronic part of the thermal conductivity, κe, was calculated using the Wiedemann–Franz law as κe = L0σT, where L0 is the ideal Lorenz number, 2.45∙10−8 W∙Ω∙K–2, σ is the electrical conductivity, and T is the absolute temperature (Figure 8). The lattice part of the thermal conductivity is calculated as the difference of the total thermal conductivity and its electronic part is also shown in Figure 8 for comparison. Clearly, the electronic contribution of the thermal conductivity for Cu26−xFexV2Sn6S32 with x = 2, 3, 4 is small and constitutes less than 15% of the total thermal conductivity. The Cu25Fe1V2Sn6S32 compound is different; it exhibits almost similar electronic and lattice contributions at 700 K. Therefore, this sample demonstrates the highest electronic thermal conductivity but the lowest lattice and total thermal conductivity. Normally, the lattice part of thermal conductivity diminishes with increasing disorder in the crystal structure. It can be proposed that, in the case of the x = 1 sample, low values of the lattice thermal conductivity may originate by such structural features as the splitting of the tin 6c atomic position and mixing of tin and vanadium on the 2a site; both features are absent in the crystal structures of all other samples. Additionally, other factors than phonon scattering on the lattice defects may influence the phonon part of the total thermal conductivity, which requires further investigations.
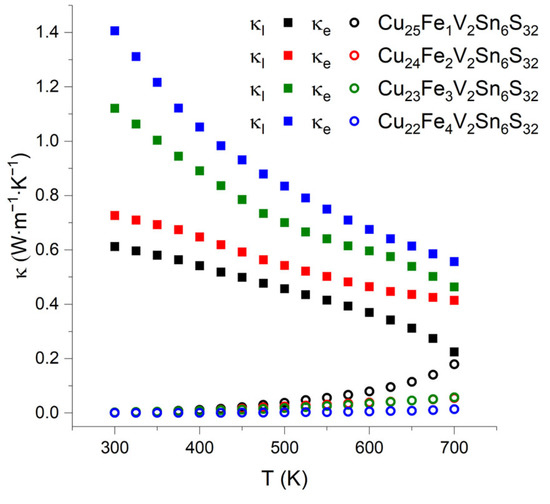
Figure 8.
Electronic (circles) and lattice (squares) parts of the total thermal conductivity for Cu26−xFexV2Sn6S32 (x = 1, 2, 3, 4) samples.
The relatively high values of the Seebeck coefficient and the electrical conductivity as well as low thermal conductivity result in appreciably high values of the thermoelectric figure-of-merit, ZT, for all samples. In general, the ZT increases with the temperature. Specifically, for the sample with x = 1, ZT = 0.78 is reached at 700 K. We note that the literature gives a range of ZT values for iron-free Cu26V2Sn6S32 between 0.01 and 0.93 evidently depending on the synthetic route [37,42,54,55,56]. We propose that such a discrepancy may stem from the intrinsic nonstoichiometry in Cu26V2Sn6S32. For comparison, it is documented in the literature that pristine tetrahedrite is always sulfur-deficient, Cu12Sb4S13−x, where x is about 0.2, and the stoichiometric composition does not belong to the homogeneity range of this phase [50,57].
The ZT value of 0.78 found for the composition with x = 1 is the greatest of all studied samples and is comparable with the high thermoelectric figure-of-merit for other synthetic copper-based minerals, such as germanites of the general formula Cu22Fe8Ge4S32 [13,58] and tetrahedrites featuring partial substitution of a d-metal for copper [22,23,59]. Comparing iron-bearing colusites studied in this work with iron-based tetrahedrites, one can notice that the greatest ZT is observed for the compositions, in which all iron is present in the oxidation state of +3 [23,24].
4. Conclusions
We have prepared iron-bearing colusites of the general formula Cu26−xFexV2Sn6S32, with x(max) lying between 4.2 and 4.5. The crystal structure formally belongs to the colusite type. The compounds with x = 2, 3, and 4 feature a slight mixing of cations in an ideal colusite structure. For x = 1, various structural defects including the anti-site effect and positional disorder of the tin atom were found. The Mössbauer spectroscopy and magnetization study have shown that iron is present in different forms in the title colusites. For x = 1, only Fe3+ is observed, whereas for colusites with higher iron content, Fe3+ and Fe2+ coexist. Moreover, whereas the magnetization study revealed weak antiferromagnetic interactions between iron cations, the Mössbauer study pointed to the fast, on the 57Fe Mössbauer time scale (107–109 s−1), electron hopping Cu+ + Fe3+ ↔ Cu2+ + Fe2+, which is manifested as a relaxation component in the spectra. The analysis of the thermoelectric properties revealed the substantial influence of the iron oxidation state on the transport properties. Specifically, the sample with x = 1 demonstrated the highest slope of the temperature dependence of the Seebeck coefficient, the lowest electrical resistivity, and the greatest electronic contribution, almost 50%, to the total thermal conductivity. Combined, these peculiarities resulted in the greatest thermoelectric figure-of-merit demonstrated by this sample, reaching ZT = 0.78 at 700 K. Although the exact reasons for the increased thermoelectric figure-of-merit for the samples where iron is present in the oxidation state of +3 are not fully understood, we note that this trend is shared by at least two synthetic Fe-bearing minerals, colusites, and tetrahedrites. Evidently, further studies are necessary to understand the role of electronic correlations in synthetic analogs of sulfide minerals, which will pave a way to more efficient non-toxic thermoelectric materials.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/compounds3020027/s1. Figure S1: Rietveld refinement of the crystal structure of Cu26−xFexV2Sn6S32 (x = 1, 2, 3, and 4) against synchrotron X-ray diffraction data; Figure S2: Local environment of Sn1 and Sn11 atoms in the crystal structure of Cu25Fe1V2Sn6S32; Figure S3: Reciprocal magnetic susceptibility as a function of temperature for Cu26−xFexV2Sn6S32 in magnetic field of 5 T; Figure S4: Relaxation frequencies distribution (left panel) of the “relax” component at 300 K; quadrupole splitting distribution (right panel) at 15 K; Table S1: Atomic parameters in the crystal structures of Cu26−xFexV2Sn6S32; Table S2: Interatomic distances in the crystal structures of Cu26−xFexV2Sn6S32; Table S3: Composition of the Cu26−xFexV2Sn6S32 samples from crystal data and EDX spectroscopy; Annex S1: Calculation of the lattice contribution to the EFG in Cu25FeV2Sn6S32. Refs. [60,61,62] are cited in the supplementary materials.
Author Contributions
Conceptualization, A.V.S. (Andrei V. Shevelkov); methodology, A.V.S. (Alexey V. Sobolev), V.Y.V. and A.V.S. (Andrei V. Shevelkov); formal analysis, A.V.S. (Alexey V. Sobolev), V.Y.V. and R.S.; investigation, A.O.P., I.S.G. and J.L.; writing—original draft preparation, A.V.S. (Andrei V. Shevelkov); writing—review and editing, A.O.P., A.V.S. (Alexey V. Sobolev), I.A.P., R.S. and A.V.S. (Andrei V. Shevelkov); supervision, A.V.S. (Andrei V. Shevelkov); funding acquisition, A.V.S. (Andrei V. Shevelkov). All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the Ministry for Science and Higher Education of Russian Federation, grant No. 075-15-2021-1353.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge ESRF for granting the beam time at ID22 and thank C. Giacobbe and M.W. Mogodi for their kind support during the high resolution XRD measurements. We thank D.I. Nasonova for assistance with the synthesis, T.B. Shatalova for DSC measurements, E. Guilmeau for thermoelectric measurements and discussion, and P. Lemoine for discussion. Magnetization measurements in Tallinn were supported by the European Regional Development Fund project TK134 and the Estonian Research Council project PRG1702. The use of the Labox-625 SPS machine is supported by the Lomonosov Moscow State University Program of Development.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cai, B.; Hu, H.; Zhuang, H.L.; Li, J.F. Promising materials for thermoelectric applications. J. Alloys Compd. 2019, 806, 471–486. [Google Scholar]
- Zhu, T.; Liu, Y.; Fu, C.; Heremans, J.P.; Snyder, J.G.; Zhao, X. Compromise and Synergy in High-Efficiency Thermoelectric Materials. Adv. Mater. 2017, 29, 1605884. [Google Scholar] [CrossRef]
- Shevelkov, A.V. Chemical aspects of the design of thermoelectric materials. Russ. Chem. Rev. 2008, 77, 1–19. [Google Scholar] [CrossRef]
- Powell, A.V. Recent developments in Earth-abundant copper-sulfide thermoelectric materials. J. Appl. Phys. 2019, 126, 100901. [Google Scholar] [CrossRef]
- Suekuni, K.; Takabatake, T. Research Update: Cu–S based synthetic minerals as efficient thermoelectric materials at medium temperatures. APL Mater. 2016, 4, 104503. [Google Scholar] [CrossRef]
- Hébert, S.; Berthebaud, D.; Daou, R.; Bréard, Y.; Pelloquin, D.; Guilmeau, E.; Gascoin, F.; Lebedev, O.; Maignan, A. Searching for new thermoelectric materials: Some examples among oxides, sulfides and selenides. J. Phys. Condens. Matter. 2016, 28, 013001. [Google Scholar] [CrossRef]
- Qiu, X.; Qiu, P.; Deng, T.; Huang, H.; Du, X.; Shi, X.; Chen, L. Thermoelectric Properties of Nano-grained Mooihoekite Cu9Fe9S16. Z. Anorg. Allg. Chem. 2020, 646, 1116–1121. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, K.; Du, B.; Reece, M.J. Screening for Cu–S based thermoelectric materials using crystal structure features. J. Mater. Chem. A 2017, 5, 5013–5019. [Google Scholar] [CrossRef]
- Li, J.M.; Li, D.; Song, C.J.; Wang, L.; Xin, H.X.; Zhanga, J.; Qin, X.Y. Realized high power factor and thermoelectric performance in Cu3SbSe4. Intermetallics 2019, 109, 68–73. [Google Scholar] [CrossRef]
- Pavan Kumar, V.; Paradis-Fortin, L.; Lemoine, P.; Le Caër, G.; Malaman, B.; Boullay, P.; Raveau, B.; Guélou, G.; Guilmeau, E. Crossover from Germanite to Renierite-Type Structures in Cu22−xZnxFe8Ge4S32 Thermoelectric Sulfides. ACS Appl. Energy Mater. 2019, 2, 7679–7689. [Google Scholar] [CrossRef]
- Hashikuni, K.; Suekuni, K.; Watanabe, K.; Bouyrie, Y.; Ohta, M.; Ohtaki, M.; Takabatake, T. Carrier concentration tuning in thermoelectric thiospinel Cu2CoTi3S8 by oxidative extraction of copper. J. Solid State Chem. 2018, 259, 5–10. [Google Scholar] [CrossRef]
- Pavan Kumar, V.; Barbier, T.; Lemoine, P.; Raveau, B.; Nassif, V.; Guilmeau, E. Crucial Role of Selenium for Sulphur Substitution in the Structural Transitions and Thermoelectric Properties of Cu5FeS4 Bornite. Dalton Trans. 2017, 46, 2174–2183. [Google Scholar] [CrossRef]
- Pavan Kumar, V.; Paradis-Fortin, L.; Lemoine, P.; Caignaert, V.; Raveau, B.; Malaman, B.; Le Caër, G.; Cordier, S.; Guilmeau, E. Designing a Thermoelectric Copper-Rich Sulfide from a Natural Mineral: Synthetic Germanite Cu22Fe8Ge4S32. Inorg. Chem. 2017, 56, 13376–13381. [Google Scholar] [CrossRef] [PubMed]
- Ang, R.; Ullah Khan, A.; Tsujii, N.; Takai, K.; Nakamura, R.; Mori, T. Thermoelectricity Generation and Electron–Magnon Scattering in a Natural Chalcopyrite Mineral from a Deep-Sea Hydrothermal Vent. Angew. Chem. Int. Ed. 2015, 54, 12909–12913. [Google Scholar] [CrossRef] [PubMed]
- Goto, Y.; Sakai, Y.; Kamihara, Y.; Matoba, M. Effect of Sn-Substitution on Thermoelectric Properties of Copper-Based Sulfide, Famatinite Cu3SbS4. J. Phys. Soc. Jpn. 2015, 84, 044706. [Google Scholar] [CrossRef]
- Liang, D.-D.; Zhang, B.-P.; Zou, L. Enhanced thermoelectric properties of Cu1.8S by Ti-doping induced secondary phase. J. Alloys Compd. 2018, 731, 577–583. [Google Scholar] [CrossRef]
- Qiu, P.; Zhu, Y.; Qin, Y.; Shi, X.; Chen, L. Electrical and thermal transports of binary copper sulfides CuxS with x from 1.8 to 1.96. APL Mater. 2016, 4, 104805. [Google Scholar] [CrossRef]
- Dennler, G.; Chmielowski, R.; Jacob, S.; Capet, F.; Roussel, P.; Zastrow, S.; Nielsch, K.; Opahle, I.; Madsen, G.K.H. Are binary copper sulfides/selenides really new and promising thermoelectric materials? Adv. Energy Mater. 2014, 4, 1301581. [Google Scholar] [CrossRef]
- Liu, H.; Shi, X.; Xu, F.; Zhang, L.; Zhang, W.; Chen, L.; Li, Q.; Uher, C.; Day, T.; Snyder, G.J. Copper ion liquid-like thermoelectrics. Nat. Mater. 2012, 11, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Morelli, D.T.; Xia, Y.; Zhou, F.; Ozolins, V.; Chi, H.; Zhou, X.; Uher, C. High Performance Thermoelectricity in Earth-Abundant Compounds Based on Natural Mineral Tetrahedrites. Adv. Energy Mater. 2013, 3, 342–348. [Google Scholar] [CrossRef]
- Chetty, R.; Prem Kumar, D.S.; Rogl, G.; Rogl, P.; Bauer, E.; Michor, H.; Suwas, S.; Puchegger, S.; Giesterg, G.; Mallik, R.C. Thermoelectric properties of a Mn substituted synthetic tetrahedrite. Phys. Chem. Chem. Phys. 2015, 17, 1716–1727. [Google Scholar] [CrossRef] [PubMed]
- Heo, J.; Laurita, G.; Muir, S.; Subramanian, M.A.; Keszler, D.A. Enhanced Thermoelectric Performance of Synthetic Tetrahedrites. Chem. Mater. 2014, 26, 2047–2051. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Pi, J.-H.; Lee, G.-E.; Kim, I.-H. Synthesis of Fe-Doped Tetrahedrites Cu12−xFexSb4S13 and Characterization of Their Thermoelectric Properties. Korean J. Met. Mater. 2020, 58, 340–347. [Google Scholar] [CrossRef]
- Tippireddy, S.; Chetty, R.; Naik, M.H.; Jain, M.; Chattopadhyay, K.; Mallik, R.C. Electronic and Thermoelectric Properties of Transition Metal Substituted Tetrahedrites. J. Phys. Chem. C 2018, 122, 8735–8749. [Google Scholar] [CrossRef]
- Barbier, T.; Lemoine, P.; Gascoin, S.; Lebedev, O.I.; Kaltzoglou, A.; Vaqueiro, P.; Powell, A.V.; Smith, R.I.; Guilmeau, E. Structural stability of the synthetic thermoelectric ternary and nickel-substituted tetrahedrite phases. J. Alloys Compd. 2015, 634, 253–262. [Google Scholar] [CrossRef]
- Suekuni, K.; Tsuruta, K.; Kunii, M.; Nishiate, H.; Nishibori, E.; Maki, S.; Ohta, M.; Yamamoto, A.; Koyano, M. High-performance thermoelectric mineral Cu12−xNixSb4S2 tetrahedrite. J. Appl. Phys. 2013, 113, 43712. [Google Scholar] [CrossRef]
- Suekuni, K.; Tsuruta, K.; Ariga, T.; Koyano, M. Thermoelectric properties of mineral tetrahedrites Cu10Tr2Sb4S13 with low thermal conductivity. Appl. Phys. Express 2012, 5, 51201. [Google Scholar] [CrossRef]
- Suekuni, K.; Kim, F.S.; Nishiate, H.; Ohta, M.; Tanaka, H.I.; Takabatake, T. High-performance thermoelectric minerals: Colusites Cu26V2M6S32 (M = Ge, Sn). Appl. Phys. Lett. 2014, 105, 132107. [Google Scholar] [CrossRef]
- Suekuni, K.; Kim, F.S.; Takabatake, T. Tunable electronic properties and low thermal conductivity in synthetic colusites Cu26−xZnxV2M6S32 (x ≤ 4, M = Ge, Sn). J. Appl. Phys. 2014, 116, 63706. [Google Scholar] [CrossRef]
- Hagiwara, T.; Suekuni, K.; Lemoine, P.; Supka, A.R.; Chetty, R.; Guilmeau, E.; Raveau, B.; Fornari, M.; Ohta, M.; Al Orabi, R.A.R.; et al. Key Role of d0 and d10 Cations for the design of colusite structure: Highly Performant Thermoelectric Sulfides Cu26Ti2Sb6S32. Chem. Mater. 2021, 33, 3449–3456. [Google Scholar] [CrossRef]
- Pavan Kumar, V.; Supka, A.R.; Lemoine, P.; Lebedev, O.I.; Raveau, B.; Suekuni, K.; Nassif, V.; Al Orabi, R.A.R.; Fornari, M.; Guilmeau, E. High Power Factors of Thermoelectric Colusites Cu26T2Ge6S32 (T = Cr, Mo, W): Toward Functionalization of the Conductive “Cu-S” Network. Adv. Energy Mater. 2019, 9, 1803249. [Google Scholar] [CrossRef]
- Pavan Kumar, V.; Guélou, G.; Lemoine, P.; Raveau, B.; Supka, A.; Al Orabi, R.A.R.; Fornari, M.; Suekuni, K.; Guilmeau, E. Copper-rich thermoelectric sulfides: Size mismatch effect and chemical disorder in the [TS4]Cu6 complexes of Cu26T2Ge6S32 (T = Cr, Mo, W) colusites. Angew. Chem. Int. Ed. 2019, 58, 15455–15463. [Google Scholar] [CrossRef] [PubMed]
- Raveau, B. Copper Mixed Valence Concept: “Cu(I)–Cu(II)” in Thermoelectric Copper Sulfidess—An Alternative to “Cu(II)–Cu(III)” in Superconducting Cuprates. J. Supercond. Nov. Magn. 2020, 33, 259–263. [Google Scholar] [CrossRef]
- Lemoine, P.; Pavan Kumar, V.; Guélou, G.; Nassif, V.; Raveau, B.; Guilmeau, E. Thermal Stability of the Crystal Structure and Electronic Properties of the High Power Factor Thermoelectric Colusite Cu26Cr2Ge6S32. Chem. Mater. 2020, 32, 830–840. [Google Scholar] [CrossRef]
- Bourgès, C.; Bouyrie, Y.; Supka, A.R.; Al Orabi, R.A.R.; Lemoine, P.; Lebedev, O.I.; Ohta, M.; Suekuni, K.; Nassif, V.; Hardy, V.; et al. High-Performance Thermoelectric Bulk Colusite by Process Controlled Structural Disordering. J. Am. Chem. Soc. 2018, 140, 2186–2195. [Google Scholar] [CrossRef]
- Kim, F.S.; Suekuni, K.; Nishiate, H.; Ohta, M.; Tanaka, H.I.; Takabatake, T. Tuning the charge carrier density in the thermoelectric colusite. J. Appl. Phys. 2016, 119, 175105. [Google Scholar] [CrossRef]
- Guélou, G.; Lemoine, P.; Raveau, B.; Guilmeau, E. Recent developments in high-performance thermoelectric sulphides: An overview of the promising synthetic colusites. J. Mater. Chem. C 2021, 9, 773–795. [Google Scholar] [CrossRef]
- Nasonova, D.I.; Presniakov, I.A.; Sobolev, A.V.; Verchenko, V.Y.; Tsirlin, A.A.; Wei, Z.; Dikarev, E.V.; Shevelkov, A.V. Role of iron in synthetic tetrahedrites revisited. J. Solid State Chem. 2016, 235, 28–35. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr.—Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Matsnev, M.E.; Rusakov, V.S. An application for Mössbauer spectra modeling and fitting. AIP Conf. Proc. 2012, 1489, 178–185. [Google Scholar]
- Lemoine, P.; Guélou, G.; Raveau, B.; Guilmeau, E. Crystal structure classification of copper-based sulphides as a tool for the design of inorganic functional materials. Angew. Chem. Int. Ed. 2022, 61, e202108686. [Google Scholar] [CrossRef]
- Suekuni, K.; Shimizu, Y.; Nishibori, E.; Kasai, H.; Saito, H.; Yoshimoto, D.; Hashikuni, K.; Bouyrie, Y.; Chetty, R.; Ohta, M.; et al. Atomic-Scale Phonon Scatterers in Thermoelectric Colusites with a Tetrahedral Framework Structure. J. Mater. Chem. A 2019, 7, 228–235. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Fatseas, G.A. Mössbauer 57Fe isomer shift as a measure of valence in mixed-valence iron sulfides. J. Solid State Chem. 1982, 41, 1–22. [Google Scholar] [CrossRef]
- Macovicky, E.; Tippelt, G.; Forcher, K.; Lottermoser, W.; Karup-Mǿller, S.; Amthauer, G. Mössbauer study of Fe-bearing synthetic tennantite. Can. Mineral. 2003, 41, 1125–1134. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Presniakov, I.A.; Nasonova, D.I.; Verchenko, V.Y.; Shevelkov, A.V. Thermally Activated Electron Exchange in Cu12−xFexSb4S13 (x = 1.3, 1.5) Tetrahedrites: A Mössbauer Study. J. Phys. Chem. C 2017, 121, 4548–4557. [Google Scholar] [CrossRef]
- Macovicky, E.; Forcher, K.; Lottermoser, W.; Amthauer, G. The role of Fe2+ and Fe3+ in synthetic Fe-substituted tetrahedrite. Miner. Petrol. 1990, 43, 73–81. [Google Scholar] [CrossRef]
- Borgheresi, M.; Di Benedetto, F.; Romanelli, M.; Reissner, M.; Lottermoser, W.; Gainov, R.R.; Khassanov, R.R.; Tippelt, G.; Giaccherini, A.; Sorace, L.; et al. Mössbauer study of bornite and chemical bonding in Fe-bearing sulphides. Phys. Chem. Miner. 2018, 45, 227–235. [Google Scholar] [CrossRef]
- Tjon, J.A.; Blume, M. Mössbauer spectra in a fluctuating environment II. Randomly varying electric field gradients. Phys. Rev. 1968, 165, 456–461. [Google Scholar] [CrossRef]
- Nasonova, D.I.; Sobolev, A.V.; Presniakov, I.A.; Andreeva, K.D.; Shevelkov, A.V. Position and oxidation state of tin in Sn-bearing tetrahedrites Cu12−xSnxSb4S13. J. Alloys Compd. 2019, 778, 774–778. [Google Scholar] [CrossRef]
- Nasonova, D.I.; Verchenko, V.Y.; Tsirlin, A.A.; Shevelkov, A.V. Low-Temperature structure and thermoelectric properties of pristine synthetic tetrahedrite Cu12Sb4S13. Chem. Mater. 2016, 28, 6621–6627. [Google Scholar] [CrossRef]
- Matsui, T.; Matsuno, H.; Kotegawa, H.; Tou, H.; Suekuni, K.; Hasegawa, T.; Tanaka, H.I.; Takabatake, T. First-Order Metal–Semiconductor Transition Triggered by Rattling Transition in Tetrahedrite Cu12Sb4S13: Cu-Nuclear Magnetic Resonance Studies. J. Phys. Soc. Jpn. 2019, 88, 054710. [Google Scholar] [CrossRef]
- Acharya, S.; Anwar, S.; Mori, T.; Soni, A. Coupling of Charge Carriers with Magnetic Entropy for Power Factor Enhancement in Mn Doped Sn1.03Te for Thermoelectric Applications. J. Mater. Chem. C 2018, 6, 6489–6493. [Google Scholar] [CrossRef]
- Vaney, J.-B.; Aminorroaya Yamini, S.; Takaki, H.; Kobayashi, K.; Kobayashi, N.; Mori, T. Magnetism-mediated thermoelectric performance of the Cr-doped bismuth telluride tetradymite. Mater. Today Phys. 2019, 9, 100090. [Google Scholar] [CrossRef]
- Hegedüs, M.; Achimovičová, M.; Hui, H.; Guélou, G.; Lemoine, P.; Fourati, I.; Juraszek, J.; Malaman, B.; Baláž, P.; Guilmeau, E. Promoted Crystallization and cationic ordering in thermoelectric Cu26V2Sn6S32 colusite by eccentric vibratory ball milling. Dalton Trans. 2020, 49, 15828–15836. [Google Scholar] [CrossRef] [PubMed]
- Bourgés, C.; Gilmas, M.; Lemoine, P.; Mordvinova, N.E.; Lebedev, O.I.; Hug, E.; Nassif, V.; Malaman, B.; Daou, R.; Guilmeau, E. Structural analysis and thermoelectric properties of mechanically alloyed colusites. J. Mater. Chem. C 2016, 4, 7455–7463. [Google Scholar] [CrossRef]
- Candolfi, C.; Guélou, G.; Bourgès, C.; Supka, A.R.; Al Orabi, R.A.R.; Fornari, M.; Malaman, B.; Le Caër, G.; Lemoine, P.; Hardy, V.; et al. Disorder-Driven Glasslike Thermal Conductivity in Colusite Cu26V2Sn6S32 Investigated by Mössbauer Spectroscopy and Inelastic Neutron Scattering. Phys. Rev. Mater. 2020, 4, 025404. [Google Scholar] [CrossRef]
- Mashadieva, L.F.; Mammadli, P.R.; Babanly, D.M.; Ashirov, G.M.; Shevelkov, A.V.; Yusibov, Y.A. Solid-Phase Equilibria in the Cu-Sb-S System and Thermodynamic Properties of Copper-Antimony Sulfides. JOM 2021, 73, 1522–1530. [Google Scholar] [CrossRef]
- Paradis-Fortin, L.; Guélou, G.; Pavan Kumar, V.; Lemoine, P.; Prestipino, C.; Merdrignac-Conanec, O.; Durand, G.R.; Cordier, S.; Lebedev, O.I.; Guilmeau, E. Structure, Microstructure and Thermoelectric Properties of Germanite-Type Cu22Fe8Ge4S32 Compounds. J. Alloys Compd. 2020, 831, 154767. [Google Scholar] [CrossRef]
- Chetty, R.; Bali, A.; Mallik, R.C. Tetrahedrites as thermoelectric materials: An overview. J. Mater. Chem. C 2015, 3, 12364–12378. [Google Scholar] [CrossRef]
- Stadnik, Z.M. Electric field gradient calculations in rare-earth iron garnets. J. Phys. Chem. Solids 1984, 45, 311–318. [Google Scholar] [CrossRef]
- Yatsenko, A.V. Analysis of the electronic dipole polarizability of ions in cubic oxides, fluorides, and sulfides of alkaline earth elements. Crystallogr. Rep. 2010, 55, 668–672. [Google Scholar] [CrossRef]
- Haas, H.; Menninger, M.; Andreasen, H.; Damgaard, S.; Grann, H.; Pedersen, F.T.; Petersen, J.W.; Weyer, G. EFG sign for Sn in Zn, Cd, and Sb. Hyperfine Interact. 1983, 15/16, 215–218. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).