The Effect of Strain on the Aromatic Character of Infinitene
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Garratt, P.J. Aromaticity; John Wiley & Sons: New York, NY, USA, 1986; p. 55. [Google Scholar]
- Solà, M. Aromaticity rules. Nat. Chem. 2022, 14, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Solà, M. Why aromaticity is a suspicious concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Cook, M.J.; Katritzky, A.R.; Linda, P. Aromaticity of heterocycles. In Advances in Heterocyclic Chemistry; Katritzky, A.R., Boulton, A.J., Eds.; Academic Press: New York, NY, USA, 1974; Volume 17, pp. 255–356. [Google Scholar]
- Cyransky, M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef]
- Wodrich, M.D.; Wannere, C.S.; Mo, Y.; Jarowski, P.D.; Houk, K.N.; von Ragué Schleyer, P. The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations. Chem. Eur. J. 2007, 13, 7731–7744. [Google Scholar] [CrossRef] [PubMed]
- Clesielski, A.; Stepień, D.K.; Dobrowolski, M.A.; Dobrzycki, L.; Cyranski, M.K. On the aromatic stabilization of benzenoid hydrocarbons. Chem. Commun. 2012, 48, 10129–10131. [Google Scholar] [CrossRef] [PubMed]
- Bird, C.W. A new aromaticity index and its application to five-membered ring heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to six-membered ring heterocycles. Tetrahedron 1986, 42, 89–92. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity.8. the influence of N-oxide formation on heterocyclic aromaticity. Tetrahedron 1993, 49, 8441–8448. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of π-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Von Ragué Schleyer, O.; Maerker, C.; Dransfeld, A.; Jiao, H.; von Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Corminboeuf, C.; Heine, P.C.; Seifert, G.; von Ragué Schleyer, P.; Weber, J. Induced magnetic fields in aromatic [n]-annulenes—Interpretation of NICS tensor components. Phys. Chem. Chem. Phys. 2004, 6, 273–276. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyranski, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1419. [Google Scholar] [CrossRef]
- Stanger, A. What is … aromaticity: A critique of the concept of aromaticity—Can it really be defined? Chem. Commun. 2009, 1939–1947. [Google Scholar] [CrossRef] [PubMed]
- Jagadeesh, M.N.; Makur, A.; Chandrasekhar, J. The interplay of angle strain and aromaticity: Molecular and electronic structure of [0n]paracycliphanes. J. Mol. Model. 2000, 6, 226–233. [Google Scholar] [CrossRef]
- Frizzo, C.P.; Martins, M.A.P. Aromaticity in heterocycles: New HOMA index parametrization. Struct. Chem. 2012, 23, 375–380. [Google Scholar] [CrossRef]
- D’Auria, M. The use of D’ index in the determination of the aromatic character of organic compounds. Comparison with HOMHED and NICS. ChemistrySelect 2020, 5, 2816–2823. [Google Scholar] [CrossRef]
- D’Auria, M. An approach to the aromaticity based on the energy of the occupied orbitals. Curr. Org. Chem. 2016, 20, 971–983. [Google Scholar] [CrossRef]
- Krzeszewski, M.; Ito, H.; Itami, K. Infinitene: A helically twisted figure-eight [12]circulene. J. Am. Chem. Soc. 2022, 144, 862–871. [Google Scholar] [CrossRef]
- Martínez, A.; Zeeshan, M.; Zaidi, A.; Sliwka, H.-R.; Naqvi, K.R.; Partali, V. On infinitenes—Reliable calculation of λ∞ and molecular modeling of lemniscate structured carotenoids. Comput. Theor. Chem. 2018, 1125, 133–141. [Google Scholar] [CrossRef]
- Orozco-Ic, M.; Valiev, R.R.; Sundholm, D. Non-intersecting ring currents in [12]infinitene. Phys. Chem. Chem. Phys. 2022, 24, 6404–6409. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Chen, P.; Sheng, H.; Li, C.; Jingang Wang, J. Physical mechanism on linear spectrum and nonlinear spectrum in double helical carbon nanomolecule–infinitene. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 282, 121674. [Google Scholar] [CrossRef] [PubMed]
- Freixas, V.M.; Tretiak, S.; Fernandez-Alberti, S. Infinitene: Computational Insights from Nonadiabatic Excited State Dynamics. J. Phys. Chem. Lett. 2022, 13, 8495–8501. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Zanasi, R.; Summa, F.F. Magnetic Characterization of the Infinitene Molecule. J. Phys. Chem. A. 2022, 126, 3717–3723. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Becke, A.D. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]

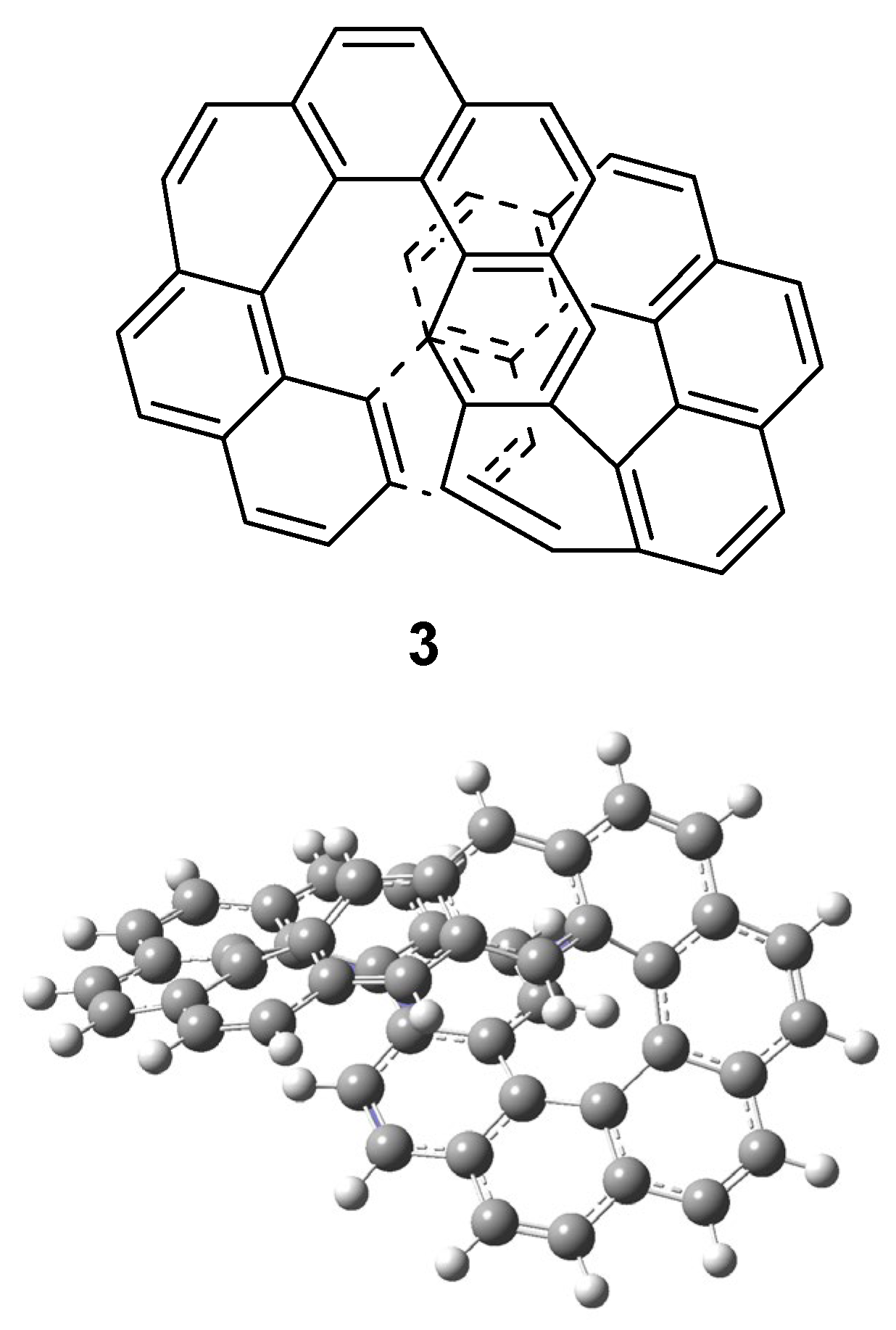

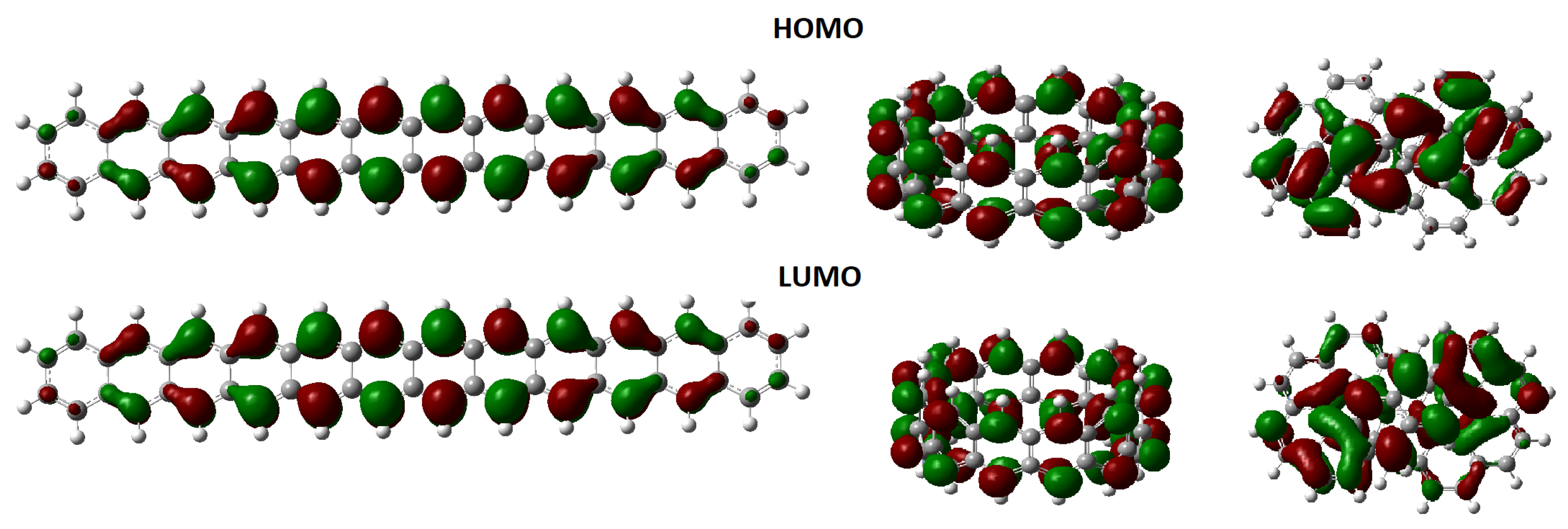
| Orbital | Dodecacene | [12]Circulene | Infinitene |
|---|---|---|---|
| π1 | −11.34 | −11.66 | −11.10 |
| π2 | −11.23 | −11.58 | −11.03 |
| π3 | −11.05 | −11.58 | −10.44 |
| π4 | −10.80 | −11.42 | −9.74 |
| π5 | −10.48 | −11.42 | −9.68 |
| π6 | −10.10 | −10.99 | −9.23 |
| π7 | −9.66 | −10.99 | −9.13 |
| π8 | −9.15 | −8.97 | −9.04 |
| π9 | −8.73 | −8.79 | −8.76 |
| π10 | −8.60 | −8.79 | −8.51 |
| π11 | −8.60 | −8.79 | −8.24 |
| π12 | −8.40 | −8.79 | −8.16 |
| π13 | −8.14 | −8.25 | −7.91 |
| π14 | −8.00 | −8.25 | −7.83 |
| π15 | −7.56 | −7.45 | −7.30 |
| π16 | −7.42 | −7.45 | −7.17 |
| π17 | −7.38 | −7.38 | −7.00 |
| π18 | −6.95 | −6.47 | −6.91 |
| π19 | −6.48 | −6.18 | −6.18 |
| π20 | −6.46 | −6.18 | −6.18 |
| π21 | −6.43 | −4.70 | −5.88 |
| π22 | −5.85 | −4.70 | −5.68 |
| π23 | −5.23 | −4.32 | −5.47 |
| π24 | −4.59 | −11.66 | −5.05 |
| π25 | −4.01 | ||
| D′ | 1.45 | 1.45 | 1.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Auria, M. The Effect of Strain on the Aromatic Character of Infinitene. Compounds 2023, 3, 336-340. https://doi.org/10.3390/compounds3020025
D’Auria M. The Effect of Strain on the Aromatic Character of Infinitene. Compounds. 2023; 3(2):336-340. https://doi.org/10.3390/compounds3020025
Chicago/Turabian StyleD’Auria, Maurizio. 2023. "The Effect of Strain on the Aromatic Character of Infinitene" Compounds 3, no. 2: 336-340. https://doi.org/10.3390/compounds3020025
APA StyleD’Auria, M. (2023). The Effect of Strain on the Aromatic Character of Infinitene. Compounds, 3(2), 336-340. https://doi.org/10.3390/compounds3020025







