Dynamics and Elastic Properties of Glassy Metastable States
Abstract
1. Introduction
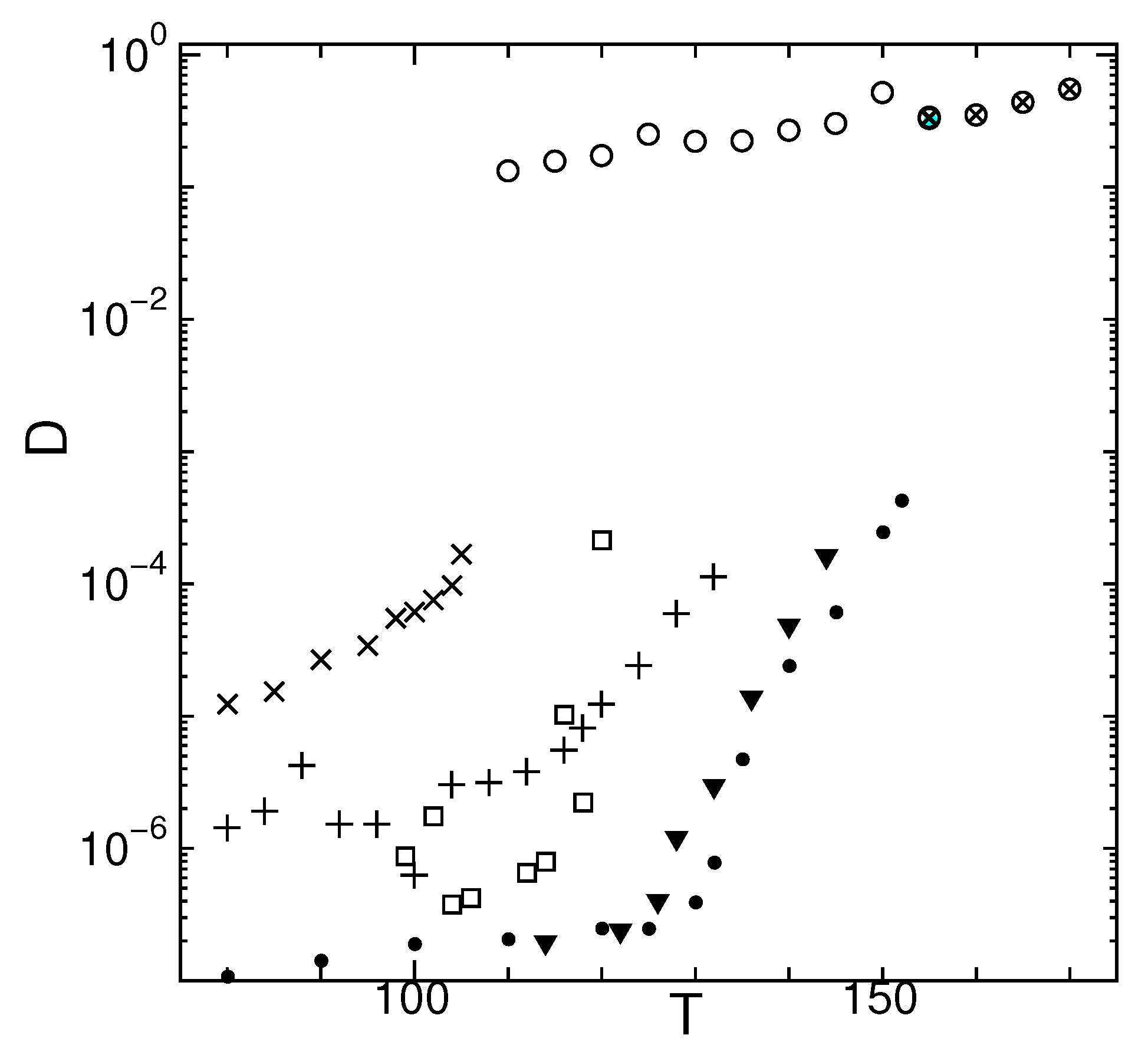
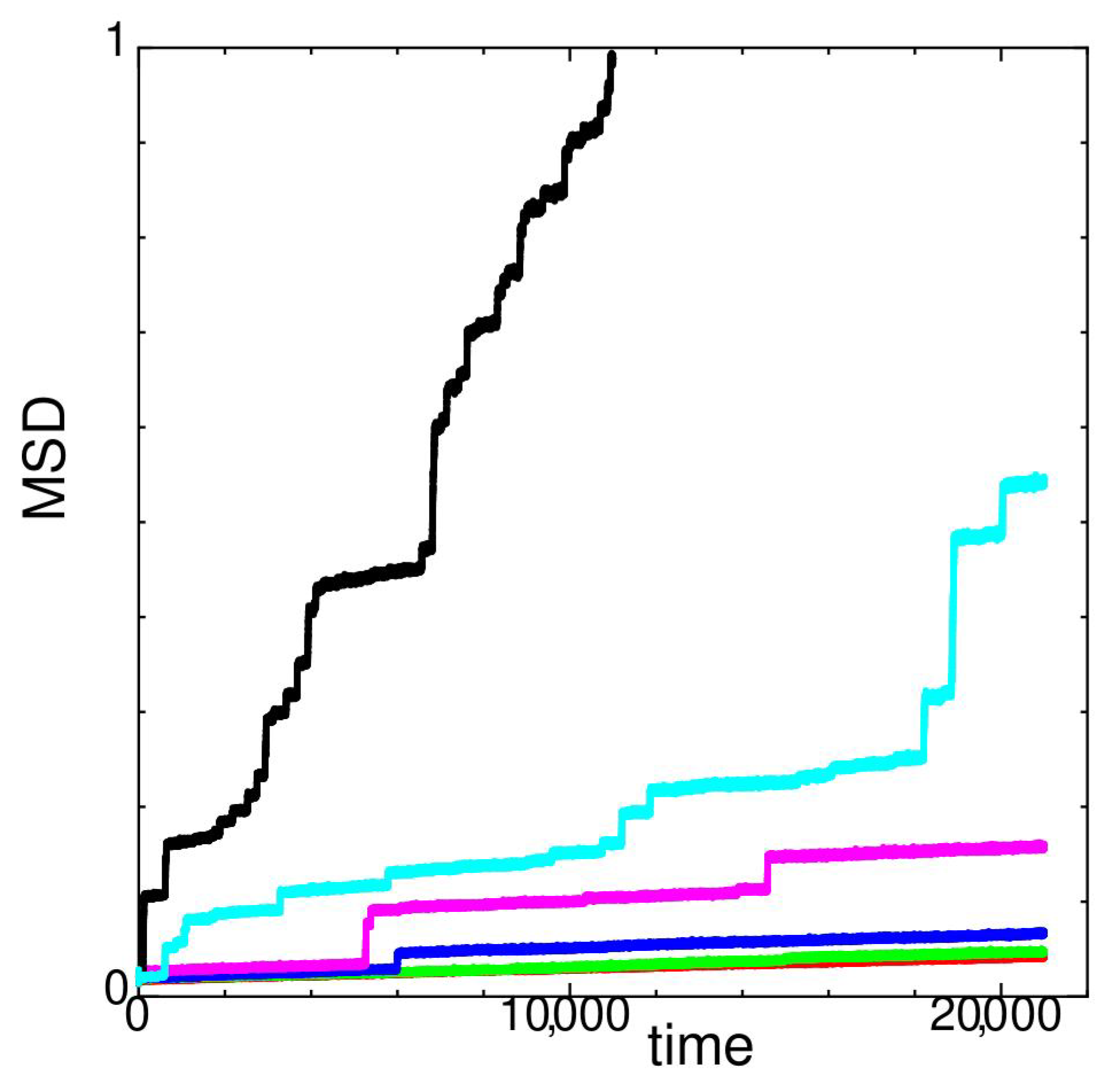
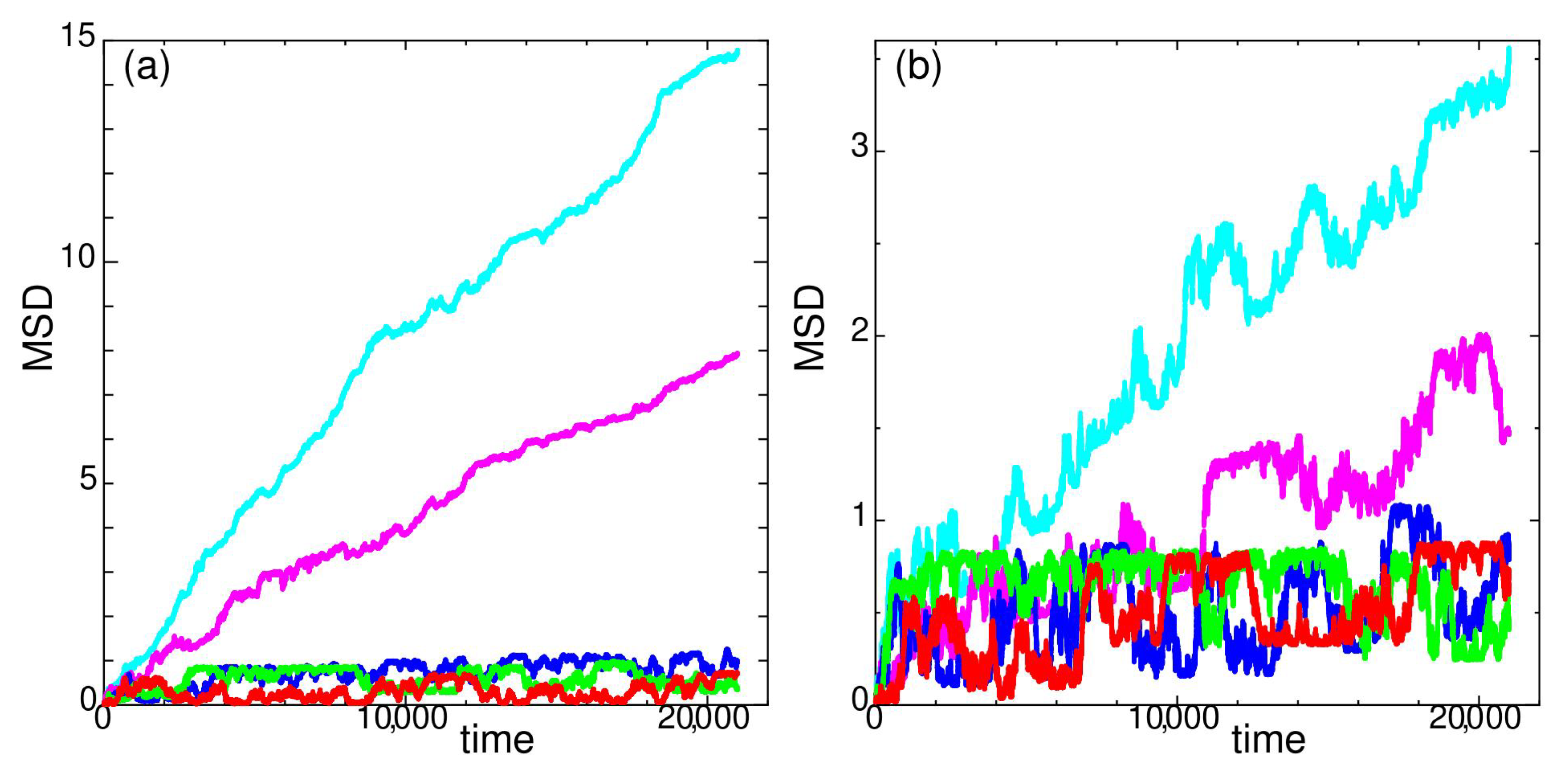
2. Dynamic Properties
2.1. Temperature Dependence
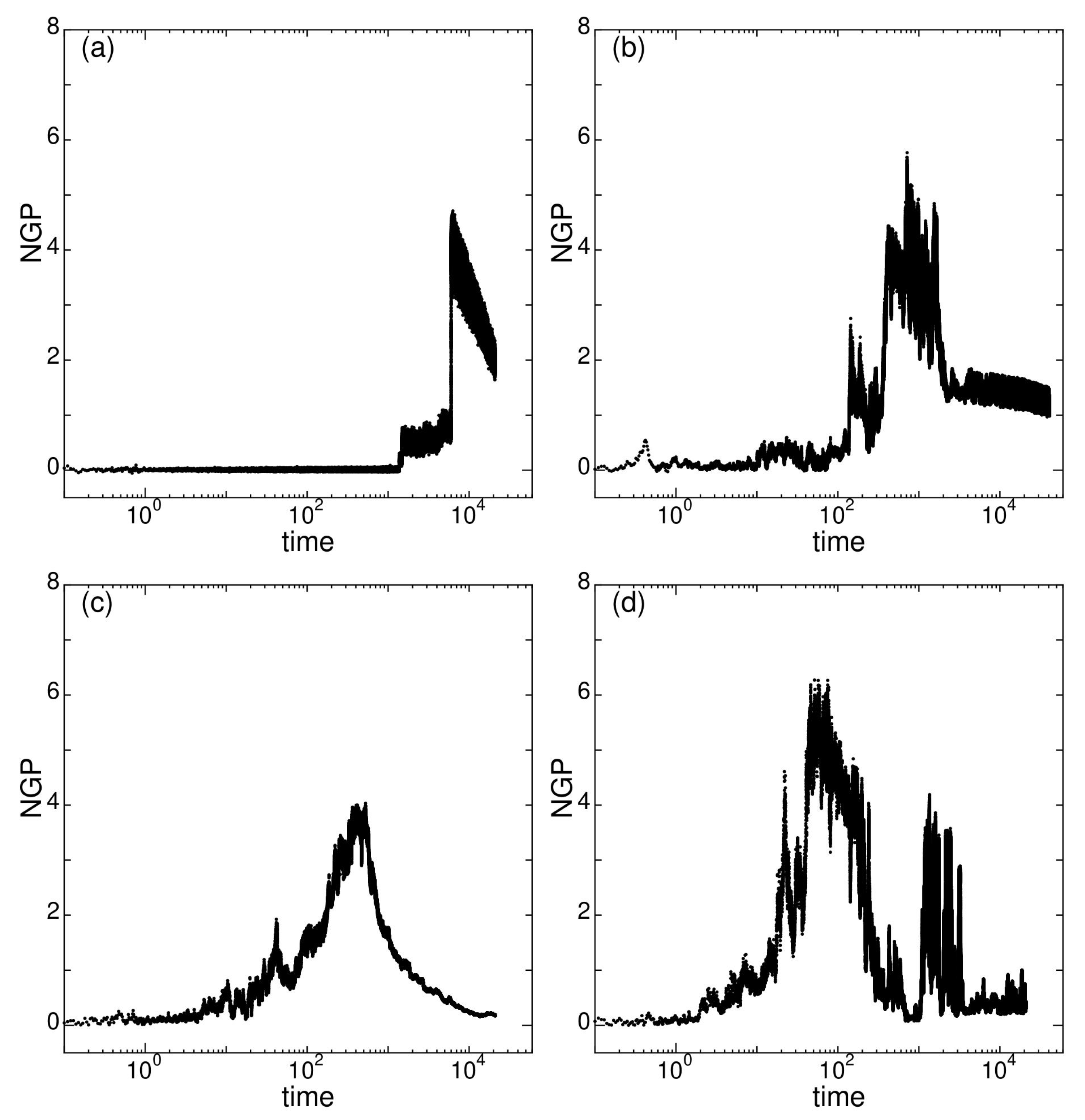
2.2. State G
2.3. State J
2.4. State M
2.5. State O
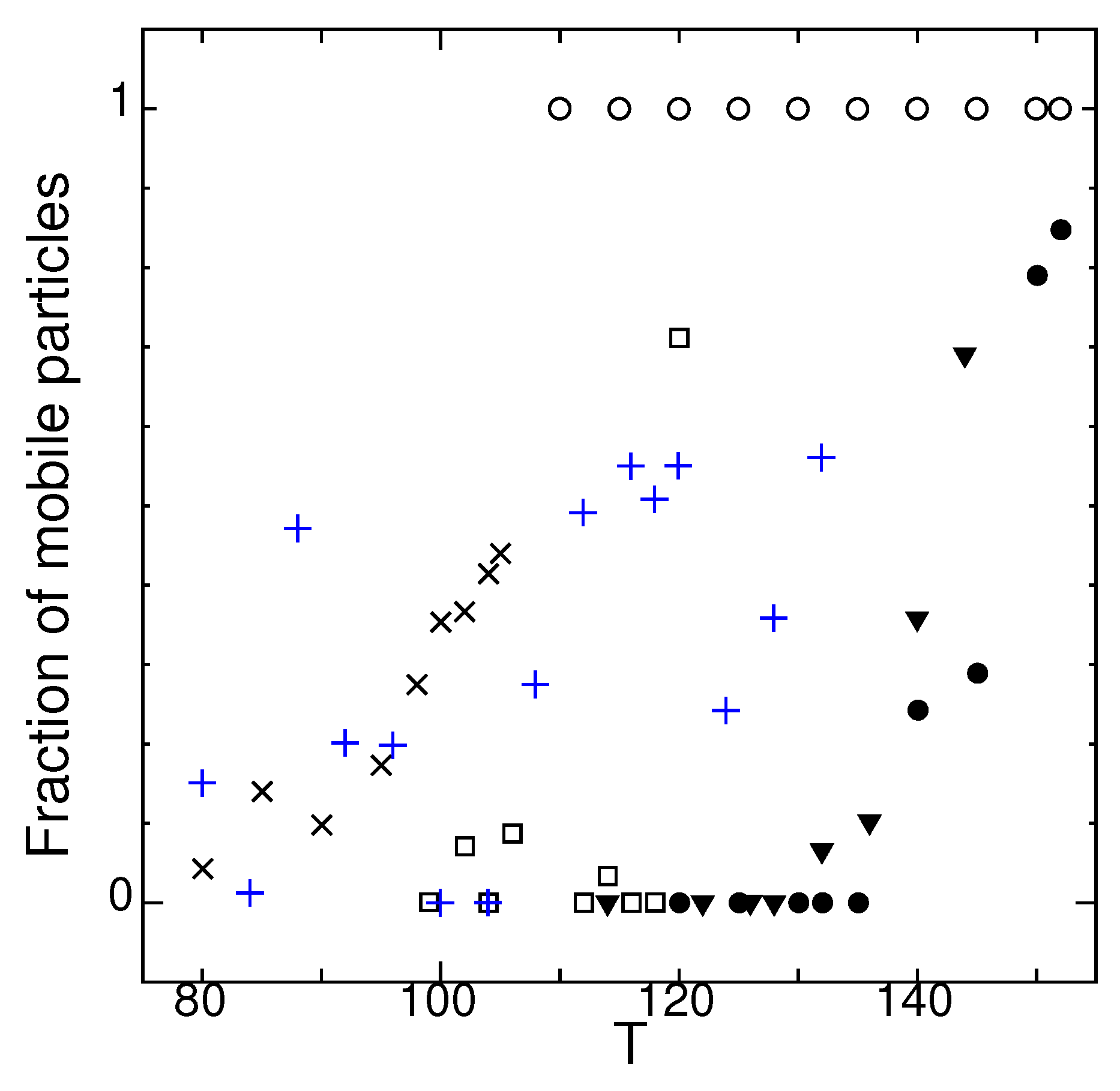
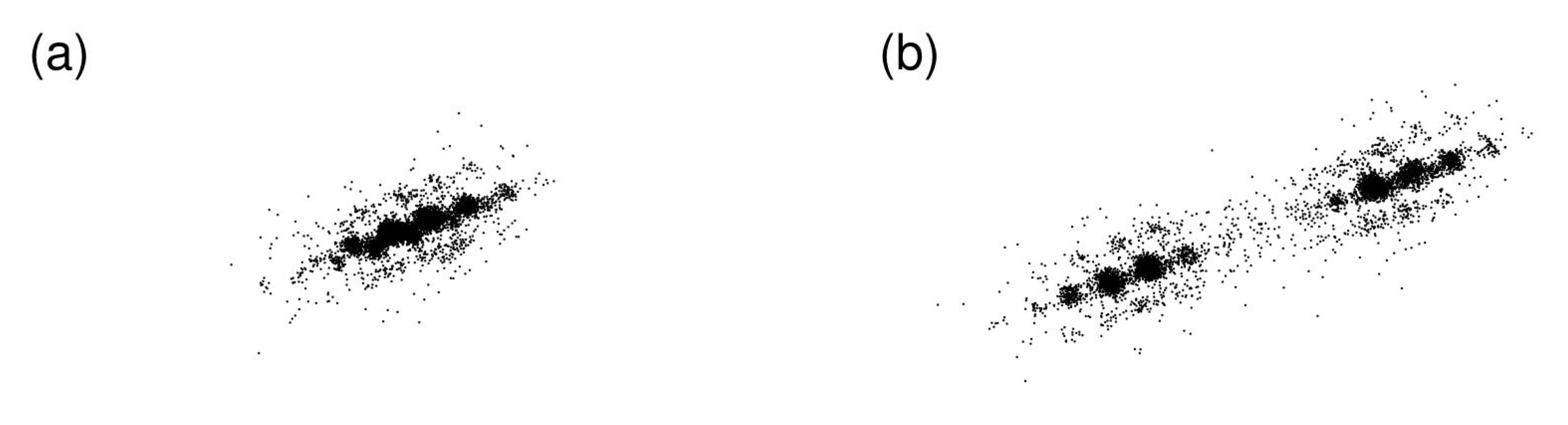
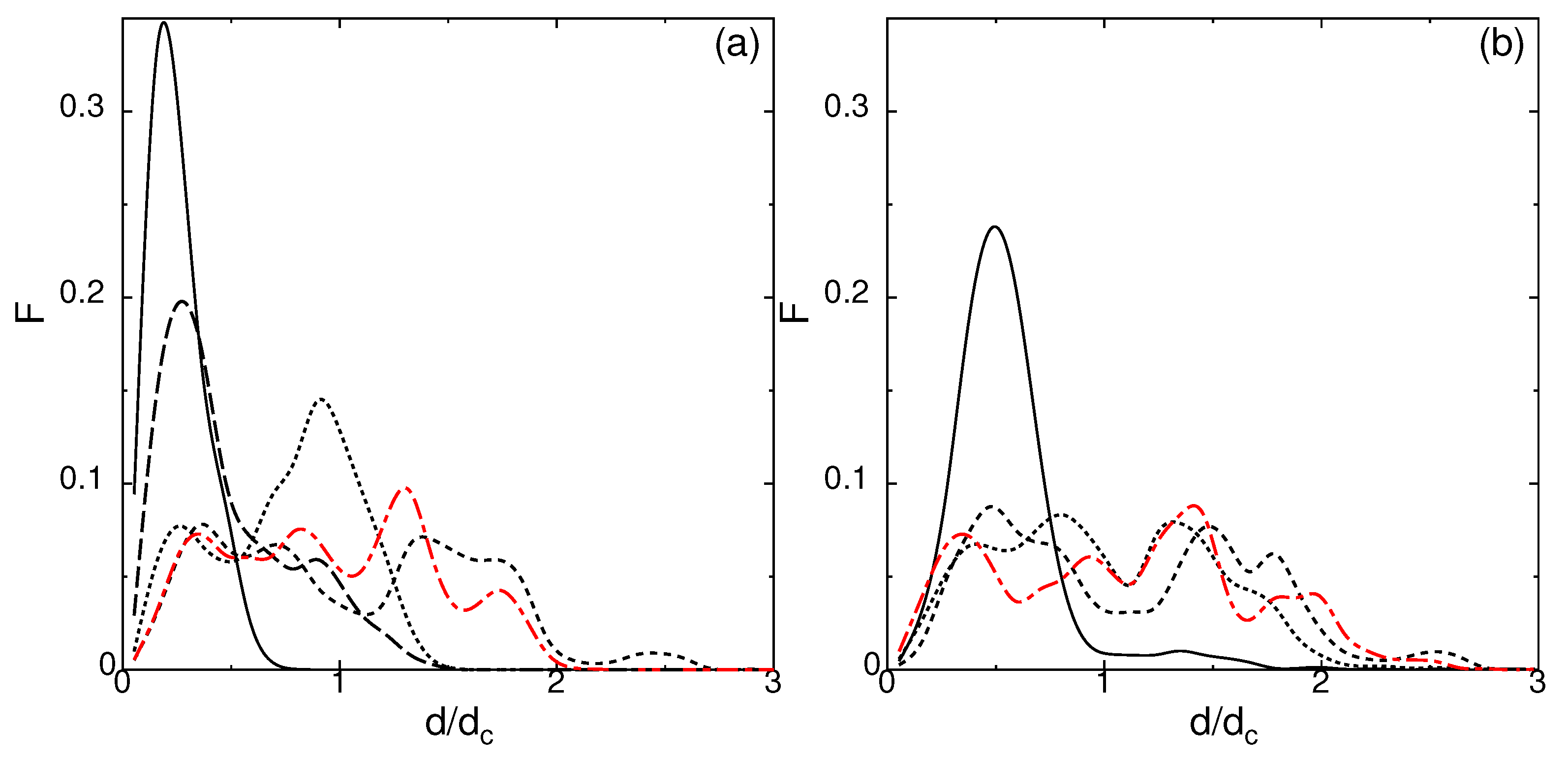
2.6. Dynamical Heterogeneity at
3. Elastic Properties
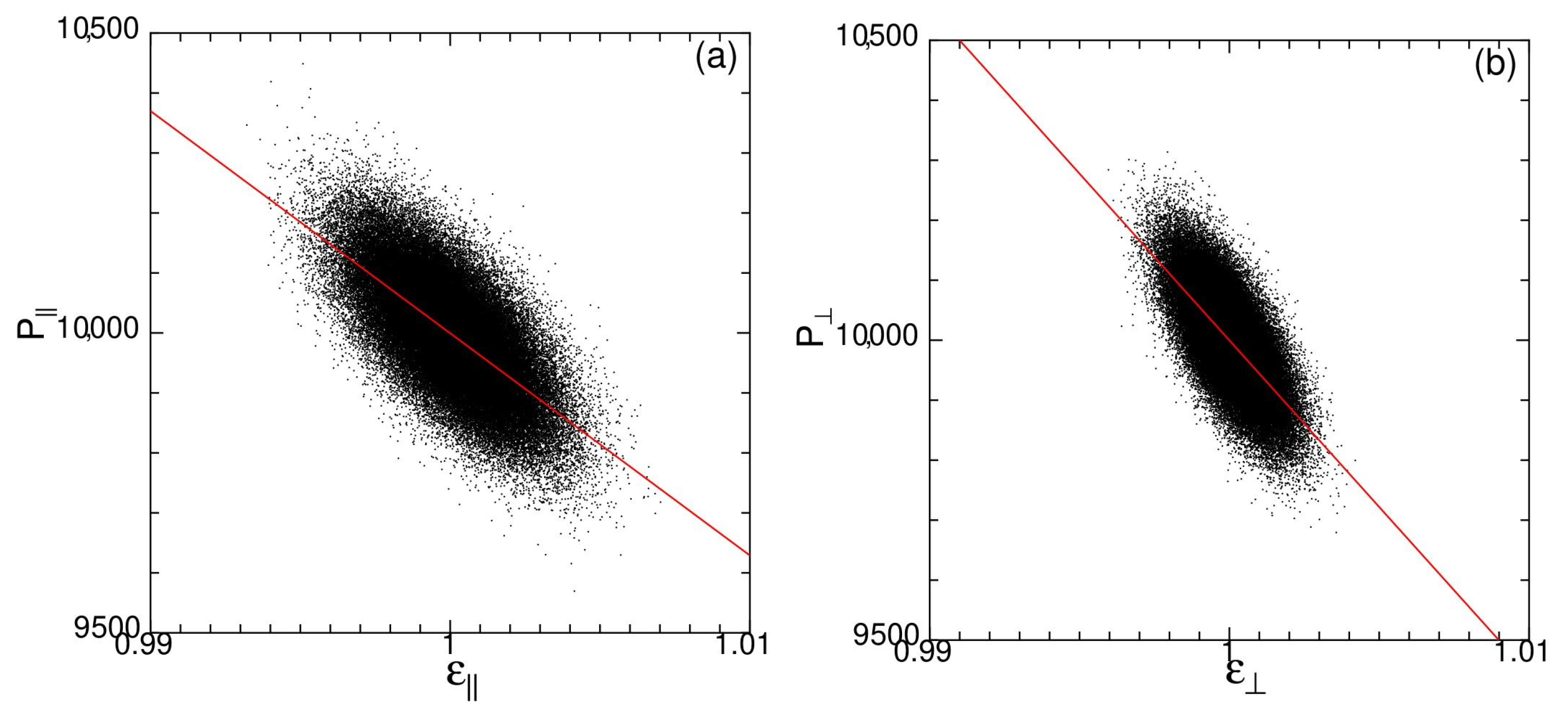
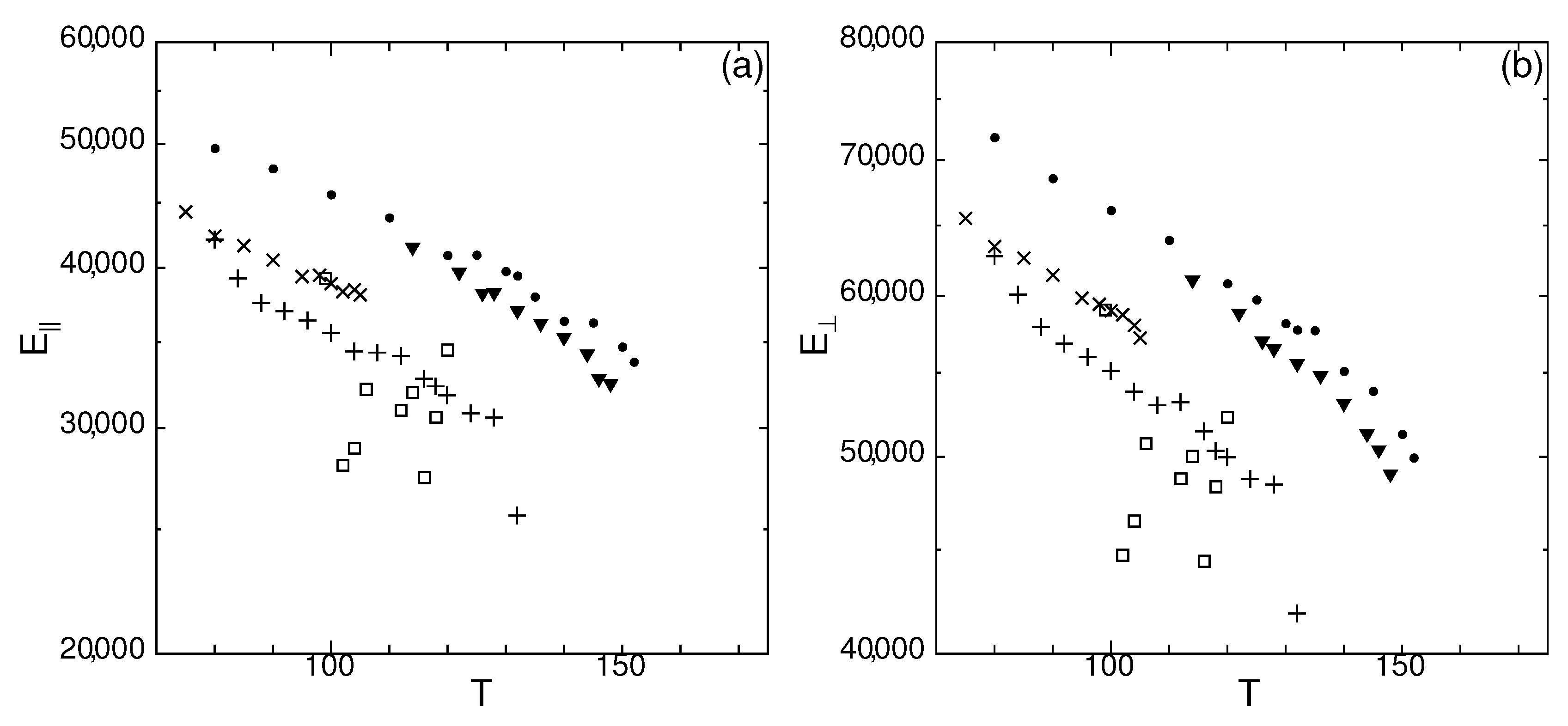
3.1. Temperature Dependence of Modulus of Spontaneous Elastic Tension/Compression
3.2. Temperature Dependence Spontaneous Strain Ratio
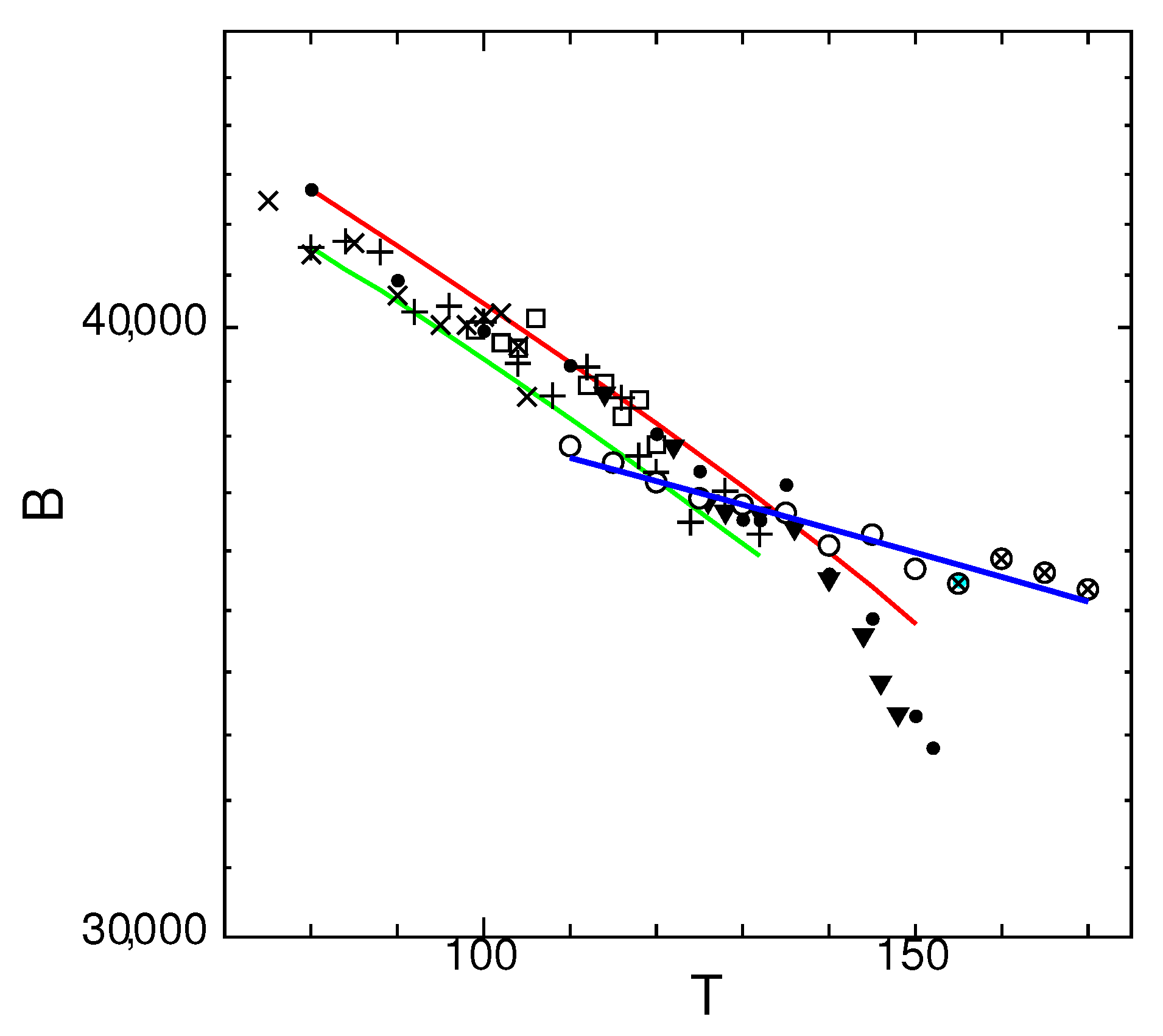
3.3. Temperature Dependence of Spontaneous Bulk Modulus
4. Concluding Remarks
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Computer Simulation Methods
Appendix A.1. Symplectic Integrator for Soft Matter
Appendix A.2. Calculation of Metastable States
Appendix A.3. Model and Initial Configurations
Appendix A.4. Calculation of Transport Coefficient
Appendix A.5. Calculation of Elastic Properties

References
- Shelby, J.E. Introduction to Glass Science and Technology, 2nd ed.; The Royal Society of Chemistry: Cambridge, UK, 2005. [Google Scholar]
- Bernu, B.; Hiwatari, Y.; Hansen, J.P. Soft-sphere model for the glass transition in binary alloys: Pair structure and self-diffusion. J. Phys. C 1985, 18, L371. [Google Scholar] [CrossRef]
- Wahnström, G. Molecular-dynamics study of a supercooled two-component Lennard-Jones system. Phys. Rev. A 1991, 44, 3752. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture I: The van Hove correlation function. Phy. Rev. E 1995, 51, 4626. [Google Scholar] [CrossRef]
- Sollich, P. Predicting phase equilibria in polydisperse systems. J. Phys. Condens. Matter 2002, 14, R79–R117. [Google Scholar] [CrossRef]
- Brazhkin, V.V. Can high pressure experiments shed light on the puzzles of glass transition? The problem of extrapolation. J. Phys. Condens. Matter 2008, 20, 244102. [Google Scholar] [CrossRef]
- Angell, C.A.; Borick, S. Specific heats Cp, Cv, Cconf and energy landscapes of glass forming liquids. J. Non-Cryst. Solids 2002, 307–310, 393–406. [Google Scholar] [CrossRef][Green Version]
- Aoki, K.M.; Fujiwara, S.; Sogo, K.; Ohnishi, S.; Yamamoto, T. One-, Two-, and Three-dimentional Hopping Dynamics. Crystals 2013, 3, 315–332. [Google Scholar] [CrossRef]
- Aoki, K.M.; Fujiwara, S.; Sogo, K.; Ohnishi, S.; Yamamoto, T. Molecular Dynamics Simulations of One-, Two-, Three-dimensional Hopping Dynamics. JPS Conf. Proc. 2014, 1, 012038. [Google Scholar]
- Aoki, K.M.; Yoneya, M. Order Parameter Discretization in Metastable States of Hexatic Smectic B Liquid Crystal. J. Phys. Soc. Jpn. 2011, 80, 124603. [Google Scholar] [CrossRef]
- Aoki, K.M. Network Analysis of Free Energy Landscaper of Metastable States of Hexatic Smectic B Liquid Crystal. J. Phys. Soc. Jpn. 2014, 83, 104603. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determinig the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237. [Google Scholar] [CrossRef]
- Aoki, K.M. Symplectic Integrator Designed for Simulating Soft Matter. J. Phys. Soc. Jpn. 2008, 77, 044003. [Google Scholar] [CrossRef]
- Aoki, K.M. Molecular Dynamics Simulation of Anisotropic Molecules as a Model of Liquid Crystals. Ph.D. Thesis, Keio University, Yokohama, Japan, 1993. [Google Scholar]
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Extended methods of molecular dynamics simulations under hydrostatic pressure and/or isostress. J. Chem. Phys. 2003, 118, 9926. [Google Scholar] [CrossRef]
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Molecular dynamics simulation methods for anisotropic liquids. J. Chem. Phys. 2004, 120, 5576. [Google Scholar] [CrossRef]
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Constant surface-tension molecular-dynamics simulation methods for anisotropic systems. J. Chem. Phys. 2006, 124, 064705. [Google Scholar] [CrossRef]
- Aoki, K.M. Anisotropy in condensed matter - liquid crystals, glass, and phase coexistence. J. Phys. Conf. Ser. 2019, 1252, 012004. [Google Scholar] [CrossRef]
- Abraham, S.; Harrowell, P. The origin of persistent shear stress in supercooled liquids. J. Chem. Phys. 2012, 137, 014506. [Google Scholar] [CrossRef] [PubMed]
- Fuereder, I.; Ig, P.I. Influence of inherent structure shear stress of supercooled liquids on their shear moduli. J. Chem. Phys. 2015, 142, 144505. [Google Scholar] [CrossRef]
- Petry, W.; Bartsch, E.; Fujara, F.; Kiebel, M.; Sillescu, H.; Frago, B. Dynamic anomaly in glass transition region of orthoterphenyl. Z. Phys. B Condens. Matter 1991, 83, 175–184. [Google Scholar] [CrossRef]
- Buchenau, U.; Zorn, R. A Relation between Fast and Slow Motions in Glassy and Liquid Selenium. EuroPhys. Lett. 1992, 18, 523–528. [Google Scholar] [CrossRef]
- Angell, C.A. Formation of Glasses from Liquids and Biopolymers. Science 1995, 267, 1924–1939. [Google Scholar] [CrossRef] [PubMed]
- Magazù, S.; Maisano, G.; Migliardo, F.; Mondelli, C. Mean-Square Displacement Relationship in Bioprotectant Systems by Elastic Neutron Scattering. Biophys. J. 2004, 86, 3241–3249. [Google Scholar] [CrossRef]
- Niss, K.; Dalle-Ferrier, C.; Frick, B.; Russo, D.; Dyre, J.; Alba-Simionesco, C. Connection between slow and fast dynamics of molecular liquids around the glass transition. Phy. Rev. E 2010, 82, 021508. [Google Scholar] [CrossRef]
- Capaccioli, S.; Ngai, K.L.; Ancherbak, S.; Paciaroni, A. Evidence of Coexistence of Change of Caged Dynamics at Tg and the Dynamic Transion at Td in Solvated Proteins. J. Phys. Chem. B 2012, 116, 1745–1757. [Google Scholar] [CrossRef] [PubMed]
- Vural, D.; Glyde, H.R. Intrinsic mean-square displacements in proteins. Phys. Rev. E 2012, 86, 011926. [Google Scholar] [CrossRef]
- Kegel, W.K.; van Blaaderen, A. Direct Observation of Dynamical Heterogeneities in Colloidal Hard-Sphere Suspensions. Science 2000, 287, 290–293. [Google Scholar] [CrossRef]
- Weeks, E.R.; Crocker, J.C.; Levitt, A.C.; Schofield, A.; Weitz, D.A. Three-Dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition. Science 2000, 287, 627–631. [Google Scholar] [CrossRef]
- Weeks, E.R.; Weitz, D.A. Properties of Cage Rearrangements Observed near the Colloidal Glass Transition. Phys. Rev. Lett. 2002, 89, 095704. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, L.J.; Weitz, D.A. Direct imaging of repulsive and attractive colloidal glasses. J. Chem. Phys. 2006, 125, 074716. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, S.; Sood, A.K.; Ganapathy, R. Deconstructing the glass transition through critical experiments on colloids. Adv. Phys. 2016, 65, 363. [Google Scholar] [CrossRef]
- Rouxel, T. Elastic Properties and Short-to Medium-Range Order in Glasses. J. Am. Ceram. Soc. 2007, 90, 3019. [Google Scholar] [CrossRef]
- Novikov, V.N.; Sokolov, A.P. Poisson’s ratio and the fragility of glass-forming liquids. Nature 2004, 431, 961. [Google Scholar] [CrossRef]
- Yannopoulos, S.N.; Johari, G.P. Poisson’s ratio of glass and a liquid’s fragility? Nature 2006, 442, E7–E8. [Google Scholar] [CrossRef] [PubMed]
- Mott, P.H.; Dorgan, J.R.; Roland, C.M. The bulk modulus and Poisson’s Ratio of “incompressible” materials. J. Sound Vib. 2008, 312, 572. [Google Scholar] [CrossRef]
- Anderson, D.L. Theory of Earth; Blackwell Scientific Publications: Boston, MA, USA, 1989; Chapter 5. [Google Scholar]
- Ha, A.; Cohen, I.; Zhao, X.; Lee, M.; Fischer, T.; Strouse, M.J.; Kivelson, D. Supercooled Liquids and Polyamorphism. J. Phys. Chem. 1996, 100, 1–4. [Google Scholar] [CrossRef]
- Cohen, I.; Ha, A.; Zhao, X.; Lee, M.; Fischer, T.; Strouse, M.J.; Kivelson, D. A Low-Temperature Amorphous Phase in a Fragile Glass-Forming Substance. J. Phys. Chem. 1996, 100, 8518–8526. [Google Scholar] [CrossRef]
- Angell, C.A. The amorphous state equivalent of crystallization: New glass types by first order transition from liquids, crystals, and biopolymers. Solid State Sci. 2000, 2, 791–805. [Google Scholar] [CrossRef]
- Kurita, R.; Tanaka, H. On the abundance and general nature of the liquid–liquid phase transition in molecular systems. J. Phys. Condens. Matter 2005, 17, L293–L302. [Google Scholar] [CrossRef]
- Kobayashi, M.; Tanaka, H. The reversibility and first-order nature of liquid–liquid transition in a molecular liquid. Nat. Commun. 2016, 7, 13438. [Google Scholar] [CrossRef] [PubMed]
- Murata, K.; Tanaka, H. Link between molecular mobility and order parameter during liquid–liquid transition of a molecular liquid. Proc. Natl. Acad. Sci. USA 2019, 116, 7176–7185. [Google Scholar] [CrossRef]
- Walton, F.; Bolling, J.; Farrell, A.; MacEwen, J.; Syme, C.D.; Jiménez, M.G.; Senn, H.M.; Wilson, C.; Cinque, G.; Wynne, K. Polyamorphism Mirrors Polymorphism in the Liquid-Liquid Transition of a Molecular Liquid. J. Am. Chem. Soc. 2020, 142, 7591–7597. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H. Liquid-liquid transition and polyamorphism. J. Chem. Phys. 2020, 153, 130901. [Google Scholar] [CrossRef] [PubMed]
- Helfand, E.; Rice, S.A. Principle of Corresponding States for Transport Properties. J. Chem. Phys. 1960, 32, 1642–1644. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Claredon Press: Oxford, UK, 1987; Appendix B. [Google Scholar]
- Hoover, W.G.; Gray, S.G.; Johnson, K.W. Thermodynamic Properties of the Fluid and Solid Phases for Inverse Power Potentials. J. Chem. Phys. 1971, 55, 1128–1136. [Google Scholar] [CrossRef]
- Aoki, K.M.; Yonezawa, F. Scaling properties of soft-core parallel spherocylinder near crystal-smectic-phase transition. Phys. Rev. E 1993, 48, 2025–2027. [Google Scholar] [CrossRef]
- Aoki, K.M.; Yoneya, M.; Yokoyama, H. Entropy and heat capacity calculations of simulated crystal-hexatic smectic-B- smectic-A liquid-crystal phase transitions. Phys. Rev. E 2010, 81, 021701. [Google Scholar] [CrossRef]
- Aoki, K.M. Structural transformation of smectic liquid crystals under surface tension. Mol. Cryst. Liq. Cryst. 2017, 647, 92–99. [Google Scholar] [CrossRef][Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aoki, K.M. Dynamics and Elastic Properties of Glassy Metastable States. Solids 2021, 2, 249-264. https://doi.org/10.3390/solids2020016
Aoki KM. Dynamics and Elastic Properties of Glassy Metastable States. Solids. 2021; 2(2):249-264. https://doi.org/10.3390/solids2020016
Chicago/Turabian StyleAoki, Keiko M. 2021. "Dynamics and Elastic Properties of Glassy Metastable States" Solids 2, no. 2: 249-264. https://doi.org/10.3390/solids2020016
APA StyleAoki, K. M. (2021). Dynamics and Elastic Properties of Glassy Metastable States. Solids, 2(2), 249-264. https://doi.org/10.3390/solids2020016





