Gene Expression Programming (GEP) Modelling of Sustainable Building Materials including Mineral Admixtures for Novel Solutions
Abstract
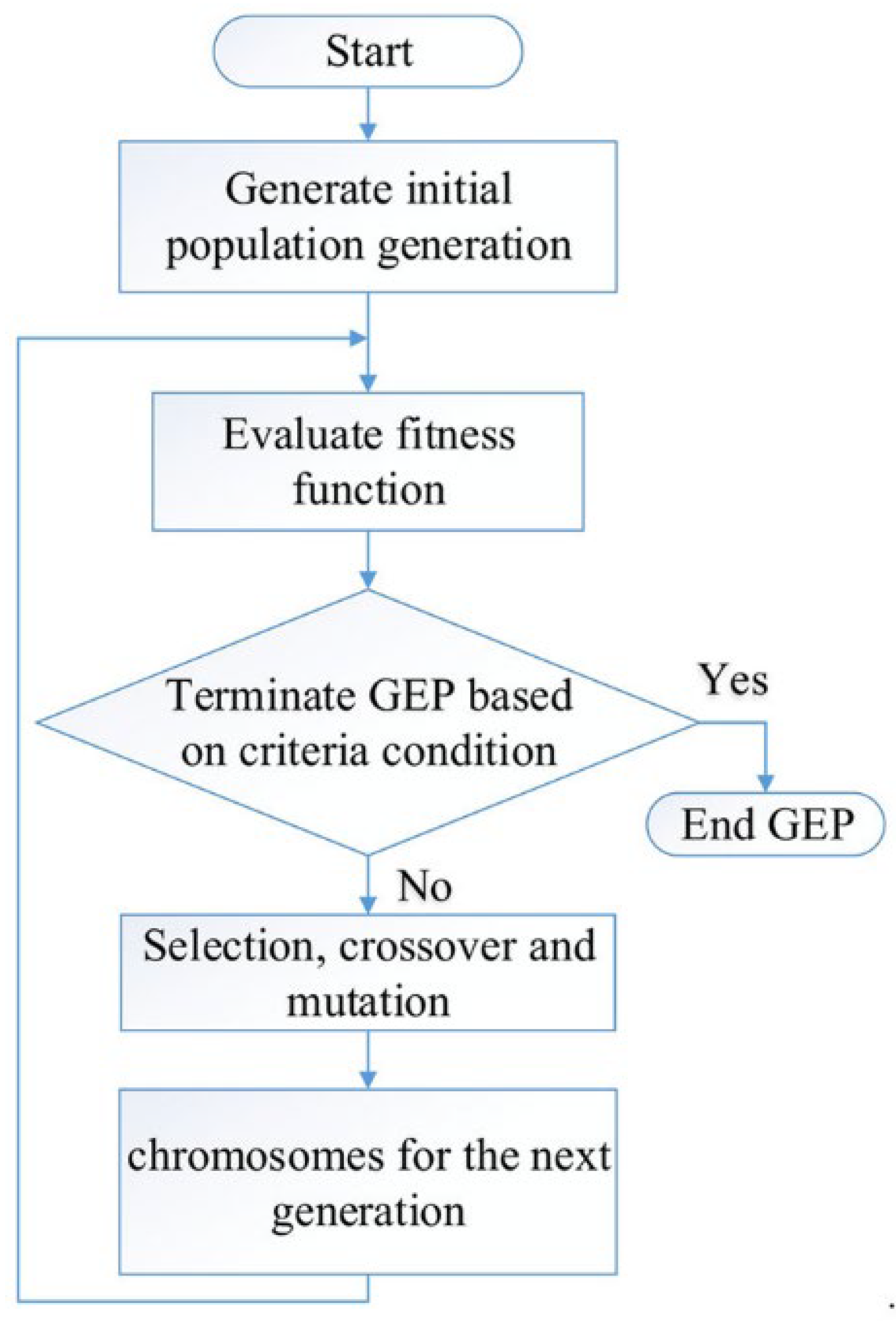
1. Introduction
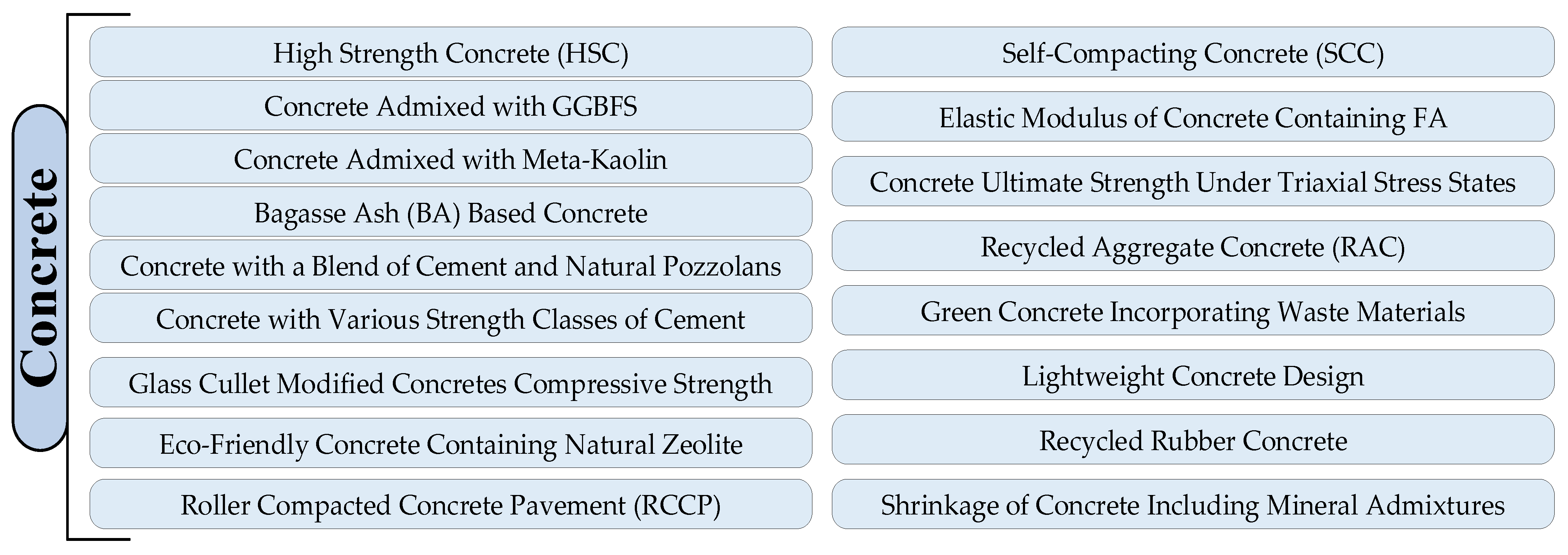
2. Concrete
2.1. High Strength Concrete (HSC)
2.2. Concrete Admixed with GGBFS
2.3. Concrete Admixed with Meta-Kaolin
2.4. Bagasse Ash (BA) Based Concrete
2.5. Concrete with a Blend of Cement, Limestone, Slag, and Natural Pozzolans
2.6. Concrete with Various Strength Classes of Cement
2.7. Glass Cullet Modified Concretes Compressive Strength
2.8. Eco-Friendly Concrete Containing Natural Zeolite Compressive Strength and Electrical Resistivity
2.9. Compressive Strength of “Roller Compacted Concrete Pavement” (RCCP)
2.10. Self-Compacting Concrete (SCC)
2.11. Elastic Modulus of Concrete Containing FA
2.12. Concrete Ultimate Strength under Triaxial Stress States
2.13. Recycled Aggregate Concrete (RAC) Compressive Strength
2.14. Green Concrete Incorporating Waste Materials
2.15. Lightweight Concrete Design
2.16. Recycled Rubber Concrete
2.17. Shrinkage of Concrete including Mineral Admixtures
3. Soil
3.1. CBR Value of Fine-Grained Soils
3.2. Compression Index of Fine-Grained Soils
3.3. Collapsibility Potential of Soils
3.4. Ice-Seabed Interaction Analysis in Sand
3.5. Sand-Waste Tire Mixtures
4. Mortar
4.1. Effect of “Nano Silica” (NS) and “Micro Silica” (MS) on Mortar Cement
4.2. Impact of Porosity on Both Flexural and Compressive Strengths of Cement Mortar Having Micro and Nano Silica
4.3. Compressive Strength of Ferrosialate Based Geopolymer Mortars
4.4. Compressive Strength of Lightweight Geopolymer Mortars
5. Asphalt (Pavement)
5.1. Viscosity Mixing Rule for Asphalt Blends
5.2. Dynamic Modulus of Asphalt
5.3. Fracture Energy of Asphalt Mixtures
5.4. Rutting Depth of Asphalt Mixtures
5.5. Effects of Aggregate Angularity on Asphalt Mixture Permanent Deformation
5.6. Unconfined Compressive Behavior of Hot Mix Asphalt (HMA)
5.7. The Service Life of Flexible Pavement (RSL)
6. Tailings
6.1. Mineral Tailings
6.2. Filling Slurry in Cemented Tailings Backfill
7. Concluding Remarks on the GEP Modeling
- Like many other numerical approaches, GEP would involve advantages and shortcomings. The most significant distinction in GEP modeling is flexibility, which can be readily adopted, and evolutions can be initiated, incorporating user-selected or user-defined functions, constant ranges, and fitness functions. The outcome of the evolutions would lead to closed-form explicit formulations. If the input parameters can be evaluated through simple laboratory or rapid measurements, and a comprehensive experimental database was available, the models can be constructed.
- Compared to the ANN based formulations, which are often too complex to be used, GEP-based derived models provide estimation equations that are reasonably simple and can be used for practical design purposes, and can even be used for hand calculations. Many popular models, such as best-fitted curves based on regression analyses, MLR, MNLR, and MNVR, can be used for construction materials properties modeling. However, due to the nonlinearity and complexity of the target properties, the models developed using regression analysis may not reveal their precise nature. Besides, regression models may not considerably measure the additive component’s effect on construction materials properties, such as concrete compressive strength. The lack of generality in regression models comes from the fact that some functions are defined for regression in classical regression techniques; while in the GEP approach, there is no predefined function to be considered, and it reproduces or omits various combinations of parameters to provide the formulation that fits the experimental outcomes.
- Flexibility in choosing the complexity and fitness functions, such as RMSE and MSE, might lead to better performance of the approach and well-capturing the governing pattern behind the material’s characteristics. Thus, GEP can be accepted to be superior to conventional and classical regression techniques and ANN. Another merit of the GEP is the automatic feature selection in the evolution process. Input variables inter-correlated to other contributing parameters, or having minor contributions to the target, would be put aside and omitted automatically in the model evolution iterations. Different combinations of the input variables can be considered for GEP modeling with no specific pre-processing, which is not the case in ANN.
- The results of GEP based models may sometimes show lower accuracies when compared to artificial neural networks and support vector machines. In some cases, the lower precision might be attributed to the limited number of considered genes, chromosomes, and heads, which are the predefined characteristics in the GEP model development process. However, the explicit mathematical expressions, which can be easily implemented in the design and analysis process, may cover the minor inaccuracies compared to ANN and SVM approaches. Based on the presented review, it would sometimes be better to provide more than one GEP model and consider different combinations of input contributing variables to afford the possible initial feed for a more settled and comprehensive model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steinfeld, B.; Scott, J.; Vilander, G.; Marx, L.; Quirk, M.; Lindberg, J.; Koerner, K. The Role of Lean Process Improvement in Implementation of Evidence-Based Practices in Behavioral Health Care. J. Behav. Heal. Serv. Res. 2015, 42, 504–518. [Google Scholar] [CrossRef] [PubMed]
- Alaneme, G.U.; Onyelowe, K.C.; Onyia, M.E.; Bui Van, D.; Mbadike, E.M.; Ezugwu, C.N.; Dimonyeka, M.U.; Attah, I.C.; Ogbonna, C.; Abel, C. Modeling Volume Change Properties of Hydrated-Lime Activated Rice Husk Ash (HARHA) Modified Soft Soil for Construction Purposes by Artificial Neural Network (ANN). Umudike J. Eng. Technol. 2020, 6, 88–110. [Google Scholar]
- Onyelowe, K.C.; Iqbal, M.; Jalal, F.E.; Onyia, M.E.; Onuoha, I.C. Application of 3-Algorithm ANN Programming to Predict the Strength Performance of Hydrated-Lime Activated Rice Husk Ash Treated Soil. Multiscale Multidiscip. Model. Exp. Des. 2021, 4, 259–274. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Gnananandarao, T.; Nwa-David, C. Sensitivity Analysis and Prediction of Erodibility of Treated Unsaturated Soil Modified with Nanostructured Fines of Quarry Dust Using Novel Artificial Neural Network. Nanotechnol. Environ. Eng. 2021, 6, 37. [Google Scholar] [CrossRef]
- El-Bosraty, A.H.; Ebid, A.M.; Fayed, A.L. Estimation of the Undrained Shear Strength of East Port-Said Clay Using the Genetic Programming. Ain Shams Eng. J. 2020, 11, 961–969. [Google Scholar] [CrossRef]
- Kayadelen, C.; Taşkıran, T.; Günaydın, O.; Fener, M. Adaptive Neuro-Fuzzy Modeling for the Swelling Potential of Compacted Soils. Environ. Earth Sci. 2009, 59, 109. [Google Scholar] [CrossRef]
- Goharzay, M.; Noorzad, A.; Ahmadreza Mahboubi, A.; Mostafa, J. A Worldwide SPT-Based Soil Liquefaction Triggering Analysis Utilizing Gene Expression Programming and Bayesian Probabilistic Method. J. Rock Mech. Geotech. Eng. 2017, 9, 683–693. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Narayanasamy, M.S.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43. [Google Scholar] [CrossRef]
- Mohammadzadeh, D.; Kazemi, S.-F.; Mosavi, A.; Nasseralshariati, E.; Tah, J.H.M. Prediction of Compression Index of Fine-Grained Soils Using a Gene Expression Programming Model. Infrastructures 2019, 4, 26. [Google Scholar] [CrossRef]
- Johari, A.; Javadi, A.A.; Najafi, H. A Genetic-Based Model to Predict Maximum Lateral Displacement of Retaining Wall in Granular Soil. Sci. Iran. 2016, 23, 54–65. [Google Scholar] [CrossRef]
- Johari, A.; Hooshmand Nejad, A. Prediction of Soil-Water Characteristic Curve Using Gene Expression Programming. Iran. J. Sci. Technol. Trans. Civ. Eng. 2015, 39, 143. [Google Scholar]
- Uysal, F. Prediction of Collapse Potential of Soils Using Gene Expression Programming and Parametric Study. Arab. J. Geosci. 2020, 13, 1038. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hajihassani, M.; Yagiz, S.; Motaghedi, H. Application of Several Non-Linear Prediction Tools for Estimating Uniaxial Compressive Strength of Granitic Rocks and Comparison of Their Performances. Eng. Comput. 2016, 32, 189–206. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; Volume 21. [Google Scholar]
- Ferreira, C. Gene Expression Programming and the Evolution of Computer Programs. In Recent Developments in Biologically Inspired Computing; Nunes de Castro, L., Von Zuben, F., Eds.; IGI Global: Hershey, PA, USA, 2005; pp. 82–103. [Google Scholar] [CrossRef][Green Version]
- Ferreira, C. Gene Expression Programming in Problem Solving. In Soft Computing and Industry; Roy, R., Köppen, M., Ovaska, S., Furuhashi, T., Hoffmann, F., Eds.; Springer: London, UK, 2002; pp. 635–653. [Google Scholar] [CrossRef]
- Abdollahzadeh, G.R.; Jahani, E.; Kashir, Z. Genetic Programming Based Formulation to Predict Compressive Strength of High Strength Concrete. Civ. Eng. Infrastruct. J. 2017, 50, 207–219. [Google Scholar] [CrossRef]
- Castelli, M.; Vanneschi, L.; Silva, S. Prediction of High Performance Concrete Strength Using Genetic Programming with Geometric Semantic Genetic Operators. Expert Syst. Appl. 2013, 40, 6856–6862. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tsai, C.-F. Concrete Compressive Strength Analysis Using a Combined Classification and Regression Technique. Autom. Constr. 2012, 24, 52–60. [Google Scholar] [CrossRef]
- Yildiz, E. Lateral Pressures on Rigid Retaining Walls: A Neural Network Approach. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2003. [Google Scholar]
- Sarıdemir, M. Effect of Specimen Size and Shape on Compressive Strength of Concrete Containing Fly Ash: Application of Genetic Programming for Design. Mater. Des. 2014, 56, 297–304. [Google Scholar] [CrossRef]
- Farooq, M.A.; Sato, Y.; Niitani, K. Experimental investigation of monotonic behavior and stress-strain models of AE and non-AE high strength concrete with BFS fine aggregates under freezing and thawing. Constr. Build. Mater. 2020, 249, 118679. [Google Scholar] [CrossRef]
- Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Faisal Javed, M.F.; Aslam, F.; Alyousef, R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Soleymani, A.; Esfahani, M.R. Effect of Concrete Strength and Thickness of Flat Slab on Preventing of Progressive Collapse Caused by Elimination of an Internal Column. J. Struct. Constr. Eng. 2019, 6, 24–40. [Google Scholar] [CrossRef]
- Bagheri, M.; Chahkandi, A.; Jahangir, H. Seismic Reliability Analysis of RC Frames Rehabilitated by Glass Fiber-Reinforced Polymers. Int. J. Civ. Eng. 2019, 17, 1785–1797. [Google Scholar] [CrossRef]
- Wang, X.-Y. Effect of Carbon Pricing on Optimal Mix Design of Sustainable High-Strength Concrete. Sustainability 2019, 11, 5827. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Investigating Loading Rate and Fibre Densities Influence on SRG-Concrete Bond Behaviour. Steel Compos. Struct. An. Int. J. 2020, 34, 877–889. [Google Scholar]
- Jahangir, H.; Rezazadeh Eidgahee, D. A New and Robust Hybrid Artificial Bee Colony Algorithm—ANN Model for FRP-Concrete Bond Strength Evaluation. Compos. Struct. 2021, 257, 113160. [Google Scholar] [CrossRef]
- Jahangir, H.; Esfahani, M.R. Experimental Analysis on Tensile Strengthening Properties of Steel and Glass Fiber Reinforced Inorganic Matrix Composites. Sci. Iran. 2020, 28, 1152–1166. [Google Scholar] [CrossRef]
- Akin, O.O.; Ocholi, A.; Abejide, O.S.; Obari, J.A. Prediction of the Compressive Strength of Concrete Admixed with Metakaolin Using Gene Expression Programming. Adv. Civ. Eng. 2020, 2020, 8883412. [Google Scholar] [CrossRef]
- Akin, O.O.; Abejide, O.S. Modelling of Concrete Compressive Strength Admixed with GGBFS Using Gene Expression Programming. J. Soft Comput. Civ. Eng. 2019, 3, 43–53. [Google Scholar] [CrossRef]
- Bilim, C.; Atiş, C.D.; Tanyildizi, H.; Karahan, O. Predicting the Compressive Strength of Ground Granulated Blast Furnace Slag Concrete Using Artificial Neural Network. Adv. Eng. Softw. 2009, 40, 334–340. [Google Scholar] [CrossRef]
- Chidiac, S.E.; Panesar, D.K. Evolution of Mechanical Properties of Concrete Containing Ground Granulated Blast Furnace Slag and Effects on the Scaling Resistance Test at 28 days. Cem. Concr. Compos. 2008, 30, 63–71. [Google Scholar] [CrossRef]
- Angulo-Ramírez, D.E.; Mejía de Gutiérrez, R.; Puertas, F. Alkali-activated Portland blast-furnace slag cement: Mechanical properties and hydration. Constr. Build. Mater. 2017, 140, 119–128. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Akbarzadeh Bengar, H.; Ghanbari, S. Compressive Strength Prediction of Eco-Efficient GGBS-Based Geopolymer Concrete Using GEP Method. J. Build. Eng. 2020, 31, 101326. [Google Scholar] [CrossRef]
- Kristóf, J.; Frost, R.; Kloprogge, J.; Horváth, E.; Makó, É. Detection of Four Different OH-Groups in Ground Kaolinite with Controlled-Rate Thermal Analysis. J. Therm. Anal. Calorim. 2002, 69, 77–83. [Google Scholar] [CrossRef]
- Badogiannis, E.; Kakali, G.; Tsivilis, S. Metakaolin as Supplementary Cementitious Material. J. Therm. Anal. Calorim. 2005, 81, 457–462. [Google Scholar] [CrossRef]
- Phonphuak, N.; Chindaprasirt, P. Types of Waste, Properties, and Durability of Pore-Forming Waste-Based Fired Masonry Bricks. In Eco-Efficient Masonry Bricks and Blocks; Elsevier: Amsterdam, The Netherlands, 2015; pp. 103–127. [Google Scholar] [CrossRef]
- Faria, K.C.P.; Gurgel, R.F.; Holanda, J.N.F. Characterization of Sugarcane Bagasse Ash for Use in Ceramic Bodies. Mater. Sci. Forum 2010, 660–661, 1049–1052. [Google Scholar] [CrossRef]
- Javed, M.F.; Amin, M.N.; Shah, M.I.; Khan, K.; Iftikhar, B.; Farooq, F.; Aslam, F.; Alyousef, R.; Alabduljabbar, H. Applications of Gene Expression Programming and Regression Techniques for Estimating Compressive Strength of Bagasse Ash Based Concrete. Crystals 2020, 10, 737. [Google Scholar] [CrossRef]
- Shah, M.I.; Javed, M.F.; Aslam, F.; Alabduljabbar, H. Machine learning modeling integrating experimental analysis for predicting the properties of sugarcane bagasse ash concrete. Constr. Build. Mater. 2022, 314, 125634. [Google Scholar] [CrossRef]
- Wang, X.-Y. Optimal Design of the Cement, Fly Ash, and Slag Mixture in Ternary Blended Concrete Based on Gene Expression Programming and the Genetic Algorithm. Materials 2019, 12, 2448. [Google Scholar] [CrossRef]
- Wang, X.Y. Evaluation Compressive Strength of Cement-Limestone-Slag Ternary Blended Concrete Using Artificial Neural Networks (ANN) and Gene Expression Programming (GEP). Key Eng. Mater. 2020, 837, 119–124. [Google Scholar] [CrossRef]
- Wang, X.-Y. Prediction of Flexural Strength of Natural Pozzolana and Limestone Blended Concrete Using Machine Learning Based Models. IOP Conf. Ser. Mater. Sci. Eng. 2020, 784, 012005. [Google Scholar] [CrossRef]
- Mermerdaş, K.; İpek, S.; Bozgeyik, M.B. Experimental Evaluation and Modeling of the Compressive Strength of Concretes with Various Strength Classes of Cements. Cumhur. Sci. J. 2020, 41, 482–492. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Mirzahosseini, M.R.; Nejad, F.M. Nonlinear Genetic-Based Models for Prediction of Flow Number of Asphalt Mixtures. J. Mater. Civ. Eng. 2011, 23, 248–263. [Google Scholar] [CrossRef]
- Mirzahosseini, M.; Jiao, P.; Barri, K.; Riding, K.A.; Alavi, A.H. New Machine Learning Prediction Models for Compressive Strength of Concrete Modified with Glass Cullet. Eng. Comput. 2019, 36, 876–898. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Akbarzadeh Bengar, H.; Jahani, E. Predicting Compressive Strength and Electrical Resistivity of Eco-Friendly Concrete Containing Natural Zeolite via GEP Algorithm. Constr. Build. Mater. 2019, 229, 116883. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Akbarzadeh Bengar, H.; AzariJafari, H. Life Cycle Assessment of Eco-Friendly Concrete Mixtures Incorporating Natural Zeolite in Sulfate-Aggressive Environment. Constr. Build. Mater. 2020, 268, 121136. [Google Scholar] [CrossRef]
- Banthia, N.; Pigeon, M.; Marchand, J.; Boisvert, J. Permeability of Roller Compacted Concrete. J. Mater. Civ. Eng. 1992, 4, 27–40. [Google Scholar] [CrossRef]
- Lam, M.N.-T.; Jaritngam, S.; Le, D.-H. Roller-Compacted Concrete Pavement Made of Electric Arc Furnace Slag Aggregate: Mix Design and Mechanical Properties. Constr. Build. Mater. 2017, 154, 482–495. [Google Scholar] [CrossRef]
- Duran Atiş, C. Strength Properties of High-Volume Fly Ash Roller Compacted and Workable Concrete, and Influence of Curing Condition. Cem. Concr. Res. 2005, 35, 1112–1121. [Google Scholar] [CrossRef]
- Ashrafian, A.; Gandomi, A.H.; Rezaie-Balf, M.; Emadi, M. An Evolutionary Approach to Formulate the Compressive Strength of Roller Compacted Concrete Pavement. Measurement 2020, 152, 107309. [Google Scholar] [CrossRef]
- Castel, A.; Foster, S.J. Bond Strength between Blended Slag and Class F Fly Ash Geopolymer Concrete with Steel Reinforcement. Cem. Concr. Res. 2015, 72, 48–53. [Google Scholar] [CrossRef]
- Nagalia, G.; Park, Y.; Abolmaali, A.; Aswath, P. Compressive Strength and Microstructural Properties of Fly Ash–Based Geopolymer Concrete. J. Mater. Civ. Eng. 2016, 28, 04016144. [Google Scholar] [CrossRef]
- AzariJafari, H.; Taheri Amiri, M.J.; Ashrafian, A.; Rasekh, H.; Barforooshi, M.J.; Berenjian, J. Ternary Blended Cement: An Eco-Friendly Alternative to Improve Resistivity of High-Performance Self-Consolidating Concrete against Elevated Temperature. J. Clean. Prod. 2019, 223, 575–586. [Google Scholar] [CrossRef]
- Adesina, A.; Awoyera, P. Overview of Trends in the Application of Waste Materials in Self-Compacting Concrete Production. SN Appl. Sci. 2019, 1, 962. [Google Scholar] [CrossRef]
- Nazari, A.; Pacheco Torgal, F. Modeling the Compressive Strength of Geopolymeric Binders by Gene Expression Programming-GEP. Expert System. Apple 2013, 40, 5427–5438. [Google Scholar] [CrossRef]
- Majeed, S.S.; Haido, J.H.; Atrushi, D.S.; Al-Kamaki, Y.; Dinkha, Y.Z.; Saadullah, S.T.; Tayeh, B.A. Properties of self-compacted concrete incorporating basalt fibers: Experimental study and Gene Expression Programming (GEP) analysis. Comput. Concr. 2021, 28, 451–463. [Google Scholar] [CrossRef]
- Barbuta, M.; Diaconescu, R.-M.; Harja, M. Using Neural Networks for Prediction of Properties of Polymer Concrete with Fly Ash. J. Mater. Civ. Eng. 2012, 24, 523–528. [Google Scholar] [CrossRef]
- Chu, H.H.; Khan, M.A.; Javed, M.; Zafar, A.; Khan, M.I.; Alabduljabbar, H.; Qayyum, S. Sustainable use of fly-ash: Use of gene-expression programming (GEP) and multi-expression programming (MEP) for forecasting the compressive strength geopolymer concrete. Ain Shams Eng. J. 2021, 12, 3603–3617. [Google Scholar] [CrossRef]
- Khan, M.A.; Zafar, A.; Akbar, A.; Javed, M.F.; Mosavi, A. Application of Gene Expression Programming (GEP) for the Prediction of Compressive Strength of Geopolymer Concrete. Materials 2021, 14, 1106. [Google Scholar] [CrossRef]
- Yadollahi, M.M.; Benli, A.; Demirboğa, R. Prediction of Compressive Strength of Geopolymer Composites Using an Artificial Neural Network. Mater. Res. Innov. 2015, 19, 453–458. [Google Scholar] [CrossRef]
- Awoyera, P.O.; Kirgiz, M.S.; Viloria, A.; Ovallos-Gazabon, D. Estimating Strength Properties of Geopolymer Self-Compacting Concrete Using Machine Learning Techniques. J. Mater. Res. Technol. 2020, 9, 9016–9028. [Google Scholar] [CrossRef]
- Özgür Deneme, İ. Modelling of Compressive Strength of Self-Compacting Concrete Containing Fly Ash by Gene Expression Programming. Rev. La Construcción 2020, 19, 346–358. [Google Scholar] [CrossRef]
- Sarıdemir, M.; Billir, T. Modeling of Elastic Modulus of Concrete Containing Fly Ash by Gene Expression Programming. In Proceedings of the Fourth International Conference on Sustainable Construction Materials and Technologies, Las Vegas, NV, USA, 7–11 August 2016. [Google Scholar]
- Gandomi, A.H.; Babanajad, S.K.; Alavi, A.H.; Farnam, Y. Novel Approach to Strength Modeling of Concrete under Triaxial Compression. J. Mater. Civ. Eng. 2012, 24, 1132–1143. [Google Scholar] [CrossRef]
- Babanajad, S.K.; Gandomi, A.H.; Mohammadzadeh, S.D.; Alavi, A.H. Numerical Modeling of Concrete Strength under Multiaxial Confinement Pressures Using Linear Genetic Programming. Autom. Constr. 2013, 36, 136–144. [Google Scholar] [CrossRef]
- Hampel, T.; Speck, K.; Scheerer, S.; Ritter, R.; Curbach, M. High-Performance Concrete under Biaxial and Triaxial Loads. J. Eng. Mech. 2009, 135, 1274–1280. [Google Scholar] [CrossRef]
- Babanajad, S.K.; Gandomi, A.H.; Alavi, A.H. New Prediction Models for Concrete Ultimate Strength under True-Triaxial Stress States: An Evolutionary Approach. Adv. Eng. Softw. 2017, 110, 55–68. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Shahmansouri, A.A.; Fakoor, M. Post-Fire Compressive Strength of Recycled PET Aggregate Concrete Reinforced with Steel Fibers: Optimization and Prediction via RSM and GEP. Constr. Build. Mater. 2020, 252, 119057. [Google Scholar] [CrossRef]
- Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.-N.; Moayedi, H. A Novel Artificial Intelligence Technique to Predict Compressive Strength of Recycled Aggregate Concrete Using ICA-XGBoost Model. Eng. Comput. 2020, 37, 3329–3346. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Soomro, M.; Evangelista, A.C.J. A Review of Recycled Aggregate in Concrete Applications (2000–2017). Constr. Build. Mater. 2018, 172, 272–292. [Google Scholar] [CrossRef]
- González-Taboada, I.; González-Fonteboa, B.; Martínez-Abella, F.; Pérez-Ordóñez, J.L. Prediction of the Mechanical Properties of Structural Recycled Concrete Using Multivariable Regression and Genetic Programming. Constr. Build. Mater. 2016, 106, 480–499. [Google Scholar] [CrossRef]
- Abdollahzadeh, G.; Jahani, E.; Kashir, Z. Predicting of Compressive Strength of Recycled Aggregate Concrete by Genetic Programming. Comput. Concr. 2016, 18, 155–163. [Google Scholar] [CrossRef]
- Gholampour, A.; Gandomi, A.H.; Ozbakkaloglu, T. New Formulations for Mechanical Properties of Recycled Aggregate Concrete Using Gene Expression Programming. Constr. Build. Mater. 2017, 130, 122–145. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Liu, Q.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of Mechanical Properties of Green Concrete Incorporating Waste Foundry Sand Based on Gene Expression Programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
- Murad, Y.; Imam, R.; Abu Hajar, H.; Habeh, D.; Hammad, A.; Shawash, Z. Predictive Compressive Strength Models for Green Concrete. Int. J. Struct. Integr. 2019, 11, 169–184. [Google Scholar] [CrossRef]
- Jafari, S.; Mahini, S.S. Lightweight Concrete Design Using Gene Expression Programing. Constr. Build. Mater. 2017, 139, 93–100. [Google Scholar] [CrossRef]
- Jalal, M.; Grasley, Z.; Gurganus, C.; Bullard, J.W. Experimental Investigation and Comparative Machine-Learning Prediction of Strength Behavior of Optimized Recycled Rubber Concrete. Constr. Build. Mater. 2020, 256, 119478. [Google Scholar] [CrossRef]
- Mermerdaş, K.; Arbili, M.M.; Ghaffoori, F.K. Statistical Analysis of the Performance of the Soft Computing Based Prediction Model for Shrinkage of Concrete Including Mineral Admixtures. In Proceedings of the 1st International Conference on Engineering and Innovative Technology, SU-ICEIT 2016, Kurdistan, Iraq, 12–14 April 2016. [Google Scholar]
- Alam, S.K.; Mondal, A.; Shiuly, A. Prediction of CBR Value of Fine Grained Soils of Bengal Basin by Genetic Expression Programming, Artificial Neural Network and Krigging Method. J. Geol. Soc. India 2020, 95, 190–196. [Google Scholar] [CrossRef]
- Taskiran, T. Prediction of California Bearing Ratio (CBR) of Fine Grained Soils by AI Methods. Adv. Eng. Softw. 2010, 41, 886–892. [Google Scholar] [CrossRef]
- Tenpe, A.R.; Patel, A. Utilization of Support Vector Models and Gene Expression Programming for Soil Strength Modeling. Arab. J. Sci. Eng. 2020, 45, 4301–4319. [Google Scholar] [CrossRef]
- Tenpe, A.R.; Patel, A. Application of Genetic Expression Programming and Artificial Neural Network for Prediction of CBR. Road Mater. Pavement Des. 2020, 21, 1183–1200. [Google Scholar] [CrossRef]
- Mitch, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Azimi, H.; Shiri, H. Ice-Seabed Interaction Analysis in Sand Using a Gene Expression Programming-Based Approach. Appl. Ocean. Res. 2020, 98, 102120. [Google Scholar] [CrossRef]
- Edil, T.B.; Bosscher, P.J. Engineering Properties of Tire Chips and Soil Mixtures. Geotech. Test. J. 1994, 17, 453–464. [Google Scholar]
- Humphrey, D.N. Effectiveness of Design Guidelines for Use of Tire Derived Aggregate as Lightweight Embankment Fill. In Recycled Materials in Geotechnics, Proceedings of the ASCE Civil Engineering Conference and Exposition, Baltimore, MD, USA, 19–21 October 2004; American Society of Civil Engineers: Reston, VA, USA, 2004; pp. 61–74. [Google Scholar]
- Tanchaisawat, T.; Bergado, D.T.; Voottipruex, P.; Shehzad, K. Interaction between Geogrid Reinforcement and Tire Chip–Sand Lightweight Backfill. Geotext. Geomembr. 2010, 28, 119–127. [Google Scholar] [CrossRef]
- Rezazadeh Eidgahee, D.; Haddad, A.; Naderpour, H. Evaluation of Shear Strength Parameters of Granulated Waste Rubber Using Artificial Neural Networks and Group Method of Data Handling. Sci. Iran. 2019, 26, 3233–3244. [Google Scholar] [CrossRef]
- Haddad, A.; Eidgahee, D.R. An Investigation on the Shear Strength Parameters of Sand-Rubber Mixtures Under the Applied Stress Paths. In Fundamentals of Soil Behaviours, Proceedings of the 4th Geo Shanghai 2018 International Conference, Shanghai, China, 27–30 May 2018; Springer: Singapore, 2018; pp. 148–156. [Google Scholar]
- Pamukcu, S.; Akbulut, S. Thermoelastic Enhancement of Damping of Sand Using Synthetic Ground Rubber. J. Geotech. Geoenviron. Eng. 2006, 132, 501–510. [Google Scholar] [CrossRef]
- Edincliler, A.; Cabalar, A.F.; Cevik, A.; Isik, H. New Formulations for Dynamic Behavior of Sand-Waste Tire Mixtures in a Small Range of Strain Amplitudes. Period. Polytech. Civ. Eng. 2017, 62, 92–101. [Google Scholar] [CrossRef]
- Rafiai, H.; Moosavi, M. An Approximate ANN-Based Solution for Convergence of Lined Circular Tunnels in Elasto-Plastic Rock Masses with Anisotropic Stresses. Tunn. Undergr. Sp. Technol. 2012, 27, 52–59. [Google Scholar] [CrossRef]
- Li, L.G.; Zhu, J.; Huang, Z.H.; Kwan, A.K.H.; Li, L.J. Combined Effects of Micro-Silica and Nano-Silica on Durability of Mortar. Constr. Build. Mater. 2017, 157, 337–347. [Google Scholar] [CrossRef]
- Tanyildizi, H.; Çevik, A. Modeling Mechanical Performance of Lightweight Concrete Containing Silica Fume Exposed to High Temperature Using Genetic Programming. Constr. Build. Mater. 2010, 24, 2612–2618. [Google Scholar] [CrossRef]
- Azimi-Pour, M.; Eskandari-Naddaf, H. ANN and GEP Prediction for Simultaneous Effect of Nano and Micro Silica on the Compressive and Flexural Strength of Cement Mortar. Constr. Build. Mater. 2018, 189, 978–992. [Google Scholar] [CrossRef]
- Emamian, S.A.; Eskandari-Naddaf, H. Effect of Porosity on Predicting Compressive and Flexural Strength of Cement Mortar Containing Micro and Nano-Silica by ANN and GEP. Constr. Build. Mater. 2019, 218, 8–27. [Google Scholar] [CrossRef]
- Emamian, S.A.; Eskandari-Naddaf, H. Genetic Programming Based Formulation for Compressive and Flexural Strength of Cement Mortar Containing Nano and Micro Silica after Freeze and Thaw Cycles. Constr. Build. Mater. 2020, 241, 118027. [Google Scholar] [CrossRef]
- Mahdinia, S.; Eskandari-Naddaf, H.; Shadnia, R. Effect of Cement Strength Class on the Prediction of Compressive Strength of Cement Mortar Using GEP Method. Constr. Build. Mater. 2019, 198, 27–41. [Google Scholar] [CrossRef]
- Yeddula, B.S.R.; Karthiyaini, S. Experimental investigations and GEP modelling of compressive strength of ferrosialate based geopolymer mortars. Constr. Build. Mater. 2020, 236, 117602. [Google Scholar] [CrossRef]
- Mermerdaş, K.; Oleiwi, S.M.; Abid, S.R. Modeling Compressive Strength of Lightweight Geopolymer Mortars by Step-Wise Regression and Gene Expression Programming. Hittite J. Sci. Eng. 2019, 6, 157–166. [Google Scholar] [CrossRef]
- Mehrotra, A.K. Modeling the Effects of Temperature, Pressure, and Composition on the Viscosity of Crude Oil Mixtures. Ind. Eng. Chem. Res. 1990, 29, 1574–1578. [Google Scholar] [CrossRef]
- Baghban, A.; Abbasi, P.; Rostami, P. Modeling of Viscosity for Mixtures of Athabasca Bitumen and Heavy N-Alkane with LSSVM Algorithm. Pet. Sci. Technol. 2016, 34, 1698–1704. [Google Scholar] [CrossRef]
- Barati-Harooni, A.; Najafi-Marghmaleki, A. Implementing a PSO-ANFIS Model for Prediction of Viscosity of Mixed Oils. Pet. Sci. Technol. 2017, 35, 155–162. [Google Scholar] [CrossRef]
- Marini, F.; Magrì, A.L.; Bucci, R.; Magrì, A.D. Use of Different Artificial Neural Networks to Resolve Binary Blends of Monocultivar Italian Olive Oils. Anal. Chim. Acta 2007, 599, 232–240. [Google Scholar] [CrossRef]
- Eleyedath, A.; Swamy, A.K. Prediction of Dynamic Modulus of Asphalt Concrete Using Hybrid Machine Learning Technique. Int. J. Pavement Eng. 2022, 23, 2083–2098. [Google Scholar] [CrossRef]
- Witczak, M.W.; Fonseca, O.A. Revised Predictive Model for Dynamic (Complex) Modulus of Asphalt Mixtures. Transp. Res. Rec. J. Transp. Res. Board 1996, 1540, 15–23. [Google Scholar] [CrossRef]
- Esfandiarpour, S.; Shalaby, A. Local Calibration of Creep Compliance Models of Asphalt Concrete. Constr. Build. Mater. 2017, 132, 313–322. [Google Scholar] [CrossRef]
- Ceylan, H.; Schwartz, C.W.; Kim, S.; Gopalakrishnan, K. Accuracy of Predictive Models for Dynamic Modulus of Hot-Mix Asphalt. J. Mater. Civ. Eng. 2009, 21, 286–293. [Google Scholar] [CrossRef]
- Far, M.S.S.; Underwood, B.S.; Ranjithan, S.R.; Kim, Y.R.; Jackson, N. Application of Artificial Neural Networks for Estimating Dynamic Modulus of Asphalt Concrete. Transp. Res. Rec. J. Transp. Res. Board 2009, 2127, 173–186. [Google Scholar] [CrossRef]
- Daneshvar, D.; Behnood, A. Estimation of the Dynamic Modulus of Asphalt Concretes Using Random Forests Algorithm. Int. J. Pavement Eng. 2022, 23, 250–260. [Google Scholar] [CrossRef]
- Majidifard, H.; Jahangiri, B.; Buttlar, W.G.; Alavi, A.H. New Machine Learning-Based Prediction Models for Fracture Energy of Asphalt Mixtures. Measurement 2019, 135, 438–451. [Google Scholar] [CrossRef]
- Majidifard, H.; Jahangiri, B.; Rath, P.; Urra Contreras, L.; Buttlar, W.G.; Alavi, A.H. Developing a Prediction Model for Rutting Depth of Asphalt Mixtures Using Gene Expression Programming. Constr. Build. Mater. 2020, 267, 120543. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Kim, S.; Ceylan, H.; Khaitan, S.K. Natural Selection of Asphalt Mix Stiffness Predictive Models with Genetic Programming. In Proceedings of the ANNIE 2010, Artificial Neural Networks in Engineering, St. Louis, MO, USA, 1–3 November 2010. [Google Scholar]
- Liu, J.; Yan, K.; You, L.; Liu, P.; Yan, K. Prediction Models of Mixtures’ Dynamic Modulus Using Gene Expression Programming. Int. J. Pavement Eng. 2017, 18, 971–980. [Google Scholar] [CrossRef]
- Leon, L.P.; Ray, I. Estimating Unconfined Compressive Behavior of HMA Using Soft Computing. Innov. Infrastruct. Solut. 2021, 6, 19. [Google Scholar] [CrossRef]
- Nabipour, N.; Karballaeezadeh, N.; Dineva, A.; Mosavi, A.; Mohammadzadeh, S.D.; Shamshirband, S. Comparative Analysis of Machine Learning Models for Prediction of Remaining Service Life of Flexible Pavement. Mathematics 2019, 7, 1198. [Google Scholar] [CrossRef]
- Heshmati, R.A.A.; Salehzadeh, H.; Shahidi, M. Prediction of the Void Ratio Parameter in Mineral Tailings Using Gene Expression Programming. Adv. Civ. Eng. 2020, 2020, 8838104. [Google Scholar] [CrossRef]
- Sajedi, F.; Razak, H.A. Comparison of Different Methods for Activation of Ordinary Portland Cement-Slag Mortars. Constr. Build. Mater. 2011, 25, 30–38. [Google Scholar] [CrossRef]
- Wang, A.; Gao, Q.; Yang, Z. Optimization of the Parameters of the Filling Slurry Based on Genetic Programming and Genetic Algorithm. Electron. J. Geotech. Eng. 2016, 21, 10599–10610. [Google Scholar]
- Sadeghi, G.; Najafzadeh, M.; Ameri, M. Thermal Characteristics of Evacuated Tube Solar Collectors with Coil inside: An Experimental Study and Evolutionary Algorithms. Renew. Energy 2020, 151, 575–588. [Google Scholar] [CrossRef]
- Sadeghi, G.; Najafzadeh, M.; Safarzadeh, H. Utilizing Gene-Expression Programming in Modelling the Thermal Performance of Evacuated Tube Solar Collectors. J. Energy Storage 2020, 30, 101546. [Google Scholar] [CrossRef]
- Naderpour, H.; Akbari, M.; Mirrashid, M.; Kontoni, D.-P.N. Compressive Capacity Prediction of Stirrup-Confined Concrete Columns Using Neuro-Fuzzy System. Buildings 2022, 12, 1386. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontoni, D.-P.N.; Onyelowe, K.C.; Ebid, A.M.; Jahangir, H.; Rezazadeh Eidgahee, D.; Soleymani, A.; Ikpa, C. Gene Expression Programming (GEP) Modelling of Sustainable Building Materials including Mineral Admixtures for Novel Solutions. Mining 2022, 2, 629-653. https://doi.org/10.3390/mining2040034
Kontoni D-PN, Onyelowe KC, Ebid AM, Jahangir H, Rezazadeh Eidgahee D, Soleymani A, Ikpa C. Gene Expression Programming (GEP) Modelling of Sustainable Building Materials including Mineral Admixtures for Novel Solutions. Mining. 2022; 2(4):629-653. https://doi.org/10.3390/mining2040034
Chicago/Turabian StyleKontoni, Denise-Penelope N., Kennedy C. Onyelowe, Ahmed M. Ebid, Hashem Jahangir, Danial Rezazadeh Eidgahee, Atefeh Soleymani, and Chidozie Ikpa. 2022. "Gene Expression Programming (GEP) Modelling of Sustainable Building Materials including Mineral Admixtures for Novel Solutions" Mining 2, no. 4: 629-653. https://doi.org/10.3390/mining2040034
APA StyleKontoni, D.-P. N., Onyelowe, K. C., Ebid, A. M., Jahangir, H., Rezazadeh Eidgahee, D., Soleymani, A., & Ikpa, C. (2022). Gene Expression Programming (GEP) Modelling of Sustainable Building Materials including Mineral Admixtures for Novel Solutions. Mining, 2(4), 629-653. https://doi.org/10.3390/mining2040034







