A Computational Algorithm to Understand the Evolution of Size Distribution with Successive Breakage Events at Grinding †
Abstract
:1. Introduction
2. Materials and Methods
Particle Selection Algorithm for Breakage
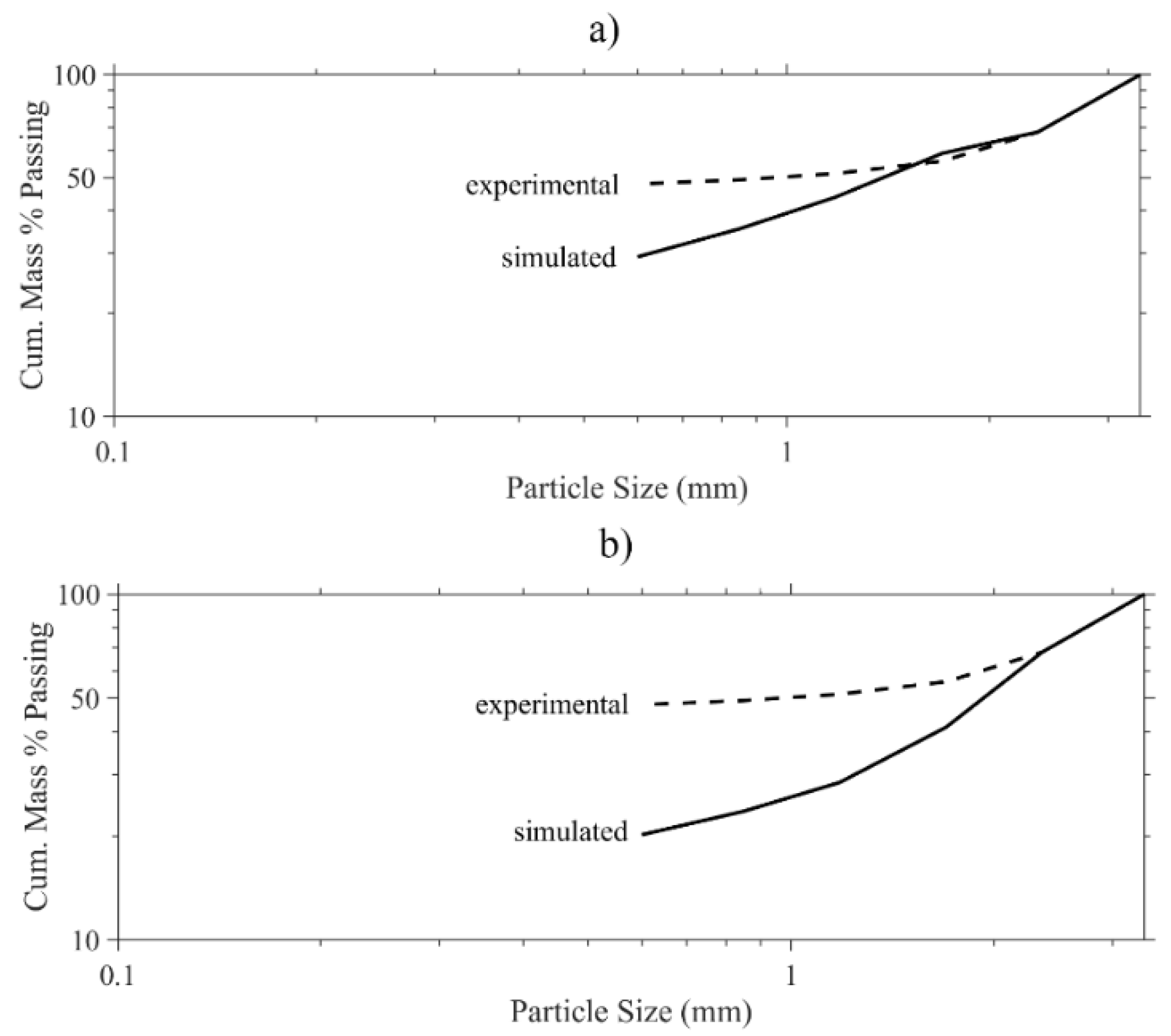
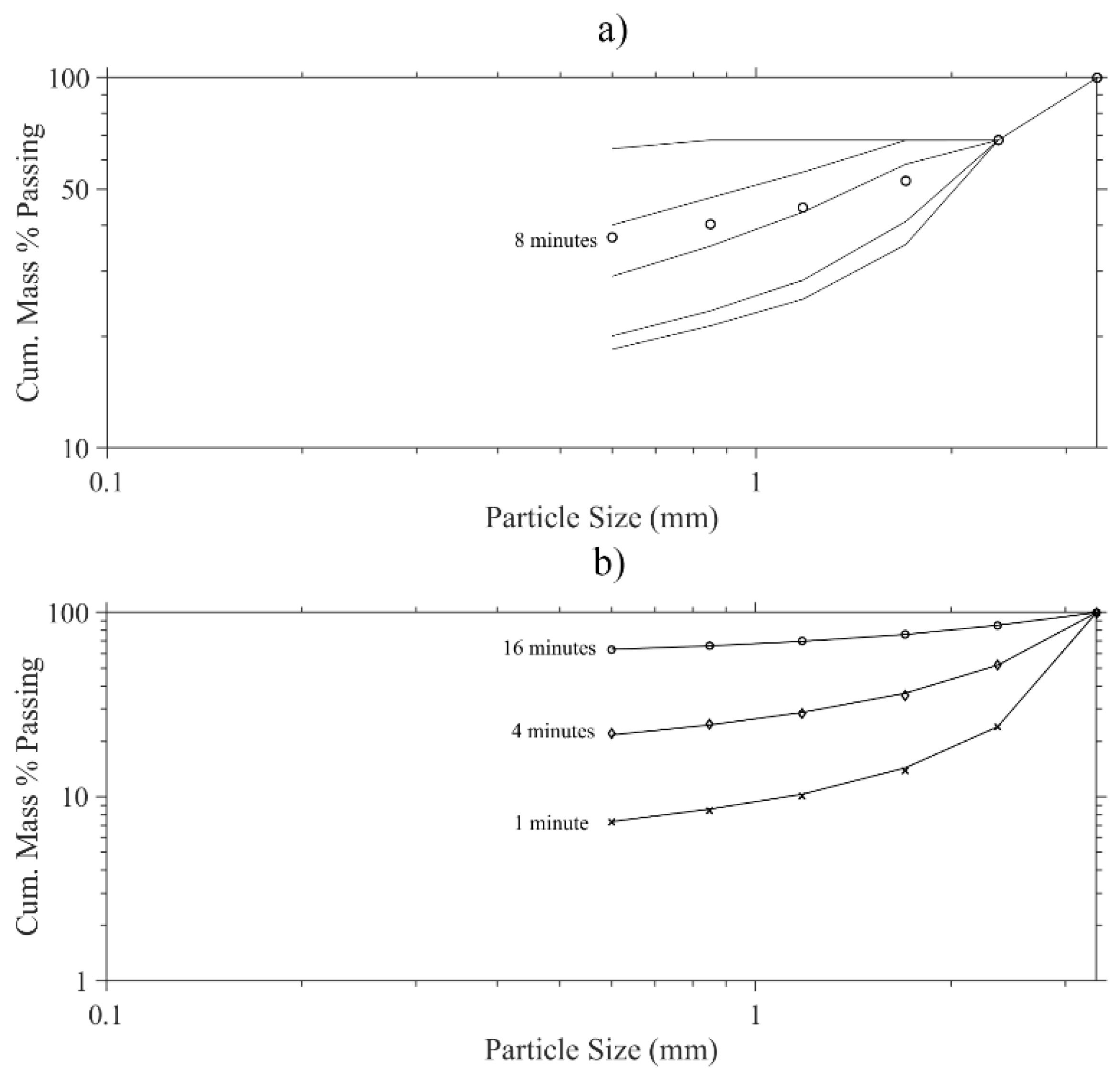
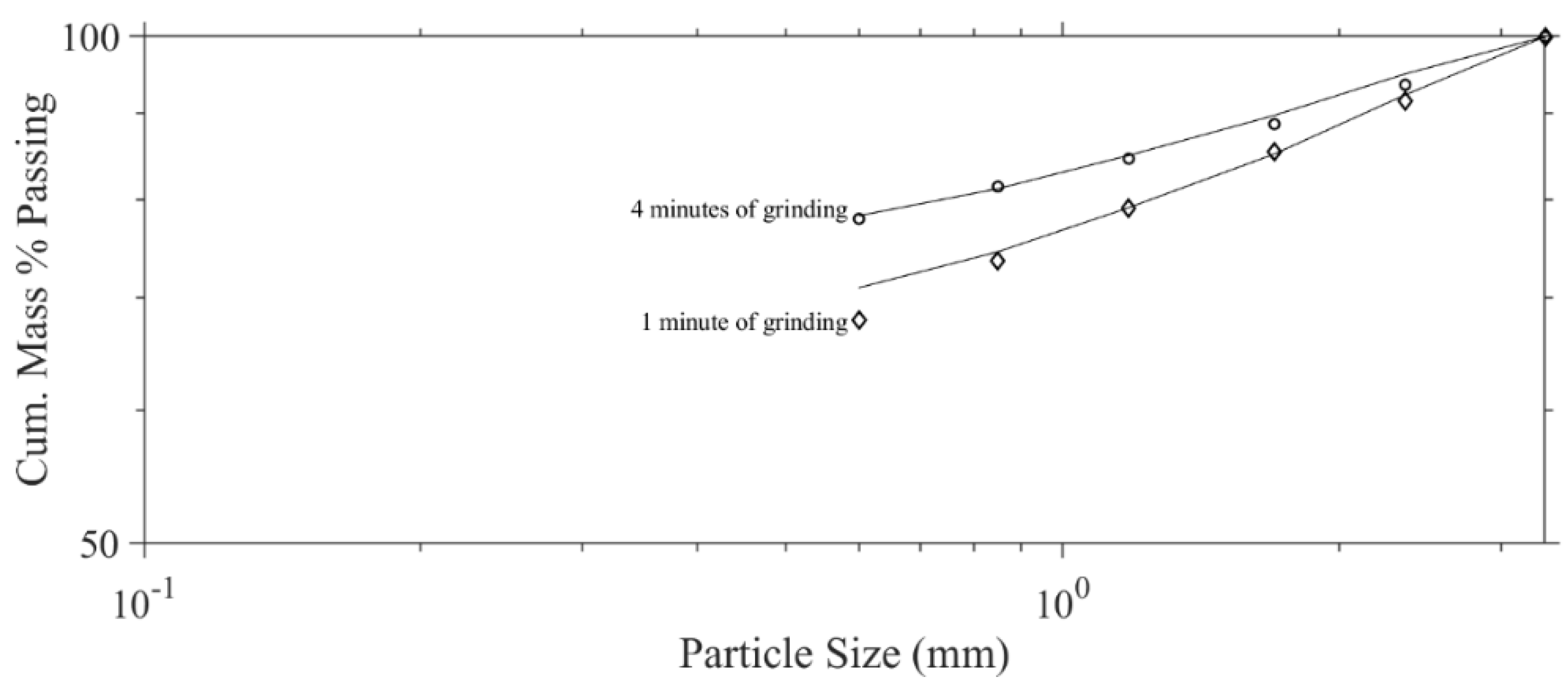
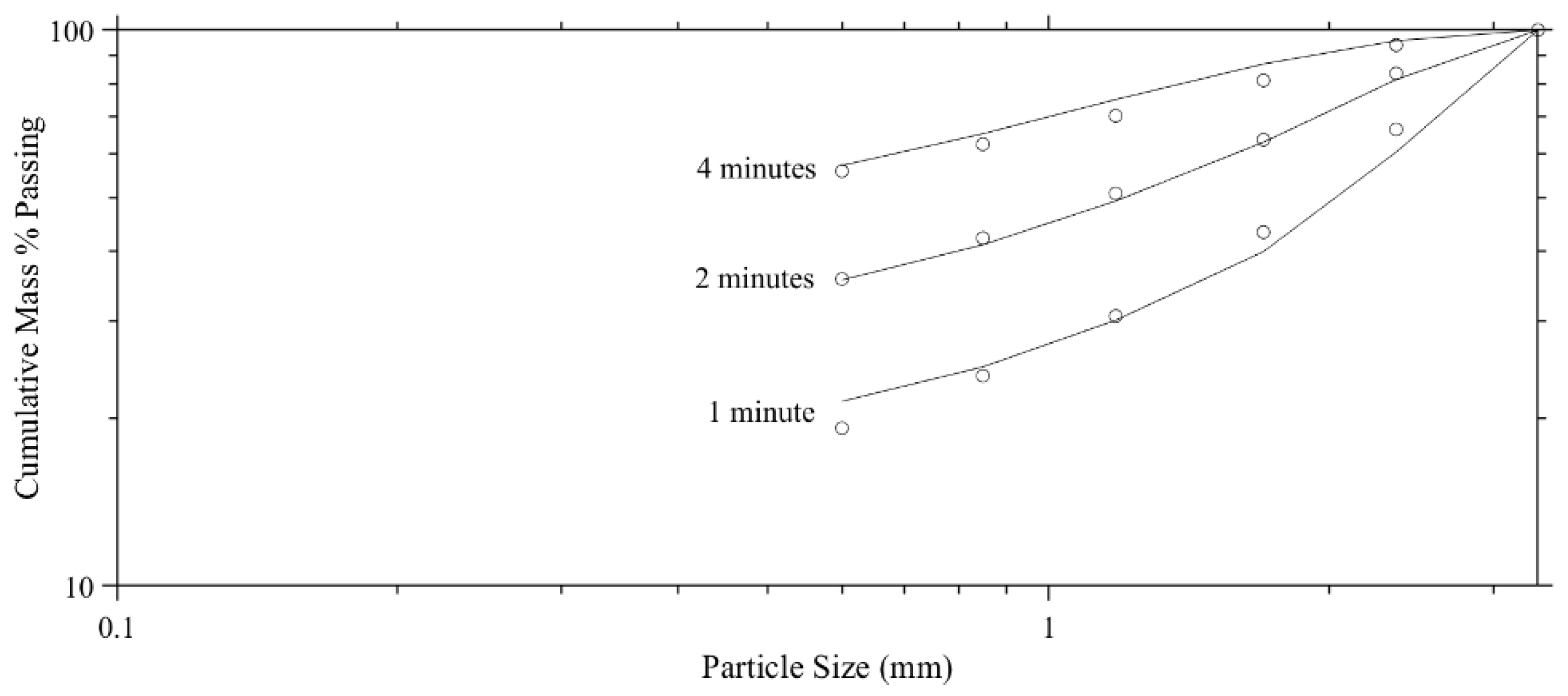
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, A.; Yan, D.S. Mineral Processing Design and Operation; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Austin, L.G.; Klimpel, R.R.; Luckie, P.T. Process Engineering of Size Reduction: Ball Milling; AIME: New York, NY, USA, 1984; ISBN 0895204215. [Google Scholar]
- Li, W. Exploring the Fundamentals of Impact Breakage Events in Grinding. Master’s Thesis, McGill University, Montreal, QC, Canada, 2005. [Google Scholar]
- King, R.P. Modeling and Simulation of Mineral Processing Systems; Butterworth-Heinmann Publications: Oxford, UK, 2001. [Google Scholar]
- Bilgili, E.; Scarlett, B. Population balance modeling of non-linear effects in milling processes. Powder Technol. 2005, 153, 59–71. [Google Scholar] [CrossRef]
- Bilgili, E. On the consequences of non-first-order breakage kinetics in comminution processes: Absence of self-similar size spectra. Part. Part. Syst. Charact. 2007, 24, 12–17. [Google Scholar] [CrossRef]
- Gupta, V.K.; Kapur, P.C. A Pseudo-Similarity Solution to the Integro-Differential Equation of Batch Grinding. Powder Technol. 1975, 12, 175–178. [Google Scholar] [CrossRef]
- Kapur, P.C. Self-preserving size spectra of comminuted particles. Chem. Eng. Sci. 1972, 27, 425–431. [Google Scholar] [CrossRef]
- Peterson, T.W.; Scotto, M.V.; Sarofim, A.F. Comparison of Comminution Data with Analytical Solutions of the Fragmentation Equation. Powder Technol. 1985, 45, 87–93. [Google Scholar] [CrossRef]
- Williams, M.M.R. An exact solution of the fragmentation equation. Aerosol Sci. Technol. 1990, 12, 538–546. [Google Scholar] [CrossRef]
- Brown, W.K. Comparison of a theory of sequential fragmentation with the initial mass function of stars. Astrophys. Space Sci. 1986, 122, 287–298. [Google Scholar] [CrossRef]
- Ziff, R.M. New solutions to the fragmentation equation. J. Phys. A Math. Gen. 1991, 24, 2821–2828. [Google Scholar] [CrossRef]
- Rao, B.V.; Datta, A. Analysis of nonlinear batch grinding in stirred media mills using self-similarity solution. Powder Technol. 2006, 169, 41–48. [Google Scholar] [CrossRef]
- Bilgili, E.; Yepes, J.; Scarlett, B. Formulation of a non-linear framework for population balance modeling of batch grinding: Beyond first-order kinetics. Chem. Eng. Sci. 2006, 61, 33–44. [Google Scholar] [CrossRef]
- Anticoi, H.; Guasch, E.; Ahmad Hamid, S.; Oliva, J.; Alfonso, P.; Bascompta, M.; Sanmiquel, L.; Escobet, T.; Escobet, A.; Parcerisa, D.; et al. An Improved High-Pressure Roll Crusher Model for Tungsten and Tantalum Ores. Minerals 2018, 8, 483. [Google Scholar] [CrossRef]
- Nikolov, S. A performance model for impact crushers. Miner. Eng. 2002, 15, 715–721. [Google Scholar] [CrossRef]
- Li, H. Discrete Element Method (DEM) Modelling of Rock Flow and Breakage within a Cone Crusher. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2013. [Google Scholar]
- Whiten, W.J. A matrix theory of comminution machines. Chem. Eng. Sci. 1974, 29, 589–599. [Google Scholar] [CrossRef]
- Weedon, D.M. A perfect mixing matrix model for ball mills. Miner. Eng. 2001, 14, 1225–1236. [Google Scholar] [CrossRef]
- Opoczky, L. Fine Grinding and Agglomeration of Silicates. Powder Technol. 1977, 17, 1–7. [Google Scholar] [CrossRef]
- Beke, B. The Process of Fine Grinding; Akademiai Kiado: The Hague, The Netherlands, 1981; ISBN 9789400982604. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Wong, C.K.; Easton, M.C. An Efficient Method for Weighted Sampling without Replacement. SIAM J. Comput. 1980, 9, 111–113. [Google Scholar] [CrossRef]
- Xu, Y.; Song, D.; Chu, F. Approach to the Weibull modulus based on fractal fragmentation of particles. Powder Technol. 2016, 292, 99–107. [Google Scholar] [CrossRef]
- Tavares, L.M. Breakage of Single Particles: Quasi-Static. In Handbook of Powder Technology; Salman, A.D., Ghadiri, M., Hounslow, M.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 12, pp. 3–68. ISBN 978-0-444-53080-6. [Google Scholar]
- Schmöle, J.; Dragosits, M.; Hepach, H.; Aspelmeyer, M. A micromechanical proof-of-principle experiment for measuring the gravitational force of milligram masses. Class. Quantum Gravity 2016, 33. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 9788578110796. [Google Scholar]
- Leite, F.L.; Bueno, C.C.; Da Róz, A.L.; Ziemath, E.C.; Oliveira, O.N. Theoretical models for surface forces and adhesion and their measurement using atomic force microscopy. Int. J. Mol. Sci. 2012, 13, 12773–12856. [Google Scholar] [CrossRef]
- Speake, C.; Quinn, T. The search for Newton’s constant. Phys. Today 2014, 67, 27–33. [Google Scholar] [CrossRef]


| Probability Vector | Formulation | Description of the Terms |
|---|---|---|
| Mass | : the weight % of the size class i in the mill feed (or new feed) before an iteration. : the geometric mean size of the monosize class i n: an empirical constant | |
| Power (P) | ||
| Mass & Power (MP) |
| Feed Size | Range of n [Minimum, Maximum] |
|---|---|
| −3.35 + 2.36 mm | [−4.9, −3.7] |
| −2.36 + 1.7 mm | [−4.3, −4.1] |
| −1.7 + 1.18 mm | [−3.9, −3.8] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camalan, M. A Computational Algorithm to Understand the Evolution of Size Distribution with Successive Breakage Events at Grinding. Environ. Sci. Proc. 2021, 6, 7. https://doi.org/10.3390/iecms2021-09381
Camalan M. A Computational Algorithm to Understand the Evolution of Size Distribution with Successive Breakage Events at Grinding. Environmental Sciences Proceedings. 2021; 6(1):7. https://doi.org/10.3390/iecms2021-09381
Chicago/Turabian StyleCamalan, Mahmut. 2021. "A Computational Algorithm to Understand the Evolution of Size Distribution with Successive Breakage Events at Grinding" Environmental Sciences Proceedings 6, no. 1: 7. https://doi.org/10.3390/iecms2021-09381
APA StyleCamalan, M. (2021). A Computational Algorithm to Understand the Evolution of Size Distribution with Successive Breakage Events at Grinding. Environmental Sciences Proceedings, 6(1), 7. https://doi.org/10.3390/iecms2021-09381






