Silicon Self-Diffusion in Stishovite: Calculations of Point Defect Parameters Based on the cBΩ Thermodynamic Model †
Abstract
1. Introduction
2. Methodology
2.1. The cBΩ Thermodynamic Model
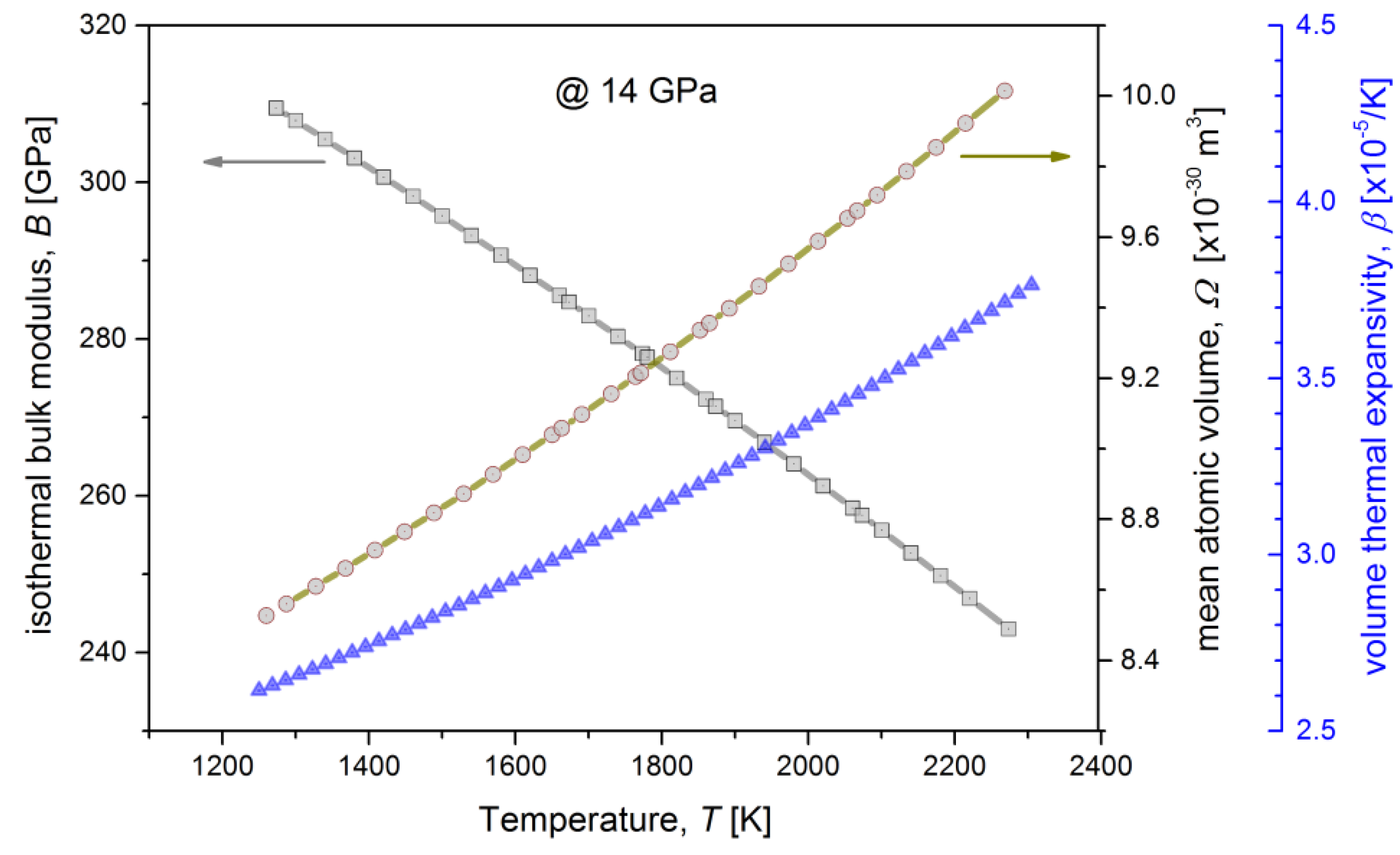
2.2. Bulk Properties of Stishovite
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nishihara, Y.; Nakayama, K.; Takahashi, E.; Iguchi, T.; Funakoshi, K.-Ì. P-V-T equation of state of stishovite to the mantle transition zone conditions. Phys. Chem. Miner. 2005, 31, 660–670. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, Q.; Meng, Y.; Walter, M.; Mao, H.K. Evidence for the stability of ultrahydrous stishovite in Earth’s lower mantle. Proc. Natl. Acad. Sci. USA 2020, 117, 184–189. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Yamazaki, D.; Sakamoto, N.; Sun, W.; Fei, H.; Yurimoto, H. Silicon and oxygen self-diffusion in stishovite: Implications for stability of SiO2-rich seismic reflectors in the mid-mantle. Earth Planet. Sci. Lett. 2017, 459, 332–339. [Google Scholar] [CrossRef]
- Karato, S.-I. (Ed.) Rheological properties of minerals and rocks. In Physics and Chemistry of the Deep Earth; John Wiley & Sons, Ltd.: Chichester, UK, 2013. [Google Scholar] [CrossRef]
- Shatskiy, A.; Yamazaki, D.; Borzdov, Y.M.; Matsuzaki, T.; Litasov, K.D.; Cooray, T.; Ferot, A.; Ito, E.; Katsura, T. Stishovite single-crystal growth and application to silicon self-diffusion measurements. Am. Mineral. 2010, 95, 135–143. [Google Scholar] [CrossRef]
- Katsura’s Lab/High-Pressure Research in Earth Science. Available online: https://katsurabgi.jimdo.com/english-home/lecture-note/past-studies/silicon-self-diffusion-in-stishovite/ (accessed on 5 September 2020).
- Varotsos, P.; Alexopoulos, K. Thermodynamics of Point Defects and their Relation with the Bulk Properties; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Varotsos, P.; Alexopoulos, K. Calculation of diffusion coefficients at any temperature and pressure from a single measurement. I. Self diffusion. Phys. Rev. B 1980, 22, 3130–3134. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Calculation of diffusion coefficients at any temperature and pressure from a single measurement. II. Heterodiffusion. Phys. Rev. B 1981, 24, 3606–3609. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Connection between the formation volume and formation Gibbs energy in noble-gas solids. Phys. Rev. B 1984, 30, 7305–7306. [Google Scholar] [CrossRef]
- Varotsos, P. Comparison of models that interconnect point defect parameters in solids with bulk properties. J. Appl. Phys. 2007, 101, 123503–123508. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, X.; Xu, J.; Zhou, R. Application of the cBΩ model for the calculation of oxygen self-diffusion coefficients in minerals. J. Appl. Phys. 2010, 108, 053505–053506. [Google Scholar] [CrossRef]
- Vallianatos, F.; Saltas, V. Application of the cBΩ model to the calculation of diffusion parameters of He in olivine. Phys. Chem. Miner. 2014, 41, 181–188. [Google Scholar] [CrossRef]
- Zhang, B.; Shan, S.; Wu, X. Modeling H, Na, and K diffusion in plagioclase feldspar by relating point defect parameters to bulk properties. Phys. Chem. Miner. 2016, 43, 151–159. [Google Scholar] [CrossRef]
- Saltas, V.; Chroneos, A.; Vallianatos, F. A thermodynamic approach to self-diffusion in silicon: Evidence of a single diffusion mechanism? Mater. Chem. Phys. 2016, 181, 204–208. [Google Scholar] [CrossRef]
- Saltas, V.; Chroneos, A.; Cooper, M.W.D.; Fitzpatrick, M.E.; Vallianatos, F. Investigation of oxygen self-diffusion in PuO2 by combining molecular dynamics with thermodynamic calculations. RSC Adv. 2016, 6, 103641–103649. [Google Scholar] [CrossRef]
- Saltas, V.; Chroneos, A.; Vallianatos, F. A thermodynamic approach of self- and hetero-diffusion in GaAs: Connecting point defect parameters with bulk properties. RSC Adv. 2016, 6, 53324–53330. [Google Scholar] [CrossRef]
- Saltas, V.; Chroneos, A.; Vallianatos, F. Composition and temperature dependence of self-diffusion in Si1−xGex alloys. Sci. Rep. 2017, 7, 1374. [Google Scholar] [CrossRef]
- Saltas, V.; Chroneos, A.; Vallianatos, F. Thermodynamic modelling of fast dopant diffusion in Si. J. Appl. Phys. 2018, 123, 161527. [Google Scholar] [CrossRef]
- Skordas, E.S.; Sarlis, N.V.; Varotsos, P.A. Applying the cBΩ thermodynamical model to LiF using its equation of state obtained from high pressure diamond anvil cell measurements. Solid State Ion. 2020, 354, 115404. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D.; Tzanis, A.; Anastasiadis, C.; Stavrakas, I. Electric earthquake precursors: From laboratory results to field observations. Phys. Chem. Earth 2004, 29, 339–351. [Google Scholar] [CrossRef]
- Vallianatos, F.; Eftaxias, K. The application of the cBΩ model for the calculation of the variation of the activation volume for creep with depth in the Earth’s lower mantle. Phys. Earth Planet. Inter. 1992, 71, 141–146. [Google Scholar] [CrossRef]
- Wang, F.; Tange, Y.; Irifune, T.; Funakoshi, K. P-V-T equation of state of stishovite up to mid-lower mantle conditions. J. Geophys. Res. 2012, 117, B06209. [Google Scholar] [CrossRef]
- Panayiotatos, Y.; Saltas, V.; Chroneos, A.; Vallianatos, F. Tin diffusion in germanium: A thermodynamic approach. J. Mater. Sci. Mater. Electron. 2017, 28, 9936–9940. [Google Scholar] [CrossRef][Green Version]
- Kube, R.; Bracht, H.; Hüger, E.; Schmidt, H.; Hansen, J.L.; Larsen, A.N.; Ager, J.W.; Haller, E.E.; Geue, T.; Stahn, J. Contributions of vacancies and self-interstitials to self-diffusion in silicon under thermal equilibrium and nonequilibrium conditions. Phys. Rev. B 2013, 88, 085206. [Google Scholar] [CrossRef]


| Direction | |||||||
|---|---|---|---|---|---|---|---|
| [110] | 0.182 ± 0.016 | (350–429) ± 19 | 322 ± 28 1 | (5.7–8.6) ± 0.3 | (289–267) ± 17 | (3.9–5.6) ± 0.6 | 6.0 ± 1.0 2 |
| [001] | 0.188 ± 0.021 | (359–438) ± 21 | 334 ± 39 1 | (5.9–8.9) ± 0.3 | (299–276) ± 17 | (4.0–5.8) ± 0.6 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saltas, V.; Vallianatos, F. Silicon Self-Diffusion in Stishovite: Calculations of Point Defect Parameters Based on the cBΩ Thermodynamic Model. Environ. Sci. Proc. 2021, 6, 6. https://doi.org/10.3390/iecms2021-09341
Saltas V, Vallianatos F. Silicon Self-Diffusion in Stishovite: Calculations of Point Defect Parameters Based on the cBΩ Thermodynamic Model. Environmental Sciences Proceedings. 2021; 6(1):6. https://doi.org/10.3390/iecms2021-09341
Chicago/Turabian StyleSaltas, Vassilios, and Filippos Vallianatos. 2021. "Silicon Self-Diffusion in Stishovite: Calculations of Point Defect Parameters Based on the cBΩ Thermodynamic Model" Environmental Sciences Proceedings 6, no. 1: 6. https://doi.org/10.3390/iecms2021-09341
APA StyleSaltas, V., & Vallianatos, F. (2021). Silicon Self-Diffusion in Stishovite: Calculations of Point Defect Parameters Based on the cBΩ Thermodynamic Model. Environmental Sciences Proceedings, 6(1), 6. https://doi.org/10.3390/iecms2021-09341







